A Comparative Evaluation of Voxel-based Spatial Mapping in Diffusion Tensor Imaging

Abstract

This paper presents a comparative evaluation of methods for automated voxel-based spatial mapping in diffusion tensor imaging studies. Such methods are an essential step in computational pipelines and provide anatomically comparable measurements across a population in atlas-based studies. To better understand their strengths and weaknesses, we tested a total of eight methods for voxel-based spatial mapping in two types of diffusion tensor templates. The methods were evaluated with respect to scan-rescan reliability and an application to normal aging. The methods included voxel-based analysis with and without smoothing, two types of region-based analysis, and combinations thereof with skeletonization. The templates included a study-specific template created with DTI-TK and the IIT template serving as a standard template. To control for other factors in the pipeline, the experiments used a common dataset, acquired at 1.5T with a single shell high angular resolution diffusion MR imaging protocol, and tensor-based spatial normalization with DTI-TK. Scan-rescan reliability was assessed using the coefficient of variation (CV) and intraclass correlation (ICC) in eight subjects with three scans each. Sensitivity to normal aging was assessed in a population of 80 subjects aged 25 to 65 years old, and methods were compared with respect to the anatomical agreement of significant findings and the R² of the associated models of fractional anisotropy. The results show that reliability depended greatly on the method used for spatial mapping. The largest differences in reliability were found when adding smoothing and comparing voxel-based and region-based analyses. Skeletonization and template type were found to have either a small or negligible effect on reliability. The aging results showed agreement among the methods in nine brain areas, with some methods showing more sensitivity than others. Skeletonization and smoothing were not major factors affecting sensitivity to aging, but the standard template showed higher R² in several conditions. A structural comparison of the templates showed that large deformations between them may be related to observed differences in patterns of significant voxels. Most areas showed significantly higher R² with voxel-based analysis, particularly when clusters were smaller than the available regions-of-interest. Looking forward, these results can potentially help to interpret results from existing white matter imaging studies, as well as provide a resource to help in planning future studies to maximize reliability and sensitivity with regard to the scientific goals at hand.

1. Introduction

Diffusion MR imaging enables the quantitative measurement of water molecule diffusion, which exhibits anisotropy in brain white matter due to axonal morphometry and coherence [1]. The diffusion tensor [2] is a commonly used model that reflects aggregate properties of tissue microstructure [3] that are relevant to the studies of brain white matter, such as normal differences in age, sex, and cognition [4] [5] [6], as well as neuropsychiatric conditions, such as schizophrenia, depression, and bipolar disorder [7] [8]. Diffusion tensor imaging studies typically make anatomically-comparable measurements across participants through spatial normalization [9] to a template using image registration [10]. Then, a spatial mapping step is used to probe features of white matter across the population, typically with either voxel-based or tractography-based localization. Voxel-based analyses can either look at individual voxels or regions-of-interest (ROIs), while tractography-based analyses instead look at features of geometric models representing large-scale fiber bundle anatomy [11] [12]. While there are known limitations of tractography that warrant evaluation [13] [14], we restrict the scope of this paper to the evaluation of voxel-based methods.

This paper is motivated by the general need to better understand the computational tools used in voxel-based diffusion tensor imaging studies [15]. As there are numerous choices at each step of the standard population imaging pipeline, there is value in understanding their net effect on the results [16]. While much is known about how data acquisition, preprocessing, and image registration affect results, fewer studies have evaluated the spatial mapping step. In this study, we examine a wide range of choices for this step and evaluate them with respect to scan-rescan reliability and sensitivity to normal aging.

Prior Work

Numerous studies have thoroughly examined the relationship between reliability and imaging data acquisition parameters. For example, several works have looked at variation across scanner manufacturers and imaging units [17] [18] [19] and found acceptable reliability across sites with a common magnet strength. Furthermore, other studies have also shown reliability across magnet strengths ranging from 1.5T to 4T [20] [21] [22]. Studies that tested gradient strength have found reliable estimates of diffusion parameters in each of a variety of gradients encoding schemes [23]; however, there is evidence of possible bias in diffusion parameters when combining estimates from different voxel sizes and gradient encoding schemes [24], although bias correction [20] and covariate analysis [25] are possible solutions. Together, these results are especially important for conducting longitudinal and multi-center studies as well as accommodating scanner upgrades within an imaging unit.

In addition, previous work has examined the effect of preprocessing and image registration algorithms on reliability. Robust preprocessing that includes denoising, motion correction, and outlier rejection has been shown to improve reliability across scanners [26] [27]. The choice of registration algorithm has also been shown to greatly affect reliability, specifically when comparing linear, deformable, and tensor-based registration [20] [21] [23]. Deformable tensor-based registration has been shown to perform better than registration with scalar maps, especially when used in combination with study-specific template construction [28]. Linear intra-subject registration has also been shown to improve reliability in longitudinal studies [26]. Overall, this indicates there is potential for significantly different outcomes based on the choice of preprocessing and registration, so it is important to have consistency in both applications and evaluations.

Each of these studies necessarily includes spatial mapping, either as a single method used in the pipeline or as part of a larger comparison of methods. The most common approaches are global histogram analysis [17], manually drawn ROIs [24] [23] [19], and standard atlas ROIs registered to each subject [18] [22] [29]. In addition to these studies, others have explicitly evaluated methods for spatial mapping, with a similar goal to this paper. For example, evaluations of manually drawn ROI approaches have tested the reliability of different ROI shapes [30] and drawing methods [31] [32], and compared to a variety of global histogram measures [25]. Voxel-based analysis has also been evaluated to quantify the effects of filter size [33], software package [34], and to compare results with ROI-based methods [35] [36]. There has also been extensive testing of skeleton-based analysis to understand its strengths and limitations [28] [26] [37] as well as comparing to voxel-based analysis and region-based analysis [20] [21]. Previous work has also evaluated the choice of template type, showing the advantages of study-specific and high-quality templates [38] [39] [40] [41]. This paper builds on these prior findings by expanding the range of methods simultaneously compared in evaluation.

Finally, the design of some of these studies not only included scan-rescan analysis, but also tested reliability in conjunction with applications to clinical and scientific studies. These studies have included populations consisting of aging adults and children [30] [24] [36], as well as patients with schizophrenia [33] [34], Alzheimer’s disease [28], and multiple sclerosis [25]. This kind of evaluation provides an additional benchmark for comparing the practical value of such methods, which is important, as a perfectly reliable measurement might still disregard anatomical features that are of scientific or clinical value. In this paper, we take a similar approach and test the sensitivity of each method to the anatomical effects of normal aging in an adult population.

Contributions

The main contribution of this paper is a comparative evaluation of spatial mapping in voxel-based diffusion tensor imaging studies. To avoid confounding effects, these tests were conducted with a common dataset and state-of-the-art tensor-based spatial normalization using DTI-TK. The evaluation includes experiments that examined reliability across scans and sensitivity to normal aging in an adult population. The first experiment characterized scan-rescan reliability across eight subjects with three scans each using the coefficient of variation and intraclass correlation. The second experiment characterized sensitivity to normal aging in a population of 80 adult subjects aged from 25 to 65 years old by examining the statistical relationship between age and diffusion parameters across the brain. Both experiments included a quantitative analysis of performance in the various methods and a qualitative analysis showing the results in relation to brain anatomy. The experimental conditions included eight methods for spatial mapping, four commonly used diffusion parameters, and two types of templates. The tested spatial mapping methods included voxel-based with and without smoothing, two types of region-based analysis, and combinations of these with skeletonization-based analysis. The tested diffusion parameters included fractional anisotropy (FA), mean (MD), radial (RD), and axial (AD) diffusivity. The aging analysis presented in the paper only shows effects in FA due to space limitations; however, all results are available for download with the link provided at the end of the paper. The experiments were conducted using both a study-specific template and the IIT standard template. In total, this represents a total of 64 conditions examined in each experiment.

2. Materials and Methods

2.1. Data Acquisition

Under an IRB-approved protocol, diffusion-weighted MR images were acquired from a population of healthy volunteers, including a group of 80 normal aging healthy controls and eight from a scan-rescan cohort. The 80 subjects comprised a cross-sectional normal aging population, which consisted of nearly equal number of each sex and roughly uniformly distributed ages ranging from 25 to 65 years old. The data from the other eight subjects were acquired for scan-rescan analysis and included three repeats each, except for one subject that only had two repeats (i.e. 23 sessions). Imaging was conducted on a GE 1.5T scanner with 2×2×2mm voxels and image resolution 128×128×72. For each diffusion scan, seven baseline volumes were acquired, and the diffusion-weighted images used a single-shell high angular resolution diffusion encoding scheme with 64 distinct gradient encoding directions at a b-value of 1000 s/mm².

2.2. Image Preprocessing

The diffusion-weighted MR images were preprocessed using FSL 5.0 [42]. The first step included motion and eddy current correction by arfine registration of each diffusion-weighted volume to the baseline volume using FSL FLIRT with the mutual information criteria. Along with this step, the b-vectors were reoriented to account for rotation induced by each transformation [43]. Skull stripping was performed using FSL BET with a threshold of 0.3. For each dataset, diffusion tensors were fit using FSL DTIFIT.

2.3. Spatial Normalization and Template Construction

Following this, a study-specific template [44] was created from the 80 normal subjects. This was performed using the tensor-based deformable registration algorithm in DTI-TK [45] with finite strain tensor reorientation and the deviatoric tensor similarity metric. Each subject’s tensor image was transformed to atlas space using the associated deformation and resampled to 1 mm³ isotropic voxels using Log-Euclidean tensor interpolation. This process was applied to both the scan-rescan cohort and the normal aging cohort.

In addition, the study examined the use of a standard template. The IIT DTI template version 4.1 [46] [47] was used for this purpose due to its high quality and use in related evaluation studies [40]. The imaging data was downloaded from the publicly available distribution on NITRC [48]. To facilitate the joint visualization and quantitative comparison of results from both templates, an additional deformable registration was performed between the IIT and study-specific template using DTI-TK. The study-specific analysis was conducted solely with the study-averaged imaging data, and the statistical results were deformed for comparison using nearest-neighbor interpolation. As there were shape differences between the study-specific and standard templates, the logarithm of the Jacobian determinant (LogJacDet) of the deformation was computed to show the spatial pattern of these shape differences.

2.4. Spatial Mapping

Next, eight methods of spatial mapping were applied (Table 1 and Figure 1) using each of the two templates (study-specific and standard) and each of four diffusion parameters (FA, MD, RD, and AD), giving a total of 64 conditions. For consistency, the methods shared the same white matter mask in each template. The masks were created by applying a threshold of 0.2 to the FA volume of each template and removing all but the largest connected component. The details of each method are described as follows.

Table 1.

A summary of methods for spatial mapping that are compared in the experiments. The dimensionality of the methods in the study-specific template are listed, as well as the average volume of the voxels/regions representing each measurement.

Method	Dimension	Mean Volume
VBA	353903	1 mm3
SMOOTH	353903	1 mm3
JHU	48	2814 mm3
SUPER	321	1098 mm3
VBA+TBSS	76586	1 mm3
SMOOTH+TBSS	76586	1 mm3
JHU+TBSS	48	648 mm3
SUPER+TBSS	318	240 mm3

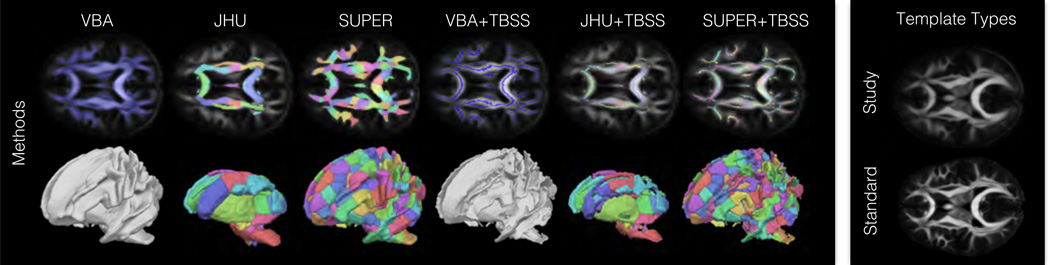
Figure 1.

The left panel shows an illustration of methods for spatial mapping compared in the experiments. Smoothing was included in voxel-based and skeleton-based analysis but is not depicted here. The right panel illustrates the two template types tested.

Voxel-based analysis was performed using the standard approach [49] [50] in all white matter voxels. This included processing without smoothing (denoted VBA) and with smoothing (denoted SMOOTH) using an isotropic Gaussian filter with σ = 2, FWHM = 4.7, which is comparable to a previous VBA evaluation [36]. Region-based analysis [51] was also performed by averaging diffusion parameters within ROIs. This included two types of region-based analysis, described as follows.

The first region-based method (denoted JHU) used manually defined regions from the Johns Hopkins University white matter atlas [52] included in FSL. For each template type, the ROIs were deformed to the template volume using FNIRT This was necessary as the JHU regions are defined in an FA atlas requiring scalar-based registration; however, the rest of the experiments used tensor-based registration between subject data and the templates.

The second region-based analysis (denoted SUPER) used automatically defined “supervoxel” ROIs that were computed for each template using a clustering algorithm [53]. The clustering algorithm includes parameters to control the relative contribution the voxel positions (α), fiber orientations (β), and number of clusters (λ) make to the overall optimization. The parameter settings were α = 1, β = 15, and λ = 20, resulting in a total of 321 study-template regions and 318 standard template regions. In addition, the supervoxel ROIs were post-processed to assign distinct labels to topologically disconnected regions with the same clustering label, e.g. in the cingulum, and to remove outlier regions less than 50 mm³ in volume.

These four methods were also each performed in conjunction with skeleton-based analysis using Tract-Based Spatial Statistics [54]. This was implemented in a custom VBA+TBSS pipeline modified to use the tensor-based registration algorithm in DTI-TK instead of the default scalar-based registration with FNIRT [42] [55]. The standard template analysis used the associated skeleton available on NITRC, and the study-specific template analysis used a study-derived skeleton. Both template skeleton masks were created with an FA threshold of 0.2. This resulted in four additional skeleton-based methods: voxel analysis without smoothing (denoted VBA+TBSS), voxel analysis with smoothing (denoted SMOOTH+TBSS), JHU ROI analysis (denoted JHU+TBSS), and supervoxel ROI analysis (denoted SUPER+TBSS).

2.5. Scan-rescan Reliability

Next, reproducibility and reliability were tested for each condition with the scan-rescan dataset, which consisted of eight subjects with three repeated scans each. This included two statistical evaluation metrics: the coefficient-of-variation (CV) [56] and intra-class correlation (ICC) [57]. The CV is a nor-malized measure of percentage change in each measurement across scans and is considered acceptable below 10%. Given the within-subject average µ_w and within-subject standard deviation σ_w, the CV is given by σ_w/µ_w. The ICC is a measure of reliability that gauges the fraction of variance between subjects. It is normalized between zero and one and is considered accept-able above 0.7. Given the between-subjects variance ${\sigma }_b^2$ and within-subjects variance ${\sigma }_w^2$, the ICC is given by ${\sigma }_b^2/({\sigma }_b^2+{\sigma }_w^2)$. For each condition, CV and ICC were computed for individual voxels/regions and then aggregated across the whole brain to estimate mean performance and its uncertainty. All statistical analysis was implemented using R 3.1.1 [58], with the ggplot2 package for plotting [59], and the ICC package from Wolack et al. [60].

2.6. Sensitivity to Normal Aging

Next, the methods were evaluated with respect to their sensitivity to normal aging in an adult population, a process which has been shown to include anatomical changes in white matter that are reflected in diffusion parameters [61] [62]. The experiments investigated the localization of age-related changes in specific areas of the brain. This was performed by fitting linear regression models in each voxel and region to relate the diffusion parameters to age. Sex and intracranial volume were included as covariates to control for changes not related to mi-crostructural decline due to aging. Specifically, this can potentially avoid attributing seemingly local changes in diffusion parameters to partial volume effects that can occur with global volumetric changes in brain size due to age. For each model, statistics of the regressions were retained for comparison, including the R², as well as the coefficient estimate, standard error, t-statistic, and p-value associated with age variable. Because the methods differ largely in their dimensions (Table 1), they cannot be directly compared. To account for this, we used False Discovery Rate (FDR) with the Benjamini-Hochberg procedure [63] to correct for multiple comparisons within each method. This procedure transforms the p-values to q-values that can be more fairly compared across methods. Volumetric maps representing the model parameters were created to explore the differences between methods. These images were manually reviewed to identify brain areas with agreement among multiple methods. The comparison focused on FA only, which is the most commonly analyzed diffusion parameter; however, the results for MD, AD, and RD are included as supplementary material. When clusters of significant voxels were encountered, the voxel with the lowest q-value was recorded to represent the result. This process resulted in a list of brain areas with significant results for each experimental condition. The results were also quantitatively analyzed to assess the performance across the conditions. All statistical analysis was implemented in R 3.1.1 [58], with the ggplot2 package for plotting [59].

3. Results

3.1. Scan-rescan Reproducibility

Quantitative results of the scan-rescan experiment are shown in Figure 2, and qualitative results showing the spatial distribution of scan-rescan reproducibility are shown in Figures 3 and 4. For both CV and ICC, statistical tests were performed to assess performance characteristics of the methods, including groupings of methods by several factors: method type, region-based, skeleton-based, smoothed, and template type.

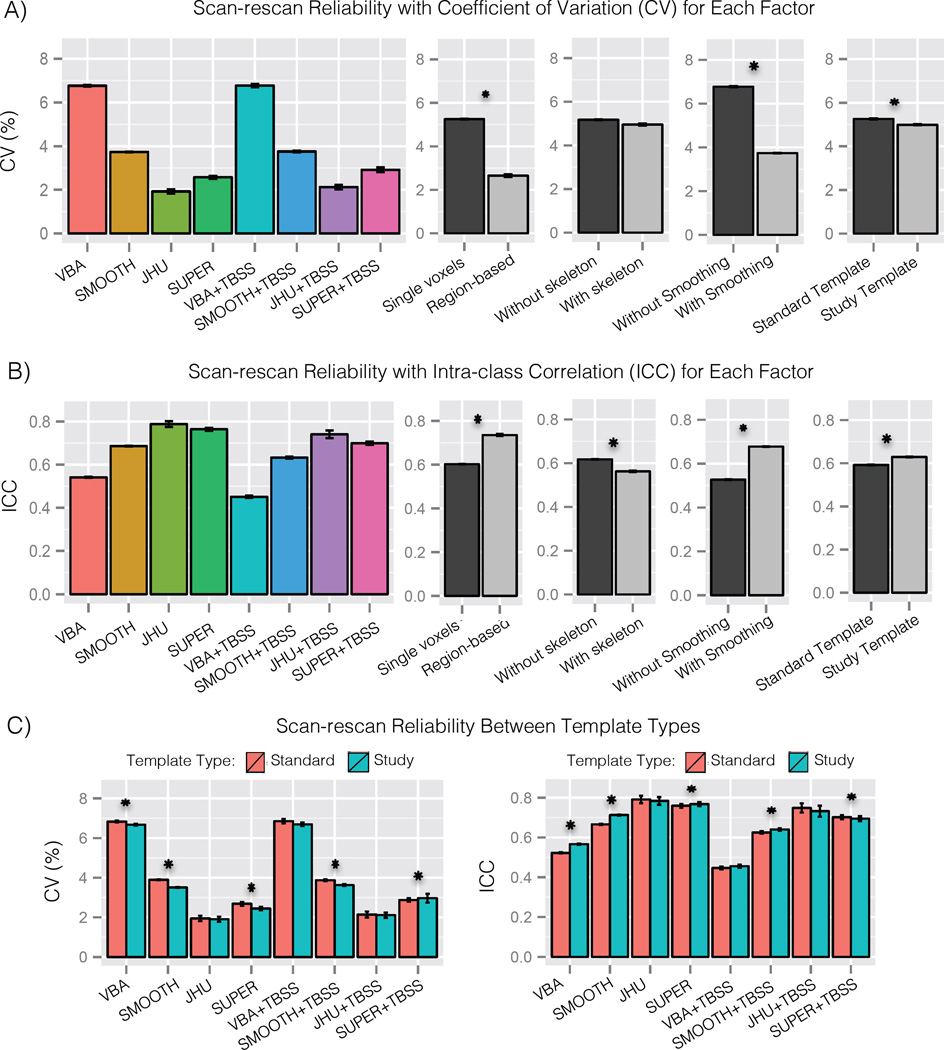
Figure 2.

Results from the scan-rescan experiment in Sec. 3.1 showing reliability across methods and between the major factors among the methods. Panel A shows the coefficient of variation (CV), which indicates the percentage of variation across scans of the same subject (smaller is better). Panel B shows the intraclass correlation, which indicates what proportion of variance is between subjects (larger is better). Panel C shows the relative performance of study-specific and standard templates in each of the tested methods. The results show high variation across methods. Among the major factors, smoothing and region-based analysis had large effects related to reproducibility, while template type and skeletonization had smaller effects. Statistically significant differences (p ≤ 0.05) are marked with an asterisk.

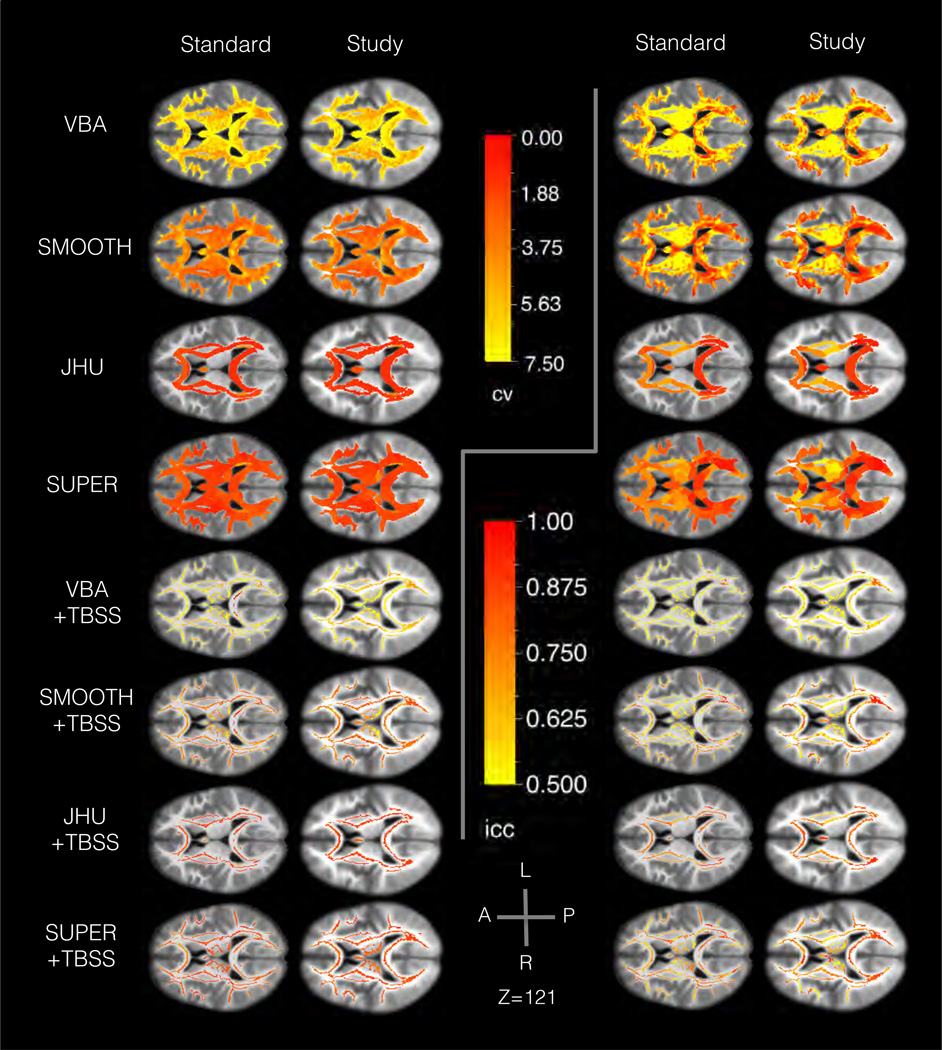
Figure 3.

Results from the scan-rescan experiment in Sec. 3.1 showing the spatial distribution of the reliability an axial slice. The background image shows the template T₁ -weighted map. The left panels show the coefficient of variation (CV), and the right panels show the intraclass correlation (ICC). Within each side, the slices are organized to show a different method in each row and a different template type in each column. The results generally show large spatial variation across methods, with higher variation in voxel-based than region-based methods. Voxel-based analysis tended to have higher reliability in deep white matter and lower in superficial white matter. Region-based analysis tended to have more uniform error rates than methods analyzing individual voxels.

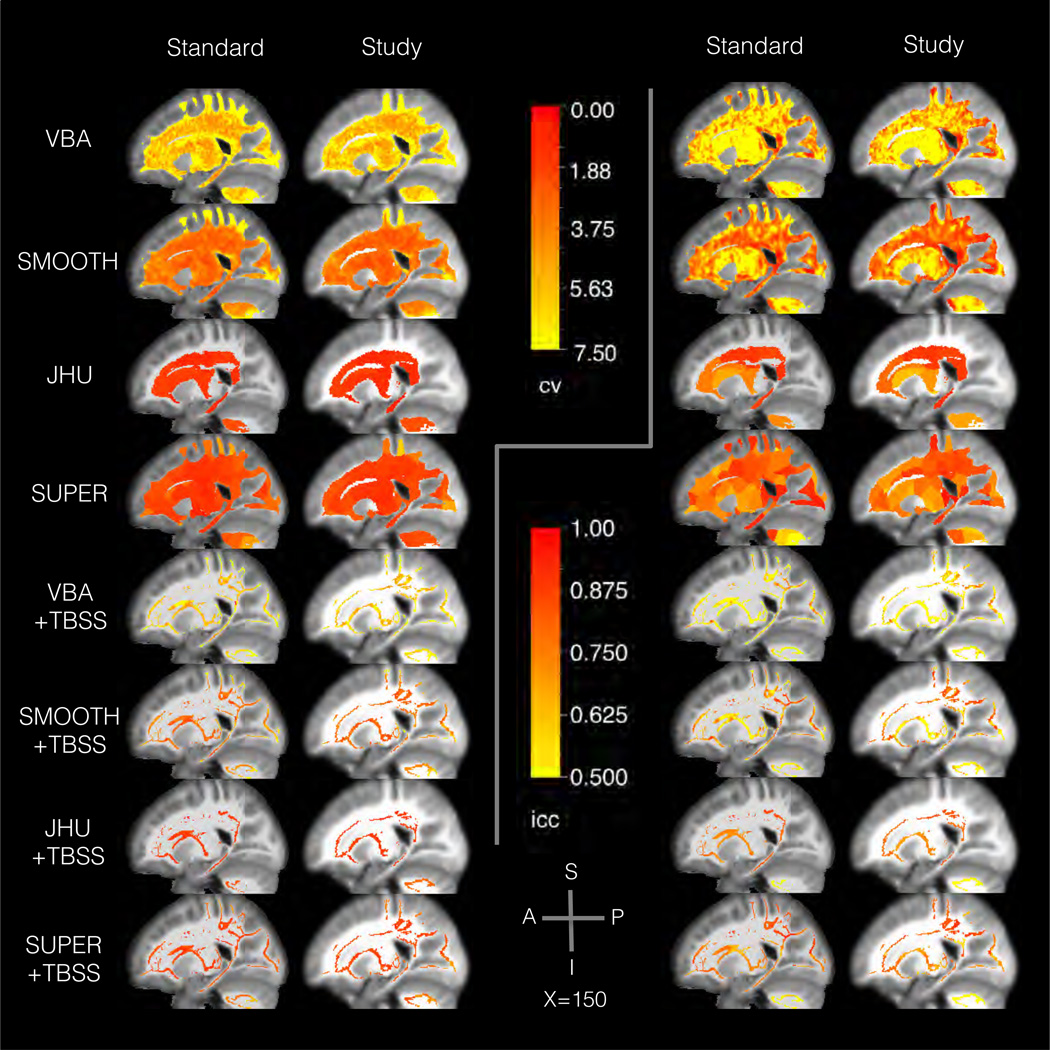
Figure 4.

Results from the scan-rescan experiment in Sec. 3.1 showing the spatial distribution of the reliability a sagittal slice. The background image shows the template T₁-weighted map. The left panels show the coefficient of variation (CV), and the right panels show the intraclass correlation (ICC). Within each side, the slices are organized to show a different method in each row and a different template type in each column. The results generally show large spatial variation across methods, with higher variation in voxel-based than region-based methods. Voxel-based analysis tended to have higher reliability in deep white matter and lower in superficial white matter. Region-based analysis tended to have more uniform error rates than methods analyzing individual voxels.

The results in CV show reliability varies significantly across methods (one-way ANOVA, p < 1 × 10⁻¹⁵, η² = 0.78). Smoothing was found to have a significant effect on CV (t-test, p < 1 × 10⁻¹⁵, d = 0.75, ΔCV = 3.3), with higher CV without smoothing (CV = 7.6 ± 1.0) than with smoothing (CV = 4.2 ± 0.5). Region-based analysis was also found to have a significant and large effect on CV (t-test, p < 1 × 10⁻⁸, d = 2.0, ΔCV = 3.4), with higher CV when analyzing single voxels (CV = 5.9 ± 0.8) compared to regions (CV = 2.5 ± 0.24). Template type was found to have a significant but small effect on CV (paired t-test, p < 1 × 10⁻⁷, d = 0.18, ΔCV = 0.44) with higher CV in the standard template (CV = 4.4 ± 0.9) compared to the study template (CV = 4.0 ± 0.8). From additional tests within each method, JHU, VBA+TBSS, and JHU+TBSS were not significantly different in CV between template types, unlike the main effect. Skeletonization was not found to have a significant effect on CV (paired t-test, p = 0.29). In reviewing the spatial distribution of CV across the brain, VBA and VBA+TBSS showed the greatest spatial variability, with better CV scores in deep white matter and worse CV in superficial and periventricular white matter. Smoothing tended to also smooth this spatial distribution of CV scores. Region-based analysis showed more spatially uniform CV results than voxel-based analysis, particularly in superficial white matter with supervoxel-based analysis.

The results in ICC also show reliability varies significantly across methods (one-way ANOVA, p < 1 × 10⁻¹⁵, η² = 0.90). Smoothing was found to have a significant effect on ICC (t-test, p < 1 × 10⁻¹⁵, d = 0.61, ΔICC = 0.15), with lower ICC without smoothing (ICC = 0.50 ± 0.04) than with smoothing (ICC = 0.66 ± 0.04). Region-based analysis was also found to have a significant and large effect on ICC (t-test, p < 1 × 10⁻⁹, d = 2.1, ΔICC = 0.17), with lower ICC when analyzing single voxels (ICC = 0.58 ± 0.04) compared to regions (ICC = 0.74 ± 0.02). Template type was found to have a significant but small effect on ICC (paired t-test, p < 1 × 10⁻⁴, d = 0.17, ΔICC = 0.02) with lower ICC in the standard template (ICC = 0.65 ± 0.04) compared to the standard template (ICC = 0.67 ± 0.04). From additional tests within each method, JHU, VBA+TBSS, and JHU+TBSS were found not to have a significant difference in ICC between template types, unlike the main effect. Skeletonization was found to have a significant but small effect on ICC (paired t-test, p < 1 × 10⁻¹², d = 0.66, ΔICC = 0.07) with a lower ICC with skeletonization (ICC = 0.62 ± 0.04) than without (ICC = 0.70 ± 0.03). In reviewing the spatial distribution of ICC across the brain, VBA and VBA+TBSS showed the greatest spatial variability, with a distinct pattern from CV and a more heterogeneous spatial distribution. Smoothing tended to also smooth this spatial distribution of ICC scores. Region-based analysis showed more spatially uniform ICC results than voxel-based analysis, particularly in superficial white matter with supervoxel-based analysis, although there was more variation than in CV.

3.2. Sensitivity to Normal Aging

The following nine brain areas were found to have a significant relationship between FA and age: right anterior pericallosal white matter (R_PERI), the fornix (FORN), the left superior cerebellar peduncle (L_SCP), left uncinate (L_UNC), middle cerebellar peduncle (MCP), splenium (SPLN), right posterior thalamic radiation (R_PTR), right superior frontal white matter (R_SUPF), and right inferior frontal white matter (R_INFF). To varying extents, there were bilateral effects in the superior cerebellar penduncles, inferior frontal white matter, and percal-losal white matter, but the hemisphere with the larger effect is reported for brevity.

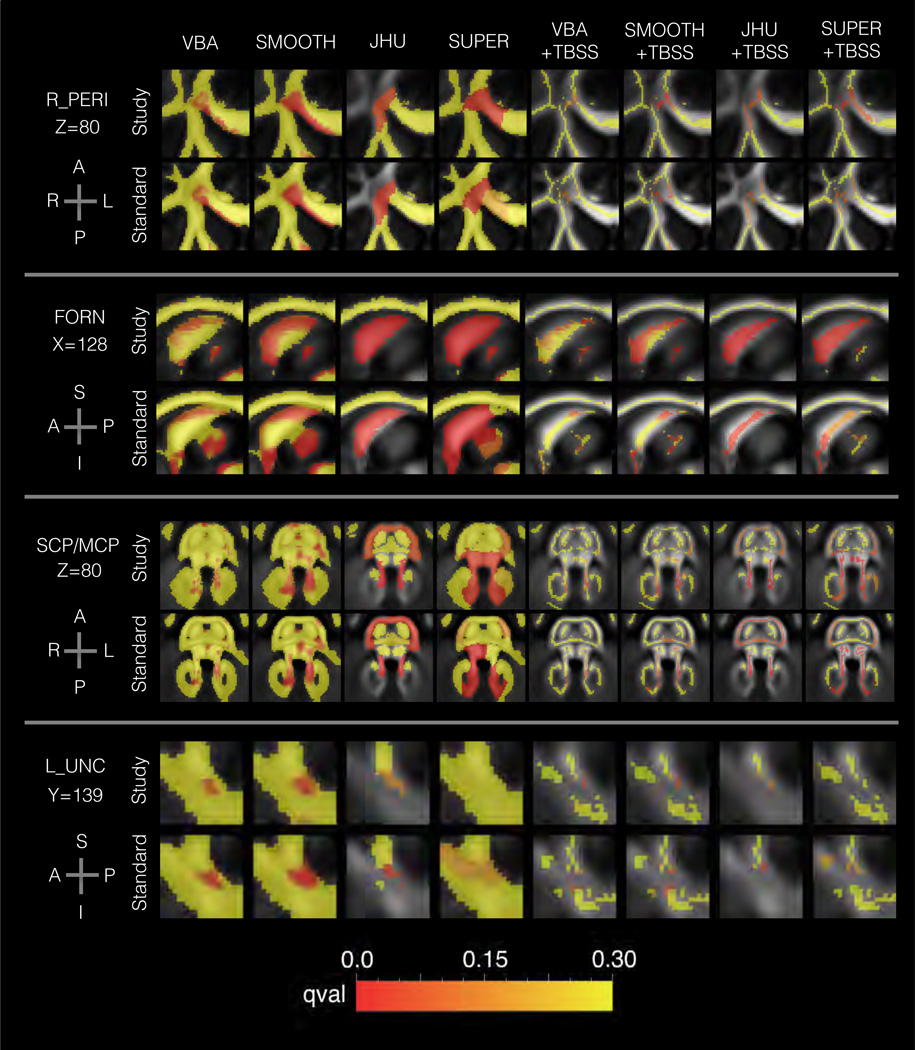
Among these regions, the qualitative results (Figure 5) show agreement with respect to the general location of the effects, but some variation was found with respect to the fine anatomical differences. In pericallosal white matter, voxel-based analysis exhibited a cluster that extended into the genu, an aspect that was not typical of most TBSS conditions. In the fornix, the study-specific results tended to show significant effects along the length of the bundle; however, most standard template conditions instead showed distinct clusters located at anterior and posterior positions along the visible portion of the bundle. In the middle cerebellar peduncle, there was high anatomical variability across methods, where some methods showed lateral concentrations of significant results. In the uncinate, the models were less sensitive in the SUPER conditions, but the spatial patterns were similar across methods. Across all regions, smoothing was found to generally increase the size of the cluster of significant voxels. Regarding the direction of the change with age, the following areas showed decreased FA with age: R_PERI, FORN, R_PTR, RINFF, and the following areas showed increased FA with age: L_SCP, MCP, L_UNC, SPLN, R_SUPF.

Figure 5.

Results from the aging analysis in Sec. 3.2 showing the spatial patterns of age-related change in FA for each method. The background shows the template FA map, and the foreground shows the FDR q-value. Four areas are shown: right anterior pericallosal white matter (R_PERI), the fornix (FORN), the superior and middle cerebellar penduncles (SCP/MCP), and left uncinate fasciculus (L_NC). The plots are colored to show FDR q-value, with redness indicating greater significance. Note that there is transparency to show the FA map, which may slightly change the perceived q-value. The results show general agreement among methods, although several differences can be noted. VBA, SMOOTH, and SUPER analysis of R_PERI showed a greater extent of significant voxels than other methods. The fornix showed distinct spatial patterns for each template type, namely a greater concentration of significant results in the anterior and posterior portions in the standard template conditions.

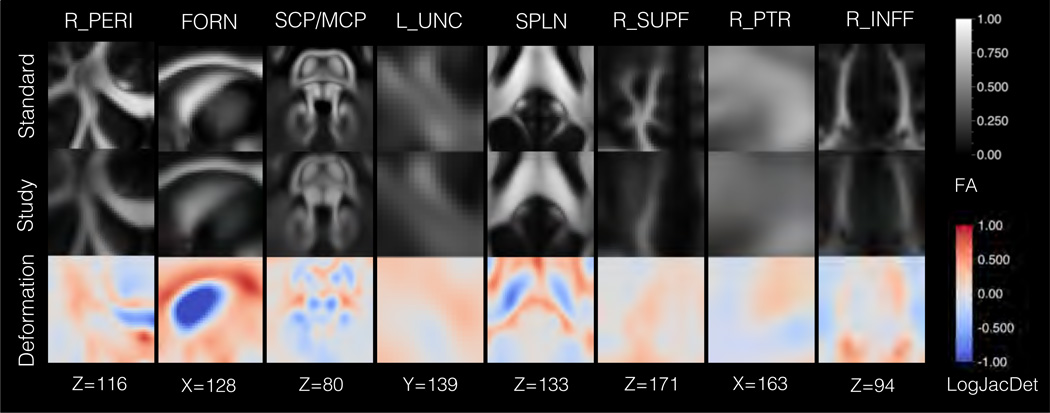
A comparison of the study-specific and standard templates showed shape differences that varied with respect to anatomical location (Figure 6). The LogJacDet maps were reviewed to determine the magnitude of local volumetric changes, where a negative value indicates that a contraction was required to deform the standard template to the study template, and positive indicates that an expansion was required. The fornix showed the greatest difference between the template types, where the study-specific template had a substantially thinner fornix than the standard template (LogJacDet ≈ −1.5). The following regions also exhibited smaller local volumes in the study-specific template: genu of the corpus callosum (LogJacDet ≈ −1.0), splenium of the corpus callosum (LogJacDet ≈ −0.5), posterior limb of the internal capsule (LogJacDet ≈ −0.5), superior cerebellar peduncle (LogJacDet ≈ −0.5), and middle cerebellar peduncle (LogJacDet ≈ −0.4). Conversely, the following regions showed greater local volume in the study-specific template: body of the corpus callosum (LogJacDet ≈ 0.5) and palladium (LogJacDet ≈ 0.5).

Figure 6.

Results from aging analysis in Sec. 3.2 showing the structural differences between the study and standard templates. Eight regions are shown: right anterior pericallosal white matter (R_PERI), the fornix (FORN), the superior and middle cerebellar penduncles (SCP/MCP), left uncinate fasciculus (L_UNC), splenium (SPLN), right superior frontal white matter (R_SUPF), right posterior thalamic radiation (R_PTR), and right inferior frontal white matter (R_INFF). The top row shows the standard template FA map, and the second row shows the study template FA map, which has been deformed to the standard template. The third row depicts the deformation field between the templates, with coloring to indicate the logarithm of the Jacobian determinant (LogJacDet). The LogJacDet measures the local volumetric changes induced by the deformation, where blueness indicates that contraction was required to match the standard template to the study template and redness indicates that expansion was required. The results show the greatest diiferences were in the region of the fornix, which was smaller in the study template.

Statistical tests were performed to assess performance characteristics of the methods according to R² with groupings by the following factors: method type, region-based, skeleton-based, smoothed, and template type (Figure 7, Table 2). The results show significant variation across methods (one-way ANOVA, p < 1 × 10⁻¹⁰, η² = 0.38). Smoothing was not found to have a significant effect on R² (t-test, p = 0.43). Region-based analysis was found to have a significant effect on R² (t-test, p < 1 × 10⁻¹³, d = 1.50, ΔR² = 0.10), with higher R² when analyzing single voxels (R² = 0.22 ± 0.01) compared to regions (R² = 0.11 ± 0.01). Template type was found to have a small but statistically significant effect on R² (paired t-test, p = 0.01, d = 0.18, ΔR² = 0.016). When compared across methods, the difference in template type was significant only in SMOOTH (paired t-test, p = 0.02), VBA+TBSS (paired t-test, p = 0.05), and SMOOTH+TBSS (paired t-test, p = 0.01). When compared across anatomical region, the difference in template type was significant only in the superior cerebellar peduncle (paired t-test, p = 0.02) and left uncinate (paired t-test, p = 0.02). Skeletonization was not found to have a significant effect on R² (paired t-test, p = 0.60 d = 0.03, ΔR² = 0.01).

Figure 7.

Results from the aging analysis in Sec. 3.2 showing a quantitative comparison of the methods. The plots show the R² of linear regression models relating age to FA. The left plot shows results aggregated for each method and template type. The right plot shows results aggregated for each region and template type. Nine areas are shown: right anterior pericallosal white matter (R_PERI), the fornix (FORN), the superior and middle cerebellar penduncles (SCP/MCP), left uncinate fasciculus (LJJNC), splenium (SPLN), right superior frontal white matter (R_SUPF), right posterior thalamic radiation (R_PTR), and right inferior frontal white matter (RJNFF). Statistically significant diiferences (p ≤ 0.05) are marked with an asterisk. The results show that single voxel analysis performed better than region-based analysis. Skeletonization and smoothing did not significantly change performance, but the standard template performed better than the study template when used in conjuction with single voxel-based TBSS. There was moderate variability in performance across regions, and models of L_SCP and L_UNC were found to perform better with the standard template.

Table 2.

A summary of findings from the evaluation in normal aging.

Region	Method	Standard Template			Study Template
		R2	t-value	q-value	R2	t-value	q-value
R_PERI	VBA	0.28	−5.3	0.0049	0.26	−5.0	0.016
R_PERI	SMOOTH	0.32	−5.8	5.5 × 10−4	0.27	−5.2	0.0027
R_PERI	JHU	0.10	−2.9	0.037	0.096	−2.8	0.075
R_PERI	SUPER	0.15	−3.4	0.047	0.14	−3.4	0.041
R_PERI	VBA+TBSS	0.16	−3.9	0.077	0.17	−3.8	0.073
R_PERI	SMOOTH+TBSS	0.19	−4.1	0.027	0.20	−4.2	0.022
R_PERI	JHU+TBSS	0.077	−2.4	0.10	0.095	−2.8	0.087
R_PERI	SUPER+TBSS	0.14	−3.0	0.096	0.14	−3.5	0.031
FORN	VBA	0.25	−5.0	0.0077	0.21	−4.4	0.041
FORN	SMOOTH	0.32	−5.9	4.4 × 10−4	0.28	−5.4	0.0021
FORN	JHU	0.14	−3.3	0.022	0.22	−4.3	7.9 × 10−4
FORN	SUPER	0.20	−4.1	0.0078	0.24	−4.8	0.0029
FORN	VBA+TBSS	0.24	−4.7	0.019	0.17	−3.9	0.068
FORN	SMOOTH+TBSS	0.33	−5.9	0.0013	0.28	−5.4	0.0040
FORN	JHU+TBSS	0.13	−3.0	0.041	0.21	−4.2	0.0010
FORN	SUPER+TBSS	0.17	−3.7	0.026	0.18	−3.9	0.016
L_SCP	VBA	0.24	4.8	0.012	0.22	4.5	0.036
L_SCP	SMOOTH	0.23	4.7	0.0068	0.21	4.5	0.011
L_SCP	JHU	0.30	5.1	6.4 × 10−5	0.29	4.7	2.6 × 10−4
L_SCP	SUPER	0.16	3.8	0.017	0.13	3.3	0.044
L_SCP	VBA+TBSS	0.25	4.8	0.017	0.20	4.2	0.035
L_SCP	SMOOTH+TBSS	0.25	4.8	0.0065	0.23	4.7	0.0093
L_SCP	JHU+TBSS	0.33	5.5	1.1 × 10−5	0.34	5.8	6.1 × 10−6
L_SCP	SUPER+TBSS	0.19	4.1	0.012	0.15	3.5	0.031
L_UNC	VBA	0.22	4.5	0.022	0.22	4.3	0.045
L_UNC	SMOOTH	0.23	4.6	0.0074	0.18	3.8	0.039
L_UNC	JHU	0.13	3.1	0.031	0.086	2.4	0.16
L_UNC	SUPER	0.16	2.8	0.20		(n.s.)
L_UNC	VBA+TBSS	0.25	4.8	0.017	0.24	4.8	0.018
L_UNC	SMOOTH+TBSS	0.21	4.3	0.017	0.18	3.9	0.036
L_UNC	JHU+TBSS	0.14	3.1	0.041	0.087	2.4	0.16
L_UNC	SUPER+TBSS	0.14	2.6	0.17		(n.s.)
MCP	VBA	0.25	4.4	0.024	0.21	4.3	0.045
MCP	SMOOTH	0.19	4.0	0.025	0.18	3.9	0.030
MCP	JHU	0.11	3.0	0.031	0.11	2.7	0.078
MCP	SUPER	0.16	3.0	0.16	0.16	2.8	0.15
MCP	VBA+TBSS	0.23	4.5	0.026	0.19	4.3	0.035
MCP	SMOOTH+TBSS	0.22	4.6	0.0098	0.18	3.8	0.037
MCP	JHU+TBSS	0.13	2.8	0.059	0.14	2.6	0.12
MCP	SUPER+TBSS	0.12	2.9	0.11	0.12	3.1	0.079
SPLN	VBA	0.22	4.4	0.025	0.27	5.1	0.015
SPLN	SMOOTH	0.23	4.7	0.0068	0.13	2.8	0.18
SPLN	VBA+TBSS	0.26	4.8	0.017	0.27	5.1	0.013
SPLN	SMOOTH+TBSS	0.24	4.8	0.0068	0.22	4.5	0.012
SPLN	JHU+TBSS	0.13	2.7	0.072	0.083	2.2	0.19
SPLN	SUPER+TBSS		(n.s.)		0.11	3.0	0.099
R_PTR	VBA	0.19	−4.0	0.053	0.17	−3.7	0.085
R_PTR	SMOOTH	0.21	−3.5	0.058	0.18	−3.1	0.12
R_PTR	SUPER		(n.s.)		0.17	−2.7	0.20
R_PTR	VBA+TBSS	0.17	−3.9	0.077	0.14	−3.3	0.15
R_PTR	SMOOTH+TBSS	0.14	−3.2	0.11	0.12	−3.0	0.14
R_SUPF	VBA	0.26	4.7	0.014	0.29	5.2	0.013
R_SUPF	SMOOTH	0.23	4.6	0.0083	0.25	4.7	0.0063
R_SUPF	SUPER	0.25	4.7	0.0025		(n.s.)
R_SUPF	VBA+TBSS	0.33	5.5	0.0045	0.26	4.7	0.019
R_SUPF	SMOOTH+TBSS	0.29	4.9	0.0059	0.28	5.2	0.0040
R_SUPF	SUPER+TBSS	0.19	3.8	0.023	0.15	2.9	0.10
R_INFF	VBA+TBSS	0.13	−3.2	0.18	0.14	−3.1	0.19
R_INFF	SUPER+TBSS	0.11	−2.7	0.15	0.11	−2.5	0.18
R_INFF	SMOOTH+TBSS	0.13	−3.1	0.13		(n.s.)
R_INFF	VBA	0.19	−3.8	0.075	0.14	−3.0	0.19
R_INFF	SMOOTH	0.14	−3.2	0.094		(n.s.)

The following regions had variation in FA that was related to age: right anterior pericallosal white matter (R_PERI), fornix (FORN), left superior cerebellar peduncle (L_SCP), left uncinate (L_UNC), middle cerebellar peduncle (MCP), splenium (SPLN), right posterior thalamic radiation (R_PTR), right superior frontal white matter (R_SUPF), right inferior frontal white matter (R_INFF). If a method is not shown or marked (n.s.), it had q > 0.2. For comparison, each test is represented by the R², t-value, and FDR q-value of the regression with age.

4. Discussion

Scan-rescan Reliability

The first main finding in scan-rescan reliability was large variability in the overall reliability across methods despite using identical data, preprocessing steps, and registration. The most readily observed pattern was that methods looking at single voxels, e.g. VBA and VBA+TBSS, were less reliable than region-based methods, e.g. JHU and SUPER, as measured with both CV and ICC. Previous work has demonstrated a trade-off in spatial specificity between these methods [36], and the results of this study further support a trade-off in reliability between voxel-based and region-based analysis. This difference is perhaps due to the voxelwise averaging used in region-based analysis, which could also tend to average out the effects of noise. Smoothing is perhaps another way to accomplish this, but it includes a greater risk of mixing different tissues. Past work has also found that the results of voxel-based analysis depend greatly on the filter parameters and implementing package [34] [33], and the results of this study show related changes in reliability. Specifically, reliability in voxel-based and skeleton-based analysis tended to improve with smoothing, while performance depended on the particular diffusion parameter being tested, which supports previous findings [36]. Regarding region-based analysis, the results were also comparable to previous findings of intra-rater variability less than 3% in manually drawn ROIs [30] [17] [21], which is perhaps evidence that de-formable tensor-based registration is comparable in quality to anatomical matching of manually drawn region masks.

The second main result was that all methods exhibited spatial variability in CV and ICC estimates of reliability. This reinforces similar results demonstrated in prior work that examined the spatial distribution of reliability estimates [18] [22] [35], although these studies were typically limited to tests of only one or two methods for spatial mapping each. The results of this study show voxel-based methods tended to have the most spatial variability and had concentrated high reliability in deep white matter, similar to previous work [20]. This could be related to higher registration accuracy in deep white matter, as seen in fiber coherence maps derived form population data [45]. However, it could also be that reliability is highest where the tensor model is most representative of the underlying diffusion process, i.e. predominantly single fiber regions in deep white matter [64]. This could be more thoroughly studied by examining reliability of multi-fiber extensions of TBSS [65], possibly with multi-compartment model smoothing [66]. Voxel-based analysis had low reproducibility in superficial and periventric-ular white matter, with CV above 7% and ICC below 0.5 in some cases; however, region-based analysis was found to have lower spatial variability and better performance in these areas. This is likely due to the variance reducing effects of averaging within each supervoxel, perhaps also indicating that the registration quality in these superficial areas is at least as accurate as the supervoxel size. In general, ICC had more spatial variability than CV with a different spatial distribution. This demonstrates how CV and ICC reflect different aspects of reliability, as CV directly represents error, while ICC depends on the variation across subjects. For this reason, results in ICC may be more specific to the populations and datasets used for evaluation.

Sensitivity to Normal Aging

The first main result in aging was a substantial agreement of significant effects among methods, despite the differences in reliability found in the previous experiment. However, there were differences in sensitivity between methods warranting discussion. The most prominent factor was whether individual voxels were analyzed, as most region-based conditions were less sensitive. An inspection of the spatial distribution of effects shows the significant clusters to be small and locally restricted effects not well characterized by the relatively larger ROIs available in the JHU atlas and supervoxels. This shows a major limitation of ROI analysis, as small local effects may be washed out by other voxels when the ROI is larger than the extent of the effect. One possible solution is to explore regions in a hierarchical way at varying levels of detail. Supervoxel-based analysis may offer a way to implement this by algorithmically varying the size of extracted regions. However, there were also brain areas in which region-based analysis performed best. These might represent anatomical changes that are more distributed and characteristic of disconnection [67].

Another main result was the negligible effect of skeletonization and smoothing. Previous evaluations have found skele-tonization to improve performance in deep white matter ROIs [37]; however, the improvement in models with FA here were not significant. This may support other results showing that high quality registration is as important as skeletonization in improving sensitivity [68] and related findings showing more heterogeneous results [37]. Smoothing tended to increase the size of the significant clusters, although the effect size did not change. Related to this, it is worth noting that the VBA and VBA+TBSS conditions still include smoothing to some extent, as the native data is interpolated to a considerably smaller template voxel resolution. While this may help to avoid possibly missing a small effect, it may also introduce further smoothing and spatial correlations of noise.

In relation to template type, the observed differences are of interest, as previous findings have shown that study-specific templates provide greater sensitivity and accuracy than standard templates [39]. The results in this study show a slight improvement in reliability when using a study-specific template; however, in three methods and two regions, age modeling slightly improved with the standard template. This perhaps supports previous findings that a high quality standard template combined with low-artifact data can provide comparable results to a study-specific template [40], unless a disease group is being studied [41]. However, we also found that the standard template was much sharper than the study template, so the consequent differences in white matter masks may have also been a factor. Furthermore, there were significant structural differences between the template that may have influenced the results, for example, in the pattern of significant results in the fornix. The study template results in the fornix were perhaps more anatomically plausible, as they followed the trajectory of the bundle, while the standard template results were not significant in those voxels with the largest magnitude deformation.

The biological significance of the results can also be related to previous studies of white matter aging. The pattern of the results supports the anteroposterior gradient and frontocerebellar synergism hypotheses of aging [69]. The specific findings in the genu, anterior pericallosal white matter, fornix, and spelenium are consistent with previous work [70] [71] [72]. The results in the cerebellum also support recent findings in the superior cerebellar peduncles [73], perhaps adding related findings in the middle cerebellar peduncle. One general concern with the results, however, is the effect of partial voluming, which may confound microstructural changes with volumetric changes, particularly in the fornix [74] [75]. Another consideration is the limitations of the aging population, specifically, the maximum age of 65 years, which is less than some previous studies [69].

Limitations and Open Problems

It is also worth discussing the design of the study. In particular, the experiments were designed to control for a number of potential biases that could severely effect the results, such as dataset, preprocessing steps, and registration algorithm. This allows us to more certainly attribute the observed differences in reliability and predictive modeling to the choice of spatial mapping algorithm and not to other factors. This is a somewhat stronger result than could be gained by summarizing the results of multiple studies, which inevitably have major differences in data and implementation. However, the major limitation of this design is that only one factor of the pipeline was studied, and the results possibly depend on variation in these other factors, e.g. registration algorithm. A full factorial design is quite challenging due to the increasing number of choices available at each step of the pipeline; however, it is likely a fruitful avenue of research to pursue. Looking beyond voxel-based analysis, it would also be tremendously valuable to expand this kind of evaluation to include tractography-based spatial mapping. However, a similar challenge is posed by the vast number of methods currently in use, as each tractography reconstruction is a complex product of diffusion modeling, image interpolation, seed and selection masks, and termination criteria.

The results of this study are also somewhat limited with respect to the VBA smoothing step. Only a single bandwidth and smoothing technique were tested, but a variety of approaches can be found in the literature [76] [77] [78]. While the effect of smoothing bandwidth has been well studied [33] [34], a relatively less understood aspect is the effect of filter type and the filtering domain. For example, smoothing can be done with a variety of types of filters, including Gaussian, median, and anisotropic filtering, and unlike some other modalities, there are several possible filtering domains, such as the diffusion-weighted signals, the diffusion models fitted to the signal, or scalar features derived from the models. Smoothing in the signal domain is attractive for the theoretical guarantees of linear systems and sampling theory, but it not commonly used in VBA, perhaps due to challenges inherent to reorienting q-space data after registration. Model-based smoothing of tensors can possibly preserve anisotropy and fiber orientation [79]; however, the most common approach is to smooth in the feature domain [80]. Previous work has also shown that anisotropic smoothing in particular can offer improved accuracy and sensitivity [81]. This study aimed to represent the most common technique of feature-domain Gaussian smoothing with a bandwidth that is comparable to previous studies with comparable voxel size [82] [83] and recommended in a previous evaluation [36]; however, there remain many questions to answer related to these aspects of smoothing in VBA.

5. Conclusion

In conclusion, this paper presented a comparative evaluation of methods for voxel-based spatial mapping as measured by scan-rescan reliability and sensitivity to normal aging. The results show reliability depends greatly on the method of spatial mapping, as well as anatomical location. The largest differences were found when adding smoothing and comparing single voxel and region-based methods. In contrast, skeletoniza-tion and template type were found to have either a small or negligible effect on reliability. The aging results showed agreement among the methods in nine brain areas, although some methods were more sensitive than others. Skeletonization and smoothing were not found to change sensitivity to aging; however, template type had a small but significant effect. In comparing templates, the results show how a standard template can provide acceptable performance compared to study-specific templates when analyzing a healthy population, but also, how structural differences between the them can may be reflected in the patterns of significant results. The results also show how sensitivity to aging is limited by the spatial extent of the method, and whether these effects are small and localized or distributed in nature. These reliability results may help in the design and interpretation of future studies, as they indicate care must be taken to establish baseline reliability and statistical power of a study based on the specific anatomical hypotheses and method of spatial mapping. The results of the aging application may also help to understand how the choice of spatial mapping method affects sensitivity in white matter imaging studies. To further this goal, the complete results of this study are available for download from the following link: https://doi.org/10.7301/Z0ZC80SW