Resting-state test-retest reliability of a priori defined canonical networks over different preprocessing steps

Abstract

Resting-state functional connectivity analysis has become a widely used method for the investigation of human brain connectivity and pathology. The measurement of neuronal activity by functional MRI, however, is impeded by various nuisance signals that reduce the stability of functional connectivity. Several methods exist to address this predicament, but little consensus has yet been reached on the most appropriate approach. Given the crucial importance of reliability for the development of clinical applications, we here investigated the effect of various confound removal approaches on the test-retest reliability of functional-connectivity estimates in two previously defined functional brain networks. Our results showed that grey matter masking improved the reliability of connectivity estimates, whereas de-noising based on principal components analysis reduced it. We additionally observed that refraining from using any correction for global signals provided the best test-retest reliability, but failed to reproduce anti-correlations between what have been previously described as antagonistic networks. This suggests that improved reliability can come at the expense of potentially poorer biological validity. Consistent with this, we observed that reliability was proportional to the retained variance, which presumably included structured noise, such as reliable nuisance signals (for instance, noise induced by cardiac processes). We conclude that compromises are necessary between maximizing test-retest reliability and removing variance that may be attributable to non-neuronal sources.

1 Introduction

Functional magnetic resonance imaging (fMRI) relies on the measurement of changes in blood oxygenation (i.e., BOLD) and plays a vital role in understanding normal and abnormal brain functioning. For instance, functional connectivity of distant brain regions can be investigated through the statistical analysis of coherent low frequency BOLD fluctuations. Synchronized signal fluctuations can be observed even when the subject is at rest, without performing any task, and the analysis of resting-state data has become a popular means of studying ongoing brain activations and functional connectivity between brain regions (Biswal et al. 1995; Fox and Raichle 2007). There are both indirect (from comparison with task co-activation patterns, (Kwong et al. 1992; Hinke et al. 1993; Buckner et al. 1996; Huettel et al. 2004; Barch et al. 2013)) as well as direct (from invasive recordings (He et al. 1999; Lai et al. 2011; Lu et al. 2014) support towards this notion. Several confounding effects including system noise, thermal noise, and noise induced by non-neuronal physiological processes may influence the measured signal and hence apparent brain activity. Therefore, interpretation of brain activity depends on the ability to mitigate their influences (Fox et al. 2009).

Participant-induced artifacts, such as motion and physiologically induced artifacts (i.e., due to respiration and cardiac processes) comprise the largest component of noise affecting the BOLD signal (Windischberger et al. 2002). Motion artifacts have been shown to produce spurious correlations in a systematic way (Van Dijk et al., 2012; Power et al., 2012; Satterthwaite et al., 2013), implying that the removal of motion related artifacts is a prerequisite for further analysis. Various approaches have been proposed for dealing with noise effects post-hoc, i.e., after the data have been acquired (Behzadi et al. 2007; Fox et al. 2009; Murphy et al. 2009; Chai et al. 2012; Griffanti et al. 2014; Patriat et al. 2015; Power et al. 2015; Soltysik et al. 2015; Wong et al. 2016). Besides motion-related artifacts, one particular aspect that has received a lot of attention is the use of nuisance regressors reflecting global signals, either derived from the whole brain or from specific tissue types such as white-matter or cerebrospinal fluid. However, removal of various global nuisance regressors alters the variance of the residual signal and has been shown to modify the correlational structure (Fox et al. 2009). In line with it, Friston 2011 showed that changing the signal to noise ratio can change the correlation coefficient, which indicates that the level of observable noise influence the correlation coefficient.

Both the definition of the ROI from which BOLD signals are extracted, and the means by which voxel-wise signals are summarized across a given ROI, are critical considerations in a functional connectivity analysis. An ROI can be derived through various approaches, including (most simply) a single voxel or sphere of a fixed radius around a voxel, histological parcellation in standard space (Eickhoff et al. 2005), clustering approaches based on functional or structural connectivity estimates (Eickhoff et al. 2015), thresholded statistical maps, or meta-analytic approaches such as ALE (Eickhoff et al. 2009; Eickhoff et al. 2012). In this study, we focused on region-to-region connectivity within a priori meta-analytically-defined networks (Schilbach et al. 2014; Schilbach 2016). This approach has several advantages. In particular, meta-analyses provide robust, functionally specific ROIs based on observations across many studies. Analyzing functional connectivity on this network combines its functional specificity with the advantages of task-free imaging, i.e., an acquisition that poses little demands on the subjects and is not confounded by a specific task paradigm. Similarly, the extraction of a summary signal across an ROI can be performed in various ways that may impact the reliability of connectivity estimates. In particular, the exclusion of voxels based on their grey matter probabilities may help improve signal-to-noise by removing signal not originating in the grey matter tissue of interest. In the current study, we compared three signal extraction approaches using different grey-matter masking techniques.

Many clinical studies currently rely on functional connectivity measures in understanding normal and abnormal brain functioning. The appeal for resting-state functional connectivity analyses in clinical applications lies in the fact that such data are easy to acquire without any specific setup, do not require active participation by the subjects, and in contrast to task-based data are less influenced by compliance and performance. Nevertheless, several concerns have been raised regarding the reproducibility and statistical power of classical neuroimaging studies (Button et al. 2013a; Button et al. 2013b). Clinical application, however, can only be useful if the analyses yield reliable measures. Various studies have also been performed to test the reliability of functional or effective connectivity measures using different modalities (such as fMRI or diffusion MRI) and reported moderate to high test-retest reliability of connectivity measures across moderate to long-term scans. (Chen et al. 2015; Frässle et al. 2016; Song et al. 2016; Zhong et al. 2015). In 2009, Shehzad et al. investigated the test-retest reliability of global connectivity patterns using resting-state fMRI and observed that significant connectivity scores are more reliable than non-significant connectivity scores. In 2011, Wang et al. evaluated short-term (less than 1 hour apart) and long-term (more than 5 months apart) test-retest reliability for topological metrics of functional networks and observed that long-term scans had better reliability than short-term scans. Later, Raemaekers et al., (2012) analyzed the reliability of BOLD activation and reported that patterns of BOLD activation were relatively stable across sessions, while the amplitude of the activations is more variable. In 2013, Gorgolewski et al. studied the test-retest reliability of confound removal at the subject level (by focusing on the single subject reliability) and showed that subject motion can detrimentally impact reliability. Yan et al., (2013b) investigated the influence of post-acquisition standardization techniques on traditional fMRI measures, test-retest reliability, and phenotypic relationships, as well as nuisance variables (mainly mean global signal) and reported that global signal regression is identical to grey matter regression and both should be avoided. Subsequently, Birn et al., (2014) evaluated the influence of various physiological noise correction methods on test-retest reliability and found that it was reduced by physiological noise correction, as it reduced the variability between subjects as well as within the subject. Shirer et al., (2015) investigated various means of confound removal across multiple outcome measures and demonstrated that noisiness, reliability, and heterogeneity of the data varies based on the preprocessing parameter chosen. In turn, the influence of various grey matter masking approaches on the reliability hasn’t been addressed in any of the previous test-retest studies. Therefore, using meta-analytically derived networks, we assessed the influence of different signal extraction and noise regression approaches on the reliability of the resting-state functional connectivity measures.

In this study, we evaluated test-retest reliability of resting-state functional connectivity in a cohort of 42 subjects scanned twice with a between-scan interval of 175 ± 75 days. We assessed two networks: the extended socioaffective default mode network (eSAD) (Amft et al. 2014); and the working-memory network (WMN) (Rottschy et al. 2012). Both networks were derived from previous meta-analytic studies, which used anatomical likelihood estimation (ALE; (Eickhoff et al. 2009; Eickhoff et al. 2012)) to identify regions that are robustly activated across studies, for specific task paradigms. Both networks have been hypothesized to anti-correlate with each other (Fox et al. 2005; Reid et al. 2015). Thus, the reliability of connectivity estimates within, as well as between, the specified meta-analytically derived networks was evaluated.

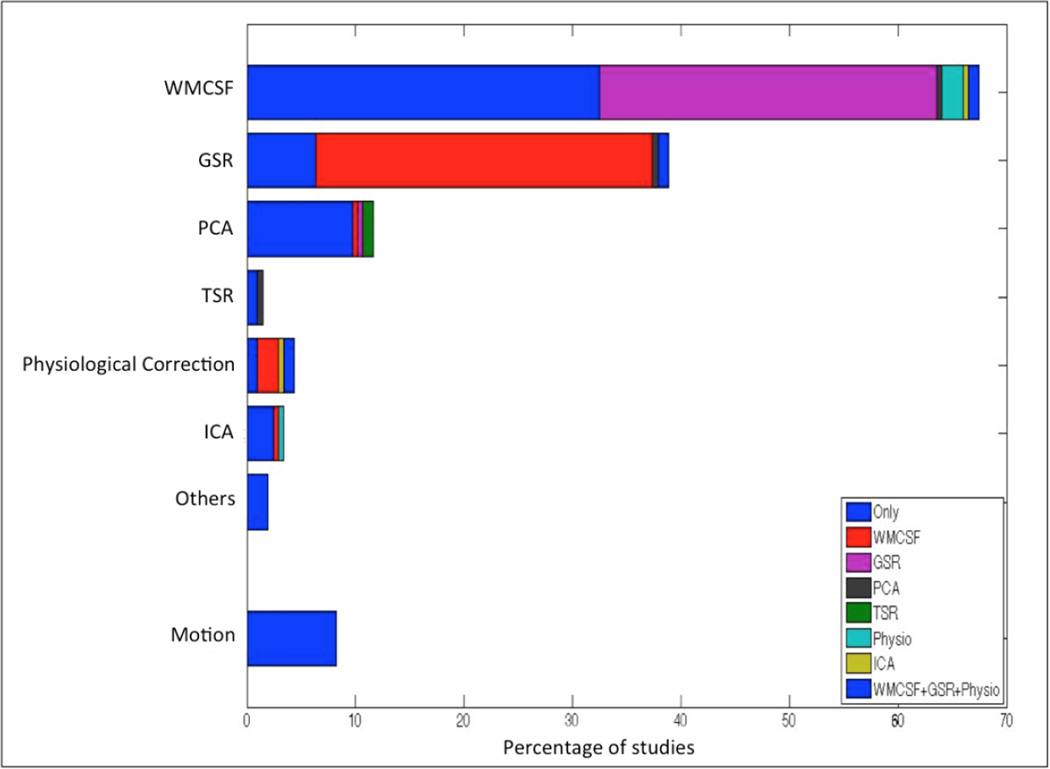
A literature survey was conducted, in order to investigate the popularity of various methods for confound removal in recent fMRI studies. Using PubMed database, all the articles with the terms “fMRI”, “resting-state” and “Seed-based”, published from the beginning of 2014 until the time of this study (June, 2016) were identified, reflecting the recent work most in line with the focus of our work on seed-based analyses. A total number of 239 studies were identified. Among them 33 studies had to be excluded because the articles were either not relevant to the study (such as, studies on animals) or not accessible. Therefore, a total number of 206 studies were investigated. We then computed the percentage of studies using the different confounds removal methods, which is illustrated in Figure 1. The frequency of studies when using a certain confound has been demonstrated separately (in the categories of ‘Only’) and in combination with the other confounds in the Figure 1.

Figure 1.

Percentage of studies using a certain confound removal method (i.e., White matter and Cerebral spinal fluid signal regression (WMCSF), Global signal regression (GSR), Principle component analysis based corrections (PCA), Tissue signal regression (TSR), Physiological recordings based corrections (Physiological Correction), Independent component analysis based corrections (ICA) and other correction methods such as ANATICOR or grey matter atrophy regression (Others)). The colors represent the interactions of each method with other methods. The first fraction of section which is consistent over the approaches, represented with the word “Only” (in blue) shows the percentage of studies performing only a certain confound removal without any interactions. Additional colors assigned to the other confound removal appears only when there is an interaction. Of note, the interactions of motion regression with other methods are not explicitly shown in Figure 1. However, almost all the studies involved in this literature survey, have removed the motion effects along with the other confound removal approaches demonstrated in the figure.

Based on this literature examination, we assessed the effects of the most commonly used confound removal approaches in resting state fMRI studies; namely global and tissue-class specific (either only WM and CSF or in addition also GM) mean signal regression, as well as principal components analysis (PCA) de-noising. We also examined three approaches for extracting the regional time-series based on different methods for grey-matter masking. Above mentioned approaches were assessed separately and in combination with each other. In order to observe the consequences of the interactions, the approaches were evaluated in combinations (cf. Section 2.3). We note that physiological noise regression (i.e., elimination of artifacts induced by respiration and cardiac processes) requires recordings of parameters such as heartbeat and breathing. Such physiological recordings, however, are rarely acquired in standard (clinical) resting-state acquisitions and were hence not considered in the current investigation. Independent component analysis (ICA) based denoising is another emerging approach to confound removal (Griffanti et al. 2014; Salimi-Khorshidi et al. 2014; Pruim et al. 2015a; Pruim et al. 2015b). However, ICA-based denoising approaches (excluding the ICA-AROMA, as the pre-defined spatial features included within in the package itself) require effective individual segmentation from high-resolution T1 images, which were not available for the current data. Acknowledging the future potential of ICA based denoising, we thus focused our work on the evaluation of the presently most widely used approaches.

Another common application of ICA is the examination of the functional connectivity networks. Recently, such ICA method followed with the dual regression is used to assess the functional connectivity for group comparisons, instead of seed-based functional connectivity. Zuo et al. 2010, reported moderate to high test-retest reliability. Furthermore, Smith et al. 2014 claimed that ICA followed with the dual regression performs better than the seed-based connectivity measures. Even though, such methods may lead to higher reliability. Zuo et al. 2010, reported moderate to high test-retest reliability, while computing the functional connectivity networks using ICA combined with the dual regression. Furthermore, Smith et al. 2014 investigated that ICA followed with the dual regression performs better than the seed-based connectivity measures. Even though, such methods may lead to higher reliability (Zuo et al. 2010), seed-based functional connectivity is still very widely used for the examination of a priori hypotheses in both basic and clinical studies (Smith et al. 2014). Thus, we here focused on the test-retest reliability of the seed-based functional connectivity measures.

Importantly, reliability can be examined from two perspectives: at the subject level and at the connection level. One the one hand, meaningful group comparisons largely depends on reliability at the subject level, i.e., over scans the order of subjects should remain as similar as possible for any given connection. One the other hand, network modeling capitalizing on within-subject connectivity requires reliability at the connection level (cf section 2.4), i.e., for any given subjects, the order of connectivity strengths should remain as similar as possible over scans. Therefore, in the present study, we investigated reliability from the two different but complementary perspectives, that is, reliability at the subject level (RoSO) and reliability at the connection level (RoCO). To sum up, the present study aimed to identify the combination of signal extraction and confound removal approaches that yields the highest test-retest reliability when assessing resting-state functional connectivity in meta-analytically defined networks, using standard acquisitions as feasible in clinical practice. In other words, this study aims to provide a ranking of methods in terms of their potential to yield stable connectivity patterns over time.

2 Material and Methods

2.1 Networks of interest

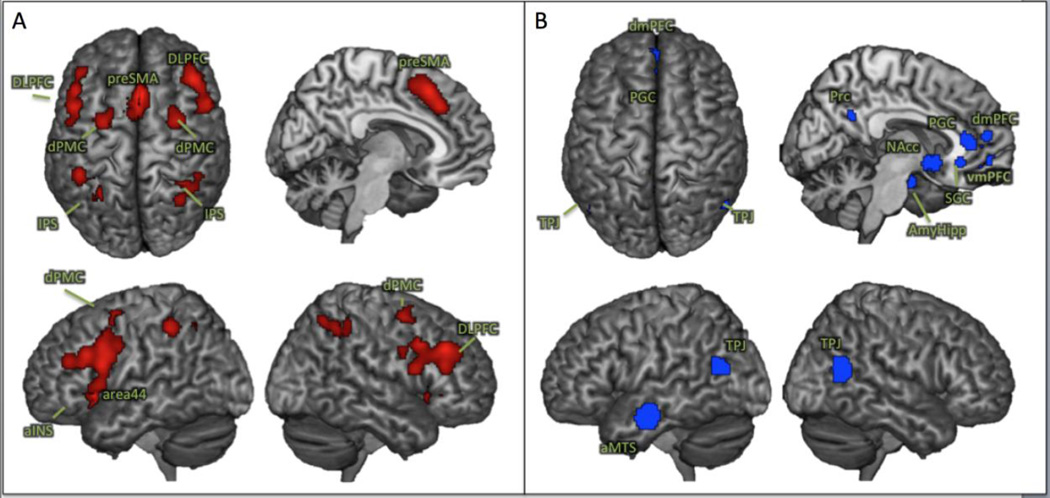
The influence of different processing steps on the test-retest reliability of resting-state functional connectivity analyses was assessed in two canonical networks related to cognitive and socio-affective processing. In particular, the two networks were defined by large-scale synthesis of neuroimaging findings using coordinate-based meta-analyses (Fox et al. 2014). As a prototypical “task-positive” cognitive network (regions exhibiting increase in activity during task performance), we assessed the core working memory network (WMN) described by Rottschy et al., (2012), consisting of 9 bilateral fronto-parietal regions (Figure 2A & Table. 1). As a “task-negative” network (regions exhibiting decrease in activity during task performance), we included the extended socio-affective default mode (eSAD) network identified by Amft et al., (2014), which extended a previous meta-analytical definition of the default mode (Schilbach et al. 2012) and comprised 12 regions mainly corresponding to cortical midline structures (Figure 2B & Table. 1). Importantly, both of these networks have shown a strong positive coupling among their respective nodes but were anti-correlated with each other. They may thus be considered as robustly a priori defined network models for the often-proposed large-scale anti-correlated systems in the human brain (Fox et al. 2005).

Figure 2.

Nodes of meta-analytically derived networks used for the reliability assessment. A: the core working memory network (Rottschy et al., 2012); B: the extended socio-affective default mode network (Amft et al., 2015)

Table 1.

Coordinate details and cluster size (k) of the regions, within the WMN & eSAD involved in this study.

					MNI Coordinates in standard RAS orientation
	Macro-anatomical labels	Abbreviation	Side	k (Voxels of size 3.1mm isotropic)	X	Y	Z
Working Memory Network (WMN) nodes
1	Anterior insula	aINS	L	276	32	22	−4
2			R	182	34	28	−2
3	Dorsolateral prefrontal cortex	DLPFC	L	1331	50	12	22
4			R	1032	44	34	32
5	Pre-supplementary motor area	preSMA		1035	2	20	50
6	Intraparietal sulcus	IPS	L	543	30	56	48
7			R	310	36	48	44
8	Dorsal premotor cortex	dPMC	L	190	28	0	58
9			R	243	30	2	56
Extended socio-affective default mode (eSAD) network nodes
10	Pregenual anterior cingulate cortex	ACC		180	0	36	10
11	Anterior middle temporal sulcus	aMTS	L	468	54	10	−20
12	Amygdala/hippocampus	Amy/Hippo	L	86	24.0	10	−20
13			R	141	24	−8.0	−22.0
14	Basal ganglia	BG	L	146	−6	10	−8
15			R	188	6	10	−8
16	Dorsomedial prefrontal cortex	dmPFC		204	−2	52	14
17	Precuneus	PrC		145	−2	52	26
18	Subgenual anterior cingulate cortex	sACC		244	−2	32	−8
19	Temporo-parietal junction	TPJ	L	251	46	66	18
20			R	373	50	60	18
21	Ventromedial prefrontal cortex	vmPFC		114	−2	50	−10

2.2 Sample characteristics, preprocessing and RS-FC computation

2.2.1. Images acquisition

Resting state fMRI data of 42 healthy subjects including 19 females with an average age of 42 ± 20 (mean ± std) years were obtained in two sessions with an average time interval of 175 ± 75 (mean ± std) days. In each session, 250 resting state EPI images were obtained on a Siemens 3T Scanner (Scanning parameters: TR: 2200ms, TE: 30ms, flip angle: 90 degrees, 36 slices, a voxel size: 3.1mm isotropic) corresponding to a scanning time of 9.2 minutes, which stays well in line with the reliable intersession scanning time of 8–12min suggested by (Birn et al. 2013). High-resolution T1 weighted structural images were not acquired for the dataset used in this study. The original study protocol of the data used here has been approved by the local ethics committees of the university hospital Aachen and informed consent was obtained by all the participants prior to the examination. The current data were analyzed anonymously.

2.2.2. Images preprocessing

Prior to further processing (using SPM8, www.fil.ion.ucl.ac.uk/spm) the first four images were discarded allowing for magnetic field saturation. The EPI images were corrected for head movement by affine registration using a two-pass procedure. In a two-pass procedure, all the EPI images were aligned to the 1^st EPI image. Then, a mean over the aligned EPI images was computed. Finally, all the EPI images were again aligned to the first pass mean EPI image. The mean EPI image for each subject was non-linearly normalized to the MNI152 non-linear template space template using the “unified segmentation” approach (Ashburner and Friston 2005). The ensuing deformation field was applied to the individual EPI volumes and smoothed with a 5-mm FWHM Gaussian kernel. Preprocessed images were visually checked for any processing artifacts.

Each node of the assessed functionally defined networks (cf. Section 2.1) available in the same space was represented by its peak’s coordinate. The time-series for all voxels within a priori meta-analytically derived clusters were then extracted. Following grey-matter masking if applicable (cf. Section 2.3), we then employed a multiple regression approach to control for different confounds in the EPI time series. While the choices for dealing with global signals were outlined below, we always included the six motion parameters derived from the image realignment as well as their derivative as first (linear) and second order (quadratic) terms as evaluated by (Satterthwaite et al., 2013). That is, in addition to the approach-specific confounds, these 24 movement regressors were used in all analyses. Following the removal of any variance in the individual voxels’ time-series that could be explained by the respective confounds, the data were band pass filtered preserving BOLD frequencies between 0.01 and 0.08 Hz (Biswal et al. 1995; Fox and Raichle 2007). We computed the frame-to-frame differences from the six motion parameters derived from the image realignment to assess frame-wise displacements (FD). An FD threshold of 0.5 mm was used to discard potentially motion-contaminated images, before band pass filtering (Power et al. 2012; Yan et al. 2013a). Finally, the characteristic time-series of each seed was computed as the first eigenvariate of the preprocessed time-series for the individual voxels within that seed. The functional connectivity between every pair of nodes was then computed as the correlation coefficient between these time series, which were transformed to Fischer’s Z scores to render them normally distributed (Figure 3). Here in this study, tissue class segmentation is performed on a mean EPI volume due to the lack of high resolution T1 structural scans. Nevertheless, the registration of EPI images to T1 structural scans may fail to detect the non-linear distortions of the EPI images, especially in the absence of the field maps or such relevant images. However, partial volume effects may exist in the mean EPI volume based segmentation. In order to avoid such partial volume effects, grey matter masking along with a median-split approach, which extracts the signal only from 50% of the voxels with high grey matter probability, has been implemented and evaluated in this study. In addition, median-split approach has an advantage of accounting similar number of voxels while extracting the signal, particularly when using meta-analytically derived clusters.

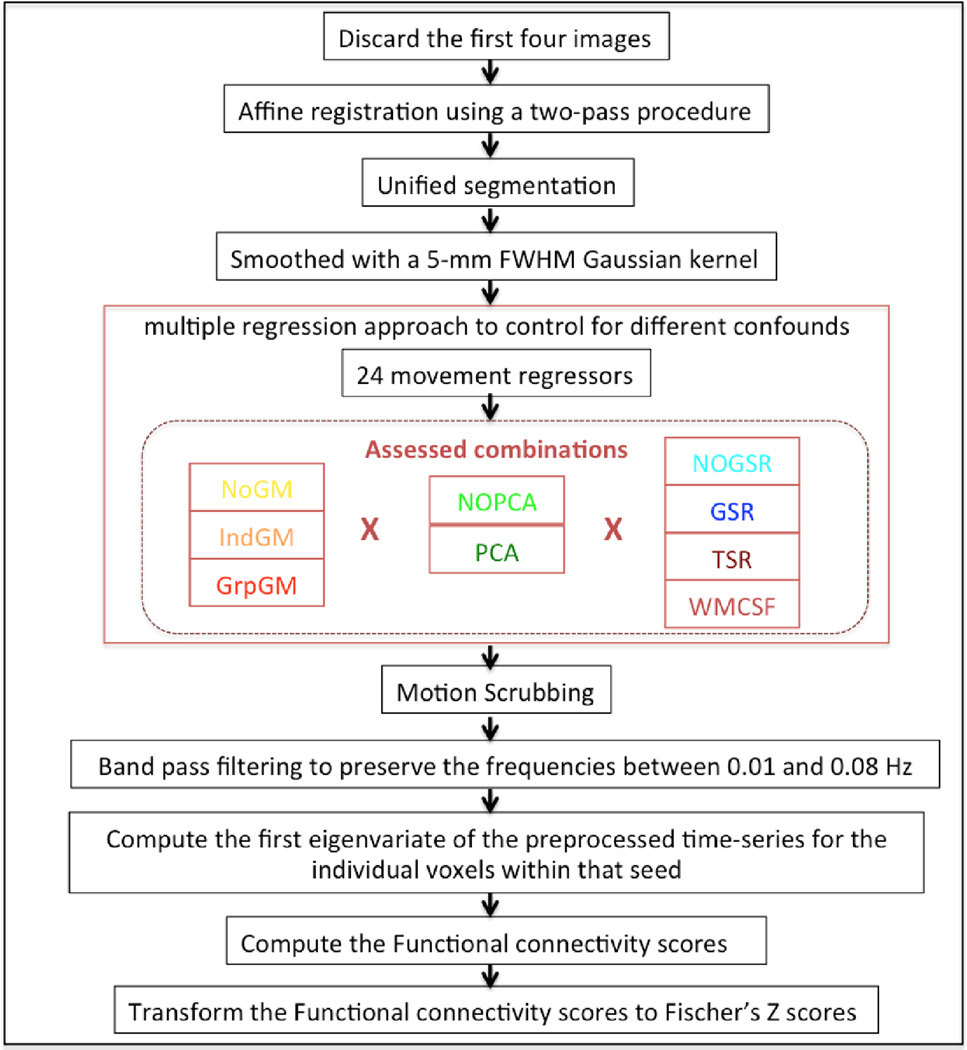
Figure 3.

Pipeline of the entire preprocessing steps until the RS-FC computation: The assessed combinations (inside the red dotted box) indicate the signal processing methods for which the reliability is evaluated in three different domains (I. Extraction of time series, II. PCA-denoising, III. Global signal removal).

2.3 Assessed (combinations of) signal processing steps

As the key aim of this study was to assess the impact of different commonly used processing steps on the reliability of RS-FC measurements, we focused on three different domains as follows:

I) Extraction of time series: Evidently, meaningful signal should mainly be found in grey matter (GM). Hence, the voxels within 5 mm of the seed’s coordinate might be anatomically constrained based on tissue class segmentation as provided by SPM (Ashburner and Friston 2005). Here we evaluated three options:

No grey matter mask (NoGM): All voxels within 5 mm of the seed-coordinate were included, processed by confound removal and temporal filtering and summarized by their first eigenvariate. No grey matter masking is the most commonly used approach in RS-FC analysis. Conceptually, NoGM considered the influence of cortical anatomy as minor relative to the spread of BOLD data and spatial smoothing.

Individual grey matter mask (IndGM): The GM probability as estimated by the unified segmentation for that particular subject was extracted for each voxel within 5 mm of the seed-coordinate and a median-split was then performed retaining those 50% of voxels with highest GM probabilities. This approach was based on the argument that the individual anatomy should be most important for tissue classification.

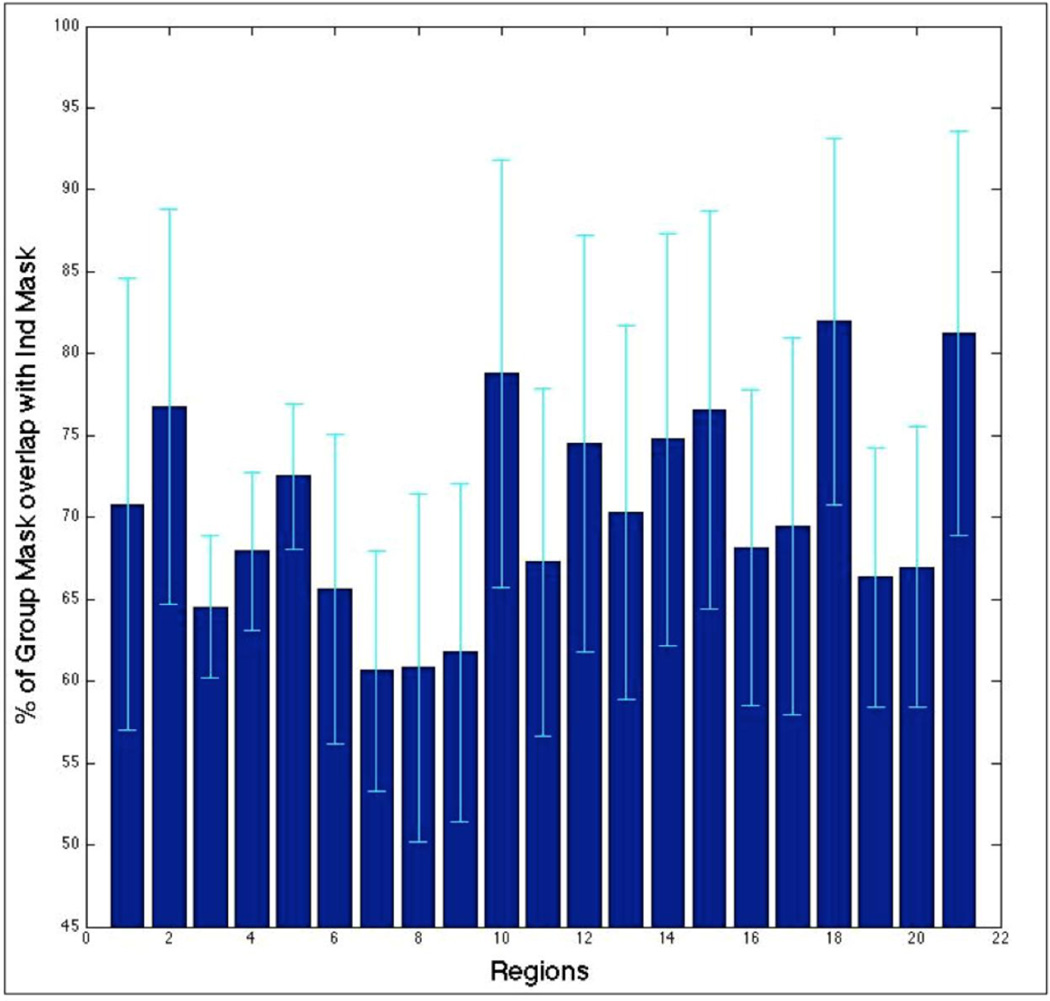
Group grey matter mask (GrpGM): The tissue class segmentations of all individual subjects were first averaged and a median split of the voxels was then performed based on these average GM probabilities. In this method, the focus on GM was retained but rather than basing the masking on the (prominently noisy) individual segmentation, group data (considered as more robust) were used. For reader’s information, the overlap between the IndGM and GrpGM was computed and illustrated in Figure 4.

Figure 4.

Percentage of voxels that overlap between the individual and group masks, relative to the GrpGM for each of the 21 seed regions

II) PCA de-noising: It has been suggested (Behzadi et al. 2007; Soltysik et al. 2015), that computing a principal component analysis (PCA) decomposition across the WM and CSF regions of the brain and removing variance associated with the most dominant 5 components might remove many sources of artificial and confounding signals and hence increase the specificity of RS-FC results. We thus performed all analyses both with (PCA) and without (NoPCA) PCA de-noising.

III) Global signal removal: As removing the global signal had received a lot of attention in recent discussions (Murphy et al. 2009; Chai et al. 2012; Saad et al. 2012; Fox et al. 2013), we assessed seven different methods for this particular aspect. In that context, tissue class specific global signals were computed based on the SPM8 segmentation of the (mean) EPI into GM, WM and CSF regions, then averaged the signal time-series of the voxels specific to each tissue class.

Global signal regression (GSR): Removes all variance explained by the first order effects of the global (average across all voxels at each time-point) signal.

Tissue signal regression (TSR): Removes variance explained by the first order effects of the mean GM, WM and CSF signals.

WM and CSF signal regression (WMCSF): The mean signals of the WM and CSF were removed i.e., only the first order effects.

No Global signal regression (NoGSR): No removal of any global signal.

Importantly, the different choices for each of the three main factors may be implemented independently of the other factors, allowing for a full permutation of the different analyses options and hence 42 (3×2×7) different combinations for signal extraction and confound removal. We therefore performed reliability analysis for all of these 42 combinations, i.e., analytical approaches.

2.4 Indices of Reliability

To quantify the test-retest reliability of the 42 different approaches, we used two complementary measures that were each applied from two different perspectives. Test-retest reliabilities are quite often assessed using Intra class correlations (ICC), which takes into account inter-subjects variability in relation with the intra-subject variability. The intention of our study, however, was to examine one effect at a time, i.e., to evaluate inter-subject variability (i.e., RoSO) separately from intra-subject variability (i.e., RoCO). Therefore, reliability was tested using two measures. The first employed measure was the Kendall’s rank correlation (in order to quantify the consistency in relative order (Zang et al. 2004; Shehzad et al. 2009; Guo et al. 2011; Thomason et al. 2011; Li et al. 2012; Patriat et al. 2013)) between the functional connectivity scores obtained at the first and second session, which quantifies the degree to which the order of observations is similar across both sessions. Modifications in the signal extraction and confound removal methods alters the residual signal fluctuations, which leads to variation in the connectivity measures. Thus, the stability of the relative orders when comparing different connections/subjects was measured using Kendall’s correlations. Complementing this index, we computed the absolute difference between functional connectivity scores to probe the numerical test-retest reliability. This index should be less sensitive to single outliers, in comparison to other alternatives like sum of squared measures. Thus, numerical differences when comparing different connections/subjects was measured using mean absolute differences.

These indices were computed from two different perspectives, reflecting the reliability at the subject level and at connection level, respectively. In that context, reliability at the connection level (RoCO) addresses the question “are, for a given subject, the connections in the same order across sessions?” which was a prerequisite for any within-subject network modeling. We thus computed for each subject the correlation (across connections) between first and second session (Figure 5A) as well as the absolute difference between the two sessions by averaging them over connections (Figure 5C). This perspective thus yields for every approach as many data-points as there were subjects’ within/between the two networks. Reliability at the subject level (RoSO) addresses the question “are, for a given connection, the subjects in the same order across sessions”, which was a prerequisite for group comparisons. Here we computed for each connection the correlation (across subjects) between first and second session (Figure 5B) as well as the absolute differences between the two sessions by averaging them over subjects (Figure 5D). This perspective thus yields, for every approach, the same number of data points, as there are connections in the respective network.

Figure 5.

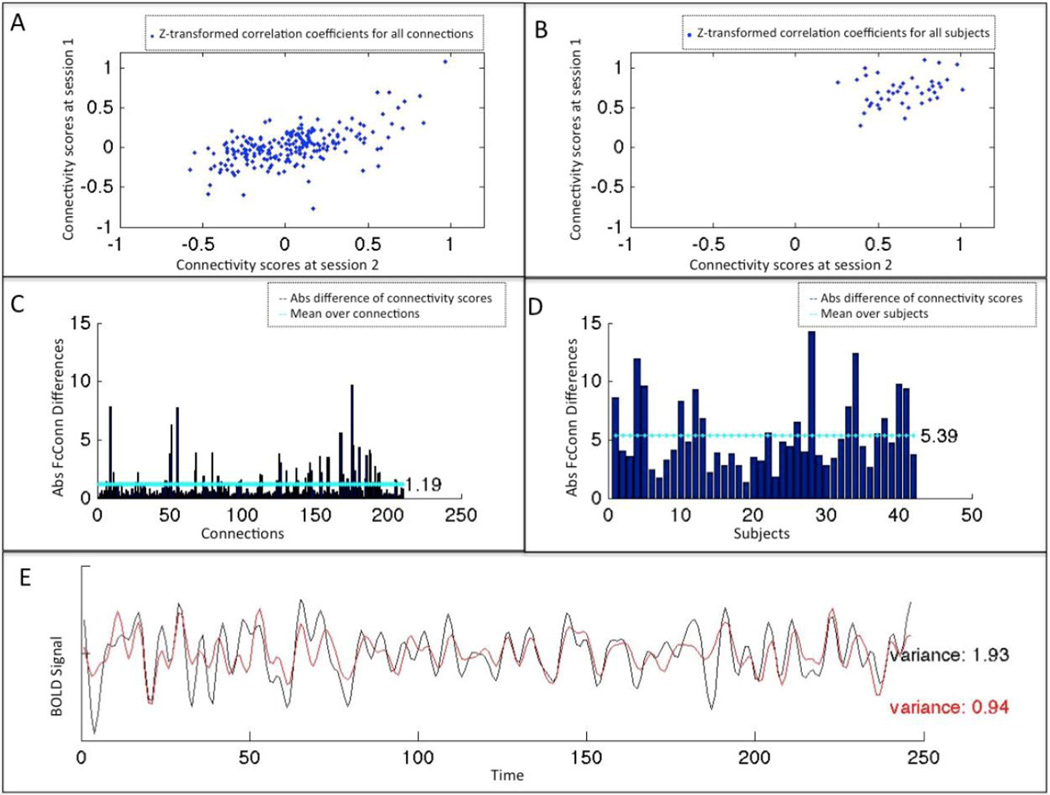
Indices of the reliability: The 4 indices of reliability used here are illustrated. A&B shows functional connectivity at two time points (A) at connection level, i.e. for all connections within a given subject (B) at subject level, i.e. for all the subjects within a given connection. (Here between left and right anterior insula (LaIns - RaIns)). C&D represent absolute differences of functional connectivity scores between the two sessions (C) at the connection level, i.e. the mean of the absolute differences over subjects for the 210 connections, and (D) at the subject level, i.e. the mean of the absolute differences over connections for the 42 subjects. E illustrates the variance within the BOLD signal time series of the left anterior Insula for two different combinations of signal processing methods (“GrpGM NoPCA NoGSR” (black), “NoGM PCA TSR” (red)).

Finally we computed two further important parameters in addition to these indices of reliability. First, the amount of variance within the extracted time series at the two time-points was computed for each combination of methods to quantify the influence of confound removal on the variance of the residual resting-state signal (Figure 5E). Second, for every approach we computed percentage of positive connectivity scores among within-network (i.e., within eSAD and WMN regions) and between-network connections (i.e., between eSAD and WMN regions).

2.5 Aggregation and evaluation

The 42 different approaches defined by the combination of different masking / confound removal approaches were compared using a non-parametric Friedman ANOVA for each of the assessed parameters (correlations and absolute differences, each assessed at subject and connection level (Supplementary figures S5–S7), as well as residual variance in the time-series). In order to aggregate these findings, the individual approaches were ranked according to their reliability scores for each parameter. Subsequently, these reliability ranks were added over the different perspectives to obtain an overall reliability ranking. The overall reliability ranks allowed to identify reliable combination of different confound removal approaches at different perspectives.

2.6 Supplementary analysis

Given that the focus of our study was to investigate, which (combination of) analytical choices result in the best test-retest reliability functional connectivity estimates for meta-analytically defined networks, the main analyses used the entire significant clusters of the previously defined eSAD and WM networks as regions of interest (ROIs). Acknowledging the alternative strategy of representing these ROIs by spheres around their center coordinates, we then repeated all analyses using spherical ROIs of 5 mm radius.

3 Results

The setup of our study allows us to perform a large number of different analyses. We first provide an overview on the test-retest reliability as reflected by the two different measures, i.e., rank-correlations and absolute differences. Here the rankings based on the reliability of subject-order (RoSO) and those based on the reliability of connection-order (RoCO) are combined. Next, we present an overview on the reliability from either perspective, combining the two measures. Finally, we provide the overall summary together with the ranking based on the residual variance in the time-series as well as the information on the proportion of positive vs. negative connections. The individual test retest rankings by the two different methods and different perspectives are presented in the supplementary results (cf Supplementary figures S1–S4).

In addition, we would like to note that we present findings for “within-network” and “between-network” connectivity. The former represents a summary of the rankings obtained for the extended socio-affective default mode as well as the working memory network, each showing strong, positive coupling among their respective nodes. The latter represents the connections between all possible pairs of nodes from either of these two major networks that are often conceptualized as being antagonistic to each other.

3.1 Reliability using different indices

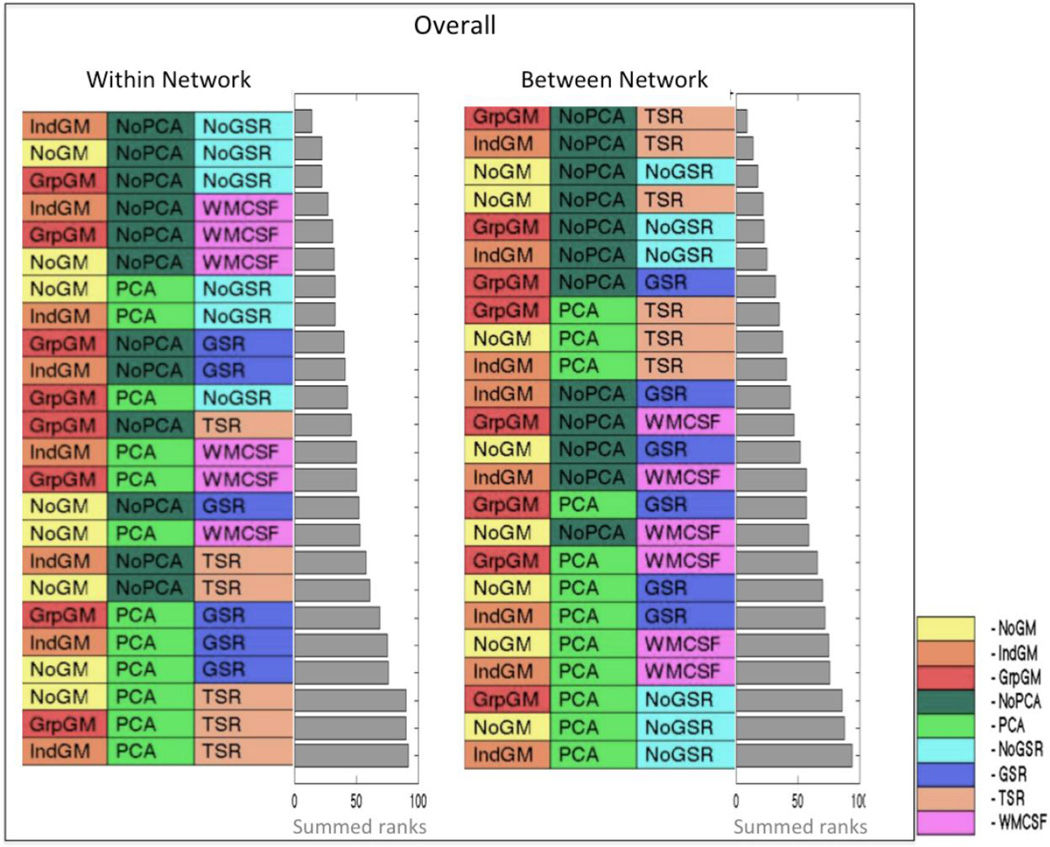
The combined ranks, based on Kendall’s rank correlations as the measure of subject- and connection-order, are illustrated in Figure 6. The approaches are ordered such that the most reliable method is placed on the top, the least reliable on the bottom. It may be noted that for both within- and between-network connections, PCA denoising seems to have a rather detrimental effect on test-retest reliability, as most combinations including PCA denoising rank in the lower half and none is found in the top 10. On the other hand, grey matter masking, which is part of more than half of the ten most reliable approaches, seems to improve reliability. In particular, individual grey matter masking for within-network connections and group grey matter masking for between-network connections provide a better reliability. Global signal removal seems to have detrimental effect on the overall pattern for both within- and between-network connections. No removal again provided the most reliable correlation values for between-network connections. Nevertheless, the rank order stability of within-network connections was improved by removal of WM and CSF signals (WMCSF).

Figure 6.

Combined rankings of the test-retest reliability at the subject and connection level for Kendall’s correlations and absolute differences. The “Within Networks” ranking refers to intra-network connections of the working memory and the default mode network and the “Between Networks” to inter-network connections. The grey bar represents the summed ranks for the respective categories.

The assessment of reliability, by measuring absolute differences rather than measuring the Kendall’s correlations, corroborated most of these observations. In particular, we again found that using grey matter masking and refraining from PCA denoising yielded more reliable estimates of functional connectivity. While this pattern is not as clear-cut as for the correlation-based measure, it again held true for both within- and between-network connections. There is, however, a striking change in the overall pattern with respect to the effects of global signal removal. No removal again provided the most reliable absolute values for within-network connections. Nevertheless, the numerical stability of between-network connections was clearly improved by removing the global signal in all three-tissue classes (TSR).

3.2 Reliability from the subject and connection perspective

As noted in the methods, RoSO assesses how well the relative differentiation between subjects is reproduced at a second time-point and is hence of particular relevance for between-subject analyses, e.g., in clinical application. In contrast, RoCO assesses how well the relative differentiation between connections in a particular subject is reproduced and is hence of particular relevance for within-subject analyses, e.g. in connectome modeling.

Several major trends of reliability noted in the previous section are again well observable in this analysis (Figure 7). In particular, we again found that PCA denoising has a rather detrimental effect on reliability. In contrast, when considering within-network RoCO, PCA denoising has improved the reliability, namely in the absence of global signal regression. Moreover, grey matter masking, in particular when using the mean tissue probabilities across the entire group, generally yields more reliable estimates of functional connectivity. Although, individual grey matter masking is more prominent when considering within-network connections, especially RoCO. With respect to the influence of global signal removal, we again found a more heterogeneous pattern with a clear distinction between within-network and between-network connections. With respect to the former, both RoSO and RoCO are highest when no global signal removal is performed, followed by approaches involving the removal of WM and CSF signals (WMCSF). For between-network connections, linear removal of the global signal for all three-tissue classes (TSR) yields the highest RoSO and RoCO, but for RoCO neither removing any global signal nor performing a PCA denoising yields the highest reliability with no grey matter masking.

Figure 7.

Summary rankings for RoSO and RoCO. Reliability for within network (WMN and eSAD) and between networks is shown separately each combining Kendall’s correlations and absolute difference. The grey bar represents the summed ranks for the respective categories.

3.3 Summary of reliability ranking

The summary ranking across both indices (Kendall’s correlations and absolute differences) and both perspectives (RoSO and RoCO) of reliability reflects the major patterns noted in the individual analyses (Figure 8). Grey matter masking, improves reliability. PCA denoising leads to lower test-retest reliability. Within-network connections are most reliably estimated when using no global signal regression and with removing the global WM and CSF signal representing the next-best approach. In contrast, between-network connections are most reliably measured by linear and second order removal of global signals of all three-tissue classes.

Figure 8.

Summary rankings of reliability across Kendall’s correlations and absolute differences as well as RoSO and RoCO, separately for within (WMN and eSAD) and between networks. The grey bar represents the summed ranks for the respective categories.

3.4 Proportion of positive vs. negative connectivity scores and residual variance in the time series

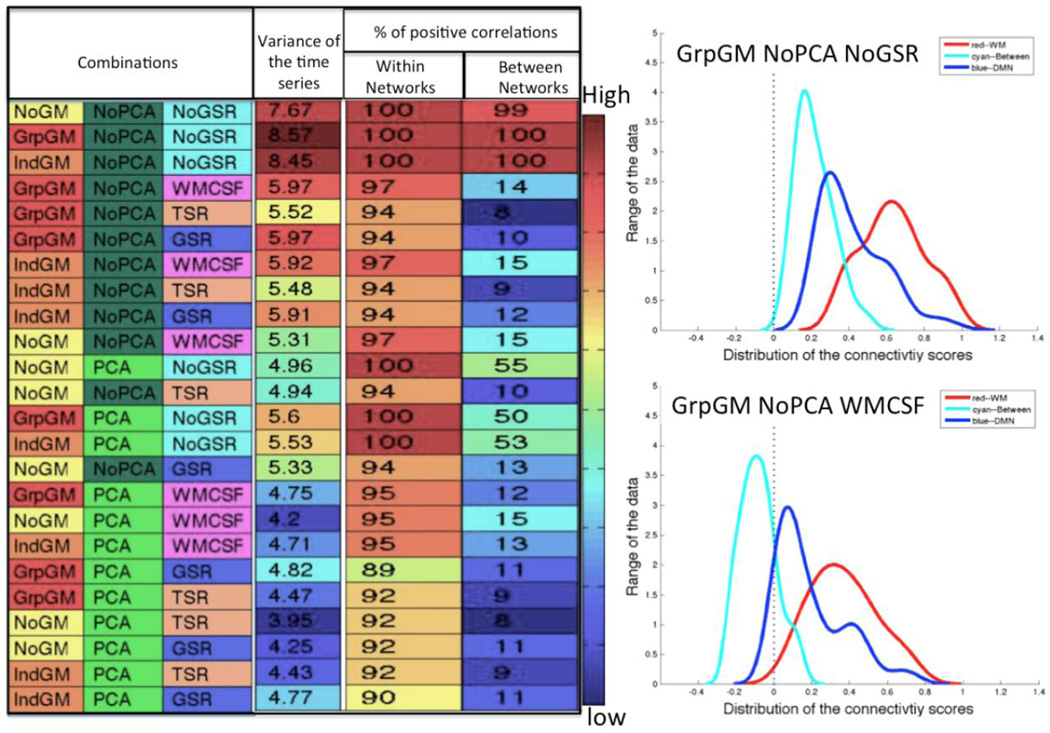
Addressing the issue of anti-correlations, we assessed the proportion of positive vs. negative connections, i.e. connections with r (and hence Z-scores) below zero (Figure 9). As expected, within-network connections are predominantly positive. It is moreover interesting to note that the least reliable approaches, i.e. those at the bottom of the list, also featured (somewhat) less consistent positive connections. The more striking observation, however, relates to the between-network connections. These are consistently negative when any form of global signal regression is used. If neither global signal regression nor PCA denoising are used, however, all connections are positive. Finally, when PCA denoising but no global signal regression is used, roughly half of the connections are positive.

Figure 9.

The variance left within the time series (far left column) and the percentage of positive correlations (columns on the far right) for both within and between networks arranged by the overall ranking of the reliability. The plots on the right side exemplify the difference of the distribution of the connectivity scores at different combinations (“GrpGM NoPCA NoGSR” (Top), “GrpGM NoPCA WMCSF” (bottom))

Assessment of residual variance in the extracted time-series expectedly reveals that refraining from PCA denoising and using no global signal regression retained more variance. Grey matter masking also seemed to perform well with regard to this measure.

3.5 Supplementary analysis

The results of the supplementary analysis conducted using spherical ROIs of 5 mm radius rather than the actual cluster volumes are detailed in the supplementary material. The summary ranking across both indices (Kendall’s correlations and Absolute differences) and both perspectives (RoSO and RoCO) of reliability reflect the major patterns noticed in the main analysis, except for the grey matter masking. The supplementary results associated with the PCA denoising and the mean global signal regression remain the same as in the main analysis. In turn, the supplementary results illustrates that using spherical ROI of 5mm radius (i.e., smaller VOIs) favor No GM masking (cf Supplementary figure S7).

4 Discussion

The key idea behind resting-state fMRI analyses is to estimate functional connectivity between distant brain regions based on the correlation of their BOLD time-series (Biswal et al., 1995; Biswal et al., 1997). The fundamental assumption behind this conceptualization is that the extracted time series reflect the effects of ongoing neuronal computation through hemodynamic coupling, such that correlated signal changes reflect interregional synchronization. However, systematic sources of non-neuronal fluctuations in EPI signals likely influence these functional connectivity estimates (Biswal et al. 1995; Friston et al. 1996; Fox and Raichle 2007; Buckner 2010; Cole et al. 2010). Addressing these non-neuronal signals is therefore a critical consideration in any functional connectivity approach. In the current study, we investigated the influence of various preprocessing approaches meant to deal with this issue, including grey matter masking, PCA denoising, and global signal regression. Our findings are based on investigating two a priori defined networks (the extended socio-affective default mode network and the working-memory network) in a sample of 42 subjects scanned twice, with an average retest-delay of 175 days. We found that grey matter masking based on group-average GM probabilities improved reliability, while confound removal approaches (either PCA denoising or global signal regression) reduced it. However, the study has yielded some mixed results that will be discussed in this section.

Recently, Shirer et al., (2015) investigated a confound removal pipeline that optimizes resting state fMRI data, which is comparable to our study. They performed a reliability study dealing with confound removal combined with various band pass filter selections. In contrast, in the present study, the focus is mainly on seed region time series extraction methods based on different methods for grey-matter masking, combined with various confound removal techniques. There are several additional differences between both studies. Shirer et al., (2015) used 10 components for the PCA model (5 from WM and 5 from CSF) and computed WM and CSF signals using a 3mm radius spherical ROI centered on (arbitrary) WM and CSF regions. In contrast, we here used a 5 components PCA model, noting that 5 dominant principle components have been shown to effectively remove the relevant noise (Chai et al. 2012). Moreover, the mean WM and CSF signal was computed using the entire segmented WM and CSF regions in our study, assuming that signal from small regions may not model the appropriate noise term. In addition, they performed reliability analyses to evaluate the motion parameters, whereas we included them in the standard pre-processing given convincing previous evidence for using a 24-parameter motion regression model (Power et al., 2015; Satterthwaite et al., 2013) and band pass filtered frequencies between 0.01 and 0.08 Hz (Biswal et al. 1995; Cordes et al. 2001; Fox et al. 2005; Zou et al. 2008; Van Dijk, K. R., Sabuncu, M. R., & Buckner 2012; Tsvetanov et al. 2015). Therefore, both studies deal with similar issues but address complementary aspects.

4.1 Different perspectives

Reliability of subjects (RoSO) and reliability of connections (RoCO) represent two fundamentally different views on reliability of resting-state measurements (Gorgolewski et al. 2013). Conceptually, assessing the RoSO allows us to identify which combinations of processing steps that yield a reproducible relationship between subjects for each connection, while RoCO identify the combinations that yield the relationship between different connections in the same subject. RoSO is fundamental for any analysis focusing on between-subject differences. Example applications would include brain-phenotype associations, e.g., the correlation of connectivity estimates with neuropsychological or other behavioral measures (Müller et al. 2014), including clinical analyses comparing patients to healthy control subjects (Zhang and Raichle 2010; Hoptman et al. 2012; Müller et al. 2013). In contrast, RoCO is most relevant when performing any within-subject modeling, either as a primary goal, e.g., when performing connectivity-based parcellation, or in order to compute derivative measures characterizing the individual connectome (Eickhoff et al. 2011; Bzdok et al. 2013; Clos et al. 2013). Examples of the latter include graph-theory-based analyses that compute characteristic network measures from the individual connectome (Shen et al. 2010; Wang et al. 2011; Reid and Evans 2013). In other words, the results from the RoSO are particularly pertinent, when the focus is on group comparison or across-subject associations, whereas the results from the RoCO are relevant when the focus is on the structure of an individual subject’s connectivity matrix.

4.2 Assessed (combinations of) signal processing steps

Here, we addressed the effects of grey-matter masking during the ROI time-series extraction (which has received rather little attention up to now), the influence of PCA denoising (which has at times been suggested but is not commonly used) and global signal regression (which is still highly controversial). The extracted ROI time-series characterizes the temporal dynamics of the selected region as captured by the evoked BOLD response. While ROI time-series extraction plays a key role when studying the regional specific BOLD signal, the respective methods are rarely discussed even though it may affect reliability of subsequent analyses. For example, grey-matter masking is frequently used to restrict signal extraction to grey matter as much as possible, even though the benefits of doing so have not been explicitly demonstrated. In this study, we thus investigated this issue by examining the reliability of various grey-matter masking approaches.

Probably the best-investigated source of spurious variance in RS time-series is head motion (Van Dijk et al. 2012; Satterthwaite et al. 2013; Griffanti et al. 2014; Patriat et al. 2015; Power et al. 2015; Wong et al. 2016). Satterthwaite et al., (2013), using a 24-parameter motion regression approach, found that the first derivative as well as the quadratic effects of both realignment parameters and derivatives could account for these effects. Additionally in this study, the residual signal after removal of the variance associated with confounds variables is band pass filtered between 0.01 and 0.08Hz, which is unfortunately known to be influenced by various noise components (Birn et al., 2006). Niazy et al. 2011 indicated that resting-state networks show temporal correlations across a wide frequency range, even though the resting-state networks are dominated by low frequencies of the BOLD signal. However, there is ample evidence that the BOLD signal which is measured by fMRI and from which functional connectivity maps are derived is dominated by low frequency fluctuations (Biswal et al. 1995; Cordes et al. 2001). Thus, in order to stay in line with standard applications and we followed the well-established standard of band pass filtering and motion regression (Satterthwaite et al., 2013). Furthermore, it has been argued that global signal regression may be beneficial to deal with motion effects (Murphy et al., 2009; Power et al., 2012). In contrast, previous studies addressing the influence of global signal removal (Weissenbacher et al. 2009; Chai et al. 2012; Chen et al. 2012) and those assessing test-retest reliability (Shehzad et al. 2009; Gorgolewski et al. 2013; Birn et al. 2014) used less extensive motion regression protocols. Acknowledging new approaches based on automatically classifying and removing noise components have recently emerged (Behzadi et al. 2007), we here focused on three steps commonly used in settings in which physiological noise recording is not available and data quality is not sufficient for reliable estimation of noise components in individual subjects. Therefore, the paper aims to study the reliability and reproducibility of functional connectivity patterns in “clinical quality” data rather than in optimal datasets with low spatial and temporal resolution as well as physiological recordings.

4.2.1 Grey matter masking during time-series extraction

The time series extracted from an ROI represents the time-varying BOLD fluctuations within that region. Using one of the common approaches (Friston et al. 2006), we computed the first eigenvariate to obtain the characteristic time-series for each ROI that accounts for the largest proportion of the variance in the set of voxel-wise time-series. In general, voxels comprising the ROI may extend into the WM or CSF region, especially for a priori meta-analytically defined clusters, which usually don’t respect the tissue class locations of the subjects under study. However, signals obtained from either WM or CSF voxels are not of interest in the functional connectivity analysis, as they should be of non-neuronal origin. One approach to reduce the influence of these unwanted signals and locally optimize the time-series extraction towards the biologically relevant voxels is to use grey matter masking. In that context, however, a fixed threshold for GM segmentation seems inappropriate, given that it could lead to exclusion of entire regions as well as having no effect in others. Our results indicates that using grey-matter masking when extracting the time series, i.e., considering only those voxels in the ROI that are above the median GM probability, yield more reliable connectivity scores.

Since there are no previous investigations into the effect of performing local optimization of ROIs towards greymatter voxels, we here investigated two different approaches (median split based on the individual and groupaveraged GM probabilities) and compared them to the “baseline” approach of using the entire ROI volume without masking. Factors like head motion could influence the outcome of various GM masks used for time series extraction investigated in this study. Subjects with higher head motion may benefit either less (due to reduced fit) or more (due to poor individual segmentation) from the group-level GM masking. Therefore, the rationale for evaluating both approaches is that individual GM probabilities should best reflect a particular subject’s anatomy after spatial normalization, but comes at the disadvantage of being potentially noisier given that they are based on a single scan. In contrast, group-level GM probabilities should be less specific but more robust. Our results are particularly true when the mean tissue probabilities across the entire group were used. In our view, this not only indicates the beneficial effects of grey-matter masking and hence supports the aforementioned motivation to perform a local optimization, but also suggests that group-level masking, albeit potentially less specific, may be the preferable choice due to increased robustness. In addition, individual GM probabilities produce reliable results for within subject studies. Nevertheless, the segmentations and spatial normalization of the EPI images might be less precise as compared to that of high-resolution T1 images, due to the lower resolution and poorer contrast. This may entail somewhat higher registration inaccuracies, which in turn may have had some influence on the results. A straightforward and more traditional approach for grey matter masking would be to use a population-based a priori tissue mask (e.g. ICBM grey matter map). However, the use of such mask to define grey matter in the ROI may be more sensitive to (systematic) registration errors stemming, e.g., from differences in the studied population to the population that was used to construct the a priori tissue masks. In summary, we would thus recommend the use of a study specific group grey matter mask when dealing with large clusters such as derived from neuroimaging meta-analyses.

Interestingly, a somewhat different pattern emerges when representing the regions of interest not by the full highly-threshold clusters derived from the meta-analyses (cf Table.1) but rather by spheres of 5 mm radius around their peak coordinate (cf Supplementary figures S5–S7). These definitions differ from those used in the main analysis in several aspects. In particular, these spherical ROIs contain a more uniform (compared to the cluster-based ones) and smaller number of voxels. In analyzing the effect of grey-matter masking on these spherical ROIs, we found that no masking yielded the best reliability and would propose two possible explanations (cf Supplementary figures S5–S7). Firstly, the smaller extent of these spherical ROIs most likely yielded a lower proportion of voxels located in WM and CSF, as indicated by a higher mean GM probability, although this is not a criterion for their definition. Secondly, given the smaller size of the spherical ROIs, the performed median-split may have resulted in a critical further reduction of available voxels that renders the results unstable due to session-to-session misalignment, noise, or other factors. As a conclusion, it is advisable to implement grey matter masking for larger, a priori defined clusters based on the group-averaged GM probabilities in order to improve the reliability. In turn, when using smaller, spherical ROIs, no grey matter masking seems preferable.

4.2.2 PCA de-noising

Cleaning the data with PCA de-noising has been introduced by Behzadi et al., (2007) and frequently used since (e.g., Kellermann et al., 2013). In the present study, we performed PCA de-noising by using the time-course of the 5 most dominant principal components as confound regressors, effectively removing signal correlated to these. In an evaluation study, Chai et al., (2012) reported that removing principal components derived from WM and CSF regions is advisable to reduce the influence of physiologically induced artifacts, as components derived from WM and CSF regions are unlikely to include neural activity. In particular, it has been argued that physiologically induced artifacts should be particularly present within WM, ventricles and large vessels (Chang et al. 2009). In addition, PCA de-noising should remove effects that are widely distributed over the brain, including again variance related to physiological sources (Chai et al. 2012). Finally, it is worth mentioning that the 1^st principle component is closely related to the global mean signal.

Our results focusing on test-retest reliability from two different perspectives (RoSO and RoCO), however, indicate that PCA denoising is not beneficial under either perspective, irrespectively of the remaining settings. These findings thus replicate the findings by Power et al. (2014) that PCA denoising does not yield encouraging results. Additionally, Shirer et al., (2015) observed a decrease in test-retest reliability with PCA denoising. We note that, following the proposed method by Behzadi et al., (2007), the main analysis presented here obtain the principal components from the segmented white matter and CSF masks. As an alternative approach, principle components may also be computed from the whole brain mask, i.e., GM, WM and CSF. We thus performed an additional analysis using PCA components derived from the entire brain, but observed similar results to those obtained from using WM/CSF derived components (cf Supplementary figures S8–S10). These results converge with those of Soltysik et al., (2015), which reveal that PCA extracted from whole brain yield similar results to those obtained from using WM and CSF regions. In summary, we would thus argue that PCA denoising has no beneficial effect on the test-retest reliability of RS-FC estimates, at least within the settings evaluated in this study. When investigating resting-state functional connectivity between a priori specified regions of interest refraining from PCA denoising should hence provide the more reliable results.

4.2.3 Global signal regression

Global signal regression, i.e., the removal of variance in the individual voxels’ time-series that can be explained by the average (global) signal across the entire brain has become a controversial topic recently. Historically, it was based on the global scaling approaches utilized in the early (functional) PET studies, which were necessary to allow inference on localized and hence specific changes in blood flow. The key idea behind this approach has been retained in virtually all MRI-based neuroimaging studies, rendering global signal regression a common feature for both task- and resting-state fMRI. Similar to its origins in PET, the purpose is again to facilitate the detection of localized neuronal effects. Using GSR assumes that meaningful effects (reflecting activations or functional connectivity) are based on local variations in neuronal activity. Consequently, global signals, which are thought to mainly originate from physiological rather than neuronal sources, should be treated as a confounding influence. In line with this view, Power et al., (2014) observed that global signal regression is also an effective means of reducing motion-related effects in resting-state fMRI data.

Following the outlined logic, global signal removal has been the standard approach for many years until, more recently, it has been argued (Murphy et al. 2009; Weissenbacher et al. 2009; Saad et al. 2012) that GSR might introduce artificial anti-correlations. Additionally, Chen et al., (2012) quantified the global noise levels and based on the noise level within the data set, they advised to determine whether to include or exclude the global signal regressors based on this information. Ultimately, the issue of whether GSR should be employed or not remains contentious. Likewise, the effects of removing global vs. tissue-class specific mean signals, in particular only those for WM and CSF are still unclear. In the present study, we thus investigated 7 different variants of global signal removal involving global, mean tissue class and mean WM/CSF signal removal at first or second order as well as no GSR.

Regarding the effects of global signal removal on test-retest reliability, our investigation yields somewhat mixed results. Overall, we found that without any mean signal regression yields the highest reliability over both subjects and connections. However, when looking at the results in more detail, it may be noted, that these overall findings are strongly driven by the within-network analyses. Here not removing any GSR clearly yields the most reliable measures of functional connectivity. In turn, estimates for functional connectivity between the two assessed networks (WMN & eSAD) are most reliable when mean signal time courses for all three-tissue classes were removed from the data. Finally, we noted that removing the mean WM & CSF signal seems to provide a good compromise, as this approach yields reliable estimates of within- and between-network connections, although it is not the best approach in either case. Furthermore, Yan et al., (2013b) suggested that global signal regression is nearly identical to grey matter regression. Thus, both the results from Yan et al., (2013b) as well as our present data argue for using only the mean WM & CSF signal (but not the mean grey matter) for nuisance signal regression.

The issue of global signal regression is strongly tied to the question of (spurious or induced) anti-correlations. This is also evident in our data. Without any global signal removal, both within- and between-network connections correlate positively. This indicates that global fluctuations override any potential local anti-correlations. Yet, when variance explained by the global signal or the mean WM & CSF is removed, between-network connections become predominantly negative. That is, only when global changes in the BOLD signal are removed, do the estimated functional connectivity values reflect the repeatedly advocated anti-correlated structure of “task-positive” and “task-negative” networks. Should these thus be considered spurious? One argument against this rather critical view comes from task-based fMRI studies (Greicius et al. 2003; Greicius and Menon 2004), which have clearly shown that regions such as the eSAD reduce their activity during cognitive tasks, which in order recruit fronto-parietal networks such as the working-memory network investigated here. However, global signal removal or, more commonly, scaling is also a standard approach also in task-fMRI (Macey et al. 2004). Another possibility is that global signal may be comprised primarily of non-neuronal sources, rendering the positive correlation between any two parts of the brain in the absence of global signal regression spurious (Murphy et al. 2009). We would therefore argue, that global (positive) correlation and between-network anti-correlations might be considered as two aspects of a more complex situation. In particular, it seems that anti-correlative structures between large-scale networks are superimposed on larger waves of global signal changes, which may be non-neuronal in origin (Fox et al. 2009). Nevertheless, more recently, Schölvinck et al., (2013) suggested that the global signal is tightly coupled to the neuronal signal. In addition, Pisauro et al. 2016 showed that global components in mice are coupled to pupil dilation as a measure of sympathetic function. Thus, they may be partially neuronal and non-neuronal in origin. In such case, removal of global signals likewise acts as a focus on (smaller) local effects of anti-correlated nature while ignoring the large-scale synchronization of BOLD patterns. In turn, not removing any global signal would preserve the latter and hence bring the positive relation between all time-series that is present in the acquired data into focus.

4.3 General discussion

When assessing the test-retest reliability of resting-state fMRI connectivity estimates, one unlikely but still important caveat must be considered. It is possible that increased reliability, i.e., higher correlation and lower absolute difference, will be caused by excessive removal of variance. In the extreme case, when the time-series would be reduced to a flat line, test-retest reliability would be perfect. But also beyond this hypothetical extreme case, the relationship between reliability and variance is interesting; as it sheds light on the question to what extent our methods remove noise (in that case residual variance and reliability would be positively related) or relevant signal (which would render the relationship negative). In our assessment, we found that methods providing results that are more reliable also feature higher residual variance within the extracted time series (Figure 9, the correlation between residual variance and reliability scores is 0.87) Therefore, reliability seems proportional to the retained variance, reinforcing the observations by Birn et al., (2014) and Yan et al., (2013a).

Another point to consider is the relationship between reliability and validity. The underlying idea of all preprocessing approaches is to remove variance in the data that may be attributable to noise or, more generally, non-neuronal sources. This naively assumes that more aggressive confound removal should increase the biological validity of the obtained results. However, this assumption has been challenged, most notably with respect to global signal regression. Here it has been argued that removing global signal as a confound may actually introduce a bias in the analysis (Murphy et al. 2009; Weissenbacher et al. 2009; Saad et al. 2012), that may lead to reduction in validity. Conversely, the argument has been made that global signal regression is the most effective approach to remove the effect of motion-related variance (Power et al. 2014) and hence should increase validity. This already illustrates that the relationship between data preprocessing, and in particular confound removal, and validity is not trivial. The present results add another layer of complexity by showing, that refraining from using global signal regression and PCA denoising, i.e., using less confounds removal, actually lead to better test-retest reliability. In other words, removing variance that is related to potentially confounding factors reduces reliability, pointing to the possibility that structured noise may be beneficial for test-retest reliability. And indeed, it may be assumed that vascular of physiological factors remain largely stable between sessions and hence help to increase reliability, even though their removal should, in theory, improve the validity of the results. Maximizing (test-retest) reliability and biological specificity / validity may hence represent (partially) conflicting aims.

The functional connectivity strength (i.e., correlation coefficients) between regions might vary with changes in the level of observation noise (Friston 2011). In this study, two resting-state networks (eSAD and WMN), which may be considered as robustly a priori defined resting state networks has been chosen, with prior assumptions such as strong positive coupling among them and anti-correlated with each other (Fox et al. 2005). When there isn’t any change in the observational noise, then the functional connectivity strength (i.e., correlation coefficients) are expected to be stable (Friston 2011). Therefore, instead of quantifying the connectivity strengths, we mainly focused on reproducibility of the connectivity strength with a certain confound removal within a subject from one session to another session. Furthermore, following the current standard in the field, our study quantified functional connectivity by the Pearson correlations between the time-series of two regions. Consequently, other regions within or outside the network could influence such correlations. Such influences, however, were not specifically investigated, given that they should be likewise present in both sessions and, most importantly, the focus of our work is to provide an assessment of how the reproducibility of the widely used time-series correlation measures are based on different approaches to confound removal. That is, we here addressed the pragmatic question, which confound removal strategy yields the highest reliability for a standard analysis approach, rather than addressing which analysis approach may yield the most appropriate representation of a network. Evidently, more investigations are needed to better understand the sources of both noise and signal in resting-state fMRI data, a question that is complicated by a lack of ground truth. Nevertheless, the current results thus point to a potential trade-off between reliability (which may benefit from structured noise) and biological validity (which should be optimal if all non-neuronal variance is removed (Huettel et al. 2004; Chang et al. 2009; Kim and Ogawa 2012). Based on the present results, we would thus tentatively propose that in cases in which reliability should be of particular importance, for example in clinical applications, it may be advisable to refrain from global signal regression and PCA denoising to maximize the reliability albeit potentially through the influence of structured noise.

ICA based denoising is one of the recently emerging confound removal approaches. A recent study showed that it can effectively remove the artifacts coupled with motion (Pruim et al. 2015b) and potential other sources of noise (Griffanti et al. 2014). The entire resting-state scan is decomposed into independent components (IC) (using FSL melodic, http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/MELODIC). ICs coupled with various artifacts were identified with the help of a classifier. ICs classified as noise is then regressed out of the raw fMRI time series. Thus, ICA based denoising aims to automatically classify and remove the components representing mostly noise rather than neuronal signal (Salimi-Khorshidi et al. 2014; Pruim et al. 2015b). The effectiveness of the strategies mainly depends on the feature selection and the sensitivity of the classifier, as these parameters play a major role in identifying the artifactual signals. In recent evaluation studies, ICA based denoising strategies resulted in an increase of the between subjects reproducibility (Griffanti et al. 2014; Pruim et al. 2015a). In the current study, however, we did not address ICA based denoising approaches, as we mainly focused on the currently most widely used approaches. In turn, ICA based denoising is a very promising but yet emerging approach as also demonstrated in our survey. Therefore, further investigations are needed to address the reliability of ICA-based approach both in comparison to and in combination with conventional confound removal strategies. Along with it, there are methods that mainly address local and global artifacts induced by the hardware and Partial volume effects (Such as: ANATICOR (Jo et al. 2010; Jo et al. 2013)). As the current study mainly studied the influences of biologically induced artifacts, methods like ANATICOR were not addressed here. Furthermore, it has been observed from the literature survey (Figure 1) that ANATICOR (which has been reported in the categories named ‘others’) is not a standard method and poorly used in the recent studies.

In this study, the connectivity measures were obtained with standard Pearson correlations. Other approaches have also been applied to this computation, with partial correlation becoming an increasingly advocated alternative (Cole et al. 2010). Partial correlation computes the correlations between two ROIs after regressing out the shared variance of all other ROI time series in the model. However, we are here concerned with testing the effects of several widely used analysis-choices on the reliability of the most common approach. So given that the overwhelming majority of all resting-state analyses employ full correlations, we here performed a practical evaluation of the impact of currently debated analyses choices on the estimation of functional connectivity by Pearson correlations. Nevertheless, testing the test-retest reliability using partial correlation could be one perspective study of the current one. Furthermore, the subjects were instructed to close their eyes during the resting state session, in order to reduce the external (visual) stimulation and eye movements. All the subjects included in this study had confirmed to be awake while debriefing. The condition of Eyes closed (EC) may be considered as a limitation of the study, as Patriat et al. 2013 showed higher reliability with Eyes open (EO) condition rather than eyes closed (EC) condition. However, Patriat et al. 2013 also reported that the connectivity strengths are not sensitive to the global noise variations. Therefore, further investigations of reliability of EO & EC with and without global noise regression are needed to provide recommendations regarding this parameter. Finally, it has to be noted that the recommendations in this paper may not necessarily apply to brain-behavior analysis examining the relationship between behavioral measures and functional connectivity measures. That is, we here focused on a priori defined meta-analytical networks and their (known) relationships to each other as large-scale anti-correlated systems in the human brain (Fox et al. 2005). What remains to be assessed using a dedicated sample for which test-retest data not only of imaging measures but also behavioral information is available is this, whether the methods yielding the best reliability in our analysis also provide the most reliable brain-behavior relationships. Likewise, it remains to be tested, whether the identified recommendations also hold for multivariate analyses, e.g., in the context of group classification.

5 Conclusions

The present study assessed test-retest reliability of resting-state fMRI analyses based on a priori ROIs using methods that are applicable without direct recordings of physiological signals (heartbeat, breathing), as is common in clinical and neuro-scientific practice. In particular, our results showed that, when using the larger clusters as regions of interest, grey matter masking based on the group-average GM probabilities is advisable. However, In addition, PCA de-noising reduces the reliability of connectivity estimates. Finally, with respect to global signal regression, we observed that refraining from this approach enhances test-retest reliability but comes at the expense of potentially poorer biological validity, including missing anti-correlations between what has been previously described as antagonistic networks. Here removal of global white matter and CSF signals seems to provide a good compromise, as this approach yielded more reliable and potentially meaningful estimates of within- and between-network connections. Importantly, we note that reliability is proportional to the retained variance, presumably including structured noise. Consequently, a compromise exists between maximizing the test-retest reliability and removing variance that may be attributable to non-neuronal sources.