Shaped and Feedback-Controlled Excitation of Single Molecules in the Weak-Field Limit

Abstract

Coherent control uses tailored femtosecond pulse shapes to influence quantum pathways and drive a light-induced process toward a specific outcome. There has been a long-standing debate whether the absorption properties or the probability for population to remain in an excited state of a molecule can be influenced by the pulse shape, even if only a single photon is absorbed. Most such experiments are performed on many molecules simultaneously, so that ensemble averaging reduces the access to quantum effects. Here, we demonstrate systematic coherent control experiments on the fluorescence intensity of a single molecule in the weak-field limit. We demonstrate that a delay scan of interfering pulses reproduces the excitation spectrum of the molecule upon Fourier transformation, but that the spectral phase of a pulse sequence does not affect the transition probability. We generalize this result to arbitrary pulse shapes by performing the first closed-loop coherent control experiments on a single molecule.

With the advent of femtosecond technology, it has become not only feasible to study molecular relaxation and vibration in real time,¹ but also to control molecular processes by tailoring the shapes of femtosecond excitation pulses.²⁻⁷ A particularly intriguing and intensely debated approach to coherent control investigates the degree to which the molecular response can be manipulated already during the interaction with a single photon.⁸⁻¹⁴ Such weak-field coherent control between molecular states could provide new approaches to quantum computing¹⁵ and may even enable an understanding and control of biological processes at excitation intensities similar to natural conditions.^9,16 Coherent control theory originally considered it impossible to change the outcome of a light-induced process by manipulating the spectral components or phase of a single photon.¹⁷ On the other hand, seminal experiments with phase-locked pulse pairs on molecular iodine revealed spectroscopic signatures consistent with interference between nuclear wavepackets, analogous to Young’s double slit experiment.¹⁸ The use of collinear, isoenergetic pulses, however, made the experiment subject to spectral interference already in the excitation field, which can explain the observed intensity oscillations by solely considering the spectral overlap of the modulated excitation spectrum with the molecular absorption spectrum. Subsequent experiments on retinal in bacteriorhodopsin,⁹ rhodamine 101,⁸ and coumarin 6¹¹ employed genetic algorithms to search for more complex optimal pulse shapes, and reported significant active control as a function of the incident light field. In the case of bacteriorhodopsin, the authors attributed changes in isomerization yield to control of wavepacket motion on the excited state. The contradiction with previous coherent control theory was later alleviated by invoking dissipation¹⁰ or the noncommutation of the isomerization outcome with the molecular Hamiltonian.¹²

A shortcoming of all the above control approaches is that they act on the average response of an ensemble of chromophores. Single molecule microscopy has revealed that photophysical properties often vary from molecule to molecule,^19,20 so that full control could only be reached if the pulse shape is tailored to each absorber individually. A simple example is the effect of inhomogeneous broadening: differences in the Franck–Condon factors of the individual molecules lead to variations in the vibronic wavepacket evolution after excitation. Experiments in solvents of different viscosity suggested that dephasing is the main limiting factor for control in an ensemble.¹¹ In addition, it is not always trivial to distinguish intramolecular pathways from ensemble interactions or collective effects,²¹ and while some response phenomena like synchronized oscillations may be studied in ensembles, other effects like stepwise bleaching, blinking, and spectral diffusion are only visible for a single molecule.¹⁹ Experiments on the single molecule level probe the purest accessible quantum system and coherent control approaches could in principle take advantage of unknown quantum pathways, which are not distinguishable in the ensemble. Hence, there have been continuous efforts to perform coherent control experiments at the single-molecule level.²² Such experiments on one molecule at a time currently have to rely on fluorescence detection, in which the background can be suppressed with spectral filters. Up to now, several pulse pair schemes have been applied to single dye molecules,²³⁻²⁷ and light harvesting complexes.¹⁶ In the strong interaction regime, ultrafast emission changes have been discussed in terms of saturation effects^23,24 and strongly damped Rabi oscillations.^25,26 In the weak-field, one-photon, regime a modulation of single fluorophore emission was observed when changing the interpulse delay and ascribed as in the case of the original iodine experiments¹⁸ to wave packet interference.^16,27 A systematic investigation of the effect different pulse shapes have on a single molecule were up to now out of reach, and the use of closed optimization loops to search a wider parameter space was even deemed impossible on the single-molecule level.²²

Here, we present a versatile and robust experimental approach to comprehensively investigate the effect of spectral phase and pulse shape of femtosecond excitation on the emission intensity of a single fluorescent molecule in a crystalline matrix in the weak-field, one-photon limit. We quantitatively compare the result of different pulse shapes in open-loop experiments on the same molecule, both in the time and in the frequency domains, and disentangle effects of the absolute spectral phase from amplitude modulations caused by spectral interference. As a general test for phase shaping in the one photon limit, we present the first closed-loop coherent control experiments on a single molecule at room temperature.

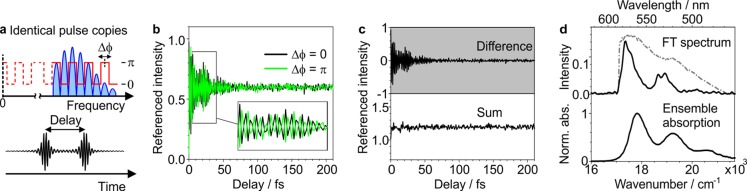
We use terrylene molecules embedded in a p-terphenyl matrix, a single-molecule system with high photostability under ambient conditions.^28,29 We begin with the conceptually simplest pulse shaping experiment, in which we excite a single molecule with a pair of identical phase-locked pulses of 12 fs duration. To achieve this, we use a spatial light modulator (SLM) that acts on the pulse in the frequency domain by applying a cosine amplitude mask |cos([2π(ν – ν₀)τ + Δϕ]/2)| and a square wave phase mask π/2[sgn (cos([2π(ν – ν₀)τ + Δϕ]/ 2)) + 1] to the SLM (Figure 1a), where ν is the optical frequency, τ is the delay, and Δϕ is the phase difference of the pulses at ν₀.^30,31 When scanning the interpulse delay τ in subcycle (0.7 fs) steps for ν₀ = 0, we observe rapid oscillations in the detected single molecule fluorescence intensity (Figure 1b). Changing the phase difference from Δϕ = 0 to Δϕ = π for the same molecule inverts the sign of the oscillations, as observed in previous pulse pair experiments.²⁷ By forming the difference and the sum of the phase-cycled traces, we separate the phase-dependent oscillations from the phase-independent background (Figure 1c). The duration of the time-dependent variations in fluorescence intensity far exceeds the temporal overlap of the excitation pulses alone, indicating that it is also a function of the molecular properties and indeed the linear autocorrelation trace of the excitation process. Accordingly, an inverse Fourier transform yields the single-molecule fluorescence excitation spectrum (Figure 1d, top). The resulting spectrum resembles the ensemble absorption spectrum of terrylene in toluene (Figure 1d, bottom), but interaction with the p-terphenyl matrix introduces a 460 cm^–1 red-shift, and the single-molecule spectrum reveals more detail in the band structure likely due to the absence of inhomogeneous broadening.

Figure 1.

Femtosecond pulse pair experiment on a single molecule. (a) Schematic illustration of the electric field of the pulse in the frequency and time domains, with the spectral phase given in red. (b) Delay-dependent single molecule fluorescence for phase differences of Δϕ = 0 and Δϕ = π between the pulses. (c) The difference and sum of the traces in b separate the phase-dependent part from the phase-independent background. (d) Fourier transformation of the difference trace yields the single molecule fluorescence excitation spectrum (top, black). Overlaid is the spectrum of the excitation pulse (dashed gray). Bottom: Ensemble absorption spectrum of terrylene in toluene.

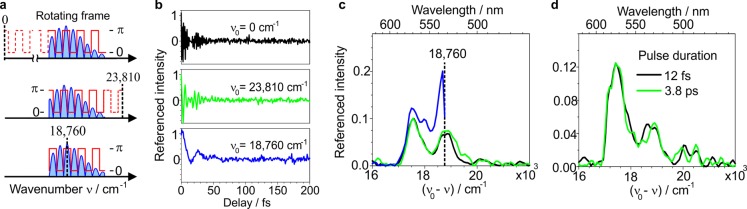
The rapid oscillations of the fluorescence signal in Figure 1 can here be directly identified as pure interference from the correspondence with the optical frequencies of the absorbed light. The appearance of the detected fluorescence modulations changes drastically as the phase locking frequency ν₀ approaches the absorption center of mass (Figure 2a,b), since setting a nonzero phase locking frequency ν₀ is equivalent to performing the experiment in a rotating frame—an effect exploited in Fourier transform spectroscopy to reduce the required sampling rate for acquisition.³²⁻³⁴ Measurements on the same single molecule with different phase locking frequencies ranging from ν₀ = 0 to ν₀ = 23 810 cm^–1 (420 nm) and ν₀ = 18 760 cm^–1 (533 nm) exhibit oscillations with decreasing frequencies (Figure 2b), but are almost indistinguishable in the inverse Fourier transform when displayed on a frequency-corrected axis (Figure 2c). Choosing the locking frequency within the excitation band reduces the extractable information, because it mirrors spectral intensity about the locking frequency so that only the sum of components above and below ν₀ is obtained.

Figure 2.

Pulse pair experiments in the rotating frame, and the effect of pulse duration. (a) Changing the phase locking frequency ν₀ (dashed black line) shifts the origin of the periodic amplitude (blue) and phase (red) modulation for the same delay scan. (b) Fluorescence intensity difference traces (cf. Figure 1c) for three different phase locking frequencies. (c) Fourier transform spectra of the fluorescence traces on a frequency-corrected axis. (d) Effect of pulse duration on the Fourier transform (fluorescence excitation) spectrum.

The experimental observation of oscillation periods for ν₀ = 0 much shorter than the incident pulse duration suggests that the femtosecond nature of the excitation pulses may not be critical for the occurrence of the reported fluorescence modulations. Indeed, repeating the experiment in the presence and absence of a glass block, which chirps the pulses from 12 fs to 3.8 ps, shows no measurable effect on the observed oscillations, as evidenced by the Fourier transform spectra in Figure 2d and the corresponding delay traces in Supporting Information Figure 8. Hence, while the fluorescence intensity oscillations are sensitive to the phase difference between the pulses they appear to be insensitive to the absolute spectral phase of the pulses.

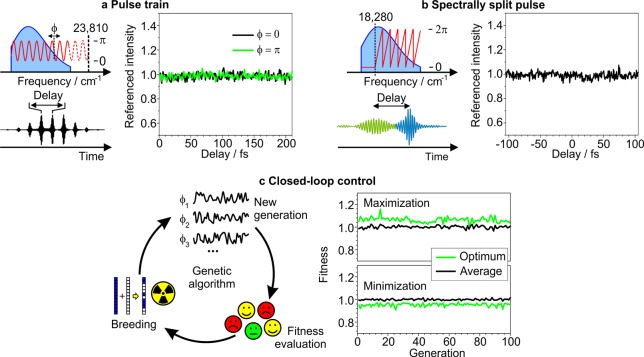
In order to corroborate the independence of the excitation probability on the spectral phase, we conduct additional phase-only shaping experiments (Figure 3). First, we apply a spectral phase oscillation π sin(2π(ν – ν₀)τ + ϕ), for which we set ν₀ to 23 810 cm^–1 and the phase ϕ either to zero or π (Figure 3a). In the time domain, the electric field splits into a multipulse with equally spaced interpulse delays τ, but without net spectral interference,³⁵ and fluorescence detection ensures that subpulse interference effects as reported in transient absorption measurements are averaged out.³⁶ In a delay scan experiment, the recorded fluorescence intensity is independent of the interpulse delay and the oscillation phase ϕ (Figure 3a). Spectral interference can also be avoided if the two pulses of a pulse pair have nonoverlapping spectra. Such an experiment should expose interference effects mediated by the molecule. We therefore split the original pulse into two spectrally distinct pulses by delaying the components above ν₀ = 18 280 cm^–1 (547 nm) with a linear phase of slope τ, wrapped to the range 0–2π (Figure 3b). We choose the splitting frequency ν₀ to lie between the first two absorption maxima, so that both pulses together can excite a vibrational superposition of the strongly Franck–Condon active backbone stretch. As previously, the resulting trace does not exhibit any modulation upon changing the interpulse delay (Figure 3b). We do not find oscillations as reported for coupled excitonic transitions in light harvesting complexes.¹⁶ Instead, the lack of delay-dependent effects matches the results on individual exciton bands presented in the Supporting Information of ref (16).

Figure 3.

Effect of phase-only shaping on single-molecule fluorescence intensity. (a) Phase oscillations (red) in the frequency domain produce an equally spaced pulse train in time domain. The interpulse delay is scanned for two different oscillation phases ϕ. (b) The pulse is spectrally split at 18 280 cm^–1 (547 nm), and the blue part is delayed by a linear phase wrapped between 0 and 2π. (c) In a closed loop approach, a genetic algorithm varied the phase mask to selectively maximize or minimize the fluorescence intensity. The algorithm has a genetic pool of 40 initially random phase masks ϕ₁, ϕ₂, ϕ₃..., for which in each generation the fitness is evaluated as the ratio of fluorescence intensity with the phase mask to be tested and with a spectrally flat phase mask. The genetic pool is modified by fitness-based breeding steps. The traces show the optimum and average fitnesses of all individuals in each generation. The optimum fitness intrinsically deviates from unity even with no control effect, because the algorithm selects the outer values of a normal distribution.

Finally, we perform a closed-loop optimization experiment with a genetic algorithm to probe if any nontrivial phase masks are capable of changing the excitation probability at the single molecule level (Figure 3c). The resulting traces indicate that even though we can determine the optimum fitness with a noise level of 2% rms of the detected signal, the algorithm does not identify any phase masks, which can significantly enhance or diminish the fluorescence intensity.

Fluorescence monitors the total population transfer from the ground to the excited state, and our experiment is analogous to single-molecule and ensemble studies on other simple laser dyes, which reported coherent population control in the weak-field regime.^8,11,27 Population control in such systems would either affect the absorption process itself,^18,27 or manipulate the nonradiative coupling of ground and excited states by directed wavepacket motion.¹¹ Our experimental results are consistent with an intuitive model describing the excitation of a molecule in the weak-field limit by its intrinsic absorption properties alone. When employing pulse forms that lead to net spectral interference, the spectral overlap of the intensity beating pattern with the absorption spectrum controls the excitation efficiency of the molecule (Figure 1). The result would qualitatively not change when normalizing to the total excitation intensity. In this picture, a delay scan experiment is analogous to other interferometric techniques, which depend on the phase difference but not on the absolute spectral phase of the incident pulses. The resulting oscillating fluorescence signal is a linear autocorrelation trace, which converts to the single-molecule fluorescence excitation spectrum upon inverse Fourier transformation. The same result would have been obtained by recording the fluorescence intensity while scanning a monochromatic laser over the absorption band.³⁷ Choosing an appropriate rotating frame can down-sample the fast optical oscillations into the regime commonly expected for molecular vibrations, but the observations are not affected by the incident pulse duration (Figure 2d) and, thus, do not directly represent excited or ground state nuclear wavepacket motion. This interpretation is confirmed by pulse shaping experiments that are not subject to spectral interference, none of which exhibit a phase-dependent fluorescence intensity and thus excitation probability (Figure 3). These results emphasize the importance of experimentally avoiding optical interference effects when investigating the feasibility of coherent control approaches.

Femtosecond time-resolved measurements on the single-molecule level pose a great experimental challenge, and linear multipulse experiments have been proposed as alternatives to nonlinear approaches like transient absorption spectroscopy commonly employed in ensemble studies.²² Our results show that for systems such as ours, linear measurements do not contain information about molecular relaxation beyond what is obtainable from stationary spectroscopy. Nuclear wavepacket evolution can be deduced from the vibrational progression in the absorption spectrum,³⁸ but we do not find any spectral phase to control this motion in a way to modify the excited state population.

The population of a system eigenstate commutes in contrast to the outcome of the isomerization result in bacteriorhodopsin with the system Hamiltonian, so that, according to the current theoretical understanding in such a case, phase control in the weak field limit has to be mediated by coupling of the system and bath modes.^10,12−14 Weak-field population control of the excited state as sought in this study was reported before for similar stable fluorescent dyes: for the terrylene homologue dinaphtoquaterrylenebis(dicarboximide) (DNQDI)²⁷ as well as for rhodamine 101⁸ and coumarin 6.¹¹ In our case, the crystalline matrix provides a well-defined environment, for which indications of light-induced coupling between chromophore modes and p-terphenyl ring torsion modes have been found.^39,40 Hence, the system is not a priori less suited to weak-field coherent control than the other strong fluorophores investigated previously.^8,11,27 In fact, the vibrational progression in the absorption spectrum of terrylene indicates extensive wavepacket oscillation compared to the relatively featureless absorption of, for example, rhodamine 101. On the other hand, terrylene in p-terphenyl can be regarded as a model for dye molecules in a nonpolar medium. The lack of any phase control suggests that the nonpolar interactions of terrylene with the p-terphenyl matrix are too weak to support phase control. As for the nature of the system, the polarity and nature of the solvent alone cannot be the reason for the absence of phase control, since weak field coherent control has been reported in various polar^8,25,27 and nonpolar¹¹ solvents.

We conclude that coherent population control in the weak-field limit is not a generally applicable approach: It is not sufficient to tailor the pulse shape alone, but—if possible at all—it also requires fine-tuning of the chromophore-bath interactions, which operate on much shorter time scales than fluorescence emission.

Experimental Methods

Visible 12 fs pulses covering the range of 470–595 nm (gray in Figure 1 d, top) at an 8 MHz repetition rate were provided by a home-built white light laser detailed in the Supporting Information. Spectral phase and amplitude of the excitation pulses were controlled with a spatial light modulator (Jenoptik SLM-320d) in a grating-based 4f setup, which was used in double-pass geometry to avoid spatiotemporal coupling artifacts.⁴¹ The single-molecule samples were prepared according to the spin-coating procedure described in ref (28). Single aligned terrylene molecules were excited by focusing the s-polarized excitation beam with a reflective objective (Newport, 0.52 NA) via a pick-off mirror at 75 degree incidence angle onto the sample. The illumination was kept at a power density below 30–100 W/cm² in all experiments. A 1.42 NA objective (Olympus PLAPON 60×) collected the fluorescence, which was then focused onto an EM-CCD camera (Andor iXon3) to produce wide field images of the sample with 300× magnification. A combination of a 3 mm wide beam block and spectral filters (Thorlabs FELH0600/FEL0600, SEMROCK FF02-617/73-25) suppressed excitation light background. Delay traces report the total fluorescence intensity of an isolated emitter, averaged over 40 to 100 scans with 100 ms exposure per delay time. Typically, a maximum of 2000 photons/s were collected per molecule, which corresponds at an estimated 5% detection efficiency⁴² and close to unit quantum efficiency to on average 0.005 excitations per laser shot and a Poissonian probability for double excitation of only 10^–5 per pulse. All intensities are presented relative to the emission with compressed pulses. As a result, in amplitude-shaping experiments, a small offset occurs due to limited shaping contrast. For the measurement in Figure 2d, pulses were chirped by passing them through 2.5 cm of SF1 glass (Thorlabs). The closed-loop coherent control experiments used a genetic algorithm based on a selection-round system detailed in the Supporting Information. The spectral phase was parametrized into 3.2 nm spaced values, which were then connected with cubic spline interpolation. The fitness of an individual was defined as the fluorescence intensity relative to a reference measurement with a flat spectral phase. The optimum fitness intrinsically deviates from unity even with no control effect, because the algorithm selects the outer values of a normal distribution and divides through the statistical average. Further experimental details are given in the Supporting Information.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.5b01748 The data underpinning the results presented in this manuscript can be accessed free of charge at http://ora.ox.ac.uk.

• Experimental Details: The 8 MHz white light source, pulse characterization, single molecule excitation, background correction, confirmation that single molecules were studied, Fourier transformation, the genetic algorithm, and test of the genetic algorithm performance. Effect of pulse duration on a pulse pair experiment: additional results. Single-molecule weak-field excitation in the Liouville picture. (PDF)

The authors declare no competing financial interest.