Comparative analysis of system identification techniques for nonlinear modeling of the neuron-microelectrode junction

Abstract

Applications of non-invasive neuroelectronic interfacing in the fields of whole-cell biosensing, biological computation and neural prosthetic devices depend critically on an efficient decoding and processing of information retrieved from a neuron-electrode junction. This necessitates development of mathematical models of the neuron-electrode interface that realistically represent the extracellular signals recorded at the neuroelectronic junction without being computationally expensive. Extracellular signals recorded using planar microelectrode or field effect transistor arrays have, until now, primarily been represented using linear equivalent circuit models that fail to reproduce the correct amplitude and shape of the signals recorded at the neuron-microelectrode interface. In this paper, to explore viable alternatives for a computationally inexpensive and efficient modeling of the neuron-electrode junction, input-output data from the neuron-electrode junction is modeled using a parametric Wiener model and a Nonlinear Auto-Regressive network with eXogenous input trained using a dynamic Neural Network model (NARX-NN model). Results corresponding to a validation dataset from these models are then employed to compare and contrast the computational complexity and efficiency of the aforementioned modeling techniques with the Lee-Schetzen technique of cross-correlation for estimating a nonlinear dynamic model of the neuroelectronic junction.

1. Introduction

Development of technology for non-invasive interfacing of live neurons to electronic devices has important applications in the fields of prosthetic devices, biological computation and whole cell-biosensors for high-throughput drug screening and toxin detection ^1–6. All these applications, in turn, depend critically on an efficient decoding and processing of the information exchanged between the neuron and the electronic sensor device. However, non-invasive extracellular recordings from neurons interfaced to microelectrode and field effect transistor arrays also suffer from problems of low signal to noise ratio, signal attenuation due to counter-ion diffusion from the bulk extracellular medium into the ~20–110 nm wide neuron-electrode cleft and a modification of the shape of the neuron-generated potentials. Therefore, it is important to develop or estimate computational models of the neuron-electrode interface that can efficiently simulate or model the neuron-electrode junction and predict its output despite these problems.

Primarily, to date, linear point or area contact equivalent circuit models have been employed for modeling the neuron-electrode interface. Equivalent circuit models, however, fail to reproduce the correct amplitude and shape of the extracellular signals recorded using planar microelectrode or field effect transistor arrays ^{7, 8}. Therefore, researchers have recently started to explore the development of models that incorporate the physics of electrodiffusion of ions at the neuron-electrode interface ^7–9 with the aim of developing and implementing strategies for engineering the neuron-sensor interface using surface chemical modification of the electrode surface, microelectrode design or novel electrode materials ^10–15. The physics of electrodiffusion of ions is governed by the Poisson-Nernst-Planck system of equations that are time-dependent coupled nonlinear partial differential equations. However, this system of equations does not lend itself to computationally inexpensive simulation or analytic solutions for representing the dynamics of the neuron-electrode interface. Although important for advancing an understanding of the mechanism of signal transduction at the neuron-electrode interface and to engineer it for a better signal to noise ratio, such an approach cannot be adapted for a real time modeling of the neuron-electrode junction for applications in whole-cell biosensing, biological computation or neural prosthetic devices. Therefore, it becomes imperative to develop computationally efficient alternate models for representing signals recorded at the neuron-electrode interface. Nonlinear dynamic models of the neuron-electrode interface estimated using system identification techniques through a use of the experimental input-output data recorded from the neuron-electrode junctions are, we believe, particularly well poised to provide such an alternative.

In this regard, it is notable that an experimental stimulation of the neuron-electrode junction with band-limited white noise was recently employed to estimate a non-parametric ‘data-true’ Volterra-Wiener (V-W) model of the neuroelectronic interface ¹⁶ using Lee-Schetzen cross-correlation technique ¹⁷. The estimated V-W model represented the complete nonlinear dynamics (up to second order) of the interface that accounted for all possible linear and nonlinear physicochemical processes, including electrodiffusion of ions and dielectric relaxation of the interfacial medium, occurring at the interface in response to the neuron generated electric signals. Furthermore, the estimated first and second order V-W kernels, representing the linear and nonlinear impulse response of the neuron-electrode junction, yielded an excellent prediction of the extracellular output recorded on the planar microelectrode corresponding to an intracellular action potential ¹⁶. However, the computational complexity for an estimation of the V-W kernels using cross-correlation of the input band-limited white noise with its corresponding extracellular output recorded at the planar microelectrode scales up as O(N^p) for a system characterized by memory length N and order of nonlinearity p. Besides, it also requires very long data records (up to 100 seconds at a sampling rate of ~10 kHz) from the neuron-electrode junction to achieve a reasonable convergence of the V-W kernels. As a consequence, the use of the Lee-Schetzen cross-correlation technique to model the neuron-electrode junction proves to be computationally very expensive and inefficient. This paper follows up on the work reported by Thakore et al ¹⁶ to explore a viable alternative of a computationally inexpensive and efficient system identification technique by representing input-output data from the neuron-electrode junction using (i) a parametric Wiener model, and (ii) a Nonlinear Auto-Regressive network with eXogenous input trained using a dynamic Neural Network (NARX-NN model). We then compare and contrast the computational complexity and efficiency of employing parametric Wiener and NARX-NN modeling with the Lee-Schetzen technique of cross-correlation for estimating a nonlinear dynamic model of the neuroelectronic junction.

The remainder of this paper is organized as follows. Section 2 focuses on materials and methods, and covers cell-culture and electrophysiological protocols, theoretical background on Wiener and NARX-NN modeling techniques and numerical methods employed to estimate these models. In Section 3, results from Wiener and NARX-NN modeling of the neuron-electrode junction are presented while Section 4 discusses and compares these results with those obtained from a V-W model ¹⁶ using Lee-Schetzen cross-correlation. The conclusions from the results presented in this paper are then summarized in Section 5.

2. Materials and Methods

2.1. Cell-culture and electrophysiological protocols

Briefly, NG108-15 neurons were cultured on top of substrate embedded microelectrode arrays and electrophysiological recordings were performed on them in voltage and current clamp modes. The neuronal differentiation of the NG108-15 cells was confirmed by recording sodium and potassium currents in the voltage clamp mode and by measuring action potentials in the current clamp mode using a 200 ms depolarization stimulus. Experiments employing white noise stimulation of the neuron-electrode junction were performed if the access resistance for the neuron was less than 15 MΩ and the action potential evoked a detectable signal on the extracellular electrode. For obtaining the input output data records, neurons were stimulated through the intracellular patch pipette in voltage clamp mode with band limited (0–500 Hz) Gaussian white noise sampled at a rate of 9.8 kHz for 100 seconds. The white noise signal was generated in MATLAB (The MathWorks, Natick, MA) and imported to pClamp as a stimulus file. Whole cell capacitance and resistance were compensated but no series-resistance compensation was used. The holding membrane potential was −10 mV and the white noise stimulus spanning an amplitude range of ± 50 mV was superposed on this signal. The extracellular signal was high and low pass filtered at 1Hz (using a second order Bessel filter) and 1 kHz (using a fourth order Bessel filter) respectively. For more details on cell-culture and electrophysiology protocols the reader is referred to ^{3, 16, 18}.

2.2. Mathematical Models

2.2.1. Wiener Model

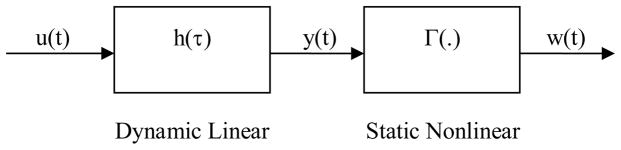
The Wiener model consists of two parametric blocks, a dynamic linear subsystem followed by a static non-linear element (Figure 1), which assumes no a priori underlying structure for the system. The estimation of the parameters of the Wiener model was carried out by a minimization of the error between predicted and actual output. Thus, employing a prediction error model, the dynamic linear subsystem can be represented in discrete time as

Figure 1.

Wiener Model Structure.

$$y(t)A(q)=B(q)u(t-n_k)+e(t)$$ (1)

where t is the discrete time, q is the time delay operator, y(t) is the output of the linear subsystem, e(t) is the process disturbance or noise in the system, A and B are the functions of the delay operator and n_k is the number of input samples that occur before the input affects the output, also called the ‘dead time’ in the system. The corresponding transfer function H(q), can then be written as

$$H(q)=\frac{B(q)}{A(q)}=\frac{b_1+b_2{q}^{-1}+\dots +b_{n_b}{q}^{-n_b+1}}{1+a_1{q}^{-1}+\dots +a_{n_a}{q}^{-n_a}}$$ (2)

where n_a and n_b denote the number of poles and zeros of the linear subsystem. The nonlinear gain at the output in the Wiener model is approximated by a p^th order polynomial in y(t) given by

$$\mathrm{\Gamma }(t)={\gamma }_{1}y(t)+{\gamma }_2{y}^2(t)+\cdots +{\gamma }_p{y}^p(t).$$ (3)

2.2.2. NARX-NN Model

Neural networks can be classified broadly into static and dynamic networks. Dynamic networks employ feedback to model systems in which the output is influenced by both the preceding input and output states of the system while static networks are used to model systems that do not have any feedback affecting their output states. At the neuron-microelectrode junction, the magnitude of the ionic currents flowing across the neuronal membrane through ion channels is governed by the potential difference across the membrane. The electrodiffusing ions influence the ionic concentrations in the interfacial medium that fills the narrow cleft (~ 20–110 nm in width) between the neuronal membrane and the microelectrode. Since the electric potential depends on the associated charge density distribution, the changing ionic concentrations in the nanoscale neuron-electrode cleft form a feedback mechanism that in turn regulates the potential across the membrane. Therefore, for modeling the time series data experimentally recorded at the microelectrode from the neuron-electrode junction, a dynamic neural network employing feedback was trained using nonlinear autoregression with the intracellular bandlimited white noise input to the junction serving as an exogenous input.

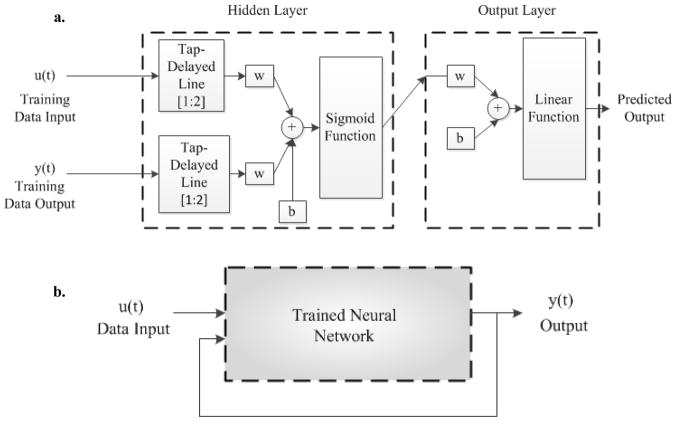
Multiple steps were employed for estimating a NARX-NN model of the mesoscopic neuron-electrode junction. The estimated model was trained using a series parallel model for the nonlinear autoregressive neural network with an exogenous input. A schematic of the NARX neural network with an exogenous input employing tap-delayed values of the true output is shown in Figure 2a. In the prediction phase, a parallel configuration was utilized as shown in Figure 2b ¹⁹. For realizing the neural network structure, an additional input was added to the simple feed-forward neural network besides the data signal at the input layer. The nonlinear dynamic process for such a network can then be represented as

Figure 2.

(a) NARX neural network series parallel model used for training phase. (b) NARX neural network parallel model used for prediction phase.

$$\widehat{y}(t)=f(\mathbf{x}(t))$$ (4)

where ŷ(t) is the predicted output and the regression vector x(t) is given as,

$$\mathbf{x}(t)=[u(t),\cdots ,u(t-k+1),y(t-1),\cdots ,y(t-n)]$$ (5)

2.3. Numerical methods

The estimation of the parametric Weiner and NARX-NN models of the neuron-microelectrode junction was carried out using in-built functions available in MATLAB’s System Identification and Neural Network toolboxes. For both the models, experimental input-output data from the band-limited white noise stimulation of the neuroelectronic interface was used for an estimation of the model parameters. After an estimation of the parameters, the Weiner and NARX-NN models were validated by a prediction of the experimental extracellular output recorded on the microelectrode corresponding to a neuron generated intracellular action potential (AP).

2.3.1. Wiener model

For estimating the parameters of the Wiener model for the neuron-microelectrode junction, a two step approach was employed. The first step involved a determination of the number of zeros and poles of the transfer function for the dynamic linear subsystem using regression. For this purpose, the struc function was used to generate all possible model order configurations in a n_a×n_b matrix for n_a and n_b values of the number of poles and zeros, ranging from 1 to 10, respectively. This n_a×n_b matrix was then employed as an input to arxstruc for an estimation of the ARX model of the linear subsystem through a determination of the coefficients a_i and b_i in the denominator and the numerator of the transfer function in Equation (2) corresponding to each model configuration of zeros and poles. This facilitated a comparison of the predicted output for the different pole-zero configurations with the actual output from the experimental bandlimited white noise stimulation of the neuroelectronic junction. Through a calculation of the prediction errors for the estimated ARX models, this comparison then allowed the choice of an optimal pole-zero configuration for the linear subsystem.

The Wiener model for the neuron-microelectrode junction was then constructed using the system-identification toolbox function nlhw(data, [z_b n_a n_k], InputNL, OutputNL) that creates and estimates a Hammerstein-Wiener model by specifying an input nonlinearity InputNL and output nonlinearity OutputNL, as a nonlinearity estimator object or string representing the nonlinearity estimator type. Employing this function to estimate a Wiener model required specification of InputNL as a first order 1-dimensional linear polynomial while OutputNL was specified as a 1-dimensional second order polynomial. The order of the linear subsystem was specified using the variables z_b and n_a that, respectively, represented the number of zeros n_b plus 1 and the number of poles from the optimal pole-zero configuration estimated in the previous step.

2.3.2. NARX-NN

The implementation of a neural network requires definition of the training functions along with a structure of the network. For this purpose, a sigmoid characterized by its nonlinear behavior was employed as an activation function. Its asymmetry about the origin allowed the inputs to be normalized resulting in an average value close to zero. For the training of the NARX neural network, a batch-learning process was utilized that allowed an update on the weights following each batch process leading to an improved rate of convergence. The availability of the experimental extracellular output at the microelectrode corresponding to the intracellular bandlimited white noise input facilitated the use of back-propagation using Bayesian regularization ²⁰. Essentially, Bayesian regularization also uses the Levenberg-Marquadt algorithm ²¹ for optimizing the weights and biases but helps in generalizing the network better when compared to the latter. Both Bayesian regularization (trainbr) and Levenberg-Marquadt (trainlm) algorithms were employed to compare the performance of the evolved network. The NARX neural network was implemented in MATLAB using an in-built function narxnet (inputDelays, feedbackDelays, hiddenLayerSize) of the neural network toolbox. The input and feedback delays ranged from 1–2 while the hidden-layer size was systematically optimized. The outputs of the hidden layer were mapped using mapminmax function to conform to the range of the sigmoid function output node. A delayed version of the input time series data was prepared using the function preparets that automatically shifted the input and target time series as many steps as were needed to fill the initial input and layer delay states. These input and layer states were then employed as inputs to the MATLAB’s in-built neural network training function train(net, inputs, targets, inputStates, layerStates).

2.3.3. Comparison of parametric Wiener and NARX-NN models with the Volterra-Wiener Model

The performance of the three modeling approaches was analyzed based on the speed of convergence of the algorithm used for model estimation and the mean square error (mse) of the predicted extracellular output with respect to the experimental extracellular output recorded on the planar microelectrode corresponding to an intracellular action potential. The algorithms employed for representing the neuron-microelectrode junction were benchmarked for convergence speed on a workstation with two 2.66 GHz Intel quad core processors and 8GB RAM.

3. Results

3.1. Wiener Model

The dynamics of the neuron-microelectrode interface were represented by a linear transfer function and the associated nonlinearities were evaluated using static nonlinear functions placed at the input and the output of the linear system. For an estimation of the linear transfer function for the Wiener model of the neuron-electrode junction, various pole-zero configurations were explored using the function arxstruc. Table 1 shows the loss function and the fitness percentage for the various pole-zero and dead-time [n_a n_b n_k] configurations of the linear dynamic subsystem of the Wiener model. The optimal pole-zero and dead-time configuration was chosen after an examination of the fitness percentages from both training and validation datasets. It can be seen from Table 1 that comparable fitness values were obtained for the [n_a n_b n_k] configurations in each of [4 4 0], [4 4 1], [4 4 2], [4 5 1] and [5 5 0] on the training dataset; however, the fitness percentages on the validation dataset showed that the optimal [n_a n_b n_k] configuration was [4 4 0]. The loss function, presented in Table 1, is defined as the determinant of the covariance matrix of the prediction error given by det[E′ E]/N, where E is the residual error matrix and N is the total number of time samples, while the fitness of the model output was calculated using 100×(1−|y−ŷ|/|y−ȳ|) where y is the target output, ŷ is the predicted output and ȳ is the mean of the target output.

Table 1.

Loss function and fitness percentage of the Wiener model using different configurations of the linear transfer function with 1^st order input and 2^nd order output nonlinearities.

[na nb nk]	Performance
	Training dataset		Validation dataset Fitness (%)
	Loss function	Fitness (%)
[4 3 0]	2.047 × 10−5	36.89	−116.5
[4 3 1]	2.475 × 10−5	36.89	−116.5
[3 4 0]	2.045 × 10−5	36.92	−115.6
[3 4 1]	2.045 × 10−5	36.92	−115.6
[4 4 0]	1.962 × 10−5	38.25	42.91
[4 4 1]	1.959 × 10−5	38.26	42.71
[4 4 2]	1.951 × 10−5	38.27	42.54
[4 5 0]	2.058 × 10−5	36.92	−115.7
[4 5 1]	1.958 × 10−5	38.28	42.21
[4 5 2]	2.046 × 10−5	36.91	−116.7
[5 5 0]	1.958 × 10−5	38.28	42.15
[5 5 1]	2.046 × 10−5	36.91	−116.3

Then using the function nlhw, a linear transfer function H(q) as given in Equation (2) for the Weiner model was estimated as

$$H(q)=\frac{-8.919e^{-006}+3.309e^{-005}{q}^{-1}-4.219e^{-005}{q}^{-2}+1.802e^{-005}{q}^{-3}}{1-3.492q^{-1}+4.586q^{-2}-2.693q^{-3}+0.599q^{-4}}$$ (6)

After an evaluation of the coefficients for the linear sub-system, different combinations of the higher order polynomials for the nonlinear blocks were further tested using the function nlhw. Static nonlinear blocks of order higher than quadratic, when used to model the input-output corresponding to the bandlimited white noise stimulation of the junction, increased the level of misfit. For example, with a pole-zero configuration of n_a= 4, n_b= 4 and a dead time of n_k= 0, using a cubic polynomial for output nonlinearity reduced the fitness to 39.34% while a change of the input nonlinearity to a quadratic polynomial decreased the fitness metric to 33.34%. The performance of the Wiener model was also evaluated by incorporating a wavelet network for modeling the output nonlinearity (data not presented here) however no significant difference was observed in the fitness percentage even after an increase in the number of training epochs to 100. Thus, following an evaluation of the model configurations for the best fit, the input and output nonlinearities were modeled using one-dimensional polynomial estimators of first and second degree given by

$$\mathit{InputNL}=0.9323u+0.4098$$ (7)

$$\mathit{OutputNL}=-9.6925\times {10}^{-9}{y}^2-4.4521\times {10}^{-5}y+1.3259\times {10}^{-4}$$ (8)

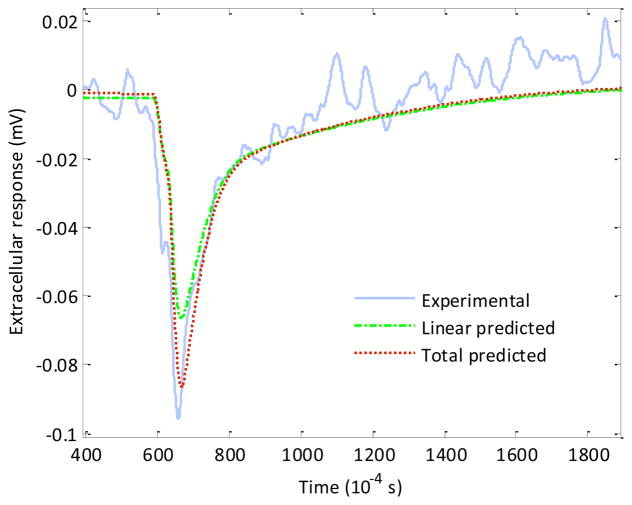
respectively. The model was then validated on the intracellular action potential dataset provided by Thakore et al ¹⁶. A good fit of the predicted extracellular output from the Wiener model for a validation dataset corresponding to an intracellular action potential was obtained as shown in Figure 3.

Figure 3.

Experimental extracellular output recorded on the planar microelectrode (solid line) and the linear (dot-dash line) and total predicted (dotted line) outputs from the Wiener model.

3.2. NARX-NN model

The implementation of the NARX neural network structure for modeling the neuroelectronic interface required a two phase process of training and testing of the trained neural network. The training phase involved tuning the values of the weights and biases of the network to optimize network performance as defined by the network performance function. The performance function employed for optimization of the networks was the mean square error (mse) between the network output and the target output. In the training phase, there are two recurring steps in each epoch known as forward pass and backward pass ²². During the forward pass, the training dataset is applied and the outputs are calculated. Then, these outputs are compared with the actual target outputs and the corresponding error is calculated. During the backward pass, this output error is then propagated back through the layers to alter the weights and biases of the network nodes for minimizing the output error. With each epoch, for every input-output data pair, the procedure involving a forward pass followed by a backward pass is repeated until the error is low enough to satisfy the specified error tolerance. At each input of the input layer, two tapped delays were also employed.

Next, the performance of the evolved networks was compared to find the one that best minimized the error with respect to the training dataset. In our case, Bayesian regularization in conjunction with early stopping ²³ was employed to avoid over-training of the network for estimating a NARX-NN model of the neuron-electrode junction. Also, compared to Levenberg-Marquadt algorithm, it was observed that for an identical network size and number of epochs, Bayesian regularization gave a better fit to the predicted output. The results for a hidden layer with different sizes showed that while NARX-NN models, estimated with higher number of nodes and epochs (Table 2), provided a low mean square error on the input-output dataset used for training (corresponding to the bandlimited white noise stimulation of the neuron-electrode junction), they also led to a problem of over-fitting which negatively affected the prediction of the validation data set. Hence, for a better generalized model of the neuron-microelectrode junction, we avoided the over-fit using early stopping in the training phase.

Table 2.

Mean square error for different numbers of hidden nodes and training epochs in a NARX-NN model.

Number of hidden nodes	Performance on the training dataset (mse)
	10 epochs	20 epochs
5	11.5 × 10−6	7.06 × 10−6
10	7.38 × 10−6	7.19 × 10−6
15	7.18 × 10−6	7.06 × 10−6

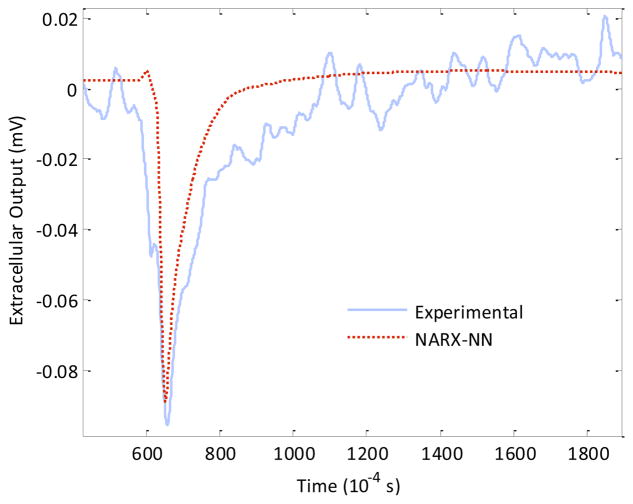
For the testing phase, the output of each of the trained networks was tested and compared against the validation dataset It was observed that results on the validation dataset for a network trained using 30 epochs and comprising the optimal number of fifteen hidden nodes gave an mse of 6.232×10⁻⁴ while for the same network, trained with fifteen epochs, the mse on the validation dataset was observed to be 7.160 × 10⁻⁵ thereby justifying an early stopping at the 15^th epoch in the training phase (Table 3). Further, it was observed that the best fitting results were obtained for an optimized network comprising fifteen hidden nodes which was trained using fifteen epochs (Figure 4).

Table 3.

Mean Squared Error for a network realized using fifteen hidden nodes and trained with various numbers of epochs in a NARX-NN model for the validation dataset.

Number of epochs	Performance on the validation dataset (mse)
10	5.913 × 10−4
13	1.567 × 10−4
14	1.567 × 10−4
15	7.160 × 10−5
16	4.544 × 10−4
17	4.544 × 10−4
20	2.653 × 10−4
30	6.232 × 10−4

Figure 4.

Comparison of the experimentally obtained extracellular output (solid line) from the neuron-electrode junction with the predicted output obtained from the NARX-NN model (dotted line) of the junction.

4. Comparison and Discussion

4.1. Comparison of parametric Wiener and NARX-NN models with the Volterra-Wiener Model

A comparison of the V-W model estimated using Lee-Schetzen cross-correlation technique with the Wiener model showed that although the mean square error was lower for the V-W model and it offered a better prediction of the system output, the complexity of computing Volterra-Wiener kernels was quite high with an increase in the order of nonlinearity. The results for the comparative performance of the sse on the validation data are shown in Table 4 which indicate that the best performance was obtained using V-W model while the mean square error was highest for the NARX-NN model.

Table 4.

Comparison of parametric Wiener and NARX-NN techniques of estimating a model of the neuron-electrode junction with the non-parametric Volterra-Wiener model estimated using Lee-Schetzen cross-correlation technique.

Non-linear model	Performance (mse)	Model complexity
Wiener Model	6.15 × 10−5	11 coefficients
NARX-NN Model	7.16 × 10−5	75 weights and 16 bias constants
V-W Model 16	4.10 × 10−5	~ 3.6 × 104 kernel elements (up to 2nd Order)

Estimation of the Wiener model required just eleven coefficients including four coefficients each for the poles and zeros, one for the first degree polynomial describing the input nonlinearity InputNL and two for the second order output nonlinearity OutputNL. For the training dataset, the simulations took fewer than 10 minutes for the computations to provide us with a supervised model for the Wiener system. In the case of the neural network-based model, it is well known that the computational complexity increases with an increase in the number of hidden nodes ²⁴. The computational complexity of the neural network is further linked to the type of back-propagation algorithm which is used for minimizing the error on the training dataset. The description of the estimated NARX-NN model for the neuron-electrode junction required a total of ninety-one coefficients that included thirty weights each for the tap-delayed autoregressive and exogenous inputs, fifteen bias weights for each hidden layer node and fifteen weights for each hidden layer node in the output layer along with a bias weight. Using the same quad-core machine, which was employed for Wiener model estimation, it took approximately 2 hours to obtain the trained neural network. In the case of Volterra-Wiener model estimated using Lee-Schetzen cross-correlation technique ¹⁶, although the predicted output of the estimated model showed efficient mapping on the validation data, the Volterra-Wiener series representation required a very large number of coefficients (~ 3.6 × 10⁴) computed in about 2–3 days to characterize the neuron-electrode junction. Generally, a Volterra system with memory length N and order p has O(N^P) coefficients ²⁵ resulting in slower convergence rates and longer computation times compared to the time required for estimating Wiener or NARX-NN models.

4.2. Discussion

For the comparison of the system under discussion, two criteria can be employed to measure their performance. From the point of computational complexity, a comparison of the models with regard to their convergence speed to obtain the best fit was made. It was observed that among all three techniques, the Wiener model utilized the fewest number of coefficients and accordingly presented the fastest convergence for the given dataset. A comparison of the performance with regard to obtaining the lowest mean square error on the validation dataset showed that the best value was obtained from the V-W model estimated using the Lee-Schetzen technique of cross-correlation ¹⁶. The NARX-NN model presented moderate computational complexity but its convergence was inferior to the Weiner model which was also nearly an order of magnitude lower in computational complexity. Thus, a choice can be made between the Weiner model and the V-W model depending on the specifications on convergence and complexity. The advantage of using a V-W model is that it is non-parametric and it does not rely on the distribution of the intracellular action potential. On the other hand, using a parametric Wiener model, a reliable estimate is obtained but the linear model is parameterized according to the experimentally obtained data for intracellular action potential.

5. Conclusions

In this paper, we first estimated two parametric nonlinear dynamic models of the neuron-electrode junction using the computationally efficient data-true techniques of Wiener and NARX-NN modeling. Further, these models were employed to predict the extracellular output recorded from the neuron-electrode junction corresponding to an intracellular action potential. The predicted outputs thus obtained from these models were then compared and contrasted with the outputs from the V-W model estimated using Lee-Schetzen cross-correlation technique. Analysis of computational complexity, that directly impacts the computation time required for estimating a model, showed that Wiener model outperformed both the NARX-NN model and the V-W model estimated using Lee-Schetzen cross-correlation. Mean square error analysis, on the other hand, showed that V-W model performed the best in prediction of the extracellular output recorded at the neuron-electrode junction which was closely followed by the Wiener model. The computational efficiency of the NARX-NN technique lay closer to the Wiener model but it did not offer any significant advantage over either the Wiener model or the V-W model in terms of obtaining a better mean square error for the predicted extracellular output.

Non-invasive techniques of interfacing live neurons to electronic devices are important because they offer promising applications in the development of high-throughput drug screening and toxin detection platforms, devices exploiting biological computation and neural prosthetic devices. The efficacy and performance of each of these applications, in turn, depends critically on the speed with which the information obtained through a neuroelectronic interface can be exchanged, decoded and processed. It is in this context that the use of computationally efficient parametric ‘data-true’ Wiener modeling for estimating a nonlinear dynamic model of the neuron-electrode junction provides a promising and powerful new alternative to the use of equivalent circuit models and modeling approaches based on the physics of electrodiffusion for representing signals recorded through the neuroelectronic interface.

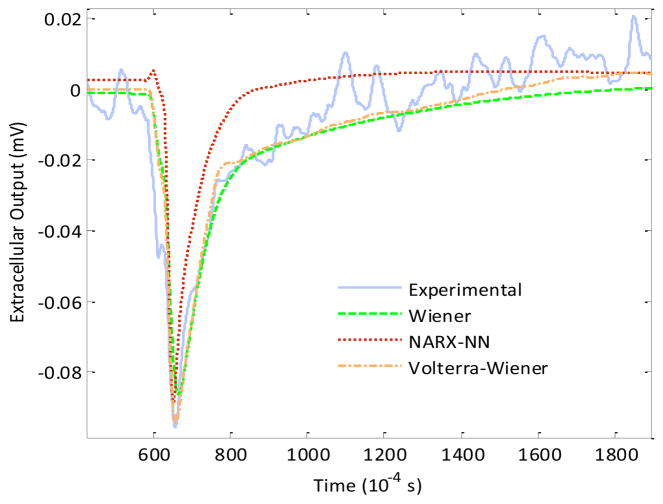
Figure 5.

Comparison of experimentally measured extracellular output (solid line) recorded on the planar microelectrode with the predicted outputs obtained using estimated Wiener (dashed line), NARX-NN (dotted line) and V-W models (dot-dash line) of the neuron-electrode junction.