Polymorphism of Bismuth Sesquioxide. II. Effect of Oxide Additions on the Polymorphism of Bi₂O₃

Abstract

The effect of small oxide additions on the polymorphism of Bi₂O₃ was studied by means of high-temperature x-ray diffractometry. Solidus and occasional liquidus temperatures were approximated, so that tentative partial phase diagrams for 33 oxide additions were constructed. Only the monoclinic and the cubic forms of Bi₂O3 were found to be stable. Other phases, frequently reported by previous investigators, such as tetragonal and body-centered cubic (b.c.c.), were shown to form metastably from cooled liquid or cubic. An impure b.c.c. phase of distinct but variable composition appeared in systems of ZnO, PbO, B₂O₃, Al₂O₃, Ga₂O₃, Fe₂O₃, SiO₂, GeO₂, TiO₂, and P₂O₅. The impure b.c.c. phase in the systems with SiO₂, GeO₂, and TiO₂ melted congruently about 100 °C above the m.p. of Bi₂O₃. The impure b.c.c. phase was formed metastably in systems with Rb₂O, NiO, MnO, CdO, V₂O₅, and Nb₂O₅; the conditions of formation were dependent on composition, preparation, and heating schedules. The impure b.c.c. phases, both stable and metastable, had smaller unit cell dimensions than that of pure Bi₂O₃.

1. Introduction

Part I of this paper was an attempt to clarify the stable and metastable relationships of pure Bi₂O₃. It can be seen in table 1 of that part, however, that I several investigators [1,2,3]1 have reported phases of Bi₂O₃ which contained, or were contaminated by, other oxides. Sillén [1] obtained a body centered cubic (b.c.c.) form by fusing Bi₂O₃ in porcelain, or with A1₂O₃ or Fe₂O₃, for 5 min at 900 °C. He suggested the unit cell formula Me₂Bi₂₄O₄₀. Fusion of Bi₂O₃ in a porcelain crucible for 20 min yielded cubic Bi₂O₃. Schumb and Rittner [2] also obtained the impure b.c.c. phase by fusing Bi₂O₃ at 875 °C in porcelain or with SiO₂. By quenching the fused mixture in water, they produced an impure cubic (C) phase. Gattow and Schröder [3] reported impurity forms of b.c.c., C, and tetragonal-symmetry, designated respectively, as γ*, δ*, β*.

Table 1.

Unit cell demensions of rhombohedral phases formed in Bi₂O₃ systems

Oxide addition	Starting composition	Final heat treatment	Additional phases present	Ionic radius of cation (Ahrens)	Unit cell dimensions
					Hexagonal			Rhombohedral
		°C/hr			a	c	c/a	a	α
					A	A		A
CaOa	6Bi2O3:CaO	700°/107	None	0.99	3.941	27.95	7.09	9.590	23°44′
SrOa,b	19Bi2O3:2SrO	699°/144	Mon Bi2O3 (moderate)	1.12	3.952	28.09	7.11	9.637	23°40′
BaOa	6Bi2O3:BaO	700°/107	b.c.c. Bi2O3 (small)	1.34	3.972	28.54	7.185	9.786	23°26′
Sm2O3	12Bi2O3:Sm2O3	700°/107	tr?	1.00	3.950	27.93	7.07	9.585	23°46′
La2O3	12Bi2O3: La2O3	700°/107	b.c.c. Bi2O3 (moderate)	1.14	3.975	28.10	7.07	9.644	23°48′

^aRhombohedral phase described by Aurivillius [7].

^bRhombohedral phase described by Sillen and Aurivillius [8].

The previous work can be questioned on two grounds: Firstly, in most cases the exact compositions were not controlled and were not known; secondly, in no instances were the phases studied at temperature and, consequently, might not represent stable equilibrium phases. Quenched liquids, for example, could hardly be expected to give equilibrium phases for any temperature. Furthermore, as the stable phases of Bi₂O₃ have been shown to be monoclinic and cubic-bismuth oxide, any other phase, e.g., impure tetragonal (Tet) or b.c.c. must represent either a metastable form of Bi₂O₃ or a discrete phase, whose composition limits does not include Bi₂O₃.

The major objective of this portion of the study, therefore, was to obtain information on the impure forms of bismuth oxide, in particular, on the b.c.c. phase. To eliminate objections applicable to previous work, mixtures were formulated from pure materials and of known compositions and were studied in a high-temperature x-ray diffractometer furnace.

2. Materials and Methods

2.1. Materials

For the admixture study, reagent grade chemicals (ACS) or those of higher purity were used. Starting materials for formulating oxide mixtures with Bi₂O₃ were as follows: Li₂CO₃, Rb₂CO₃, NiO, ZnO, CdO, MgO, CaCO₃, SrCO₃, BaCO₃, PbO, B₂O₃, Al₂O₃, Ga₂O₃, Fe₂O₃, MnCO₃, Sb₂O₃, Lu₂O₃, Sm₂O₃, La₂O₃, SiO₂, GeO₂, TiO₂, TeO₂, SnO₂, ZrO₂, CeO₂, P₂O₅, V₂O₅, Sb₂O₅, Ta₂O_s, Nb₂O₅, Cr₂O₃, WO₃, and MoO₃. These materials were chosen from crystal chemistry considerations, such as charge, ionic radius, coordination number, and polarizability of the cations.

2.2. Preparation of Mixtures

Binary mixtures were formulated from Bi₂O₃ and a second substance, to give an atomic ratio in most cases of 12Bi to 1Me, where Me represents the second cation. The intent was to determine which oxides formed Sillén’s [1] impure b.c.c. phase at the above ratio. Thus for monovalent, trivalent, and pentavalent cations, oxide compositions would correspond to 12Bi₂O₃:Me₂O, 12Bi₂O₃:Me₂O₃, and 12Bi₂O₃:Me₂O₅. For divalent, tetravalent, and hexavalent cations, oxide compositions would correspond to 6Bi₂O₃:MeO, 6Bi₂O₃:MeO₂, and 6Bi₂O₃: MeO₃. Additional compositions were prepared in many of the systems, as designated on the individual phase diagrams.

Preliminary treatment of the mixtures consisted of three cycles of grinding together calculated amounts of the starting materials, pressing the material in a mold, and then heating the disk at a temperature below the solidus, as described in previous publications [4,5].

2.3. Apparatus

The high-temperature, x-ray diffractometer furnace noted in Part I was used also for the admixture study. The modification of the sample holder [6] which permitted the use of a thin layer of powered specimen was of especial importance for this part of the study. X-ray diffraction patterns of crystalline phases could be obtained in the presence of liquid, which did not flow off the platinum holder. Thus, it was possible to approximate solidus temperatures (±10°) and under favorable conditions even the liquidus temperatures.

3. Results and Discussion

3.1. Phase Diagrams

a. General Remarks

The data obtained by use of the high-temperature x-ray furnace can be presented in the form of phase diagrams, as shown in figures 1 through 6. Arrangement of the figures is according to the Periodic Table. Within each figure, diagrams are arranged, in general, according to a combination of the Periodic Table subgroups and ionic radii of the atoms. As no table of data is given, figure captions include selected notes. In most instances, the rate of disappearance of old phases and of the appearance of new ones on the indicated boundary curves was not rapid but took place over a temperature interval. Phases which have been interpreted as nonequilibrium ones are not shown in the diagrams.

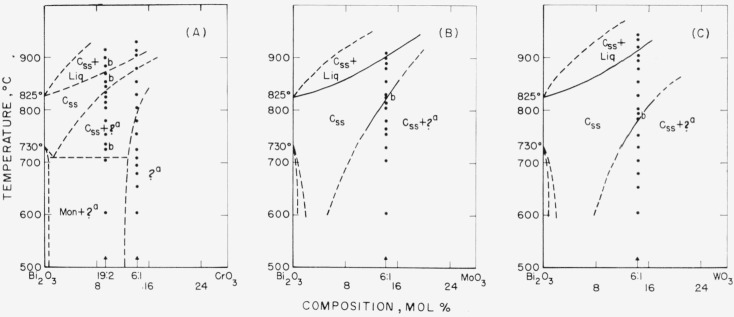
Figure 1. Bi₂O₃ rich regions of Bi₂O₃–R₂O systems, as determined from high-temperature x-ray diffraction data.

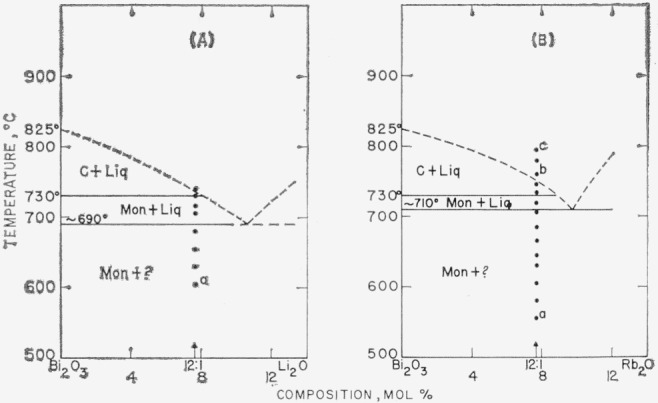
Phases: Mon—monoclinic, C—cubic, ?—unknown, Liq—liquid

(A) Bi₂O₃–Li₂O

a—Trace of unknown phase observed.

(B) Bi₂O₃–Rb₂O

a—No second phase seen,

b—Rb₂O apparently volatilizes from liquid,

c—Liquid cools to b.c.c. phase: a=10.22A.

Figure 6. Bi₂O₃ rich regions of Bi₂O₃—RO₃ systems, as determined from hiqh-temperature x-ray diffraction data.

Phases: Mon—monoclinic, C—cubic, ss—solid solution, ?—unknown, Liq— liquid

(A) Bi₂O₃—CrO₃

Compositions formulated from Cr₂O₃. Diagram shown on CrO₃ basis because on calcining, specimens changed in color from green to red, and ? phase is similar to that formed with the hexavalent ions.

a—Unknown composition, apparently pseudotetragonal (similar to the phase in the Bi₂O₃—MoO₃ and Bi₂O₃—WO₃ systems).

b—Phases found at these temps, do not agree entirely with postulated phase boundaries, because system may be pseudobinary.

(B) Bi₂O₃—MoO₃

a—Unknown composition, apparently pseudotetragonal (similar to the phase in the Bi₂O₃—CrO₃ and Bi₂O₃—WO₃ systems).

b—Reversibility demonstrated with high-temp, x ray.

(C) Bi₂O₃—WO₃

a—Unknown composition, apparently pseudotetragonal (similar to the phase in the Bi₂O₃—CrO₃ and Bi₂O₃—MoO₃ systems).

b—Reversibility demonstrated with high-temp, x ray.

It is emphasized that these phase diagrams represent the best interpretation of the data within the limitations of the experimental method. The major limitation is due to volatility of the samples or of the constituents. The high surface-to-volume ratio inherent with a thin film method, increases the effect of volatilization on composition. Thus, verification of equilibrium by long soaking periods, especially at high temperatures, was precluded.

b. General Conclusions

From inspection of all of the diagrams, several general conclusions become evident:

1. The only stable phases of pure bismuth oxide are Mon and C. The b.c.c. or Tet phases of pure Bi₂O₃ do not appear. The conclusion is consistent with the stability relationships for Bi₂O₃ as deduced in Part I.

2. Monoclinic Bi₂O₃ shows little or no solid solution.

3. The C phase of Bi₂O₃, however, may show extensive solid solution: and in such cases, the Mon to C transition temperature is lowered.

4. Except for the CdO and PbO systems (fig. 2 G& H), the effect of solid solution in the C phase is to raise solidus and liquidus temperatures.

5. A b.c.c. phase distinct from that of pure Bi₂O₃ appears in a number of systems. This b.c.c. phase may vary in composition for different systems (see figs. 2F, 3B & C, 4A, 5A), may melt congruently (fig. 4A, B & C), or melt incongruently (figs. 2H, 3A & B), and when stable is separated from Bi₂O₃ by a two-phase region.

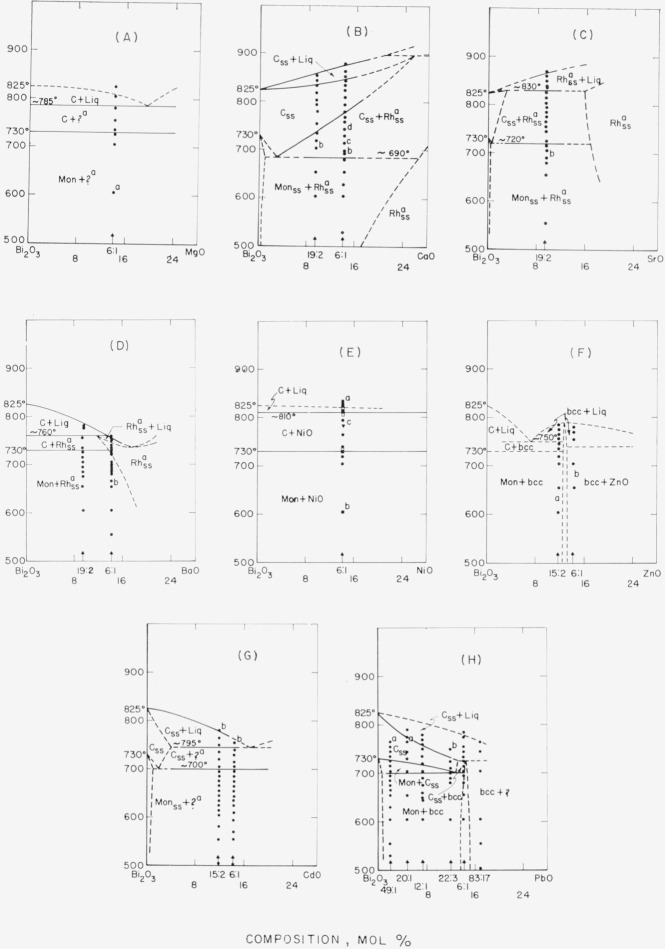
Figure 2. Bi₂O₃ rich regions of Bi₂O₃–RO systems, as determined from high-temperature x-ray diffraction data.

Phases: Mon—monoclinic, C—cubic, b.c.c.—body-centered cubic, ?—unknown, Rh—rhombohedral, ss—solid solution, Liq—liquid

(A) Bi₂O₃–MgO

a—Second phase, possibly MgO.

(B) Bi₂O₃–CaO

a—Described by Aurivillius (1943) [7].

b—Cubic Bi₂O₃ ss starting to form,

c—Cubic Bi₂O₃ ss increasing; Mon Bi₂O₃ decreasing,

d—Mon Bi₂O₃ gone.

The 6:1 composition slow-cooled from 700 °C (after 107 hr soaking period) shows single phase Rh_ss. See table 1 for unit cell dimensions.

(C) Bi₂O₃–SrO

a—Described by Sillén and Aurivillius (1939) [8].

b—Rh_ss increasing; Mon decreasing. See table 1 for unit cell dimensions.

(D) Bi₂O₃–BaO

a—Described by Aurivillius (1943) [7].

b—Rh_ss increasing; Mon decreasing. See table 1 for unit cell dimensions.

(E) Bi₂O₃—NiO

a—Liq cools to b.c.c.

●—First heat

□—b.c.c. reheated

■—Superposition of ● and □.

▼ -Reheated sample cooled from liq to 780 °C

b—b.c.c. decomposing to Mon.

c—Cubic phase when cooled to room temperature shows b.c.c.

(F) Bi₂O₃—ZnO

a—No Mon detected.

b—ZnO detected only in specimen soaked 107 hr at 700 °C and then slow-cooled.

The two compositions studied indicate that the b.c.c. phase is stable and melts congruently.

Beyond this the diagram is conjectural.

G) Bi₂O₃—CdO

a—Possibly one of Sillén’s reported CdO—Bi₂O₃ phases [9].

b—Liq cools to b.c.c.

(H) Bi₂O₃—PbO

a—C_ss cools to b.c.c.

b—C_ss+ Liq cools to b.c.c.

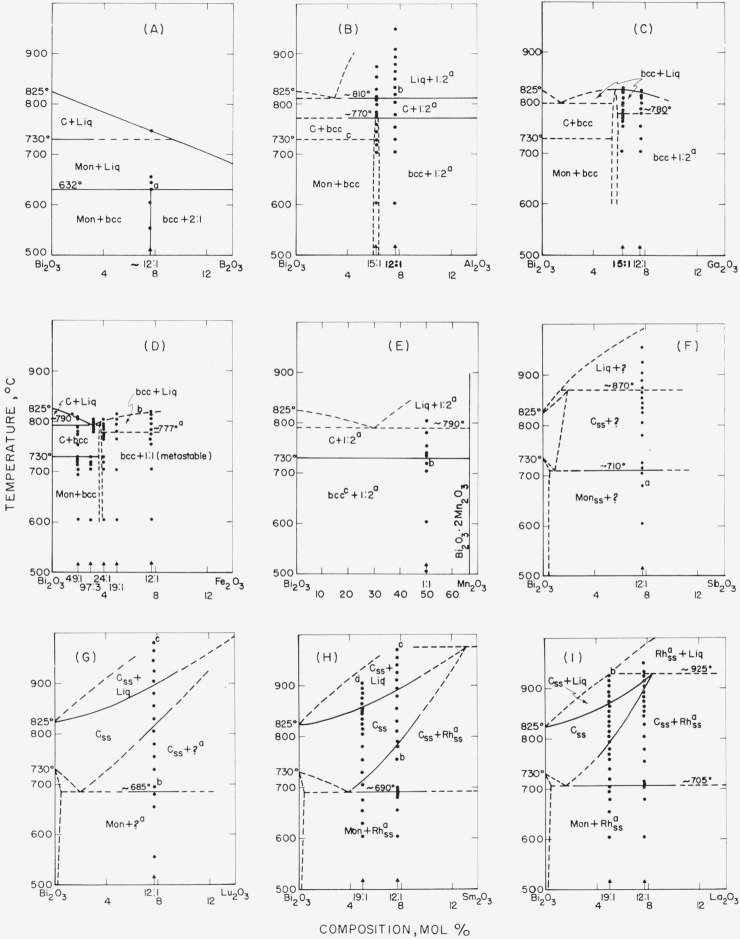
Figure 3. Bi₂O₃ rich regions of Bi₂O₃–R₂O₃ systems, as determined from high-temperature x-ray diffraction data.

Phases: Mon—inonoclinic, C—cubic, b.c.c.—body-centered cubic, ?—unknown, Rh—rhombohedral, ss—solid solution, Liq—liquid.

(A) Bi₂O₃—B₂O₃

Diagram taken from Levin et al. [4].

a—Unreacted 2Bi₂O₃·B₂O₃(2:1) and Mon Bi₂O₃ at lower temperatures form single phase b.c.c.

B) Bi₂O₃—Al₂O₃

a—Isostructural with 1:2 compounds in systems of Bi₂O₃ with Fe₂O₃, Ga₂O₃, and Mn₂O₃, according to unpublished work of R. S. Roth.

b—Very strong peak at d value about 2.9A; probably orientation of Bi₂O₃·2Al₂O₃.

c—Effect of Al₂O₃ on Mon to C transition temperature not determined.

(C) Bi₂O₃—Ga₂O₃

a—Isostructural with 1:2 compounds in systems of Bi₂O₃ with Fe₂O₃, Al₂O₃, Mn₂O₃, according to unpublished work of R. S. Roth.

The two compositions studied indicate that the b.c.c. phase is stable and melts congruently. Beyond this the diagram is conjectural.

(D) Bi₂O₃—Fe₂O₃ (Does not obey phase rule.)

a—May represent metastable eutectic between b.c.c. and metastable BiFeO₃.

b—Liquidus curve does not show maximum temperature at melting of b.c.c. phase.

The BiFeO₃ phase is believed to be metastable because the compound composition can never be made single phase, according to the unpublished work of R. S. Roth.

(E) Bi₂O₃—Mn₂O₃ (Note different composition scale.) MnCO₃ used as starting material, and mixture ground in alcohol, which tends to give b.c.c.[17].

a—Isostructural with 1:2 compounds in systems of Bi₂O₃ with Fe₂O₃, Al₂O₃, Ga₂O₃, according to unpublished work of R. S. Roth,

b—Samples at this temperature and below show b.c.c., believed to be metastable, as it disappears at Mon to G inversion (730 °C).

c—Mon Bi₂O₃ probably stable phase (see b).

(F) Bi₂O₃—Sb₂O₃

a—Above about 650 °C oxidation state of the antimony is unknown. Starting with Sb₂O₅, same phases occur, but solidus appears to be lower (~855 °C).

(G) Bi₂O₃—Lu₂O₃

a—Second phase observed, with major d value at 2.95A.

b—As Mon transorms to C, unreacted Lu₂O₃ transforms to ? phase.

c—Liq+C_ss cools to metastable tetragonal_ss.

(H) Bi₂O₃—Sm₂O₃

a—Essentially isostructural with Rh_ss phase in CaO—, SrO—, and BaO — Bi₂O₃ systems. See table 1 for unit cell dimensions.

b—When cooled to 450 °C shows Rh_ss+ tetragonal (Tet)_ss (metastable).

c—Liq+C_ss cools to Tet_ss+C_ss (both metastable).

d—Liq+C_ss cools to Tet_ss (metastable). Single phase Tet_ss (19:1) reheated to 625 °C transforms first to C_ss+Rh_ss, then the C_ss transforms to the equilibrium Mon phase.

(I) Bi₂O₃—La₂O₃

a—Essentially isostructural with Rh_ss phase in CaO—, SrO —, and BaO — Bi₂O₃ systems. See table 1 for unit cell dimensions.

b—Cools to C_ss (metastable)

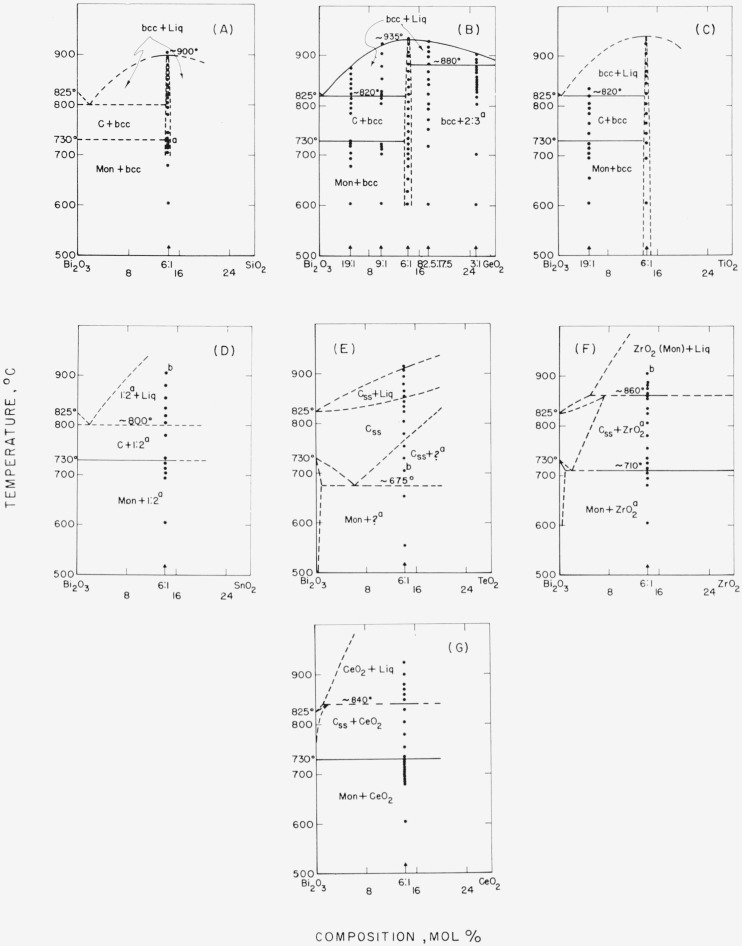
Figure 4. Bi₂O₃ rich regions of Bi₂O₃ —RO₂ systems, as determined from high-temperature x-ray diffraction data.

Phases: Mon—monoclinic, C—cubic, b.c.c.—body-centered cubic, ?—unknown, ss—solid solution, Liq—liquid

(A) Bi₂O₃-SiO₂

a—Unreacted Mon transforms to C, on heating.

Composition studied shows that the b.c.c. phase (6:1) melts congruently. Beyond this the diagram is conjectural.

(B) Bi₂O₃–GeO₂

a—Unpublished work of C. R. Robbins, NBS.

Compositions studied show that the b.c.c. phase melts congruently, near to but not necessarily at the 6:1 composition.

(C) Bi₂O₃—TiO₂

Compositions studied show that the b.c.c. phase melts congruently, near to but not necessarily at the 6:1 composition.

(D)Bi₂O₃—SnO₂

a—Compound described by R. S. Roth [14].

b—1:2 + Liq cools to 1:2 + Mon + b.c.c. (trace).

(E) Bi₂O₃–TeO₂

Oxidation state of tellurium at high temperature is unknown.

a—Unknown composition, apparently of cubic symmetry.

b—Unit cell dimensions at 700 °C: C_ss, a=5.63A; ?, a=5.57A

(F) Bi₂O₃—ZrO₂a—ZrO₂ does not show in x-ray pattern below solidus.

b—Liq + ZrO₂ (Mon) cools to Tet Bi₂O_3ss.

No b.c.c. found in this system although reported by Aurivillius and Sillén [15].

(G) Bi₂O₃—CeO₂.

No b.c.c. found in this system although reported by Aurivillius and Sillén [15].

Figure 5. Bi₂O₃ rich regions of Bi₂O₃—R₂O₅ systems, as determined from high-temperature x-ray diffraction data.

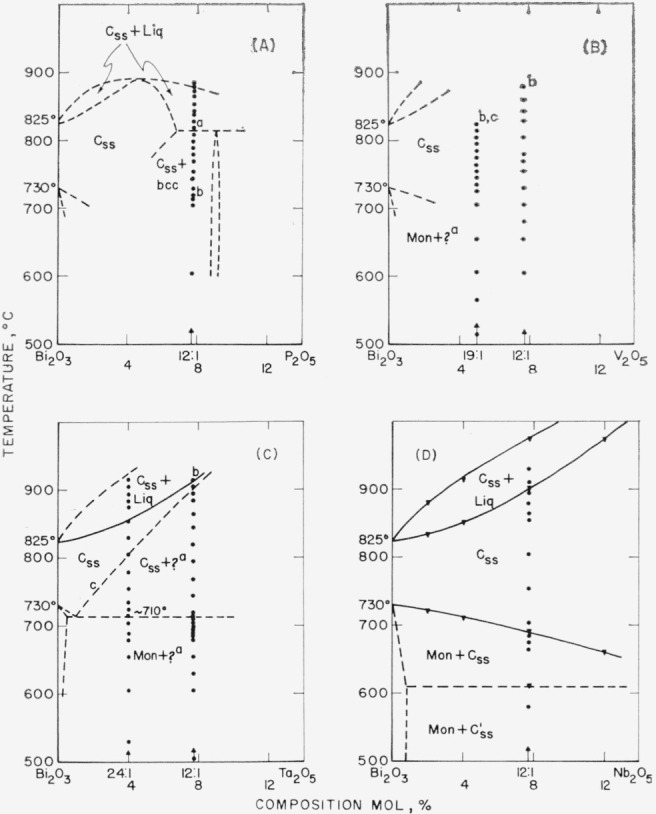
Phases: Mon—monclinic, C—cubic, C′—pseudocubic, b.c.c.—body-centered cubic, ?—unknown, ss—solid solution, Liq—liquid

(A) Bi₂O₃–P₂O₅

a—The b.c.c. phase decreases markedly in amount at about 815 °C, but persists in diminishing amounts to about 850 °C. It is possible, therefore, that the true solidus is at 850 °C and (1) a 2-phase region of C_ss + ? exists between 815 ° and 850 °C or (2) the decomposition temp, of b.c.c. should be raised to 850 °C.

b—The Mon to C transition with the high-temp, x ray occurs at about 720 °C. However, a sample held at 700 °C for 107 hr and slow-cooled does not show Mon. Therefore, the temperature of the Mon to C inversion is in doubt.

(B) Bi₂O₃—V₂O₅

A more complete phase diagram could not be postulated because of inconsistencies in the temperatures of transitions and the relative amounts of phases present.

a—b.c.c., if a stable phase; otherwise, unknown phase.

b—Above 815 °, only C_ss; between 715° and 815 °C, C_ss + b.c.c.; below 715 °C, phases present depend on previous heat treatment. Stability and approximate composition of b.c.c. could not be ascertained, c—C_ss cools to b.c.c.

(C) Bi₂O₃–Ta₂O₅

a—Apparently cubic symmetry; composition may correspond to C′ phase in Bi₂O₃—Nb₂O₅ system [17] (about 4:1).

b—Liq + C_ss cooled slowly shows only C_ss at all temps.

c—Because of nonreversibility (see b), this boundary may actually be much lower, as in the Bi₂O₃—Nb₂O₅ system (D).

(D) Bi₂O₃–Nb₂O₅

▼—Values taken from phase diagram of Roth and Waring [17].

c. Individual Phase Diagrams

In the following section, individual figures and selected diagrams will be discussed. Only two alkali oxide systems, representing extremes in cation radii, were studied (fig. 1). Both Li₂O and Rb₂O, in the region studied, were simple eutectic types with no solid solutions. It should not be inferred, however, that oxides of the intermediate cations necessarily would behave similarly.

For oxides of the divalent cations (fig. 2) the phase diagrams showed a number of variations, e.g., simple eutectic system (A), congruently melting b.c.c. phase (F), incongruently melting b.c.c. phase (H), C solid solution with liquidus and solidus raised (B), and C solid solution with liquidus and solidus lowered (H).

In the systems with CaO, SrO, and BaO, the rhombohedral solid solution phase described previously [7, 8] was found to be an equilibrium phase. Sillén and Aurivillius had found the phase in samples cooled rapidly from the liquid. The unit cell dimensions at 700 °C for the bismuth oxide-rich compositions of the solid solution phase are given in table 1.

Sillén and Sillén [9] report finding several phases in the Bi₂O₃-CdO system, one of which might be the unknown phase in the present study of the cadmium oxide system (fig. 2G).

The PbO-Bi₂O₃ system (fig. 2H) is interesting for several reasons. It varies significantly from the reported phase diagram of Belladen [10, 11]. The latter shows neither the Mon to C transition, nor the solid solution of PbO in Bi₂O₃, nor the b.c.c. phase at the 6Bi₂O₃·PbO composition. It is evident from the present diagram that the molal heat of fusion of Bi₂O₃ calculated by Kelley [12] from the liquidus curve of Belladen’s diagram (6800 cal/mole) is in error. The molal heat of fusion of Bi₂O₃ was discussed by Levin and McDaniel [4].

With regard to the systems of bismuth oxide with oxides of the trivalent cations, the Bi₂O₃-B₂O₃ system (fig. 3A) was reported previously [4], as determined by the quenching technique. However, one composition, 12Bi₂O₃:B₂O₃, was used to compare both methods and to show that agreement was satisfactory.

Apparently isostructural 1:2 compounds were found in systems of Bi₂O₃ with Al₂O₃ (fig. 3B), Ga₂O₃ (fig. 3C), and Mn₂O₃ (fig. 3E). An isostructural 1:2 compound also exists in the Bi₂O₃–Fe₂O₃ system; however, the high-temperature x-ray study revealed only a 1:1 compound (fig. 3D). The BiFeO₃ phase is believed to be metastable, because according to the unpublished work of R. S. Roth, the compound composition can never be made single phase. It should also be noted that the portion of the diagram to the right of the b.c.c. phase does not obey the phase rule. Royen and Swars [13] who also have studied this system reported two Tet phases of approximately 30:1 and (12–13):1 compositions, a b.c.c. phase of composition 15:1, as well as 2:1 and 1:1 compounds. The present work does not substantiate the 30:1, (12–13) :1, and 2:1 compounds; and the composition of the b.c.c. phase appeared slightly greater than 24Bi₂O₃ :Fe₂O₃. As Royen and Swars obtained their compounds from fused mixtures, it is believed that some of them represented metastable states.

The system with the rare earth oxides Sm₂O₃ (fig. 3H) and La₂O₃ (fig. 3I), showed the same rhombohedral solid solution phase as was found in the CaO, SrO, and BaO systems (fig. 2B–D). The unit cell dimensions are given in table 1. The phase did not form in the Lu₂O₃ system (fig. 3G) nor in the MgO system (fig. 2A); consequently, the minimum cationic radius required for formation of this phase lies between that of Lu³⁺ and Ca²⁺ or between 0.85 and 0.99A (Ahrens).

In the systems studied with the group IV cations (fig. 4), SiO₂ (A), GeO₂ (B), and TiO₂ (C) showed a congruently melting b.c.c. phase at or near the 6:1 composition. The phase diagrams provide positive proof, for the first time, that the impure b.c.c. phase is a discrete composition and not a solid solution phase of Bi₂O₃.

The Bi₂O₃-SnO₂ system (fig. 4D) contains a 1:2 compound described by R. S. Roth [14] as having a distorted pyrochlore-type structure.

No b.c.c. phase was found in the ZrO₂ and CeO₂ systems, although this phase was obtained from fused mixtures by Aurivillius and Sillén [15]. As will be discussed later under the b.c.c. phase, cooling of the liquid or C phases tends to form metastable phases.

In the group V cations (fig. 5), systems with P₂O₅ (A) and V₂O₅ (B) showed inconsistencies which could not be reconciled, and these diagrams are most questionable. The systems with Ta₂O₅ (C) and Nb₂O₅ (D) are similar, and it is possible that the boundary curve in the Ta₂O₅ system between (Css+ ?) and Css should descend continuously as in the Nb₂O₅ system (see b and c in legend to fig. 5C).

Finally, in the Bi₂O₃–RO₃ systems (fig. 6), the three systems studied are similar, including the occurrence of a phase of apparently pseudotetragonal symmetry but of unknown composition. Gattow [16] prepared a mixed oxide 2Bi₂O₃·MoO₃, by precipitation from solution, and studied it by means of x-ray and thermal analysis. Because of insufficient data, however, it was not possible to compare the unknown phase in the present study with Gattow’s.

3.2. Metastable Phases

The results of the high-temperature x-ray experiments were especially informative regarding the occurrence of metastable phases observed at room temperature in samples cooled from higher temperatures. Such information is included in the figure captions. Illustrative examples are as follows:

1. Liquid cooled to a metastable b.c.c. phase in Bi₂O₃ systems with Rb₂O (see c to caption of fig. IB), NiO (a of fig. 2E), and CdO (b of fig. 2G).

2. Cubic or cubic solid solution cooled to a metastable b.c.c. phase in systems with NiO (c of fig. 2E) and V₂O₅ (c of fig. 5B).

3. Liquid+cubic solid solution cooled to metastable cubic solid solution in systems with La₂O₃ (b of fig. 3I), Ta₂O₅ (b of fig. 5C), and Nb₂O₅ [17].

4. Liquid+cubic solid solution also cooled to metastable Tet in systems with Lu₂O₃ (c of fig. 3G), Sm₂O₃ (b and d of fig. 3H), and Nb₂O₅ [17].

5. In the zirconia system, liquid+ZrO₂ cooled to metastable tetragonal.

It is emphasized that an exhaustive study of the formation of metastable phases was not attempted. In general, only one cooling cycle for a limited number of compositions was studied in each system. It is apparent, however, from the frequency and diversity of the matastable phases found, that phases obtained by the cooling of fused mixtures or of high-temperature forms may well represent nonequilibrium states at all temperatures. It is not surprising, therefore, that previous investigators [1, 2, 13, 15] studying fused samples of unknown compositions obtained various impurity phases. Many of these are metastable phases and have no place in the equilibrium diagrams.

3.3. Body-Centered Cubic Phase

Table 2 gives the unit cell dimensions for the stable and metastable b.c.c. phases of bismuth oxide found in this study. The unit cell dimensions were obtained at room temperature; and except for Rb₂O and Bi₂O₃ (see footnotes d and e, respectively) the samples were heated in sealed platinum tubes according to the schedule given in the column under “Final Heat Treatment”. As observed from the x-ray diffraction patterns, most of the compositions studied were not single phase but showed a second phase.

Table 2.

Unit cell dimensions of body-centered cubic phases formed by small additions of oxides to Bi₂O₃

Stable phases
Oxide addition	Starting composition	Final heat treatment	Additional phases present	Ionic radius of cation (Ahrens)	Levin and Roth	Aurivilliusa and Sillen [15]
		° C/hr		A	A	Aa
ZnO	6Bi2O3:ZnO	700°/107	Trace ZnO	0.74	10.201
PbO	6Bi2O3:PbO	725°/1	None	1.20	10.258	10.25b
B2O3	12Bi2O3:B2O3	600°/65	Trace Bi2O3+ trace 2:1	0.23	10.124
Al2O3	12Bi2O3: Al2O3	700°/107	Trace Bi2O3·2Al2O3	.51	10.169	10.16
Ga2O3	12Bi2O3: Ga2O3	700°/107	Trace Bi2O3·2Ga2O3	.62	10.176
Fe2O3	19Bi2O3:Fe2O3c	700°/3	Trace BiFeO3	.64	10.183	10.18
Tl2O3				.95		10.17
SiO2	6Bi2O3:SiO2	700°/107	Small amt. Bi2O3	.42	10.104	10.10
GeO2	6Bi2O3: GeO2	700°/107	Trace GeO2	.53	10.143
TiO2	6Bi2O3:TiO2	700°/107	None	.68	10.176
P2O5	12Bi2O3:P2O5	700°/107	Trace?	.35	10.164
Metastable phases
Rb2O	12Bi2O3: Rb2O	795°/0.1d	Trace Bi2O3	1.47	10.22
NiO	Bi2O3:NiOc	785°/1	NiO	0.69	10.227
MnO	Bi2O3:MnOc	735°/1	Moderate amt. Bi2O3·2Mn2O3	.80	10.221
CdO	6Bi2O3:CdO	700°/107	Trace CdO	.97	10.225
Bi2O3	Bi2O3	780°/0.1e	Small amt. Mon Bi2O3	1.20f	10.268	10.264g
ZrO2				0.79		10.23
CeO2				.94		10.22
V2O5	12Bi2O3: V2O5	700°/107	Small amt. Tet. Bi2O3 ss	.59	10.210
Nb2O5	6Bi2O3:Nb2O5c	700°/3	Moderate amt. cubic (C′ [17])	.69	10.19
Nb2O5	24Bi2O3: Nb2O5 c	700°/3	Trace cubic (C′ [17])	.69	10.263

^aConverted from kx units.

^bCation is tetravalent according to Aurivillius and Sillen [15].

^cStarting materials ground together in alcohol.

^dSample cooled from liq. in high-temp., x-ray furnace.

^eSlow-cooled in high-temp., x-ray furnace.

^fAhrens gives 0.96Å, which is low. See [4].

^gAgrees with value obtained by Schumb & Rittner [2].

Concerning the systems with a stable b.c.c. phase, it is seen that an exact 12Bi to 1Me atom ratio was not substantiated in most cases. Except for PbO and B₂O₃, systems with divalent and trivalent cations would show single phase b.c.c. at ratios of Bi to Me greater than 12:1. Systems with the tetravalent ions Si⁴⁺, Ge⁴⁺, and Ti⁴⁺ approached most closely the ideal ratio of 12Bi: 1Me, proposed by Sillén [1]. This conclusion is more apparent from figure 4A,B,C, where the b.c.c. phase in these systems is seen to melt congruently at a temperature about 100 °C above the melting point of Bi₂O₃. With the oxide of the pentavalent cation, P⁵⁺, the single phase b.c.c. composition appears to be less than 12Bi:1Me (fig. 5A). It can be seen from table 2 that within each valence group increased ionic radius of the cation is associated with increased unit cell dimensions of the b.c.c. phase. Unit cell dimensions versus ionic radius for all of the cations are plotted in figure 7. The general correlation between the two for the stable phases (solid points) is seen to be good, although not linear.

Figure 7. Unit cell dimensions versus ionic radius for impure body-centered cubic phases of Bi₂O₃.

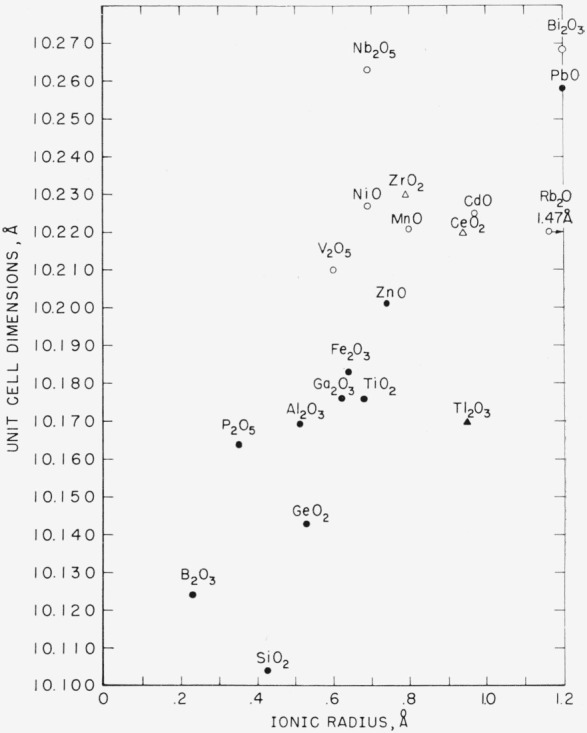
Oxides shown in the figure refer to the impurity additions. See figures 2 through 5 for approximate compositions of the phases.

●—equilibrium phases

○—metastable phases

▲, △—unit cell dimensions after Aurivillius and Sillén [15].

An interesting and surprising finding is that oxides of cations so diverse in ionic radius, oxygen coordination number, and polarizability as Zn²⁺, B³⁺, Ti⁴⁺, and Pb²⁺ can form with bismuth oxide a discrete phase of the same symmetry. An appealing explanation is the concept of a clathrate- or cage-type structure, in which as postulated by Sillén [1] for Si₂Bi₂₄O₄₀, central Si atoms are surrounded by spheres of Bi₁₂O₂₀ atoms. For the case of a central ion with valence different from 4, charge balance would be achieved through cation or oxygen adjustments.

Regarding the metastable b.c.c. phase, the monovalent ion Rb⁺ formed the phase on cooling in the high temperature x-ray experiments. The compositions containing NiO, MnO, and Nb₂O₅, which in the process of preparation were ground in alcohol, also formed the b.c.c. phase, metastably. These results would seem to support the conclusion that an impure b.c.c. phase of Bi₂O₃ might be formed (metastably) with most cations, under the proper conditions of composition, grinding, and heating schedules.

It is seen from figure 7 that with the exception of PbO the unit cell dimensions of the metastable phases are larger than those of the stable phases. The cell dimensions of the metastable impure phases, also, are less than those for the b.c.c. metastable phase of pure Bi₂O₃. Therefore, the compositions of the impure metastable phases cannot be that of pure Bi₂O₃. However, contrary to the case of the stable b.c.c. phases, no correlation exists between unit cell dimensions and ionic radius for the metastable b.c.c. phases. The x-ray diffraction patterns of the b.c.c. phases of the stable and metastable impurity forms are similar in d spacings and intensities to the pattern for pure Bi₂O₃. It is a reasonable assumption that the structures are similar.

To summarize (see fig. 7), the b.c.c. phase of pure Bi₂O₃ has the largest unit cell dimensions, and the addition of a foreign ion to Bi₂O₃ tends to decrease the dimensions. This decrease is least for the larger ions, which tend to form the metastable b.c.c. phase. The decrease in cell dimensions is greatest for the smaller ions, which tend to form the stable b.c.c. phase. Whereas the stable b.c.c. phases show correlation with ionic radius, the metastable phases do not. These findings are compatible with a cage-type structure in which a central cation, including Bi, is surrounded by a sphere of atoms of approximately Bi₁₂O₂₀ composition.

4. Summary

The important phase equilibria relationships for the bismuth-rich portions of the phase diagrams are shown schematically in figure 8. Elements in boldfaced type refer to the respective oxide mixtures studied. Elements enclosed in heavy outlines represent oxides which formed the stable b.c.c. phase with bismuth oxide. Composition of the b.c.c. phase was found to be variable for different systems, but most nearly approached the ideal 12Bi:1Me ratio for oxides of the tetravalent ions Si⁴⁺, Ti⁴⁺, and Ge⁴⁺. Designations in the upper right-hand corners of the boxes for the stable b.c.c. phases refer to the nature of melting, e.g., congruent, incongruent, or decomposition. Oxides of elements which formed the metastable b.c.c. phase are indicated by an M in the upper right-hand corner of the box, and those that formed the rhombohedral solid solution phase, by Rh. The nature of the liquidus curves is indicated by a designation in the lower right-hand corner of each box, as follows: E, simple eutectic; ss_r, solid solution type with liquidus and solidus raised; ss_L, solid solution type with liquidus and solidus lowered.

Figure 8. Summary of some phase equilibria data on the effect of oxide additions to Bi₂O₃. Elements shown in boldfaced type on the Periodic Table refer to oxide additions.

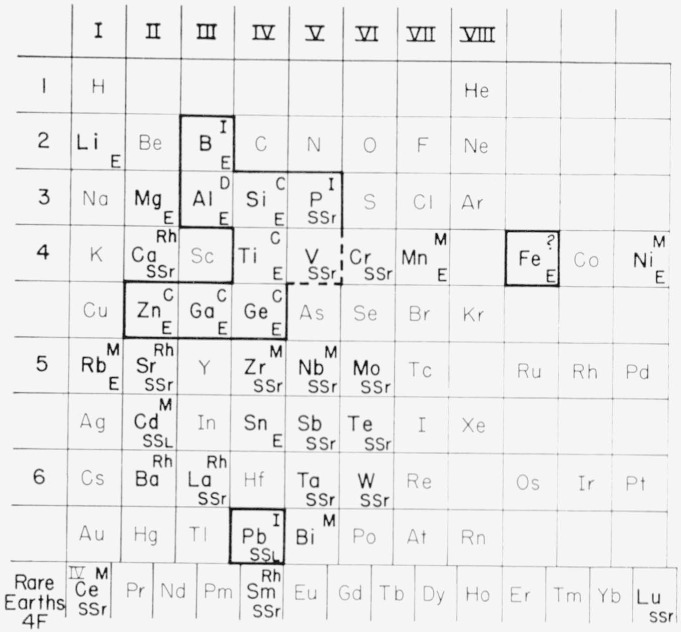
Elements enclosed in heavy outlines represent oxides which form stable body- centered cubic phases with bismuth oxide:

C—congruently melting

I—incongruently melting

D—decomposes

M—metastable body-centered cubic phase

E—eutectic-type system

SS_r—solid solution of oxide in Bi₂O₃, with solidus and liquidus raised

SS_L—solid solution, with solidus and liquidus lowered

Rh—rhombohedral solid solution phase [7, 8].