A theoretical and experimental study of calcium, iron, zinc, cadmium, and sodium ions absorption by aspartame

Abstract

Aspartame (L-Aspartyl-L-phenylalanine methyl ester) is a sweet dipeptide used in some foods and beverages. Experimental studies show that aspartame causes osteoporosis and some illnesses, which are similar to those of copper and calcium deficiency. This raises the issue that aspartame in food may interact with cations and excrete them from the body. This study aimed to study aspartame interaction with calcium, zinc, iron, sodium, and cadmium ions via molecular dynamics simulation (MD) and spectroscopy. Following a 480-ns molecular dynamics simulation, it became clear that the aspartame is able to sequester Fe²⁺, Ca²⁺, Cd²⁺, and Zn²⁺ ions for a long time. Complexation led to increasing UV–Vis absorption spectra and emission spectra of the complexes. This study suggests a potential risk of cationic absorption of aspartame. This study suggests that purification of cadmium-polluted water by aspartame needs a more general risk assessment.

Introduction

Aspartame (C₁₄H₁₈N₂O₅) (N- (L-Aspartyl) -L-phenylalanine, 1-methyl ester) (Fig. 1) was discovered in 1965 by James Schlatter. It is an artificial dipeptide sweetener [1, 2] approved for use in food products by the U.S. Food and Drug Administration (FDA) in 1981 [3]. Aspartame is about 200 times sweeter than sucrose, leaves no bitter taste in the mouth, and is widely used in the food industry in beverages, conserve foods, candies, and pastries. Aspartame is sold under the brand names Equal, NutraSweet, and Canderel [4]. Today, millions of people around the world consume foods and soft drinks containing NutraSweet. Long-term consumption of aspartame causes adverse effects including sight problems, depression, insomnia, spasms, neurological disorders, and sensory ataxia [5].

Fig. 1.

Structure of aspartame

Calcium is vital for all organisms. Entry and exit pathways for the calcium ion into the cell cytoplasm are used as a signal for many cellular processes. Mineralization of bone, teeth, and shells are dependent on the calcium so that it is the most abundant element by mass in many animals [6]. Calcium does not exist naturally because it will react quickly with other elements. Calcium deficiency leads to rickets in children [7]. Common diseases such as osteoporosis, arisen from the use of aspartame, may cause more than 8.9 million fractures annually [8]. The National Institute for Health and Clinical Excellence (NICE) estimates that in England and Wales more than 2 million women are thought to have osteoporosis [9].

Iron exists in all cells in the human body with many functions, such as oxygen transferring from the lungs to the tissues; acting as a transport medium for electrons within the cells; facilitating oxygen use and storage in the muscles and as an integral part of enzyme reactions in various tissues. When there is too little iron in the body, the above vital functions can be interfered with and result in morbidity (anemia latent iron deficiency or iron-deficient erythropoiesis) and death [10].

Another essential element for humans, other animals, plants, and for microorganisms is zinc [11], which is found in almost 100 specific enzymes [12]. Acting as structural ions in transcription factors, zinc is stored and transferred in metallothioneins. The amino acid side chains of aspartate, glutamate, cysteine, and histidine residues are usually correlative with zinc ions [11]. Zinc is mainly present in the brain, muscle, bones, kidney, and liver, with the highest concentrations in the prostate and parts of the eye [12]. With a wide range of organic ligands, which regulates apoptosis, zinc is involved in the multitude of metabolic processes such as DNA and RNA, signal transduction, and gene expression. Insufficient dietary intake, associated with malabsorption, acroesthesia, chronic liver disease, chronic renal disease, sickle cell disease, diabetes, malignancy, and other chronic illnesses, may lead to zinc deficiency [13, 14].

An essential nutrient that regulates blood volume, blood pressure, osmotic equilibrium, and pH with a minimum physiological requirement of 500 mg per day, is sodium [15]. The ultimate source of sodium is sodium chloride, which comes from processed foods. Sodium is essential in nerve cells, osmoregulation, extracellular fluid, and Na⁺/K⁺-ATPase pump, so sodium is the most prominent cation in extracellular fluids.

Although cadmium has no biological role in higher organisms, a cadmium-dependent carbonic anhydrase has been found in some marine diatoms [16]. Usually, the diatoms live in the sea where the concentration of zinc is low and cadmium can perform functions normally carried out by zinc in other anhydrases. This finding was done using X-ray absorption fluorescence spectroscopy. The vast majority of human cadmium is known to accumulate in the kidneys, and up to about 30 mg of cadmium is commonly inhaled throughout childhood and adolescence. Cadmium is able to block calcium channels in chicken sensory neurons [17, 18].

Molecular dynamics simulation is a very powerful method for modern molecular modeling. It allows following and understanding structure and dynamics with extreme details—literally on scales where the motion of individual atoms can be tracked [19]. Alder and Wainwright (1957) were the first to perform molecular dynamics [20]. Since the 1970s, advances in computer technology and algorithmic improvements has made MD simulation a valuable tool in many areas of science, such as proteins or nucleic acids [21]. Currently, conventional MD simulations are being used to study the interactions between proteins and ions in dilute salt solutions [22–24].

Studies have shown that that aspartame can enhance the absorption of ions. For example, experimental studies show that aspartame can affect calcium levels in the body and long-term use of it may lead to osteoporosis [25]. In addition, Kongkachuici et al. (1997) showed that 2 μg of aspartame increase the iron uptake and transport rate by Caco-2 cells [26]. The voltammetric behavior of aspartame in the presence of Cu(II), Ni(II), and Zn(II) was investigated by Cakir et al. (2003), showing that with increasing the aspartame concentration, copper, zinc, and nickel ions were reduced [27]. Due to negatively charged carboxyl oxygens and the aromatic ring of phenylalanine in the aspartame structure, it was postulated that aspartame might be able to enhance or stimulate cation uptake and transport. So far, no theoretical study has been done regarding the cationic absorption of aspartame. This study therefore aimed to demonstrate potential cation absorption of aspartame via molecular dynamic simulation and UV–Vis and fluorescence spectroscopy.

Methods

Theoretical methods

The three-dimensional structure of aspartame was drawn via HyperChem 7 software [28] and minimized by molecular mechanics method through MM⁺ force field. This structure was used as a starting structure for the molecular dynamics simulation.

Acpype/Antechamber software was used to generate a topology file of aspartame [29] based on GAFF (General AMBER force filed). The total charges of aspartame were set to zero and RESP atomic charges were calculated with the Merz−Kollman electrostatic potential fitting procedure. Thus, the Gaussian 98 quantum chemistry program using this command: HF/6-31G* Pop = MK IOp (6/33 = 2, 6/41 = 10, 6/42 = 17) [30] was used and then transferred to a topology file of the aspartame.

We also used Amber99 force field for ion parameters. The nonbonded parameters of Zn²⁺, Ca²⁺, Na⁺, and Fe²⁺ exist in the Gromacs library by default. The nonbonded parameters for VDW interaction (C6, C12) of cadmium were C6 = 1.06733 × 10⁻³ nm⁶kJ/mol and C12 = 6.145441 × 10⁻⁸ nm¹²kJ/mol based on Brewager’s paper [31] and inserted into ffnonbonded.itp file of the GROMACS software package.

At first, 80-ns MD simulation of aspartame in pure water was performed. The final structure was then used for five molecular dynamics simulations in which three cations (Ca⁺² or Fe⁺² or Zn⁺² or Cd⁺²) or six Na⁺ and six Cl⁻ ions and one aspartame molecule were enclosed in a fully hydrated simulation box. Molecular dynamics simulation was performed using the GROMACS 4.5.7 package [32, 33].

The aspartame was embedded into a box containing about 10,000 TIP4P water that extended for at least 3.2 nm between aspartame and the edge of the box. Ionic strength was set to 50 mM [34] and the ions were replacing the water molecules in random positions. At first, the whole system became minimized using steepest descent and conjugate gradient algorithms. After the minimization, an MD equilibration run was performed under position restraints for 500 ps in NVT and 1,000 ps in NPT ensemble. The latter was made using Berendsen’s coupling algorithm to keep the temperature and the pressure constant (P = 1 bar, τ _P = 0.5 ps; T = 300 K; τ _T = 0.1 ps) [35]. During the equilibration run, the LINCS algorithm was used to constrain the lengths of hydrogen-containing bonds and the waters molecules were restrained using the settle algorithm [36]. The time step for the simulation was 2 fs. Van der Waals forces were treated using a cutoff of 1.2 nm. Long-range electrostatic forces were treated by using the particle mesh Ewald method [37] using a cutoff of 1.4 nm. The coordinates were saved every 0.5 ps. An 80-ns MD simulation was performed for each system with a time step 2 fs.

The pqr and APBS maps (dx files) were made by PDB2PQR Server (version 1.8) (http://nbcr-222.ucsd.edu/pdb2pqr_1.8/) [38]. Three-dimensional density maps of cations around the aspartame over an 80-ns MD trajectory were created via a grid count using g_ri3Dc and a_ri3Dc utilities [39]. All images were generated by the VMD 1.8.5 software [40].

Experimental methods

UV–Vis absorption spectroscopy

UV–Vis spectroscopy, used in the study of covalent and non-covalent interactions, involves the absorption of electromagnetic radiation from the 200–800 nm range and the subsequent excitation of electrons to higher energy states. Specific functional groups in the molecules can absorb light at characteristic wavelengths in the UV–Vis region. This technique can be used to determine the presence of these groups in the sample with investigating the complexation reaction and sustaining structural information obtained from other methods [41, 42]. The UV–Vis absorption spectra were measured using an Ultrospec 3100 pro Pharmacia UV–Vis spectrophotometer at 25 °C and pH = 7 and spectra were recorded between 200 and 300 nm. The samples were thermally equilibrated for at least 5 min before measuring in quartz cuvettes. No time-dependence UV–Vis spectra were detected. At various concentrations of NaCl, CdCl₂, ZnCl₂, and CdCl₂, the concentration of aspartame was 0.005 M. Stoichiometry of cations relative to aspartame molecule was 0:1, 1:1, 2:1, 3:1, 4:1, and 5:1 in samples S0, S1, S2, S3, S4, S5, respectively, for each cation. Changes in absorbance values were recorded at 256 nm [43]. All compounds were purchased from Sigma Company.

Fluorescence spectroscopy measurements

The binding of a ligand to a protein may directly affect the fluorescence of aromatic residues by acting as a quencher, or by physically interacting with the fluorophore, thereby changing the polarity of its environment and their accessibility to the solvent [44]. Steady-state fluorescence measurements studies were performed using a Shimadzu RF-5301 fluorescence spectrophotometer equipped with a temperature adjustable cell holder. The emission spectra, excited at 256 nm, were measured at 25 °C and emission wavelength 260–350 nm [45]. The slit widths for excitation and emission were 3 and 5 nm, respectively. Fluorescence spectra were recorded in each step of temperature elevating processes. All studies were carried out in quartz cells with the same concentration of UV–Vis spectroscopy. The samples were thermally equilibrated for at least 5 min before measuring in quartz cuvettes. No time-dependence of fluorescence spectra was detected.

Results

Theoretical results and discussion

MD simulation results of aspartame in the presence or absence of different cations

Table 1 shows the root mean square deviation (RMSD) of aspartame atoms relative to the initial positions and average energy of the entire simulation box, radius of gyration (Rg), temperature, accessible surface area (ASA) of aspartame, and average of intermolecular hydrogen bonds between aspartame and water during the last 60 ns of 80 ns MD simulation in the absence and presence of different cations. During the simulation, the stability of the aspartame was evaluated by the root mean square deviation (RMSD) of aspartame relative to the starting structure. As shown in Table 1, the RMSD of aspartame atoms in the presence of each cation was steady over time, exhibiting fluctuations that reached maximal values of about 0.05 nm in the simulation. The RMSD of aspartame atoms represents the equilibration of all systems after about 20 ns of MD simulations. This consistency dictates that the aspartame was stable under the simulation conditions. The kinetic and potential energy fluctuations were in equal and opposite directions in all phases during MD simulation. Based on the achieved small standard deviation of the radius of gyration and accessible surface area of aspartame in the presence of each cation during the last 60 ns of simulation, different cations caused no changes in the volume and three-dimensional structure of aspartame. Also, variations of the potential energy the entire simulation box and temperature during the last 60 ns of MD simulation were small. This indicates that there was thermal equilibrium in all systems.

Table 1.

The average of RMSD, Rg, accessible surface area (ASA) of aspartame, temperature, intermolecular hydrogen bonds between aspartame and water, and potential energy of entire simulation box during the last 60 ns of 80 ns MD simulation of aspartame in absence and presences of different cations

Cation	RMSD of aspartame atoms (nm)	Rg (nm)	ASA of aspartame (nm2)	Temperature (K)	Intermolecular hydrogen bonds between aspartame and water molecules	Potential energy of entire simulation box (kJ/mol)
Without ion	0.19 ± 0.03	0.36 ± 0.01	5.35 ± 0.19	300 ± 1.83	10.8 ± 1.55	−413891 ± 776
Cd+2	0.2 ± 0.03	0.35 ± 0.01	4.34 ± 0.15	300 ± 1.7	7.16 ± 1.32	−423846 ± 687
Fe+2	0.2 ± 0.03	0.35 ± 0.01	4.41 ± 0.15	300 ± 1.8	7.32 ± 1.35	−421690 ± 721
Ca+2	0.2 ± 0.02	0.35 ± 0.01	4.40 ± 0.15	299.9 ± 1.7	9.06 ± 2.25	−419757 ± 714
Zn+2	0.18 ± 0.05	0.36 ± 0.01	5.34 ± 0.19	299.8 ± 1.8	7.42 ± 1.42	−394553 ± 549
Na+	0.2 ± 0.04	0.36 ± 0.01	4.43 ± 0.15	300 ± 1.8	10.87 ± 1.6	−419900 ± 642

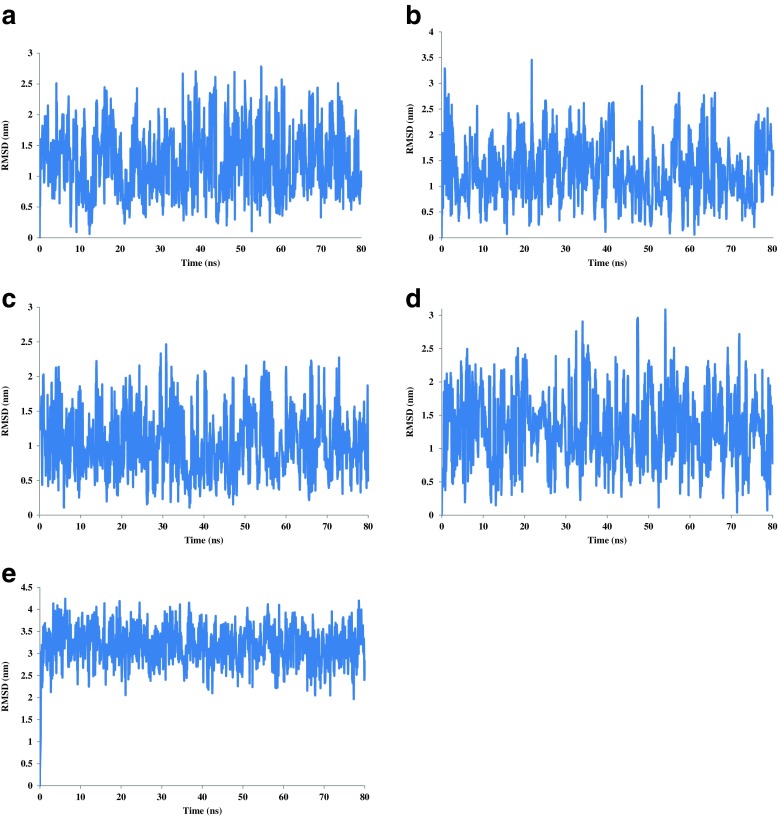
In addition, RMSD of cations relative to start positions during 80-ns simulation are shown in Fig. 2. As seen, the fluctuation in RMSD for all cations is about 0.5 nm and some deal with stable positions.

Fig. 2.

Root mean square deviation (RMSD) of cations during 80-ns MD simulation in the presence of calcium (a), zinc (b), iron (c), cadmium (d), and sodium (e) ions

Root mean square fluctuation (RMSF) of atoms is a measure of the average atomic mobility or flexibility of atoms. RMSFs of aspartame atoms in the absence or presence of each cation are shown in Fig. 3, which suggests almost equivalent flexibility of the aspartame atoms in the absence or presence of different cations.

Fig. 3.

Root mean square fluctuation (RMSF) of aspartame in absence or presence of different cations

The RMSF of all cations except Na⁺ is close to 1 nm (Table 2). This means that locomotion of divalent cations in the simulation was equivalent. However, in the case of Na⁺, the RMSF is about 3 nm, which means that the mobility of Na⁺ was more than other cations. This could be rational because Na⁺ has less positive charge relative to other cations. Again, small standard deviations of the RMSF of cations indicate that cations almost reached a stable position during MD simulation.

Table 2.

The ratio of the total energy drifts to the average of total energy and the average of RMSD and RMSF of cations and computational and experimental diffusion coefficient of all cations

Cation	Drift1 × 10−4	Average RMSD of cations (nm)	Average RMSF of cations (nm)	Computational diffusion coefficient of cations × 10−5 (cm2/s)	Experimental diffusion coefficient of cations × 10−5 (cm2/s)
Cd+2	3.3	1.3 ± 0.52	1.03 ± 0.11	0.12 ± 0.2	0.719
Fe+2	7.3	1.03 ± 0.43	0.94 ± 0.13	0.43 ± 1.1	0.719
Ca+2	2	1.26 ± 0.48	1.15 ± 0.14	0.89 ± 0.38	0.792
Zn+2	0.32	1.84 ± 0.61	1.02 ± 0.182	2.18 ± 1.1	0.703
Na+	0.08	3.16 ± 0.4	2.9 ± 0.25	2.6 ± 0.2	1.33

The ratio of the total energy drifts to average of total energy

The ratio of the total energy drift to the average of total energy in all systems was lower than 0.001 (Table 2). This fact shows that there was a low drift in the total energy during MD simulations and that the simulation times were sufficient and stable under convergence conditions. The computational and experimental diffusion coefficients [46] of all ions are shown in Table 2. As shown, in spite of the simplicity of the water model and the small number of ions, the simulation of the Brownian motion of the ions is realistic and theoretical and experimental diffusion coefficients are compatible. Of course, experimental diffusion coefficients were calculated in an infinitely dilute solution but theoretical diffusion coefficients were calculated at a concentration of 16.6 mM for each cation.

Figure 4 shows the minimum distance between each cation and aspartame during 80-ns MD simulation. The results show that aspartame can absorb cations and put them into its negative potential cavity, but after some time it voids due to the Brownian motion. In other words, at least one of the Ca²⁺, Fe⁺², Cd⁺², or Zn²⁺ ions can be trapped by aspartame during long-time MD simulations, but Na⁺ ions are weakly absorbed by aspartame during 80-ns MD simulation. The minimum distance distances between Cl⁻ ions and aspartame in each system does not show any absorption by aspartame either (data not shown).

Fig. 4.

Minimal distance (nm) between calcium (a), zinc (b), iron (c), cadmium (d), and sodium (e) ions and aspartame during 80-ns MD simulation

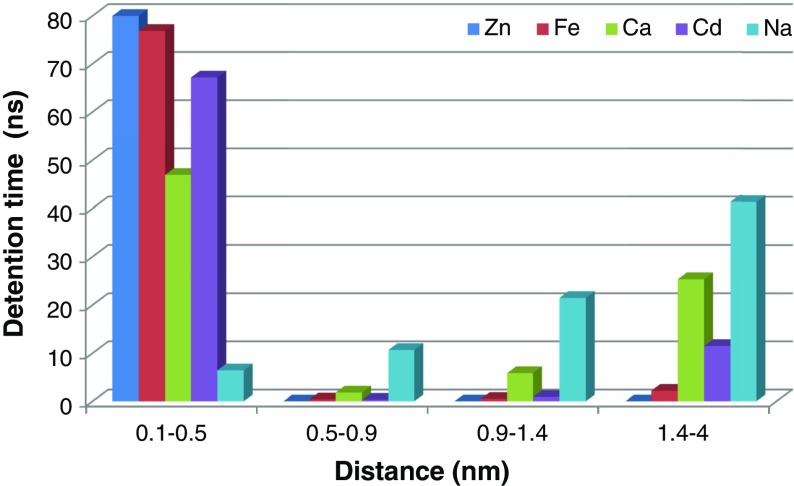
Figure 5 shows retention time versus the minimum distance between the cations and aspartame as a histogram during 80-ns MD simulation. As seen, aspartame can detain Cd²⁺, Fe²⁺, Ca²⁺, and Zn²⁺ ions at least in the half-way of the simulation time for the distance range from 0.1 to 0.5 nm.

Fig. 5.

Detention time for cations versus distance from aspartame atoms during 80-ns MD simulation

Using the Einstein–Smoluchowski equation, and in the absence of external force, the relation between displacement of a particle and diffusion coefficient with time is as follows: t = <∆²>/6D [47], where <∆²> is the mean square displacement of a particle (equals 5 Å in this study), and D is the computational diffusion coefficient of a particle (mentioned in Table 2) around the aspartame’s surface. It can then be calculated that cadmium, iron, calcium, zinc, and sodium ions will propagate to 5 Å within aspartame in 0.34, 0.097, 0.04, 0.02, and 0.016 ns, respectively. As seen in Fig. 5, tens of nanoseconds appear to be correlated with at least one ion, which remains in 5 Å from aspartame. Also, because cations are sequestered around aspartame for a long time, then their movement must be biased by the presence of it.

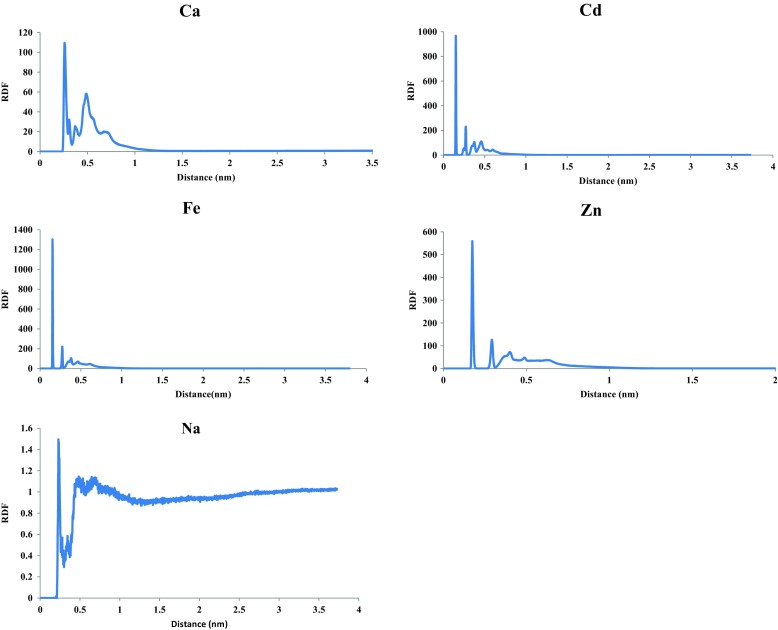
Radial distribution function (RDF) or pair correlation function (r), describes how the atomic density varies as a function of the distance from one particular atom. The structure of a system, particularly liquid, can easily be described by the RDF. Figure 6 shows the RDFs of cations with respect to the aspartame. The peak positions of cations in relation to the aspartame atoms were at 0.14, 0.15, 0.17, 0.23, and 0.26 nm for Cd²⁺, Fe²⁺, Zn²⁺, Na⁺, and Ca²⁺ ions, respectively. This is due to the strong attractive forces between cations and aspartame. These results also verify the previous results for ion absorption of aspartame.

Fig. 6.

Radial distribution functions of aspartame to cations during 80-ns MD simulation

Cations can be absorbed to aromatic rings through cation-π interactions [48]. In order to compare the attractiveness of the carboxyl oxygens (four atoms) or aromatic ring of phenylalanine with cations, the minimum distance between these groups and cations for each simulation were calculated. The average number of contacts below 0.6 ns between them and cations during the last 60 ns of 80 ns MD simulation are shown in Table 3. The results show the power of the carboxyl oxygens is more than the aromatic ring of phenylalanine for cation absorption. Cations stay near the carbonyl and carboxyl oxygens, either at a van der Waals contact distance or separated by a single solvation layer. Although we did not perform quantitative electronic structure calculation for comparison of electrostatic interaction between carboxyl oxygens or benzene ring with cations, but it appears that electrostatic interactions of carboxyl oxygens (with a total charge of -3.38898 e) with cations are more important than π interactions of the benzene ring (with a total charge of -0.02249 e) with cations.

Table 3.

Average minimum distances (nm) benzene ring of phenylalanine or carbonyl and carboxyl oxygens with each cation and the number of contacts below 0.6 ns between them during the last 60 ns of 80-ns MD simulation

Cations	Minimum between cations with benzene ring	The number of contact cations with benzene ring	Minimum distance cations with carbonyl and carboxyl oxygens	The number of contact cations with carbonyl and carboxyl oxygens
Cd+2	0.63 ± 0.14	1.45 ± 2.22	0.15 ± 0	3.77 ± 0.45
Fe+2	0.69 ± 0.14	0.93 ± 2.4	0.15 ± 0	3.43 ± 0.56
Ca+2	1.30 ± 0.86	0.53 ± 1.4	1.02 ± 1.03	2.06 ± 1.77
Zn+2	0.74 ± 0.137	0.17 ± 0.37	0.18 ± 0.004	1 ± 0.05
Na+	1.59 ± 0.6	0.04 ± 0.21	1.55 ± 0.64	0.23 ± 0.78

Interaction energies

Table 4 shows the average electrostatic and van der Waals energies between aspartame and cations and also the electrostatic and van der Waals energies and intermolecular potential energy (electrostatic + van der Waals) between aspartame and water in the presence and absence of cations during the last 60 ns of 80-ns MD simulation.

Table 4.

Average electrostatic and van der Waals energies between aspartame and cations or water and intermolecular potential energy of aspartame with water during the last 60 ns of 80-ns MD simulation and the time fraction of cations (TF) in distance 5 Å from aspartame and free energy of detainment ∆G_det (kJ/mol) of the nearest cations to aspartame

Cation	Average electrostatic energy between aspartame and cations (kJ/mol)	Average van der Waals energy between aspartame and cations (kJ/mol)	Average electrostatic energy between aspartame and water (kJ/mol)	Average van der Waals energy between aspartame and water (kJ/mol)	Intermolecular potential energy aspartame with water	TF	∆Gdet
Without ions	–	–	−622.4 ± 53.8	−39.67 ± 23.7	−662.07	–	–
Cd+2	−868.6 ± 76.1	0	−231.4 ± 52.8	62.8 ± 26.5	−168.6	0.84	−14.35
Fe+2	−754.8 ± 48.4	60 ± 12	−286 ± 57	−43 ± 20	−329	0.96	−18.2
Ca+2	−196 ± 172	13.3 ± 1.4	−440.6 ± 154	−67.5 ± 33	−508.1	0.59	−11.1
Zn+2	−507.2 ± 29.5	45.9 ± 13.7	−217.4 ± 42.6	−28.6 ± 20.4	−246	1	IF*
Na+2	−6.9 ± 31	0.4 ± 2.6	−594.4 ± 75	−42.6 ± 21.7	−637	0.08	−2.41

*IF: The value of ∆G_det cannot be calculated via the mentioned formula because TF = 1 and ∆G_det approaches −∞

There was a good correlation between the number of hydrogen bonds of aspartame with water molecules (Table 1) and electrostatic energy (R ² = 0.97) or intermolecular potential energy of aspartame with water molecules (R ² = 0.93). In contrast, there was a weak correlation between van der Waals energy of aspartame’s interactions with water molecules and hydrogen bonds of aspartame with water molecules. Thus, it appears that a decrease in the number of hydrogen bonds of aspartame with water molecules in the presence of Cd²⁺, Fe²⁺, and Zn²⁺ (about seven), compared to no-cation state (about 11) or an increase in electrostatic (or intermolecular potential) energy between these cations and water molecules to be of great significance, which leads to a decrease of aspartame solubility in water (similar to salting-out phenomenon).

The electrostatic interactions of aspartame with cations are more negative and are more important than van der Waals interactions which exist between them. Thus, it can be concluded that electrostatic interactions play an important role in the interaction of aspartame with cations. The ranking order for negative electrostatic interactions or attractions between aspartame and cations is the same as the average minimum distance between aspartame and cations, i.e., Cd²⁺, Fe²⁺, Zn²⁺, Ca²⁺, and Na⁺ from the most negative to the less negative energy, respectively (Table 4).

In addition, in order to measure the affinity of the different cations to aspartame, a two-state model was used for the absorption of ions. In this model, if ions are less than 5 Å away from the aspartame, they are considered to be internment. They are otherwise free. According to this definition, the equilibrium constant for detainment (K_det) is calculated as follows: K_det = TF/(1 − TF)C, where C is the concentration of the cations in solution (0.0332 M for sodium and 0.0166 M for other cations) and TF is the time fraction of cations within 5 Å distance from the aspartame (Table 4). Then, the free energy of internment was obtained by this equation: ΔG_det = − RT ln K _det [22]. It is worth mentioning that these energies are based on the nearest cation to the aspartame and not the average detainment energy of all three of the cations used for each simulation. In other words, it is detainment energy of the only entrapped cation in the negative cage of aspartame.

The electrostatic potential map

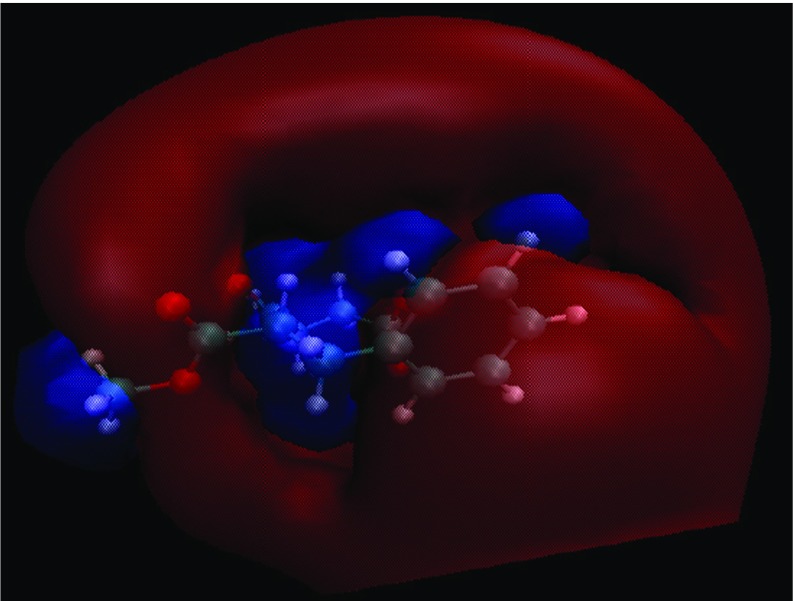
Figure 7 shows the electrostatic potential surfaces around aspartame (final structure) after 80-ns MD simulations of aspartame in pure water without ions. The electrostatic potential about the aspartame was calculated using the PDB2PQR website [38] with a grid spacing of 0.4 Å and solvent dielectric value ɛ = 78.4 and a solute dielectric value ɛ = 2.

Fig. 7.

Electrostatic potential surface around aspartame in the absence of ions. Negative isocontours are in red and positive isocontours are in blue. Isovalues were considered +1 and −1 for positive and negative charges respectively in picture generation

The potential field consists of two main lobes, one positive (blue), and the other negative (red); the ions are attracted to the oppositely charged lobes, and interact with the atoms enclosed within this space. The Coulomb cages for the positive and negative domains are drawn at the distance where the electrostatic potential equals 1 k_BT/e. As seen, the Coulomb cage of negative charges are bigger than positive charges, therefore aspartame can absorb more cations than anions. Thus, close inspection of the electrostatic potential surfaces is the first step for cationic absorption of aspartame and this figure confirms the other results.

The space distribution of cationic ions around the aspartame

Figure 8 shows the 3D density maps of the cations around aspartame during the last 50 ns MD simulation. The spatial distribution of Cd²⁺, Fe²⁺, and Zn²⁺ ions is smaller than sodium ions. It can then be concluded that the power of absorption of aspartame for Cd²⁺, Fe²⁺, and Zn²⁺ is more than for sodium ions.

Fig. 8.

3D density of cations around aspartame during the last 50 ns of MD simulation

Figure 9 shows the average accessible surface area (ASA) (Ų) of the aromatic ring of aspartame phenylalanine during the last 60 ns of simulation. These results show a partial reduction of the aromatic ring surface (about 0.1 Å²) following cation absorption via aspartame. This could be due to the low number of cations and trivial absorption of the aromatic ring in the theoretical study.

Fig. 9.

The average of accessible surface area (ASA) (Ų) of aromatic ring of phenylalanine during the last 60 ns of simulation

Experimental results

Spectroscopy results

To obtain insight into the interaction of cations with aspartame experimentally, UV–Vis absorption spectra were recorded. The UV–Vis absorption spectra of aspartame in the absence and presence of different concentrations of cations were between 200 and 300 nm. We obtained a peak for amide and carboxylate group at about 210 nm and a peak at 256 nm for benzene ring. The differences of absorbance in carboxyl and amide peak were ambiguous. However, the differences in absorbance at 256 nm were clear and obvious; then we used the peak of absorption at 256 nm for our study. Although carbonyl oxygens are more reactive than the aromatic ring, the spectroscopic method can often detect the changes in the microenvironment of aromatic groups so that the environment of Phe residues changed after interaction of aspartame with cations. These complexes had a higher molar extinction coefficient than the unabsorbed states with an absorption peak at the same position. The addition of chloride salts (cations) at pH = 7 to the aspartame solution or increasing cation concentration resulted in an absorbance increase at 256 nm, which are shown in Fig. 10.

Fig. 10.

UV–Vis absorbance spectra of aspartame cations at 256 nm in the presence of different ratios of cations to aspartame. S0 Without cations, S1 one cation, S2 two cations, S3 three cations, S4 four cations, S5 five cations versus one aspartame molecule

Spectroscopic results are consistent with the theoretical results of cation absorption of aspartame (Table 3). Also, the interaction of cations with aspartame at room temperature was evaluated by monitoring the intrinsic fluorescence intensity changes of the aspartame upon the addition of cations. Aspartame is a dipeptide with a Phe residue and its intrinsic fluorescence is mainly contributed by the Phe residue alone. However, the phenylalanine residue has a low quantum yield. Aspartame in solution was excited at 256 nm and emission spectra were recorded in the wavelength range of 260–350 nm (emission maximum at 281 nm) at 25 °C. The fluorescence spectra in the presence and absence of various concentrations of cations are shown in Fig. 11. The fluorescence intensity of aspartame gradually increased after the addition of cations but a red or blue shift was not observed when the concentration of aspartame was fixed. In other words, the intrinsic fluorescence of the aspartame Phe residue demonstrated no significant shift (data not shown) in the presence of different cations. These observations could be attributed to the binding interactions of cations to the aspartame. The increased fluorescence intensity is consistent with the partial reduction of the accessible surface area of the aromatic ring of phenylalanine induced by absorption of cations (Fig. 9). In addition, the emission of aspartame in the presence of sodium is more than that of other cations. The results are consistent with the conclusion that the largest decrease in accessible surface area of the aromatic ring (relative to no-cation state) occurs in the presence of sodium ions (Fig. 9). Therefore, changes in the fluorescence intensity of the aspartame due to the binding of cations to aspartame would affect the microenvironment around the Phe residue. In sum, both UV–Vis and fluorescence spectroscopy confirm cation–aspartame interactions.

Fig. 11.

Intensity of fluorescence emission (IFE) at 281 nm in the presence of different ratios of cations to aspartame. S0 Without cations, S1 one cation, S2 two cations, S3 three cations, S4 four cations, S5 five cations versus one aspartame molecule

Conclusions

Theoretical ion absorption has been studied by some authors [22–24, 34, 40–52]. For example, Friedman et al.’s study showed that a protein could sequester Na⁺ ions [22]. Also, Saffar et al. showed that a mutated SmtA protein could absorb cadmium ions [24]. In addition, experiments on ion Europium (III) absorption with the zwitterion form of amino acids by means of UV–Vis spectroscopy were studied by Heller et al. [42]. Then ionic absorption of proteins can be studied by theoretical and experimental methods. Because of the similarity between symptoms of calcium deficiency and illnesses caused by aspartame consumption, we conjectured that aspartame may interact with cations in foods or blood and remove them from the body. In this study, to investigate the absorption of calcium, iron, zinc, sodium, and cadmium ions by aspartame, MD simulations were carried out in explicit solvent. The average minimum distance and attractive (negative) electrostatic interactions and the first peak of the radial distribution function between aspartame and cations and other results indicate that aspartame can sequester cations for a long time in its proximity or near its surface and bias Brownian motions of cations. The ranking of cation detention of aspartame according to our results is Cd⁺²>Fe⁺²>Zn⁺²>Ca⁺²>Na⁺.

In addition, UV–Vis and fluorescence spectroscopy showed the interaction and absorption of cations with aspartame.

In the experimental study, the concentration of cations was variable with a high number of cations in each sample. In contrast, in the theoretical study, the concentration of cations was constant with a lower number of cations (only three cation in each simulation state). Thus, it appears that, while predicting UV–Vis spectra from MD simulation is not straightforward, a comparison of the ranking order of experimental (UV–Vis results and fluorescence spectroscopy) and theoretical method is not authentic.

In addition, because of more negatively charged oxygens in the aspartame than in the benzene ring, it seems that in the interactions with cations, electrostatic interactions of carboxyl oxygens are more important than cation-π interactions of the benzene ring. Similar results were obtained via Heller et al. in complexation of alanine with Europium (III) in water. They also showed that the complex stability constants of the carboxyl group of side chain aspartic and glutamic acid with Europium (III) ion were high [42].

This study suggests that one of the potential risks of aspartame in blood and in the digestive system is the absorption of essential cations. Experimental studies showed that aspartame consumption causes osteoporosis after long exposure [25]. This fact is compatible with calcium absorption through aspartame obtained in this study.

Cadmium, as one of the most toxic elements, has serious adverse effects on the environment. Aspartame (or poly-aspartame attached to a polymer), is a potential drug candidate for the treatment of cadmium toxicity because it is able to absorb Cd²⁺ and other cationic ions.