A dynamical model of immune responses to antigen presentation predicts different regions of tumor or pathogen elimination

Abstract

The immune system must discriminate between agents of disease and an organism’s healthy cells. While the identification of an antigen as self/non-self is critically important, the dynamic features of antigen presentation may also determine the immune system’s response. Here, we use a simple mathematical model of immune activation to explore the idea of antigen discrimination through dynamics. We propose that antigen presentation is coupled to two nodes, one regulatory and one effecting the immune response, through an incoherent feedforward loop and repressive feedback. This circuit would allow the immune system to effectively estimate the increase of antigens with respect to time, a key determinant of immune reactivity in vivo. Our model makes the prediction that tumors growing at specific rates evade the immune system, despite the continuous presence of antigens indicating disease, a phenomenon closely related to clinically observed “two-zone tolerance.” Finally, we discuss a plausible biological instantiation of our circuit using combinations of regulatory and effector T cells.

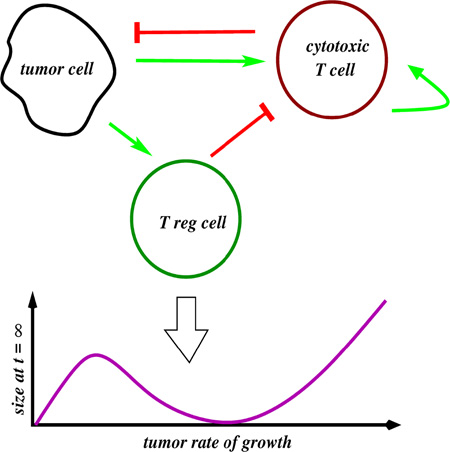
Graphical abstract

INTRODUCTION

In vertebrates, the innate and adaptive immune systems combine to provide a finely orchestrated multicomponent host defense mechanism, which protects against infective pathogens and also helps to identify and eliminate malignantly transformed cells (Kindt et al. 2013; Abbas, Lichtman, and Pillai 2016). A prerequisite for successful immune action is the ability to distinguish agents of disease from an organism’s own healthy cells. A central role in this discriminatory ability is played by antigens, which are molecules capable of inducing an immune response. Nonself antigens appear not only in pathogens, but also in malignantly transformed cells due to their overexpression of normal proteins, mutated proteins, or oncogenic viruses. In its normal functioning, the immune system is trained not to react improperly to self-antigens. This paradigm of “self/nonself pattern” recognition traces back to Burnet (F. Burnet 1957), and related ideas in (Talmage 1957).

The static view, however, is not entirely consistent with a number of phenomena which hint to a role for discrimination based on the antigen’s dynamic features, as suggested by the following examples: (1) The presence of commensal bacteria (microbiome) is stably tolerated by the immune system, despite the presence of bacterially derived, non-self molecules that exist in intimate proximity to the host (Pradeu 2012). (2) Slow-growing tumors are known to evade the immune system (Grossman and Berke 1980) despite their expression of non-self antigens. (3) Decreased activation of natural killer cells is observed under chronic receptor activation (Pradeu, Jaeger, and Vivier 2013) despite the continued presence of antigens. (4) The reduced capacity of a host to respond to the pro-inflammatory stimuli of bacterial signatures such as lipopolysaccharides after a first exposure to the same type of stimulus, a phenomenon called endotoxin tolerance in macrophages (also known as deactivation, desensitization, adaptation, or reprogramming) (West and Heagy 2002). Notably, autoimmune diseases also offer examples of the immune system responding to changes in antigen presentation. For example, Pradeu and collaborators argue (Pradeu 2012) that many autoimmune diseases appear during puberty, when relatively fast changes occur in the physiology of the host, or due to a sudden exposure to chemical or biological agents and, conversely, allergy treatment by slow desensitization through antigen exposure leads to tolerance (Burks et al. 2012). These examples suggest that to understand the immune response, one might want to also consider dynamic features of antigen presentation as a complement to discrimination mechanisms which are only based on a static response that depends on the presence or absence of antigen.

During the past 30 or so years, a number of authors, most notably Zvi Grossman and collaborators (Grossman and Berke 1980) and Pradeu and collaborators (Pradeu 2012), have proposed the necessity of incorporating dynamics of antigen presentation when attempting to understand the body’s decision to initiate the immune response. They support this line of reasoning by experimental observations that (a) lymphocytes mount a sustained response only when faced with a sufficiently steep increase in their level of stimulation (for example, acute antigen presentation, proliferation rates of infected cells or tumors, stress signals) and (b) even when a new motif triggers an immune response, its chronic presence may result in adaptation: downregulation or even complete termination of the inflammatory response. One mathematical formulation was introduced by Grossman and Paul (Grossman and Paul 1992), who postulated the “tunable activation threshold” model for immune responses: effector cells in the innate or adaptive systems should become tolerant to continuously expressed motifs, or even gradually increasing ones, but should induce an effector response when a steep change is detected. Among recent variations upon this theme are the “discontinuity theory” postulated by Pradeu, Jaeger, and Vivier (Pradeu, Jaeger, and Vivier 2013), and the “growth threshold conjecture” due to Arias, Herrero, Cuesta, Acosta, and Fernández-Arias (Arias et al. 2015) (see Document S1 for details). Here, I present an extremely simple, conceptual mathematical model that describes how the immune system may discriminate between immune challenges based on their dynamics. I go on to demonstrate that it can capture a clinically important behavior, “two-zone tolerance,” in which tumors growing at specific rates evade the immune system.

Results

My model consists of three ordinary differential equations, as I will describe in detail below. They are:

$$\dot{u}=(\lambda -\kappa y)u$$

$$ẋ=-{\delta }_{x}x+\beta u$$ [sys:production.expo

$$ẏ=h(u/x)+f(y)$$

(dots indicate time derivatives), see Figure 1. The constants λ, κ, δ_x, β, are positive, and they represent reaction constants as discussed below. The function h is continuous, strictly increasing, and satisfies h(0) = 0; for our purposes we could simply take a linear function, h(p) = μp where μ is a constant and p represents u/x. Qualitatively, the plot of the function f is as in the left panel of Figure 1(B).

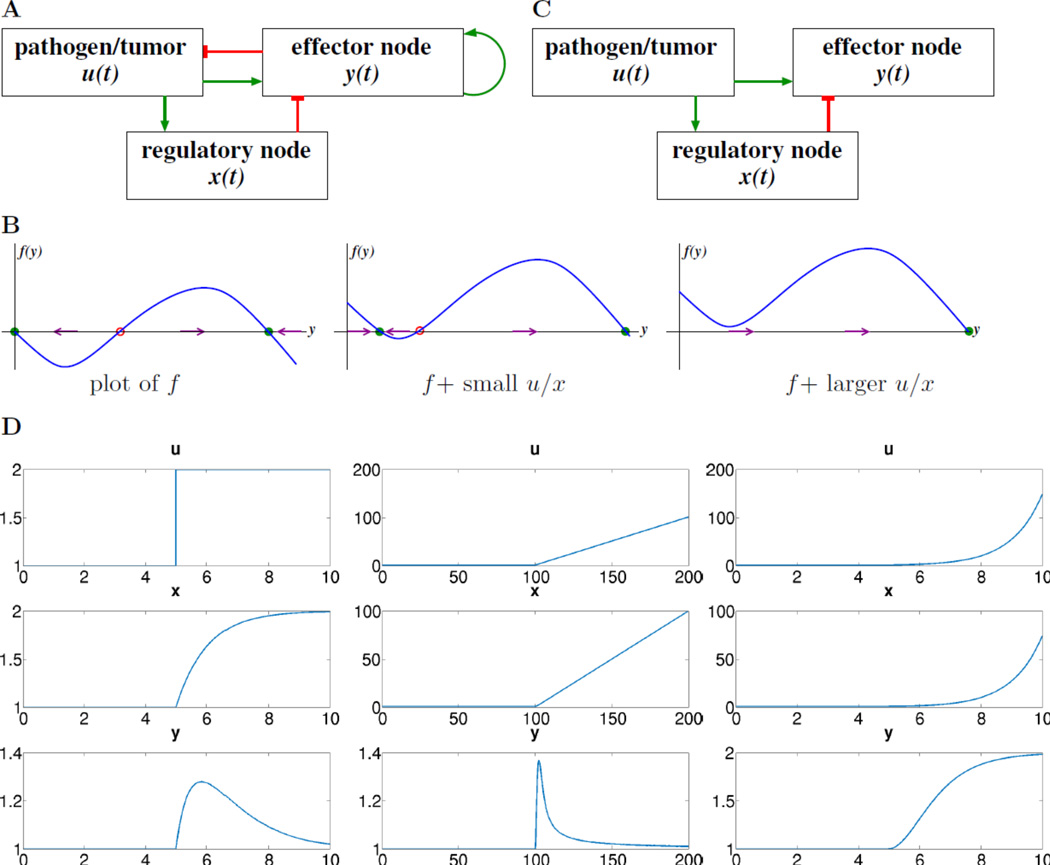
Figure 1.

A. The model being considered in this paper. Blunt-end red arrows denote repression, green arrows denote activation or autocatalytic feedback. B. Plot of the nonlinear function f that endows the system with bistability (left), and two translates of this plot; open red and filled green circles denote unstable and stable states respectively. C. Simplified model when feedbacks are ignored, an incoherent feedforward loop (IFFL). D. Simulations of system, with input u(t) switching in the middle of the interval from u(t) = 1 to a new constant value u(t) = 2, a shifted ramp u(t) = t, and a shifted exponential u(t) = e^t respectively; also shown are x(t) and y(t). In every case, the horizontal axis is time, t. Parameters used: δ_x = β = μ = δ_y = 1; initial conditions x(0) = y(0) = 1.

We view the system described by equations as a “toy model” that encompasses immune suppression as well as pattern discrimination based on antigen dynamics. The variable u represents an immune challenge, such as the volume or number of cells in a tumor, an infection, or the number of antigen-presenting cells (APC) of a certain type, and the term λu in the equation for u represents its exponential rate of growth. The variable x represents what I will call an “intermediate regulatory node,” because it driven by u and in turn regulates y. This node has an explicit biological correlate, such as the number of T regulatory cells in a defined tumor microenvironment. Within the model, this variable evolves according to a linear activation, proportional to the immune challenge, and decays linearly (inactivation or degradation). The variable y represents an agent that can eliminate the challenge u, such as the number of tumor-specific cytotoxic T cells (CTL) in the same environment. This elimination is represented by the mass-action term −κyu in the equation for u. As I will discuss in detail below, the variable y increases in proportion to the ratio of u to x, which implies that y is driven by the rate of growth of u. The function f(y) combines both degradation of y and a positive autocatalytic feedback between the presence of y and its induction, such as is observed when T cell activation is induced by cytokines; this function is chosen so as to endow the y component with bistable behavior, as explained next.

Initial intuition regarding the system can be obtained by thinking of p = h(u/x) as a parameter in the scalar differential equation ([sys:production.expo]c), writing ẏ = p + f(y) and temporarily ignoring that in the full model p is not constant but it depends on y through a feedback repression of u. Note that in this thought exercise the plot of p + f(y) is a vertical translation by p of the plot of f. If p is small, then, starting from the initial condition y(0) = 0, the solution y(t) approaches asymptotically a low value of y, the left-most stable green-labeled point in the center plot in Figure 1(B). However, once that p has a value large enough that this first equilibrium disappears (in what is known as a “saddle-node bifurcation”) then y(t) will converge, instead, to a comparatively large value, the green stable point in Figure 1(B), right. This higher equilibrium represents the triggering of a substantially increased immune response.

Further intuition can be gleaned from another simplification. Let us think of u as an input to equations ([sys:production.expo]b,c), once again ignoring the repression of u by y, see Figure 1(C). In addition, let us take h(u/x) = μu/x and let the function f include only degradation or deactivation but no autocatalytic feedback. Thus ([sys:production.expo]b,c) simplify to:

$$ẋ=-{\delta }_{x}x+\beta u$$ [sys:openloop]

$$ẏ=\mu u/x-{\delta }_{y}y$$

where β, μ, δ_x, δ_y are some positive constants and u is viewed as an external stimulus. The resulting system is a type of incoherent feedforward loop (IFFL), a “motif” which is ubiquitous in biological networks (Milo et al. 2002; Alon 2006), and is statistically enriched in many intracellular networks (metabolic pathways, genetic circuits, kinase-mediated signaling) as well as the intercelullar level. IFFL’s are characterized by the existence of two antagonistic (“incoherent”) alternative pathways from the input to the output; these paths can be direct or indirect, see Figure 1C

For our model, in there is an activating, direct path within the IFFL from the stimulus u (given as a step function, for example, in the left panel of Figure 1(D)) to the effector node y. In addition, there is an inhibitory, indirect path from stimulus u to node y:u activates regulatory node x which in turn represses y. This structure endows IFFL’s with powerful signal processing capabilities, studied in detail in Alon’s textbook (Alon 2006). As the indirect effect requires an accumulation of x over time, there is typically a delay in the downregulation of y, leading to a response that consists of a short activity burst followed by a return to a basal value which is the same no matter what was the magnitude of the input, as shown in the left plots in Figure 1(D). The return to a basal value independent of the excitation magnitude is a phenomenon called “perfect adaptation” (Alon 2006; Sontag 2003), and holds also for ramps (linearly increasing) inputs u(t), see, for example, the center plots in Figure 1(D). However, when instead we consider an exponentially growing input, such as the solution u(t) = u(0)e^νt of the differential equation u̇ = νu, then the response y(t) approaches a constant multiple of the rate ν, instead of returning to its basal value, see right plots in Figure 1(D). Combining these two observations, we see that the system has two interesting properties. First, it effectively estimates the growth constant ν, if the input is exponentially growing, and second, it does not respond persistently to sub-exponential inputs. Supplementary Materials section B includes a formal proof of this property. In this context, if we the autocatalytic feedback term in f into account, then a large value of u/x, which depends on the steepness of the input u, may trigger an irreversible transition to a higher state for y, which persists even after the excitation goes away. An important property of our system, which will allow us to simplify considerably its mathematical analysis, is that it incorporates a subsystem, the IFFL system just discussed, that has the “fold change detection” or “scale invariance” property: if the input is scaled by a positive constant p, then the same response y is obtained, provided that the regulatory variable x is also scaled by p. One uses the term “fold detection” for the initial activity burst, motivated by the response to an input that switches from u(t) = u₋ for t < 0 to u(t) = u₊ for ≥ 0: assuming that x(0) is adapted to u₋, the initial amplitude of u/x, which triggers the initial change in response in y, is (δ_x/β)u₊/u₋, and u₊/u₋ is the fold change in the input. In the IFFL system [sys:openloop], an input that is scaled by a positive constant p leads to the same response y, provided that the regulatory variable x is also scaled by p, since one has

$$(ṗx)=-{\delta }_x(px)+\beta (pu)$$

and

$$ẏ=\mu u/x-{\delta }_{y}y=\mu (pu)/(px)-{\delta }_{y}y.$$

In mathematical terms, this says that the equations do not change under the one-parameter Lie group of transformations

$$(u,x,y)\to (pu,px,y).$$

In other words, this system is “scale invariant” (or, in different terminology, it is a “fold change detector”) (Shoval et al. 2010). Supplementary Materials section D includes a more detailed discussion of scale invariance for this system. Irrespectively of it being a property that is very useful in our mathematical analysis, scale-invariance allows a system to detect relative, as opposed to absolute, changes in input signals, and to do so robustly even when intermediates in signaling pathways are varied (Shoval et al. 2010).

In summary, our model combines three central motifs in modern systems biology: (1) an IFFL for estimating the rate of growth of u(t), which is scale-invariant, (2) multi-stable dynamics for y(t), and (3) feedback control of y(t) that represses the input u(t).

In spite of its extreme simplicity, analysis of the model reveals a key biological implication: an immune challenge, for instance a tumor, can be eliminated in more than one range of growth rates. Specifically, we find three thresholds, λ₁, λ₂, λ₃, so that:

• if the per-capita rate of growth λ of the tumor is less than λ₁, then it is eventually eliminated by the immune system;

• when the tumor is more aggressive, λ > λ₁ but λ < λ₂, it cannot be eliminated (it is “tolerated” by the immune system);

• for an even more aggressive challenge, with λ > λ₂ but λ < λ₃, again the tumor is eliminated; and

• if λ > λ₃, again there is no elimination (the tumor “escapes”).

Intuitively, in the intermediate range λ₂ < λ < λ₃ the immune system goes into “overdrive,” engaging additional resources through activation of a positive feedback mechanism, and this level is powerful enough to effectively repress the challenge. As we mentioned earlier, the impact of growth rates on immune responses has been a hot topic of discussion in the immunology literature, and it has been proposed that different rates provide a way to differentiate among threats based on their aggressivity. “Non-self” and potentially dangerous cells presumably reproduce faster, compared to “self” and also beneficial microorganisms. As we will discuss, the role of exponential rates in determining immune response has also been the subject of experimental research, including a recent immunotherapy patent, and the role of T suppressor cells in providing what we may now view as the regulatory node in an incoherent feedforward loop has been well-established experimentally as well.

The prediction of the existence of disjoint regions of tumor elimination, depending on rate of growth, remains to be tested. However, this behavior is strongly reminiscent of the well-known phenomenon of “two-zone” tumor tolerance, which has been observed in the experimental literature since the mid-1960s (Gatenby, Basten, and Creswick 1981), (Kolsch and Mengersen 1976), (Li et al, 2016). This phenomenon is analogous to our predictions, the only difference being the “zones” are now determined by the magnitude of an initial tumor inocula in animal subjects instead of tumor growth rates. Moreover, the model is capable of logarithmic sensing and scale invariance. These phenomena, and the origins of two-zone tolerance, will be discussed in detail below.

RESULTS

A key step in our analysis will be an exact reduction to a certain two-dimensional system, as such a system is far easier to analyze than the full three-variable one. Indeed, scale invariance under the transformations (u, x, y) ↦ (pu, px, y) suggests performing a change of variables in which x is replaced by p = u/x. As x = u/p, the original variables (u, x, y) can be recovered from (u, p, y), so the transformation is invertible. Rearranging the order of equations, we will from now study the system in these new coordinates:

$$ẏ=h(p)+f(y)$$ [eq:changed_coordinates]

$$ṗ=p({\delta }_x+\lambda -\kappa y-\beta p)$$

$$\dot{u}=(\lambda -\kappa y)u.$$

Writing the equations in these new coordinates has a major advantages for analysis, because the equations for y and p are now decoupled from u, and therefore we may study the two-dimensional (y, p) system using techniques suitable for planar systems, such as phase planes and nullclines. Information regarding the asymptotic behavior of u can be inferred from that of the (y, p) system. Suppose that we have determined that a solution (y(t), p(t)) tends to an equilibrium (ȳ, p̅) with p̅ ≠ 0. This implies that λ − κy → λ − κȳ as t → ∞, and, because δ_x + λ − κȳ − βp̅ = 0 at any equilibrium with p̅ ≠ 0, asymptotically u(t) ∝ e^νt with ν = λ − κȳ = βp̅ − δ_x. This allows us to decide if u(t) converges to zero or infinity (that is, whether the immune challenge is eliminated or grows without limit):

$$\overline{p}<{\delta }_x/\beta \Rightarrow \nu <0:\text{ elimination }(\text{rejection})$$

$$\overline{p}>{\delta }_x/\beta \Rightarrow \nu >0:\text{ proliferation }(\text{escape},\text{tolerance}).$$

Thus, from now on we study ([eq:changed_coordinates]a,b). Recall the plot of f is as in Figure 1(B), and that h is assumed to be strictly increasing with h(0) = 0, which we will later specialize to h(p) = μp. We are only interested in solutions with y(t) ≥ 0 and p(t) ≥ 0.

The equilibria of system ([eq:changed_coordinates]a,b) are obtained by simultaneously solving

$$h(p)+f(y)=0$$

and

$$p({\delta }_x+\lambda -\kappa y-\beta p)=0.$$

When p = 0 the first of these is simply f(y) = 0 (because h(0) = 0), and when p > 0, the second gives δ_x + λ − κy − βp = 0. The y and p nullclines of this system are the subsets of the first quadrant where ẏ = 0 and ṗ = 0, that is,

$$N_1=\{(y,p)|y\ge 0,p\ge 0,p=h^{-1}(-f(y))\}$$

and

$$N_2=\{p=0\}\cup \{(y,p)|y\ge 0,p\ge 0,p=(1/\beta )({\delta }_x+\lambda -\kappa y)\}$$

respectively. Note that (y, p) can only belong to N₁ if − f(y) is in the range of h, and in particular this means that f(y) ≤ 0, thus ruling out the values of y for which the plot of f is positive. Similarly, (y, p) can only belong to N₂ if y ≤ (δ_x + λ)/κ. The equilibria of the system are the points at the intersection of these two sets.

We are interested in analyzing the behavior of the system for different values of the parameter λ which quantifies the initial growth rate of the immune challenge. The only place where λ plays a role is the equation for the line p = (1/β)(δ_x + λ − κy), picking one of its parallel translates. See Figure 2.

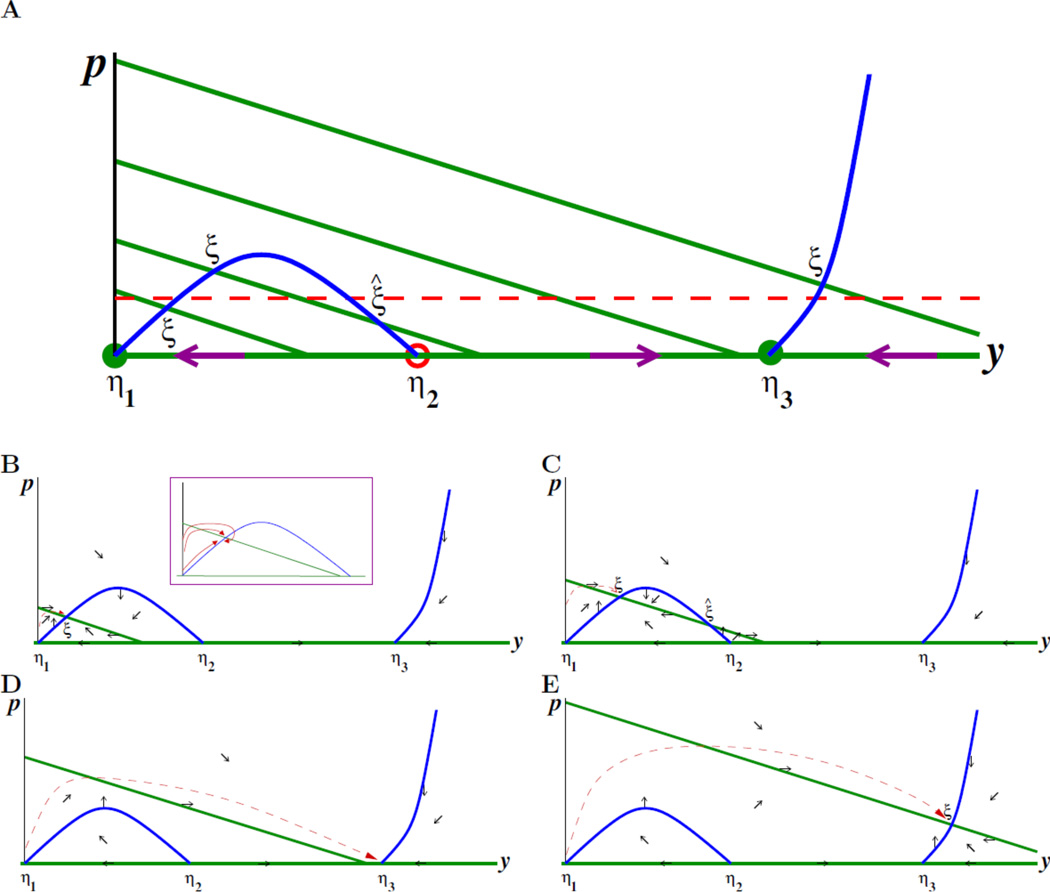
Figure 2.

A. Nullclines for the system ([eq:changed_coordinates]a,b) on the quadrant y ≥ 0, p ≥ 0. Blue curve is y-nullcline. Green lines are p-nullclines, shown for four typical values of λ. There are two different types of equilibria: the η’s are equilibria with p = 0 and the ξ’s with p > 0. The four points labeled ξ are stable for the reduced dynamics, for the respective λ’s, as discussed in the text. The intercepts of the green lines with the p axis (vertical) are at the locations p = (1/β)(δ_x + λ_i), i = 1,2,3,4. Red dashed horizontal line is threshold p = δ_x/β discussed in the text. B–E. Directions of movement in each region determined by the nullclines, along with typical trajectories, respectively, low to high for each of the values of λ represented in A. Inset in B shows various possibilities for approach of trajectory to point labeled ξ.

We assume, for simplicity, there are no more than two positive intersections between any (green) line p = (1/β)(δ_x + λ − κy) and the (blue) y nullcline; this means that the slope −κ/β is not ≈ 0. We also assume for the values of λ that we analyze that there is at most one intersection, like ξ̂, on the decreasing branch of the blue curve. (If there are such additional intersections, the theoretical analysis is somewhat more complicated, but is analogous.) The dashed line is the threshold that determines the behavior of u: if (y(t), p(t)) converges to an equilibrium that has p̅ < δ_x/β, then u(t) → 0 as t → ∞, but if p̅ > δ_x/β, then u(t) → ∞.

The Jacobian matrix for the system ([eq:changed_coordinates]a,b), evaluated at a generic equilibrium (ȳ, p̅), is:

$$J=\left(\begin{array}{cc}\hfill f^{\prime }(ȳ)\hfill & \hfill h^{\prime }(\overline{p})\hfill \\ \hfill -\kappa \overline{p}\hfill & \hfill {\delta }_x+\lambda -\kappa ȳ-2\beta \overline{p}\hfill \end{array}\right)$$

and therefore

$$J=\left(\begin{array}{cc}\hfill f^{\prime }(ȳ)\hfill & \hfill h^{\prime }(0)\hfill \\ 0& \hfill {\delta }_x+\lambda -\kappa ȳ\hfill \end{array}\right)$$

if p̅ = 0 and

$$J=\left(\begin{array}{cc}\hfill f^{\prime }(ȳ)\hfill & \hfill h^{\prime }(\overline{p})\hfill \\ \hfill -\kappa \overline{p}\hfill & \hfill -\beta \overline{p}\hfill \end{array}\right)$$

if p̅ > 0, where we used that

$${\delta }_x+\lambda -\kappa y-2\beta \overline{p}=-\beta \overline{p}$$

when p̅ > 0 (since the equilibrium condition is δ_x + λ − κy − βp̅ = 0 in that case). Note that these cases correspond, respectively, to points labeled η and ξ in Figure 2.

At points with p̅ = 0, the eigenvalues of the upper triangular matrix J are f′(ȳ) and δ_x + λ − κȳ. Referring to the plot of f in Figure 1(B), f′(ȳ) > 0 at the point η₂ and f′(ȳ) < 0 at the points η₁ and η₃. This is because the blue curve in Figure 2 is h⁻¹(−f(y)) and therefore is qualitatively like an upside-down version of the plot of f, so that positive (respectively negative) f′ corresponds to negative (respectively positive) slope at the equilibrium. Thus η₂ is unstable. At the point η₁, the second eigenvalue is δ_x + λ − κȳ = δ_x + λ, which is positive, so η₁ is also unstable (a saddle point). The stability of η₃ depends on the sign of δ_x + λ − κȳ: η₃ is stable if this sign is negative, that is, if

$${\delta }_x+\lambda -\kappa ȳ<0,$$

and unstable otherwise. Suppose that all parameters are fixed except for λ. We use Figure 2 to determine stability: if λ is such that the corresponding line

$$p=(1/\beta )({\delta }_x+\lambda -\kappa y)$$

intersects the y axis at a point y₀ to the left of η₃, that is, if y₀ < ȳ, then δ_x + λ − κy₀ = 0 implies δ_x + λ − κȳ < 0, and hence η₃ is stable. If, on the other hand, λ is larger and p = (1/β)(δ_x + λ − κy) intersects the y axis at a point y₀ to the right of η₃, then δ_x + λ − κy₀ = 0 implies δ_x + λ − κȳ < 0 so we conclude that η₃ is unstable. In the figure, only for the largest λ (top line) is η₃ unstable.

We next analyze stability of the equilibrium points for which p̅ > 0, labeled ξ or ξ̂ in Figure 2. Stability is equivalent to the trace of J being negative and its determinant positive (Hirsch and Smale 1974; Sontag 1998), that is:

$$-\text{tr}J=\beta \overline{p}-f^{\prime }(ȳ)>0$$

and

$$(1/\overline{p})\text{ det}J=\kappa h^{\prime }(\overline{p})-\beta f^{\prime }(ȳ)>0.$$

Since h is increasing and all constants are positive, these expressions are both positive when f′(ȳ) < 0. Remembering again that the blue curve is an “upside down” version of f, we conclude that all the intersections ξ shown in Figure 2 are stable, with the possible exception of the intersection labeled ξ̂, which needs further analysis. At the point ξ̂, the slope of the green line is −κ/β and the slope of the blue line is the derivative of h⁻¹(−f(y)) evaluated at y = ȳ, where h(p̅) + f(ȳ) = 0, so this slope is −f′(ȳ)/h′(p̅). Since the slope of the green line is larger (less negative) than the slope of the blue line, we have that −κ/β > −f′(ȳ)/h′(p̅), or equivalently κh′(p̅) − βf′(ȳ) < 0, so the determinant of J is negative, which means that ξ̂ is a saddle point and therefore unstable.

These theoretical results strongly suggest that, for trajectories that start with small p = u/x, convergence will be to one of the points labeled ξ in Figure 2, or η₃ in the case of the line that does not intersect the blue curve. In other words, if λ, the reproduction rate of the immune challenge, such as a tumor, is small, then we’ll have an intersection below the threshold (dashed line), meaning that the challenge will be eliminated. For a larger, but not too much larger, λ, the intersection is above the threshold, so the challenge will be “tolerated” (it will grow). For λ’s such that there are no intersections with the blue curve, solutions should converge to η₃, which is again under the threshold, implying a second zone of elimination of the challenge. Finally, for very large λ, the immune system is not capable of eradicating the challenge (ξ is over the threshold), so escape again occurs. This “two-zone tolerance” (at both intermediate and large λ) is reminiscent of analogous experimental findings, see Box 1. The analysis based on stability of equilibria can be complemented by numerical simulations, done in Box 1 for an example, as well as a global phase-plane analysis, done below. A simplified case is analyzed further in Supplementary Section B.

Observe that ẏ > 0 in those regions of the phase plane where h(p) + f(y) > 0, that is to say, where

$$p>h^{-1}(-f(y)).$$

Geometrically, this means that the flow of the vector field defining the system will point to the right at points that lie over the blue curve (y nullcline); it will point left under the blue curve and will be exactly vertical (or an equilibrium) on the curve itself.

Similarly, for p > 0, ṗ > 0 in those regions of the phase plane where

$${\delta }_x+\lambda -\kappa y-\beta p>0,$$

that is to say, where

$$p<(1/\beta )({\delta }_x+\lambda -\kappa y).$$

Geometrically, this means that the flow of the vector field defining the system will point up at points that lie under the green lines (p nullcline); it will point down over the green lines and will be exactly horizontal (or an equilibrium) on the lines. At p = 0, the vector field is horizontal.

In summary, motions are “Northeast”, etc., as per these rules in each region delimited by the blue curve and the line δ_x + λ − κy − βp = 0:

1. NE: over blue, under green

2. SE: over blue, over green

3. NW: under blue, under green

4. SW: under blue, over green

Figure 2 shows the directions of movement in each region, for each of the sample nullclines shown earlier, as well as what a typical trajectory might look like, consistently with these directions of movement and converging to the stable points ξ or η₃. (The precise approach depends on the functional forms of f and h and their parameters. The inset in Figure 2B shows several possibilities.) As λ is increased, the equilibrium shown lies under, above, under, and finally again above the threshold. Box 1 discusses a specific model where these predictions are verified, and relates our results to experimental evidence of similar phenomena.

Biology Box: Case Study: A concrete mathematical model featuring Treg cells and cytokines

In aggregate, the results of our model analysis show that (1) the role of the underlying IFFL as an estimator of the exponent λ of immune challenge growth and (2) the existence of four regimes, alternating tolerance and rejection, which correspond to different values of λ. In our abstract theoretical arguments, we did not specify the function f(y), except for the requirement that its graph be as in Figure 1B. We view the model as qualitative and phenomenological, merely as an illustration of behaviors that can arise from, and can be easily explainable by, simple motifs, and not necessarily instantiated by a specific biological system. Nonetheless, it is fair to ask if there is a plausible biological system that gives rise to an f(y) of this form, and for which our conclusions hold true. We address this issue now, using as a guide simplified versions of standard models in immune dynamics such as found in (Kuznetsov et al. 1994; Kirschner and Panetta 1998), and using simulations to verify for this system the theoretically predicted four-regime behavior.

We will pick h(p) = μp, a linear function, and

$$f(y)=\frac{V{y}^2}{K+y}-\epsilon y^2-{\delta }_{y}y.$$

The term $\frac{V{y}^2}{K+y}$ in this expression can be thought of as representing a cytokine-mediated positive feedback, as discussed in Supplementary Materials section D. Motivated by a similar term in (Khailaie et al. 2013), the term −εy² can be thought of as representing cell-contact-dependent activation-induced cell death (“fratricide”) through the Fas receptor / FasL (“death ligand”) mechanism for T-cell homeostasis suggested by Callard, Stark, and Yates (Callard, Stark, and Yates 2003). Finally, the term −δ_yy represents a linear constitutive deactivation and/or degradation. The resulting system is therefore as follows

$$\dot{u}=(\lambda -\kappa y)u$$

$$ẋ=-{\delta }_{x}x+\beta u$$

$$ẏ=\mu \frac{u}{x}+\frac{V{y}^2}{K+y}-\epsilon y^2-{\delta }_{y}y$$

and the reduced system written in (y, p) coordinates is

$$ẏ=\mu p+\frac{V{y}^2}{K+y}-\epsilon y^2-{\delta }_{y}y$$

$$ṗ=p({\delta }_x+\lambda -\kappa y-\beta p).$$

We take the units of time to be days. Cell populations (u, x, y) are in units of 10⁶ cells, but p = u/x is non-dimensional. In this model, u, x, y represent, respectively, populations of tumor, Treg, and effector T cells. The parameters that we used, and corresponding units, are as follows: μ = 10 day⁻¹, V = 0.25 day⁻¹, δ_x = 0.1 day⁻¹, δ_y = 0.1 day⁻¹, β = 1 day⁻¹, ε = 10⁻⁵ day⁻¹ (10⁶ cells)⁻¹, K = 100 (10⁶ cells), κ = 10⁻⁵ (10⁶ cells)⁻¹ day⁻¹. The particular choice of algebraic forms and parameters is discussed in Supplementary Materials section D; basic descriptions of the model’s behavior can be found in Supplementary Materials section E.

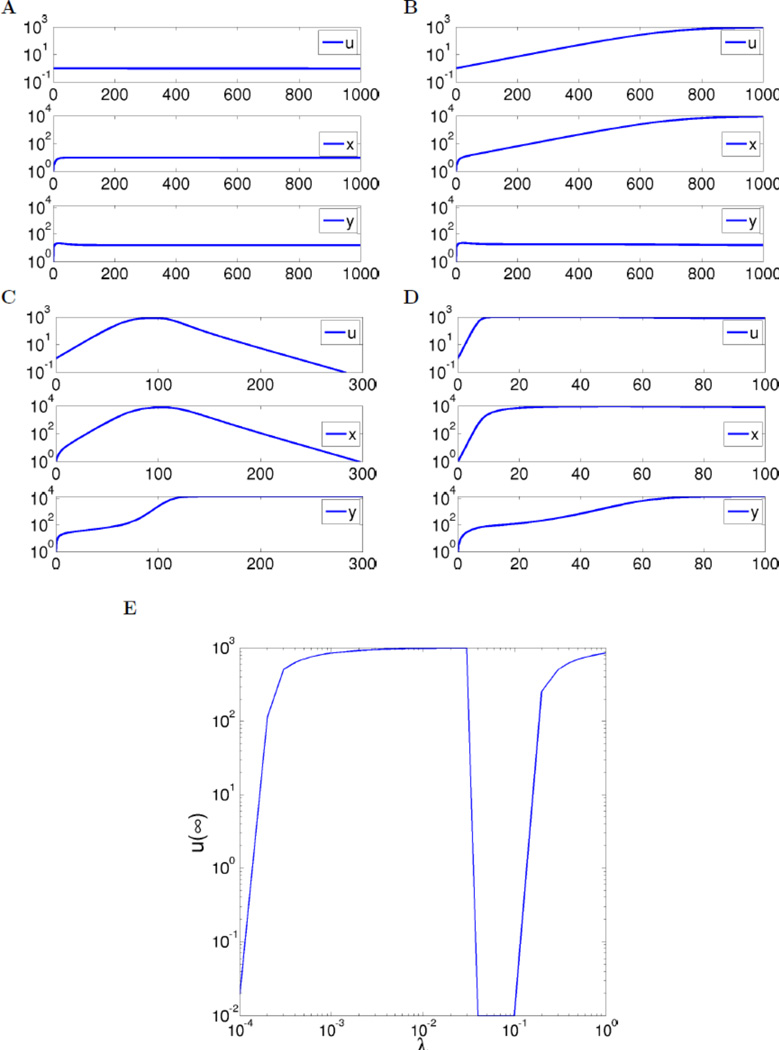
Shown in Figure 3(A–D) are simulations of the complete closed-loop system, where we now included a carrying capacity term for the immune challenge: u̇ = [λ(1 − Bu) − κy]u. When u is small, the term Bu is dominated by the other terms, but we include this term for numerical convenience in order to avoid blow-up of solutions in the case when u is unstable; in any event, such a term is biologically realistic. We picked, specifically, B = 10⁻³; (see Supplementary Materials section D). As predicted, for increasing λ there are alternating decay and growth behaviors for u(t). Notably, for the third value, λ = 10⁻¹, the immune challenge load u(t) only starts decreasing after about 120 days. This time scale happens to be, purely coincidentally, the start of remission observed in some patients under Ipilimumab [CTLA-4 checkpoint blockade therapy (Wolchok 2010). For this model and parameters, Figure 3(E) shows the asymptotic value of u, the immune challenge, as a function of the parameter λ, clearly illustrating the four-regime phenomenon. In Supplementary Materials section E, similar results are shown to hold for a model in which the effect of regulatory variables is through an inactivation of a helper-cell population.

Figure 3.

A–D. Simulations of full system as described in text, for λ = 10⁻⁴, 10⁻², 10⁻¹, and 1. (In A, u(t) converges to zero as t → ∞, but very slowly.) Parameters as described in text. Initial states are always u = 1, x = 1, y = 0. E. Values of u(∞) plotted against λ, showing four regimes of elimination, tolerance, elimination, and escape (zero values shown as 10⁻² to fit in log scale).

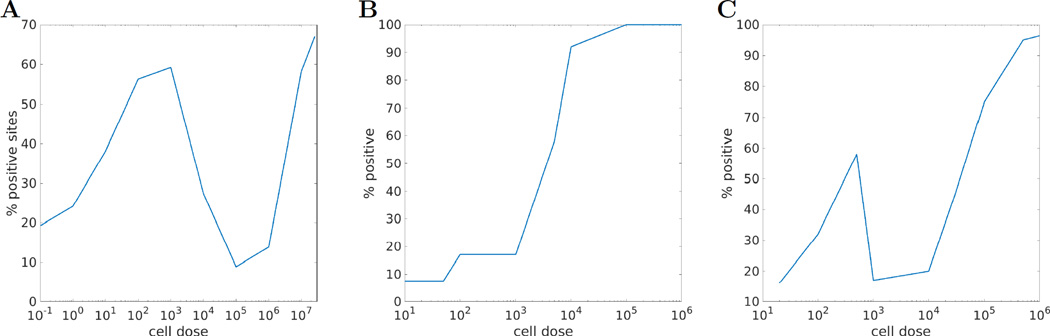
The existence of disjoint regions of tumor elimination depending on rate of growth is reminiscent of “sneaking through.” The idea of tumors “sneaking through” from immune control can be traced to the mid 1960s, when Klein (Klein 1966) found the “preferential take of tumours after small size inocula to a similar degree with that seen with large size inocula, compared to the rejection of medium sized inocula.” Put simply, there is an intermediate region in which tumors can be eliminated. This picture is at least consistent with a larger initial rate of increase in exposure leading to tumor suppression, as in our model. These ideas were explored experimentally in (Gatenby, Basten, and Creswick 1981) and (Kolsch and Mengersen 1976), and are analogous to behavior that can be seen in our model, see Figure 4, but with the important proviso that the numbers represent tumor incidence, and that we work with rates of increase instead of initial tumor size (see Supplementary Section G for more discussion).

Figure 4.

A: four regions of “sneaking through”, and B: no sneaking-through when eliminating suppressor T cells, plots drawn from data in (Gatenby, Basten, and Creswick 1981). Very low zone (less than 100 cells): low tumor incidence; low zone (10² – 10³ cells): tolerance of tumor; moderate zone (10³ – 10⁵ cells): immunogenic (low tumor); high zone (> 10⁶): again tolerogenic. C: Another illustration of the same general idea of four regions. Plot drawn from data in (Kolsch and Mengersen 1976). The x axis in these plots case measures the initial number of tumor cells, and not the rate of growth λ of tumor as it did as in Figure 3. In both cases, the y-axis measures the percentages of mice in which tumors were detected by some predetermined point. Supplemental Section G discusses experiments in more detail.

Our analysis is merely a phenomenological “toy model” which does not specify immune components. Nonetheless, one might speculate that, as far as T cell activation and deactivation, regulatory T cells (Tregs) may play a role as a regulating intermediate variable x. Tregs are a type of CD4⁺ cell that play “an indispensable role in immune homeostasis” (Josefowicz, Lu, and Rudensky 2012). They arise during maturation in the thymus from autoreactive cells (“natural Tregs”), or are induced at the site of an immune response in an antigen-dependent manner (“induced Tregs”). They are thought to play a role in limiting cytotoxic T-cell responses to pathogens, and Treg⁻ mice have been shown to suffer from extreme inflammatory reactions. It is known from animal studies that Tregs inhibit the development of autoimmune diseases such as experimentally induced inflammatory bowel disease, experimental allergic encephalitis, and autoimmune diabetes (Owen, Punt, and Stranford 2009). Moreover, the involvement of T suppressor cells (now Tregs) in regulating the immune response to tumor has a long history, see for instance (Fujimoto, Greene, and Sehon 1976).

Our analysis suggests that the immune system might act as an estimator of the rate of growth of an immune challenge, and more specifically the rate of exponential increase. In recent work, Kündig and coauthors (Johansen et al. 2008) emphasized the role of antigen kinetics in determining immune reactivity, with exponentially increasing antigenic stimulation recognized by the immune system as a pattern associated with pathogens and thus leading to strong immune responses. They showed that the dynamics of immune stimulation (through dendritic cell vaccination and for T cells stimulated in vitro) was by itself a factor in determining the strength of T cell and anti-tumor responses, and obtained a patent for the idea of using exponential increasing antigen stimulation (Kundig et al. 2008). See Supplemental Section G for more discussion.

DISCUSSION AND CONCLUSIONS

The study of immune systems and their interactions with tumors has long been the focus of theoretical and mathematical immunology (Jerne 1974; Bell, Perelson, and (editors) 1978). Two influential contributions were the 1980 paper by Stepanova (Stepanova 1979) in which a set of two ODE’s was used to represent tumor and immune system cells, and the 1994 paper by Kuznetsov, Makalkin, Taylor, and Perelson (Kuznetsov et al. 1994) in which a similarly simple model was used to provide an explanation for the sneaking-through phenomenon, though with escape of small tumors and with no mechanism for detection of rates of change of the immune challenge. It is impossible here to review the literature in this very active area of research; some reviews and textbooks are (Bell, Perelson, and (editors) 1978; Callard and Yates 2005; Andrew, Baker, and Bocharov 2007; Eftimie, Bramson, and Earn 2011; Wodarz and Komarova 2014; Pillis and Radunskaya 2014; Vodovotz et al. 2017).

In this paper, we proposed a very simple phenomenological model that recapitulates some of the basic features of interactions between the immune systems and tumors (or more generally at this level of abstraction, other immune challenges) in the context of the estimation of tumor growth rates. The model leads to interesting conclusions regarding transitions between tolerance and elimination and the role of dynamics in self/nonself discrimination, and makes contact with several theory and experimental papers. Obviously, our model represents a purely phenomenological, macroscopic, and hugely over-simplified view of a highly complex, intricate, and still poorly understood network of interactions between different components of the immune system, as well as immune interactions with pathogens and tumors, Paraphrasing the well-known quote, our model is “as simple as possible but not simpler” to illustrate the particular phenomena of interest.

Since Paul Ehrlich’s work in 1909, (Ehrlich 1909) the interplay with the immune system has been a controversial, though recently accepted, aspect of cancer biology. These ideas were formalized in Burnet’s immune surveillance hypothesis (M. Burnet 1957), as an interaction between cancers that continuously arise and their repression by immune system, resulting in eventual elimination. Initial interest in this work was soon tempered by early experiments, but eventually new data led to a revival of these ideas in the late 1990s (Dunn et al. 2002). There is little doubt nowadays that immunosurveillance acts as a tumor suppressor, although it is also widely understood that the immune system can facilitate tumor progression by “sculpting” the immunogenic phenotype of tumors as they develop. Indeed, one current paradigm (Dunn, Old, and Schreiber 2004) is the so-called “three Es of cancer immunoediting” hypothesis: elimination, equilibrium, and escape. The first of this corresponds with the classical immunosurveillance idea: the immune system successfully eradicates the developing tumor. In the equilibrium or immune sculpting phase, the host immune system and any tumor cells that have survived the elimination phase enter into a dynamic quasi-steady state equilibrium during which the tumor cell population stays at sub-clinical levels. Ultimately, however, genetic and epigenetic heterogeneity in tumors, coupled by the Darwinian selection pressure exerted by the immune system, lead to the emergence of dominant clones with reduced immunogenicity which expand and become clinically detectable, and this is termed the escape phase. Our model does not directly address the effect of genetic or epigenetic modifications, and expanding it to do so remains a most interesting direction for further work.

Clinically, the interactions between the immune system and tumors are the focus of much current research because of the promise of novel immunotherapies such as checkpoint inhibitors (Pardoll 2012). It is worth pointing out the role of dynamical responses in immunotherapies, compared to classical chemotherapy and pathway inhibitors, which is emphasized in the UpToDate physician reference guide, from which we quote from the 01 Sep 2015 version: “patients may have a transient worsening of disease, manifested either by progression of known lesions or the appearance of new lesions, before disease stabilizes or tumor regresses.” (Interestingly, the solution in Figure 3B has this behavior.) This statement helps justify, in our view, the introduction of dynamical systems concepts into the field of immunotherapy.