Afferent control of locomotor CPG: insights from a simple neuromechanical model

Abstract

A simple neuromechanical model has been developed that describes a spinal central pattern generator (CPG) controlling the locomotor movement of a single-joint limb via activation of two antagonist (flexor and extensor) muscles. The limb performs rhythmic movements under control of the muscular, gravitational and ground reaction forces. Muscle afferents provide length-dependent (types Ia and II) and force-dependent (type Ib from the extensor) feedback to the CPG. We show that afferent feedback adjusts CPG operation to the kinematics and dynamics of the limb providing stable “locomotion.” Increasing the supraspinal drive to the CPG increases locomotion speed by reducing the duration of stance phase. We show that such asymmetric, extensor-dominated control of locomotor speed (with relatively constant swing duration) is provided by afferent feedback independent of the asymmetric rhythmic pattern generated by the CPG alone (in “fictive locomotion” conditions). Finally, we demonstrate the possibility of reestablishing stable locomotion after removal of the supraspinal drive (associated with spinal cord injury) by increasing the weights of afferent inputs to the CPG, which is thought to occur following locomotor training.

Introduction

The mammalian spinal cord can generate locomotor activity in the absence of rhythmic inputs from higher brain centers and sensory feedback.¹ These observations led to the concept of the locomotor central pattern generator (CPG) that is located in the spinal cord and generates a primary locomotor rhythm and alternating pattern of motoneuron activations.^2-5 Substantial evidence for this concept came from studies of “fictive locomotion,” in which sustained stimulation of the brain stem mesencephalic locomotor region in decerebrate, immobilized cats can evoke rhythmic locomotor activity with flexor-extensor and left-right alternations specific for locomotion.^3-9 Fictive locomotion studies have also demonstrated that electrical stimulation of flexor and extensor afferents can modulate the fictive locomotor pattern, change the timing of locomotor phase transitions (and hence the durations of locomotor phases), control locomotor speed (i.e., overall step cycle duration), and produce various types of rhythm resetting.^10-13 Although the spinal CPG can generate locomotor rhythm in the absence of sensory feedback, during normal overground locomotion it operates under feedback control. The latter plays a critical role in stabilizing the locomotor movement, contributes to weight support during stance phase, and adjusts the locomotor pattern to the biomechanical characteristics of limbs and body and the characteristics of the environment (terrain, obstacles, etc.).^14,15

An important feature of normal overground locomotion in mammals, including cats,^16,17 rats,^18,19 and humans,²⁰ is that the speed of locomotion normally changes due to a shortening of the stance (extensor) phase duration while the swing (flexor) phase duration remains relatively constant, which represents the so-called “extensor (or stance) phase dominance” in control of locomotion speed. In principle, the physiological basis for this extensor-dominated locomotion could derive from one (or combination) of the following²¹: (1) an extensor/flexor asymmetry in the organization of CPG per se,^22,23 (2) an asymmetry in the descending drive from the brainstem to the flexor and extensor half-centers,^24-26 or (3) afferent control of the CPG.^21,27-31 Despite extensive studies in different animals and experimental preparations, this issue remains unresolved and is continuously debated in the literature.^21,26,30

Another important issue is the potential role of afferent feedback in the recovery of locomotor function after spinal cord injury (SCI). Complete SCI results in the loss of descending propriospinal inputs from above the level of transection as well as supraspinal (cortical and brainstem) inputs to the CPG, which is expected to interrupt the normal CPG operation and hence to stop generation of locomotor oscillations.^32-34 At the same time, many studies have provided evidence that locomotor function can be recovered by locomotor training alone or in combination with afferent stimulation or pharmacological treatment.^4,15,35-39 It is commonly accepted that the recovery of locomotor function after SCI by locomotor training occurs, at least in part, due to an increase in the strength of afferent inputs to the CPG which re-enforces its operation despite the loss of supraspinal drive.^{4,15,35,36,38} However, the feasibility of such re-enforcement of the spinal CPG and locomotor pattern generation by afferent feedback after removal of supraspinal drive has never been theoretically investigated.

In this study, we have developed a simple neuro-mechanical model that describes a locomotor CPG controlling the movement of a simple biomechanical system and used this model to investigate the possible role of afferent feedback from flexor and extensor muscles in the control of locomotor oscillations, including the extensor-dominated control of locomotor speed, and in the recovery of locomotor function after the loss of supraspinal drive to the CPG (to model SCI conditions).

Model description

The model schematic is shown in Figure 1. The two-level half-center CPG represents a simplified version of a previous model^6,7 and consists of a half-center rhythm generator (RG, containing flexor, RG-F, and extensor, RG-F, half-centers/neurons), pattern formation (PF) circuits (represented by PF-F and PF-E neurons) and inhibitory interneurons (In-F and In-E) which mediate reciprocal inhibition between flexor and extensor half-centers. The CPG receives tonic “supraspinal” drive and generates a basic “locomotor” rhythm providing alternating activation of flexor and extensor neurons within the CPG and alternating activation of flexor and extensor motoneurons (Mn-F and Mn-E). The controlled biomechanical system represents a simplified model of a single-joint limb described as a pendulum. The forces acting at the limb include: (1) forces of two antagonistic muscles (flexor, F, and extensor, E, activated by Mn-F and Mn-E, respectively), (2) gravitational force, and (3) ground reaction force, whose moment (M_GR) is applied during the “stance phase” when the limb moves counterclockwise (i.e., with angular velocity q̇ > 0). Muscle afferents provide the length-dependent (type Ia from both muscles and type II from the flexor) and force-dependent (Ib from the extensor) feedback to the CPG through additional excitation to the homonymous (F or E) interneurons of the CPG. This afferent feedback affects motoneuron activity through the CPG by controlling the timing of phase transitions at the RG level and the excitability of the PF circuits. Sensory feedback from the extensor muscle also accesses an additional circuit (In and Inab-E) providing disynaptic excitation of Mn-E during extension.^40,41

Figure 1.

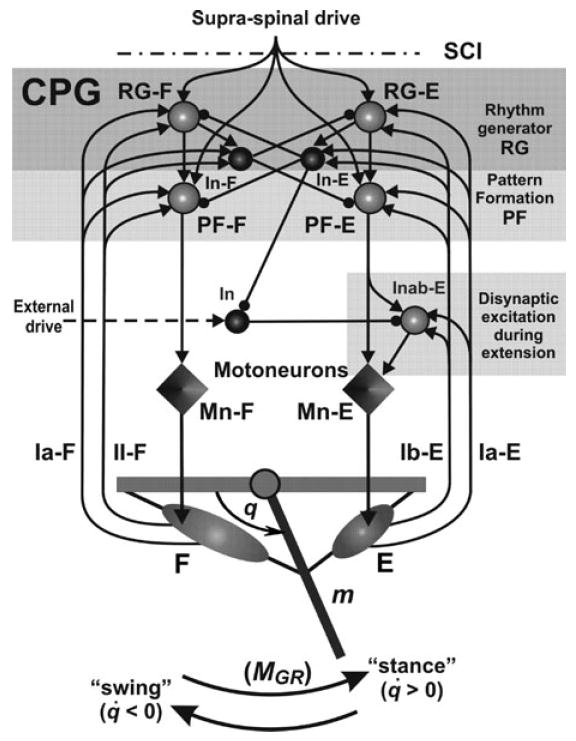
Model schematics. The two-level spinal CPG consists of a half-center rhythm generator (RG, containing flexor, RG-F, and extensor, RG-E, half-centers), pattern formation (PF) circuits (PF-F and PF-E neurons) and inhibitory interneurons (In-F and In-E), which mediate reciprocal inhibition between flexor and extensor sides of the CPG. The CPG receives tonic “supraspinal” drive and generates a basic “locomotor” rhythm providing alternating activation of all flexor and extensor CPG neurons and corresponding flexor and extensor motoneurons (Mn-F and Mn-E). An additional circuit including In and Inab-E interneurons is incorporated to provide disynaptic excitation of Mn-E by extensor afferents during extension (see text for details). All interneurons are represented by spheres: light spheres are excitatory, and dark spheres are inhibitory interneurons. Motoneurons are represented by diamonds. Excitatory and inhibitory synaptic connections are shown by arrows and small circles, respectively. The biomechanical system represents a simplified model of a single-joint limb that is forced to oscillate by the forces of two antagonistic muscles (flexor, F, and extensor, E, activated by Mn-F and Mn-E, respectively). Muscle afferents provide length-dependent (Ia type from both muscles, and type II type from the flexor muscle) and force-dependent (Ib from the extensor) feedback to the CPG providing excitation to the homonymous (F or E) interneurons of the CPG (see text for details).

Biomechanical model of single-joint limb

The biomechanical model of a single-joint limb consists of a rigid segment of mass m and length l_s connected to a stationary rigid base by a hinge joint (see Fig. 1). The segment oscillates in the sagittal plane by rotating around the suspension point under control of two muscles, flexor (F) and extensor (E). The muscles are attached to the segment and the stationary base. Motion of the segment is described by a second order differential equation:

$$\begin{array}{lll}I\cdot \ddot{q}& =& 0.5\cdot m\cdot g\cdot l_s\cdot \cos q\\ & & -b\cdot \dot{q}+F_F(q,\dot{q},t)\cdot h_F(q)\\ & & -F_E(\mathrm{\pi }-q,-\dot{q},t)\cdot h_E(q)+M_{\mathit{GR}}(q),\end{array}$$ (1)

where q is the generalized coordinate (joint angle); I is the moment of inertia of the segment with respect to the suspension point ( $I=m\cdot l_s^2/3$); b is the angular viscosity in the hinge joint; F_F is the flexor muscle force; F_E is the extensor muscle force; h_F is the flexor muscle moment arm; and h_E is the extensor muscle moment arm. The generalized force on the right side of equation (1) consists of moment of gravitational force, moment of friction force in hinge joint, moments of muscle forces, and moment of external forces (M_GR) emulating the effect of ground reaction forces during “stance.” Contracting the flexor muscle produces negative moment while contracting the extensor muscle produces positive moment applied to the segment. The following parameters were used in our simulations: m = 300 g; l_s = 300 mm; b = 0.002 g · mm²/(ms · rad).

Length of muscles (L) is calculated as the distance from origin to attachment point, and the moment arm (h) is calculated as the shortest distance from the muscle to the joint. For the flexor muscle:

$$\begin{array}{l}L=\sqrt{a_1^2+a_2^2-2a_1\cdot a_2\cdot \cos q};\\ h=\frac{a_1\cdot a_2\cdot \sin q}{L},\end{array}$$ (2)

where a₁ is the distance between suspension point and muscle origin, (a₁ = 60 mm) and a₂ is the distance between suspension point and muscle attachment to the segment (a₂ = 7 mm). For the extensor muscle, the same description (2) was used by substituting q with π–q.

Muscle velocities are defined as:

$${\upsilon }_F=\dot{q}\cdot h_F;{\upsilon }_E=-\dot{q}\cdot h_E,$$ (3)

where q̇ is the segment angular velocity and h is the moment arm of the corresponding muscle.

Calculation of muscle forces is based on the Hill-type model proposed by Harischandra and Ekeberg.⁴² The total force F in each muscle (F_F and F_E) is defined by the normalized length- (F_l) and velocity- (F_v) dependent variables describing the muscle contractile component and the passive parallel component F_p as follows:

$$F=F_{\max }\cdot (f(V)\cdot F_l\cdot F_{\upsilon }+F_p),$$ (4)

where f (V) is the neural activation (output activity of the corresponding motoneuron, Mn-F or Mn-E, respectively, see Fig. 1 and neuron description below; 0 ≤ f (V) < 1) and F_max is the maximal isometric force of the corresponding muscle (F_max for the flexor and extensor muscles was set to 72.5 and 37.7 N, respectively).

Muscle lengths (L) are normalized with respect to L_opt (the length of muscle for which F_l = 1; L_opt = 68 mm for both muscles); the normalized muscle lengths l = L/L_opt.

The force–length dependence F_l in (4) is given by:

$$F_l=\exp (-{\mid \frac{l\cdot \mathrm{\beta }-1}{\mathrm{\omega }}\mid }^{\mathrm{\rho }})$$ (5)

with parameters β = 2.3, ω = 1.26, and ρ = 1.62.⁴²

The force–velocity dependence F_v in (4) is calculated as:

$$F_{\upsilon }=\{\begin{array}{cc}\frac{b_1-c_1\cdot \upsilon }{\upsilon +b_1},& \mathrm{if}\upsilon <0;\\ \frac{b_2-c_2(l)\cdot \upsilon }{\upsilon +b_2},& \mathrm{if}\upsilon \ge 0,\end{array}$$ (6)

where υ is muscle velocity; c₁ = 0.17, b₁ = −0.69, c₂(l) = −5.34·l² + 8.41·l − 4.7, and b₂ = 0.18. Negative velocities correspond to shortening of the muscles.

The passive force F_p in (4) is calculated as follows⁴²:

$$\begin{array}{cc}{F}_p=& 3.5\cdot \mathrm{In}(\exp ((l-1.4)/0.005)+1.0)\hfill \\ & -0.02\cdot \exp (-18.7\cdot (l-0.79))-1.0).\end{array}$$ (7)

To simulate the effect of the ground, we assumed that increasing segment angle q (in counterclockwise direction of movement in Fig. 1) corresponds to the stance phase, and decreasing q (in clockwise direction) corresponds to the flexion phase. The moment of ground reaction forces is described as:

$$M_{\mathit{GR}}(q)=\{\begin{array}{cc}-M_{\mathit{GR}\max }\cdot \cos q,& \mathrm{if}\dot{q}\ge 0(\mathit{stance});\\ 0,\mathrm{if}\dot{q}<0(\mathit{swing}),& \end{array}$$ (8)

where M_GRmax > 0 is a constant (M_GRmax = 585 N · mm).

Activity of muscle afferents

Only length-dependent feedback from the flexor muscle (primary Ia-F and secondary II-F) and primary length- and force-dependent afferents from the extensor muscle (Ia-E and Ib-E) have been considered (see Fig. 1). The descriptions of muscle afferent activities are derived and modified from the formulas suggested by Prochazka^43,44:

$$\begin{array}{l}\mathit{Ia}=k_{\upsilon }\cdot {\upsilon }_{\mathrm{norm}}^{p_{\upsilon }}+k_{\mathit{dI}}\cdot d_{\mathrm{norm}}+k_{\mathit{nI}}\cdot f(V)+{\mathit{const}}_I;\\ \mathit{Ib}=k_F\cdot F_{\mathrm{norm}};\\ \mathit{II}=k_{\mathit{dII}}\cdot d_{\mathrm{norm}}+k_{\mathit{nII}}\cdot f(V)+{\mathit{const}}_{\mathit{II}},\end{array}$$ (9)

where υ_norm is the normalized muscle velocity (υ_norm = υ/L_th); p_v = 0.6; d_norm is the normalized muscle lengthening (d_norm = (L −L_th)/L_th, if L ≥ L_th, and 0 otherwise); L_th is the minimal muscle length evoking afferent activation; f (V) is the output activity of the corresponding (flexor or extensor) motoneuron; const_I and const_II are constant components; F_norm is the normalized muscle force (F_norm = (F − F_th)/ F_max, if F ≥ F_th, and 0 otherwise); k_v, k_dI, k_nI , k_F , k_dII , and k_nII are coefficients (L_th = 59 mm; F_th = 3.38 N; k_v = 6.2; k_dI = 2; k_dII = 1.5; k_nI = k_nII = 0.06; k_F = 1).

Modeling neurons and the CPG

The CPG model is a simplified version of a previous model^6,7 and includes a half-center rhythm generator that receives tonic supraspinal drive and generates the locomotor rhythm producing alternating activation of flexor and extensor motoneurons. Because our major focus was on the afferent control of the CPG, the classical reflex circuits and low-level interactions involving Ia interneurons and Renshaw cells have not been included in the model. We however incorporated circuits simulating disynaptic excitation of extensors by group I extensor afferents (In and Inab-E interneurons in Fig. 1, see details in Rybak et al.⁷).

Each neuron in the model represents a neural population and is described by an activity-based neuron model, in which the dependent variable V represents the average membrane voltage of neurons within the population, and the output activity f (V) represents the average or integrated population activity. At the same time, the neuron model was formulated to include an explicit representation of some voltage-gated ionic currents such as potassium rectifier (I_K) and persistent sodium (I_NaP) currents. These currents in RG-F and RG-E neurons in combination with reciprocal inhibition between these neurons define the rhythm-generation mechanism in RG.^6,45 Specifically, the membrane potential of CPG neurons (RG-F, RG-E, PF-F, and PF-E) and motoneurons (Mn-F and Mn-E) is described by the following differential equation:

$$C\cdot \frac{\mathit{dV}}{\mathit{dt}}=-I_{\mathit{NaP}}-I_K-I_{\mathit{Leak}}-I_{\mathit{SynE}}-I_{\mathit{SynI}}.$$ (10)

The membrane potential of all other neurons (InE, In-F, Inab-E, and In) is described as follows:

$$C\cdot \frac{\mathit{dV}}{\mathit{dt}}=-I_{\mathit{Leak}}-I_{\mathit{SynE}}-I_{\mathit{SynI}}.$$ (11)

In the above equations, C is the neuronal capacitance, I_Leak is the leakage current, I_SynE and I_SynI are the excitatory and inhibitory synaptic currents, respectively. The ionic currents are described as follows:

$$\begin{array}{ccc}{I}_{\mathit{NaP}}& =& {\overline{g}}_{\mathit{NaP}}\cdot m_{\mathit{NaP}}\cdot h_{\mathit{NaP}}\cdot (V-E_{\mathit{Na}});\hfill \\ I_K& =& {\overline{g}}_K\cdot m_K^4\cdot (V-E_K);\hfill \\ I_{\mathit{Leak}}& =& {\overline{g}}_{\mathit{Leak}}\cdot (V-E_{\mathit{Leak}});\hfill \\ I_{\mathit{SynE},i}& =& {\overline{g}}_{\mathit{SynE}}\cdot (V_i-E_{\mathit{SynE}})\hfill \\ & & \cdot (\sum _j{\alpha }_{\mathit{ji}}\cdot f(V_j)+\sum _m{c}_{mi}\cdot d_m\hfill \\ & & +\sum _k{w}_{ki}\cdot f{b}_k);\hfill \\ I_{\mathit{SynI},i}& =& {\overline{g}}_{\mathit{SynI}}\cdot (V_i-E_{\mathit{SynI}})\cdot \sum _j{b}_{ji}\cdot f(V_j),\hfill \end{array}$$ (12)

where ḡ_NaP , ḡ_K , ḡ_Leak, ḡ_SynE, and ḡ_SynI are the maximal conductances of the corresponding ionic channels; E_Na, E_K , E_Leak, and E_SynI are the corresponding reversal potentials; a_ji defines the weight of the excitatory synaptic input from neuron j to neuron i; b_ji defines the weight of the inhibitory input from neuron j to neuron i; c_mi defines the weight of the excitatory drive d_m to neuron i; w_ki defines the synaptic weight of afferent feedback fb_k to neuron i (see Fig. 1).

The nonlinear function f (V) defines the output activity of each neuron:

$$f(V)=\{\begin{array}{l}1/(1+\exp (-(V-V_{1/2})/k)),\mathrm{if}V\ge V_{th};\\ 0,\mathrm{if}V<V_{th},\end{array}$$ (13)

where V _1/2 is the half-activation voltage, k defines the slope of the output function and V_th is the threshold for each neuron.

Activation of the potassium rectifier and persistent sodium currents is considered instantaneous. Voltage dependent activation and inactivation variables and time constants for the potassium rectifier and persistent sodium channels are described as follows⁶:

$$\begin{array}{ccc}{m}_K& =& 1/(1+\exp (-(V+44.5)/5)),\\ m_{\mathit{NaP}}& =& 1/(1+\exp (-(V+47.1)/3.1)),\hfill \\ {\mathrm{\tau }}_{\mathit{hNaP}}& \cdot & \frac{d}{\mathit{dt}}{h}_{\mathit{NaP}}=h_{\infty \mathit{NaP}}-h_{\mathit{NaP}},\hfill \\ h_{\infty \mathit{NaP}}& =& 1/(1+\exp ((V+51)/4)),\hfill \\ {\mathrm{\tau }}_{\mathit{hNaP}}& =& {\mathrm{\tau }}_{h\mathit{NaP}\max }/\cosh ((V+51)/8).\hfill \end{array}$$ (14)

The following values of neuronal parameters were used: C = 20 pF; E_Na = 55 mV, E_K = −80 mV, E_SynE = −10 mV, E_SynI = −70 mV, E_Leak = −64 mV for RG and PF neurons and motoneurons and −60 mV for all other neurons; ḡ_K = 4.5 nS, ḡ_Leak = 1.60 nS, ḡ_SynE = ḡ_SynI = 10.0 nS, ḡ_NaP = 3.5 nS for RG neurons, 0.5 nS for PF neurons, and 0.3 nS for motoneurons; τ_{hNaP max} = 600 mS. Parameters of f (V) function were V _1/2 = –30 mV, V_th = −50 mV, and k = 3 mV for motoneurons and 8 mV for other neurons.

The weights of the synaptic connections are shown in Table 1. To change the rate of oscillations (locomotion speed) in the model, we change the supraspinal drive (d₁) in the range of 0.7−3.6. The values of afferent feedback connections in Table 1 correspond to “intact case.” To simulate the loss of supraspinal drive after spinal cord injury, we set d₁ = 0. To simulate the effects of training on locomotor recovery, the weights of all length-dependent afferent connections (Ia-F, II-F, and Ia-E) to all target neurons were increased by 31%, and the weights from Ib-E to all target neurons were increased five-fold, which “recovered” stable locomotor oscillations in the absence of a supraspinal drive.

Table 1.

Weights of synaptic connections in the model

Source	Target neuron
	RG-F	RG-E	In-F	In-E	PF-F	PF-E	In	Inab-E	Mn-F	Mn-E
Connections from drives, cmi
Supraspinal drive, d1	0.08	0.08			0.4	0.4
External drive, d2 = 1							0.18
Excitatory connections, aji
RG-F			0.41		0.7
RG-E				0.41		0.7
PF-F									1.95
PF-E								0.35		1.30
Inab-E										0.82
Inhibitory connections, bji
In-F		2.2				6.6
In-E	2.2				6.6		2.8
In								0.55
Afferent feedback connections, wki
Ia-F	0.06		0.27		0.19
II-F	0.0348		0.1566		0.1102
Ia-E		0.06		0.44		0.10		0.16
Ib-E		0.066		0.484		0.11		0.176

The model was implemented using Matlab 7.5.0. Differential equations were solved using a variable order multistep differential equation solver ode15s available in Matlab.

Results and discussion

Model performance under normal conditions

Generation of the locomotor rhythm in the model is performed by the half-center rhythm generator comprised of RG-F and RG-E neurons reciprocally inhibiting each other via In-F and In-E inhibitory interneurons, respectively (see Fig. 1). The generation of this rhythm relies on the dynamics of the persistent sodium current (I_NaP) in RG-F and RG-F neurons and the mutual inhibition between them.^6,45 The generation of this rhythm in the “intact” case requires tonic (“supraspinal”) drive to the CPG (see Fig. 1) but does not require afferent feedback. The afferent feedback, however, controls the performance of the CPG and modifies the locomotor pattern generated, adjusting the latter to the behavior of the controlled biomechanical system.

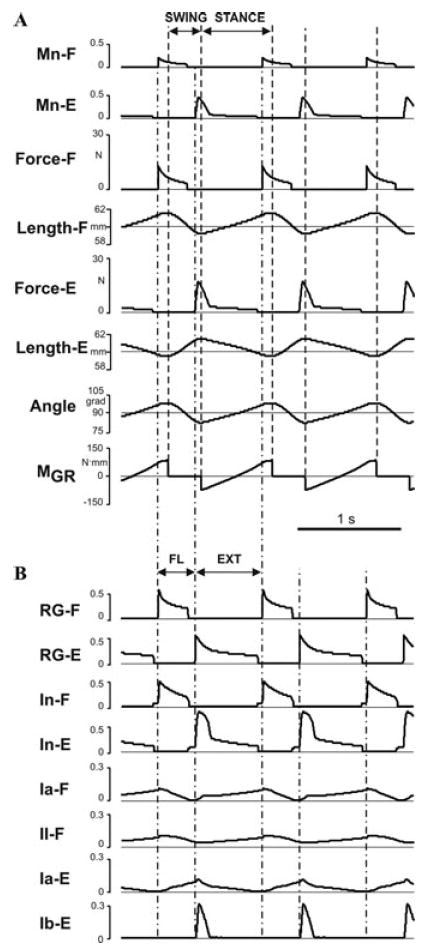
Changes in the major characteristics of the biomechanical system during locomotion are shown in Figure 2A. The two top traces in this figure show alternating activity of motoneurons Mn-F and Mn-E, which activate flexor (F) and extensor (E) muscles, respectively. The next four traces represent the corresponding changes in forces and lengths of F and E muscles. The next trace represents changes in the (“hip”) angle (q), and the bottom trace shows changes in the moment of ground reaction forces (M_GR) acting during the “stance” phase (when q̇ > 0). Figure 2B represents the activity of RG neurons (RG-F and RG-E) and corresponding inhibitory interneurons (four top traces) and the activity of all four muscle afferents controlling the RG in the model (see Fig. 1). One important feature of the locomotor oscillations in the model is the existence of a delay (about 100 ms, which slightly changes with the rate of oscillations) between the onsets of flexion (FL) and extension (EXT) (defined by the onset of the corresponding RG neurons and motoneurons) and the onsets of the stance (STANCE) and swing (SWING) phases (defined by the “interaction with the ground,” see M_GR trace in Fig. 2A). This simulation result exactly reproduces the delay between the onsets of EMG bursts in flexor and extensor muscles and the corresponding onsets of the swing and stance phases (defined by the timing of limb’s touch-down and lift-off) observed during real locomotion.^4,5,15,34,37

Figure 2.

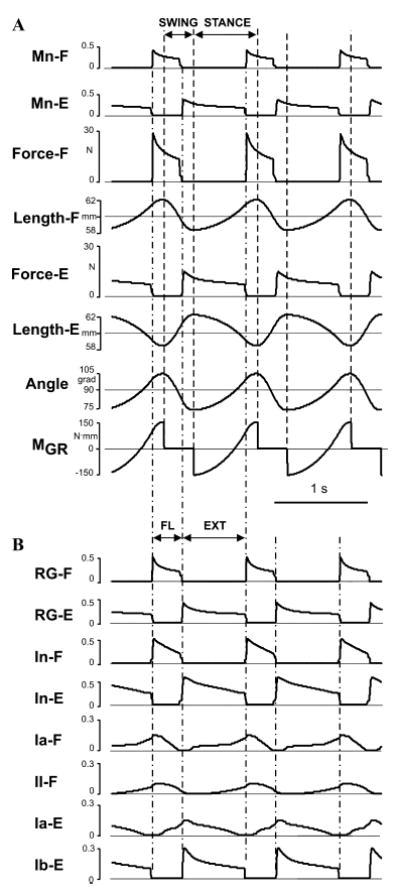
Model performance under normal conditions (A) Changes in limb biomechanical output during locomotor movement (see text for details). (B) Rhythmic activity of RG neurons (RG-F and RG-E) and corresponding inhibitory interneurons (four top traces) and the activity of all four afferents controlling the RG (see text for details). The activity of all neurons in (A) and (B) represent changes of output neural variable of each neuron f (V). The vertical dashed lines in (A) separate the swing and stance phases (defined by the changes in the moment of ground reaction forces (M_GR)); the vertical dash–dotted lines in (A) and (B) separate the flexor (FL) and extensor (EXT) phases defined by the onset of activity of RG-F and RG-E neurons.

The locomotor oscillations produced by the model can be represented by a limit cycle in a 2D diagram (q, q̇) (see Fig. 3). Our analysis has shown that the produced locomotor oscillations are stable with respect to both the initial conditions (initial limb position and velocity, e.g., see examples in Figs. 3A and B) and external perturbations (additional moments of force applied in different phases of the step cycle (see examples in Figs. 3C and D)). Stability of these oscillations in the model is provided by afferent control of the CPG. Specifically, the activity of the force-dependent extensor afferents (Ib-E), that provide positive feedback to the extensor motoneuron via both the CPG (PF-E) and disynaptic excitation (Inab-E), plays a major role in compensating for the ground reaction forces and effects of external perturbations during stance.

Figure 3.

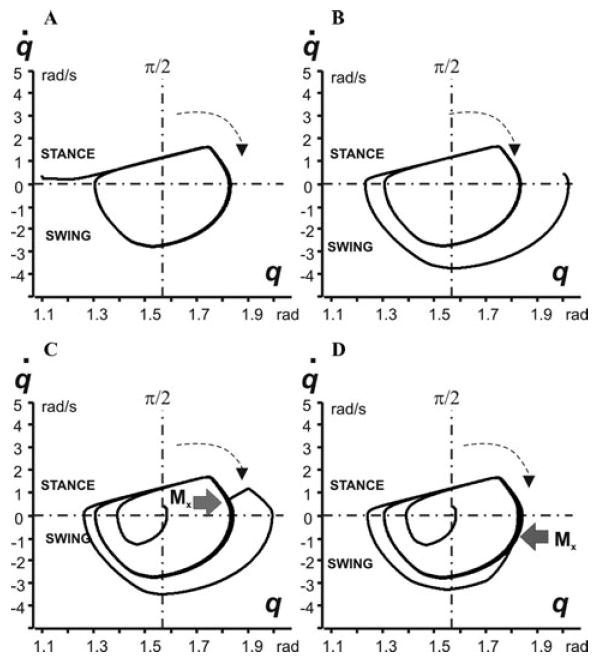
Locomotor oscillations in the model represented as 2D (q, q̇) diagrams. In each diagram, the horizontal dash–dotted line at q̇ = 0 splits trajectory into the stance (top) and swing (bottom) parts; the vertical dash–dotted line corresponds to the vertical position of the limb (q = π/2); the arrows show the direction of movement. In diagrams (A) and (B), oscillations started from different initial angles (q₀ at t = 0). (C) and (D) show the effect of disturbances, a moment of external force M_x = 150 N · mm applied for 100 ms in different phases of the step cycle (during stance in (C) and swing in (D)).

Control of locomotor speed

An increase in the supraspinal drive to the CPG in the model (Fig. 1) increases the speed of locomotion (rate of oscillation), so that the step cycle duration decreases due to the shortening of the stance phase with a relatively constant swing phase duration (Figs. 4A and C). Hence, the model with afferent feedback produces an extensor-dominated locomotor pattern (Fig. 4C), which fits the experimental observations in cats^16,17 (see Fig. 4D), rats,^18,19 and humans.²⁰ Interestingly, an increase of locomotor speed is also accompanied by a symmetrical increase in the amplitude of angular limb deviation from the midpoint vertical position (q = π/2) which is kept almost constant (Fig. 4B).

Figure 4.

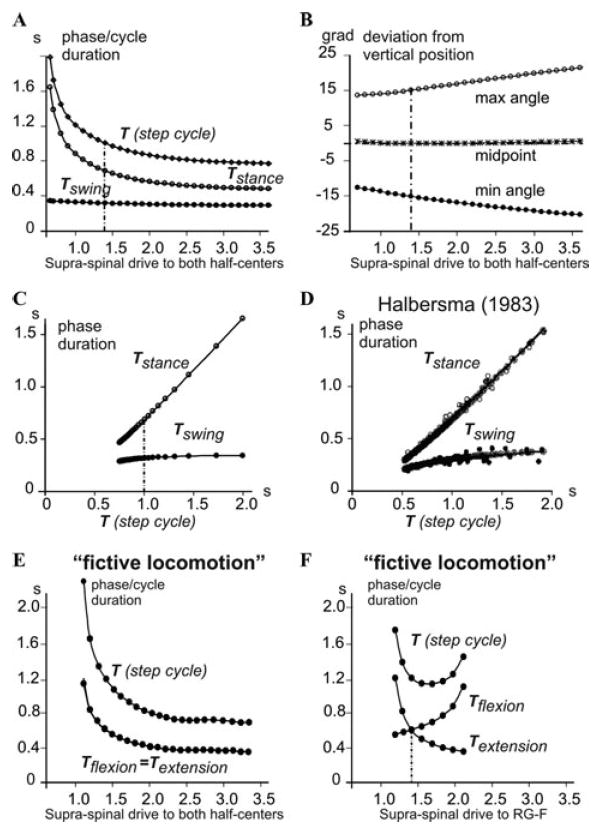
Control of the locomotor speed. (A) Changes in the durations of the swing and stance phases and the overall step cycle in the intact model with an increase in the supraspinal drive to the CPG (both half-centers receive the same drive). (B) Changes in the amplitude of the angular deviation from the midpoint (vertical limb position at q = π/2) with an increase in the supraspinal drive to the CPG. (C) The durations of simulated swing and stance phases plotted against the step-cycle period, the same data as in A. The vertical dash-dot lines in A–C indicate the drive value of 1.4 which was used in all simulations shown in Figures 2 and 3. (D) The durations of simulated flexor and extensor phases in the model plotted against the step-cycle period for treadmill locomotion in intact cats (from Halbertsma¹⁷). (E) Changes in the durations of flexor and extensor phases and the overall step cycle in the CPG pattern generated in the absence of afferent feedback (“fictive locomotion” state) when both half-centers receive the same drive. (F) Changes in the durations of flexor and extensor phases and the overall step cycle in the CPG pattern generated in the absence of afferent feedback (“fictive locomotion” state), when the drive to RG-E was kept constant (1.4, marked by a dashed line), whereas the drive to RG-F was varied from 1.1 to 2.1.

It has been proposed that the physiological basis for the extensor-dominated locomotion may result from an asymmetry in the organization of the CPG per se,^22,23 or an asymmetry in the descending drive to the flexor and extensor CPG half-centers.^24-26 To investigate this possibility we have comparatively investigated the generation of locomotor pattern by the CPG with and without afferent feedback. The latter may be considered as a “fictive locomotion” state. Our simulations have demonstrated that in the symmetrical case (when both half-centers of the RG received the same supraspinal drive), both flexor and extensor phases were equally shortened by an increase of the drive (Fig. 4E). In an asymmetrical case, both flexor-dominated and extensor-dominated “fictive” pattern could be obtained by applying different drives to the RG half-centers.^6,40 For example, Figure 4F shows the case when the drive to RG-E was kept constant, whereas the drive to RG-F was progressively varied, producing gradual transition from an extensor-dominated to a flexor-dominated “fictive” locomotor pattern. Two of the patterns generated during “fictive locomotion” (with no afferent feedback) by different drives to RG-F, one flexor-dominated and one extensor-dominated, are shown in Figures 5(A1 and B1) and (A2 and B2), respectively. However, as seen in Figures 5C1 and C2, incorporating afferent feedback changed both patterns to “normal” extensor-dominated patterns with a relatively constant duration of the flexor phase. Moreover, to provide stable oscillations, afferent feedback prolonged the extensor phase in the first case (Fig. 5C1) and shortened it in the second case (Fig. 5C2).

Figure 5.

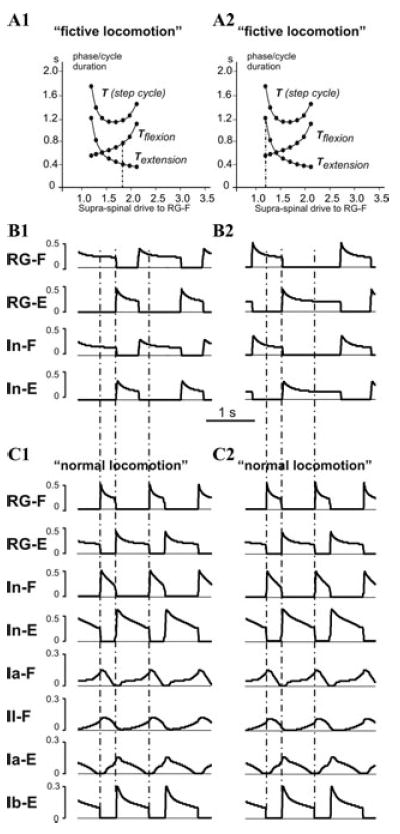
Locomotor oscillations with asymmetric drive to CPG half-centers. (A1) and (A2) repeat the diagram shown in Figure 4F, with vertical dash-dot line indicating drives used in simulations shown in (B1) and (B2), respectively. (B1) An example of a flexion-dominated “fictive locomotion” pattern generated by the CPG (with no afferent feedback) with drive to RG-E set to 1.4, and drive to RG-F set to 1.8 (see in (A1)). (B2) An example of an extensor-dominated “fictive locomotion” pattern generated by the CPG with drive to RG-E set to 1.4, and drive to RG-F set to 1.2 (see in (A2)). (C1) and (C2) The extensor-dominated pattern of “normal locomotion” with the same values of drives as in (B1) and (B2), respectively, with afferent feedback intact. Note that feedback prolongs the extensor phase in (C1) and shortens it in (C2).

In summary, our simulations show that afferent feedback can adjust and maintain an asymmetric, extensor-dominated pattern during normal locomotion relatively independent of the pattern (flexor- or extensor-dominated) expressed in the “fictive locomotion” case (without afferent feedback). Specifically, the timing of extension-flexion transition in the CPG is controlled by both the reduction of Ib-E activity (unloading of Mn-E) and the increase in length-dependent flexor (Ia-F and II-F) afferent activity (see Fig. 2B), which make the duration of stance dependent on the locomotor speed. In contrast, the timing of flexion-extension transition in the CPG is mainly controlled by the length-(and velocity-) dependent extensor afferent activity (Ia-E) which adjusts the duration of flexion to limb kinematics during swing, keeping the duration of swing relatively constant. Hence our simulations support the suggestion of Juvin et al.²¹ and Hayes et al.³⁰ regarding the critical role of afferent feedback in shaping and maintaining the extensor-dominated asymmetry observed during normal locomotion.

Role of afferent feedback in locomotor recovery after loss of supraspinal drive

During the last decade, many studies have provided evidence that after SCI (which removes supraspinal inputs to the spinal CPG) locomotor function can be recovered by locomotor training alone or by various combinations of locomotor training with pharmacological treatment and/or afferent stimulation. It is believed that locomotor training (and other successful treatments) restores locomotor function by an increase of proprioceptive input to the CPG.^{4,15,35,36,38} This possibility, however, has not been theoretically investigated with the models. Therefore, as a part of this study, we address the question of whether an augmentation of afferent feedback to the CPG (which supposedly simulates the effect of locomotor training) can reestablish locomotor rhythm generation and stable locomotor movement after the loss of the supraspinal drive (emulating the effect of SCI).

Removal of the supraspinal drive in the model (Fig. 1) stopped the generation of the locomotor rhythm. To simulate the proposed effect of locomotor training, we proportionally increased the weights of flexor and extensor length-dependent (Ia and II) and force-dependent (Ib) afferents to all target neurons in the model. We found that progressive increase of these weights can quickly reestablish the generation of locomotor oscillations by the CPG. However, the locomotor movements of the limb remained unstable (the limb simply “fell” during either stance of swing phase in the first step or after a few steps) until the weights of the extensor Ib-E afferents were increased fivefold, and the weights of Ia and II afferents (Ia-F, Ia-E, and II-F) were increased by 31%. After that, the model was able to demonstrate stable locomotor movements without “falling” (see Figs. 6 and 7). The locomotor movement after recovery, however, was less stable in respect to initial conditions and applied perturbations. An additional analysis has shown that a dramatic increase in weights of the force-dependent extensor (Ib-E) afferent inputs to CPG is critical for “locomotor recovery” after supraspinal drive removal.

Figure 6.

Model performance after removal of supraspinal drive and recovery. (A) Changes in the limb biomechanical output during locomotor movement. (B) Rhythmic activity of RG neurons (RG-F and RG-E) and corresponding inhibitory interneurons (four top traces) and the activity of all four afferents controlling the RG. For the meaning of the dashed and dash–dotted lines see Figures 2A and B.

Figure 7.

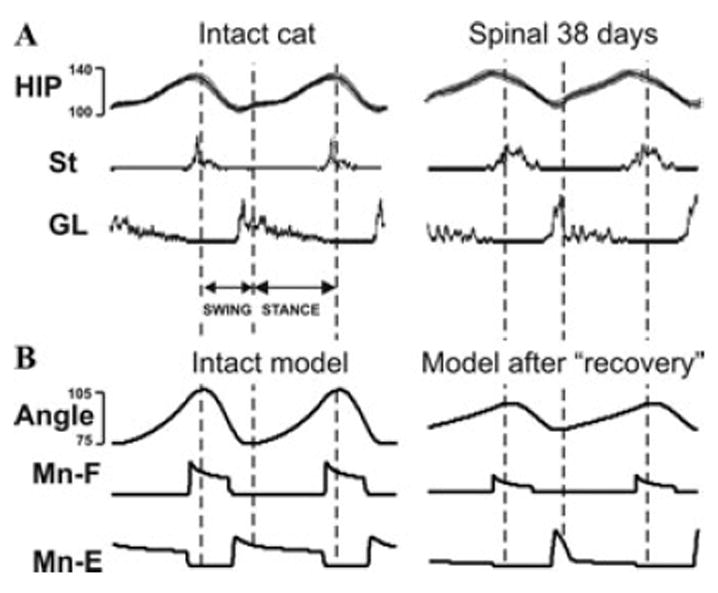
Comparison of simulation results to data obtained during cat locomotion on a treadmill. (A) Changes in hip angle and activity (EMG) of semitendinosus (St) and gastrocnemius lateralis (GL) muscles during locomotion on a treadmill (0.3 m/s) in the intact cat (left) and in the same spinal cat after locomotor training (right) (adapted from Rossignol and Bouyer³⁷). (B) Changes of limb angle and flexor and extensor motoneuron activity produced by the model during normal conditions (left, from Figs. 2A and B) and after recovery (right, from Figs. 6A and B).

Figure 6A shows the changes in the biomechanical output of the model during locomotor movement after “locomotor recovery” (compare with Fig. 2A), and Fig. 6B represents, correspondingly, the activity of RG neurons (RG-F and RG-E), inhibitory interneurons, and all 4 afferents controlling the RG (compare with Fig. 2B). Comparison with the intact model (Figs. 2A and B) shows that after removal of the supraspinal drive and “recovery”: (a) the delay between the onsets of flexion and extension and the corresponding onsets of stance and swing phases was reduced; (b) the ratio of flexor phase duration to the step cycle was increased; (c) the angle changes during stance became more linear; and (d) a dramatic increase in extensor motoneuron (Mn-E) activity occurred at the beginning of extension preceding the onset of stance. Interestingly, all these features appear (at first glance) to fit the changes of these characteristics observed in intact versus spinal cats after locomotor training (see Fig. 7A).

Conclusions

In this study, a simple neuromechanical model was used to investigate the role of afferent feedback in the control of the locomotor CPG. Despite the simplicity of the model, it may provide important insights into afferent control of locomotion. Specifically, our simulations have demonstrated the essential role of afferent feedback for the adjustment of CPG operation and the locomotor pattern generated to the biomechanical characteristics of the limb and its interactions with the ground. We have also shown that afferent feedback can provide asymmetric, extensor-dominated control of locomotor speed (with a relatively constant swing phase duration) independent of the asymmetric pattern (flexor- or extensor-dominated) generated by the CPG alone (in “fictive locomotion” conditions). Finally, we have demonstrated the possibility of re-establishing stable locomotion after removal of the supraspinal drive by increasing the weights of afferent inputs to the CPG, which supposedly occurs with locomotor training. These findings will be further investigated using a more detailed and realistic model of neural control of locomotion. The simplified model described in this study has not considered the possible effects of SCI and locomotor recovery on the intrinsic properties of motoneurons and interneurons as well as on the circuits of various spinal reflexes, which will be incorporated and considered in future models.