Beyond static structures: Putting forth REMD as a tool to solve problems in computational organic chemistry

Abstract

Computational studies of organic systems are frequently limited to static pictures that closely align with textbook style presentations of reaction mechanisms and isomerization processes. Of course, in reality chemical systems are dynamic entities where a multitude of molecular conformations exists on incredibly complex potential energy surfaces (PES). Here, we borrow a computational technique originally conceived to be used in the context of biological simulations, together with empirical force fields, and apply it to organic chemical problems. Replica‐exchange molecular dynamics (REMD) permits thorough exploration of the PES. We combined REMD with density functional tight binding (DFTB), thereby establishing the level of accuracy necessary to analyze small molecular systems. Through the study of four prototypical problems: isomer identification, reaction mechanisms, temperature‐dependent rotational processes, and catalysis, we reveal new insights and chemistry that likely would be missed using static electronic structure computations. The REMD‐DFTB methodology at the heart of this study is powered by i‐PI, which efficiently handles the interface between the DFTB and REMD codes. © 2015 The Authors. Journal of Computational Chemistry Published by Wiley Periodicals, Inc.

Introduction

Studies of organic systems frequently utilize computational results as an essential tool to elucidate mechanistic reaction details that are difficult or impossible to access experimentally.1, 2 The literature is rife with examples of reaction pathways in which reactants, intermediates, and products, as well as their associated transition states, are cartooned as a series of static geometries each possessing a specific reaction enthalpy. Often, a picture of this type successfully captures the key aspects of a system allowing, for example, identification of the primary mechanistic pathway3, 4, 5, 6, 7, 8, 9 or rationalization of the presence of a specific intermediate.9, 10, 11, 12, 13 Such descriptions, however, are occasionally insufficient to chemistry occurring in an experimental setting,14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33 in the most extreme cases leading to disastrous failures.34 Inside the computer, a host of factors that govern “real world” chemical reactions must necessarily be approximated or ignored altogether in a static picture. Chiefly among these is a precise description of a reaction's free energy, as opposed the frequently reported enthalpy. While estimates of the free energy within a harmonic approximation are provided by most quantum chemistry codes, techniques based on molecular dynamics (MD) represent a more appealing option to fully access the entropic contribution to the stability of different molecular states, that can also be extended to explicitly include environmental effects (e.g., temperature, pressure, etc.).

From the perspective of the computational organic community, an ideal methodology would directly provide ab initio free energies at accessible computational costs, for example, by combining the physical quantities associated with the free energy obtained from MD simulations with the accuracy of static quantum chemical computations. Roughly speaking, the current state of MD simulations to estimate these quantities can be subdivided into two classes: classical or molecular mechanics (MM) and ab initio (AIMD) methods. On one hand, conventional MM force fields, such as those successfully used in molecular biology and pharmaceutical chemistry,35, 36 rely only on the nuclear coordinates of a system, making them very fast. Unfortunately, in most cases they are incapable of describing chemical processes involving the breaking and formation of bonds (Reactive force fields capable of simulating chemical reactions do exist, but are relatively few in number).37 This makes MD simulations based on MM force fields very useful to examine biological phenomena such as protein folding.38 On the other hand, AIMD is capable of describing chemical reactions involving bond breaking and formation. Indeed, the combination of density functional theory (DFT) with AIMD methods has already been used within the framework of Car‐Parrinello39 and Born–Oppenheimer40, 41 MD to resolve problems associated with reaction pathways, 42, 43, 44 phase transitions,45, 46 and solute/solvent interactions.47, 48 The above mentioned examples utilize GGA functionals and plane‐waves, which benefit from being both relatively fast39, 49 and highly scalable,50, 51, 52, 53 but are, nonetheless not ideal for the organic community as chemically intuitive concepts and properties are lost owing to the delocalized nature of the planewaves and the inevitable use of effective core potentials. In contrast, Born–Oppenheimer MD simulations, using typical localized basis set quantum chemistry codes featuring the more reliable global hybrid functionals and post‐Hartree Fock methods, are rather sparse (see e.g., Refs. 54, 55, 56) (For a seminal implementation on GPU see Ref. [56]). A serious limitation involves the duration for which a simulation can be propagated in time. Naturally, the increased computational expense of AIMD simulations, which require computing potentials from a first principle method such as DFT, limits their applicability to short ∼10²–10³ ps intervals. Depending on the complexity of the potential energy surfaces (PES), chemically relevant interconversions between different possible states may not appear on such short time scales. One feasible solution is to lengthen the simulation time by reducing the computational expense of determining the first principles potential by replacement with a potential derived from semiempirical methods, such as density functional tight binding57, 58 (DFTB). For instance, replacing the DFT by a semiempirical DFTB potential permits access to simulations that are three orders of magnitude longer (on the 1–10 ns time scale) while also accommodating a tenfold increase in the number of atoms.59 Despite these improvements, the complexity of the PES of many organic reactions remains sufficiently large that visiting all chemically relevant regions remains essentially impossible. To ensure that all of the PES is explored, additionally computational tricks must be used.

MD simulations of systems containing a large, complex PES necessitate the use of enhanced sampling techniques that facilitate thorough exploration of the free energy landscape. These techniques are required to overcome problems associated with running insufficiently short simulations by reducing the amount of time that a system spends trapped in a local energy minimum. Such enhanced sampling techniques can be roughly divided into two groups. The first is concerned with the identification of pathways between known initial and final states. This category includes, for instance, transition path sampling60 or constrained dynamics.61 However, these approaches do not facilitate searching for the free‐energy global minima or other important configurations of a system within a complex free energy landscape.62, 63, 64, 65 The second category of enhanced sampling methods is better suited to tackle this problem, as it is aimed at obtaining a thorough exploration of the low‐energy portions of the free energy landscape. Some of these techniques, such as metadynamics62 or accelerated MD66 (aMD), rely on modified potentials. While most of these methodologies were originally envisioned for the study of biological systems using classical MD,36, 67, 68 both metadynamics69, 70 and aMD71 have been used to study chemical reactions requiring quantum mechanical treatments. The principal disadvantage, in this case, is that some insight about the system's reactivity is needed to choose an appropriate reaction coordinate, which could in turn affect the outcome of the simulation.

In contrast, modified sampling approaches, such as replica exchange MD72 (REMD), do not require any prior insight. However, they have mostly been used in the context of biological simulations together with empirical force fields, and have only rarely been used in concert with quantum chemical methods. The few existing studies are limited to molecular clusters containing only a handful of atoms.73, 74, 75 The basic idea of parallel tempering replica exchange is to simulate N replicas of a system at a range of different temperatures. Replicas propagated at high temperature freely explore a large amount of the PES in an unencumbered manner by overcoming any barriers present, while low temperature replicas explore local minima regions from which they are unable to escape. The key to the improved sampling seen in REMD involves exchanging complete configurations from replicas at different temperatures via a Metropolis–Teller algorithm,76 thereby enhancing exploration of the entire free energy landscape.

In principle, the coupling of potentials derived from semiempirical methods with REMD would allow access to additional information and larger systems than for the first principles potentials obtained in AIMD. Such a tool would be very useful within the realm of organic chemistry, where the PES landscapes of reactions may be quite complex. Moreover, the importance of directly determining free energies can assist in exploring the chemistry of systems where entropy is known to play an important role. Here, we present results obtained by coupling the i‐PI interface for advanced molecular simulations77 with the DFTB357, 58, 78, 79 semiempirical framework to conduct REMD with the objective of exploring the free energy surfaces of organic systems. Such an approach is appealing as it combines the thorough statistical sampling enabled by enhanced MD with the reliability of approximate quantum chemical techniques, which are capable of accurately describing the energetics of structures of organic systems at an affordable cost. Through coupling with i‐PI, we highlight the abilities of the REMD@DFTB3 method to address prototypical cases relevant to the computational organic community including: (i) exploration of the conformational space of a dithiacyclophane molecule possessing multiple local minima, (ii) estimation of the minimum energy pathway and free energy barrier of the Cope rearrangement (CR) of semibullvalene (SBV), (iii) distinguishing entropically versus enthalpically favored conformational states of a molecular rotor, and (iv) identifying the key conformations of a widely used organocatalyst, cinchona alkaloid.

Computational Details

All forces are computed at the DFTB3/3OB80, 81 using the Universal Force Field parameters to account for dispersion forces as implemented in the DFTB+ program.82 The DFTB+ code was interfaced with the dynamic driver i‐PI after minor modifications. The Hubbard derivatives and the h‐damping factor were chosen according to Refs. [80,81]. A finite electron temperature of 300 K was selected to improve the convergence of the geometries arising from the hottest replicas. While a serious drawback for systems sensitive to solvent effects, the current implementation is restricted to gas phase simulations. Regardless, many valuable aspects of a system's behavior can still be extracted from gas phase data. In turn, this newly revealed information may lead to more informed predictions about how the same system would behave in the condensed phase.

The i‐PI software drives the REMD, which evolves in the NVT ensemble within a cubic box length of 1000 Å. The large box avoids the spurious interaction between replicas within the periodic boundary conditions. For a given system, the simulations were initiated from the same structure and velocities. Gaussian distributions centered at 900 K provide the atomic velocities for each replica. A time step of 0.25 fs was found to be sufficient to integrate the Newton equation without observing any drift on the conserved quantity (see Supporting Information Fig. S6). Exchanges between replicas (Fig. 1) were attempted stochastically every 50 steps83 on average using the following probability (The exchange time was chosen in accordance with the current state‐of‐the‐art, as is frequently done in the literature):

$$p=\min \left(1,e^{(E_i-E_j)(\frac{1}{k_{\mathrm{B}}{T}_i}-\frac{1}{k_{\mathrm{B}}{T}_j})}\right)$$ (1)

where k _B is the Boltzmann constant and T_i and T_j are the temperature of the exchanged replica. In this way, the mapping of the PES is canonical, meaning that the free energy profile obtained at each temperature corresponds to the free energy profile that would be obtained in a normal MD with much improved sampling efficiency.

Figure 1.

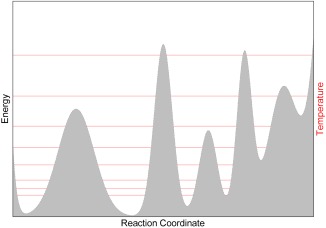
Illustration of replica exchange: the PES of a hypothetical system is represented in gray. The red lines illustrate the replicas (i.e., trajectories) at different temperatures. Frequent exchanges are attempted between the replicas based on a Metropolis criterion [with a probability given by eq. (1)], which guarantees that at any time the statistical distribution of each replica is consistent with its current temperature. Thanks to the exchanges, each replica can go up and down across the red lines and visit all the minima and maxima on the PES.

A Langevin thermostat, with a time constant of 100 fs, was used to maintain a constant temperature for each replica. The temperature ranges from 300 K for the coldest replica to 1500 K for the hottest. Sixteen replicas were found to be sufficient (i.e., provided enough round‐trips among the replicas during the simulation time) for the dithiacyclophane molecule and the CR of SBV. Larger molecules—the cinchona alkaloid and the molecular rotor needed 48 replicas to effectively exchange among replicas. A table with all temperatures is provided in the Supporting Information (Table S1). Snapshots of atomic configurations were saved every 50 steps, and used for further processing.

The initial 10,000 steps were used for equilibration, and discarded from subsequent analysis. Data from different replicas were combined by weighting each frame by $w=e^{{\beta }_r-{\beta }_t}$ and computing the observables separately for each parallel tempering temperature. The different replica were then combined with the weighing factors chosen as $\frac{{〈w〉}^2}{{〈w〉}^2-{〈w〉}^2}$ according to the error estimates in reweighed averages given in Ref. 84.

Smooth histograms were constructed using kernel binning with a triangular windows function much smaller than the extent of the main features in the free energy landscape. With respect to timing, for each system considered the REMD@DFTB3 computations presented herein could be performed within 2–4 days (real time) depending on the size of the system on Intel‐based (Xeon E5‐2660) cores. A patch for DFTB+ (version 1.2) is available on demand.

The REMD free energies reported in Table 1 (cinchona alkaloid) and Supporting Information Table S2 (dithiacyclophane) for each relevant region (i.e., a basin i) are computed through evaluation of the following integral:

$$F_i=k_{\mathrm{B}}T \log \hspace{0.17em}{\displaystyle \underset{N_i}{\int }{e}^{-F(x)/k_{\mathrm{B}}T}}dx$$

where each of the nonoverlapping integration regions (N_i) covers a neighborhood of the local free‐energy minima. This equation permits one to account for the thermal fluctuations that distort in a different manner the geometries of the various configurations.

Table 1.

Relative electronic and free energies (in kcal mol⁻¹) of the cinchona alkaloid conformers determined from gas phase static computations or from the REMD simulations (DFTB3/3OB‐UFF) at 300 K. The geometries for computing the static DFTB3 energies are optimized at the same DFTB3 level. The BP86‐D results are taken from Ref. [132].

	DFTB3/3OB‐UFF		BP86‐D/TZP132
	(Static) Electronic energy	REMD free energy	Static free energy
Anti‐open (1)	1.3	0.00	0.6
Syn‐open (4)	0.0	1.57	0.0
Anti‐closed (2)	6.5	2.11	5.4
3	1.7	1.94	–

Static electronic structure computations for the dithiacyclophane and CR included optimizations at the M06‐2X85, 86/def2‐SVP level using the “Ultrafine” grid as implemented in Gaussian09.87 Alternative energy assessments were obtained at the PBE088, 89‐dDSC90, 91, 92, 93/TZ2P (for dithiacyclophane) and CCSD(T)/cc‐pVTZ (for the CR) using ADF94, 95, 96 and Molpro,97, 98 respectively. Reported static free energies include unscaled free energy corrections from M06‐2X/def2‐SVP computations. Reported static DFTB3/3OB‐UFF electronic energies are computed at the DFTB3 optimized geometry.

Results and Discussion

Dithiacyclophane

Understanding the conformational analysis of molecules represents a cornerstone of organic chemistry. Free energy mapping provides direct relationships between structure and energy and assists in understanding molecular behavior. In this context, a dynamic exploration of the free energy surface may not only alter, but possibly even reverse pictures provided by static relative energy computations. More importantly, it may also reveal unexpected energetically low‐lying conformations that were not envisioned owing to preconceived user‐based biases about a system. The conformations of dithiacyclophane (Fig. 2), previously investigated by two of the authors,99, 100 perfectly illustrates this aspect. This highly flexible molecule was originally found to possess several low‐lying conformers featuring both π‐stacked (structure 1, meta‐stable) and open conformations (structure 2, lower in energy) using accurate electronic structure methods. Not surprisingly, Born–Oppenheimer MD simulations performed at both the DFT (i.e., PBE) and DFTB3 levels were shown to be highly sensitive to the inclusion of a dispersion correction.99, 100 As might be expected, in the absence of van der Waals corrections, the π‐stacked conformation readily converted into the open conformers (on a scale as fast as 250 fs), whereas the stacked meta‐stable conformer persisted for a few picoseconds in the dispersion‐corrected trajectories. The current REMD@DFTB3 results add a new element to the former picture, revealing a somewhat less intuitive “disarticulated” conformational state (structure 3, Fig. 2). More importantly, this new conformational region is thermodynamically favored from the MD free energy and static electronic or free energy perspective (see Supporting Information Fig. S1 and Table S2), and thus would affect any measured properties (e.g., NMR chemical shifts, infrared spectrum, etc.). Note, however, that the conformational entropic contributions are the largest for 2 as indicated by its larger basin (larger number of conformations) and by the small REMD free energy difference between 2 and 3 in comparison to the static picture (see Supporting Information Table S2). The population of 3 remains barely dominant at 300 K, when accounting for the full entropic contribution. The two‐dimensional (2D) plot of Figure 2 provides further insights into the conformational dynamics inaccessible from a static picture. For instance, the direct paths connecting the open conformational regions with the two other areas (2 ↔ 1, 2 ↔ 3) contrast with the absence of a low‐energy pathway directly connecting the closed and “disarticulated” conformer (1 ↔ 3). Having access to information of this type could be useful when, for example, aiming to alter dynamic fluctuation through chemical modification. Finally, it is worth noting that “standard” Born–Oppenheimer MD simulations (as opposed to REMD) performed on an even longer timescale (i.e., 1.3 ns see Supporting Information Fig. S2) than those in Refs. [38] and [39] remained, for most of the time, trapped in its original stacked conformational region without identifying the thermodynamically more important region associated with the new conformation.99, 100

Figure 2.

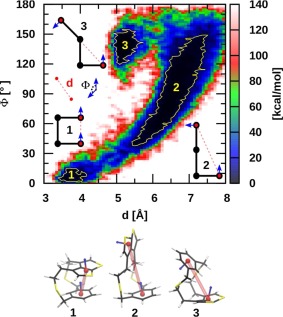
Two‐dimensional representation of the free energy landscape obtained from the REMD@DFTB3 of the dithiacyclophane molecule. The relevant collective variables are shown in the plot. 1 kcal mol⁻¹ isocontours are shown in yellow.

Cope rearrangement of semibullvalene

Aside from the identification of chemically important conformers presented in the previous example, REMD can also be used to explore the PES of organic reactions. This second type of case has been explored less often, as most REMD simulations to date have been performed together with a fixed‐bonds, nonreactive force field. The CR of SBV represents a prototypical example for which a great deal of mechanistic detail has already been amassed, including information regarding: the (a)synchronous nature and the role of tunneling in the reaction mechanism,101, 102, 103, 104, 105, 106, 107 the presence and magnitude of homoaromaticity in the transition state,108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121 and the link between molecular properties and structure.122 In its simplest form, the CR transitions between two equivalent structures each characterized by three‐membered ring on one side of the bridging ethyl subunit (Fig. 3). Utilizing a static picture derived from electronic structure theory [CCSD(T)/cc‐pVTZ//M06‐2X/def2‐TZVP], the transition state connecting these structures possesses equivalent C2—C8 and C4—C6 bond distances (2.00 Å) associated with a concerted reaction mechanism with an overall barrier height of 7.3 kcal mol⁻¹.

Figure 3.

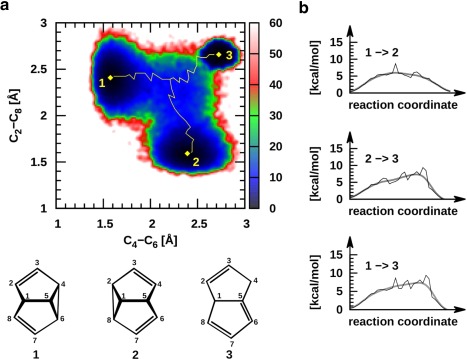
Cope rearrangement of semibullvalene. a) Two‐dimensional free energy map obtained from REMD@DFTB3 simulations indicating the expected CR (minimum energy pathway, 1 ↔ 2, given in yellow) as well as an unexpected region corresponding to opening of the SBV structure to give dihydropentalene (1 ↔ 3, 2 ↔ 3). b) Qualitative plots of the minimum energy pathways between the stable conformations presented in 3a.

From the organic chemist's perspective, this reaction likely appears far too simple to merit study using MD techniques, predominantly because the essential mechanistic components appear well described from static computations. In contrast, our exploration of the PES using REMD@DFTB3 reveals considerably more information than might have been anticipated (Fig. 3). More than 600,000 structures were analyzed to generate a 2D free energy plot, that identifies chemically meaningful regions including the expected SBV minima (1 and 2) and the CR TS (blue central area), as well as the minimum energy reaction pathways connecting these structural regions (yellow). From this data, the relative height of the TS barrier (+8.7 kcal mol⁻¹ is the highest point along the DFTB3 MEP) and any free energy differences between the reactant and products can be estimated (zero in this case) by the upper most reaction coordinate plot of Figure 3b, which closely mirror the type of energy plots typically associated with static computations. A quantitative assessment of the reaction rate, however, would require a careful analysis of deviations from transition‐state theory that are to be expected whenever the order parameters chosen to describe the transition are not ideal.

Perhaps, the most relevant feature of Figure 3a is the presence of three minima, as opposed to the two that we expected. As mentioned earlier, regions 1 and 2 correspond to the two symmetric SBV structures, however, the third black region (3, upper right) represents conformations that possess significant lengthening of both the C2—C8 and C4—C6 interatomic distances. Molecular structures of this type are no longer three‐dimensional cages, instead adopting quasiplanar conformations, as exemplified by dihydropentalene (3, Fig. 3). Indeed, such structures are linked to SBV by two distinct, yet directly connected TS structures and a valley‐ridge inflection point indicative of a surface bifurcation.17, 123 Examining the 3 ↔ 1 and 3 ↔ 2 MEPs reveals this feature: the structure must first pass over a relatively high barrier close to region 3 (Fig. 3a, also visible 1→3 and 2→3 reaction coordinate plots, Fig. 3b). Overcoming this first, energetically more costly TS barrier leads to the second TS associated with the CR transition between the two symmetric SBV structures. As we observe just a few transitions toward region 3, we cannot deem simulations to be converged and we cannot be confident of the quantitative accuracy of the free energy landscape we computed. More sophisticated REMD implementations or combinations of REMD and metadynamics124 are probably needed to obtain reversible sampling. Similar in nature to the bare SBV picture, placing an electron withdrawing substituents onto selected positions either enhances or suppresses the CR TS barrier.108, 109, 125, 126 For instance, the placement of a CN‐ onto the C8 carbon results in a decrease in the CR transition state barrier as well as creating asymmetrical products and reactants, yet the substituted dihydropentalene is again present (see Supporting Information Fig. S3).

Clearly, the inherent nature of sampling the PES using REMD provides an enhanced view of the ways in which organic systems move between different conformers or along competing energetic pathways. For the example provided here, the three energetic basins corresponding to structural minima, as well as the minimum energy pathways connecting them, were obtained with no prior knowledge of the system. Assessments with no a priori knowledge that are provided by enhanced sampling techniques are likely to become of increasing importance, particularly for systems featuring a more complex PES. Taken to its extreme, REMD can be used to better understand the behavior of systems consisting of thousands of isomers, such as shape‐shifting organic molecules (e.g., bullvalene).127

Molecular rotor

The dynamics of a recently investigated molecular rotor128 (Fig. 4), is a further illustrative case study highlighting the importance of accessing conformational states associated with both entropically and enthalpically favored regions. For this rotor, structural changes occur upon increases in temperature, which are directly visible in the variable temperature ¹H NMR spectra. The measured chemical shifts imply that enthalpy favored conformational states, characterized by CH/π interactions between the hydrogen of the central rotating phenylene unit and the aromatic ring of the steroid, are at the origin of the pronounced upfield ¹H chemical shift evident at low temperatures. Increasing the temperature results in an increasing population of CH/π unbound rotational states, leading to the displacement of the ¹H NMR signal of the rotator C—H group toward lower fields. In such a situation, static computations can help to identify a handful of relevant conformers of both types (bound and unbound), yet the direct one‐to‐one relationship between the most prevalent conformational states at a given temperature and the observed chemical shifts remains undetectable. REMD, conversely, delivers a more comprehensive picture by disclosing key changes in the relative populations associated with temperature‐dependent rotational processes. The REMD@DFTB3 results in Figure 5a for a temperature of 300 K are analyzed in terms of ring current chemical shielding at the position of the hydrogen atoms H₁ and ${\mathrm{H}}_1^{\prime }$ for each structure. The shielding cone created by the aromatic ring of the steroids at proton H₁ and ${\mathrm{H}}_1^{\prime }$ were evaluated using Pople's ring current model129 (see Supporting Information Fig. S4). The region above 0 ppm is characterized by CH/π bound states, whereas values around 0 ppm are representative of CH/π unbound states. Accordingly, the results show that the enthalpy driven region corresponds to a set of conformers possessing only one CH/π interaction. In other words, if a CH/π interaction exists with one of the steroid aromatic rings ( ${\delta }_{{\mathrm{H}}_1\hspace{0.17em}\text{or}\hspace{0.17em}{\mathrm{H}}_1^{\prime }\hspace{0.17em}}$> 0 ppm in Fig. 5a), the other side is essentially unbound ( ${\delta }_{{\mathrm{H}}_1^{\prime }}$ or ${\delta }_{{\mathrm{H}}_1}$ = 0 ppm) at 300 K. Increasing the temperature displaces the population toward the CH/π unbound states (around 0,0) with both hydrogen atoms lying outside the shielding zone (Fig. 5b). The overall picture is clearly visible in the variable temperature ¹H NMR experiment128 but the REMD data provides significantly deeper insight into the dynamic process by revealing the relative conformational population evolution when varying the temperature as well as the direct temperature dependence of the measure properties (Fig. 5b). For such processes, it is rather unrealistic to neglect the conformational entropic contributions and calculate the “static” population of a few representative conformers randomly extracted from a minimum‐energy structures search, as is often done in computational chemistry.

Figure 4.

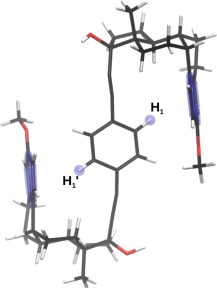
Schematic representation of the molecular rotor and the key hydrogen atoms.

Figure 5.

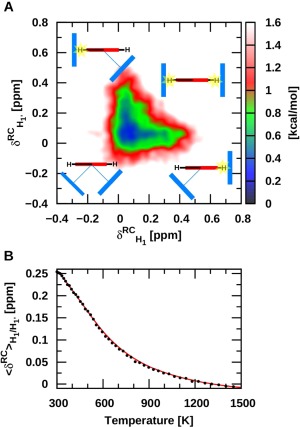
a) Two‐dimensional map of the shift induced by the current created by the aromatic ring of the steroids on H₁ and ${\mathrm{H}}_1^{\prime }$. Pople's ring current model was used to calculate the ring current chemical shifts (see Supporting Information Figure S4 for details). b) The averaged ring current chemical shifts with respect to temperature.

Cinchona alkaloid

The final illustrative application of REMD@DFTB focuses on asymmetric catalysis, more specifically on the use of cinchona‐based primary amines as chiral phase‐transfer catalysts (Fig. 6). This class of compounds, derived from natural sources, has been identified as a promising alternative to other amino‐catalysts such as proline.130, 131, 132, 133 (A) As well as its quinidine diasteteroisomer activate various carbonyl compounds with a consistently high level of stereocontrol. Rather than addressing the origin of the stereoselectivity, which depends heavily on: concentration and nature of the acid co‐catalyst, formation of hydrogen bond motifs, solvent effects, and so forth, here we revisit the gas phase conformational behavior of (A), which is one of the primary elements responsible for the control of stereochemistry.

According to our simulations, the rich conformational behavior of (A) is not easily rationalized in terms of four relevant (anti/syn and closed/open) conformations.132, 134 The 2D conformational map with 5, 10, 15, and 20 kcal mol⁻¹ isocontours given in Figure 6 suggests a somewhat richer conformational picture consisting of four easily accessible conformational regions (1–4) and one that is less frequently visited (2′). The most populated region, 1, essentially encompasses a 60° range for the C₈—C₉— ${{\mathrm{C}}^{\prime }}_4$—C_4a angle with no significant energy barrier. The most illustrative conformation associated with 1 (i.e., lowest free energy) is characterized by an angle around 90°. Previous NMR measurements135 in apolar solvents along with static computations132 established the anti‐open (1) and syn‐open (4) conformers as being energetically comparable and ∼5 kcal mol⁻¹ more stable than the “closed” conformers, with the quinuclidine nitrogen lone pair in gauche arrangement with respect to quinoline group (e.g., 2, see Table 1). The information extracted from REMD follows this interpretation while also revealing an additional accessible conformational space (3) lying between the free energy of 1 (or 4) and 2, and a flatter PES around the lower free energy minimum. The broader conformational space of 1 is particularly illustrative of the importance of capturing the full entropic and anharmonic contributions to the free energy to establish the relative stabilities between 1 and 4. In fact, while region 4 is slightly favored at both static DFTB3 and DFT‐D levels,132 the REMD free‐energy conformational minimum corresponds to 1 (Table 1). Another crucial aspect for catalysis concerns interconversion between the different conformational regions. It is clear from Figure 6 that complete rotation around the C₈—C₉ bond is much more favorable in comparison to rotation around the C₉— ${\mathrm{C}}_4^{\prime }$ bond, which is hindered by the contact between the two polycyclic groups. Even though regions 1 and 4 lie close in energy the syn‐open conformers (4) are trapped and cannot easily convert into other conformational states. Finally, it is interesting to stress that, in line with previous observation, the diastereomers of quinidine, which carry opposite sterochemistries at carbons 8 and 9, essentially behaves like an enantiomer130 as illustrated by the 2D conformational energy map provided in Supporting Information Figure S5.

Figure 6.

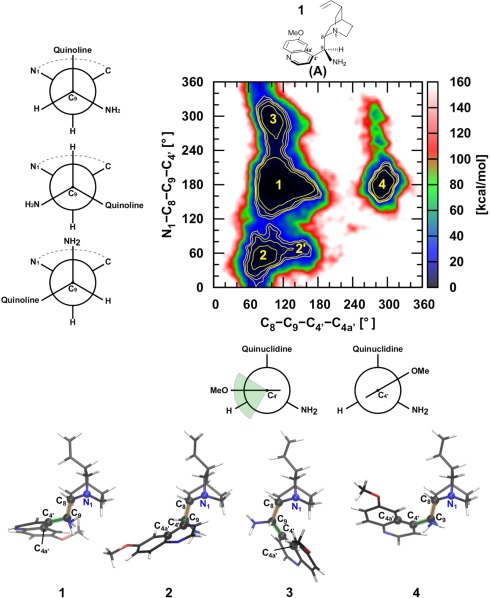
Two‐dimensional free energy map of the cinchona alkaloid catalyst a). 5, 10, 15, and 20 kcal mol⁻¹ isocontours are shown in yellow. The representative structural figures of the four relevant minima are shown at the bottom.

Regarding the crucial role played by lowest‐energy conformers and by conformational barriers in the enantiodifferentiation processes, clearly having access to the conformational free‐energy landscape is an undeniable asset. While we stress that the present analysis was performed at a fairly low electronic structure level (DFTB3) and in the gas phase (a limitation of the current implementation), the key findings related to the conformational landscape and population remain valid. Based on these finding, we believe that computational studies in the field of asymmetric catalysis would benefit greatly from accessing more realistic pictures of the conformational and reaction dynamics for each step of the catalytic cycle.

Conclusion

Here, the coupling of REMD with DFTB (REMD@DFTB3) via the i‐PI dynamic driver has been introduced and its utility demonstrated as a tool to solve problems in computational organic chemistry. Through the study of four illustrative examples, we have highlighted the importance of mapping the free energy of the PES to increase chemical understanding. As opposed to static electronic structure computations, exploring chemistry via REMD often reveals unexpected or unimagined features even for seemingly quite simple systems. This fact is exemplified by the search for low energy conformers of dithiacyclophane and analysis of the CR of SBV. Chemically more complex examples further illustrate this point by showing the important role played by dynamics in reproducing experimentally observable properties (such as proton chemical shifts) and the understanding of underlying chemical structure and its role in determining stereochemistry during organocatalysis. In general, we hope to have shown the utility of using enhanced sampling approaches, such as REMD, to better understand and solve problems of interest to computational organic chemists.

Supporting information

Supporting Information

How to cite this article: Petraglia R., Nicolaï A., Wodrich M. D., Ceriotti M., Corminboeuf C.. J. Comput. Chem. 2016, 37, 83–92. DOI: 10.1002/jcc.24025