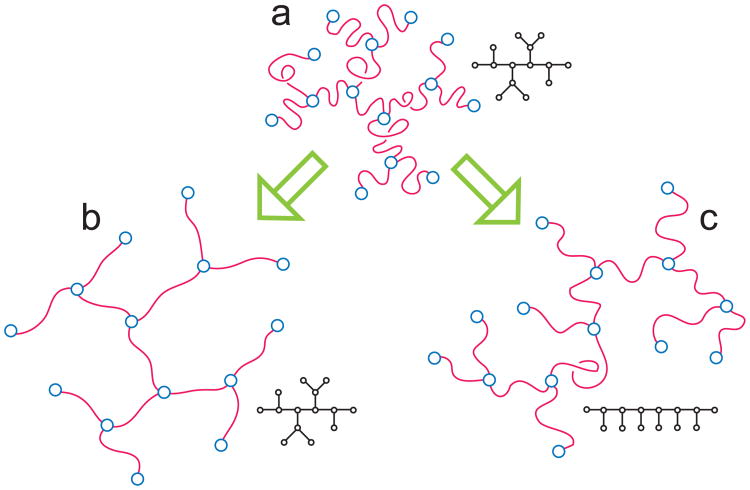
Abstract
Randomly branched polymer chains (or trees) are a classical subject of polymer physics with connections to the theory of magnetic systems, percolation and critical phenomena. More recently, the model has been reconsidered for RNA, supercoiled DNA and the crumpling of topologically-constrained polymers. While solvable in the ideal case, little is known exactly about randomly branched polymers with volume interactions. Flory theory provides a simple, unifying description for a wide range of branched systems, including isolated trees in good and θ-solvent, and tree melts. In particular, the approach provides a common framework for the description of randomly branched polymers with quenched connectivity and for randomly branching polymers with annealed connectivity. Here we review the Flory theory for interacting trees in the asymptotic limit of very large polymerization degree for good solvent, θ-solutions and melts, and report its predictions for annealed connectivity in θ-solvents. We compare the predictions of Flory theory for randomly branched polymers to a wide range of available analytical and numerical results and conclude that they are qualitatively excellent and quantitatively good in most cases.
Graphical abstract
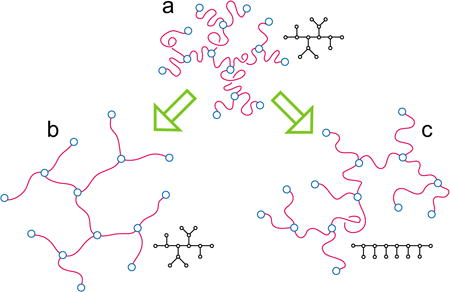
Different swelling modes for branched polymers (a) with quenched (b) and annealed connectivity (c) are explained by the Flory theory.
1 Introduction
Randomly branched polymers, or trees for brevity, are of interest in a number of scientific fields. Branched polymers can be synthesised by deliberately incorporating monomers with higher functionality into the polymerisation processes as a means of modifying materials properties1,2. In industrial applications they represent the norm rather than the exception, since most polymerisation processes for linear chains also introduce a certain amount of branching, a feature that strongly affects the dynamics3.
In the same way as random walks can be used as models for linear polymers, random trees are models for branched polymers. In this article, we use the term “tree” not only for the model, but also as a convenient short-hand notation for the object.
Theoretical models for trees date back to the early days of polymer physics4, and have been successfully employed since then in the description of a wide range of phenomena including percolation5 and gelation1. More recently, these models have been reconsidered in the context of biological molecules. In fact, the large RNA's of some viruses (Fig. 1a) behave in many ways like branched polymers owing to the presence of (small) multi-loops in the secondary structure which effectively act as branching points6–8. Similarly, supercoiled circular DNA inside the bacterial nucleoid folds into plectonemic structures9,10 which can branch on larger scales (Fig. 1b). In Statistical Mechanics, the closely related subject of lattice animals11–13 has deep connections with magnetic spin systems and has been studied by field theoretic methods14–17. Our own (renewed) interest in these systems18–20 is due to the analogy between their behavior and the crumpling of topologically constrained ring polymers21–25 (Fig. 1c) and, ultimately, chromosomes26–30.
Fig. 1.
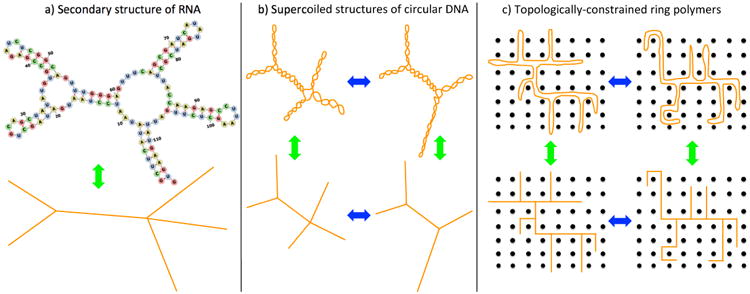
(a) Due to the Watson-Crick base pair mechanism and neglecting the difference of excluded volumes between loops and stems, single filaments of RNA have a branched secondary structure (here, visualized by the FORNA31 software). These structures have been shown6–8 to play a crucial functional role in the RNA behavior inside viral capsids. (b) The increase of the level of supercoiling in circular polymers (rings) gives rise to the formation of plectonemes: by neglecting plectonemes torsional properties, rings assume the shape of branched structures9 which reproduce the experimental behaviour of circular DNA inside the bacterial nucleoid10. According to the total amount and distribution of supercoiling the ring may continuously switch between different branched structures. (c) By neglecting the excluded volume interactions between double-folded strands, a single ring polymer constrained in a matrix of fixed obstacles21–23 resembles a branched polymer with annealed connectivity: in this situation, an “elk” may change into a “camel” and viceversa.
While there is a number of exact results for ideal, non-interacting trees4,32,33, even the simplest theory of the systems described above may not ignore the excluded volume interactions between the constituents of the trees. The treatment of these interactions is notoriously difficult even for linear polymers34. In practice1,35, descriptions are often limited to the level of scaling arguments36 and Flory theory37. In the case of branched chains, there is a single exactly known exponent for isolated three-dimensional self-avoiding trees14, highlighting the need for approximate treatments. Here we focus on Flory theories11,18,33,38, which provide a unifying description of the rich behaviour of a wide range of tree systems. Our aim is twofold: firstly, we provide a pedagogical, comprehensive review of the theory; secondly, we compare the predictions to available theoretical14,16,39–49 and computational50–63 results to gauge the reliability of the approach. We find that predictions of Flory theory are qualitatively excellent. The predicted values of the Flory exponent ν describing the scaling of polymer size with its mass are quantitatively accurate and agree with best numerical estimates in many cases.
The work is structured as follows. In Section 2 we introduce the model and discuss the theoretical difficulties arising from branching. Furthermore we briefly review the observables and exponents, which serve to characterize the connectivity and spatial configuration of randomly branched polymers. In particular, we carefully distinguish between randomly branched polymers with quenched connectivity (in short, quenched trees), whose connectivity remains “frozen” after their initial preparation, and randomly branching polymers with annealed connectivity (in short, annealed trees), whose connectivity can adapt to the environmental conditions. Section 3 is devoted to a review of Flory theory. We discuss the underlying ideas and work out the predictions for isolated trees in good and θ-solvent as well as for tree melts. In all cases, we discuss trees with annealed connectivity as well as trees with the quenched connectivity of ideal random trees. In Section 4 we compare the results to available theoretical and numerical estimates of the asymptotic exponents. Finally, in Section 5 we draw the conclusions by also commenting briefly on the theoretical limitations of the Flory theory.
2 Interacting trees
Trees are spatially embedded graphs, which are free of closed paths or loops. Ideal random trees are composed of N + 1 nodes or monomers, which are randomly connected by N bonds. We treat these bonds as having a uniform (Kuhn) length, lK. In the absence of branching, ideal trees reduce to freely jointed chains of contour length, L = lKN, and mean-square end-to-end distance, 〈(r⃗N − r⃗0)2〉 = lKL. The subject of this article are interacting random trees, i.e. trees whose nodes/monomers interact with each other via short-range excluded volume interactions.
The theory of branched polymers is more difficult than linear ones for at least three reasons. First, branched polymers are considerably more compact than their linear counterparts and therefore volume interactions play a more important role. Indeed, for isolated non-interacting randomly branched polymers, the root-mean-square gyration radius scales with polymerization degree N as compared to N1/2 for ideal linear polymers4. Second, to characterise a branched polymer, or an ensemble of randomly branched polymers, one has to describe two aspects – their connectivity (or topology of branching, or internal geometry) as well as their conformations (or embedding in space). The latter, in the simplest case, is commonly characterised through the root mean square gyration radius, , or root-mean-square spatial distance between monomers, just as in the linear polymer case. But the former is peculiar for branched systems only. A useful measure of connectivity is the average value of the contour distance between all possible pairs of monomers i, j, L ∼ 〈ℓij〉, which is equally a measure of the average length of linear paths on the tree. Thus, even the simplest theory of branched polymers has to operate with two distinct observables, R and L. And the third inherent peculiarity of branched systems is the necessity to distinguish between annealed (randomly branching) and quenched (randomly branched) polymers, or trees38. Let us explain this point in more detail.
According to accepted terminology, quenched trees are the ones in which the topology of branches, or simply the value of L, is fixed during synthesis and does not change afterwards. In contrast, the topology of annealed trees, or their L parameter, is not fixed by synthesis, but instead varies in response to external conditions and fluctuates due to thermal motion. Note that linear chains in this context can be thought of as a trivial limit of quenched tree with L ∼ N. As one example, chemically synthesized branched polymers have almost always quenched connectivity. RNA can rearrange its secondary structure, therefore, it should be viewed as annealed branching polymer (Fig. 1a). Also ring polymer placed in a lattice of immobile uncrossable obstacles (Fig. 1c) behaves like an annealed branching polymer21,22.
Considering sufficiently large polymers (N ≫ 1), we will be interested in this article only in scaling relations. We first define the usual scaling exponent ν, which characterizes the dependence of polymer size, R, on the degree of polymerization N:
| (1) |
1/ν = df is the corresponding fractal dimension. Next we define the index ρ, which characterizes the branching topology and relates the parameter L to the degree of polymerization N:
| (2) |
Finally, we define the scaling exponent νpath relating chain size R and characteristic chemical length L:
| (3) |
this index tells us how a typical linear chemical path in the tree, viewed as a linear polymer, is embedded in space; is the fractal dimension of a typical single chemical path of the tree in space.
It is immediately clear from the definitions that in general,
| (4) |
Furthermore, since chemical paths on a tree cannot include more steps than monomers present, we have ρ < 1. Similarly, the spatial extension of trees and path cannot exceed their total contour length, so that ν < 1 and νpath < 1.
There are not very many cases where critical exponents ν and ρ are known exactly. For isolated, non-interacting trees ν = 1/4 (compared to ν = 1/2 for linear chains) while ρ = 1/2, and this is true for both quenched and annealed cases4. For isolated, self-avoiding lattice trees with annealed connectivity in d = 3, the analogy to lattice animals14 allows to obtain the exact result ν = 1/2 but it gives no prediction for ρ.
3 Flory theory
Flory theories 37,64 are formulated in terms of a balance between elastic and interaction contributions to the free energy
| (5) |
Although physically appealing, this representation of the free energy is itself an approximation; in reality, these terms in the free energy are not independent from one another. As a result, although minimization of Flory free energy (5) yields very good approximations for the gyration radius for linear polymers, and, as we will see also for branched ones, the value of the free energy corresponding to this minimum itself is severely in error. Therefore, we can not overemphasize the fact that one must exercise great caution to use Flory theory for the right purpose. Elucidating corresponding applicability limits for various randomly branched systems is one of the goals of this article. Although not explicitly discussed here, it is worth mentioning that Flory theories have been equally formulated for regularly (opposed to randomly) branched polymers such as: star polymers65,66, dendrimers67,68 and dendronized polymers and forests68.
Returning to Eq. (5), the interaction free energy, ℱinter, is assumed to be independent of the connectivity and depends only on the overall density of the monomer cloud, i.e., on R. In contrast, the elastic energy of trees, ℱel, is very sensitive to the monomeric connectivity. It depends not only on the spatial distance between nodes, R, but also on their typical contour distance, L. We, therefore, begin with the discussion of this elastic free energy.
3.1 Entropic elasticity of trees
3.1.1 Quenched trees
For quenched branched polymers the parameter L is controlled by the synthesis condition and does not change in reaction to external forces or intermolecular interactions. For a given connectivity, to increase the spatial distance between any two nodes, the linear paths connecting them need to elongate/straighten in space, as sketched in Fig. 2. Qualitatively, as a consequence, the smaller L, the more energy is required to reach a given average spatial distance, R. Quantitatively, the corresponding elastic free energy is69:
Fig. 2.
Schematic representation of the two independent swelling mechanisms for interacting trees (a). (b) With quenched connectivity, branched polymers can swell only by stretching its linear sections. (c) With annealed connectivity, in addition to stretching linear sections, branching polymers can also simplify the connectivity which can become somewhat “less branched” as, for instance, in the combo-like conformation shown in the picture. Then, to achieve the same overall swelling, an annealed tree has to stretch its linear sections by a lesser amount than the quenched counterpart.
| (6) |
This expression is highly non-trivial, as it looks like stretching free energy of a single linear chain of L/lK segments, each segment corresponding to a Kuhn statistical unit70 of linear size = lK; in other words, it looks like it accounts for the deformation of only one chemical backbone out of many branches present in the polymer, while in reality all branches swell in fractal manner. A rigorous proof of Eq. (6) is given in71, where it is shown that, up to logarithmic corrections, with μ ∼ L/lK being the largest eigenvalue of the Kramers matrix† associated to the quenched branched polymer.
3.1.2 Annealed trees
In contrast to quenched polymers, annealed branching polymers swell or respond to stretching in two different ways, sketched in Fig. 2 (right): they extend their linear sections and reconfigure their branching topology, described by two terms for the elastic free energy:
| (7) |
The first term is the same as in the quenched polymer case, and it describes the same mode of swelling, while the major novelty is the second term, which describes entropy of reconfiguring the tree topology.
This term can be derived formally from the partition function of all trees of N bonds and with the L bonds between two arbitrary fixed ends. The derivation employs the diagrammatic recursive method presented in Refs. 32,33 with the simplifying assumption38 that only ends and branchings are allowed (no bifunctional units or linear parts). Suggestively, an intuitive way to understand the second term in Eq. (7) is to imagine tree-like graphs as drawn on an abstract Cayley tree. Then L/lK is just a “gyration radius” in that space, and (L/lK)2/N is just the usual elastic free energy of a Gaussian polymer.
Since L for annealed polymer is a fluctuating quantity, free energy Eq. (7) reduces after optimization of L at fixed R to obtain
| (8) |
and
| (9) |
This result is consistent with the fact that R ∼ lKN1/4 (see4,32,33) for ideal, non-interacting trees‡.
3.2 Relation between exponents
The fact that the interaction free energy in Flory approximation is independent of branching, i.e. it does not depend on L, yields an interesting testable prediction. To understand it, let us imagine for a moment, say, three annealed trees with the same N and lK, but placed in different environments: for instance, one tree may be placed alone in a solvent of a certain quality, another tree is surrounded by other trees in a melt or in a concentrated solution, and the third tree is subjected to some external forcing – such that all three happen to have the same overall size R. Then we expect all of them to have also the same value of L. To make this quantitative, let us return to the minimization of free energy (7) with respect to L, Eq. (8). If we write R ∼ Nν and L ∼ Nρ, then we arrive at the following general relation between indices ν and ρ:
| (10) |
in the light of Eq. (4), this is also equivalent to
| (11) |
Eqs. (10) and (11) are plotted in Fig. 4 as the red and green line, respectively. It is worth repeating that these relations follow from the assumed independence of interaction energy from the branching parameter L. To illustrate these relations, let us see how they work in various simple cases. If a system is fully extended, which means ν = 1, then it is predicted not to branch, ρ = 1, and to have a fully stretched stem, νpath = 1. For the radius of ideal randomly branched polymers, νideal = 1/4, one recovers the Zimm-Stockmayer result ρideal = 1/24 and Gaussian path statistics, .
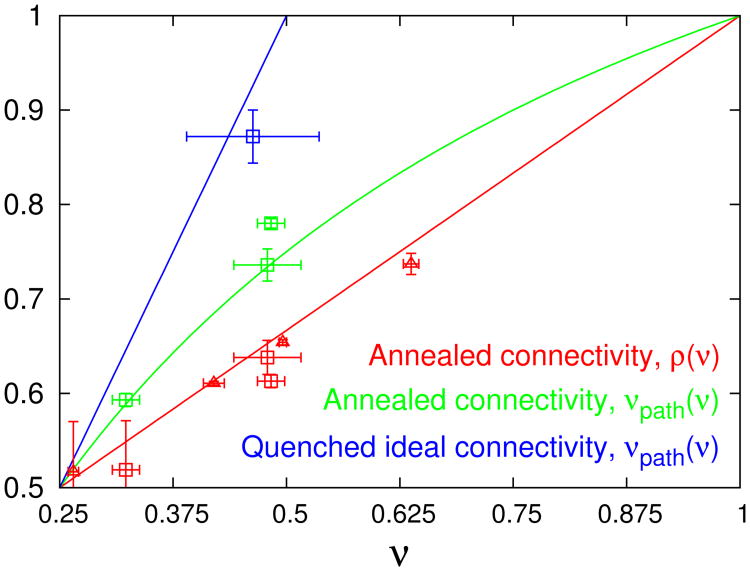
Fig. 4.
Exponents ρ and νpath are plotted as a function of ν following the expressions Eqs. (10), (11) for annealed trees (red and green lines) and with ρ = 1/2 (blue line) for trees with quenched ideal connectivity. Symbols correspond to numerical results for: (triangles) annealed dilute trees in good solvent in d = 2,3,4,855; (squares) annealed and quenched dilute trees in good solvent in d = 362 and annealed tree melts in d = 2,363.
Relations (10)-(11) suggest a peculiar way to view the problem, by considering index ν as an independent variable. This way, we look in parallel to physically different systems and even having different space dimensions, but as long as they have the same ν – they should have ρ and νpath given by equations (10)-(11) – as long as Flory theory assumption of ℱinter being independent of branching is correct. From that point of view, it is easy to establish that at any ν < 1, where and ρideal = 1/2; we can interpret this saying that path stretching contributes more to the overall swelling than rearrangement of branches, as long as the trees are not fully stretched, i.e., as long as ν < 1 (note that at ν = 1 automatically also ρ = νpath = 1). Similarly, we can consider the case when ν is close to νideal = 1/4, which corresponds to weakly swollen trees; in that case, Eqs. (10) and (11) imply that .
3.3 Flory theory for trees with volume interactions
In his original formulation for linear chains in good solvent37, Flory considered the two-body repulsion between segments, described by the second virial approximation. To cover also higher order collisions, θ-conditions, and melts, we use the more general form
| (12) |
for the pth moment of the virial expansion. Screening in a melt is accounted for by setting x ≡ 111, while for isolated chains in dilute solution x ≡ 0. Eq. (12) reduces to the standard form, , for p = 2 and x = 0. As repeatedly stated above, interaction free energy in Flory approximation does not depend on L.
Next we minimize the total Flory free energy with respect to R.
3.3.1 Quenched branched polymer
For branched polymers with quenched connectivity, the variational free energy per chain includes the elastic contribution, Eq. (6), and the interaction term, Eq. (12). Substituting L ∼ Nρ, and minimizing the sum with respect to R we find
| (13a) |
| (13b) |
where Eq. (13b) follows directly via Eq. (4). Note that ρ here is controlled by how the macromolecule was synthesized.
Every chemical path in the tree cannot be stretched more than its contour length, which implies νpath ≤ 1, but it cannot also be more compact than Gaussian, meaning νpath ≥ 1/2. These two conditions determine lower and upper critical dimensions, respectively:
| (13c) |
Above upper critical dimension excluded volume interactions become unimportant, meaning νpath = 1/2 and ν = ρ/2. On the other hand, below lower critical dimension, chemical paths are completely stretched, νpath = 1, while overall molecule size is such that ν = ρ. An additional peculiarity of quenched branched systems is that they cannot exist at all in space dimensions such that ν = ρ < 1/d: their linear portions are already completely stretched, and they lack any means to resolve frustrations arising from the interplay of excluded volume and chain connectivity.
3.3.2 Annealed branching polymer
For branching polymers with annealed connectivity, the free energy per chain includes elastic contribution, Eq. (9), and interaction term, Eq. (12). Minimizing the sum with respect to R and using also Eqs. (10) and (11) we find
| (14a) |
| (14b) |
| (14c) |
Implementing again the conditions νpath ≤ 1 and νpath ≥ 1/2, we can determine upper and lower critical dimensions:
| (14d) |
As in the quenched case, if d is above upper critical dimension, the role of excluded volume is marginal and the system connectivity is completely random, with ν = 1/4, ρ = 1/2, and νpath = 1/2. The situation at the lower critical dimension for the annealed branching polymer is dramatically different from the quenched case. Annealed tree at low dimension d not only stretches its linear sections, but also rearranges its connectivity, increasing L, or increasing ρ. As a result, lower critical dimension corresponds to the situation when not only νpath = 1 (stretched linear sections), but also ρ = 1 (the tree is effectively simplified to become a linear trunk) and ν = 1 (the whole molecule is stretched).
Below, we will explicitly consider various specific cases. All results are summarized in Fig. 3.
Fig. 3.
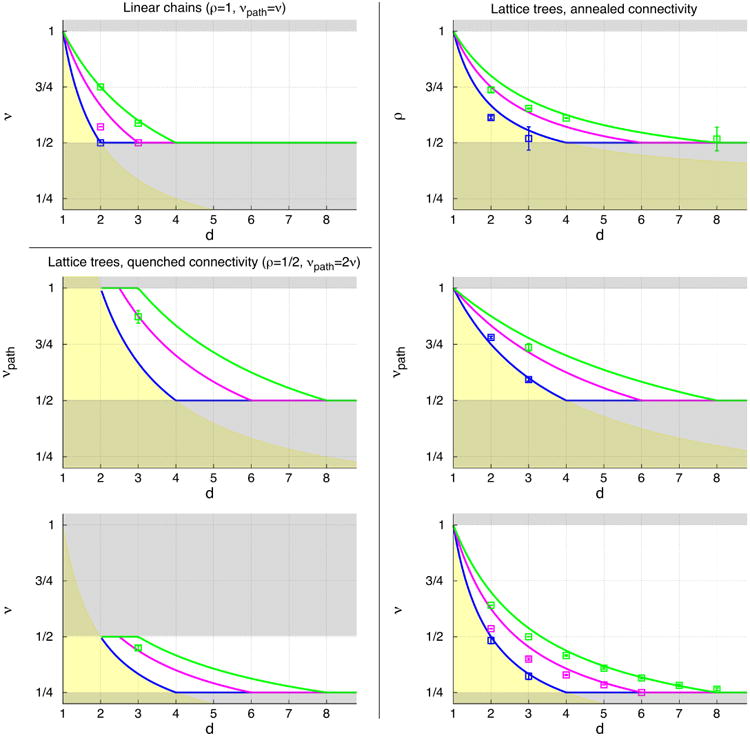
Exponents ρ, νpath and ν for: linear chains (upper panel on the left, ρ = 1 and νpath = ν), trees with quenched ideal connectivity (middle and bottom panels on the left, ρ = 1/2), trees with annealed connectivity (panels on the right). Solid lines correspond to predictions of Flory theory: green is for single chains in good solvent (Eq. (16) for linear chains, Eqs. (17a)-(17b) for quenched trees and Eqs. (18a)-(18c) for annealed trees); magenta is for single chains in θ-solvent (Eq. (20) for linear chains, Eqs. (21a)-(21b) for quenched trees and Eqs. (22a)-(22c) for annealed trees); blue is for chains in melt (Eqs. (23a)-(23b) for, respectively, linear chains and quenched trees with ideal connectivity and Eqs. (24a)-(24c) for annealed trees). Grey- and yellow-shading regions indicate violations of the following physical constraints on the values of the exponents: (grey) 1/2 ≤ ρ ≤ 1, 1/2 ≤ νpath ≤ 1 and 1/4 ≤ ν ≤ 1 for lattice trees and 1/2 ≤ ν ≤ 1 for linear chains; (yellow) the fractal dimension df = 1/ν of any object placed in space must be ≤d. For annealed trees, given Eqs. (4), (10) and (11), constraints for one exponent map to the corresponding constraints for the others. This is not the case for quenched trees, where constraints for νpath restrict corresponding values of ν to a narrower region. Symbols are for computer simulations and analytical results boldfaced in Tables 1–4.
3.4 Isolated trees in a good solvent
3.4.1 Quenched case
A single macromolecule in a dilute solution in a good solvent corresponds to p = 2 (two-body repulsion) and x = 0 (no screening). In this case
| (15a) |
| (15b) |
with critical dimensions
| (15c) |
Importantly, ρ here is controlled by how the molecule was prepared.
For instance, ρ = 1 corresponds to linear chains, and indeed Eqs. (15a)-(15c) reduce in this case to the classical Flory result (solid green line in Fig. 3, top left panel):
| (16) |
in 1 ≤ d ≤ 4 dimensions.
For random trees with quenched ideal connectivity, ρ = 1/2, one recovers the Isaacson and Lubensky11 prediction
| (17a) |
| (17b) |
| (17c) |
In d > 8, excluded volume becomes insignificant, with νpath = 1/2, leading to ν = 1/4. Conversely, in d ≤ 3 linear paths are completely stretched, with νpath = 1, and molecule size is entirely controlled by its connectivity, with ν = ρ = 1/2, as shown by the solid green line in Fig. 3 (middle and bottom left panels). Note that this line ends at d = 2 and does not continue to lower d. In fact, a quenched branched polymer with ρ = 1/2 faces and unresolvable frustration between excluded volume and chain connectivity requirements and can not exist in spaces with dimension lower than d = 2.
3.4.2 Annealed case
For a single (x = 0, no screening) swollen randomly branching polymers with annealed connectivity in a good solvent (p = 2), Eqs. (14a)-(14d) reduce to the prediction of Gutin et al. 38:
| (18a) |
| (18b) |
| (18c) |
| (18d) |
For annealed trees, the limit of full path stretching is only reached in d = 1 dimensions, where ν = ρ = νpath = 1. The results for the isolated annealed branching polymer in a good solvent are depicted by the green solid lines in Fig. 3 (right panels).
3.5 Isolated trees in a θ-solvent
3.5.1 Quenched case
For the case of dilute solutions (x = 0, no screening) in a θ-solvent (p = 3, three-body repulsion, because ν2 = 0) we have:
| (19a) |
| (19b) |
| (19c) |
For linear chains with ρ = 1 (solid magenta line in Fig. 3, top left panel):
| (20) |
and the three-body repulsion is only relevant for d < 3 dimensions, while chains become fully stretched in d = 1 and cannot exist in d < 1 because of the frustration between excluded volume and chain connectivity.
For trees with ideal connectivity, ρ = 1/2, one recovers:
| (21a) |
| (21b) |
| (21c) |
corresponding to the result by Daoud and Joanny33. The statistics of linear paths suggests that linear sections of the polymer become fully stretched for d ≤ 5/2 and ν = ρ = 1/2, as shown in the middle and bottom left panels of Fig. 3 in solid magenta lines. As in good solvent solutions, randomly branched polymers with ρ = 1/2 in θ-solutions do not fit in spaces with dimensionality below d = 2.
3.5.2 Annealed case
For trees with annealed connectivity, Eqs. (14a) to (14b) reduce to
| (22a) |
| (22b) |
| (22c) |
| (22d) |
To the best of our knowledge these relations have not been reported in the literature before and are plotted as magenta lines in Fig. 3 (right panels).
3.6 Melts of branched or branching polymers
3.6.1 Quenched case
Eqs. (13a)-(13b) can also be applied to melts of branched polymers. In melts, volume interactions are screened implying that x = 1 in the virial-type expansion of the interaction energy term, Eq. (12) 11,18, which becomes . Close inspection to these terms shows that interactions are estimated to be irrelevant, if νd > 1. Even without swelling, this is the case in d > 4 dimensions, where νideald = d/4 > 1 suggests ideal tree behavior. Conversely, in d ≤ 4 dimensions, for 1/4 < ν ≤ 1/d all terms of the series need to be taken into account, implying that the series is dominated by high-order interactions with p → ∞33. In particular, the p → ∞ limit of Eqs. (13a)-(13b) gives:
| (23a) |
| (23b) |
| (23c) |
The ν = 1/d result means that trees in the melt are “territorial”30,73, and each of them behaves as a compact object. As before, ρ is the property of the system in question. For instance, for the melt of linear chains, ρ = 1, the interval between lower and upper critical dimension, 1 ≤ d ≤ 2, does not include 3 (solid blue line in the top left panel of Fig. 3); that means the well known textbook fact that linear chains in a regular 3d melt are approximately Gaussian (Flory theorem). At dimensions below 2 they swell, at d = 1 they are completely stretched, and cannot be placed in d < 1.
In contrast to linear chains, randomly branched polymers with ideal connectivity ρ = 1/2 in the regular 3d melt are “territorial”73, they do not obey Flory theorem and their linear sub-chains are predicted to exhibit a non-trivial statistics. The results for quenched tree melts are shown as solid blue lines in the middle and bottom left panels of Fig. 3. As before, the lines stop at d = 2, because quenched polymer cannot be placed in space of lower dimension.
3.6.2 Annealed case
For trees with annealed connectivity, screening is still important, meaning x = 1, as well as many-body interactions, suggesting again the limit p → ∞. The results read:
| (24a) |
| (24b) |
| (24c) |
| (24d) |
Interestingly, territorial behavior with ν = 1/3 is expected for both, randomly branched and randomly branching, polymers in d = 3. However, the annealed trees are expected to be less strongly branched, ρ = 5/9 > 1/2, with less strongly stretched linear paths, νpath = 3/5 < 2/318. The results for annealed tree melt are given as solid blue lines in Fig. 3 (right panels).
3.7 Examples of other preparation protocols
We emphasized repeatedly that connectivity of a quenched polymer, described by L or ρ, is controlled by the preparation conditions, but we explicitly considered only two examples: ρ = 1 (linear polymer) and ρ = 1/2 (ideally branched polymer). Let us give a couple more examples and illustrate the application of our results.
Suppose we prepare (synthesize) branched polymer in a θ-solvent, then quench its connectivity, and then change solvent quality to good while keeping the solution very dilute. We have everything to describe this situation. Since the molecule is prepared in a θ-solvent, its connectivity is annealed under θ-conditions and, therefore, it is characterized by index ρ given in Eq. (22b) at d = 3, namely ρ = 7/11. Now, with this value of ρ fixed, the molecule is placed in good solvent conditions. We thus have to insert ρ = 7/11 into Eqs. (15a) and (15b) to obtain ν = 29/55 ≈ 0.53 and νpath = 29/35 ≈ 0.83. We see that linear sections of the tree are significantly stretched, which is natural given how this tree was prepared.
As a second example, suppose we prepare branched polymers in a good solvent, quench their connectivity, and then concentrate the resulting macromolecules to form a melt. To describe this situation, we first look at Eq. (18b) at d = 3, and find that the molecule in a good solvent will have ρ = 9/13. In this case, the space dimension d = 3 is above upper critical for melts, which is (see Eq. (23c)) 2/ρ = 26/9 ≈ 2.89. As a consequence, such melts are expected to be ideal with νpath = 1/2 and ν = ρ/2.
In a similar way we can consider also many other preparation protocols. Curiously, it should not be possible to generate randomly branched polymers with quenched ideal statistics along these lines: in d ≤ 3 all annealed branching systems exhibit swelling with ρ > 1/2.
4 Comparison of Flory Theory predictions to theoretical and simulation results
Flory theory37 owes its simplicity to uncontrolled approximations, the neglect of spatial correlations arising from the connectivity of the chains and to Gaussian estimate of polymer elasticity. To gauge the utility of the approach, its predictions need to be compared to exact solutions 14,44,46,47, ε-expansions 39 renormalisation group calculations 14,40,41,43,49, dimensional reduction45, series expansions16,48 exact enumerations42,50–52,54, Monte Carlo 53,55–63 and Molecular Dynamics 62 simulations. Tables 1 to 4 list available benchmark results for linear chains and for trees with annealed and with quenched ideal connectivity. Typically, analytical approaches only provide access to the overall asymptotic behaviour as characterised by the exponent ν. In contrast, numerical investigations extract estimates for ν, ρ, and νpath from data for polymers of finite size.
Table 1.
Analytical and simulation results for critical exponent ν of linear chains (ρ = 1, νpath = ν) for different solvent conditions and spatial dimensionality d. “ is the relative discrepancy between the actual and the true values (in boldface) of ν over the difference between the latter and the ideal value. Currently available exact values or best estimates (in boldface) are reported as symbols in Fig. 3, where predictions of Flory theory are shown as lines.
| Linear chains | ||||||
|---|---|---|---|---|---|---|
|
| ||||||
| d | ν | δν |
|
Technique | Reference | |
| Dilute solution in a good solvent | ||||||
|
| ||||||
| 2 | 3/4 = 0.75 | 0 | 0% | Flory theory | Flory (1969)74 | |
| 2 | 3/4 = 0.75 | – | – | Exact calculation | Nienhuis (1982)44 | |
| 2 | 0.74963±0.00008 | −0.00037 | −0.2% | Monte Carlo | Li, Madras & Sokal (1995)56 | |
| 3 | 3/5 = 0.6 | 0.0123 | 14% | Flory theory | Flory (1969)74 | |
| 3 | 0.588±0.001 | 0.0003 | 0.3% | Renormalization group | Le Guillou & Zinn-Justin (1977)40 | |
| 3 | 0.5877±0.0006 | – | – | Monte Carlo | Li, Madras & Sokal (1995)56 | |
|
| ||||||
| Dilute solution in a θ-solvent | ||||||
|
| ||||||
| 2 | 2/3 = 0.667 | 0.0952 | 133% | Flory theory | Flory (1969)74 | |
| 2 | 367/726 ≈ 0.5055 | −0.0659 | -92% | ε-expansion | De Gennes (1975)39 | |
| 2 | 4/7 ≈ 0.5714 | – | – | Exact calculation | Duplantier & Saleur (1987)47 | |
| 2 | 0.57±0.02 | −0.0014 | -2% | Monte Carlo | Wittkop, Kreitmeier & Göritz (1996)57 | |
| 3 | 1/2 = 0.5 | 0 | 0% | Flory theory | Flory (1969)74 | |
| 3 | 1/2 = 0.5 | – | – | ε-expansion | De Gennes (1975)39 | |
| 3 | 0.50±0.02 | 0.00 | 0% | Monte Carlo | Wittkop, Kreitmeier & Göritz (1996)57 | |
|
| ||||||
| Melt | ||||||
|
| ||||||
| 2 | 1/2 = 0.5 | 0 | 0% | Flory theory | Isaacson & Lubensky (1980)11 | |
| 2 | 1/2 = 0.5 | – | – | Conformal theory | Duplantier (1986)46 | |
| 3 | 1/2 = 0.5 | – | – | Flory theory | Isaacson & Lubensky (1980)11 | |
Table 4.
Analytical and simulation results for critical exponents ρ, νpath and ν of annealed lattice trees in melts for different spatial dimensionalities d. is defined as in Table 1. Currently available exact values or best estimates (in boldface) are reported as symbols in Fig. 3, where predictions of Flory theory are shown as lines. To our knowledge, analytical or simulation data for quenched branched polymers in melts are currently missing.
| Annealed branching polymers in melts | ||||||||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| d | ρ | νpath | ν | δν |
|
Technique | Reference | |
| 2 | 2/3=0.667 | 3/4=0.75 | 1/2 = 0.5 | 0.02 | 9% | Flory theory | Grosberg (2014)18 | |
| 2 | 0.613 ±0.007 | 0.780 ±0.005 | 0.48 ±0.02 | – | – | Monte Carlo | Rosa & Everaers (2016)63 | |
| 3 | 5/9=0.556 | 3/5=0.6 | 1/3 = 0.333 | 0.013 | 19% | Flory theory | Grosberg (2014)18 | |
| 3 | 0.52 ±0.05 | 0.593 ±0.007 | 0.32 ±0.02 | – | – | Monte Carlo | Rosa & Everaers (2016)63 | |
To set the stage, let us briefly review the situation for linear chains. The results presented in Table 1 show that Flory theory works remarkably well, with the only exception of 2d chains in θ-solvent. The theory correctly predicts (i) ν = 1 for all interacting systems in d = 1, (ii) the hierarchy νSAW ≥ νθ ≥ νmelt for all d, and (iii) the upper critical dimensions dSAW = 4, dθ = 3, and dmelt = 2 for the three media types. The values of the predicted exponents are mostly exact. Exceptions are self-avoiding walks in d = 3 dimensions, where the Flory estimate of νF = 3/5 slightly exceeds the best estimates40 of ν ≈ 0.588, and linear chains in θ-solvents in d = 2, where the deviation between the Flory estimate, νF = 2/3, and the exact value of ν = 4/747 is larger.
A first, visual inspection of the values listed in Tables 2 to 4 suggests that Flory theory works almost as well for trees as for linear chains. This is confirmed by Figure 3, where we compare the results (symbols) to the predictions of Flory theory (lines) for the relevant exponents ν, ρ, and νpath as a function of dimension, d. Different sets of panels are devoted to linear chains, trees with quenched ideal connectivity and trees with annealed connectivity. The theory correctly predicts (i) ν = 1 for all types of annealed trees in d = 1, (ii) the hierarchy νSAW ≥ νθ ≥ νmelt for all d, and (iii) the upper critical dimensions dSAW = 8, dθ = 6, and dmelt = 4 for the three solution types. Moreover, all known values for the exponents fall in between these bounds, see Tables 1–4. In spite of its simplicity, it is indeed quite remarkable that Flory theory correctly anticipates all observed trends.
Table 2.
Analytical and simulation results for critical exponents ρ, νpath and ν of isolated self-avoiding lattice trees in a good solvent for different spatial dimensionalities d. is defined as in Table 1. Currently available exact values or best estimates (in boldface) are reported as symbols in Fig. 3, where predictions of Flory theory are shown as lines.
| Annealed branching polymers in dilute solutions in a good solvent | ||||||||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| d | ρ | νpath | ν | δν |
|
Technique | Reference | |
| 2 | 4/5=0.8 | 7/8=0.875 | 7/10 = 0.7 | 0.0592 | 15% | Flory theory | Gutin et al. (1993)38 | |
| 2 | – | – | 0.637 | −0.0038 | -1% | Renormalization group | Family (1980)41 | |
| 2 | – | – | 0.6408 ±0.0003 | – | – | Renormalization group | Derrida & de Seze (1982)43 | |
| 2 | – | – | 0.640 ±0.004 | −0.0008 | -0.2% | Exact enumeration | Margolina et al. (1984)52 | |
| 2 | – | – | 0.6394 ±0.0067 | −0.0014 | -0.4% | Exact enumeration | Privman (1984)51 | |
| 2 | – | – | 0.640 ±0.004 | −0.0008 | -0.2% | Scanning method | Meirovitch (1987)53 | |
| 2 | – | – | 0.644 ±0.004 | 0.0032 | 0.8% | Exact enumeration | Ishinabe (1989)54 | |
| 2 | 0.74 ±0.01 | – | 0.637 ±0.009 | −0.0038 | -1% | Monte Carlo | J. van Rensburg & Madras (1992)55 | |
| 2 | – | – | 0.6412±0.0005 | 0.0004 | 0.1% | Monte Carlo | Hsu et al. (2005)60 | |
| 3 | 9/13=0.692 | 7/9=0.778 | 7/13 = 0.538 | 0.0385 | 15% | Flory theory | Gutin et al. (1993)38 | |
| 3 | – | – | 1/2 | – | – | Exact calculation | Parisi & Sourlas (1981)14 | |
| 3 | 0.654 ±0.003 | – | 0.496 ±0.004 | −0.004 | -2% | Monte Carlo | J. van Rensburg & Madras (1992)55 | |
| 3 | – | – | 0.49 ± 0.01 | −0.01 | -4% | Monte Carlo | Cui & Chen (1996)58 | |
| 3 | – | – | 0.500 ±0.002 | 0.000 | 0% | Monte Carlo | Hsu et al. (2005)60 | |
| 3 | 0.64±0.02 | 0.74 ±0.02 | 0.48 ±0.04 | 0.02 | -8% | Monte Carlo | Rosa & Everaers (2016)62 | |
| 4 | 5/8=0.625 | 7/10=0.7 | 7/16 = 0.438 | 0.022 | 13% | Flory theory | Gutin et al. (1993)38 | |
| 4 | – | – | 0.425 | 0.009 | 5% | Series expansion | Kurtze & Fisher (1979)16 | |
| 4 | – | – | 0.450 ±0.035 | 0.034 | 21% | Exact enumeration | de Alcantara et al. (1980)42 | |
| 4 | – | – | 0.42 | 0.04 | 2% | Renormalization group | Parisi & Sourlas (1981)14 | |
| 4 | – | – | 0.45 ±0.05 | 0.034 | 21% | Exact enumeration | Gaunt et al. (1982)50 | |
| 4 | – | – | 0.417 | 0.001 | 0.6% | Dimensional reduction | Dhar (1983)45 | |
| 4 | – | – | 0.425 ±0.015 | 0.009 | 5% | Series expansion | Adler et al. (1988)48 | |
| 4 | 0.611 ±0.002 | – | 0.42±0.01 | 0.004 | 2% | Monte Carlo | J. van Rensburg & Madras (1992)55 | |
| 4 | – | – | 0.416 ±0.003 | – | – | Monte Carlo | Hsu et al. (2005)60 | |
| 5 | 11/19=0.579 | 7/11=0.636 | 7/19 = 0.368 | 0.009 | 8% | Flory theory | Gutin et al. (1993)38 | |
| 5 | – | – | 0.359 ±0.004 | – | – | Monte Carlo | Hsu et al. (2005)60 | |
| 6 | 6/11=0.545 | 7/12=0.583 | 7/22 = 0.318 | 0.003 | 5% | Flory theory | Gutin et al. (1993)38 | |
| 6 | – | – | 0.315 ±0.004 | – | – | Monte Carlo | Hsu et al. (2005)60 | |
| 7 | 13/25=0.52 | 7/13=0.538 | 7/25 = 0.28 | −0.002 | -6% | Flory theory | Gutin et al. (1993)38 | |
| 7 | – | – | 0.282 ± 0.005 | – | – | Monte Carlo | Hsu et al. (2005)60 | |
| 8 | 1/2=0.5 | 1/2=0.5 | 1/4 = 0.25 | −0.015 | −100% | Flory theory | Gutin et al. (1993)38 | |
| 8 | 0.52 ±0.05 | – | 0.265 ±0.006 | – | – | Monte Carlo | J. van Rensburg & Madras (1992)55 | |
|
| ||||||||
| Quenched branched polymers in dilute solutions in a good solvent | ||||||||
|
| ||||||||
| d | ρ | νpath | ν | δν |
|
Technique | Reference | |
|
| ||||||||
| 3 | 1/2 | 1 | 1/2 = 0.5 | 0.05 | 25% | Flory theory | Isaacson & Lubensky (1980)11 | |
| 3 | 1/2 | – | 0.45 ±0.01 | – | – | Monte Carlo | Cui & Chen (1996)58 | |
| 3 | 1/2 | 0.87 ±0.03 | 0.46 ±0.07 | 0.01 | 5% | Molecular Dynamics | Rosa & Everaers (2016)62 | |
The key element of the Flory theory for annealed trees is the description of the tree elasticity summarised in Sec. 3.1.2, which implies that the swelling of annealed trees results from a combination of modified branching and path stretching. This and the dominance of the path stretching mode (Sec. 3.2) are qualitatively confirmed by the benchmark results wherever independent information is available for the exponents ρ or νpath. Interestingly, the benchmark results are in good agreement with the predicted relations, Eqs. (10) and (11), between the exponents for annealed trees (Fig. 4). The same holds for the comparison of annealed trees and trees with quenched ideal connectivity, ρ = 1/2. The latter are predicted to exhibit less overall swelling than trees with annealed connectivity, even though they are expected to be stretched more strongly on the path level (Eqs. (17a) and (17b) vs. Eqs. (18a) and (18c)). These features are directly observed in numerical simulations58,62 and confirm that trees with annealed and quenched ideal connectivity fall into different universality classes38.
Nevertheless, Flory theory is no more exact for trees than for linear chains. For instance, there is a tendency to overestimate the exponent ν in good and θ-solvents. For example, Flory theory predicts ν = 7/13 instead of the exact result14 ν = 1/2 for self-avoiding trees with annealed connectivity in d = 3 dimensions. The absolute deviations is much larger for trees (0.038) than for linear chains (0.012), but the relative errors of the predicted effects, (7/13 – 1/2)/(1/2 – 1/4) = 15% and (3/5 – 0.588)/(0.588 – 1/2) ≈ 14%, are of comparable magnitude. Another example are annealed branching polymers in dilute θ-solutions in d = 2 dimensions. Flory theory predicts ν = 5/8 instead of the best numerical result61 0.5359±0.0003 for trees with annealed connectivity. In this case, the absolute errors are comparable for annealed trees (0.089) and linear chains (0.095), but the relative error for annealed trees, (5/8 – 0.5359)/(0.5359 – 1/4) = 31%, is much smaller than for linear chains, where Flory theory is off by (2/3 – 4/7)/(4/7 – 1/2) ≈ 133%.
5 Summary and conclusion
In the present article, we have reviewed the Flory theory of branched polymers with volume interactions as pioneered in Refs.11,18,33,38 and completed the theory for the case of annealed branching polymers in dilute θ-solvent solutions. An important point is the distinction38 between annealed and quenched trees. To reduce the number of unfavorable contacts, the latter can only swell by modifying the conformational statistics of linear paths to values νpath > 1/2 (Fig. 3, middle panels). The former have the additional option to increase their overall size by adjusting the branching statistics, ρ > 1/2 (Fig. 3, right panels). The predicted behaviour for trees is considerably richer than for linear chains 75, which represent the limiting case of trees with quenched connectivity characterised by ρ = 1 (Fig. 3, left panel).
The predictions of Flory theory are shown to be in excellent qualitative agreement with available theoretical and numerical results (compare symbols to solid lines in Figs. 3 and 4). While quantitative predictions from Flory theory need to be taken with a grain of salt, the approach thus provides a simple and unifying description of the average swelling behaviour of a wide range interacting tree systems.
However, there are other quantities such as entropies60 and internodal contact probabilities62,63, which Flory theory fails to describe even for linear chains75. A forthcoming article76 discusses how to go beyond Flory theory and the Gaussian approximation by analyzing the distribution functions characterising the tree conformations and connectivity.
Table 3.
Analytical and simulation results for critical exponents ρ, νpath and ν of annealed isolated self-avoiding lattice trees in a θ-solvent for different spatial dimensionalities d. is defined as in Table 1. Currently available exact values or best estimates (in boldface) are reported as symbols in Fig. 3, where predictions of Flory theory are shown as lines. To our knowledge, analytical or simulation data for quenched isolated branched polymers in θ-solutions are currently missing.
| Annealed branching polymers in dilute solutions in a θ-solvent | ||||||||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| d | ρ | νpath | ν | δν |
|
Technique | Reference | |
| 2 | 3/4=0.75 | 5/6=0.833 | 5/8 = 0.625 | 0.0891 | 31% | Flory theory | This work | |
| 2 | – | – | 0.54±0.03 | 0.0041 | 1% | Monte Carlo | Madras & J. van Rensburg (1997)59 | |
| 2 | – | – | 0.5359±0.0003 | – | – | Monte Carlo | Hsu & Grassberger (2005)61 | |
| 2 | – | – | 0.52±0.03 | −0.0159 | -6% | Renormalization group | Janssen & Stenull (2011)49 | |
| 3 | 7/11=0.636 | 5/7=0.714 | 5/11 = 0.455 | 0.055 | 36% | Flory theory | This work | |
| 3 | – | – | 0.400 ±0.005 | – | – | Monte Carlo | Madras & J. van Rensburg (1997)59 | |
| 3 | – | – | 0.396 ±0.007 | −0.004 | -3% | Renormalization group | Janssen & Stenull (2011)49 | |
| 4 | 4/7=0.571 | 5/8=0.625 | 5/14 = 0.357 | 0.028 | 35% | Flory theory | This work | |
| 4 | – | – | 0.329 ± 0.002 | – | – | Renormalization group | Janssen & Stenull (2011)49 | |
| 5 | 9/17=0.529 | 5/9=0.556 | 5/17 = 0.294 | 0.0091 | 26% | Flory theory | This work | |
| 5 | – | – | 0.2849 ± 0.0002 | – | – | Renormalization group | Janssen & Stenull (2011)49 | |
| 6 | 1/2=0.5 | 1/2=0.5 | 1/4 = 0.25 | 0 | 0% | Flory theory | This work | |
| 6 | – | – | 0.25 | – | – | Renormalization group | Janssen & Stenull (2011)49 | |
Acknowledgments
RE, MR, and AYG are grateful for the hospitality of the Kavli Institute for Theoretical Physics (Santa Barbara, USA) and support through the National Science Foundation under Grant No. NSF PHY11-25915 during their visit in 2011. AR acknowledges grant PRIN 2010HXAW77 (Ministry of Education, Italy). MR acknowledges financial support from the National Science Foundation under grants DMR-1309892, DMR-1436201, and DMR-1121107, the National Institute of Health under grants P01-HL108808 and 1UH2HL123645, and the Cystic Fibrosis Foundation.
Footnotes
The method of the Kramers matrix1,7,71,72 allows for a systematic treatment of the elasticity of a quenched branched polymer. The Kramers matrix G is an N × N matrix, every element of it Gkm corresponds to two bonds in the graph, k and m. These two bonds delineate one portion of the tree with K(k) monomers on one side of bond k, another portion with M(m) monomers on the other side of bond m, with the rest of the monomers between two bonds, and then Gkm = ±K(k)M(m)/N2, where the sign+ or − is chosen according to a simple rule. The trace of the Kramers matrix gives the mean square gyration radius of the tree without volume interactions (Kramers theorem, see1). And if the tree swells (or is being pulled) much in excess of this average, than the corresponding elastic free energy can be expressed in terms of the largest eigenvalue of the Kramers matrix, ; in this form, the expression is amenable to numerical implementation for RNA7. But as far as scaling is concerned, a separate argument is required to establish the connection between μ and L, and it shows L/lK ∼ μ, up to logarithmic corrections 71.
One may be puzzled by the fact that free energy (9) is minimal at R = 0. One way to think about it is to realize that typical fluctuation corresponds to ℱel ∼ kBT. A better way is to remember that at very small R a more accurate expression must be used for ℱel, it can be approximated as , it is minimal at the expected finite R. The additional term, which blows up at very small R, is never important in real physics, because even a minimal excluded volume will drive branched polymer to larger R. But if one wants to treat purely mathematical problem of ideal trees without any excluded volume, than extra term of free energy arises from low probability (high entropy cost) of placing all monomers in a small volume.
References
- 1.Rubinstein M, Colby RH. Polymer Physics. Oxford University Press; New York: 2003. [Google Scholar]
- 2.Burchard W. Adv Polym Sci. 1999;143:113. [Google Scholar]
- 3.Bacova P, Hawke LGD, Read DJ, Moreno AJ. Macromolecules. 2013;46:4633–4650. [Google Scholar]
- 4.Zimm BH, Stockmayer WH. J Chem Phys. 1949;17:1301–1314. [Google Scholar]
- 5.Stauffer D, Aharony A. Introduction to percolation theory. Taylor & Francis Inc; 1994. [Google Scholar]
- 6.Liu L, Hyeon C. Biophys J. 2016;110:2320. doi: 10.1016/j.bpj.2016.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kelly J, Grosberg AY, Bruinsma R. J Phys Chem B. 2016;120:6038–6050. doi: 10.1021/acs.jpcb.6b01964. [DOI] [PubMed] [Google Scholar]
- 8.Singaram SW, Gopal A, Ben-Shaul A. J Phys Chem B. 2016;120:6231–6237. doi: 10.1021/acs.jpcb.6b02258. [DOI] [PubMed] [Google Scholar]
- 9.Marko J, Siggia E. Phys Rev E. 1995;52:2912–2938. doi: 10.1103/physreve.52.2912. [DOI] [PubMed] [Google Scholar]
- 10.Mondal J, Bratton BP, Li Y, Yethiraj A, Weisshaar JC. Biophys J. 2011;100:2605–2613. doi: 10.1016/j.bpj.2011.04.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Isaacson J, Lubensky TC. J Physique Lett. 1980;41:469–471. [Google Scholar]
- 12.Seitz WA, Klein DJ. J Chem Phys. 1981;75:5190–5193. [Google Scholar]
- 13.Duarte J, Ruskin H. J Physique. 1981;42:1585–1590. [Google Scholar]
- 14.Parisi G, Sourlas N. Phys Rev Lett. 1981;46:871–874. [Google Scholar]
- 15.Fisher M. Phys Rev Lett. 1978;40:1610–1613. [Google Scholar]
- 16.Kurtze D, Fisher M. Phys Rev B. 1979;20:2785–2796. [Google Scholar]
- 17.Bovier A, Fröhlich J, Glaus U. Branched Polymers and Dimensional Reduction. In: Osterwalder K, Stora R, editors. Critical Phenomena, Random Systems, Gauge Theories. North-Holland, Amsterdam: 1984. [Google Scholar]
- 18.Grosberg AY. Soft Matter. 2014;10:560–565. doi: 10.1039/c3sm52805g. [DOI] [PubMed] [Google Scholar]
- 19.Rosa A, Everaers R. Phys Rev Lett. 2014;112:118302. doi: 10.1103/PhysRevLett.112.118302. [DOI] [PubMed] [Google Scholar]
- 20.Ge T, Panyukov S, Rubinstein M. Macromolecules. 2016;49:708–722. doi: 10.1021/acs.macromol.5b02319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Khokhlov AR, Nechaev SK. Phys Lett. 1985;112A:156–160. [Google Scholar]
- 22.Rubinstein M. Phys Rev Lett. 1986;57:3023–3026. doi: 10.1103/PhysRevLett.57.3023. [DOI] [PubMed] [Google Scholar]
- 23.Obukhov SP, Rubinstein M, Duke T. Phys Rev Lett. 1994;73:1263–1266. doi: 10.1103/PhysRevLett.73.1263. [DOI] [PubMed] [Google Scholar]
- 24.Michieletto D, Turner MS. Proc Natl Acad Sci USA. 2016;113:5195–5200. doi: 10.1073/pnas.1520665113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Michieletto D. Soft Matter. 2016;12:9485–9500. doi: 10.1039/c6sm02168a. [DOI] [PubMed] [Google Scholar]
- 26.Grosberg A, Rabin Y, Havlin S, Neer A. Europhys Lett. 1993;23:373–378. [Google Scholar]
- 27.Rosa A, Everaers R. Plos Comput Biol. 2008;4:e1000153. doi: 10.1371/journal.pcbi.1000153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Vettorel T, Grosberg AY, Kremer K. Phys Biol. 2009;6:025013. doi: 10.1088/1478-3975/6/2/025013. [DOI] [PubMed] [Google Scholar]
- 29.Mirny LA. Chromosome Res. 2011;19:37–51. doi: 10.1007/s10577-010-9177-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Halverson JD, Smrek J, Kremer K, Grosberg AY. Rep Prog Phys. 2014;77:022601. doi: 10.1088/0034-4885/77/2/022601. [DOI] [PubMed] [Google Scholar]
- 31.Kerpedjiev P, Hammer S, Hofacker IL. Bioinformatics. 2015;31:3377–3379. doi: 10.1093/bioinformatics/btv372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.De Gennes PG. Biopolymers. 1968;6:715. doi: 10.1002/bip.1968.360060508. [DOI] [PubMed] [Google Scholar]
- 33.Daoud M, Joanny JF. J Physique. 1981;42:1359–1371. [Google Scholar]
- 34.des Cloizeaux J, Jannink G. Polymers in Solution. Oxford University Press; Oxford: 1989. [Google Scholar]
- 35.Grosberg AY, Khokhlov AR. Statistical Physics of Macromolecules. AIP Press; New York: 1994. [Google Scholar]
- 36.De Gennes PG. J Physique Lett. 1976;37:L59–L61. [Google Scholar]
- 37.Flory PJ. Principles of Polymer Chemistry. Cornell University Press; Ithaca (NY): 1953. [Google Scholar]
- 38.Gutin AM, Grosberg AY, Shakhnovich EI. Macromolecules. 1993;26:1293–1295. [Google Scholar]
- 39.De Gennes PG. J Physique Lett. 1975;36:L55–L57. [Google Scholar]
- 40.Le Guillou JC, Zinn-Justin J. Phys Rev Lett. 1977;39:95–98. [Google Scholar]
- 41.Family F. J Phys A-Math Gen. 1980;13:L325–L334. [Google Scholar]
- 42.de Alcantara OF, Kirkham JE, McKane AJ. J Phys A-Math Gen. 1980;13:L247–L251. [Google Scholar]
- 43.Derrida B, de Seze L. J Physique. 1982;43:475–483. [Google Scholar]
- 44.Nienhuis B. Phys Rev Lett. 1982;49:1062–1065. [Google Scholar]
- 45.Dhar D. Phys Rev Lett. 1983;51:853–856. [Google Scholar]
- 46.Duplantier B. J Phys A-Math Gen. 1986;19:L1009. [Google Scholar]
- 47.Duplantier B, Saleur H. Phys Rev Lett. 1987;59:539–542. doi: 10.1103/PhysRevLett.59.539. [DOI] [PubMed] [Google Scholar]
- 48.Adler J, Meir Y, Harris A, Aharony A, Duarte J. Phys Rev B. 1988;38:4941–4954. doi: 10.1103/physrevb.38.4941. [DOI] [PubMed] [Google Scholar]
- 49.Janssen HK, Stenull O. Phys Rev E. 2011;83:051126. doi: 10.1103/PhysRevE.83.051126. [DOI] [PubMed] [Google Scholar]
- 50.Gaunt DS, Sykes MF, Torrie GM, Whittington SG. J Phys A-Math Gen. 1982;15:3209–3217. [Google Scholar]
- 51.Privman V. Physica A. 1984;123:428–442. [Google Scholar]
- 52.Margolina A, Family F, Privman V. Z Phys B-Condens Mat. 1984;54:321–324. [Google Scholar]
- 53.Meirovitch H. J Phys A-Math Gen. 1987;20:6059–6073. [Google Scholar]
- 54.Ishinabe T. J Phys A-Math Gen. 1989;22:4419–4431. [Google Scholar]
- 55.Janse van Rensburg EJ, Madras N. J Phys A: Math Gen. 1992;25:303–333. [Google Scholar]
- 56.Li B, Madras N, Sokal AD. J Stat Phys. 1995;80:661–754. [Google Scholar]
- 57.Wittkop M, Kreitmeier S, Göritz D. J Chem Phys. 1996;104:3373–3385. [Google Scholar]
- 58.Cui S, Chen Z. Phys Rev E. 1996;53:6238–6243. doi: 10.1103/physreve.53.6238. [DOI] [PubMed] [Google Scholar]
- 59.Madras N, Janse van Rensburg EJ. J Stat Phys. 1997;86:1–36. [Google Scholar]
- 60.Hsu HP, Nadler W, Grassberger P. J Phys A: Math Gen. 2005;38:775. [Google Scholar]
- 61.Hsu HP, Grassberger P. J Stat Mech: Theory Exp. 2005;2005:P06003. [Google Scholar]
- 62.Rosa A, Everaers R. J Phys A: Math Theor. 2016;49:345001. [Google Scholar]
- 63.Rosa A, Everaers R. J Chem Phys. 2016;145:164906. doi: 10.1063/1.4965827. [DOI] [PubMed] [Google Scholar]
- 64.Bhattacharjee SM, Giacometti A, Maritan A. J Phys: Condens Matter. 2013;25:503101. doi: 10.1088/0953-8984/25/50/503101. [DOI] [PubMed] [Google Scholar]
- 65.Daoud M, Cotton JP. J Phys France. 1982;43:531–538. [Google Scholar]
- 66.Raphael E, Pincus P, Fredrickson GH. Macromolecules. 1993;26:1996–2006. [Google Scholar]
- 67.Boris D, Rubinstein M. Macromolecules. 1996;29:7251–7260. [Google Scholar]
- 68.Kröger M, Peleg O, Halperin A. Macromolecules. 2010;43:6213–6224. [Google Scholar]
- 69.Daoud M, Pincus P, Stockmayer WH, Witten T. Macromolecules. 1983;16:1833–1839. [Google Scholar]
- 70.Doi M, Edwards SF. The Theory of Polymer Dynamics. Oxford University Press; New York: 1986. [Google Scholar]
- 71.Grosberg AY, Nechaev SK. J Phys A-Math Theor. 2015;48:345003. [Google Scholar]
- 72.Smrek J, Grosberg AY. J Phys: Condens Matter. 2015;27:064117. doi: 10.1088/0953-8984/27/6/064117. [DOI] [PubMed] [Google Scholar]
- 73.Vettorel T, Grosberg AY, Kremer K. Phys Today. 2009;62:72. doi: 10.1088/1478-3975/6/2/025013. [DOI] [PubMed] [Google Scholar]
- 74.Flory PJ. Statistical Mechanics of Chain Molecules. Interscience; New York: 1969. [Google Scholar]
- 75.De Gennes PG. Scaling Concepts in Polymer Physics. Cornell University Press; Ithaca: 1979. [Google Scholar]
- 76.Rosa A, Everaers R. Phys Rev E. 2017 doi: 10.1103/PhysRevE.95.012117. accepted for publication Preprint: http://arxiv.org/abs/1610.05230. [DOI] [PubMed]