Cubic meter volume optical coherence tomography

Abstract

Optical coherence tomography (OCT) is a powerful three-dimensional (3D) imaging modality with micrometer-scale axial resolution and up to multi-GigaVoxel/s imaging speed. However, the imaging range of high-speed OCT has been limited. Here, we report 3D OCT over cubic meter volumes using a long coherence length, 1310 nm vertical-cavity surface-emitting laser and silicon photonic integrated circuit dual-quadrature receiver technology combined with enhanced signal processing. We achieved 15 µm depth resolution for tomographic imaging at a 100 kHz axial scan rate over a 1.5 m range. We show 3D macroscopic imaging examples of a human mannequin, bicycle, machine shop gauge blocks, and a human skull/brain model. High-bandwidth, meter-range OCT demonstrates new capabilities that promise to enable a wide range of biomedical, scientific, industrial, and research applications.

1. INTRODUCTION

With over 100 million cumulative clinical imaging procedures performed in ophthalmology and the technology gaining increasing acceptance in cardiology, dermatology, and gastroenterology, optical coherence tomography (OCT) is becoming an increasingly important tool for micrometer-resolution three-dimensional (3D) sub-surface imaging [1–4]. Modern OCT systems achieve high detection sensitivity and high speed by performing measurements in the Fourier domain and Fourier transforming an interference spectrum to generate axial scans (A-scans), which characterize reflection/backscatter versus the range [5–9]. The imaging range of Fourier-domain OCT has been limited to a few centimeters [4,10,11], thereby restricting its applications. In this study, we demonstrate an order of magnitude longer imaging range than previously demonstrated [10,11]. We demonstrate 3D macroscopic imaging at a 100 kHz axial scan rate with 15 µm depth resolution, near-shot-noise-limited sensitivity, sub-surface tomographic imaging, and a meter-scale imaging range for ranging applications. This makes OCT a new macroscopic 3D imaging and ranging method alternative to other demonstrated technologies, such as laser triangulation [12,13], time of flight [14], single-pixel detector [15], and structured illumination (or modulated imaging) [16,17]. We demonstrate macroscopic imaging with applications to machine vision, 3D documentation, precision measurement, and non-destructive evaluation of materials.

State-of-the-art high-speed OCT systems using Fourier domain detection are known as either spectral-domain OCT (SD-OCT) [5,8,18] or swept-source OCT (SS-OCT) [9,19]. SD-OCT suffers from an inherent sensitivity roll-off due to spectrometer resolution limits, making long-range imaging challenging. SS-OCT has improved sensitivity roll-off but has been predominately implemented with laser technologies that tune multiple longitudinal laser modes under the tuning filter [2,9], which detrimentally affects laser coherence lengths and limits OCT imaging to a few centimeters in the depth range. Lasers based on widely tunable swept vertical-cavity surface-emitting laser (VCSEL) [20,21] technology have cavity lengths on the order of a few microns that separates the Fabry–Perot cavity resonant mode spacing to be wider than the laser tuning range to generate true single longitudinal mode, narrow linewidth emission. This research uses an optically pumped MEMS-tunable VCSEL centered at 1310 nm [Fig. 1(a)]. A ~225 m coherence length has been estimated for a similar electrically pumped MEMS-VCSEL at 1050 nm [22].

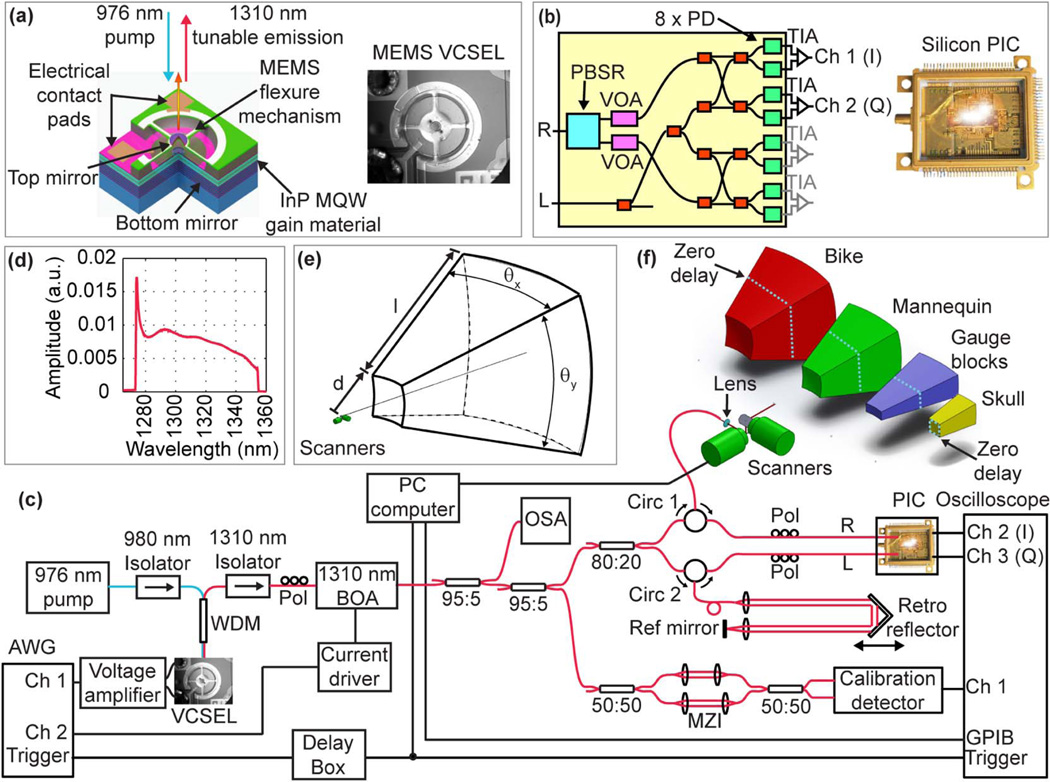
Fig. 1.

Details of the imaging system. (a) Schematic and photograph of the MEMS-tunable VCSEL swept laser source. (b) Schematic and photograph of the silicon photonic integrated circuit (PIC) IQ receiver. R, signal input; L, reference input; PBSR, polarization beam splitter; VOA, variable optical attenuators; TIA, trans-impedance amplifier. (c) Imaging system layout. AWG, arbitrary waveform generator; WDM, wavelength division multiplexer; Pol, polarization controller; BOA, booster optical amplifier; OSA, optical spectrum analyzer; Circ, circulator; MZI, Mach–Zehnder interferometer. (d) Spectrum of the BOA-amplified VCSEL emission recorded with the OSA. (e) Definition of scanning volume. (f) Representations of scanned volumes for the bicycle, mannequin, gauge blocks, and skull/brain that are proportionally accurate and show the position of the OCT zero delay.

Long imaging ranges with fine axial resolutions in SS-OCT require high detection bandwidths. We demonstrate, for the first time to our knowledge, a new photonic integrated circuit (PIC) system operating at 1310 nm [Fig. 1(b)] for OCT. The PIC integrates waveguides, polarization splitting elements, 90-deg phase shifters, and waveguide couplers to provide dual polarization and in-phase and quadrature (IQ) dual balanced detection with an optical bandwidth of 370 nm and electrical bandwidths greater than 25 GHz. IQ detection enables full-range (complex conjugate suppressed) OCT, which provides a 2 × increase in the imaging range at a given acquisition bandwidth [23]. The PIC replaces a large subsection of an equivalent fiber optic OCT interferometer with integrated optics on a silicon chip.

2. METHODS

A. Experimental Setup

Figure 1(c) shows the imaging system. The VCSEL tunable laser had a ~1310 nm center wavelength and was tuned over an 80 nm full sweep range [Fig. 1(d)] at a 100 kHz repetition rate. The VCSEL drive waveform was shaped to achieve a quasi-linear sweep in the wavenumber (see Supplement 1, Note 1 and Fig. S1). A dual-circulator OCT interferometer design used a reference arm with a retro-reflector on a translational stage to set the zero delay position. In the sample arm, the output beam from the optical fiber with a 0.14 numerical aperture was focused by a lens (f = 19 mm) and directed to a pair of galvanometers to a focused spot size of 550 µm [full width at half-maximum (FWHM)] with 20 mW power on the sample. The Rayleigh length of this design was 52.3 cm, corresponding to a confocal parameter of 104.6 cm. According to Gaussian beam propagation, the resolution degrades by a factor of $\sqrt{2}$ at the limits of the confocal range. The focused spot size and Rayleigh length were selected based on the size of the objects used for the imaging experiment. They can be easily adjusted by varying the distance between the fiber and the lens for different applications. Light from the reference and sample arms was interfered and detected by a fully packaged silicon PIC IQ receiver. The reference arm power at the input of the PIC was 3 mW. Within the silicon PIC receiver, the sample input was first separated into two orthogonal polarization channels by an integrated polarization beam-splitting element. The reference signal from each polarization channel was further split into in-phase (I) and quadrature (Q) components, mixed with the signal input, and then coupled into four integrated photodetectors whose outputs were directly coupled to two balanced trans-impedance amplifiers. A high-speed oscilloscope with a 16 GHz analog bandwidth sampled the data at 50 GS/s. For 3D imaging, the post-objective focused beam was raster-scanned to generate a pyramidal volume [Figs. 1(e)–1(f)]. The non-telecentric scan generated “fan” distortions in both the axial and lateral dimensions because the A-scan directions varied as a function of the scan angle. These distortions can be fully corrected with the methods described in Supplement 1, Note 7. More details of the imaging system can be found in Supplement 1, Note 2.

B. Signal Processing

Although a customized waveform was used to tune the VCSEL wavelength, internal mechanical resonances and limitations on MEMS actuator dynamics resulted in both sweep-to-sweep variation and a deviation from perfect wavenumber linearity in the sweep trajectory. A reference Mach–Zehnder interferometer (MZI) was used to nominally calibrate the sample interferogram on a sweep-by-sweep basis, but it was found that the transfer function phase response of the oscilloscope and detection electronics prevented the proper calibration of high-frequency (long depth range) data. We developed a phase correction method to invert the phase component of the electrical transfer function, which was applied as a first processing step to the raw acquired data (see Supplement 1, Notes 3 and 4 and Figs. S2–S4). We corrected the phase distortion from the detection electronics by fast Fourier transforming (FFT) the fringe signal and then multiplying the positive frequencies by e^iβ(f) and the negative frequencies by e^−iβ(|f|), then inverse fast Fourier transforming to obtain the corrected signal by retaining only the real component, where β(f) = β₁f ^p + β₂f ^p−1 + … + β_pf + β_p+1 is a polynomial expression representing the phase correction, β₁ through β_p+1 are the polynomial coefficients, and f is the frequency. The coefficient values of the polynomial function were pre-determined based on the optimization of multiple mirror signals over different depths. In this study, we used m = 8 mirror samples from close to DC all the way to ~70 cm, separated by about 10 centimeters. We used a sixth-order polynomial, and we set the DC term β_p+1 to zero. The first-order term was equivalent to correcting the group delay difference between the OCT signal path and the MZI calibration signal path. Higher-order terms were used to correct the transfer function of the detection electronics. The optimization to determine the coefficients was performed in MATLAB using the fmin-search function. Note that similar methods have been used to correct RF errors in quadrature detection circuits [24].

For SS-OCT, it is also important to achieve a high stability distance measurement that is robust against sweep-to-sweep variations or long-term laser drift. This was realized using a fixed k signal processing method. Specifically, the phase-corrected interferogram was resampled to be linear in wavenumber on a sweep-by-sweep basis,

$$E{[k_s^{(t)}]}_{\mathrm{O}\mathrm{C}\mathrm{T}}\stackrel{\text{arg}(E{(k)}_{\mathrm{M}\mathrm{Z}\mathrm{I}})}{\to }E{[k_l^{(k)}]}_{\mathrm{O}\mathrm{C}\mathrm{T}},$$ (1)

where [k_s] = [k_s1, k_s2, …k_sn] are uniform intervals in time and [k_l] = [k_l1, k_l2, …k_ln] are linearly spaced in wavenumber. In SS-OCT, the swept laser may have sweep-to-sweep jitter of the starting wavelength and trajectory variations in the wavelength vs. time, as well as long-term drift, which could affect measurement precision. A key observation is that if we fix the length of the accumulated span of [k_l] in the signal processing by extracting sample data corresponding to a fixed phase range in the MZI reference signal (see also Supplement 1, Note 3), the frequency of the signal in k-space after interpolation remains constant, even in the presence of laser sweep-to-sweep variations. This removes the effects of laser sweep variation so the measured sample position after the Fourier transform is repeatable and consistent. We describe further details and verify the findings by simulation in Supplement 1, Note 6 and Fig. S6.

The phase between the I and Q channels of the PIC receiver was nearly 90 deg and was stable and consistently maintained over at least several days of continuous operation. However, there was a frequency-dependent phase difference between the I and Q channels which caused deviations from 90 deg as a linear function of the wavenumber over the laser sweep range, possibly caused by a small optical path length mismatch between the two channels. We developed a linear IQ correction method to correct the frequency, phase, and amplitude differences between the two channels in order to improve the complex conjugate suppression without compromising the signal-to-noise ratio (SNR) or the dynamic range. Specifically, the frequencies of I and Q were adjusted in opposite directions to match each other:

$$M_{\mathrm{I}}^{\prime }=M_{\mathrm{I}}{e}^{i\chi /2}$$

$$M_{\mathrm{Q}}^{\prime }=M_{\mathrm{Q}}{e}^{-i\chi /2},$$ (2)

where χ = ak + b, k is the wavenumber and was arbitrarily defined in the range from −1 to 1, and a and b are coefficients of the linear model. After this operation, I and Q have the same frequency but may have a relative phase deviation from the desired 90-deg relative phase. We can correct this relative phase error by applying a linear phase ramp in the Fourier domain on the I channel,

$$M_{\mathrm{I}}^{″}=\mathrm{F}{\mathrm{T}}^{-1}(\mathrm{F}\mathrm{T}(M_{\mathrm{I}}^{\prime })e^{i\delta }),$$ (3)

where δ = cx, and x is a distance vector arbitrarily defined from −1 to 1. The coefficients a, b, and c can be found from a three-dimensional exhaustive search by maximizing mirror suppressions over different depths (including both positive and negative depths). The combined complex signal after the frequency and phase correction is

$$M_{\mathrm{I}\mathrm{Q}}=M_{\mathrm{I}}^{″}+i{M}_{\mathrm{Q}}^{\prime },$$ (4)

and since there could be amplitude differences between the I and Q components of M_IQ, they further underwent a magnitude equalization process in the Fourier domain,

$$M_{\mathrm{I}}^{*}=\mathrm{F}{\mathrm{T}}^{-1}(\mathrm{F}\mathrm{T}(\text{Re}(M_{\mathrm{I}\mathrm{Q}}))A_{\text{ave}}/|\mathrm{F}\mathrm{T}(\text{Re}(M_{\mathrm{I}\mathrm{Q}}))|)$$

$$M_{\mathrm{Q}}^{*}=\mathrm{F}{\mathrm{T}}^{-1}(\mathrm{F}\mathrm{T}(\text{Im}(M_{\mathrm{I}\mathrm{Q}}))A_{\text{ave}}/|\mathrm{F}\mathrm{T}(\text{Im}(M_{\mathrm{I}\mathrm{Q}}))|),$$ (5)

where A_ave = (|FT(Re(M_IQ))| + |FT(Im(M_IQ))|)/2.

3. RESULTS

A. Imaging System Characterization

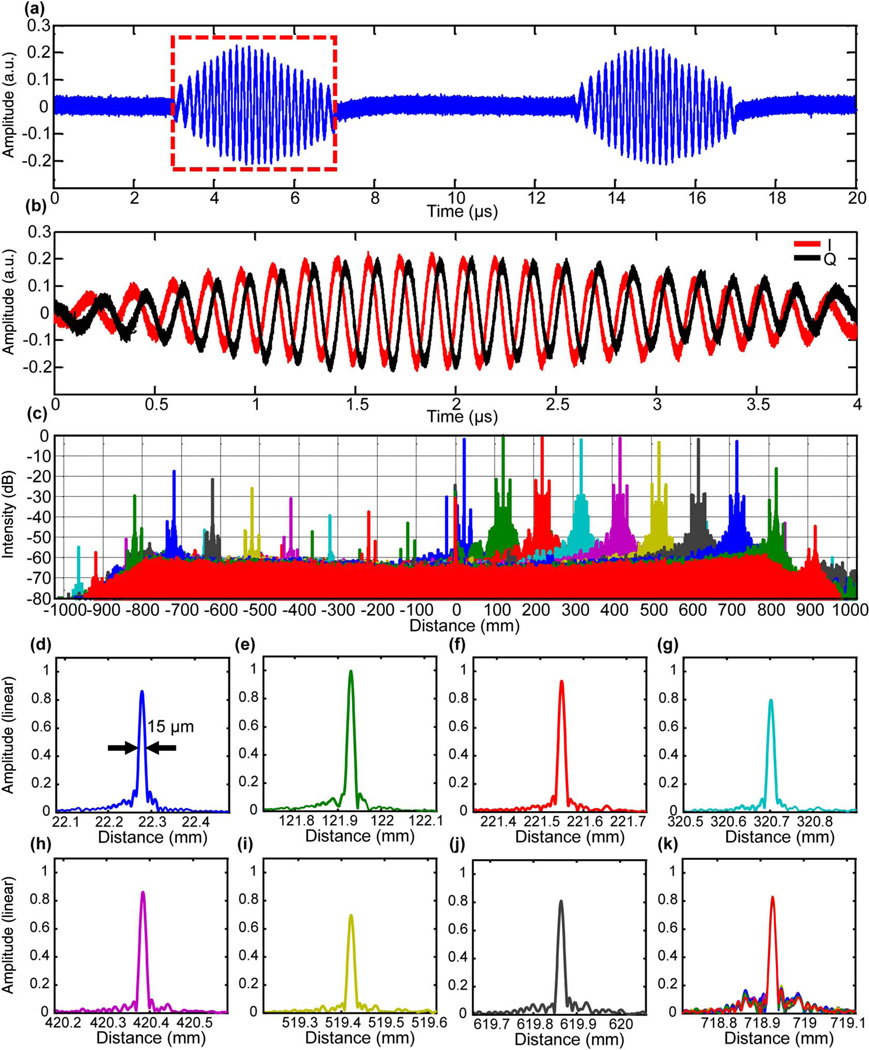
Figure 2(a) shows representative interferograms from a single reflection from a silver mirror (I channel only) from two consecutive sweeps, and Fig. 2(b) shows raw data for the I and Q channels acquired by the oscilloscope. The experimentally measured axial resolution was 15 µm FWHM for the axial point-spread function (PSF) in air (before spectral shaping) throughout the entire single channel (I only) imaging range of ~75 cm [Figs. 2(d)–2(k)], where the sensitivity rolled off by less than 4 dB. IQ processing [Fig. 2(c)] doubled the imaging range to ~1.5 m, which was limited by the oscilloscope RF bandwidth and not by the VCSEL coherence length or the PIC receiver. The symmetrical side peaks in the PSFs at a distance of 17.3 mm from the primary peak [Fig. 2(c)] were caused by spurious reflections outside the laser cavity in this first-generation source. They did not show up in previous short-range imaging experiments due to the inherent low-pass filtering in the acquisition system [25], but became apparent with the high bandwidth acquisition of the current study. The side peaks have been significantly reduced in later generations with refinements to the optical component specifications and are not inherent to the approach.

Fig. 2.

System characterization of meter-range OCT. (a) Representative interferograms from a mirror showing two consecutive laser sweeps (I channel only). (b) I and Q channel signals from one sweep showing ~90-deg phase relationship between the two channels. (c) Signal roll-off measurement on a logarithmic scale with IQ processing. Negative axis shows suppressed complex conjugates. (d)–(k) Plots of PSFs on a linear scale at different depths. (k) 10 of 100 repeated PSFs at a depth of ~718.9 mm.

The complex conjugate suppression ratios before and after IQ phase correction were 17.6 ± 4.1 and 28.8 ± 9.3 dB over the entire imaging range, respectively (see also Supplement 1, Note 5, Fig. S5). This was enough to suppress the complex conjugate artifacts in meter-range OCT unless there were strong specular reflections.

The system sensitivity was measured to be 108 dB at a 20 mW average power. The theoretical shot-noise-limited sensitivity was 118 dB. The 10 dB difference was due to the loss from the sample arm interface, circulators, the PIC receiver, and fiber optic connectors.

To assess the measurement precision, we performed 100 repeated measurements of a mirror at a long delay and found no variation of the measured mirror position to within the axial resolution of 15 µm [Fig. 2(k)]. The measurement precision was limited by environmental disturbances in our experimental configuration, as well as limitations on the precision of the MZI setting. Distance measurements in this study were calibrated by measuring a gauge block with a known size contained within the dataset. However, the absolute distance measurement would require calibration with a wavemeter.

B. Macroscopic 3D Imaging

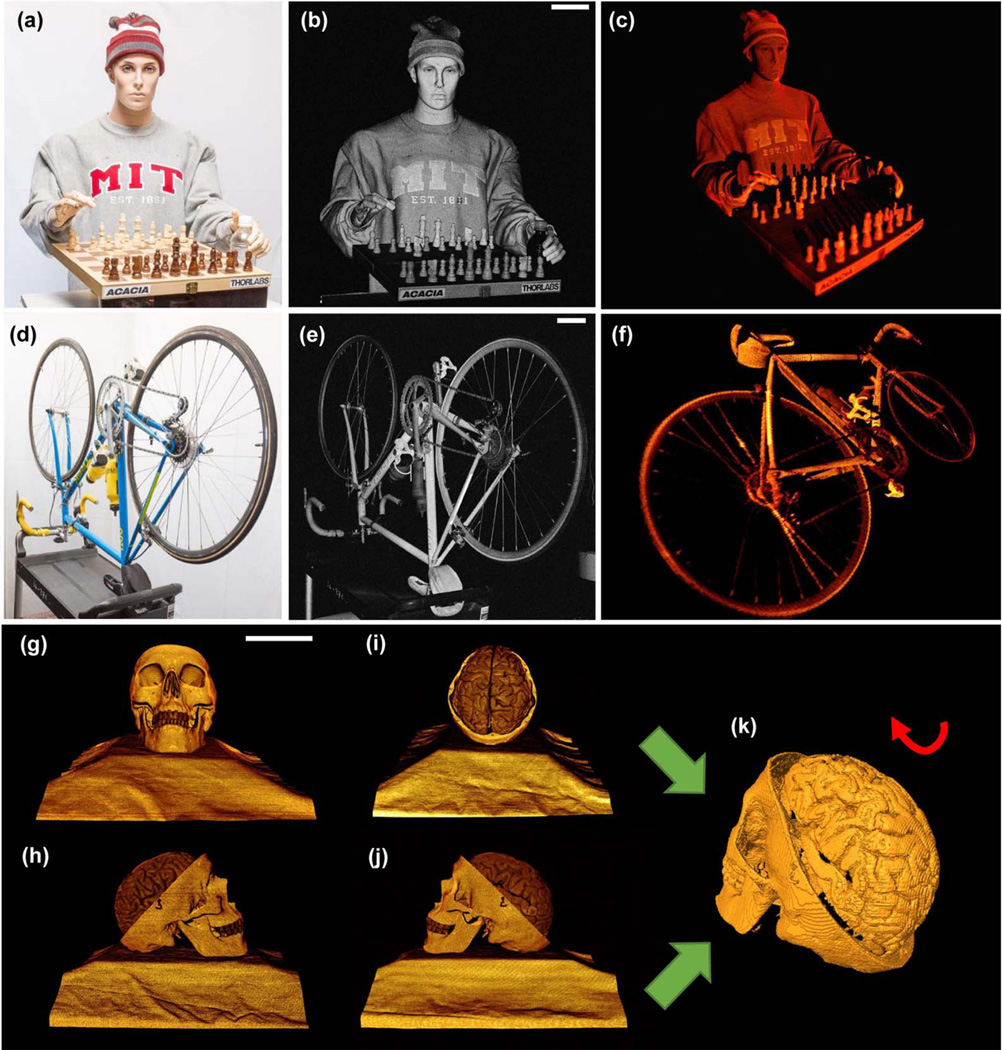
Meter-range OCT is well suited for imaging objects of humansized scales with high axial resolution. Figures 3(a)–3(c) show an example of 3D imaging of a mannequin playing chess with 200 Giga samples (raw data) for a volume size of 0.98 m³ and a dynamic range of 54 dB, defined as the intensity difference between the peak signal and mean noise floor in the volumetric data set using a logarithmic scale (here, we used the definition of dynamic range suggested in Ref. [4], Chap. 5, p. 169. It characterizes the SNR for a single acquisition volume, is limited by the digitization range of the oscilloscope, and is different from the system sensitivity, which is the minimum signal an OCT system can detect). From the 3D volume, we generated the maximum intensity projection image [Fig. 3(b)], which revealed details of the objects, including subtle facial expressions, complex folds of the sweatshirt, and fine details of the chess pieces. A full 3D rendering is shown in Fig. 3(c) and Visualization 1. This technology may provide solutions to challenging computer vision tasks such as 3D object recognition and surveillance.

Fig. 3.

(a) Photograph, (b) maximum intensity projection, and (c) 3D OCT visualization of a life-size mannequin with a chess set consisting of 1000 × 1000 A-scans before scan correction. The volume size is 0.98 m³ (d = 89 cm, l = 150 cm, θ_x = 27.5 deg, and θ_y = 27.5 deg. For display, an intensity threshold of ~10 dB above the mean noise floor was applied. (d) Photograph, (e) maximum intensity projection, and (f) 3D OCT visualization of an adult bicycle more than 1.5 m in length consisting of 1000 × 1000 A-scans before scan correction. The volume size is 1.8 m³ (d = 97 cm, l = 150 cm, θ_x = 35.7 deg, and θ_y = 35.7 deg). (g)–(j) Human skull model imaged at 0 deg (g), 90 deg (h), 180 deg (i), and 270 deg (j). Each volume has 500 × 500 A-scans and a volume of 8000 cm³ (d = 97 cm, l = 75 cm, θ_x = 10.8 deg, and θ_y = 10.8 deg). (k) 3D skull surface reconstructed by segmenting and merging the individual object surface of (g)–(j) after scan correction. Scale bars are 10 cm. 3D visualization of the objects after scan correction can be found in Visualization 1, Visualization 2, and Visualization 3.

Meter-range OCT can be used to inspect and measure weakly scattering objects with complex shapes and surface profiles. Figures 3(e) and 3(f) show an example of imaging a bicycle with a volume size of 1.8 m³ and a dynamic range of 56 dB. A full 3D rendering is shown in Visualization 2.

Macroscopic anatomical imaging of a human skull/brain model is shown as an example relevant for surgical guidance applications [Figs. 3(g)–3(k)]. The structural images were generated by taking the sum of the squares of the I and Q signals instead of quadrature processing because of the moderate imaging range requirement. By acquiring multiple volumes from four orthogonal perspectives and correcting the geometrical distortions created by the non-telecentric beam scanning (Supplement 1, Note 7, Figs. S7 and S8), it was possible to generate a complete 3D model (Visualization 3) by segmenting and merging the individual object surfaces. This may be useful for surgical planning or guidance, where position or topographic information is required over a long imaging range.

C. Non-Contact Precision Measurement

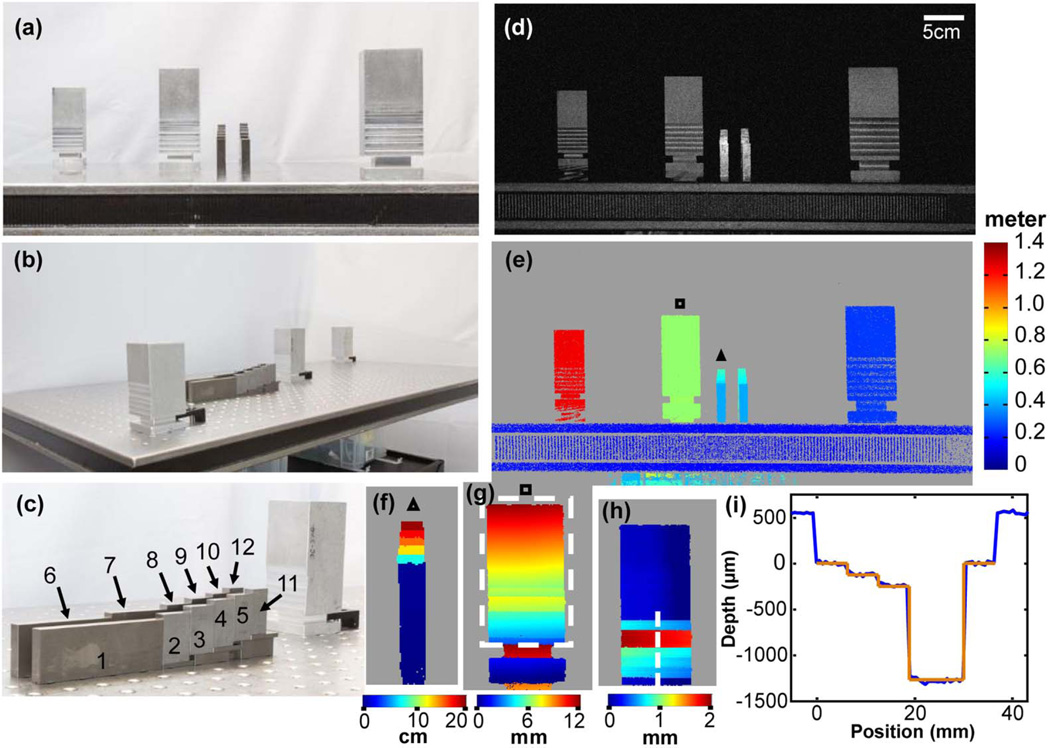
Meter-range OCT is well suited for non-contact metrology. Quantitative measurements of aluminum posts and precision steel gauge blocks from a meter scale down to a micrometer scale with a 65 dB dynamic range are shown in Fig. 4, with the results summarized in Table 1. The gauge blocks have a manufacturer-specified tolerance of 0.00005 in. The first row in Table 1 shows the manufacturer specification (Part #06461818, MSC Industrial Supply Co.). Three independent measurements of each block were also performed by a micrometer with a 0.01 mm resolution, as shown in the second row in Table 1. Block 1 was used for calibrating the axial measurement range in the 3D data set. Blocks 11 and 12 were not measured by the OCT because there were no detectable surfaces behind them. For each block, 10 consecutive measurements from 10 adjacent A-lines scanning over the block surface were performed to assess the measurement precision. The sample position was determined by locating the peak signal of each A-scan. The OCT measurements of the gauge block lengths agree with the specified dimensions with a mean error of 9.93 ± 4.94 µm. The standard deviation of the measurements over consecutive A-scans scanning across the block surface was 6.71 ± 2.78 µm, which was mainly due to the sample tilt with respect to the incident beam. In a separate demonstration, depth measurements of milled steps in the aluminum post agree with the nominal machined values [Fig. 4(i)].

Fig. 4.

(a) and (b) Photographs of the aluminum posts and steel gauge blocks on an optics table from two perspectives. (c) Photograph of the gauge blocks. (d) OCT maximum intensity projection. The OCT volume has 500 × 1000 A-scans. The volume size is 0.288 m³ (d = 98 cm, l = 150 cm, θ_x = 20.4 deg, and θ_y = 9.7 deg). (e) Distance mapping of the objects in meter scale. (f) Distance mapping of the gauge blocks on a centimeter scale. (g) Visualization of the tilt of an aluminum post with respect to the incident OCT beam on a millimeter scale. (h) Topological mapping of the aluminum surface from the box in (g) after correcting for sample tilt. (i) Relative depths of milled steps in the aluminum post surface from dotted line in (h) on a micrometer scale showing good agreement between the OCT measured surface profile (blue) and nominal depths from the milling machine digital readout (orange). Depth scale was calibrated by measurement of gauge block 1, and the transverse scale was calibrated by the nominal milled widths.

Table 1.

Quantitative Validation of the OCT Thickness Measurement of the Gauge Blocks

Length	Block 2	Block 3	Block 4	Block 5	Block 6	Block 7	Block 8	Block 9	Block 10
Manufacturer’s specification (inch)	1	0.9	0.8	0.75	3	2	0.95	0.85	0.7
Measured by a micrometer (mm)	25.4000 ±0.0000	22.8600 ±0.0000	20.3267 ±0.0058	19.0533 ±0.0058	76.2033 ±0.0058	50.8000 ±0.0000	24.1300 ±0.0000	21.5900 ±0.0000	17.7800 ±0.0000
Measured by OCT (mm)	25.3858 ±0.0063	22.8596 ±0.0065	20.3321 ±0.0059	19.0636 ±0.0065	76.1965 ±0.0059	50.7896 ±0.0048	24.1215 ±0.0039	21.6021 ±0.0069	17.7946 ±0.0137

D. Non-Destructive Evaluation of Objects

Unlike many other ranging technologies that are limited to detecting surface signals, meter-range OCT can perform sub-surface imaging of objects and transparent multilayered structures. An example image of plastic bottles is presented in Fig. S9; it would be relevant for non-destructive evaluation in manufacturing.

4. DISCUSSION AND CONCLUSION

Meter-range OCT is analogous to frequency-modulated continuous-wave coherent radar [14,26] but with orders of magnitude higher speeds. Compared with other 3D ranging technologies, such as LIDAR [14], laser trackers [27], and frequency comb lasers [28–30], OCT is better suited for sub-surface evaluation and imaging weakly scattering objects owing to its unique capability to perform tomographic imaging with shot-noise-limited sensitivity. Compared with other 3D sub-surface imaging methods, such as modulated imaging [16,17], OCT has a higher axial resolution. OCT also has the advantage that it is less sensitive to clutter or parasitic reflections. Other metrology techniques work best when there is only a single reflected signal and can be confounded by multiple reflections or parasitic reflections at different ranges. OCT can differentiate these signals and provide a high-accuracy measurement. In addition, OCT can potentially provide information about material composition, laminated structures, coatings, surface roughness, and other properties that are difficult to assess with other metrology techniques. However, the majority of applications that require a true meter range will likely be in metrology, process monitoring, non-destructive evaluation, and related areas. Medical applications may not require such a long range. By contrast, there are many medical applications that require few centimeters to tens of centimeters imaging ranges, such as macroscopic anatomic imaging for surgical guidance, upper airway imaging for the diagnosis of chronic obstructive pulmonary diseases, and endoscopic imaging of organs with a large lumen size, such as the stomach.

The imaging range of SS-OCT is governed by the light source coherence length, sweep repetition rate, detection bandwidth, and backscattered signal detection. For scattering objects, the numerical aperture of the signal collection is proportional to the confocal parameter, which scales as the square of the spot size and also determines the imaging range and transverse resolution. Synthetic aperture methods [31] might potentially be used to enhance the transverse resolution across the imaging range.

Meter-range OCT has benefitted from the tremendous progress in PIC development in recent years. There have been advances in integrating waveguides [32], photodetectors [33], swept lasers [34], and OCT interferometers on a chip [35,36]. The integrated IQ receiver used in this study is an important step towards a fully integrated OCT system, which will reduce the cost and enable new applications. With the ability to image sub-surface features, meter-range OCT is also a promising technology for large-scale non-destructive evaluation of materials [37] such as ceramics, polymers, optical elements, and glasses, and for inspecting artwork [38], flat-panel televisions, and mobile phone screens. In addition to detecting the scattering signal, additional contrast [4] from polarization, motion, spectroscopy, and elastrography can also be explored to enable new applications for future 3D macroscopic imaging and measurement.

One limitation of the current imaging system is the relatively long acquisition time for an imaging volume. Although it took only 10 ms to acquire one B-scan, the oscilloscope had very limited memory (256 MB) and could only hold one B-scan of data from three channels, which had to be copied to a disk before the acquisition of the next B-scan. The slow data transfer speed between the memory and hard disk using Tektronix software and the long rearming times of the oscilloscope significantly prolonged the total acquisition time, and it took up to 5 h to acquire 1000 B-scans for an imaging volume. It should be noted that the oscilloscope is not designed for large data acquisition and was used here out of convenience and cost. High-speed ADCs (>60 GHz) with very powerful digital signal processing have been demonstrated with integrated photonics technology and can be used to speed up the acquisition [39].

Another limitation is the long data processing time. Currently, the processing was implemented in MATLAB, and it took around 1.4 minutes to process one B-scan consisting of 1000 A-scans with 200,000 samples/A-scan. Rewriting the processing code in C/C₊₊, together with GPU-accelerated parallel processing, can significantly reduce the processing time. In addition, for meter-range OCT, only a few frequency components have the sample information, and other frequency components are nearly zero. This sparse data can be processed efficiently using sparse FFT [40,41], which is at least 10 times faster compared with regular FFT considering the size and sparsity of our data. Other compressed sensing methods may also be used. Finally, rapid advances in optical computing and high-performance digital signal processing integrated circuits might eventually enable real-time processing and rendering of meter-range OCT information.

Although meter-range OCT can still perform tomography, the penetration depth is limited to 1–2 mm in scattering samples, which makes it drastically different from true tomographic imaging modalities such as MRIs or CT scans. Therefore, for tomographic imaging applications, meter-range OCT is best suited for imaging transparent objects, such as glasses, plastics, and fluid. In addition, with the current implementation, the lateral resolution has to be sacrificed to achieve a long Rayleigh range, and this also reduces the effective axial resolution in scattering samples. However, this is true for all optical ranging methods.

In conclusion, we demonstrated 3D OCT over cubic meter volumes using a long coherence length, 1310 nm, VCSEL technology and silicon PIC dual-quadrature receiver technology combined with enhanced signal processing. The results suggest that it is a viable imaging and profiling technology that promises to enable a wide range of new industrial, research, and medical applications.