Abstract
Metabolite or substrate channeling is a direct transfer of metabolites from one enzyme to the next enzyme in a cascade. Among many potential advantages of substrate channeling, acceleration of the total reaction rate is considered as one of the most important and self-evident. However, using a simple model, supported by stochastic simulations, we show that it is not always the case; particularly at long times (i.e. in steady state) and high substrate concentrations, a channeled reaction cannot be faster, and can even be slower, than the original non-channeled cascade reaction. In addition we show that increasing the degree of channeling may lead to an increase of the metabolite pool size. We substantiate that the main advantage of channeling likely lies in protecting metabolites from degradation or competing side reactions.
Introduction
Enzyme-catalyzed cascade reactions play a crucial role in all physical-chemical processes in living systems and have numerous biotechnological applications. For instance, in glycolysis, which is probably the most ubiquitously present metabolic pathway in living organisms, glucose is transformed into pyruvate by ten sequential enzyme-catalyzed reactions. Enzymatic cascades are widely used in pharmaceutical and chemical industry, in medical research and other fields.
Enzymes are proteins with specific catalytic activities. As other catalysts, they do not change the chemical equilibrium, but increase the rate with which the equilibrium is achieved. Unlike most catalysts, enzymes are typically very specific and often accept only one substrate type for catalysis. Many enzyme-catalyzed reactions follow the Michaelis-Menten kinetics [1, 2], in which an enzyme and a substrate first form a complex, and then the substrate is converted into the product and released into the bulk solution. Other mechanisms are also known [3–7].
Metabolite or substrate channeling means a direct transfer of the product of one enzyme to another in a cascade reaction, without releasing it into the bulk solution [8–12]. This is realized through formation of enzyme-enzyme complexes, also called enzyme assemblies or metabolons. In these complexes the reaction intermediates are transfered from the active site of one enzyme to the active site of another enzyme either inside a physical tunnel [11–14] or along an ‘electrostatic highway’ [11, 12, 15, 16] (both called direct channeling), or diffusionally, but along a shortened path, in which case it is termed ‘channeling by proximity’ [17–22].
Although strong experimental evidence now exists in support of enzyme-enzyme complexes in vivo [23–27], the role of channeling, its presence and physiological significance in living cells have long been an abiding subject of debates [28–31]. In biotechnology, on the other hand, channeling is considered as an important method to reduce the amount of intermediate substances in solutions (e.g. to protect cells or bioreactors from toxic intermediates) and to accelerate the overall reaction rates [20–22, 32–34]. Indeed, it appears to be a widely accepted paradigm in biotechnology that channeling of intermediates accelerates cascade reactions. Thus, Zhang writes [32], when listing the benefits of channeling: “In addition to accelerating reaction rates through substrate channeling, potential benefits of complexes include…”, i.e. the reaction acceleration is treated as self-evident and is not even discussed. But there are also other views. For instance, Wheeldon et al. say in a very recent review article that [8] “the overall rate of a cascade reaction is not a function of channeling.” Here, we attempt to clarify whether substrate channeling influences the velocity of enzyme-catalyzed cascade reactions, and if so how and when.
For simplicity, we consider a cascade consisting of just two enzyme-catalyzed reactions,
| (1a) |
| (1b) |
in which the product of the first reaction (intermediate, I) is the substrate for the second. Here ai and di are macroscopic association and dissociation rate constants, respectively, ki is the turnover number of i’th enzyme, and we have assumed the standard Michaelis-Menten kinetics. In defiance of its simplicity, the Michaelis-Menten model describes well many enzyme-catalyzed reactions [7], including some reactions requiring co-factors, provided the co-factors are in abundance (see Supporting Information and the Discussion below).
We suppose now that in cascade reaction Eq (1) the intermediates are channeled between enzymes E1 and E2, through the formation of a complex E12 = E1E2. A particular mechanism of channeling is not important for our purposes, and will not be discussed here, instead we consider the following simple model for channeling
| (2) |
where SE12 (IE12) denotes a complex in which S (I) is attached to the active site of E1, while E12 I is a complex in which an intermediate is at the active site of E2; kch is a channeling rate constant, i.e. it is inverse of the time needed by an intermediate to travel from the active site of E1 to the active site of E2 in the E12 complex. For instance, Brownian dynamics simulations predict for the total journey time of a 4-hydroxy-2-ketovalerate in the intermolecular channel of a bifunctional DmpFG enzyme [13].
We assume for simplicity that the enzyme-catalyzed reactions and the channeling process are both irreversible, and that the enzyme complex can process one substrate molecule at a time. Extensions are possible and will be discussed below.
In what follows we assume that all non-diffusional (microscopic or intrinsic) rate constants are not altered when the enzymes form a complex. While this assumption might not generally be true, we note that if the overall reaction velocity changes because one of the microscopic rate constants differs in a complex and for the free enzymes, it is then this rate constant that is the cause of the change, rather than channeling per se. In this work we are solely interested in the effect of channeling as such, and for this reason we assume that in Eqs (1) and (2). Likewise, we will assume that microscopic (intrinsic) contributions to the macroscopic association/dissociation rate constants (a1, d1, and ach, dch) are the same for the channeled and non-channeled reactions (see below).
It is possible that enzymes are more stable in an enzyme-enzyme complex than alone. While this can undoubtedly be an important benefit of complex formation, it says little about the advantage of channeling as such. Indeed, in this case such a stabilization can potentially be achieved by complexing each enzyme separately with non-active proteins, through immobilization [35], or by placing enzymes in nanocages [36].
Channeling model (2) may or may not accurately describe the kinetics of real enzyme complexes. In particular, this is not a valid model for the majority of proximity channeling techniques (we shall consider this case in a separate article). However, this is a simple, analytically tractable model that will help us develop new physical insights and reach conclusions in fact more general than the model itself offers. To compare the overall reaction rates within this model with the rates of the original non-channeled cascade reaction, Eq (1), we assume that both systems are well stirred and formulate a set of ordinary differential equations based on the Michaelis-Menten kinetics. We support these results by Brownian dynamics simulations by which we determine the rates of diffusion-limited channeled and non-channeled reactions.
Results
There are three typical situations occurring in vivo and in biocatalytic experiments. For cellular systems, it is reasonable to assume that the concentration of substrate molecules in cells remains (roughly) constant under pleasurable conditions. In biocatalytic laboratory experiments, a popular setup is a batch reactor, in which substrate molecules are well mixed with enzymes, and the reactions are observed without any further addition of substrates. In semi-batch or continuous stirred-tank or flow reactors, the substrate molecules are continuously supplied to the system, often with a constant rate.
In the latter case it is clear that when the substrate supply velocity is not too high (that is, it does not exceed the maximum rate set by the enzyme capability, cf. Eq (7)), then the mass conservation implies that the rate of product formation at long times, i.e. in steady state, is equal to the rate of substrate supply. Obviously this is so for both channeled and non-channeled systems. Thus, we shall not discuss this case here. Instead, we focus on the case when the substrate concentration is kept constant in the system (cellular conditions), and comment on the batch reactors later.
We consider first long-time steady-state behaviour. In this case, it is straightforward to find for the product formation velocity of the channeled system (see Methods)
| (3) |
where is the Michaelis-Menten constant. Here [E12] is the total concentration of the enzyme complexes, and, likewise, [Ei] below is the total concentration of enzyme i.
The product formation velocity of the non-channeled system depends on the relation between the rates of individual reactions and the enzyme and substrate concentrations. When the first reaction in Eq (1) is rate-limiting, then the concentration of intermediates is constant at long times, which means that d[I]/dt = 0, and hence we have
| (4) |
where is the Michaelis-Menten constant of the first reaction. In the opposite case, when the second reaction is rate-limiting, the first reaction at long times will produce an excess amount of intermediates, and the concentration of intermediates will increase with time. This means that [I] → ∞ as t → ∞, and we obtain
| (5) |
The borderline between these two regimes is at the substrate concentration
| (6) |
For concentrations above [S]threshold, the first reaction outperforms the second, and the amount of intermediates will increase with time; in this case the rate of product formation is given by Eq (5). For [S] < [S]threshold, the second reaction is fast enough to convert the available intermediates, the concentration of intermediates is therefore always finite, and the production rate is given by Eq (4).
We focus now on the case when the first reaction is rate-limiting, and consider first two limiting cases of high and low substrate concentrations. For high substrate concentrations ( and but below [S]threshold) we get
| (7a) |
and
| (7b) |
This equation means that metabolite channeling slows down the overall reaction, provided of course that [E1] = [E12], which we assume is true for a fair comparison. Note that (where α = {ch,non}) are the maximum achievable rates determined by the enzyme’s capabilities. (Incidentally, in the case that the second reaction in a cascade is rate-limiting we have for [E2] = [E12].)
At low substrate concentrations we have
| (8) |
and hence whether the overall reaction is accelerated or decelerated by channeling is determined by the ratio .
Extent of diffusion-control
To study the case of low and intermediate substrate concentrations, we first split all association rate constants into their diffusional and microscopic (intrinsic) parts [37–39]; that is, we present an association constant a as the sum
| (9) |
and the corresponding dissociation constant as [38] d = kd/(1 + ka/kD). Here ka and kd are microscopic (intrinsic) rate constants and kD ≈ 4πDR the rate due to diffusion [40], where D is the mutual diffusion coefficient and R the reaction radius. Then, following Fange et al. [41], we introduce the degree of diffusion control
| (10) |
If γ ≫ 1, then ka ≫ kD and the reaction is diffusion limited (a ≈ kD). In the opposite case, γ ≪ 1, we have a ≈ ka and the reaction is limited by the intrinsic (microscopic) rate.
We now assume that, in addition to the enzyme’s turnover numbers , also the microscopic association/dissociation rate constants of the channeled and non-channeled reactions are equal (i.e. and ), and investigate how channeling affects the production velocity, depending on the degree of diffusion control of these reactions.
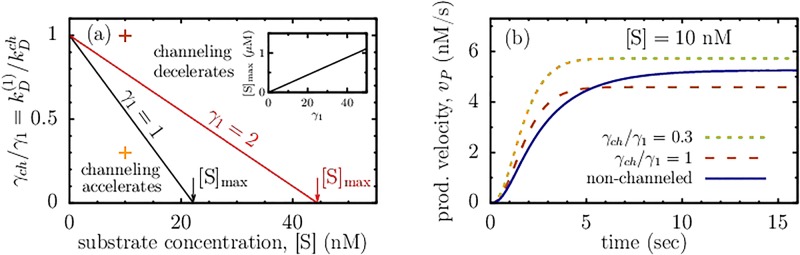
A diagram in Fig 1a shows the regions in which channeling accelerates/decelerates tandem reactions in steady-state. In accord with Eq (7), the non-channeled reaction is faster at high substrate concentrations, [S] > [S]max, at which the concentration of intermediates is sufficiently high to ensure its fast rate. At low [S], the channeled reaction can only be faster if channeling reduces the degree of diffusion control, that is if γch < γ1 and hence . This is clear as in the steady state the rates are essentially determined by the first reaction in a cascade (in the case discussed, i.e. when the first reaction is rate limiting), and the only way to accelerate the overall rate is to increase the rate due to diffusion (for otherwise equal parameters). The region in which channeling provides higher rates increases as γ1 increases. Hence the maximum substrate concentration, [S]max, below which the metabolite channeling has the potential to accelerate the reaction, also increases with γ1 (the inset in Fig 1a).
Fig 1. Effect of channeling in systems with constant substrate concentrations.
(a) Channeling diagram showing the regions in which channeling accelerates/decelerates enzyme-catalyzed tandem reactions in steady state. These regions are separated by lines calculated for different degrees of diffusion control of the first reaction in the tandem, γ1. The degree of diffusion control of the enzyme complex is denoted by γch. In general, the degree of diffusion control is γ = ka/kD, where ka is the intrinsic (microscopic) association rate constant and kD is the rate due to diffusion. Then the microscopic dissociation rate constant is kd = d(1 + γ), where d is the total dissociation constant; similarly, the microscopic association constant is ka = a(1 + γ), where a is the total association constant. γ, a and d can all be different for channeled and non-channeled reactions (i.e. a1 ≠ ach etc.), but we have assumed that the microscopic rate constants are equal, i.e. and . [S]max denotes the substrate concentration above which channeling decelerates the tandem reaction independently of the value of γch. The inset shows how [S]max depends on γ1. (b) Product formation velocity, vP, for the non-channeled reaction and for two channeled reactions with different γch/γ1, shown by symbols in (a). In all plots, the intrinsic association and dissociation rate constants are and , where i = 1,2. The enzyme’s turnover numbers are . These rate constants correspond to the first two reactions in the MAPK pathway [42]. The rate of channeling is kch = 1 s−1 (see Eq (2)).
Fig 1b shows the production velocity, vP, as a function of time for the channeled and non-channeled systems. In accord with the numerous experimental studies [20–22, 43], in all cases we looked at, vP was found higher for the channeled system at short times. The reason is that initially the concentration of intermediates is low, and hence the non-channeled system needs more time to advance to its steady state. In the long run, however, the overall production rate of a system with channeling can be lower for sufficiently large γch.
Batch reactor
In a batch reactor, substrate molecules and enzymes are mixed and the reaction is observed without any further addition of substrate molecules. In other words, the substrate supply velocity is zero. To compare the systems with and without channeling in this case, we look at the time needed by each system to reach the product concentration [P] = α[S]0, where [S]0 is the initial substrate concentration and α a comparison parameter.
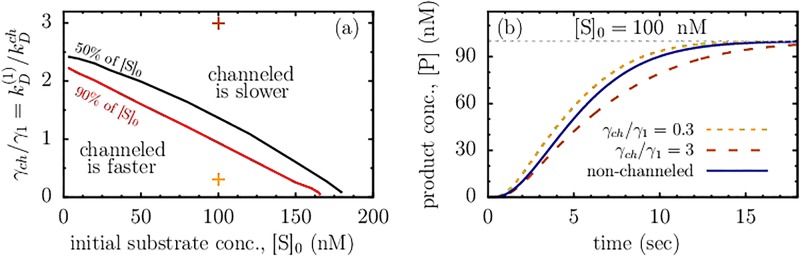
The results are summarized in Fig 2a and typical time-dependent concentration profiles are shown in Fig 2b. The diagram in Fig 2a is drawn in the plane of the initial substrate concentration ([S]0) and the degree of diffusion control of the channeled reaction, and has a topology similar to Fig 1a. It shows that the region in which the channeled reaction transforms substrates faster is narrow and essentially bound to low values of [S]0. This region shrinks as we increase the comparison parameter α. This emphasizes that we compare the systems that are not in steady states, thus the diagram also reflects how these systems would approach the steady states, were the substrate supplied to them.
Fig 2. Effect of channeling in batch reactors.
(a) Channeling diagram showing the regions in which the channeled reaction transforms the shown amount of the substrate (α[S]0) faster or slower than the non-channeled tandem reaction. The demarcation lines of this diagram were calculated by comparing the times needed by the channeled and non-channeled systems to achieve the product concentration [P] = α[S]0; these times are equal on the demarcation lines. The values of α expressed as percentage of [S]0 are denoted on the figure. γ1 and γch are the degrees of diffusion control of the first reaction in the cascade and of the channeled reaction, respectively (see Eq (10) and Fig 1). (b) Product concentration as a function of time for the non-channeled reaction and for the channeled reactions with different γch/γ1, shown by symbols in (a). The thin vertical line denotes [P](t = ∞) = [S]0. We have used γ1 = γ2 = 1 for the first and second reactions in the cascade to produce all plots. The remaining parameters are the same as in Fig 1.
Diffusion-limited rates
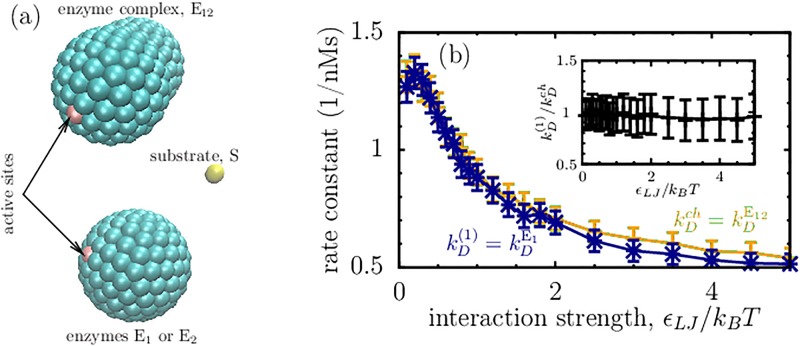
Figs 1 and 2 show that channeling can accelerate or decelerate cascade reactions depending on how the degree of diffusion control (or the reaction rate due to diffusion) changes when the enzymes form a complex. To gain some insight into this dependence, we compare the diffusion-limited association rates for a single enzyme and for an enzyme-enzyme complex, i.e. and in Eq (9). To model this situation, we consider a complex obtained by merging two identical spherical enzymes, as shown in Fig 3a. Each enzyme consists of Lennard-Jones (LJ) particles placed on the enzyme surface, while the substrate is modelled as a single LJ sphere. In the enzyme-enzyme complex, the second enzyme is put behind the active center of the first enzyme, so that it presents only minimal geometrical hindrance for a substrate to access the active site. Our purpose is to see if (and how) the formation of an enzyme-enzyme complex, i.e. the complex as such, alters the association rate, and hence the reaction velocity. To calculate the association rates we have used the Northrup-Allison-McCammon algorithm [44, 45] (see Methods).
Fig 3. Single enzymes versus enzyme-enzyme complexes.
(a) Enzymes E1 and E2 consist of Lennard-Jones (LJ) spheres of radius ≈0.37 nm placed on the surface of a sphere of radius 1.5 nm, where one of the LJ-spheres is treated as an active site. An enzyme complex (E12 = E1E2) is constructed by merging E1 and E2 together such that the active site of E1 is located on the axis connecting the centers of E1 and E2. The center-to-center distance between E1 and E2 is 1.4 nm. The substrate for E1 and E12 is a LJ-sphere of radius 0.4 nm. (b) Rates of the diffusion-limited enzyme-catalyzed reactions for the first enzyme in a tandem reaction (denoted by ) and for the enzyme-enzyme complex (denoted by ). The rates are shown as functions of the strength of the LJ potential between the substrate molecule and the LJ particles of the enzymes (ϵLJ). These rates were calculated by using Brownian dynamics simulations (see Methods).
The results are shown in Fig 3b. Both reaction rates and decrease as the strength of the interaction between the substrate and the LJ particles of the enzymes, ϵLJ, increases. This is understandable as the enzymes become ‘less soft’ for the substrate, preventing it from coming close to their active sites, while the van der Waals attraction is too weak to significantly influence the association rate in this case. Since in this case the rate is mainly determined by the substrate diffusion, both rates are comparable (see the inset in Fig 3b), except of high values of ϵLJ at which the LJ attraction starts to play a more significant role.
This result suggests γch ≈ γ1 and hence deceleration of the reaction velocity by channeling in steady-state, according to Fig 1. We note, however, that we have considered uncharged enzymes and that in some cases, e.g. when the surface of the second enzyme is charged mainly oppositely to the substrate, an enhancement of over can be expected. Whether this is sufficient to accelerate the reaction velocity depends on system (i.e. on enzyme sizes and charge distributions, substrate concentration etc.), and it will be interesting to study such cases explicitly in future work.
Discussion
We have considered a simple model for substrate channeling, Eq (2). This or similar models have been previously used in the literature in different contexts [10, 15, 29, 30, 46]. The model predicts that in steady state channeling can slow down tandem reactions in a wide range of substrate concentrations, [S]. Such a slow-down is most clearly expressed at high concentrations, at which independently of [S] and of the microscopic rate constants, the channeled reaction is slower than the original non-channeled tandem reaction (Eq (7) and Fig 1). Although this result may seem surprising at first glance, it has a simple explanation. Indeed, in our model we assumed that there is only one metabolite bound to an enzyme-enzyme complex (E12 = E1E2) at a time. This means that E12 processes metabolites in series: It first takes a substrate (S) and transforms it into an intermediate (I); next, this intermediate is transfered to the second active site of E12, where it is finally converted into the product (P). Only then the enzyme-enzyme complex is free to associate with another substrate molecule. In a non-channeled cascade, in contrast, the and reactions can proceed in parallel, provided the concentration of intermediates is sufficiently high. This can in particular be achieved in steady state at high substrate concentrations, as expressed by Eq (7).
Clearly, our model can be criticized for not allowing more than one metabolite in an enzyme-enzyme complex at the same time. It can, however, be easily extended to take this into account, for example, by introducing, in addition to reaction Eq (2), a complementary reaction where ach and dch are association/dissociation rate constants and k2 the turnover number, which we have assumed here to be the same as k1, for simplicity. This additional reaction describes a process of attaching a substrate to the complex that already contains an intermediate (for instance in the tunnel between its active sites). Thus, the modified model allows two metabolites to be simultaneously present in the complex. In this case we indeed observe an increase in the velocity of the channeled reaction, viz. at high substrate concentrations, but the overall reaction rate is still lower than in the non-channeled system (see Eq (7a)).
One might be tempted to continue this process and allow more and more metabolites in an enzyme-enzyme complex, to see when channeling becomes beneficial for the reaction velocity. It is easy to notice, however, that if the first reaction in a cascade is rate limiting, then, independently of the number of intermediates in the complex, the channeled reaction cannot exceed the product formation velocity set by the first enzyme [15], i.e. k1[E1], which is just the production rate of the non-channeled system in steady state at high substrate concentrations (see Eq (7a)).
In the opposite case, when the second reaction in a cascade is rate limiting (i.e. k2 < k1), it is theoretically possible that the channeled reaction is faster than its non-channeled counterpart (in steady-state). This can happen if channeling increases the local concentration of intermediates at the second enzyme, in comparison to the non-channeled case. Whether this is achievable in practice depends on particular system, substrate concentration, etc. However, in this case it is easy to improve the overall rate of the non-channeled system by increasing the concentration of E2, to compensate its weak activity. In particular, by taking [E2] = k1[E1]/k2 > [E1] we can increase the maximum product formation velocity to , while the maximum possible rate of the channeled system is for [E12] = [E1]. Obviously, we can also increase the concentration of enzyme-enzyme complexes to [E12] = [E2], to make a fairer comparison, but this will only lead to the rate as high as . Note that in this case the capability of the first enzyme in E12 is not fully utilized, unlike it is in the non-channeled system. This illustrates, particularly, that a non-channeled system is more flexible and provides more options for maximizing its product formation velocity.
So far we have discussed only uni-substrate reactions, while many enzymes require more than one substrate or co-factors for the reaction to occur (for instance, many dehydrohynases, oxidases, transferases, etc) [47, 48]. However, it is straightforward to extend our model, Eqs (1) and (2), to take such reactions into account. It can then be shown that, similarly to the case of uni-substrate reactions, channeling can accelerate or decelerate the reaction velocity at low substrate concentrations, depending on the relation between the various rate constants. In saturation, however, when the concentrations of all substrates are high, we obtain the limiting reaction velocities that are similar or identical to Eqs (7a) and (7b), which means that channeling cannot accelerate the reaction velocity in this case (see Supporting Information for bi-substrate reactions).
Thus, our main claim is that channeling may have small or even negative effect on the steady state velocities of cascade reactions. However, enzyme-enzyme complexes do exist in vivo [23–27], and it is thus appropriate to ask: What are the benefits of channeling that are possibly exploited by living cells? We shall discuss here two most commonly mentioned assets, viz. (i) decreasing the intermediate pool size, which is important e.g. to protect cells from toxic intermediates, and (ii) preventing intermediates from side reactions or degradation.
Decrease of the metabolite pool size
One frequently mentioned advantage of channeling is the decrease of metabolite pool size [32]. This sounds reasonable. Indeed, in the channeled system (with direct channeling) the intermediates are never released into the bulk solution, and thus, one may think, increasing the degree of channeling, i.e. the concentration of enzyme-enzyme complexes, [E12], should decrease the amount of intermediates in the system. However, Cornish-Bowden and Cárdenas [29] have shown that (in some cases) the concentration of intermediates, [I], is essentially indifferent to the amount of [E12]. Mendes et al. [30] argued that in more general cases [I] does decrease with increasing [E12], and Korzeniewski and Quant [49] demonstrated a simple mechanism to decrease the metabolite pool size by channeling.
To look into this in some details, we consider a system that contains both single enzymes (E1 and E2) and enzyme-enzyme complexes (E12) in varying proportions. It is a simple exercise to calculate the steady-state concentration of intermediates in this system. The result is
| (11) |
where is the Michaelis-Menten constant of enzyme Ei and [S]threshold is given by Eq (6). The total concentration of single (not complexed with each other) enzymes is [Ei]0 = [Ei] − [E12], i = 1,2.
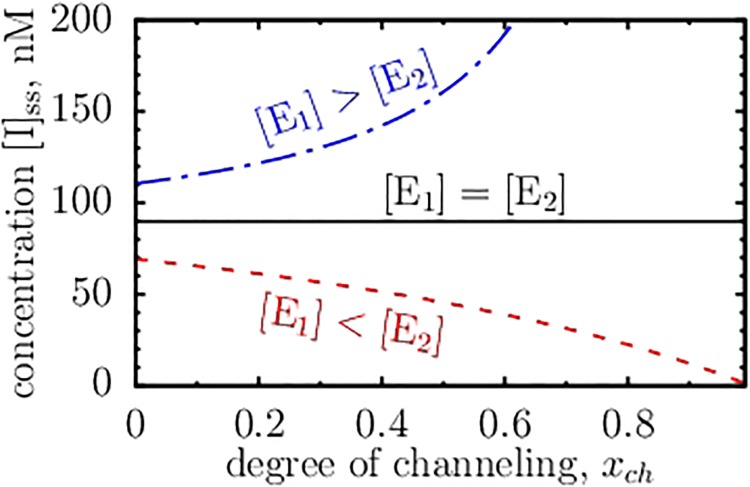
It is convenient to define the degree of channeling xch = [E12]/min([E1], [E2]). Now, it directly follows from Eq (11) that for [E1] = [E2] the steady-state concentration of intermediates is independent of xch. This corresponds to the Cornish-Bowden–Cárdenas case and is shown by the solid line in Fig 4. The dash line in this figure shows the case when channeling reduces the amount of intermediates in the system. But, inverse is also possible: For [E1] > [E2], [I] increases as the degree of channeling increases (dash-dot line in Fig 4). Such a scenario has already been pointed out by Cornish-Bowden [50].
Fig 4. Effect of channeling on the metabolite pool size.
The concentration of intermediates in the steady state is shown for systems with varying degree of channeling. The degree of channeling is xch = [E12]/min([E1], [E2]), where [E12] is the concentration of enzyme-enzyme complexes in the system and [Ei], i = 1,2, is the total enzyme concentration (i.e. free, not complexed Ei plus E12). The concentration [E1] = 50 nM and the rate constant k1 = 1.5 s−1 are the same in all three systems. The concentration of [E2] and the rate constant k2 are adjusted to satisfy k1[E1] = k2[E2], in which case the enzymes capabilities are fully utilized. We chose k2 = 1.5 s−1 = k1 and [E2] = 50 nM = [E1] (solid line); k2 = 1 s−1 < k1 and [E2] = 75 nM >[E1] (red dash line); and k2 = 2 s−1 > k1 and [E2] = 37.5 nM < [E1] (dot-dash blue line). The degree of channeling γ1 = γ2 = γch = 1 (see Eq (10)). The substrate concentration ([S] = 90 nM) and the remaining rate constants are the same as in Fig 1.
This result can be easily understood. Assume k1 = k2/2 and imagine the extreme case of just two E1 enzymes and one E2 enzyme, so that k1[E1] = k2[E2], as in Fig 4 (this relation gives the enzyme concentrations that optimize an enzymatic cascade in saturation). When E1 and E2 form a complex, some metabolites are channeled by E12, but the remaining E1 produces the intermediates that cannot be converted into the product; thus, [I] increases to infinity as we approach the steady state. In a less extreme case, we observe a finite increase of [I] as E1 and E2 dimerize into a complex. This can also be easily seen from Eq (11), which gives d[I]ss/dxch ∼ [E2] − [E1]. Interestingly, the sign of d[I]ss/dxch does not depend on the reaction constants, and thus channeling always increases the metabolite pool size in steady state if the first enzyme is abundant with respect to the second. Since we have not made any specific assumption on the enzyme environment, this conclusion should hold in vitro as well as in vivo.
Protecting intermediates from degradation or competing reactions
In living cells or in catalytic reactors, it may happen that intermediates degrade, decompose or are consumed by competing side reactions. To model this situation, it is usual to supplement the evolution equation for the intermediates by a term kdeg[I], where kdeg is the effective degradation rate constant. Then the product formation velocity in the steady state is , where corresponds to kdeg = 0 and is given by Eq (4), and [I]ss is the steady-state concentration of intermediates (note that [I]ss is not given by Eq (11); it depends on kdeg and must be found from a quadratic equation, which we solved numerically, see Methods).
Fig 5a compares the product formation velocity in the non-channeled and channeled systems (we assume that the latter is unaffected by kdeg). We have chosen the rate constants such that the channeled system is slower when kdeg = 0 (see Fig 1). As one may expect, the product formation velocity decreases as kdeg increases, however, this decrease becomes significant only when kdeg ≳ 1 s−1 (for the parameters of the plot). The velocity of the non-channeled system can be improved by increasing the concentration of enzymes, but this does not rescue the system from low production velocities at high kdeg.
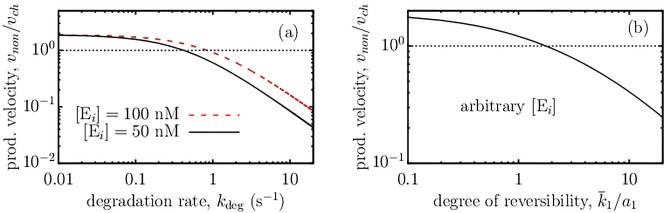
Fig 5. Effect of channeling on reaction cascades with competing reactions.
(a) Product formation velocity of the nonchanneled system, vnon, decreases as the degradation or consumption rate of intermediates, kdeg, increases. (b) Reaction velocity of the nonchanneled system falls off for increasing ‘degree of reversibility’ of the first reaction in the cascade, . In this case the reaction is in lieu of Eq (1a). In both plots vnon is compared to the velocity of the channeled system, vch. The concentrations of enzymes and enzyme-enzyme complexes are equal in both systems on both panels, i.e. [Ei] = [E1] = [E2] = [E12]; in panel (b) the ratio vnon/vch is independent of [Ei]. Substrate concentration [S] = 90 nM, the degree of diffusion control is γ1 = γch = 1 (see Eq (10)), and the rate constants are the same as in Fig 1. Thin dotted line denotes vch = vnon.
A particularly interesting example of competing reactions is a reversible reaction I ⇌ S catalyzed by the same enzyme (E1); such enzymes are numerous and include many important isomerases, aldolases, dehydrogenases, transferases and others. The peculiarity of this system is that the reverse reaction, although competing, transforms the intermediates back into the substrates, which can then be reused; however, this process effectively reduces the amount of enzyme E1 available for the direct reaction. To study this case, we consider, instead of reaction Eq (1a), a one-complex reversible reaction , and leave the channeled reaction unaltered (in a more general case of two-complex reversible reactions the channeled reaction will also be affected by reversibility). Fig 5b shows that the non-channeled reversible reaction provides higher rates for low degrees of reversibility, , while channeling becomes beneficial as increases. Unlike it is in the case of degradation of intermediates (Fig 5a), the ratio of the velocities of the channeled and non-channeled reactions is independent of the enzyme concentration, provided of course [E1] = [E2] = [E12].
Conclusions
Using a simple reaction-kinetics model, supported by Brownian dynamics simulations, we have shown that metabolite channeling does not necessarily accelerate cascade reactions and can even decelerate them (Fig 1). In addition, we demonstrated that the metabolite pool size can increase as the degree of channeling increases (Fig 4). We corroborated however that channeling provides a convenient way to increase the velocity of a cascade reaction if intermediates degrade or participate in competing reactions (Fig 5). This suggests therefore that the main advantage of channeling is unlikely the reaction acceleration or decrease of the metabolite pool size, but it rather lies in protecting intermediates from degradation or competing reactions.
Our study is by no means conclusive and complete, however. Indeed, we considered a simple homogeneous mean-field model and ignored any chemical details of enzymes and metabolites. This may be important in some situations and deserves separate studies. For instance, we performed Brownian dynamics simulations of the diffusion-controlled rates for a model system (Fig 3), and it is desirable to perform a similar study for real enzymes and enzyme-enzyme complexes. Additionally, it will be interesting to investigate the effect of diffusion slow-down [51–53] and anomalous diffusion [54–58] on channeling, which is highly important for living systems [59]. It will be particularly interesting to see how channeling influences the response of a system to external stimuli [60–62], where channeling can potentially be advantageous.
Experimental studies have mainly focused on artificial enzyme complexes and channeling by proximity [20, 21, 32, 63], while experiments on direct channeling are currently scarce. Such experiments would ideally provide a careful examination of microscopic association/dissociation rates and turnover numbers of complexed and ‘free’ enzymes, and should be performed under steady-state, rather than typically used laboratory initial conditions. While the latter is relatively easy to achieve, e.g. by constantly supplying substrates to the system or using the steady-state concentration of intermediates from the onset of a measurement, the former is challenging and demands significant advances in the experimental techniques and theory.
Thus, the question posed in the title of this article requires further and more complex theoretical and, in particular, experimental investigations, and we hope that our work will stimulate more active research and discussions in this direction.
Methods
Homogeneous well-mixed systems
We consider a mixed system containing both enzymes E1 and E2 and the enzyme-enzyme complexes E12 = E1E2. To obtain a fully channeled or a pure non-channeled system, we set the concentrations [E1] = [E2] = 0 or [E12] = 0, respectively, at all times.
Applying the mass action law to reactions Eqs (1) and (2), we obtain a system of ordinary differential equations, which is straightforward but lengthy, and is not shown here in full to save space (see Supporting Information for the whole set of equations). The first equation of this system is
| (12) |
where vS is the substrate supply velocity. In a batch system vS = 0, while in a fed-bach system it is non-zero. In a system where the substrate concentration is kept constant, d[S]/dt = 0, and vS = vS(t) ≠ 0 is in general not constant, but attains a constant value in the steady state as t → ∞.
In addition to the differential equations discussed above, there are also conservation laws for the enzyme and metabolite concentrations. For instance, [E1]tot = [E1](t) + [SE1](t), where [E1]tot is the total concentration of enzyme E1 (not dimerized with E2); it is equal to the free (i.e. not complexed) concentration of E1 at time t = 0, i.e. [E1]tot = [E1](t = 0), and similarly for other species. (The total enzyme concentrations are used on all plots in the main text, but we remove ‘tot’ to avoid clumsy notations.) This reduces the number of independent variables from 11 to 7 (in the mixed system). Nevertheless, it is difficult to solve this system of equations analytically and we used OCTAVE with Hindmarsh’s solver LSODE [64] to obtain the time-dependent profiles of various species in the system numerically.
In steady state, all concentrations approach constant values and the differential equations reduce to a system of algebraic equations, which we have solved analytically. (This reasoning applies to fed-batch and constant substrate concentration conditions, in which, however, the product concentration increases with time. Additionally, it is possible that [I] → ∞ or [S] → ∞ as t → ∞. This occurs when the substrate supply velocity is too high for the first enzyme to deal with the available substrates, and when the first enzyme is more efficient than the second enzyme so that the second enzyme is unable to deal with the increasing amount of intermediates. The condition when this happens can be readily obtained and is given by Eq (6).) The resulting equations are presented and discussed in the main text.
The evolution equation for the intermediates reads
| (13) |
where kdeg is the rate due to degradation or competing side reactions (i.e. in addition to reactions Eqs (1) and (2) we have ). In steady state, the product formation velocity of the non-channeled system is , where denotes the production velocity when kdeg = 0 and is given by Eq (4). [I]ss is the steady-state concentration of intermediates and satisfies the following equation
| (14) |
In the case when the first reaction in the cascade is one-complex reversible, the product formation velocity in the steady state is
| (15) |
where the steady-state concentration of intermediates satisfies
| (16) |
where and is the rate of the reverse reaction . We solved Eqs (14) and (16) numerically using the GNU Scientific Library [65].
Diffusion-controlled rates
We have used the ready-to-use software package browndye written by Gary Huber [66] to calculate the association rates between a substrate molecule and an enzyme or a complex of two enzymes.
Enzymes were created by placing small Lennard-Jones spheres (of radius ≈0.37 nm) on the nodes of a triangularized sphere of radius 1.5 nm. One of the small spheres was declared an active site. The triangularization was done using the GTS library [67]. An enzyme-enzyme complex was created by merging two identical enzymes such that their active sites were opposite to each other on the line connecting the centers of the two enzymes (the active site of the second enzyme in the complex did not participate in simulations, however). The distance between the enzyme centers was 1.4 nm. The substrate was a Lennard-Jones sphere of radius 0.4 nm. The enzymes and substrates were not charged.
The Northrup-Allison-McCammon algorithm was used to calculate the diffusion-limited reaction rates [44, 45]. In this algorithm the substrate and the enzyme are initially separated by some distance called b-radius and the reaction rate is calculated by estimating the probability of a substrate molecule to approach the active site of the enzyme to within a user specified reaction distance (taken 0.82 nm in our simulations). The b-radius was 5 nm and 105 independent runs (trajectories) were analyzed. In a few cases, up to 107 runs were used, leading to no significant differences.
Supporting information
This appendix includes the full set of ordinary differential equations for the evolution of concentrations of various species in the well-mixed homogeneous system of enzyme-catalyzed uni-substrate tandem reaction and its channeled counterpart. In addition it contains the steady-state equations for enzyme-catalyzed bi-substrate tandem reactions and their channeled versions; these include sequential ordered and random reactions as well as ping-pong (double-displacement) reactions.
(PDF)
Acknowledgments
This work was in part supported by BMBF Grant No. 031A129. We are grateful to Wolfgang Wiechert, Olav Zimmermann, Marco Bocola, Andrey Cherstvy, Stephan Noack and especially Antje Spieß for fruitful and stimulating discussions.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
This work was supported by Bundesministerium für Bildung und Forschung, Grant Number 031A129.
References
- 1. Michaelis L, Menten ML. Die Kinetik der Invertinwirkung. Biochem Z. 1913;49:333–369. [Google Scholar]
- 2. Pulkkinen O, Metzler R. Variance-corrected Michaelis-Menten equation predicts transient rates of single-enzyme reactions and response times in bacterial gene-regulation. Scientific Reports. 2015;5:17820 10.1038/srep17820 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Hill AV. The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J Physiol (Lond). 1910;. [Google Scholar]
- 4. Monod J, Wyman J, Changeux JP. On the nature of allosteric transitions: A plausible model. J Mol Biol. 1965;12:88–118. 10.1016/S0022-2836(65)80285-6 [DOI] [PubMed] [Google Scholar]
- 5. Koshland DEJ, Némethy G, Filmer D. Comparison of experimental binding data and theoretical models in proteins containing subunits. Biochemistry. 1966;5:365 10.1021/bi00865a047 [DOI] [PubMed] [Google Scholar]
- 6. Richard J, Cornish-Bowden A. Co-operative and allosteric enzymes: 20 years on. Euro J Biochem. 1987;166:255–272. 10.1111/j.1432-1033.1987.tb13510.x [DOI] [PubMed] [Google Scholar]
- 7. Segel IH. Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady-State Enzyme Systems. John Wiley & Sons Inc; 1993. [Google Scholar]
- 8. Wheeldon I, Minteer SD, Banta S, Barton SC, Atanassov P, Sigman M. Substrate channelling as an approach to cascade reactions. Nature Chemistry. 2016;8:299–309. 10.1038/nchem.2459 [DOI] [PubMed] [Google Scholar]
- 9. Srivastava DK, Bernhard SA. Metabolite transfer via enzyme-enzyme complexes. Science. 1986;234:1081 10.1126/science.3775377 [DOI] [PubMed] [Google Scholar]
- 10. Spivey HO, Ovádi J. Substrate Channeling. Methods. 1999;19:306–321. 10.1006/meth.1999.0858 [DOI] [PubMed] [Google Scholar]
- 11. Miles EW, Rhee S, Davies DR. The Molecular Basis of Substrate Channeling. J Biol Chem. 1999;274:12193–12196. 10.1074/jbc.274.18.12193 [DOI] [PubMed] [Google Scholar]
- 12. Huang X, Holden HM, Raushel FM. Channeling of Substrates and Intermediates in Enzyme-Catalyzed Reactions. Annu Rev Biochem. 2001;70:149–180. 10.1146/annurev.biochem.70.1.149 [DOI] [PubMed] [Google Scholar]
- 13. Smith NE, Vrielink A, Attwood PV, Corry B. Biological Channeling of a Reactive Intermediate in the Bifunctional Enzyme DmpFG. Biophys J. 2012;102:868–877. 10.1016/j.bpj.2012.01.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Smith NE, Vrielink A, Attwood PV, Corry B. Binding and Channeling of Alternative Substrates in the Enzyme DmpFG: a Molecular Dynamics Study. Biophys J. 2014;106:1681 10.1016/j.bpj.2014.03.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Elcock AH, Huber GA, McCammon JA. Electrostatic Channeling of Substrates between Enzyme Active Sites: Comparison of Simulation and Experiment. Biochem. 1997;36:16049–16058. 10.1021/bi971709u [DOI] [PubMed] [Google Scholar]
- 16. Metzger VT, Eun C, Kekenes-Huskey PM, Huber G, McCammon JA. Electrostatic Channeling in P. falciparum DHFR-TS: Brownian Dynamics and Smoluchowski Modeling. Biophys J. 2014;107:2394–2402. 10.1016/j.bpj.2014.09.039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. DeLisa MP, Conrado RJ. Synthetic metabolic pipelines. Nat Biotech. 2009;27:728–729. 10.1038/nbt0809-728 [DOI] [PubMed] [Google Scholar]
- 18. Bauler P, Huber G, Leyh T, McCammon JA. Channeling by Proximity: The Catalytic Advantages of Active Site Colocalization Using Brownian Dynamics. J Phys Chem Lett. 2010;1:1332–1335. 10.1021/jz1002007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Eun C, Kekenes-Huskey PM, Metzger VT, McCammon JA. A model study of sequential enzyme reactions and electrostatic channeling. J Chem Phys. 2014;140:105101 10.1063/1.4867286 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. You C, Myung S, Zhang YHP. Facilitated Substrate Channeling in a Self-Assembled Trifunctional Enzyme Complex. Angew Chem Int Ed. 2012;51:8787–8790. 10.1002/anie.201202441 [DOI] [PubMed] [Google Scholar]
- 21. You C, Zhang YHP. Annexation of a High-Activity Enzyme in a Synthetic Three-Enzyme Complex Greatly Decreases the Degree of Substrate Channeling. ACS Synth Biol. 2014;3:380–386. 10.1021/sb4000993 [DOI] [PubMed] [Google Scholar]
- 22. Castellana M, Wilson MZ, Xu Y, Joshi P, Cristea IM, Rabinowitz JD, et al. Enzyme clustering accelerates processing of intermediates through metabolic channeling. Nature Biotechnology. 2014;32:1011–1018. 10.1038/nbt.3018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Shearer G, Lee JC, Koo Ja, Kohl DH. Quantitative estimation of channeling from early glycolytic intermediates to CO2 in intact Escherichia coli. FEBS Journal. 2005;272:3260–3269. 10.1111/j.1742-4658.2005.04712.x [DOI] [PubMed] [Google Scholar]
- 24. Srivastava D, Schuermann JP, White TA, Krishnan N, Sanyal N, Hura GL, et al. Crystal structure of the bifunctional proline utilization A flavoenzyme from Bradyrhizobium japonicum. Proc Natl Acad Sci USA. 2010;107:2878–2883. 10.1073/pnas.0906101107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Singh H, Arentson BW, Becker DF, Tanner JJ. Structures of the PutA peripheral membrane flavoenzyme reveal a dynamic substrate-channeling tunnel and the quinone-binding site. Proc Natl Acad Sci USA. 2014;111:3389–3394. 10.1073/pnas.1321621111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Pröschel M, Detsch R, Boccaccini AR, Sonnewald U. Engineering of metabolic pathways by artificial enzyme channels. Front Bioeng Biotechnol. 2015;3:00168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Sanyal N, Arentson BW, Luo M, Tanner JJ, Becker DF. First Evidence for Substrate Channeling between Proline Catabolic Enzymes. J Biol Chem. 2015;290:2225–2234. 10.1074/jbc.M114.625483 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Wu XM, Gutfreund H, and Chock P B L S. Substrate channeling in glycolysis: a phantom phenomenon. Proc Natl Acad Sci USA. 1991;88:497–501. 10.1073/pnas.88.2.497 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Cornish-Bowden A, Cárdenas ML. Channelling can affect concentrations of metabolic intermediates at constant net flux: artefact or reality? Eur J Biochem. 1993;213:87–92. 10.1111/j.1432-1033.1993.tb17737.x [DOI] [PubMed] [Google Scholar]
- 30. Mendes P, Kell DB, Westerhoff HV. Why and when channelling can decrease pool size at constant net flux in a simple dynamic channel. Biochimica et Biophysica Acta. 1996;1289:175–186. 10.1016/0304-4165(95)00152-2 [DOI] [PubMed] [Google Scholar]
- 31. Cornish-Bowden A, Cárdenas ML, Letelier JC, Soto-Andradec J, Abarzúac FG. Understanding the parts in terms of the whole. Biol Cell. 2004;96:713–717. 10.1016/j.biolcel.2004.06.006 [DOI] [PubMed] [Google Scholar]
- 32. Zhang YHP. Substrate channeling and enzyme complexes for biotechnological applications. Biotechnology Advances. 2011;29:715–725. 10.1016/j.biotechadv.2011.05.020 [DOI] [PubMed] [Google Scholar]
- 33. Buchner A, Tostevin F, Gerland U. Clustering and Optimal Arrangement of Enzymes in Reaction-Diffusion Systems. Phys Rev Lett. 2013;110:208104 10.1103/PhysRevLett.110.208104 [DOI] [PubMed] [Google Scholar]
- 34. Jandt U, You C, Zhang YHP, Zeng AP. Compartmentalization and Metabolic Channeling for Multienzymatic Biosynthesis: Practical Strategies and Modeling Approaches. Adv Biochem Eng Biotechnol. 2013;137:41–65. [DOI] [PubMed] [Google Scholar]
- 35. Sheldon RA, van Pelt S. Enzyme immobilisation in biocatalysis: why, what and how. Chem Soc Rev. 2013;42:6223–6235. 10.1039/C3CS60075K [DOI] [PubMed] [Google Scholar]
- 36. Zhao Z, Fu J, Dhakal S, Johnson-Buck A, Liu M, Zhang T, et al. Nanocaged enzymes with enhanced catalytic activity and increased stability against protease digestion. Nature Comm. 2016;7:10619 10.1038/ncomms10619 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Collins FC, Kimball GE. Diffusion-controlled reaction rates. J Colloid Sci. 1949;4:425–437. 10.1016/0095-8522(49)90023-9 [DOI] [Google Scholar]
- 38. Berg OG. On diffusion-controlled dissociation. Chemical Physics. 1978;31:47–57. 10.1016/0301-0104(78)87025-6 [DOI] [Google Scholar]
- 39. Kim JS, Yethiraj A. Effect of Macromolecular Crowding on Reaction Rates: A Computational and Theoretical Study. Biophys J. 2009;96:1333–1340. 10.1016/j.bpj.2008.11.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Smoluchowski M. Z Phys Chem Stoechiom Verwandtschaftsl. 1917;92:129. [Google Scholar]
- 41. Fange D, Berg OG, Sjöberg P, Elf J. Stochastic reaction-diffusion kinetics in the microscopic limit. Proc Nat Acad Sci USA. 2010;107:19820–19825. 10.1073/pnas.1006565107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Takahashi K, Tǎnase-Nicola S, ten Wolde PR. Spatio-temporal correlations can drastically change the response of a MAPK pathway. Proc Nat Acad Sci USA. 2010;107:2473–2478. 10.1073/pnas.0906885107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Buchner A, Tostevin F, Hinzpeter F, Gerland U. Optimization of collective enzyme activity via spatial localization. J Chem Phys. 2013;139:135101 10.1063/1.4823504 [DOI] [PubMed] [Google Scholar]
- 44. Northrup SH, Allison SA, McCammon JA. Brownian dynamics simulation of diffusion-influenced bimolecular reactions. J Chem Phys. 1984;80:1517 10.1063/1.446900 [DOI] [Google Scholar]
- 45. Luty BA, McCammon JA, Zhou HX. Diffusive reaction rates from Brownian dynamics simulations: Replacing the outer cutoff surface by an analytical treatment. J Chem Phys. 1992;97:5682 10.1063/1.463777 [DOI] [Google Scholar]
- 46. Mendes P, Kell DB, Westerhoff HV. Channelling can decrease pool size. Euro J Biochem. 1992;204:257–266. 10.1111/j.1432-1033.1992.tb16632.x [DOI] [PubMed] [Google Scholar]
- 47. Bisswanger H. Enzyme Kinetics: Principles and Methods. Wiley-VCH Verlag GmbH & Co. KGaA; 2008. [Google Scholar]
- 48. Cornish-Bowden A. Fundamentals of Enzyme Kinetics. Wiley-VCH Verlag GmbH & Co. KGaA; 2012. [Google Scholar]
- 49. Korzeniewski B, Quant PA. A simple mechanism decreasing free metabolite pool size in static spatial channelling. Mol Cell Biochem. 1997;169:135–142. 10.1023/A:1006882029611 [DOI] [PubMed] [Google Scholar]
- 50. Cornish-Bowden A. Failure of channelling to maintain low concentrations of metabolic intermediates. Eur J Biochem. 1991;195:103–108. 10.1111/j.1432-1033.1991.tb15681.x [DOI] [PubMed] [Google Scholar]
- 51. Rohwer JM, Postma PW, Kholodenko BN, Westerhoff HV. Implications of macromolecular crowding for signal transduction and metabolite channeling. Proc Natl Acad Sci USA. 1998;95:10547–10552. 10.1073/pnas.95.18.10547 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. McGuffee SR, Elcock AH. Diffusion, Crowding & Protein Stability in a Dynamic Molecular Model of the Bacterial Cytoplasm. PLoS Comput Biol. 2010;6:e1000694 10.1371/journal.pcbi.1000694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Kondrat S, Zimmermann O, Wiechert W, Lieres Ev. The effect of composition on diffusion of macromolecules in crowded environment. Phys Biol. 2015;12:046003 10.1088/1478-3975/12/4/046003 [DOI] [PubMed] [Google Scholar]
- 54. Weiss M, Elsner M, Kartberg F, Nilsson T. Anomalous Subdiffusion Is a Measure for Cytoplasmic Crowding in Living Cells. Biophys J. 2004;87:3518–3524. 10.1529/biophysj.104.044263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Banks DS, Fradin C. Anomalous Diffusion of Proteins Due to Molecular Crowding. Biophys J. 2005;89:2960–2971. 10.1529/biophysj.104.051078 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Metzler R, Jeon JH, Cherstvy AG, Barkai E. Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys Chem Chem Phys. 2014;16:24128–24164. 10.1039/C4CP03465A [DOI] [PubMed] [Google Scholar]
- 57. Cherstvy AG, Chechkin AV, Metzler R. Ageing and confinement in non-ergodic heterogeneous diffusion processes. J Phys A: Math Theor. 2014;47:485002 10.1088/1751-8113/47/48/485002 [DOI] [Google Scholar]
- 58. Cherstvy AG, Metzler R. Ergodicity breaking, ageing, and confinement in generalized diffusion processes with position and time dependent diffusivity. J Stat Mech. 15; p. P05010. [Google Scholar]
- 59. Minton AP. Macromolecular crowding. Current Biology. 2006;16(8):R269—R271. 10.1016/j.cub.2006.03.047 [DOI] [PubMed] [Google Scholar]
- 60. Easterby JS. A generalized theory of the transition time for sequential enzyme reactions. Biochem J. 1981;199:155–161. 10.1042/bj1990155 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Easterby JS. 23. In: Cornish-Bowden A, Cárdenas ML, editors. Temporal Analysis of the Transition between Steady States vol. 190 of Control of Metabolic Processes; 1990. p. 281–290. [Google Scholar]
- 62. Kondrat S, Zimmermann O, Wiechert W, Lieres Ev. Discrete-continuous reaction-diffusion model with mobile point-like sources and sinks. Eur Phys J E. 2016;39:11 10.1140/epje/i2016-16011-0 [DOI] [PubMed] [Google Scholar]
- 63. Jeon EY, Baek AH, Bornscheuer UT, Park JB. Enzyme fusion for whole-cell biotransformation of long-chain sec-alcohols into esters. Appl Microbiol Biotechnol. 2015;99:6267 10.1007/s00253-015-6392-9 [DOI] [PubMed] [Google Scholar]
- 64.OCTAVE;. https://www.gnu.org/software/octave/. Available from: https://www.gnu.org/software/octave/.
- 65.GNU Scientific Library;. https://www.gnu.org/software/gsl/. Available from: https://www.gnu.org/software/gsl/.
- 66. Huber GA, McCammon JA. Browndye: A Software Package for Brownian Dynamics. Comput Phys Commun. 2010;181:1896–1905. 10.1016/j.cpc.2010.07.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.GNU Triangulated Surface Library;. http://gts.sourceforge.net/. Available from: http://gts.sourceforge.net/.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
This appendix includes the full set of ordinary differential equations for the evolution of concentrations of various species in the well-mixed homogeneous system of enzyme-catalyzed uni-substrate tandem reaction and its channeled counterpart. In addition it contains the steady-state equations for enzyme-catalyzed bi-substrate tandem reactions and their channeled versions; these include sequential ordered and random reactions as well as ping-pong (double-displacement) reactions.
(PDF)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.