Anisotropic phantom to calibrate high-q diffusion MRI methods

Abstract

A silicon oil-filled glass capillary array is proposed as an anisotropic diffusion MRI phantom. Together with a computational/theoretical pipeline these provide a gold standard for calibrating and validating high-q diffusion MRI experiments. The phantom was used to test high angular resolution diffusion imaging (HARDI) and double pulsed-field gradient (d-PFG) MRI acquisition schemes. MRI-based predictions of microcapillary diameter using both acquisition schemes were compared with results from optical microscopy. This phantom design can be used for quality control and quality assurance purposes and for testing and validating proposed microstructure imaging experiments and the processing pipelines used to analyze them.

Graphical abstract

Introduction

Diffusion weighted MRI (DWI) are used in a growing list of imaging methods. These include apparent diffusion coefficient (ADC) mapping[1, 2] , diffusion tensor imaging (DTI)[3, 4], q-space MRI[5, 6], diffusion spectrum imaging (DSI)[7, 8], high angular resolution diffusion imaging (HARDI)[9], q-ball MRI[10, 11], combined hindered and restricted model of water diffusion (CHARMED) MRI[12], AxCaliber MRI[13, 14], persistent angular structure (PAS) MRI[15], diffusion kurtosis imaging (DKI)[16, 17], Mean Apparent Propagator (MAP) MRI[18], multiple scattering MRI[19–22], inter alia. Isotropic MRI phantoms, consisting of containers of water[23], ice water[24, 25], sucrose[26], alkanes[27], and various polymers and polymer mixtures[26, 28, 29] have been proposed for testing MR hardware performance and accompanying data processing pipelines. While able to calibrate the three individual gradients in a conventional MRI scanner, isotropic diffusion phantoms are generally not sufficient to validate and calibrate more advanced DWI sequences. To test methods that are designed to extract microstructural information from anisotropic media that generally exhibit both restricted and free diffusion, such as brain white matter, a reliable and robust anisotropic diffusion MRI phantom is needed.

Anisotropic diffusion phantoms have been proposed consisting of packs of polytetrafluoroethylene (PTFE)[30] or Dyneema[31–34] a polyethylene fiber with an ultra-high molecular weight. While these phantoms appear to exhibit restricted diffusion within extra-fibrillar spaces, owing to the irregular geometry of this region, it is generally not possible to predict the displacement distribution of water molecules within these phantoms with a tractable physical or mathematical models, or to characterize their complex pore morphology to establish the “ground truth” for these displacements. One way to provide the “ground truth” is to construct anisotropic diffusion phantoms with simple, regular and measurable pore geometries, such as a water-filled glass capillary array (GCA)[35–37]. In such systems, it is possible to compute diffusion MRI signals based on their assumed pore morphology. In principle, these phantoms can be used to calibrate DWI-based applications designed to extract microstructural information. Using water, which has a high free diffusivity (1.8 μm² ms⁻¹ at the magnet bore ambient temperature) limits the use of such a phantom for either low q-value experiments or experiments in which diffusion-encoding gradient are applied perpendicular to the capillary axis, i.e. along the restricted direction. When acquisition scheme require high q-value applied along the direction parallel to the tubes’ axes, such as for tissue studies, the MR signal is rapidly crushed and the signal quickly resides in the noise floor[38]. To avoid the problem of hitting the noise floor while applying experimental parameters and acquisition scheme used in tissue study, a suitable anisotropic porous phantom should contain a solute whose free diffusion coefficient is an order of magnitude smaller than that of free water at the same temperature.

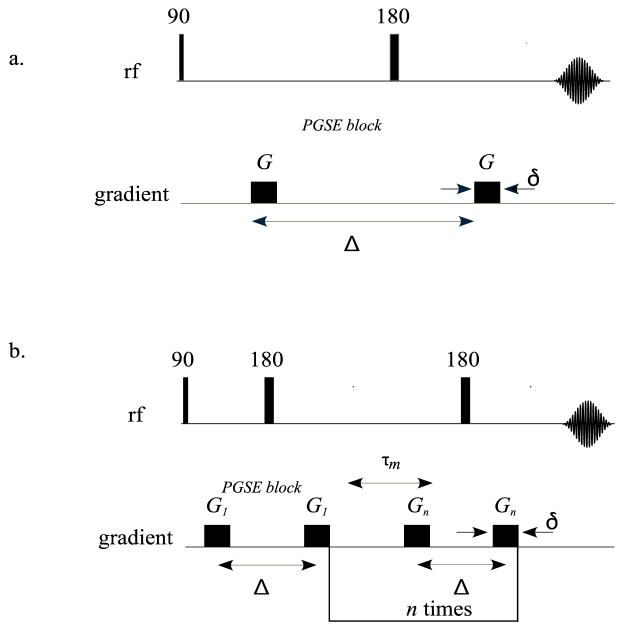
Most diffusion MRI experiments are based on the single pulsed field gradient (s-PFG)[39] MRI sequence (Figure 1a) in which the motion of the spins is encoded by a pair of magnetic field gradient pulses, separated by diffusion time, Δ. In these sequences, the degree of diffusion weighting can be characterized by the wave vector, q = γGδ/(2π), where γ is the gyromagnetic ratio, G is the magnetic field gradient strength, and δ is the duration of the magnetic field gradient pulse. In the Stejskal–Tanner sequence, the resulting signal attenuation due to dephasing is related to the net displacement distribution of the spins[40–42]. This information can be used to probe the morphology of the spaces where the spins are confined. Well-ordered white matter pathways, for example, appear to exhibit several different modes of water diffusion: free, hindered, and restricted. Newly proposed diffusion MRI methods attempt to measure different features or properties of these tissues. For instance, HARDI methods were developed specifically to identify non-Gaussian diffusion processes within an MRI voxel[43], such as the orientation distribution function (ODF), which is widely used in white matter tractography applications[44]

Figure 1.

NMR pulse sequences of a.) Stejskal–Tanner pulse field gradient method and b.) multiple scattering technique.

Another category of DWI data is produced by multiple scattering or multiple PFG (m-PFG) MRI techniques (Figure 1b). In these experiments, more than one pair of single PFG blocks is applied successively, separated by a mixing time, τ_m. The resulting signal represents correlations between net displacements of spins during the different displacement encoding periods, rather than the distribution of the net displacements themselves. As a result of adding another displacement dimension to the experiment, additional microstructural information can be obtained. The most popular multiple scattering MRI method is double-PFG (d-PFG)[19, 20, 45] recently renamed double diffusion encoding (DDE)[46] MRI, in which two s-PFG blocks are applied with the direction of the gradient of the first block set, while the direction of the gradient of the second PFG block is varied. Choosing the right τ_m allows one to tease out different microstructural features[20, 21, 47–51]. Because pore diameter can be easily determined at short τ_m, we use the MRI phantom in this regime to calibrate d-PFG MRI experiments.

Building on our recent work[52], here we describe the construction of an anisotropic diffusion MRI phantom filled with a silicon oil that is stable and safe to handle, store, and transport. Most importantly, its diffusivity is about an order of magnitude lower than free water at the same temperature, which allows one to apply high q-values along the free direction without reaching the noise floor, while still maintaining restricted diffusion conditions in the perpendicular plane. We tested this phantom on the two classes of DWI sequences described above, s-PFG and m-PFG sequences, and used a mathematical modeling framework that can predict how the displacement history of solute molecules in the phantom is related to the measured MR signal. Together, they can be used to calibrate and validate a wide range of anisotropic diffusion MRI methods, providing “ground truth” for these diffusion MRI methods.

Materials and Methods

Phantom preparation

The MRI phantom (Figure 2) described here is based on our previous design, which used a water-filled GCA[37]. In the current study, the GCA was filled with and immersed in decamethylcyclopentasiloxane: (C₁₀H₃₀O₅Si₅, hereafter referred to as “D5”) (Gelest Inc., Morrisville, PA), whose chemical structure is shown in Figure 2a. Silicon oils and polymers such as Polydimethylsiloxane are commonly used for NMR studies and gradient performance tests[28]. D5 is stable at physiological temperatures and widely used in the cosmetics industry. The MR signal (which produces only one peak in the proton NMR spectrum) comes from the chemically identical methyl groups. Owing to its boiling point (101°C at 20 mmHg) the capillaries can be filled by using the method described in our previous paper[37]. D5's viscosity of 3.9 × 10⁻⁶ m²s⁻¹ (3.9 cSt ) results in a low diffusivity (measured 0.163 ± 0.04 μm² ms⁻¹, T = 16.8°C), making it suitable for calibrating scanners used for diffusion NMR and MRI experiments with diffusion gradient pulse strengths comparable to those currently used for high q-values diffusion methods used in tissue, preclinical or clinical studies of white and gray matter.

Figure 2.

a.) D5 molecular structure and an light microscopy image of a 10 μm GCA wafer. b.) Photo of GCA phantom. Stacked GCA filled with D5 between PTFE insert and a plunger. Color-coded arrows mark positions of various diameters

The GCA phantom (Photonis, Lancaster, PA) consists of eight stacked, fused silica wafers with a 13-mm outer diameter (OD). The inner diameter (ID) of the microcapillary arrays in these wafers varies as follows: there are two 2-mm-thick wafers containing capillaries with a nominal ID of 10 μm, two 2-mm-thick wafers containing capillaries with a nominal ID of 25 μm, and four 0.75-mm-thick wafers containing capillaries with a nominal ID of 5 μm. The GCA wafers are arranged (stacked, bottom to top, see Figure 2b) as follows: 25 μm, 10 μm, 5 μm, 5 μm, 25 μm, 10 μm, 5 μm, 5 μm. In addition, the phantom contains a layer of freely diffusing D5. This arrangement permits us to use the same phantom to sample various regions of interest (ROI), enabling us to produce a wide range of mono- and polydisperse pore size distributions. The GCAs are placed in a flat-bottom 15-mm New Era NMR tube (New Era Enterprises Inc., Vineland, NJ) with a polytetrafluoroethylene (PTFE) base and plunger to reduce susceptibility differences that would otherwise produce unwanted magnetic field gradient artifacts within the sample.

Acquisition protocols

All experiments were performed on a 7T Bruker vertical wide-bore magnet with an AVANCE III MRI spectrometer equipped with a Micro2.5 microimaging probe and three GREAT60 gradient amplifiers, which have a nominal peak current of 60 A per channel. This configuration can produce a maximum nominal gradient strength of 24.65 mT m⁻¹ A⁻¹ along each of the three orthogonal directions. The ambient temperature of the magnet bore was16.8 °C.

Assuring the purity and monodispersity of the polymer used to fill the GCAs is crucial to proper phantom preparation. Materials with various molecular weights and relaxation times are not suitable as a gold standard because the resulting diffusion coefficient will depend on the diffusion time. Although the stated purity of the material we used is high (>97%) and the polydispersity is low, diffusion stability measurements were conducted on an isotropic phantom consisting only of D5. MRI stability measurements were conducted by using four diffusion times with the following parameters: TE/TR = 125/7,000 ms; 2 averages; δ = 3 ms; and Δ = 25, 50, 75, and 100 ms. Thirteen b-values ranging from 0 to 3,000 s mm⁻² were used. To fully assess whether D5 is suitable for MRI use, NMR spin-lattice (T₁) and spin–spin (T₂) relaxation times were measured. T₁ was measured by using an inversion recovery sequence with the following parameters: TR = 10,000 ms, and 20 inversion times ranging from 5.38 ms to 7,500 ms. T₂ was measured by using a Carr–Purcell–Meiboom–Gill (CPMG) sequence with the following parameters: TR = 10,000 ms and 64 echoes, resulting in a TE range of 46.88 to 3,000 ms.

DWI experiments were also done to demonstrate the advantage of D5 over water as the diffusive media of the phantom for high q-value methods. The DWI were acquired on the D5 phantom and on a similar water filled phantom[53] by using a sagittal 2D spin echo sequence with the following parameters: TE/TR = 58/3,000 ms, 1 average, FOV=16 x16 mm², coronal slice thickness = 2 mm, and spatial resolution = 125 × 125 × 2,000 μm³. Diffusion parameters were as follows: δ = 3 ms and Δ = 50 ms. Data were acquired for two q-values 26.2 and 74.1 mm⁻¹. Each q-value was applied in the parallel and in the perpendicular direction to the free axis of the capillaries.

In addition to the DWIs, we acquired images of the GCA phantom with various different MRI acquisition schemes to assess image homogeneity as well as potential MRI artifacts arising from eddy currents, susceptibility gradients, echo planar image (EPI) distortion, scanner stability, and so on. These included standard 2D spin echo EPI, and rapid acquisition relaxation enhanced (RARE) sequences. Multi-slice multi-echo (MSME) images were acquired by using the following parameters: TE/TR =1 2/5,000 ms, 1 average, field of view (FOV) = 16 × 16 mm², sagittal slice thickness = 1 mm, and spatial resolution = 125 × 125 × 1,000 μm³. Echo planar imaging (EPI) MRI data were acquired by using the following parameters: TE/TR = 12/5,000 ms, 16 segments, 2 average, FOV = 16 × 16 mm², sagittal slice thickness = 1 mm, and spatial resolution =125 × 125 × 1,000 μm³. RARE MRI data were acquired by using the following parameters: TE/TR = 12/5,000 ms; 1 average; RARE Factor = 8 and 16; effective TE = 48 and 96 ms, respectively; FOV=16 × 16 mm²; sagittal slice thickness = 1 mm; and spatial resolution = 125 × 125 × 1,000 μm³.

GCA pore diameters were independently measured by using d-PFG filtered MRI and multi-shell HARDI acquisition scheme . The s-PFG (multi-shell HARDI) data were acquired by using a sagittal 2D spin echo DWI sequence with the following parameters: TE/TR = 58/5,000 ms, 1 average, FOV=16 x16 mm², coronal slice thickness = 1 mm, and spatial resolution = 125 × 125 × 1,000 μm³. Diffusion parameters were as follows: δ = 3 ms and Δ = 50 ms. The data were acquired in five shells in q-space, with q = 15.7, 26.2, 43.7, and 74.1 mm⁻¹. In each shell, we acquired 91 samples on a semi-circle with a 2^o angular resolution; the diffusion sensitization of the first and last images was parallel to the axis of the cylinders.

Two d-PFG acquisition schemes were used in this study. The traditional 2D scheme where the diffusion encoding gradients were rotating in the perpendicular plane to the capillaries’ free axis, and a 3D scheme, where the diffusion encoding gradients were uniformly distributed on a hemisphere. The later acquisition scheme is used in tissue studies where the orientation of the fibers is unknown or vary within the image[54]. D-PFG filtered MRI data were acquired by applying a d-PFG NMR sequence followed by a 2D spin echo MRI sequence with the following parameters: TE/TR = 8/5,000 ms, 2 average, FOV=16 × 16 mm², coronal slice thickness = 1 mm, and spatial resolution = 125 × 125 × 1,000 μm³ 2D D-PFG NMR parameters were as follows: τ_m = 0; δ = 3 ms; Δ = 30 ms; ϕ, the angle between the two PFG blocks, varied from 0 to 360 with intervals of 30 degrees in the restricted plane, with q =29.7, 39.6, 49.5, 59.4, 69.3, 79.2, and 89 mm⁻¹. 3D D-PFG parameters were as follows: τ_m = 0; δ = 3 ms; Δ = 20 ms; Three shells of 7, 16, and 37 directions with q =56.6, 71.6, and 84.8 mm⁻¹ respectively. Each direction was applied with ϕ = 0 and 180.

To determine pore size with high accuracy and precision, optical microscopy measurements were conducted on the GCAs. The disks were imaged in D5 on a Zeiss LSM 780 confocal microscope with a 20x 0.8 air objective in transmission mode with a 488-nm laser. Actual pixel size was measured under the same conditions with a micrometer. Image resolution was 2048 x 2048 pixels, zoom at 1-pixel size is 0.208 mm / pixel (measured from a calibrated micrometer, Graticules LTD, Tonbridge, England). Ten images were taken at different locations on the disk, and analyzed by using ImageJ (Wayne Rasband, NIH, Bethesda, MD).

Modeling and analysis

D-PFG

The d-PFG experiment produces an NMR signal attenuation from D5 molecules restricted in cylindrical microcapillaries of radius a, E_rest(G₁,G₂,θ, φ a), which also depends on the amplitudes of the first and second gradients, G₁ and G₂, respectively, and on their directions, described by the polar (θ) and azimuthal (φ) angles. Because the phantom consists of fused glass wafers containing only microcapillaries, a free diffusion compartment was not included in our model. The average signal from eight ROIs (one for each pore size) was fitted to E_rest(G₁,G₂, θ, φ, a) to obtain estimates of a. Data analysis was performed by using in-house Matlab (R2013a, The MathWorks, Natick, MA) routines to implement the multiple correlation function (MCF) methodology[55, 56] and the library function lsqcurvefit to perform the nonlinear curve fitting by using the trust-region reflective method. To increase accuracy, the diffusion coefficient was independently estimated by using the free diffusion D5 compartment of the MRI phantom before the microcapillary diameter was estimated. The diffusion coefficient was obtained by fitting the signal that arose from the non-restricted part of the phantom to a Gaussian diffusion model.

Multi-shell HARDI

To calibrate a HARDI (e.g., Q-ball or spherical deconvolution) or a multishell q-space

MRI experiment, such as MAP MRI, we determined whether the method could generate the correct estimate of the radius of the cylindrical pores comprising the GCA. For a system with cylindrical symmetry, the MRI signal S(q) can be written as

$$S(\mathbf{q})=S_0{E}_{\mathit{circle}}(qsin\theta ;\frac{a}{\sqrt{D\mathrm{\Delta }}},\frac{\delta }{\mathrm{\Delta }})exp\left(-{\left(2\pi qcos\theta \right)}^2\left(\mathrm{\Delta }-\frac{\delta }{3}\right)D\right),$$ (1)

where S₀ is the signal without diffusion attenuation, q is the sensitization vector, q magnitude of q, θ is the angle between q and the cylinder axes, δ is the diffusion pulse width, Δ is the diffusion pulse separation, a is the radius of the pores, and D is the bulk diffusivity of the medium. For a given pulse sequence, the attenuation function $E_{\mathit{circle}}(qsin\theta ;\frac{a}{\sqrt{D\mathrm{\Delta }}},\frac{\delta }{\mathrm{\Delta }})$, in the plane perpendicular to the tube axis, can be computed by using the multiple correlation function (MCF) method[55]. Nine ROIs were defined, one in each GCA layer, plus an additional ROI in the free diffusing compartment of the phantom. The average signal was fitted twice to Equation 1: once to obtain estimates of S₀, D, and a, and then to obtain estimates of only S₀ and a, while D was fixed according to the d-PFG protocol. The data analysis was programmed in GNU octave with in-house software to implement the MCF method and the library function leasqr to perform the nonlinear curve-fitting by using the Levenberg–Marquardt method.

Results and Discussion

Compatibility and robustness of the phantom

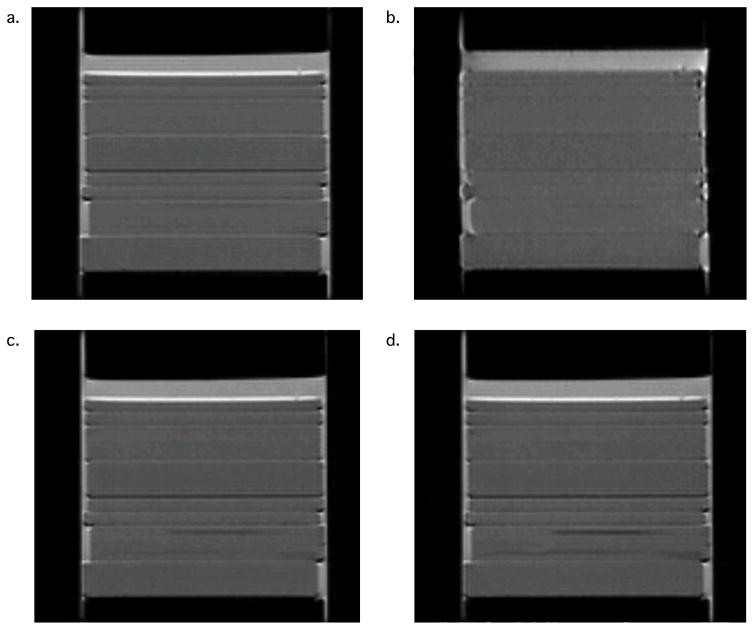
Figure 3 show DWIs of the D5 (a–d) phantom and a similar water filled phantom (e–h). All images were made with the same acquisition data as for the HARDI experiment with q-values of 26.2 and 74.1 mm⁻¹ . The low q-value of 26.2 mm⁻¹ (a., b., and e., f.) is in the range used for DTI, while the high q-value of 74.1 mm⁻¹ is within the range of the d-PFG and HARDI experiments. Diffusion gradient in a., c., and e., g., were applied in the parallel and in b., d., and f., h., in the perpendicular direction to the free axis of the capillaries. Figure 3 e and f demonstrate that the water filled phantom is preferred over the D5 phantom for calibration at low q-values. The water phantom shows strong anisotropy when diffusivity is measured perpendicular to the GCA’s free axis while still producing a signal when diffusivity is measured along the free axis. However, the water filled GCA phantom is not suitable for the high q value experiments as diffusivity measurements along the GCA’s free axis reach the noise floor.

Figure 3.

Diffusion weighted images a.-d.) D5 phantom and e.–h.) water filled phantom. a. and e.) q = 26.2 mm⁻¹ parallel to GCA free axis b. and f.) q = 26.2 mm⁻¹ perpendicular to GCA free axis c. and g.) q = 74.1 mm⁻¹ parallel to GCA free axis d. and h.) q = 74.1 mm⁻¹ perpendicular to GCA free axis

Measurements were performed to test the consistency and reproducibility of self-diffusion MR experiments by using the isotropic D5 polymer at four different diffusion times, Δ = 25, 50, 75, and 100 ms. Similar diffusion coefficients were obtained for all diffusion times, with a mean of 1.63 ± 0.04 10⁻⁴ mm²/s, indicating D5 is sufficiently monodisperse for use over a wide range of diffusion times. In contrast, with a mixture of a solute in water, the concentration can change due to water evaporation, leading to a change in the diffusion coefficient. D5 is also stable at room temperature.

Measurements of T₁ and T₂ of the D5 were 1,462 and 1,160 ms, respectively. The long relaxation times are suitable for probing long diffusion times and for implementing sequences with long acquisition times without compromising the signal-to-noise ratio (SNR) of the resulting DWIs. In addition, the diffusivity of the D5 at 17°C is roughly an order of magnitude lower than the diffusivity of water in tissue[3]. This important property allows the phantom to be scanned with experimental designs that are clinically applicable while retaining high SNR because of the smaller signal attenuation.

Multiple MRI acquisition schemes were used to image the GCA phantom to assess its homogeneity as well as potential imaging artifacts attributable to eddy currents, susceptibility gradients, and scanner stability. Figure 4, a–d, shows MSME, EPI, and RARE (Factor 8 and 16) images, respectively, of the polymer-filled phantom. The high quality of the images demonstrates that the phantom can be used with various acquisition schemes, including fast imaging methods. Although the GCA phantom is made of fused silica, with a different susceptibility from that of D5, because of careful selection of acquisition parameters the resulting DW-EPIs are of high quality and show minimal susceptibility distortions. Furthermore, the long T₂ of the silicone oil enables use of the polymer-filled CGA phantom with sequences like RARE that have long acquisition times.

Figure 4.

Phantom images resulting from multiple acquisition schemes: a.) MSME, b.) EPI, c.–d.) RARE Factors 8 and 16, respectively.

In addition to being shown robust to different imaging schemes, the proposed phantom resolves an important limitation of water-based phantoms, the so-called ''noise floor'' problem[38, 57]. In previous studies in which a water-based GCA phantom was used[53] , the usable gradient amplitude was limited by the value needed for the signal to approach the noise floor. Using D5 enabled us to play out stronger diffusion gradients without approaching the ''noise floor'' , as is evident from the high q-values reported in this study.

Estimated microstructural features

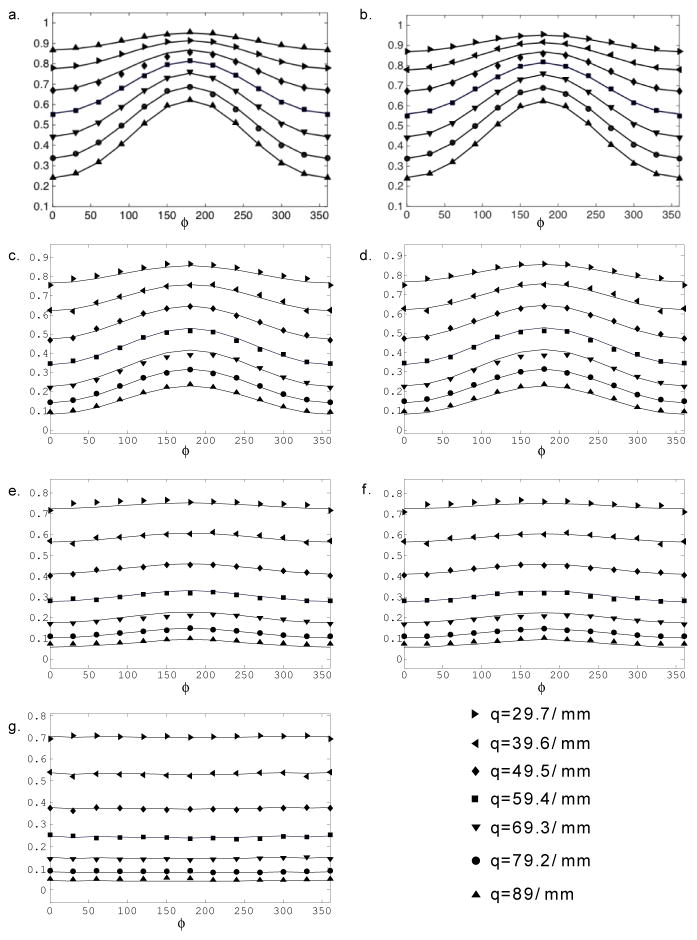
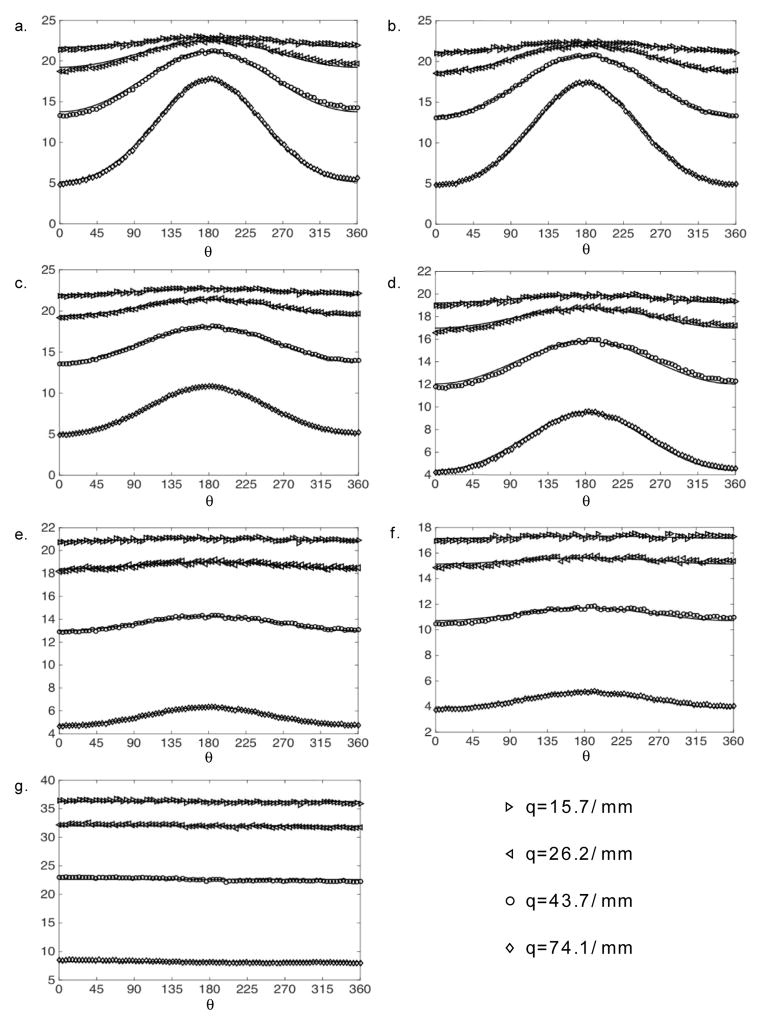
After it was verified that the phantom could be robustly used with different imaging schemes, two DWI methods, d-PFG and multishell HARDI, were used to measure the phantom’s known microstructural features. An ROI-based approach was used, thus accounting for the eight GCAs, and the three nominal pore sizes: 5, 10, and 25 μm. For each of the eight GCA layers, the signal attenuations were fitted to the theory, depending on the case (i.e., d-PFG or HARDI). Figures 5 and 6 show the d-PFG and multi-shell HARDI data and their corresponding theoretical fits. It is evident from the figures that, in both cases, the theoretical curves fit the experimental data well.

Figure 5.

d-PFG experiment (symbols) and simulations (solid line) of the corresponding echo attenuations vs. ϕ for q = 29.7, 39.6, 49.5, 59.4, 69.3, 79.2, and 89 mm⁻¹ for ROIs within the phantom: a.– b.) 5 μm, c.–d.) 10 μm, e.–f.) 25 μm, and g.) free diffusing D5

Figure 6.

Multi-shell HARDI experimental data (symbols) and simulations (solid line) of the corresponding echo attenuations vs. ϕ for q = 15.7, 26.2, 43.7, and 74.1 mm⁻¹ for different ROIs within the phantom. a.–b.) 5 μm, c.–d.) 10 μm, e.–f.) 25 μm, and g.) free diffusing D5.

Table 1 shows the calculated capillary pore diameters obtained from the 2D and 3D d-PFG, HARDI experiments (with diffusivity treated as a free and a fixed parameter) and from the optical measurements. The manufacturer precision for the pore diameter is 5% i.e. 0.25, 0.5, and 1.25 for the 5, 10, and 25 mm capillaries respectively, which is in the order of the error determined in light microscopy measurements. Bootstrapping was used to calculate the errors in the MRI data[58], resulting in errors significantly lower than the light microscopy. MRI pore diameter significant digits were matched to the light microscopy as it was used as the “gold standard”. The d-PFG experiment yielded values in good agreement with all nominal pore diameters and the ones obtained by optical microscopy (Table 1). The HARDI data with the D as a free parameter (i.e., both diameter and diffusivity were estimated) yielded accurate values only for the GCAs with pore diameters of 5 and 10 μm (Table 1). We repeated the HARDI data processing; this time fixing the diffusivity, which was independently estimated by using the free diffusion D5 compartment of the MRI phantom. In this case, the diameter estimates from the 5 and 10 μm GCAs were similar to the ones obtained with D as a free parameter. However, the estimated values for the 25μm GCAs were this time in close agreement with the nominal pore diameters and the ones obtained by optical microscopy (Table 1). While in the GCAs with pore diameters of 5 and 10 μm a large fraction of the spins sample the majority of the pore space during the diffusion time, in the case of the 25 μm pore diameter, most spins do not interact with the impermeable boundary and diffusion appears largely “free.” The failure to accurately estimate the largest compartment’s size when trying to estimate both diameter and diffusivity is might be due to the fact that half the tube diameter, 12.5 μm ≫ √DΔ ≈ .8 μm. Although this limit is violated in the case of 10 μm diameter as well, the estimation error becomes more evident as the violation becomes more pronounced.

Table 1.

Pore diameter estimates for the GCA plates making up the phantom.

	Pore Diameter
Method	5 μm	5 μm	10 μm	25 μm	5 μm	5 μm	10 μm	25 μm
HARDIa Fitted D	5.0 0.161	5.0 0.164	9.9 0.166	29 0.167	4.9 0.165	4.9 0.166	9.8 0.166	31 0.167
HARDIb	5.2	4.8	9.7	26	5.1	5.0	9.8	27
2 D d-PFG	5.4	5.3	10.1	25	5.5	5.4	10.1	26
3D d-PFG	5.2	5.1	9.9	26	5.1	5.0	10.2	27
Light microscopy	5.2 ±0.2	5.2 ±0.2	10.7 ±0.1	26 ±1	5.4 ±0.1	5.3 ±0.1	10.8 ±0.1	26 ±1

^aPore diameter estimated from the fits using diffusivity as free parameter.

^bPore diameter estimated from the fits using diffusivity as fixed parameter.

The 5- and 10-μm pore sizes represent the nominal dimensions that are already larger than those typically found in axons in the central nervous system (CNS); therefore, estimating both diameter and diffusivity should remain accurate in tissue and does not present a practical concern. However, the D5 phantom, particularly the larger pore diameter GCA wafers, can test the limits of experiments and their modeling pipelines.

In this study only pore diameter estimation was used to validate the phantom, however, more parameters such as FA, MAP-MRI metrics and more can be calculated using this phantom.

By reinforcing the GCA and sealing the tube this phantom can be suitable for a horizontal bore magnet where high q-value acquisition methods are currently in use. Since the magnetic field inside the tubes is uniform regardless of the orientation of the capillaries free axis with the main magnetic field[59–61], such modification would allows positioning the phantom in any orientation with respect to the main magnetic field. Furthermore, D5 could be used as the diffusing media in any phantom, which consists of physical barriers and constructed to resolve high q-values microstructural methods.

Conclusions

This work describes the development and use of an anisotropic diffusion MRI phantom and a computational pipeline that is suitable for simulating general s- and d-PFG MRI experiments in homogeneous porous media. The low diffusivity of the D5 medium allows testing of MRI methods with parameters that are comparable to brain white matter.

The suitability of using this phantom with a variety of standard image acquisition schemes and D5's diffusion stability and relaxation properties were all verified. Multi-shell HARDI and d-PFG MRI acquisition schemes were then used to measure and map the pore diameter in the phantom.

This robust anisotropic diffusion MRI phantom should enable calibration and validation of a wide range of diffusion MRI methods, specifically those that require applying high q- or b-values and multiple gradient orientations. The construction of the phantom lends itself to being scaled up for preclinical and clinical use.

Highlights.

• A novel glass capillary array MRI phantom for anisotropic diffusion is proposed.

• This can be a gold standard for calibrating high q diffusion MRI experiments

• Capillary diameters were validated using HARDI, DDE and light microscopy methods.