Latent growth models matched to research questions to answer questions about dynamics of change in multiple processes

Abstract

Objective

Given theoretical and methodological advances that propose hypothesis about change in one or multiple processes, analytical methods for longitudinal data have been developed that provide researchers with various options for analyzing change over time. In this paper, we revisit several latent growth curve models that may be considered to answer questions about repeated measures of continuous variables, which may be operationalised as time varying covariates or outcomes.

Study design and setting

To illustrate each of the models discussed and how to interpret parameter estimates, we present examples of each method discussed using cognitive and blood pressure measures from a longitudinal study of ageing, the OCTO Twin Study.

Result and Conclusion

Although statistical models are helpful tools to test theoretical hypotheses about the dynamics between multiple processes, the choice of model and its specification will influence results and conclusions made.

Introduction

The identification of the most appropriate statistical method to answer a research question is an essential step towards obtaining a meaningful answer to the question posed. Concurrent with advances in theoretical models [1,2] that propose dynamic associations between change in one or multiple processes, development of software [3–5] and analytical methods for longitudinal data [6–11] facilitate the implementation of these newly developed models. These advancements provide researchers with the opportunity to re-examine theoretical models of increasing complexity although they have also made the selection of the most appropriate model for answering the various possible questions posed and the interpretation of its results increasingly challenging.

Latent growth curve models (LGMs, 17) are statistical models conceptualized under the Structural Equation Modelling (SEM) framework often used for the analysis of univariate trajectories of longitudinal data [13–15]. LGM permit the estimation of mean and subject-specific curves and the inclusion of covariates that may be time invariant (i.e. variables that do not change over time, e.g. sex) or time varying (i.e. variables that change over time, e.g. blood pressure). See Appendix 1 for a mathematical formulation of an unconditional LGM, and pictorial representation of a LGM with time invariant covariates (Fig. A1). In these longitudinal models, time invariant covariates are included to explain differences between individuals (e.g., to examine hypothesis regarding differences in level and rate of cognitive change between men and women). The role of other variables that are measured repeatedly over time is less clear as they may explain change within individuals (how an individual changes compared to their previous level) whilst also explain differences between individuals (how an individual differs from another individual in the sample). The additional complexity of accounting for the different sources of information conveyed by time varying variables increases the difficulty in choosing the most appropriate analysis method. Furthermore, they can be operationalized in different ways resulting in either univariate models with time varying covariates or multivariate models of change.

The purpose of the current paper is to present an overview and discussion of a series of research questions that involve the analysis of information from variables that have been measured repeatedly over time and that may be answered by fitting univariate LGMs with time varying covariates or multivariate LGMs of change. Because these are related but substantially different models, understanding what each model offers and when they can be best applied is essential to avoid a mismatch between research questions and models used. Moreover, variations of these two models can and should be considered depending on the research question being addressed. We present exemplary questions that researchers, in the field of ageing, may ask and to illustrate the application of the different models, we also present an empirical example where we match research questions to methods. We hope this paper will be a useful tool for investigators involved in research using longitudinal designs.

Matching models to questions

To facilitate the matching of research questions to the most appropriate statistical method, we present and discuss the different models in the context of answers to a series of hypothetical questions. Even though the hypothetical questions we present here examine possible dynamics of cognitive function (CF) and blood pressure (BP), the models discussed are applicable to other research areas where similar questions are of interest. This is different from the current literature on research methods, which tends to describe the mathematical specifics of the statistical modeling approaches with less focus on the actual questions that can be answered by each model. Our approach, which highlights how the nuances between models answer slightly different questions, will be useful to all readers including those who are less mathematically oriented.

Latent Growth Curve Model with a Time-varying Covariate

Research Questions

Question 1: “What is the trajectory of CF once the effect of BP, at each concurrent time point is accounted for? ; Question 2: “Is the effect of BP on CF consistent over time, considering the fact that CF changes? ; Question 3: “Do individuals whose BP is higher than average also have higher than average CF?

Analytical approach

A Latent Growth Curve Model with a Time-varying Covariate (TVC model) can be considered to answer these 3 questions as described next. Specifically, they can be answered fitting a TVC model to CF measurements with BP measures regarded as time varying covariates.

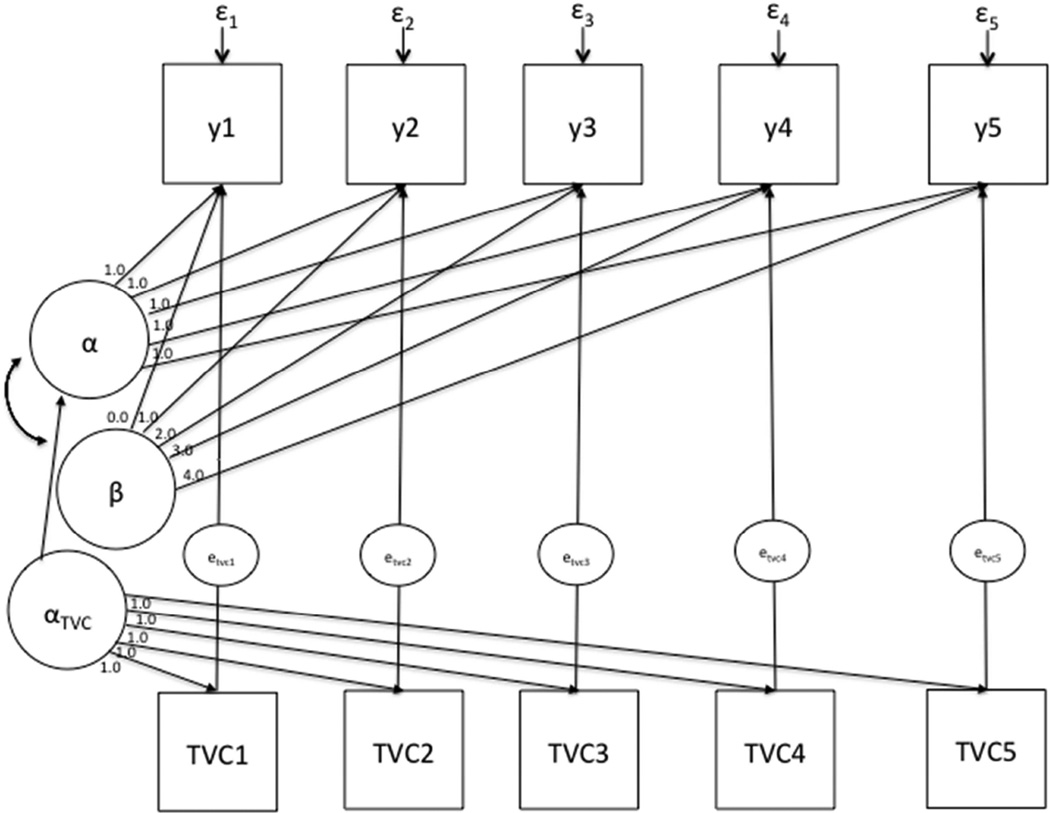
The TVC model is an extension of a LGM that permits the incorporation of covariates that, similarly to the outcome variable, are also measured repeatedly over time. It estimates the trajectory of the outcome variable (CF in our example) as a function of the metric of time, but, it does so while simultaneously controlling the outcome at each time point for some measure of the TVC (BP in our example).

The growth curve and the time specific regressions of the TVC on the outcome variable are estimated simultaneously, hence, the inclusion of a TVC in a growth model affects the interpretation of model parameters. Because the TVC directly impacts the outcome variable, the growth curve parameters (e.g. intercept and rate of change) should be interpreted as net of the effect of the TVC on the outcome. That is, they are estimates of the growth parameters after removing the effect of the TVC on the outcome. In addition, the time specific regression effects of the TVC on the outcome need also be interpreted as effects net of the influence of the growth process. Thus, TVC models provide information about occasion-specific effects of the TVC (BP) on the outcome (CF) beyond the outcome’s expected trajectory based on time alone. Although these effects are usually constrained to be equal over time, the constraint may be relaxed to obtain potentially different estimates of the effect of the TVC on the outcome at each time point [16] and by doing so, it would be possible to understand whether these effects increase, decrease or fluctuate over time. It is relevant to note that a series of independent cross sectional analysis regressing CF on the concurrent BP measurements would not result in consistent estimates as the occasion specific regression estimates obtained from a TVC model accounts for the CF’s growth, whilst the cross sectional regressions would not.

Figure 1 depicts a diagram of a common formulation of the TVC where the outcome variable at each time point is controlled for the concurrent value of the TVC although alternative formulations are possible as discussed below in the paper.

Figure 1.

Path diagram of the conditional latent growth curve model (y) with a time-varying covariate (TVC).

Conceptually, it is also relevant to note that, contrary to time invariant covariates that are variables measured once and that are included in longitudinal models to explain between person differences, the main purpose of including time varying covariates (TVCs) in longitudinal models is to control for possible sources of variance at the individual level. That is, TVCs are variables included in the level 1 or within person level equation of the model that describes a person’s curve. In longitudinal analyses, the outcome variable, which is measured repeatedly over time, is composed of two sources of variation: between person differences (differences between individuals in mean level) and changes within a person (within person change or variation about a person’s mean level). Similarly, TVCs, which are also variables measured repeatedly over time, are also composed of between and within person sources of variation that need to be properly differentiated and reported. For instance, in the previous example where BP was regarded as a TVC, there are differences in blood pressure between study participants (between individual differences, i.e. some individuals have higher BP than others) but BP is also likely to change over time within a person (within individual change, i.e. an individual’s BP may increase over time). These two sources of variation in the TVC should be separated to avoid biases in estimates of the time-specific effects of the TVC on the outcome. If not separated, these estimates will be a compound of between and within person effects of the TVC [17,18].

Working within a SEM context, Curran and colleagues [19] proposed to separate both sources of variance of the TVC by explicitly modelling the TVC with a random intercept model and regressing the outcome’s intercept on this new intercept to get the between person effect. Simultaneously, the within person effect is estimated by regressing the measure of the outcome variable at each time point on the time-specific residuals of the TVC [19]. Hoffman (2015) proposed an alternative but similar approach to modeling the TVC (gives the same estimates) but that does not require creating the additional time-specific residuals. Using Hoffman’s approach, the effect of the TVC’s intercept on the outcome’s intercept represents the contextual effect, which is defined as the difference between the within and between person TVC effects. Although used in the SEM framework here, the concept of contextual effect originates in the multilevel literature for clustered data and represents the additional effect of belonging to a group on an individual’s outcome. In longitudinal models, individuals are regarded as contexts, therefore, the contextual effect is the average characteristic of a person after controlling for the characteristic at specific occasions. That is, the effect of a person’s general BP on CF after controlling for BP level at specific occasions. The between person effect of the TVC can then be computed by adding the contextual effect to the within person effect. This additional computation of the between person effect enables researchers working with BP and CF to answer question 3 (For a more details about differences between the contextual, within, and between person effect, see Hoffman, 2015, page 346–350).

Variations of TVC model formulations

Concurrent associations between the TVC and the outcome are commonly modeled (regressing the outcome at each occasion on the TVC at that same occasion as shown in Figure 1), although alternative formulations of TVC models are possible. For example, lagged associations where the outcome variable at a specific occasion is regressed on the immediately previous measure of the TVC (as depicted in Figure A2) may be considered. These lagged associations would enable researchers to investigate whether the TVC has a delayed effect on the outcome and answer questions such as “How are cognitive functioning (CF) scores related to effects of previous blood pressure (BP) measures?”. Notably, this model does not directly permit causal inferences without verification of additional assumptions (e.g. unmeasured confounding), but, because of the temporal ordering of the variables, it makes a stronger case for these inferences. Alternatively, when no additional assumptions are verified, only claims about how one variable is associated with change in another variable measured later in time can be made. The lagged TVC model is often preferred when there is strong theoretical basis for a change process over time for the TVC on the outcome. A further extension of the TVC model involves a combination of concurrent and lagged effects of the TVC on the outcome at a specific time. These simultaneous associations would permit, for instance, to answer questions regarding the effect of baseline BP on baseline and the first follow up of the CF measure. Cross-lagged associations between the TVC and the outcome variable may also be considered. For instance, it may be of interest to model the bidirectional impact of baseline BP on cognitive scores collected at the first follow-up occasion whilst modeling the impact of baseline cognitive scores on BP at the first follow-up occasion [20]. Yet, the interpretation of the cross lagged effects in this case is slightly different, as the effects of the TVC are conditioned on the growth of the outcome variable, whilst those affecting the TVC are not conditioned on the overall growth of the TVC, as these are not directly modelled.

Often TVC variables are directly observed, but in some contexts, it may be necessary to first derive them and then include them as TVCs. For instance, researchers may be interested in the evaluation of the effect of change of an observed variable on an outcome. In this case, difference scores between two measurement occasions (not necessarily consecutive) should be first derived and then included as TVCs. This formulation however, is susceptible to limitations that are inherent to change scores [21], including poor reliability compared to the individual measures involved [22], regression to the mean effects and to the “horse racing” effect that suggests that individuals with largest change are those who start from higher values [23]. This model would be of use when the researcher is interested in the effect of the change in BP between baseline (BP_baseline) and the first follow up occasion (BP₁) on cognitive function at the first follow up occasion or between baseline and subsequent measures of blood pressure (e.g. BP₁− BP_baseline; BP₂ − BP_baseline, …) on subsequent measures of cognition. For instance, when a baseline measure of the TVC has a special significance (for example, in studies where the baseline measure was taken after the implementation of a certain intervention to reduce BP), the question “How are cognitive functioning (CF) trajectories related to the effects of changes from baseline blood pressure (BP)? ” may be particularly relevant.

Although flexible, models that include lagged effects may be sensitive to the time elapsed between measurement occasions. Researchers should carefully evaluate whether the time lapse between occasions is appropriate for the specific question they are attempting to address given that some variables change more rapidly than others and require more frequent measurement intervals. We have discussed models with a single TVC, although models with multiple TVCs may also easily be considered.

It is possible, although not yet fully explored in this context, limitations in interpretation of results arising from poor discrimination between mediators and genuine confounders may affect model results [24]. Yet, these may be minimise when models are supported by a deep understanding of the data structure and a strong theoretical underpinning.

Bivariate Linear Growth Model

Research Questions

Questions 4: “How do cognitive functioning and blood pressure change over time?”; Question 5: “After accounting for intraindividual change in CF and BP, do individuals whose cognitive scores are further away from the person’s average cognitive function have BP measures that are also further away from the person’s average BP at each occasion?” (do individuals whose cognitive scores deviate the most from the individual’s average cognitive trajectory, also have BP measures that also deviate the most from the individual’s mean BP over time?); Question 6: “Do individuals whose cognitive functioning declines at a faster rate also demonstrate a faster rate of change in BP?” and Question 7: “ Do individuals who have better cognitive performance also have higher BP at study entry?”.

Analytical approach

these 4 questions may be answered by fitting a Bivariate Latent Growth Curve Model (BLGM) to repeated measures of CF and BP. Up to this point, we have discussed models where TVCs vary over time without acknowledging their potential growth trajectories. In the case where a TVC (BP in our example) may have its own trend, modelling the TVC trajectory by adding growth factors such as a random slope is possible. In this situation, the TVC is regarded as a second outcome and the model becomes a bivariate LGM.

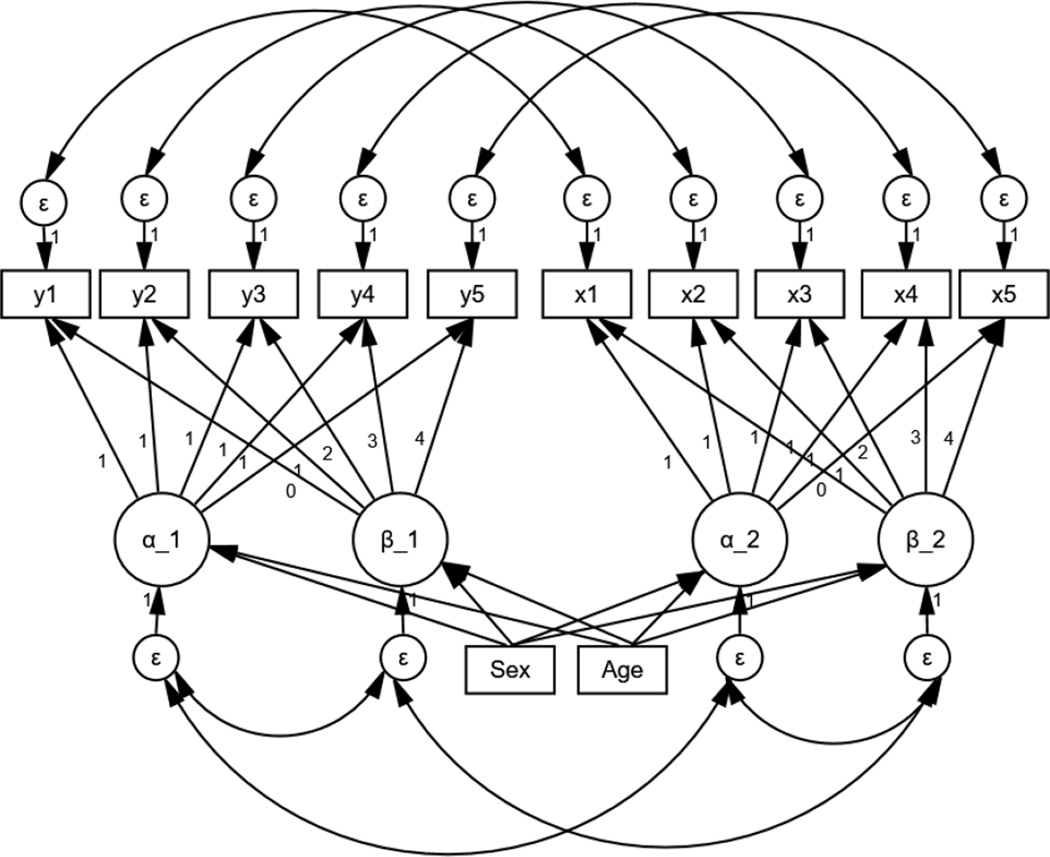
The bivariate linear growth model (sometimes called parallel growth model) is an extension of the univariate growth curve model that estimates the trajectories of two variables (known to be correlated) simultaneously whilst modeling correlations between latent growth factors of each outcome variable. So, a BLGM would allow the simultaneous estimation of the CF and BP trajectories (see Figure 2 for a pictorial representation of the BLGM) and the evaluation of correlations between their levels and change parameters, providing an answer to Question 4.

Figure 2.

Path diagram of the conditional bivariate latent growth curve model fitted to outcomes x and y, adjusted for age and sex

An interesting additional feature of the BLGM is that it permits the investigation of the association between occasion-specific residuals of each outcome after accounting for each outcome’s intraindividual change. For example, by modeling occasion-specific residuals researchers would be able to answer questions such as question 5. This is an important piece of information as it captures the short-term within person fluctuations in both variables, which can be the result of a multitude of possible unexplained factors occurring together. Questions 5 and 6 may also be answered by a BLGM, as a further feature of this model is that it permits the modelling of intercept-intercept and slope-slope correlations of the processes investigated. These correlations would provide specific answers to questions such as “Do individuals who have better cognitive performance also have higher BP at study entry?” that refer to the intercept–intercept correlation; and “Do individuals whose cognitive functioning declines at a faster rate also demonstrate a faster rate of change in BP?” that refer to slope-slope correlation.

Although the intercept-intercept and intercept-slope correlations may be important for extending our understanding of the associations between different features of the processes under examination such as level and rate of change, it is important to bear in mind that they are dependent on the placement of the intercept [25], which is usually arbitrarily chosen. The interpretation of slope-slope correlation, which may also be relevant for our understanding of how the two processes evolve, is also dependent on the parametric curve considered to describe the trajectory of the outcomes. For example, when considering a quadratic polynomial to model the trajectory of the outcomes, the linear slope (first order term of the polynomial) is interpreted as the instantaneous rate of change at the intercept whereas when the trajectory is described by a first order polynomial, the slope is interpreted as the rate of change across all occasions.

Variations of the bivariate model

The BLGM may be formulated as a directional bivariate growth model (DBGM), which, unlike the standard model which treats both repeated measures as outcomes, considers one of the variables as an outcome and the other as a TVC. Specifically, growth factors and occasion-specific residuals of the outcome variable are regressed (not correlated as in the standard BLGM) on corresponding growth factors and occasion specific residuals of the covariate, respectively. In other words, this model can also be considered as an extension of the TVC model with the additional random slope for the TVC. As regressions are part of this model, it is relevant to respect the ordering of the variables (for example, it would not be acceptable to regress the outcome’s intercept on the covariate’s slope). The DBGM is best suited to situations where theoretical support exists to test whether one variable predicts the second one, whereas the BLGM is recommended when order is unknown and the interest lies in whether the trajectories are correlated.

Finally, the BLGM can easily be extended to model more than two outcomes simultaneously. For example, it could be of interest to model change in fluid and crystallised cognitive abilities whilst also modelling blood pressure trajectories. However, it should be noted that the interpretation of results from such a model may be challenging.

Materials and Methods

To illustrate the models discussed, we present results from a series of analyses conducted using measures of global cognition and systolic blood pressure (SBP) from the Origins of Variance in the Old-Old (OCTO-Twin) study. The OCTO-Twin study includes dizygotic and monozygotic twin pairs aged 80 years of age and older [26] selected from older adults participating in the population-based Swedish Twin Registry. The initial sample consisted of 702 individuals (351 same-sex pairs). Five cycles of longitudinal data were collected at two year intervals. Global cognitive function was assessed using the Mini Mental State Examination [27], a test that takes values between 0 and 30 with high scores indicating better CF. Measurements of BP were taken by nurses using a mercury sphygmomanometer with subjects in a supine position after five minutes of rest. Descriptive statistics of MMSE and systolic BP (SBP) measures at each wave can be found in Table 1.

Table 1.

Descriptive statistics of MMSE and SBP measures at each measurement occasion of sample analysed.

	Mean (St. deviation)
	MMSE	SBP
Study entry	26.93(3.92)	159.75(22.54)
2nd. follow up occasion	26.57(4.33)	153.68(22.91)
3rd follow up occasion	26.25(5.08)	149.75(22.81)
4th follow up occasion	24.77(6.54)	143.50(21.42)
5th. follow up occasion	22.08(7.90)	140.38(20.61)

We analysed data from non-demented individuals who had no stroke history (n=397). All models were fitted using time in study as the time metric to describe change and, for simplicity, we also assumed that CF and SBP changed linearly over time. Models were adjusted for three time invariant covariates: age at study entry (centered at 83.6 years old, the sample’s average at study entry), education (centered at 7.3 years, the average years of education) and sex (male=0, female=1).

All models were fitted in Mplus version 7.2 [3], a software package that uses maximum likelihood estimation and produce robust estimates under a missing at random assumption. Cluster identifiers were used to account for the dependency among twin participants [28]. Robust maximum likelihood (MLR) estimation was used to provide adjusted chi-square and standard errors that account for non-normality. See Appendix 2 for Mplus syntax used to fit the different models discussed here.

Next, we demonstrate how each aforementioned model answers specific research questions and discuss how to interpret results obtained from fitting the models using the OCTO-Twin study. For the sake of brevity, we refer only report results relevant to the specific questions asked and because we are interested in the illustration of the analytical methods rather than in substantive results, we present results from a model where concurrent associations between systolic blood pressure and the MMSE were modelled.

Question 1: How does cognitive function change once we control for the effect of SBP, which was also measured repeatedly? Or how is the MMSE trajectory after controlling for the effect of time–varying SBP measures?

Answer 1: To answer this question, we fitted a LGM to MMSE scores including SBP as a time varying covariate. Results indicate that after accounting for the effects of SBP at each occasion, age, gender, and education differences, the MMSE expected score at study entry for a reference person (an 83.6 year old man with 7.3 years of education), was estimated at 27.74 (SE=2.12) points with an annual rate of decline of −0.38 (SE=0.08) points per year (see Table 2, third column, Q1). The BLGM should not be used to answer this question as correlations, rather than regressions, are modelled between MMSE and SBP. Therefore, the trajectory of MMSE is not net of the repeated effect of SBP. The TVC model is essentially the same as a conditional LGM except that the covariate varies over time rather than included only at baseline. One option, however, is to model a directional BLGM where an intercept and slope factor is modeled for MMSE and SBP and MMSE at each time point is regressed on SBP.

Table 2.

Unstandardized estimates and standard errors with the matching question for the latent growth model fitted to cognitive scores without and with BP measures modelled as time-varying covariates.

	LGM	TVC model
	Est(SE)	Est.(SE)	Question
Fixed effects MMSE
Intercept	26.97 (0.38)*	27.74 (2.12)*	Q1
Slope	−0.47 (0.08)*	−0.38 (0.083)*	Q1
SBP →MMSE (WP)		0.030 (0.009)*	Q2
SBP →MMSE (BP)		−0.006 (0.014)	Q3
Random effects Variance
Intercept	4.10 (1.56)*	3.82 (1.54)*
Slope	0.24 (0.06)*	0.23 (0.05)*
Error	5.32 (0.74)*	5.20 (0.70)*
Corr (Intercept, Slope)	0.47 (0.21)*	0.49 (0.20)
SBP		308.30 (21.30)*

Note. Est. = Unstandardized estimates. SE = Standard errors; WP = Within person effect; BP = Between person effect.

^*p < .05

Question 2: What is the effect of SBP on MMSE at each occasion after accounting for the MMSE growth parameters?

Answer 2: This question refers to the occasion specific regression coefficients of CF on SBP which can be answered by fitting a TVC model. Results show that, after accounting for the MMSE growth factors, a significant within person association between SBP and the MMSE was found (0.030 (SE=0.009)) such that MMSE scores were higher on occasions where SBP was also higher (Table 2, Q2). The BLGM would not be appropriate to use for this research questions as correlations rather than regressions are included between the repeated measures. That is, SBP and MMSE are both treated as outcomes rather than them being outcomes regressed on a TVC. As mentioned, one option is to model a directional BLGM where an intercept and slope factor is modeled for MMSE and SBP and MMSE at each time point is regressed on SBP.

Question 3: Do individuals with higher than average SBP also have better than average CF?

Answer 3: This question refers to between individual differences in SBP and CF and may be answered by a TVC model that includes a random intercept for SBP and that computes the between person effect. Results (−0.006 (SE=0.014)) suggest that SBP and MMSE scores were not associated (Table 2, Q3).

For the sake of comparison of estimates we also included, in Table 2, results obtained from a LGM without controlling for the repeated BP measures. It can be noted that estimates of the MMSE’s rate of change, error variance and the intercept’s residual variance are attenuated in the TVC model compared to estimates obtained from the LGM, whilst other model parameters differ only slightly. As the TVC is included at the within person level of a model, the attenuation of the error variance is expected. But because the TVC includes between and within person information, which were explicitly separated in the model by including a random intercept to model the TVC, the attenuation of the intercept’s residual variance is also expected.

Importantly, three pieces of information were gained when including the TVC: the trajectory of the outcome net of the effect of the TVC, the effect of the TVC on the outcome (which in our example indicated that after accounting for the MMSE’s growth factors, individuals performed better on occasions when their SBP was higher) and the effect of between person differences in SBP and cognitive function (which in our example is statistically non significant).

Question 4: What are the MMSE and SBP baseline levels and rate of change?

Answer 4: Although this question can be answered by fitting a LGM to MMSE and SBP measures independently, it may also be answered with a BLGM. The expected mean MMSE score at study entry for a reference person was estimated at 26.75 (SE=0.37), with an annual rate of decline of −0.37 (SE=0.082) whilst the average SBP at study entry was estimated at 157.21 (SE=2.05) mmHg with an annual rate of decline of −2.87 (SE=0.38) mmHg (Table 3, Q4). This question cannot be answered by the TVC model. Unlike the BLGM, the TVC model provides MMSE scores at study entry and rate of change after controlling for the effect of SBP.

Table 3.

Unstandardized estimates and standard errors with the matching question for the bivariate latent growth model.

	Est.(SE)	Question
Fixed effects MMSE
Intercept	26.75(0.37)*	Q4
Slope	−0.37(0.082)*	Q4
Fixed effects SBP
Intercept	157.21(2.05)*	Q4
Slope	−2.87(0.38)*	Q4
Residual Covariances
Intercept – Intercept	4.35(3.44)	Q5
Slope – Slope	0.37(0.21)	Q6
OSR – OSR	5.42(1.88)*	Q7

Note. Est. = Unstandardized estimates. SE = Standard errors. OSR = Occasion-specific residuals.

^*p < .05,

Question 5: After accounting for intraindividual change in SBP and MMSE, do individuals whose SBP measures deviate the most from the mean SBP also deviate the most from the mean MMSE at each occasion?

Answer 5: This question can be answered by modelling the correlation between occasion specific MMSE and SBP residuals. In our example, within person occasion-specific fluctuations across time in SBP were positively related to within person fluctuations in MMSE across time (Table 6, Q7). This question is different from the aforementioned Question 2 in that correlations rather then regressions are included between SBP and MMSE at each occasion and the occasion-specific relationship between both variables is controlled for intraindividual change (intercept and slope) in both SBP and MMSE rather than just for MMSE and the SBP intercept as is the case in the TVC model.

Question 6: Is change in SBP related to change in MMSE?

Answer 6: This question is concerned with the MMSE and SBP slope-slope correlation using the BLGM. In our example, rates of SBP and MMSE annual change were not found to be correlated such that those individuals who had faster (or slower SBP) decline were not found to also have faster (or slower) CF decline (Table 3, Q6). This cannot be answered by the aforementioned TVC model given that the slope of the TVC (SBP) is not modeled.

Question 7: Are the baseline levels of SBP and MMSE related? Or, is baseline SBP related to baseline MMSE?

Answer 7: This question refers to the correlation between CF and SBP intercepts in the BLGM. In our example, baseline SBP and MMSE were not found to be statistically significantly (4.35(SE=3.44)) correlated such that those individuals who had higher or lower initial SBP were not found to also have better or poorer CF (Table 3, Q5). The relationship between the MMSE and SBP can also be examined in the TVC model. However, as mentioned, regressions rather than correlations are modeled.

Conclusion

The purpose of this paper is to present a brief and didactic overview of some analytical models that may be used to answer specific questions about different potential associations that may exist between repeated measures of multiple variables, and to illustrate how to best match a set of research questions to analytical models. The discussion of substantive conclusions regarding the association between blood pressure and cognitive function was not an aim of the work presented here; therefore, we abstain from discussing these results.

Models discussed here are extensions of the univariate LGM that conceptualise repeated measures of one of the variables in two fundamentally different ways. Whilst the TVC model regards one of the longitudinal variables as an outcome and the other as a covariate, the BLGM regards both longitudinal variables as outcomes.

Differences Between SEM and MLM

Models presented in this paper were all fitted in an SEM framework, but can also be fitted in multilevel modeling (MLM). Although differences between LGMs and MLM models are minimal, some differences warrant to be discussed. For example, using a MLM framework makes it is easy to include more than two hierarchical levels whilst LGMs are more limited in this regard. Instead, because time scores are parameters in LGMs, they can be estimated, which is an advantageous feature of LGMs. Within the SEM framework, it is possible to free the residual variances across time, whereas in the long format used for the MLM framework, these are automatically fixed to be equal across time.

Some differences between SEM and MLM are model specific. For example, the between and within person effects of a TVC model are separated differently in MLM and LGMs. Within the SEM framework, the between person effect is estimated by creating a latent intercept for the TVC and regressing the outcome’s intercept on that of TVC’s intercept. The within person effect is estimated by regressing the measure of the outcome variable at each time point on the TVC [18,19]. Instead, in the MLM framework, the between and within person effects are separated using centring techniques [19]. For instance, using person- mean centering (that is, subtracting the person mean from the TVC), the level 1 effect of a person-mean centered TVC is the within person effect and the level 2 effect of the person mean predictor is the between person level effect.

In most longitudinal designs, missing data are a given. LGM assume missing data are random (i.e. probability of an observation being missing depends on observed data). As extensions of LGMs, the models presented here also produce estimates under a MAR assumption. However, limitations of LGMs such as list wise deletion in the presence of missing data on time invariant covariates are also inherited.

We presented a limited number of models but other models are possible including the autoregressive cross-lagged model [20], the bivariate autoregressive latent trajectory (ALT) model [20] and the dual change score model [29]. Further, many of these models can be extended to allow for the examination of meditational processes including the multilevel SEM (MSEM) mediation model, LGC mediation model, autoregressive mediation model, autoregressive latent trajectory mediation model, and latent difference score mediation model [10]. Mixture models may also be considered to identify subpopulations with similar trajectories [30], although their fit may be computationally demanding and technically challenging.

It is possible that multiple models are required to best understand the complex associations of various processes. We encourage researchers to carefully reflect on the features of the study design that may impact their conclusions. These include the time elapsed between data collection waves, whether designs involved variably spaced measurement occasions, age heterogeneity of sample, consistency of measures over time, and other key features likely to impact results. Further, features of the variables chosen in their investigations such as ceiling or floor effects may also need consideration.

On deciding which model would best answer questions about the complex associations between multiple continuous outcomes, theoretical questions should drive the choice of model, although features of the data may need consideration when interpreting results.

Supplementary Material

1

Figure A1. Path diagram of an unconditional latent growth curve model fitted to outcome variable y

2

Figure A2. Path diagram of a latent growth model with a lagged effect of the time varying covariate

What is new.

• *Advances in theoretical models and analytical methods provide researchers with ample opportunities for research, but mismatches between questions and methods are possible
• *When repeated measures of multiple variables are collected over time, whether longitudinal variables are operationalized as time varying covariates or outcomes depends on the question of interest and leads to the application of substantially different analytical approaches
• *We revisit and provide guidance about various latent growth curve models to help researchers identify the best methodology to answer a series of commonly asked questions about the dynamics of change in single or multiple longitudinal variables

Key message.

• In longitudinal studies, information about multiple processes is often collected simultaneously

• Latent growth curve models with time-varying covariates and multivariate models of change allow for the examination of change over time and the examination of longitudinal relationships between two or more variables.

• Variations of these longitudinal models are also possible and should be considered.

• We revisited various longitudinal models that are useful tools for answering complex dynamics of multiple longitudinal processes

• The choice of longitudinal model should be based on the research question of interest and take into account characteristics of the data used.