Abstract
When no means are available for directly measuring 3D dose distribution, online imaging could be employed for dose monitoring in image guided radiotherapy (IGRT). This paper addresses the issue of cumulative dose estimation from CBCT images in prostate cancer radiotherapy cases. It focuses on the dose received by the surfaces of the main organs at risk, namely the bladder and rectum. We have proposed both a surface-constrained dose accumulation approach and its extensive evaluation. Our approach relied on the nonrigid registration (NRR) of daily acquired CBCT images on the planning CT image. This proposed NRR method was based on a Demons-like algorithm, implemented in combination with mutual information metric. It allowed for different levels of geometrical constraints to be considered, ensuring a better point to point correspondence, especially when large deformations occurred, or in high dose gradient areas. The three following implementations of the NRR approach with different levels of constraints were considered: (i) full iconic NRR; (ii) iconic NRR constrained with landmarks defined interactively at the surface of organs (LCNRR); (iii) NRR constrained with full delineation of organs (DBNRR). To assess dose accumulation accuracy, we designed a numerical phantom based on finite-element modeling and image simulation. This model provided known deformations of organs and a reference accumulated dose. The methods were assessed on both the numerical phantom and real patient data in order to quantify uncertainties in terms of dose accumulation. The LCNRR method appeared to constitute a good compromise between dose monitoring capability and compatibility with clinical practice constraints (low interactivity level).
I. Introduction
Radiotherapy has proven to be an effective treatment method for all stages of localized prostate cancer. The main challenge this therapeutic option currently presents is delivering the prescribed dose to the clinical target for local control, while limiting the irradiation of the organs at risk (OAR), to thus avoid subsequent toxicity-related events. In prostate cancer irradiation cases, treatment is planned using a unique CT scan, then is typically fractionated into 30 to 40 daily treatment sessions using the same irradiation plan. The OARs, namely the rectum and bladder, are, however, subject to large deformations due to their differing contents, leading to displacements of the prostate gland and discrepancies between the planned dose distribution and that which is actually received. This may expose the patient to an OAR overdose or tumor underdose. One of the major innovations to come out of recent years has been the evolution of imaging devices integrated into the treatment device for image-guided radiotherapy (IGRT). Among these new devices, the most widely-employed is cone beam computed tomography (CBCT) which enables soft tissues under the treatment device to be observed, and, if required, repositionning of the patient according to tumor location [1], [2]. IGRT is therefore of particular interest in terms of correcting inter-fraction prostate motion. Yet, rigid registration of the prostate does not allow to compensate for anatomical deformations. Recently-developped concepts of adaptive and dose-guided radiotherapy (DGRT) [3], [4] could lead to improved matching between planning and treatment by considering a possible treatment replanning prior to a new fraction delivery. To determine if replanning is required, the dose actually received by the tissues must be monitored during the treatment course. When no means are available for directly measuring 3D dose distribution, embedded imaging (i.e. CBCT) could be used for dose monitoring. Taking anatomical variations into account, it primarily involves estimating the daily cumulative and total cumulated dose distributions. This is a critical issue, relying on the capability of tracking the tissues appearing on the planning CT on each CBCT scan, in order to estimate the actual dose distribution in the frame of reference of the planning CT. This tissue tracking can be performed by nonrigid image registration [5], [6]. The aim of the CBCT to CT nonrigid registration is to provide a dense deformation field that maps any tissue appearing on the planning CT to the CBCT. This deformation field can be used to warp the daily dose on the planning CT which constitutes the spatial reference for the clinician.
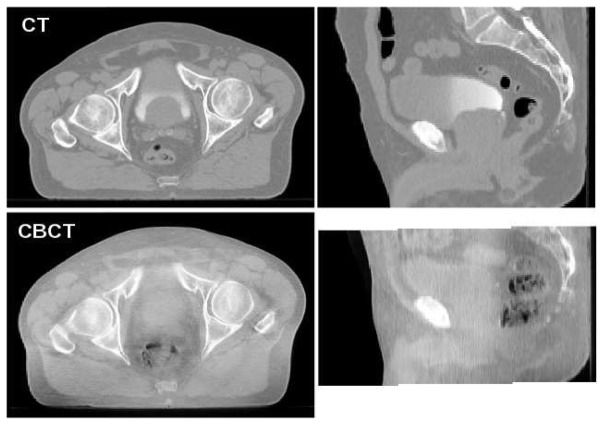
Few solutions have so far been advanced for the process of registering CBCT to CT for prostate cancer DGRT. Registering pelvic CT and CBCT is, in fact, very challenging, due to a number of different problems, including: (i) the significant deformations encountered in this anatomical area, especially for the bladder and the rectum; (ii) the poor soft tissue contrast in CBCT; (iii) the scatter effect observed in CBCT images; and (iv) the appearance and disappearance of bowel gases from one fraction to another. Fig. 1 provides an example of planning CT slices and corresponding daily CBCT slices. In this context, previous studies have suggested guiding the registration process by means of anatomical constraints. Greene et al [7] proposed a nonrigid registration solution with B-spline free-form deformations (FFD) maximizing a normalized cross correlation metric. By adding constraints to the control points of the deformations lying in soft organs and bones, the authors demonstrated improved alignment of these structures, but the method required prior segmentation. In a different study [8], Lu et al proposed an approach integrating the segmentation step. In the above mentioned studies, registration has been addressed as an isolated issue, with evaluation criteria based only on organ overlapping ratios (such as Dice score), whereas it should be addressed in the aim of dose tracking. Tissue overlaps and image similarity measures do not, in reality, ensure effective anatomical point matching [9], on which dose accumulation accuracy depends almost entirely. Some works have been reported about physical deformable phantoms [10], [11] simulating very simplified shapes. Thanks to a cylinder shaped gel dosimeter, [11] recently pointed out the need for comprehensive validation of deformable image registration in the aim of dose accumulation. A simplified finite-element model (FEM) based numerical phantom could be used for an assessment of registration, and particularly of the underlying nonrigid transformation. While these types of numerical phantoms have been considered for registration assessment [12], [13], this approach has, as far as we are aware, not been reported for dose accumulation assessment.
Fig. 1.
Top: Axial and sagittal slices of a planning CT example. Bottom: Identical corresponding slices of a rigidly registered daily CBCT
For prostate IGRT, considering patient repositioning protocol and clinical use of margins to account for geometric uncertainties on target location, the prostate is assumed to be in a homogeneous dose region at each treatment fraction. Moreover, the prostate is subject to only small deformations in the course of IGRT. The main issue is here to estimate the dose variations during treatment inside the walls of the bladder and rectum which are hollow organs.
In this study, we have proposed a full workflow for dose accumulation in the context of prostate IGRT. The proposed registration method enables different levels of geometrical constraints to be taken into consideration, ensuring more effective point-to-point correspondence at the surface of organs, especially with the presence of large deformations or in high-dose gradient areas. In order to assess dose accumulation accuracy, we designed a numerical phantom of pelvic deformation based on biomechanical modeling and image simulation. This model provided known deformations and a reference cumulated dose.
This paper takes the following structure: Section II provides a step by step description of the overall dose accumulation process for prostate IGRT, along with the NRR algorithms with different levels of constraints; Section III describes the numerical phantom we developed for accuracy assessment; Section IV outlines the methods assessment on the numerical phantom and real patient data, as well as the quantification of uncertainties on accumulated dose; and finally, we present our conclusions in Section V.
II. Dose accumulation process
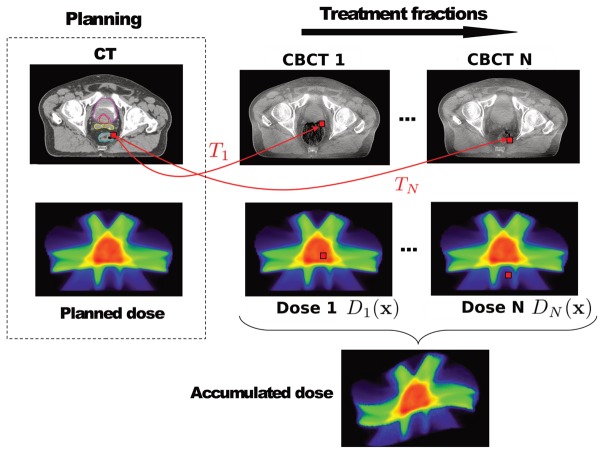
Fig. 2 provides an overview of the dose accumulation concept. At each treatment fraction n the CBCT is nonrigidly registered to the planning CT resulting in a transform Tn which provides a displacement for each voxel of the planning CT. By considering the daily dose distribution Dn, it is then possible to estimate the dose received at fraction n by any voxel of the reference CT. This estimated dose distribution, called “cumulative”, can be added to the cumulative dose distributions of the previous fractions in order to provide an estimation of the dose accumulated since treatment initiation.
Fig. 2.
Concept of tissue tracking for dose accumulation during prostate cancer IGRT. For each voxel V representing a tissue on the planning CT, a displacement Tn is estimated for each treatment fraction n. At fraction n, knowing the daily dose distribution Dn, it is then possible to estimate the cumulative dose received at voxel V and thus to accumulate the dose along the fractions.
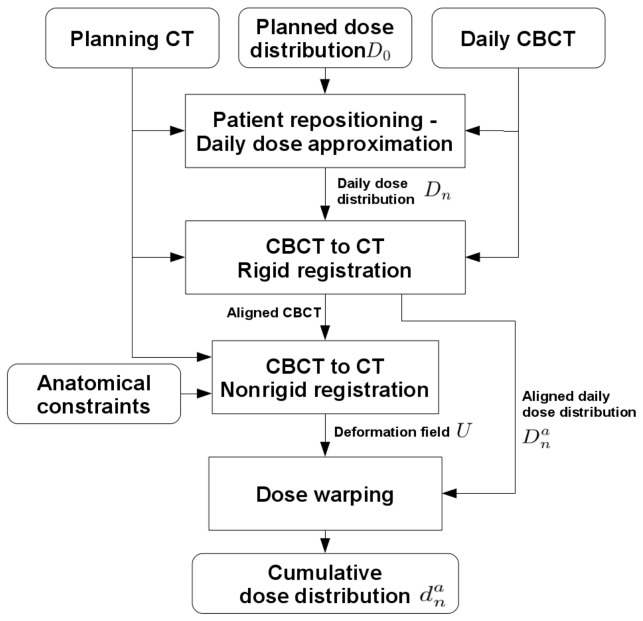
The proposed dose tracking workflow is illustrated in details in Fig. 3. First of all, the patient repositioning protocol had to be taken into account to compute the daily dose distribution. A CBCT to CT rigid registration was then required to initialize the NRR part of the process. In this study, we proposed and assessed the three following NRR approaches: (i) a fully iconic NRR between CBCT and CT (NRR); (ii) an iconic NRR constrained by interactively-defined landmarks (LCNRR); (iii) an NRR constrained by organ delineations (DBNRR). Finally, the deformation field computed by any of the NRR approaches was used to estimate the daily cumulative dose distribution. A step-by-step description of this workflow can be found in the following sections.
Fig. 3.
Overall process of dose accumulation. This process is applied for each daily CBCT.
A. Patient repositioning - Daily dose Approximation
Prior to daily irradiation, the treatment couch was shifted in the three directions according to the prostate position as observed on the CBCT scan. In our radiotherapy department, this shift was the result of a semi-automatic registration performed by the XVI Synergy® System (Elekta).
In principle, the dose distribution on the newly acquired image should be calculated using the treatment plan and taking into account the treatment couch shift. Following CBCT preprocessing and a density calibration between planning CT and CBCT [14] [15], this calculation can be performed either by the algorithms integrated into the treatment planning systems, or more accurately by means of Monte Carlo simulations [16]. Given the homogeneity of the tissues in the pelvic area, however, and their low depth variation relative to the outer contour of the patient, ”dose invariance to patient translation and organ deformation” can be assumed [17] [18] [19]. In [17] the authors compared shifted dose distributions with recalculated dose distributions. The resulting error on dose-volume metrics was inferior to 2%. In this work, we therefore approximated the dose distribution Dn at Day n by shifting the planned dose distribution D0 according to the three-dimensional couch treatment translation TS:
| (1) |
B. Rigid registration
The transform TS, corresponding to the couch shift, aligned the prostate on the CBCT with its equivalent on the CT. Since we considered the deformation of the surrounding organs, we introduced an additional rigid transform R, globally aligning the two images, to provide a better initialization for nonrigid registration. The translation and rotation parameters of R were determined by optimizing the mutual information between the two images with a gradient descent algorithm. The rigid transform was then applied in order to obtain the aligned CBCT. The daily dose distribution was also transformed using R to obtain the aligned daily dose distribution .
C. Nonrigid registration algorithm
The Demons registration algorithm has been applied in several radiotherapy studies involving CT to CT registration [20], [21], [22]. This algorithm nevertheless requires exact correspondence between the voxel intensities of the images to register, and therefore cannot be used for CBCT to CT registration. [23], [24] in a context of head-and-neck IGRT proposed to correct images intensities in order to apply the demons algorithm. However, these studies could be sensitive to the shading effect in the CBCT images. Some studies have suggested, not to correct image intensities, but to rely on metrics more robust to intensity variations like cross-correlation [25] and mutual information [26], [27]. These approaches present the advantages of the Demons algorithm while extending its field of application. In this study, we adapted a NRR algorithm proposed by [28]. The implemented method was based on a Demons-like framework, but aimed to maximize a mutual information metric. This metric is a global measure for the whole image that can be seen as the sum of local contributions SL. We then defined a global measure SG between the fixed CT image F and the moving CBCT image M as follows:
| (2) |
where iF(x) and iM(x) represent the voxel intensities at the three-dimensional coordinate x in images F and M respectively, and
| (3) |
where p(i1, i2) denotes the joint probability function and p(i1) and p(i2) the marginal probability functions computed from the whole images.
The optimisation of the similarity measure was performed iteratively by means of the following process:
M was deformed with the current global deformation field U (first iteration: no deformation) to obtain M′
p(iM′ (x)) was computed and the joint intensity probability p(iF (x), iM′(x)) was estimated by Parzen windowing of the joint histogram with a 2D Gaussian kernel.
-
For each voxel, a forward force corresponding to the point similarity gradient was computed as in the previous study [28]:
(4) as well as a reverse force Fr:(5) The deformation update at this voxel coordinate x was then calculated as:(6) where Δs represents an update length factor.
- The deformation update u was added to the global deformation field U:
(7) The global deformation field was regularized by convolution with a Gaussian kernel Ge, simulating an elastic behavior [29]: U ← U ⊗ Ge.
Convergence criteria: the registration stopped when the derivative of SL over the last ten iterations fell below a specified threshold.
The process was repeated three times in a coarse-to-fine multiresolution scheme. The images were downsampled by four at the first level, by two at the second and kept at their original resolution at the third. Variants of this algorithm have been investigated. Firstly, it appeared that the use of the symmetric force Fr in addition to the forward force Ff was essential with the considered definition of SL. Secondly, if a more natural way to combine the deformation fields by (7) would be to use a compositive transformation [30], this did not improve the results while it was computationally more expensive.
D. NRR with landmark constraints
In order to improve the dose accumulation accuracy of the NRR algorithm, we propose in this paper a constrained approach that allows to guide the CBCT-to-CT registration when the contrast is too poor on CBCT, and to establish better local anatomical correspondences on which relies the dose accumulation accuracy. In clinical practice, the structures of interest are systematically delineated on the planning CT. We propose to use this strong prior information along with some additional landmark constraints specified by the clinician, in order to increase NRR accuracy. The new proposed algorithm was identical to that which was described previously, except for the insertion of a new step between steps 5 and 6 designed to geometrically constrain the deformation field U.
A landmark constraint Cl represents a vector defined by a point belonging to a surface on the moving CBCT and by its approximate correspondence on the fixed CT. The set of N constraints is expressed as L = {C1…CN}.
Due to the frequency of errors inherent to the manual placement of landmarks on the considered 3D images, this method iteratively reevaluated each constraint Cl to allow for the point to slide on the organ surface of the CT in a defined radius of tolerance Dmax. At each iteration, every constraint Cl was then replaced by . With P denoting the set of points belonging to the organ surface on the CT:
| (8) |
with
| (9) |
L′ = {C1′…CN′} denotes the set of constraints for the current iteration.
The deformation field U at point x became a linear combination between its current estimation and the closest constraint Ck belonging to L′:
| (10) |
with
| (11) |
The coefficient Ψk was the product of two radial basis functions (RBF) ψ1 and ψ2 comprised between 0 and 1. The first RBF ψ1 aimed to decrease the influence of the constraint Ck as x is away from and from P:
| (12) |
with
| (13) |
The second RBF was the complementary of a normalized Gaussian function centered on that aimed to decrease the influence of Ck when approaches . In this way the estimation of could evolve over the iterations around the original point in the specified radius of tolerance Dmax
| (14) |
The constraints were similarly applied at all levels of the multiresolution scheme, the values of the parameters Dmax and σRBF1,2,3 expressed in millimeters being the same at all levels.
An alternative method would be to constrain the deformation field between steps 4 and 5 to keep the same regularization model as in the NRR method. With the current implementation, no regularization step followed the constraint step at the last iteration, which enabled to preserve the specified constraints.
E. Delineation based NRR
To further improve the registration, we propose a hybrid method combining a delineation of the organs with an intensity based similarity measure. It consists in registering distance maps derived from organ delineations in a similar approach as reported in [31]. The following procedure was implemented:
Given the surfaces of the prostate, the rectum and the bladder delineated on the planning CT, a 3D distance map γCT in the planning CT space was computed, representing the signed squared Euclidean distance from the closest surface point [32].
The same shape representation was computed for the delineated organs of the CBCT image: γCBCT
The distance map γCBCT was nonrigidly registered to γCT by applying the fast symmetric demons algorithm implemented in the Insight Toolkit (ITK) [33] [30]. In short, this algorithm is similar to that which was described in section II-C except in its computation of u (step 3) which depends on the gradient of the squared voxel intensity differences.
This kind of approach which employs signed distance maps has been proven able to provide dense deformation fields that closely match the surfaces, yet the probability of representing erroneous anatomical deformations increases with the distance from the organ surface. Nevertheless, since we were primarily interested in the dose in the rectum and bladder walls, which have a thickness of a few millimeters, a satisfactory cumulative dose estimation could be expected with this method.
F. Dose warping
In order to obtain a daily cumulative dose distribution , the aligned daily dose distribution was deformed following the field U and resampled in the planning CT space with a trilinear interpolation:
| (15) |
III. Numerical Phantom
This section provides a description of the generation of a FEM-based numerical phantom, consisting of a set of synthetic images with simulated simple, yet plausible deformations of the main organs. The purpose of this phantom was to evaluate and compare the performance of the three investigated NRR approaches for dose accumulation.
A. Modeling
The phantom included the following anatomical structures: prostate, seminal vesicles, bladder and rectum. The geometry of the structures were based on delineations from a typical patient with empty bladder and rectum. Mesh points defined from the delineation were imported into the ANSYS DesignModeler® modeling software. The organ surfaces were then created using B-spline curves connecting the points. The prostate and seminal vesicles were represented by volume structures, while the bladder, rectum and sigmoid colon were modeled by surface structures. The geometry was then discretized into tetrahedrons for the prostate and seminal vesicles, and triangles for the other organs.
The laws of the materials used for the bladder, rectum and sigmoid colon were derived from the mechanical characterization of pelvic tissues in [34]. For these organs, an Ogden model was then defined with the parameters provided in Table I. A linear law was used to describe the prostate and seminal vesicles behavior, with a Young’s modulus of 60 kPa and a Poisson’s ratio of 0.495.
TABLE I.
Ogden parameters of simulated organs
| Material parameters | Rectum/Sigmoid colon | Bladder |
|---|---|---|
|
| ||
| Ogden moduli μ | 0.0424 | 0.0412 |
| Exponent α | 14.598 | 6.767 |
The different contact properties between each organ and its neighbouring organs were defined as follows: bounded, frictionless or no separation. The boundary conditions were based on clinician’s observations and on [35], [36]. Stiffness in the form of an elastic support was added at the apex of the prostate that is actually maintained by the pelvic muscles. The inferoanterior part of the bladder is near to or touching the pelvis. An elastic support was added to this zone in order to simulate the presence of the pelvis and the surrounding tissues. This boundary condition limits the expansion of the bladder in this direction but authorizes tangential displacement (i.e. sliding) of the bladder surface. We assumed the lower part of the rectum to have a very low mobility as it is surrounded by muscle fibers. The extremal rectum edge was then fixed and an elastic support was added to the first 2 cm of the rectal wall. The posterior part of the rectum, located close to the spine, was further stiffened in order to limit the expansion of the rectum in the posterior direction. The parameter values of these boundary conditions were adjusted to obtain typical behavior, particularly allowing for a posteroanterior displacement of the prostate. Based on [37], [38], the bladder’s internal pressure was modified with values ranging from 0 to 5 kPa, that of the rectum with values from 0 to 2 kPa.
B. Simulation
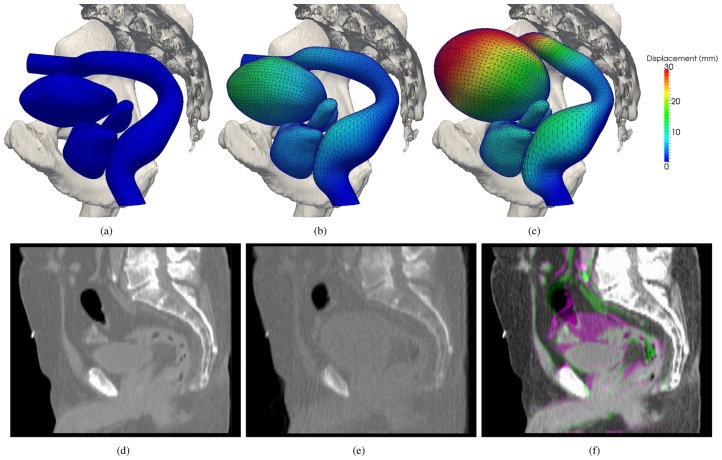
Different pressure values were applied to the initial bladder and rectum to cause deformation and observe the resulting displacements and deformations of neighbouring organs. A total of 15 pressure sets were applied using Ansys Mechanical®. With the initial organ mesh configuration, a total of 16 organ mesh configurations were obtained. The set of node correspondences between two mesh configurations defines a mesh deformation field. Fig. 4 displays the meshes of the initial anatomy configuration in (a), and two of the resulting meshes following deformation in (b) and (c). It appears that the simulation results in an anteroposterior displacement of the prostate of around 9 mm because of rectum deformations. In addition, the bladder mainly expands in the superoanterior direction, thanks to the defined boundary conditions and the contact with the sigmoid colon.
Fig. 4.
(a) Initial FEM mesh of the bladder, rectum, prostate and seminal vesicles; (b) and (c): two examples of deformation induced by pressure variation in the rectum and the bladder, with surface point displacements represented by the colormap; (d) sagittal slice of the simulated CT scan corresponding to the organ configuration in (a); (e) Sagittal slice of the simulated CBCT scan corresponding to the organ configuration in (c); (f) complementary color overlay of two simulated CT images highlighting the deformation magnitude between two extreme cases.
C. Image construction
A total of 16 synthetic images were created from the 16 simulated organ mesh sets. In order to obtain realistic CT/CBCT images, the following procedure was developed:
The delineation of the template patient’s body contour, bones, prostate, bladder, rectum and seminal vesicles was used to compute a distance map γT by means of the method described in section II-E.
The 16 organ mesh sets were then rasterized into binary volumes and for each set a distance map γn was computed as for the template patient.
γT was registered to each γn by applying the fast symmetric demons algorithm, and deformed accordingly each time, producing a synthetic CT image with organ shapes identical to the simulated ones.
The main advantage of this procedure was to generate realistic images with low contrast and additional neighbouring soft tissues existing in real images. The choice of such a registration approach to determine gray levels in the simulated images may slightly influence the results of the methods to evaluate thereafter. However, the performance of the evaluated methods will not be overestimated because the reference deformations were not directly used to compute the gray levels of the phantom images.
In order to simulate a clinical case where the patient received a critically increased dose to the rectum and bladder than planned, the planning CT was chosen as presenting the most distended rectum and bladder. Yet, many clinical test cases could be simulated by sorting the images in different orders. The 15 remaining CTs were converted to CBCT images by computing 2D x-ray projections, adding noise and blurring as in [39], and reconstructing a 3D image using the FDK algorithm implemented in the reconstruction toolkit (RTK) [40]. Fig. 4 displays a sagittal slice of the simulated planning CT in (d) and the equivalent slice of a simulated CBCT in (e). In (f), by superimposing two CT images, the deformation magnitude that must be addressed by NRR is highlighted.
D. Associated dose distributions
The simulated planning CT scan was imported in the Philips Pinnacle® treatment planning system (TPS) in order to generate a planning dose distribution D0, delivering 80 Gy to the prostate using intensity modulated radiotherapy (IMRT). The dose at each fraction was obtained by shifting D0 for prostate motion correction as described in Section II-A. The cumulative dose da at treatment fraction n was then known for each initial mesh node k of coordinates xk:
| (16) |
where S represents the mesh deformation field given by the numerical simulation. The reference accumulated dose DA for each node k was then obtained by summing up from the 15 simulated treatment fractions.
The most relevant assessment tool for the clinician is the dose-volume histogram (DVH). In short, for each given dose within a structure, it represents the volume that receives at least this dose. The bladder and rectum are, however, defined by surface meshes, and in order to compute DVHs for these two organs, we transformed S into a dense deformation field U defined at each voxel of the planning CT. U was obtained by multivariate interpolation, as shown below:
| (17) |
where K represents the number of mesh points and αk(x) the inverse of the Euclidean distance between x and the node k. Each vector of the dense deformation field is computed as a weighted average of the vectors given by the mesh deformation. The weight corresponds to the inverse of the Euclidean distance. With this interpolation, the generated field presents local deformations limited to the neighborhood of the organs.
Lastly, each daily aligned dose distribution was warped with the corresponding deformation field U as described in Section II-F in order to obtain a reference of the daily cumulative dose distribution . The 15 daily cumulative dose distributions were totaled to provide a reference for the accumulated dose DA.
IV. Experiments and results
In addition to the phantom data, the proposed workflow was also evaluated for three patients undergoing treatment for prostate cancer with daily CBCT acquisition.
The prostate, bladder and rectum were delineated by means of the ARTiView® software on 36 CBCTs for the first patient, 22 CBCTs for the second, and 32 CBCTs for the third. For the landmark constrained NRR (LCNRR), we set out guidelines for a reproducible landmark positioning method. Following these guidelines, an expert placed on each image a total of six landmark correspondences at the bladder vertices and eight on the rectum surface approximately at the apex and base of the prostate.
The process of dose accumulation as described in Section II was then applied to the phantom and the three patients for all three proposed NRR approaches.
A. Algorithm parameters
The parameters used in the registration methods were defined as follows. Firstly, we selected the parameters of the NRR method which maximized the Dice scores for five images of one patient: Δs = 0.3 and σe = 2.5 voxels.
The same parameters were kept ensuring that specifying landmark constraints locally did not modify the results in the other parts of the image when compared to the NRR method. The parameters were chosen in order to minimize the registration error with two phantom images: σRBF1 was set to 15 mm, σRBF2 to 5 mm and σRBF3 to 1 mm. The landmarks placement tolerance Dmax was set to 10 mm. For the Delineation based NRR (DBNRR), the regularization parameter used in the Demons algorithm was set to σe = 0.8 voxels.
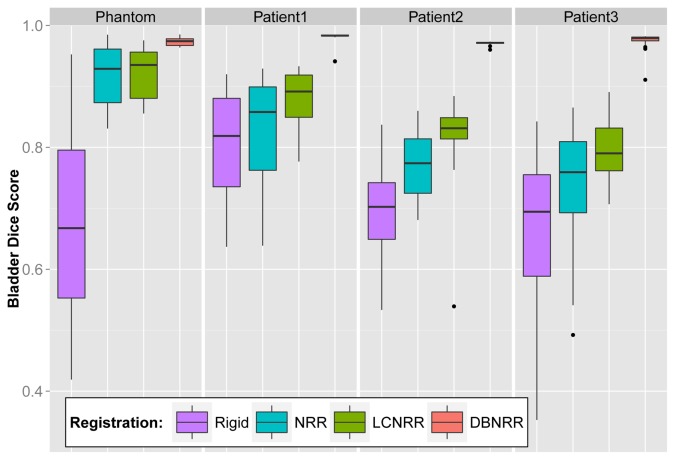
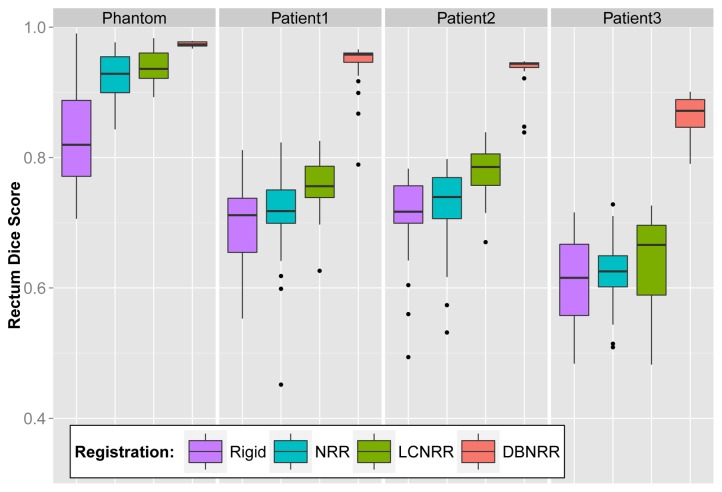
B. Dice scores
Fig. 5 and Fig. 6 display the Dice scores obtained following each registration method for the bladder and rectum. For the NRR and LCNRR, the registration performance is higher for the phantom images than for the patient images. The main reason is that the CBCT simulation ignores scatter effect which reduces contrast during real image acquisition. Nevertheless, according to the Dice scores, the performance ranking was the same for both the phantom and the patients: NRR, LCNRR and DBNRR. In case of NRR or LCNRR, interpretation of these results must take into account delineation variability. In [41], the authors quantified the inter-observer delineation variability on CBCT images. The Dice score equivalent to their overlap measure was equal to 0.85 for the bladder and the rectum. This value can therefore be considered as a reasonable Dice score objective for registration based on original image intensities.
Fig. 5.
Boxplots of bladder Dice scores obtained for each registration strategy.
Fig. 6.
Boxplots of rectum Dice scores obtained for each registration strategy.
C. Registration Errors
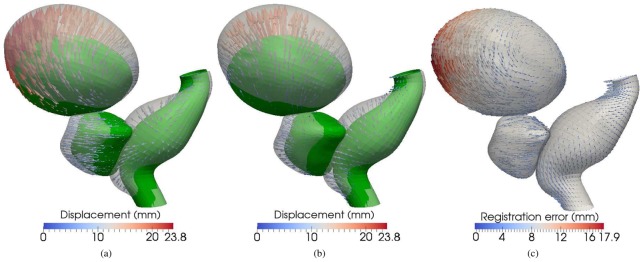
For each point of the initial phantom mesh, registration error was computed as the norm of the difference between the reference deformation field vectors and those of the deformation field estimated by registration. Fig. 7 (a) shows the reference deformation field between the initial organ configuration and that of one of the 15 phases; (b) represents the deformation field estimated with DBNRR; (c) the registration error defined by the difference between the two fields.
Fig. 7.
(a) Reference deformation field between two organ configurations ; (b) deformation field estimated with DBNRR; (c) difference between the two deformation fields in (a) and (b).
Table II provides the mean local registration errors recorded following registration of an extreme case (Fig. 4 (e)) on the planning CT (Fig. 4 (d)). As expected, the ranking was: NRR, LCNRR and DBNRR. However, even in case of DBNRR, large registration errors can occur. For example, in this case, the registration error reached 14.3 mm for the bladder despite a Dice score of 0.97. It appears in the Fig. 7 that, where there is sliding of the tissues, the displacements are the most challenging to estimate.
TABLE II.
Phantom Mean Registration Errors (mm)
| Registration | Bladder | Rectum | Prostate | Overall (3 organs) | ||||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| Mean | Max | Mean | Max | Mean | Max | Mean | Max | |
|
| ||||||||
| Rigid | 22.93 ± 10.20 | 39.98 | 4.18 ±3.36 | 11.86 | 8.81 ±0.28 | 9.43 | 13.60 ± 10.40 | 39.98 |
| NRR | 11.23 ± 7.22 | 28.84 | 3.84 ±1.91 | 9.88 | 6.68 ±1.05 | 8.70 | 7.93 ± 5.57 | 28.84 |
| LCNRR | 9.60 ± 4.63 | 22.91 | 2.91 ±1.79 | 7.00 | 5.34 ±2.26 | 12.23 | 6.56 ± 4.31 | 22.91 |
| DBNRR | 7.56 ± 3.49 | 14.30 | 2.29 ±1.22 | 6.32 | 4.96 ±2.86 | 10.84 | 5.45 ± 3.52 | 14.30 |
The impact of these registration errors on cumulative dose estimation is not yet clear. Large errors in an homogeneous dose area can, in actual fact, have less of an impact than small errors in a high-dose gradient area. For this reason, we must also assess the methods in terms of dose accumulation accuracy.
D. Cumulative dose estimation errors
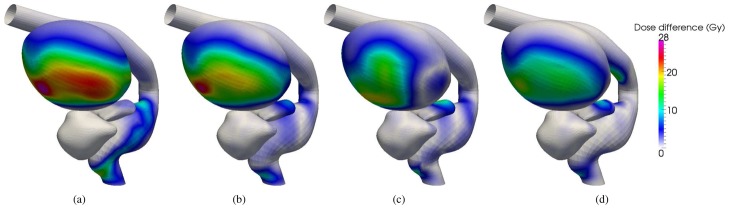
The performance of each dose accumulation method was evaluated by means of the numerical phantom. Firstly, the local dose estimation error was evaluated in each node of the organ meshes. Fig. 8 (a) displays the absolute differences between the planned and the reference accumulated doses, computed as explained in Section III-D. We verified that the prostate received the prescribed dose, primarily due to the patient repositioning (see Section II-A). Nevertheless, large differences were observed on the bladder and rectum surfaces due to organ deformations, which thus justified the need for nonrigid registration in order to estimate the deviation from the planned dose. Fig. 8 (b), (c) and (d) display the differences between the reference accumulated dose and that which was estimated using NRR, LCNRR and DBNRR, respectively. Even in case of DBNRR, large dose estimation errors were made locally (more than 15 Gy). Table III outlines the mean dose estimation error for each registration method. Both DBNRR and LCNRR outperformed NRR in terms of dose estimation accuracy. The LCNRR method could achieve almost the same error as DBNRR, in comparison with the initial error.
Fig. 8.
Absolute difference on organ surfaces between the reference accumulated dose and: (a) planned dose, (b) accumulated dose with NRR, (c) accumulated dose with LCNRR, and (d) accumulated dose with DBNRR.
TABLE III.
Phantom Mean Dose Errors (Gy)
| Registration | Bladder | Rectum | Prostate | Overall (3 organs) | ||||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| Mean | Max | Mean | Max | Mean | Max | Mean | Max | |
|
| ||||||||
| Rigid | 9.14 ± 6.73 | 28.59 | 3.56 ± 3.21 | 18.06 | 0.08 ± 0.07 | 0.52 | 4.53 ± 6.09 | 28.59 |
| NRR | 5.66 ± 5.63 | 26.82 | 1.87 ± 1.86 | 10.32 | 0.31 ± 0.27 | 1.45 | 2.83 ± 4.43 | 26.82 |
| LCNRR | 4.76 ± 4.71 | 19.38 | 1.46 ± 1.73 | 13.67 | 0.29 ± 0.23 | 1.52 | 2.36 ± 3.73 | 19.38 |
| DBNRR | 3.78 ± 4.03 | 17.49 | 1.09 ± 1.54 | 10.24 | 0.22 ± 0.20 | 1.40 | 1.86 ± 3.13 | 17.49 |
E. Sensitivity to landmarks placement uncertainties
In order to quantify the sensitivity of dose accumulation to landmark selection in the LCNRR method, we simulated 30 different sets of constraints. The 14 landmarks on the planning CT were fixed. For each simulated set of constraints, the 14 corresponding points on the CBCT were selected randomly following a uniform distribution in a radius ranging from 0 mm to 8 mm around the ground truth provided by the model. For the sake of comparison, our expert selected the landmarks at a mean distance of 4.93±2.72 mm for the bladder and 1.88±0.98 mm for the rectum. The variability of the mean dose error on the bladder and rectum surfaces, depending on the radius value is provided in table IV.
TABLE IV.
Dose estimation errors with respect to landmark placement uncertainties (Gy)
| Error radius | Bladder | Rectum | ||
|---|---|---|---|---|
|
| ||||
| Mean | Max | Mean | Max | |
|
| ||||
| 0 mm | 3.24 | 14.25 | 1.32 | 10.54 |
| 2 mm | 3.33 ± 0.14 | 14.91 ± 0.73 | 1.51 ± 0.21 | 10.08 ± 2.69 |
| 4 mm | 3.66 ± 0.29 | 15.28 ± 1.31 | 1.91 ± 0.45 | 10.39 ± 4.79 |
| 6 mm | 3.98 ± 0.46 | 16.51 ± 1.43 | 2.42 ± 0.70 | 12.48 ± 5.72 |
| 8 mm | 4.38 ± 0.77 | 18.28 ± 1.80 | 3.00 ± 0.92 | 14.93 ± 6.56 |
The LCNRR appears to be robust to the uncertainties in landmark selection. If we refer to table III, the dose estimation accuracy is improved compared to NRR even when the uncertainty radius reaches 8 mm for the bladder or when it is less than 4 mm for the rectum.
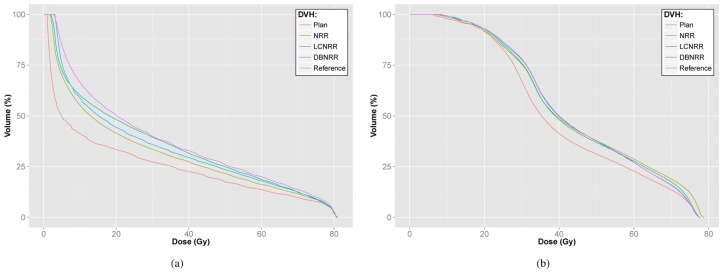
F. Global measures of dose estimation accuracy
The dose volume histograms (DVH) were computed as described in Section III-D and are presented in Fig. 9 for the rectum and bladder. To quantify the performance of each method, we defined the distance ℒ between two histograms h1 and h2 as:
| (18) |
Fig. 9.
Numerical phantom results: representation of the planned DVH, reference accumulated DVH and accumulated DVHs, as estimated with the three NRR approaches for:(a) the bladder wall; and (b) the rectum wall.
This distance is then comprised between 0 (when h1(x) and h2(x) are identical) and 100 (when, for all doses, one is equal to 100% and the other to 0%). The distances between the histogram of the accumulated and the reference DVHs are provided in Table V. According to these evaluation criteria, the ranking remained the same except for the bladder for which we obtained a better DVH with LCNRR than with DBNRR. This result depends on the relationship between the localisation of the landmark constraints and the dose distribution. According to the DVHs, it seems that, when using the LCNRR, more dose estimation errors were made for the low dose (between 3 and 5 Gy) than when using the DBNRR. On the contrary, the LCNRR improved the dose estimation in areas of higher dose (between 8 and 70 Gy) compared to the DBNRR, thanks to a locally better anatomical point matching accuracy. The low dose regions on the bladder surface being larger than the high dose regions, the mean dose errors provided in table III were in favor of the DBNRR. The higher dose area being potentially a more clinically relevant area, our proposal to place the landmark constraints at the six vertices of the bladder appears well suited to improve the dose accumulation for this organ.
TABLE V.
Dose-Volume Histograms - Distances From reference
| Dose type | Bladder wall | Rectum wall | Prostate |
|---|---|---|---|
|
| |||
| Planned | 12.0 | 4.1 | 0.03 |
| Cumulated with NRR | 5.8 | 1.6 | 0.09 |
| Cumulated with LCNRR | 2.1 | 1.0 | 0.08 |
| Cumulated with DBNRR | 3.4 | 0.2 | 0.12 |
V. Discussion
We have proposed and evaluated an approach for dose accumulation in case of prostate IGRT.
Before any consideration for clinical application, the proposed registration methods with different levels of interactions have to be deeply evaluated regarding the ultimate objective, dose monitoring in this case. The different approaches were evaluated and compared, not only with images similarity or organ overlap metrics as in previous works, but in terms of capability to match anatomical points on organ surfaces and in terms of resulting dose estimation accuracy. To achieve this, typical organs deformations were simulated with a biomechanical model of the organs of interest. The registration error and resulting cumulative dose estimation error were locally quantified on the organ surfaces.
Our contribution does not address the general issue of dose tracking within a volume. Nevertheless, we proposed a solution for dose accumulation constrained at the surface of organs at risks (rectum and bladder) that are subject to the most important deformations in the context of prostate IGRT. We think that surface constrained dose accumulation makes sense in the case of rectum and bladder since these are hollow organs with a relatively thin wall.
A limitation of the dose accumulation approaches based on CBCT is that the intrafraction motion is ignored, since images are acquired prior to treatment delivery. Even if the intrafraction motion is significantly smaller than the interfraction motion, the issue of its impact on the cumulated dose has still to be addressed.
Another limitation of this study concerns dose warping which could be prone to error because voxel volume variations were not taken into account. Previous studies have proposed more accurate methods [42], such as warping the mass or energy deposits in the images instead of directly warping the dose. However, this approach would require a simulation of the energy deposit distribution, conducted using Monte Carlo methods, and its feasibility on CBCT images has not yet been demonstrated.
There is today a need to evaluate the capability of registration algorithm to estimate right anatomical point correspondences on which depends the dose accumulation accuracy. In this paper, we focused on the evaluation of the dose accumulation on organ surfaces by means of a numerical phantom. The proposed numerical phantom simulates simplified deformations compared to the complex nature of real anatomical changes and deformations. Nevertheless, its ability to present a variety of plausible deformations, including sliding tissues, is challenging for nonrigid registration algorithms. As a consequence, we have demonstrated that a delineation-based algorithm could result in high Dice scores, but locally to large cumulative dose estimation errors. This issue has rarely been addressed in the reported work. The evaluation with the numerical phantom shows that the largest registration errors appear where tissues are sliding. The proposed registration methods are not specifically designed to estimate these kinds of displacements. Only the LCNRR partially allows to take them into account, compared to a conventional registration algorithm, provided that the expert is able to specify the actual anatomical correspondences. A further improvement of the registration method that may help to estimate the sliding would be to integrate a biomechanical model through a FEM-based approach. However, it appears challenging due to the multiple interactions between the structures and their different configurations over treatment fractions (e.g. content of the bladder and rectum). In this case, the issue of the mechanical parameters identification should be addressed.
VI. Conclusion
In this study, we have formalized a full workflow for dose accumulation in case of prostate IGRT. Three nonrigid registration approaches, requiring different user interaction levels were proposed. Our study demonstrated that the intensity based nonrigid registration method (NRR), that requires no interactive definition of constraining features (landmarks, delineations), could provide a cumulative dose estimation that came much closer to the actual delivered dose than the planned dose did. The LCNRR method relies on the NRR method and integrates local anatomical constraints on organ surfaces to guide the registration. This approach proved the feasibility of improving local cumulative dose estimation with minimal interactivity. The DBNRR method does not directly register the original images, but rather a distance field derived from prior delineation of the organs of interest. We were therefore able to considerably reduce the local difference between the reference and estimated doses. However, the delineation of one CBCT is very time consuming, and can be only considered for studies including a very limited number of patients. For clinical routine the proposed LCNRR method appears to offer a good compromise between the estimation of deviation from the planned dose and the level of user interaction. Especially given that, when used to derive global measures such as DVHs, the LCNRR yielded to results close to the ones obtained with the DBNRR.
Acknowledgments
This work has been partially supported by the French National Research Agency (ANR) through project TIGRE n° ANR-09-BLAN-0378 and through Labex CAMI (ANR-11-LABX-0004-01).
References
- 1.Jaffray DA, Siewerdsen JH, Wong JW, Martinez AA. Flat-panel cone-beam computed tomography for image-guided radiation therapy. International Journal of Radiation Oncology* Biology* Physics. 2002;53(5):1337–1349. doi: 10.1016/s0360-3016(02)02884-5. [DOI] [PubMed] [Google Scholar]
- 2.Thilmann C, Nill S, Tucking T, Hoss A, Hesse B, Dietrich L, Bendl R, Rhein B, Haring P, Thieke C, et al. Correction of patient positioning errors based on in-line cone beam CTs: clinical implementation and first experiences. Radiation Oncology. 2006;1(1):16. doi: 10.1186/1748-717X-1-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chen J, Morin O, Aubin M, Bucci M, Chuang C, Pouliot J. Dose-guided radiation therapy with megavoltage cone-beam CT. Br J Radiol. 2006;79:S87–S98. doi: 10.1259/bjr/60612178. [DOI] [PubMed] [Google Scholar]
- 4.Pouliot J. Megavoltage imaging, megavoltage cone beam CT and dose-guided radiation therapy. Front Radiat Ther Oncol. 2007;40:132–142. doi: 10.1159/000106032. [DOI] [PubMed] [Google Scholar]
- 5.Schaly B, Kempe J, Bauman G, Battista J, Dyk J. Tracking the dose distribution in radiation therapy by accounting for variable anatomy. Physics in Medicine and Biology. 2004;49:791. doi: 10.1088/0031-9155/49/5/010. [DOI] [PubMed] [Google Scholar]
- 6.Foskey M, Davis B, Goyal L, Chang S, Chaney E, Strehl N, Tomei S, Rosenman J, Joshi S. Large deformation three-dimensional image registration in image-guided radiation therapy. Physics in Medicine and Biology. 2005;50:5869. doi: 10.1088/0031-9155/50/24/008. [DOI] [PubMed] [Google Scholar]
- 7.Greene W, Chelikani S, Purushothaman K, Knisely J, Chen Z, Papademetris X, Staib L, Duncan J. Constrained non-rigid registration for use in image-guided adaptive radiotherapy. Medical image analysis. 2009;13(5):809–817. doi: 10.1016/j.media.2009.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lu C, Chelikani S, Papademetris X, Knisely J, Milosevic M, Chen Z, Jaffray D, Staib L, Duncan J. An integrated approach to segmentation and nonrigid registration for application in image-guided pelvic radiotherapy. Medical Image Analysis. 2011;15(5):772. doi: 10.1016/j.media.2011.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rohlfing T. Image similarity and tissue overlaps as surrogates for image registration accuracy: Widely used but unreliable. IEEE transactions on medical imaging. 2011 doi: 10.1109/TMI.2011.2163944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kirby N, Chuang C, Pouliot J. A two-dimensional deformable phantom for quantitatively verifying deformation algorithms. Medical Physics. 2011;38:4583. doi: 10.1118/1.3597881. [DOI] [PubMed] [Google Scholar]
- 11.Juang T, Das S, Adamovics J, Benning R, Oldham M. On the need for comprehensive validation of deformable image registration, investigated with a novel 3-dimensional deformable dosimeter. International Journal of Radiation Oncology* Biology* Physics. 2013;87(2):414–421. doi: 10.1016/j.ijrobp.2013.05.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Schnabel J, Tanner C, Castellano-Smith A, Degenhard A, Leach M, Hose D, Hill D, Hawkes D. Validation of nonrigid image registration using finite-element methods: application to breast mr images. Medical Imaging, IEEE Transactions on. 2003;22(2):238–247. doi: 10.1109/TMI.2002.808367. [DOI] [PubMed] [Google Scholar]
- 13.Nie K, Chuang C, Kirby N, Braunstein S, Pouliot J. Site-specific deformable imaging registration algorithm selection using patient-based simulated deformations. Medical physics. 2013;40:041911. doi: 10.1118/1.4793723. [DOI] [PubMed] [Google Scholar]
- 14.Cheung J, Aubry J, Yom S, Gottschalk A, Celi J, Pouliot J. Dose recalculation and the dose-guided radiation therapy (DGRT) process using megavoltage cone-beam CT. International Journal of Radiation Oncology* Biology* Physics. 2009;74(2):583–592. doi: 10.1016/j.ijrobp.2008.12.034. [DOI] [PubMed] [Google Scholar]
- 15.Richter A, Hu Q, Steglich D, Baier K, Wilbert J, Guckenberger M, Flentje M. Investigation of the usability of conebeam CT data sets for dose calculation. Radiat Oncol. 2008;3(1):42. doi: 10.1186/1748-717X-3-42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Paganetti H, Jiang H, Adams J, Chen G, Rietzel E. Monte carlo simulations with time-dependent geometries to investigate effects of organ motion with high temporal resolution. International Journal of Radiation Oncology* Biology* Physics. 2004;60(3):942–950. doi: 10.1016/j.ijrobp.2004.06.024. [DOI] [PubMed] [Google Scholar]
- 17.Sharma M, Weiss E, Siebers J. Dose deformation-invariance in adaptive prostate radiation therapy: Implication for treatment simulations. Radiotherapy and Oncology. 2012;105(2):207–213. doi: 10.1016/j.radonc.2012.10.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Baum C, Alber M, Birkner M, Nüsslin F. Treatment simulation approaches for the estimation of the distributions of treatment quality parameters generated by geometrical uncertainties. Physics in medicine and biology. 2004;49:5475. doi: 10.1088/0031-9155/49/24/006. [DOI] [PubMed] [Google Scholar]
- 19.Craig T, Battista J, Van Dyk J. Limitations of a convolution method for modeling geometric uncertainties in radiation therapy. I. the effect of shift invariance. Medical physics. 2003;30:2001. doi: 10.1118/1.1589492. [DOI] [PubMed] [Google Scholar]
- 20.Wang H, Dong L, O’Daniel J, Mohan R, Garden AS, Ang KK, Kuban DA, Bonnen M, Chang JY, Cheung R. Validation of an accelerated’demons’ algorithm for deformable image registration in radiation therapy. Physics in Medicine and Biology. 2005;50(12):2887. doi: 10.1088/0031-9155/50/12/011. [DOI] [PubMed] [Google Scholar]
- 21.Castadot P, Lee JA, Parraga A, Geets X, Macq B, Grégoire V. Comparison of 12 deformable registration strategies in adaptive radiation therapy for the treatment of head and neck tumors. Radiotherapy and oncology. 2008;89(1):1–12. doi: 10.1016/j.radonc.2008.04.010. [DOI] [PubMed] [Google Scholar]
- 22.Brock KK. Results of a multi-institution deformable registration accuracy study (midras) International Journal of Radiation Oncology* Biology* Physics. 2010;76(2):583–596. doi: 10.1016/j.ijrobp.2009.06.031. [DOI] [PubMed] [Google Scholar]
- 23.Hou J, Guerrero M, Chen W, DSouza WD. Deformable planning CT to cone-beam CT image registration in head-and-neck cancer. Medical physics. 2011;38:2088. doi: 10.1118/1.3554647. [DOI] [PubMed] [Google Scholar]
- 24.Nithiananthan S, Schafer S, Uneri A, Mirota DJ, Stayman JW, Zbijewski W, Brock KK, Daly MJ, Chan H, Irish JC, et al. Demons deformable registration of CT and cone-beam CT using an iterative intensity matching approach. Medical physics. 2011;38:1785. doi: 10.1118/1.3555037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Avants BB, Epstein CL, Grossman M, Gee JC. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Medical image analysis. 2008;12(1):26–41. doi: 10.1016/j.media.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Modat M, Vercauteren T, Ridgway GR, Hawkes DJ, Fox NC, Ourselin S. Diffeomorphic demons using normalized mutual information, evaluation on multimodal brain mr images. SPIE Medical Imaging. 2010:76 232K–76 232K. [Google Scholar]
- 27.Lu H, Reyes M, Serifovic A, Weber S, Sakurai Y, Yamagata H, Cattin PC. Multi-modal diffeomorphic demons registration based on point-wise mutual information. Biomedical Imaging: From Nano to Macro, 2010 IEEE International Symposium on; IEEE; 2010. pp. 372–375. [Google Scholar]
- 28.Rogelj P, Kovai S, Gee J. Point similarity measures for non-rigid registration of multi-modal data. Computer vision and image understanding. 2003;92(1):112–140. [Google Scholar]
- 29.Pennec X, Cachier P, Ayache N. Medical Image Computing and Computer-Assisted Intervention–MICCAI99. Springer; 1999. Understanding the demons algorithm: 3D non-rigid registration by gradient descent; pp. 597–605. [Google Scholar]
- 30.Vercauteren T, Pennec X, Perchant A, Ayache N, et al. Diffeomorphic demons using itks finite difference solver hierarchy. The Insight Journal. 2007;1 [Google Scholar]
- 31.Reaungamornrat S, Liu W, Wang A, Otake Y, Nithiananthan S, Uneri A, Schafer S, Tryggestad E, Richmon J, Sorger J, et al. Deformable image registration for cone-beam ct guided transoral robotic base-of-tongue surgery. Physics in medicine and biology. 2013;58(14):4951. doi: 10.1088/0031-9155/58/14/4951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Maurer CR, Jr, Qi R, Raghavan V. A linear time algorithm for computing exact euclidean distance transforms of binary images in arbitrary dimensions. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 2003;25(2):265–270. [Google Scholar]
- 33.Ibanez L, Schroeder W, Ng L, Cates J, et al. The ITK software guide. Vol. 8 Kitware; 2005. [Google Scholar]
- 34.Brieu M, Boukerrou M, Dubois P, Cosson M, Rubod C. Vers une modelisation du comportement de la cavite pelvienne. 18eme Congres Francais de Mecanique Grenoble; 2007; 2007. [Google Scholar]
- 35.Boubaker MB, Haboussi M, Ganghoffer JF, Aletti P. Finite element simulation of interactions between pelvic organs: Predictive model of the prostate motion in the context of radiotherapy. Journal of biomechanics. 2009;42(12):1862–1868. doi: 10.1016/j.jbiomech.2009.05.022. [DOI] [PubMed] [Google Scholar]
- 36.Keros L, Bernier V, Aletti P, Marchesi V, Wolf D, Noel A. Qualitative estimation of pelvic organ interactions and their consequences on prostate motion: study on a deceased person. Medical physics. 2006;33:1902. doi: 10.1118/1.2198190. [DOI] [PubMed] [Google Scholar]
- 37.Constantinou C, Djurhuus J, Silverman D, Towns A, Wong L, Govan D. Isometric detrusor pressure during bladder filling and its dependency on bladder volume and interruption to flow in control subjects. The Journal of urology. 1984;131(1):86–90. doi: 10.1016/s0022-5347(17)50213-x. [DOI] [PubMed] [Google Scholar]
- 38.Haynes W, Read N. Ano-rectal activity in man during rectal infusion of saline: a dynamic assessment of the anal continence mechanism. The Journal of physiology. 1982;330(1):45–56. doi: 10.1113/jphysiol.1982.sp014327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tu S, Shaw C, Chen L. Noise simulation in cone beam CT imaging with parallel computing. Physics in medicine and biology. 2006;51(5):1283. doi: 10.1088/0031-9155/51/5/017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.“Reconstruction toolkit (rtk),” http://www.openrtk.org.
- 41.Foroudi F, Haworth A, Pangehel A, Wong J, Roxby P, Duchesne G, Williams S, Tai K. Inter-observer variability of clinical target volume delineation for bladder cancer using CT and cone beam CT. Journal of medical imaging and radiation oncology. 2009;53(1):100–106. doi: 10.1111/j.1754-9485.2009.02044.x. [DOI] [PubMed] [Google Scholar]
- 42.Zhong H, Siebers J. Monte Carlo dose mapping on deforming anatomy. Physics in medicine and biology. 2009;54:5815. doi: 10.1088/0031-9155/54/19/010. [DOI] [PMC free article] [PubMed] [Google Scholar]