The accommodation index measures the perturbation associated with insertions and deletions in coiled‐coils: Application to understand signaling in histidine kinases

Abstract

Coiled‐coils are essential components of many protein complexes. First discovered in structural proteins such as keratins, they have since been found to figure largely in the assembly and dynamics required for diverse functions, including membrane fusion, signal transduction and motors. Coiled‐coils have a characteristic repeating seven‐residue geometric and sequence motif, which is sometimes interrupted by the insertion of one or more residues. Such insertions are often highly conserved and critical to interdomain communication in signaling proteins such as bacterial histidine kinases. Here we develop the “accommodation index” as a parameter that allows automatic detection and classification of insertions based on the three dimensional structure of a protein. This method allows precise identification of the type of insertion and the “accommodation length” over which the insertion is structurally accommodated. A simple theory is presented that predicts the structural perturbations of 1, 3, 4 residue insertions as a function of the length over which the insertion is accommodated. Analysis of experimental structures is in good agreement with theory, and shows that short accommodation lengths give rise to greater perturbation of helix packing angles, changes in local helical phase, and increased structural asymmetry relative to long accommodation lengths. Cytoplasmic domains of histidine kinases in different signaling states display large changes in their accommodation lengths, which can now be seen to underlie diverse structural transitions including symmetry/asymmetry and local variations in helical phase that accompany signal transduction.

Abbreviations

R₀

superhelical radius

R₁

minorhelical radius

ω₀

superhelical angular frequency

ω₁

minorhelical angular frequency

ω_α

alpha‐helical angular frequency

N_super

superhelical repeat

N_minor

minorhelical repeat

N_α

alpha‐helical repeat

d

rise per residue of the minorhelix

l

helical path length along one turn of the minorhelix

P_super

superhelical pitch

α

superhelical pitch angle

AI

accommodation index

I_A

insertion index

L_A

accommodation length

Φ₁

minorhelical phase

skip

1‐residue insertion in the heptad repeat

stutter

4‐residue insertion in the heptad repeat

stammer

3‐residue insertion in the heptad repeat

HK

histidine kinase

HAMP

domain present in Histidine kinases, Adenyl cyclases, Methyl‐accepting proteins, and Phosphatases

PAS

Per‐Arnt‐Sim domain

DHp

N‐terminal dimerization and histidine phosphotransfer domain

CA

catalytic domain

S‐helix

signaling helix

Introduction

Coiled‐coils figure largely in the protein universe.1, 2, 3 First detected in mechanically rigid structural proteins, coiled‐coils have since been shown to be critical to multiple dynamic functions. Fusion proteins often contain metastable structural domains that rearrange into thermodynamically stable but dynamically responsive coiled‐coils—the favorable driving force for coiled‐coil elongation is harnessed to overcome the unfavorable energetic barrier associated with membrane fusion.4, 5, 6, 7 In other cases, coiled‐coil proteins form hubs for the assembly of multiple cofactors involved in transcription and vesicle trafficking.8, 9, 10, 11, 12, 13, 14 Finally, coiled‐coils are often seen in highly elongated proteins involved in signal transduction, faithfully transmitting signals across membranes, sometimes signaling over hundreds of Angstroms.15, 16 In this article we describe a theory to predict the structural effects of insertions in the otherwise regular packing seen in the structures of coiled‐coils, as well as a metric that allows automatic detection and classification of insertions based on the three dimensional structure of a protein. Using histidine kinases (HKs) as a test system, we show that these defects can be accommodated in different ways in distinct signaling states. This analysis elucidates previously undiscovered relationships between seemingly disparate models that have been proposed to explain the signaling of HKs. Finally, this method provides a parametric approach to design proteins that incorporate specific structural deviations from canonical coiled‐coils.

The functional versatility of coiled‐coils emphasizes their structural diversity and dynamics; on the one hand they are abundant in highly rigid structural frameworks, and yet they are also very broadly represented in responsive proteins involved in signaling and other dynamic phenomena. The ability to dynamically assemble, disassemble, and to form environmentally responsive bistable conformations is partially a reflection of their intrinsic malleability. Decades of research have revealed that coiled‐coils can change their topology, stoichiometry, and dynamics in response to changes in environment or small changes of their sequences.17, 18, 19, 20, 21, 22, 23, 24 In our own work this malleability has been studied in early designs of three‐helix25, 26, 27, 28 and four‐helix29, 30, 31, 32, 33, 34, 35 bundles, and utilized in the design of ion channels,36, 37 transporters,38 and catalytic metalloproteins.39, 40, 41

A second, widely recognized feature of coiled‐coils involved in signaling is the presence of breaks or defects inserted into the otherwise regularly repeating sequence patterns of canonical coiled‐coils.42 Soon after coiled‐coils proteins were sequenced it became apparent that they have a seven‐residue sequence pattern regularly repeated over long stretches of the sequence. However, occasionally, one, three, or four residues are inserted between the more regular heptad repeats, and these insertions became anthropomorphically known as skips, stammers, and stutters, as discussed below. Despite their recognized importance and frequent conservation within protein sequences, our detailed understanding of how insertions dictate function has lagged behind our understanding of the more regular regions of coiled‐coil proteins. Insertions and deletions have not been extensively studied by protein designers, with the exception of the pioneering studies of Coles and Lupas, whose work has largely motivated the present manuscript.43, 44, 45, 46, 47, 48, 49, 50

Here, we apply our methods to the membrane‐spanning class of HKs, which are widely used by bacteria to sense an extracellular environmental cue—such as the presence of nutrients or periplasmic protein misfolding stress—and relay this cue to a change in the activity of its intracellular kinase domain.51, 52, 53 An activated HK then catalyzes phosphorylation of a transcriptional factor, which in turn orchestrates the transcriptional response to the extracellular signal. The major members of this class of HKs are homodimers, each containing two transmembrane helices. The extracellular sensor domains can have a number of different folds, some of which are also coiled‐coils. They transmit the signal through a membrane‐spanning four‐helix bundle and one or more coiled‐coil domains, ultimately being received by a dimeric four‐helical coiled‐coil (the DHp domain). The DHp domain has a conserved His residue that is phosphorylated by an adjacent C‐terminal ATP‐binding domain. Thus, the signal transmits sequentially through successive domains, many of which bear the hallmarks of coiled‐coils.

Early models suggested that signals were transduced within idealized coiled‐coils by one of a number of different rigid‐body shifts. Each motion was hypothesized to be important based on studies of fragments of full HK proteins.54 Examples include rotations (gearshift motion),44, 55 translation of a single helix along the long axis of the bundle (piston‐shifts),56, 57 or tilting outward of individual helices.58, 59, 60, 61 However, these motions have generally been found to be partial descriptions of more complex motions,54, 60 and often are restricted to single domains of a protein, leaving the question of how the signal transmits between adjacent domains.

Sequence analyses and experimental studies of bacterial signaling proteins have frequently demonstrated the presence of highly conserved insertions or deletions between the heptad repeats of adjoining domains through which the signal must transduce. We suggest that acting like defects in a lattice; insertions endow a protein with the ability to adopt multiple alternate conformational states of similar thermodynamic stability. Such an energetically balanced ensemble would be well suited to thermodynamically link environmental cues impinging on one “sensing” domain to the ensemble of conformational states of a neighboring “transmitting” domain, which in turn influences the conformational ensemble of each ensuing domain until the signal is read out at the terminal DHp and catalytic domains. In this view of signaling, the insertions or deletions of the heptad repeats are essential for conformational bistability and to prevent the overall structure from falling into a single conformational energy well so deep as to render it unable to respond to the energetic perturbations occasioned by the binding of ligands or other conformational cues.

While many tools are available for the analysis and design of the regular regions of coiled‐coils,43, 62, 63, 64, 65 there are few tools for analyzing the structural regions accommodating insertions and deletions within coiled‐coils.66 Typically, deviations from a heptad repeat are detected at the level of the amino acid sequence. It is, however, often difficult to pinpoint the precise point of the insertion even when a structure is known. For example, Figure 1(A,B) illustrates a sequence profile of 3466 aligned sequences of the helical region spanning from the C‐terminal helix of a “HAMP” domain through a short linker known as the “S‐helix” and into the first helix of the downstream DHp domain. In these proteins, the HAMP is a dimeric four‐helix bundle, which transmits a signal from upstream domains [not shown in Fig. 1(C)], while the DHp is the domain that receives the signal and is phosphorylated at a His sidechain. The mean hydrophobicity of each position along the sequence shows a seven‐residue repeat near the N‐terminus of the HAMP domain and the C‐terminus of the DHp domain. However, the pattern is clearly attenuated and interrupted in the intervening “S‐helix” (Fig. 1). This middle region is 15 residues in length, or one residue longer than two heptads, indicating a one‐residue insertion (Fig. 1, Supporting Information Fig. S1). The precise position at which the insertion occurs is difficult to pinpoint, however, as the strict repetition of hydrophobic residues at “a” and “d” is relaxed in the S‐helix. Despite the availability of multiple structures, the mechanisms by which the signal propagates through the HAMP and into the DHp remains a matter of stimulating debate.

Figure 1.

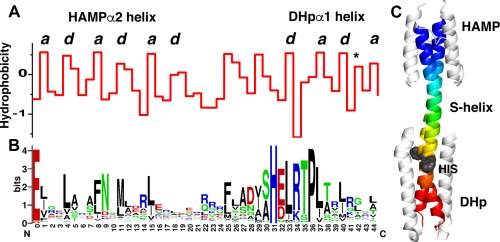
Histidine kinases with direct HAMP‐S—helix‐DHp connections contain a conserved single residue insertion. A. Average hydrophobicity at each residue position along the backbone consisting of the second helix from the HAMP and the first helix from the DHp. In both domains the a and d positions (labeled above) of the heptad repeats are clearly visible. The position with an asterisk indicates a residue position on the DHp that is important for response regulator recognition and binding.67 B. The corresponding sequence logo for the backbone showing the conserved positions. C. Structure of the HAMP‐S‐helix‐DHp region from the histidine kinase A291F AF1503‐EnvZ. The backbone is colored in rainbow, and the conserved histidine is shown as a space‐filled model in grey.

In the present manuscript, we define a structure‐based metric for the detection and classification of insertions and deletions in coiled‐coils based on experimental structures of the proteins. We introduce a suite of related profiles that automatically define: (1) the presence and nature of the insertion; (2) the number of residues over which the insertion is accommodated; (3) how the insertion is structurally accommodated in a given structure. We also use these methods to unify previous models for HK activation. The accommodation index should find manifold applications to investigations of conformational change and will provide a useful tool for de novo protein design.

Results

In the following section we review the features that define the structures of coiled‐coils as a prelude to understanding the impact of insertions on the heptad repeat. The reader already very familiar with the coiled‐coil literature might find this repetitive; if so, don't stammer or stutter, but skip to the following section.

Features that define the structures of regular coiled‐coils

One of the hallmarks of the classical left‐handed coiled‐coil is tight and specific packing of sidechains that are buried near the central axis of the structure. This packing occurs optimally when the helices cross with a slight left‐handed angle (app. −10° to −20°), which allows packing of interfacial residues in knobs‐into‐holes manner. If the helices are straight, they gradually diverge after about 10 residues on either side of the point of closest approach. However, if the helices gently supercoil with a left‐handed twist they can maintain tight and intimate packing indefinitely. Importantly, this coiling also creates a geometric pattern that repeats every seven residues. The positions in this heptad repeat are labeled “a” through “g”. By convention, the a and d residues are the two positions that project most closely towards the central superhelical axis [Fig. 2(A)]; they are generally hydrophobic, but on occasion polar residues help modulate the conformational specificity and stability of the structure. The heptad repeat is also occasionally called a 3,4 repeat because the d position lies three residues after the a position (a bc d ) while an a residue lies four positions beyond a d position (d efg a ). In summary, coiled‐coils represent a particularly frequent motif, in which a very favorable packing interaction can be achieved and repeated over long distances through the iteration of a seven‐residue geometric repeat.

Figure 2.

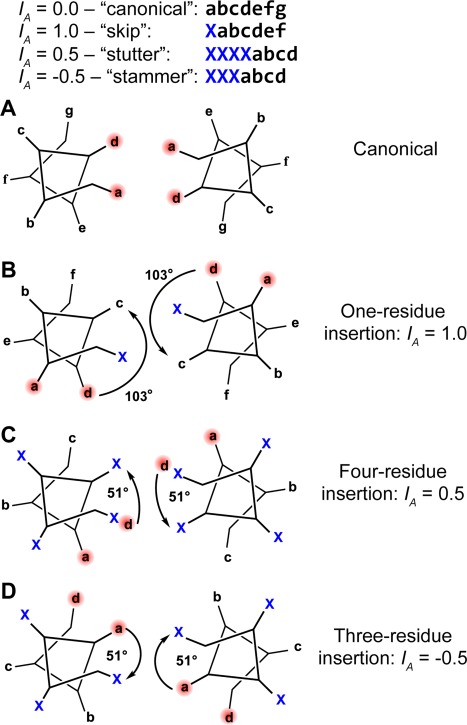
The most common types of residue insertions in coiled‐coil sequences. A. Canonical coiled‐coil heptad sequence displayed on the heptad wheel. B. A one‐residue insertion produces a 103° clockwise rotation of the residue positions following the insertion relative to their expected positions if no insertion had occurred. Realigning the a and d core residue positions requires a net −103° helical phase change within the coiled‐coil structure (arrow) relative to the canonical structure. Four‐residue insertions, C, and three‐residue insertions, D, produce 51° clockwise and 51° counterclockwise rotations of the following residue positions, respectively. These insertions are accommodated by opposite, net equivalent changes in helical phase within the coiled‐coil structure.

The detailed structures of coiled‐coils can be readily predicted following Crick's original derivation68 as follows: The α‐helix has a repeat of ∼3.6 residues/turn, which is defined by the regular pattern of i, i + 4 hydrogen bonding and favorable van der Waals interactions. By contrast, the heptad repeat of a coiled‐coil has seven residues for every two turns of the minor helix or 3.5 residues/turn. The resolution of this mismatch of 3.6 versus 3.5 residues/turn defines the structure of the coiled‐coil. In a coiled‐coil, the peptide chain is overwound by a right‐handed twist from 3.6 to 3.5 residues per turn. This right‐handed twist of the peptide chain is precisely compensated by an equal and opposite underwinding associated with the left‐handed coiling of the superhelix. The combination of these two opposing operations is a conformation in which the normal α‐helical geometry of the peptide chain is closely retained. Regularly repeating i, i + 4 hydrogen bonds are formed and the phi/psi angles remain in the α‐helical portion of the Ramachandran plot.

The overall shape of a coiled‐coil, including the helix‐crossing angle, is defined by the radius of the bundle and the offset between the α‐helical repeat (N _α = 3.6 residues/turn) and the 3.5‐residue repeat of the minor helix of a coiled‐coil (N _minor = 3.5 residues/turn). For example, we can think of the canonical left‐handed coiled‐coil as precessing by (3.6–3.5)/3.6 or 1/36 of the way around its path after completing a single turn of the minor helix. To compensate for this, the repeat of the superhelix in residues is then N _super = 3.5/(1/36) = 126 residues/turn. More generally, for any coiled‐coil (irrespective of whether it is a right‐ or left‐handed structure), the superhelical repeat expressed in amino acid residues can be approximated as:

$$N_{super}={(\frac{1}{N_{\alpha }}-\frac{1}{N_{\text{min}or}})}^{-1}$$ (Eq. 1.)

where N _α and N _minor are the repeats of the α‐helix and minor helix, respectively. This approximate relationship captures the compensating under‐ and over‐winding between the superhelix and minorhelix described above, enabling the local helical geometry to be minimally perturbed with respect to the ideal α‐helix. In fact, Eq. (1) is precisely equivalent to stating that ${\omega }_0+{\omega }_1={\omega }_{\alpha }$, as corresponding repeats and angular frequencies are related via ${\omega }_i=2\pi /N_i$ (in radians per residue), where the subscript i denotes the superhelix, α‐helix, or minorhelix. In Eq. (1) a negative value indicates the superhelix will be left‐handed, and right‐handed superhelices correspond to positive values.

Having defined N _super we can now compute the superhelical pitch and superhelical pitch angle for a given bundle radius, assuming reasonable local conformations for the peptide chain. For an ideal coiled‐coil, the length, l, of the path traced out by the minor helix axis over one complete turn of the superhelix is given by $l= N_{super} \times d$, in which d is the rise per residue of the minor helix. The superhelical pitch, P _super, depends on both the helical path, l, as well as the radius of the superhelix, R ₀, according to Eq. (2) by:

$$P_{super}=\sqrt{l^2-{\left(2\pi R_0\right)}^2}$$ (Eq. 2)

This relationship arises because the axis of the minor helix will lie along a cylinder of radius R ₀. As R ₀ increases P _super must contract for a fixed value of l.

The superhelical pitch angle, α, defined as the angle at which the minor helix axis crosses the superhelical axis, varies with the radius of the structure according to Eq. (3),

$$\tan \alpha =\frac{2\pi R_0}{P_{super}}$$ (Eq. 3)

Equations (2) and (3) can be understood by ‘unrolling’ the cylinder on which the superhelical path lies (2πR ₀ corresponds to the circumference of the cylinder and P _super the length, so the tangent provides the pitch angle, α).

This treatment provides a “first principles” description of experimentally determined structures of coiled‐coils. Using ideal values of d = 1.5 Å/residue, N _α = 3.60 residues/turn, and a superhelical radius, R ₀ = 4.85 Å, a canonical two‐stranded coiled‐coil is computed to have an α = −9.3°, which is comparable with the experimental average α = −12.0° ± 3.1° for 243 two‐chain canonical coiled‐coils from the coiled‐coil database.69

Equations 1–3 are general and can predict both right‐ and left‐handed coiled‐coils. For example, an 11‐residue repeat leads to a value of N _minor =11/3 = 3.67 residues/turn, which is larger than the expected value for N _α, leading to right‐handed instead of a left‐handed superhelix.65, 70 However, as the magnitude of the difference between N _minor and N _α becomes larger, the value of α necessary to preserve locally ideal α‐helical geometry is computed to be increasingly large, which can be difficult to accommodate with optimal inter‐helix packing. Other values of α are also possible, of course, but need to be accompanied with appropriate perturbations in local helical geometry. In the next section, we will see how Eqs. (1)–(3) predict how the peptide chain accommodates insertions and deletions into the heptad repeat.

Theoretical impact of insertions and deletions on coiled‐coils

A single residue insertion (also known as a skip) between adjoining heptads of a coiled‐coil presents a fly in the ointment. The mostly apolar a and d residues that were nicely projecting towards the core of the coiled‐coil will become exposed to the polar exterior beyond the point of the insertion, unless something is done locally to correct the situation [Fig. 2(A,B)]. These residues are now 360/3.5 ∼ 103° out of phase after the insertion. Repositioning the a and d positions back into the core of the coil requires modifying the coil geometry from that of an idealized coiled‐coil, which occurs over a stretch of the peptide chain that we define as the “accommodation region.” For a single residue insertion the minor helical frequency, ω ₁, must be underwound relative to the value for the canonical coiled‐coil to provide a cumulative change of ∼103° in the rotation of the minor helix over the length of the accommodation region. If the insertion is accommodated over a length of L _A residues, the minor helical frequency in the accommodation region needs to be underwound by ∼103°/L _A, assuming ω ₁ is constant over the accommodation region. The accommodation length, L _A, is defined as the length in residues of the accommodation region, or the region where ω ₁ differs from the ∼103° residues/turn in an ideal, or canonical coiled‐coil. The resulting minor helical frequency and minor helical repeat of the accommodation region are given by Eq. (4).

$$\begin{array}{c}{\omega }_1=103° \left(1-\frac{I_A}{L_A}\right)\\ N_{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{o}\mathrm{r}}=3.5{\left(1-\frac{I_A}{L_A}\right)}^{-1}\end{array}$$ (Eq. 4.)

The parameter I _A is defined as the “insertion index” and it defines the number of residues by which an insertion or deletion brings the chain out of register relative to the ideal 3.5‐residue/turn repeat; for a 1‐residue insertion I _A = 1.0.

If a 1‐residue insertion is accommodated over a short region (i.e., small L _A) Eqs. (1)–(4) predict geometries that are not easily accommodated by the α‐helix, but as L _A becomes longer the insertion can be more easily accommodated while maintaining unstrained conformations close to those of the ideal α‐helix. Figure 3 illustrates the minor helical repeat, N _minor, and superhelical pitch angle, α, versus L _A for a 1‐residue insertion computed using Eq. (1)–(4). With an accommodation length of 7 residues, the repeat of the minor helix is 4.1 residues/turn, matching the repeat of a π‐helix rather than that of the α‐helix. Of course, coupled with an appropriate value of α, the superhelix can compensate to make the local peptide geometry close to α‐helical, but as Figure 3(B) shows, this would require α of ∼40°. In the absence of such extreme superhelical twisting, π‐helix‐like geometries are thus needed. Indeed, insertions are sometimes accommodated by a single turn of a π‐helix (also known as helix aneurisms, π‐bulges or α‐bulges).71, 72, 73, 74 Longer accommodation lengths enable alternative solutions to maintain approximate α‐helical geometry without requiring drastic changes in either the minorhelix or the superhelix. For example, as the accommodation length is increased to 30 residues, the repeat of the minor helix comes closer to that of the α‐helical repeat, and the superhelical pitch angle comes close to 0.

Figure 3.

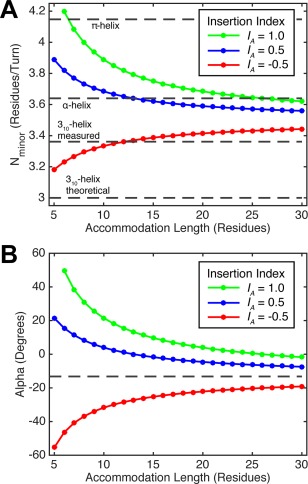
Minorhelical pitch, N _minor, and superhelical pitch angle, α, for different residue insertions in coiled‐coils over a range of accommodation lengths. A. Theoretical N _minor calculated using Eq. (4) for one‐residue insertions (I _A = 1.0, green), three‐residue insertions (I _A = −0.5, red), and four‐residue insertions (I _A = 0.5, blue). Horizontal dashes lines show N _minor for α−, π‐, and 3₁₀‐ helices for comparison. B. Theoretical α for coiled‐coils with insertions in accommodation regions of different lengths. Values are calculated using Eqs. (1)–(4) with superhelical radius, R ₀ = 4.9 Å, rise per residue, d = 1.50 Å, and α‐helical pitch, N _α = 3.60 residues/turn. The Alpha for a regular coiled‐coil (dashed line) uses N _minor = 3.5 residues/turn.

A four‐residue insertion has an insertion index, I _A = 0.5. This insertion is less disruptive to the structure of a canonical coiled‐coil, because it leads to a phase change of 51° rather than 103° for a single‐residue insertion [Fig. 2(B,C)]. Four residues is 0.5 residue greater than the 3.5 residue/turn minor helical repeat of a canonical coiled‐coil, so a four‐residue insertion effectively rotates the position following the insertion by 0.5 residues, or +51° [Fig. 2(C)]. Because the phase change is half the value seen for a one‐residue insertion, a four‐residue insertion can be accommodated over shorter lengths while maintaining reasonable i, i + 4 hydrogen‐bonding geometry of the α‐helix. For example, an accommodation length of 10 residues predicts a minor helical repeat of 3.68 residues and an α of 7° [Fig. 3(A,B)]. As the accommodation length is extended further the repeat becomes slightly lower than the ideal repeat of an α‐helix (3.64 residues/turn); the superhelical pitch angle goes through 0 and becomes slightly left‐handed. The ease of accommodating a 4‐residue insertion explains its frequent occurrence in coiled‐coils.42

A 3‐residue insertion (I _A = −0.5) corresponds to a phase change of −52° or 0.5 residues less than the 3.5‐residue repeat of a coiled‐coil. Thus, a 3‐residue insertion corresponds to a 0.5 residue deletion, and the chain must overwind in the accommodation region to reposition the a and d positions back into the core of the coil [Fig. 2(D)]. Because the 3.5‐residue repeat of a coiled‐coil is already less than the 3.60 residue repeat of an α‐helix, overwinding the minor helix in response to a 3‐residue insertion is more disruptive than the underwinding that occurs in response to a 4‐residue insertion. Accommodation of a 3‐residue insertion over a length of 10 residues leads to a minor helical repeat of 3.33 residues/turn [Fig. 3(A)], similar to the value of 3.36 residues/turn seen for the 3₁₀ helix in proteins of known structure.75 Thus, with short accommodation lengths, 3‐residue insertions might be expected to be accommodated by forming 3₁₀ helices.45 As the accommodation length increases the repeat approaches 3.5 residues/turn, and the superhelical pitch angle approaches the value seen for a canonical coiled‐coil [Fig. 3(B)].

A 1‐residue deletion (I _A = −1.0 or, equivalently a 6‐residue insertion) is predicted to be more disruptive to the structure of coiled‐coils than the 1‐, 3‐, and 4‐residue insertions described above, and indeed is quite uncommon. A 1‐residue deletion, accommodated over an entire heptad, leads to a helical repeat of ∼3.06 residues/turn, which is considerably less than that of the α‐helical repeat, or even the repeat of experimentally determined 3₁₀ helices (3.36 residues/turn). The superhelical pitch angle required to relax such geometry back to α‐helical is over 80°, representing extreme twisting. Hence this deletion type cannot be easily accommodated while maintaining physically reasonable values of the super‐ or minor‐helical parameters. This and other strongly perturbing insertions of two or five residues lead to non‐helical transitions, as recently demonstrated by Lupas et al.50

The accommodation index profile facilitates analysis of experimental structures

Here we define a new parameter, the accommodation index, AI(I _A , L _A), which allows insertions to be rapidly and accurately identified in coiled‐coil structures. The accommodation index is calculated by comparing the C_α positions of residues in coiled‐coil structures with their expected position in a canonical coiled‐coil. The minor helical frequency in a canonical coiled‐coil is ω₁ = 360°/3.5 = 102.86°/residue. The minor helical phase of the tth C_α of a residue in a canonical coiled‐coil is therefore given by Φ _ideal(t) = Φ _ideal1 + (t‐1)*ω₁, where Φ _ideal1 is the starting helical phase. The situation of a coiled‐coil containing an insertion will be more complex. As described above, near an insertion the coiled‐coil structure will deviate from the canonical coiled‐coil structure, ω₁ will differ from the canonical value, and this will produce a difference between the expected minor helical phase in a canonical coiled‐coil, Φ _ideal(t), and the phase observed in the protein structure, Φ _structure(t) (at residue position t in the structure). The accommodation index at the tth residue position in a coiled structure, AI(t), is defined as:

$$AI\left(t\right)=\frac{{\mathrm{\Phi }}_{\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}}\left(t\right)- {\mathrm{\Phi }}_{\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}}\left(t\right)}{{\mathrm{\Phi }}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}}$$ (Eq. 5.)

The step size in phase between consecutive positions along the minor helix is Φ _step = 102.86°. The accommodation index, therefore, is a measure of the increase or decrease in phase observed at a given position in a coiled‐coil structure in comparison to the structure for a canonical coiled‐coil, and is, therefore, reminiscent of Crick angle deviation analysis.76 The plot of AI(t) at every position t is called the accommodation index plot, and its profile characterizes the effects of insertions on coiled‐coil structures. An accommodation index profile (AI profile) is computed for a structure by computing AI(t) for seven‐residue windows at each successive position over each chain in the structure. The fitting procedure uses the program CCCP (http://www.grigoryanlab.org/cccp/),66 as described in Materials and Methods.

The accommodation index profile identifies the position and type of insertion, as well as the length over which it is structurally accommodated

Figure 4 compares AI profiles for experimentally determined structures of a highly regular coiled‐coil (I _A = 0) versus coiled‐coils with either a one‐residue (I _A = 1.0), three‐residue (I _A = −0.5) or four‐residue (I _A = 0.5) insertion. The AI profile of the regular coiled‐coil is flat, maintaining a constant value near zero, indicative of an ideal geometry throughout the structure [Fig. 4(A,E)]. By comparison, the AI profiles for the other three structures have sigmoidal shapes [Fig. 4(F–H)]. The AI profile for a one‐residue insertion [Fig. 4(F)] is initially flat at AI = 0 in the regular coiled‐coil region. It then transitions sigmoidally over the accommodation region, and then again plateaus at AI = 1.0. As explained above, the AI levels at a value of 1.0 for a one‐residue insertion, because a single residue insertion induces a net decrease in ω₁ (or increase in N _minor) of −102.86° in minor helical phase as compared to the minor helical phase for a canonical coiled‐coil.

Figure 4.

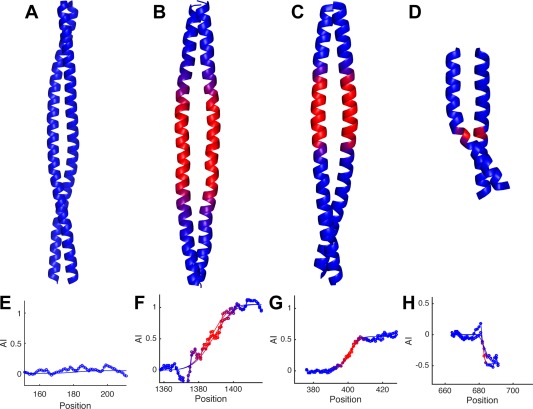
Accommodation index plots identify insertions in coiled‐coil structures and their corresponding accommodation regions. Coiled‐coils with I _A = 0.0, (A), I _A = 1.0, (B), I _A = 0.5, (C), and I _A = −0.5, (D), insertion indexes. The accommodation region is each structure is colored red, while the canonical region is blue. E–F. The AI profiles calculated from the structures above. The graphs show the AI profile data points measured from each chain in the coiled‐coil structure (lines with circle markers), as well as the corresponding fits of each AI profile (lines only).

Three‐residue and four‐residue insertions can also be easily identified from an AI profile, as they lead to a net change in the AI index of −0.5 and +0.5, respectively. The half‐integral value is a result of a net change in ω₁ of only half the value seen for a single‐residue insertion (Fig. 2). Additional AI profiles for the one‐residue, three‐residue and four‐residue insertions are provided in Figures 5, 6, 7, as well as Supporting Information Figures S2–S4. In general, the plots show no systematic dependence on the number of chains in the coiled‐coil, and chain partnering (homo‐oligomeric vs. hetero‐oligomeric). The analysis can be applied to both parallel and antiparallel coiled‐coils assuming appropriate symmetry. The structures are fit using a seven‐residue moving window in the N– to C–terminal direction, so parallel coiled‐coils are scanned in the same direction [e.g., Fig. 5(A)] and anti‐parallel chains are scanned in the opposite direction [e.g., Fig. 5(C)]. These results indicate that the accommodation index primarily measures the effects of residue insertions in coiled‐coils. Thus, the AI profile is a rapid and convenient method to objectively, automatically, and precisely determine the type and position of an insertion.

Figure 5.

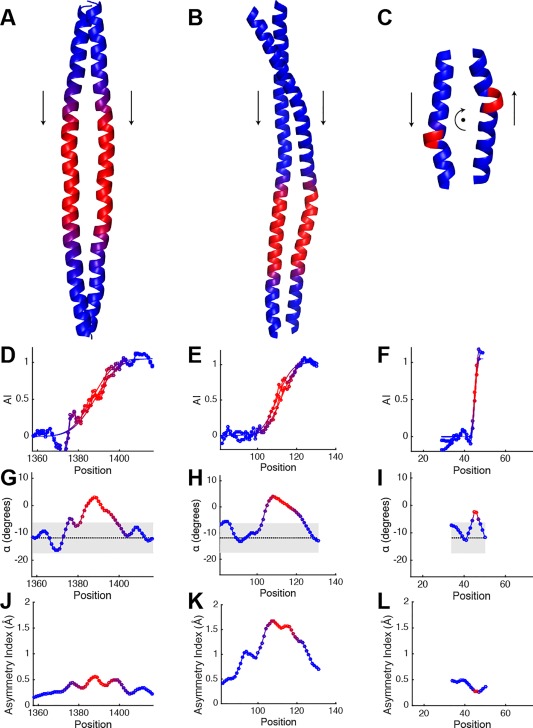
I _A = 1.0 coiled‐coils. Crystal structures of (A), the coiled‐coil surrounding the second skip in myosin‐7 (PDB ID: 4xa3), (B), the coiled‐coil domain from the Sec2p protein (PDB ID: 2eqb), and (C), a coiled‐coil in symetherin (PDB ID: 3qhc). Accommodation index plots for (D), myosin‐7, (E), Sec2p, and (F), symetherin. The plots are shown for both chains in the structure (lines with circle markers), and the corresponding fits of the accommodation index plots (lines only). (G–I) are plots of α determined by structural fits of the same region to the Crick equations, for myosin‐7, Sec2p, and symetherin, respectively, and (J–L) show their asymmetry index plots. Residue position corresponds to the first position in the seven‐residue window. Grey region in the α plots show the distribution of values from 243 two‐chain canonical coiled‐coils (median ± twice the population standard deviation). The areas where the accommodation index plot changes are indicated by blue to red color changes in the structure and plots.

Figure 6.

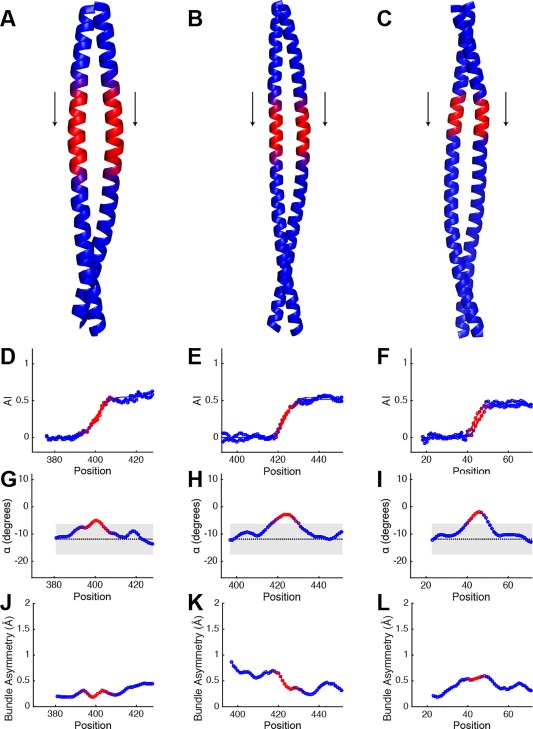
I _A = 0.5 coiled‐coils. Crystal structures of (A), the coiled‐coil domain from Huntigtin‐Interacting Protein (HIP1) (PDB ID: 2qa7), (B), keratin 5 and keratin 14 intermediate filament protein heterocomplex (PDB ID: 3tnu), (C), the coiled‐coil domain of Nuclear Distribution Protein Nude‐like 1 (Nudel) (PDB ID: 2v71). (D–F), Their accommodation index plots. Data are plotted for both chains in the structure (lines with circle markers), along with their fits (lines only). (G–I), are plots of α from the structural fits to the Crick equations for HIP1, the keratin heterocomplex, and Nudel, respectively, and (J–L) show their asymmetry plots. Plot format is identical to Figure 5.

Figure 7.

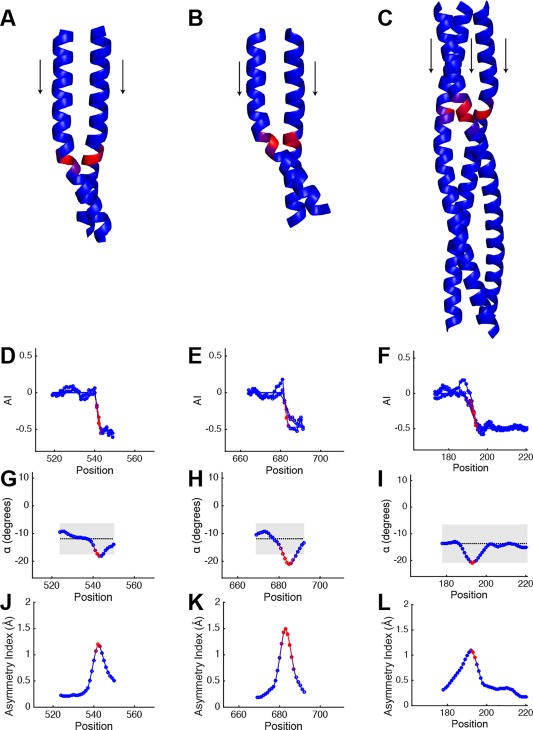
I _A = −0.5 coiled‐coils. Crystal structures of (A), and (B), coiled‐coils from Drosophila PAN3 pseudokinase (PDB ID: 4bwk and 4bwp), and (C), a trimeric autotransporter adhesion (TAA) fragment from Actinobacillus (PDB ID: 5app). (D–F), are their corresponding accommodation index plots. (G–I), are plots of α from structural fits over the same region with the Crick equations for the PAN3 pseudokinases, and TAA fragment, respectively, and (J–L) show their asymmetry plots. Plot format is identical to Figure 5.

The length of the accommodation region has an important influence on the geometry of the bundle, as described above [Eqs. (1)–(4), Fig. 3(B)]. Shorter values of L _A correspond to sharper transitions and can lead to strained bundles. For experimental structures, we estimate the accommodation length, $L_{\mathrm{A}} = 2\sqrt{2}\sigma$, based on the Gaussian width, σ, of the first derivative of the AI profile (Materials and Methods). The accommodation length, therefore, is a quantitative measure of the structural effects of insertions, and it is determined directly from AI analysis of coiled‐coil structures.

Relationships between accommodation index, accommodation length, and observed structures of helical bundles

The influence of the insertion type on the global structure of a bundle can be appreciated by comparing the AI profiles with corresponding profiles of the local superhelical pitch angle, α. As expected from Eqs. (1)–(3), the superhelical pitch angles are relatively uniform and constant at near −12° for a two‐stranded heptad repeat protein (Supporting Information Fig. S5).66, 77 Within the accommodation region, the local crossing angles transition from this canonical value in a manner that can be anticipated from Eq. (4) and Figure 3. Inspection of Figures 5, 6, 7 clearly shows that the values of α become more positive for I _A = 1.0 [Fig. 5(G–I)] or I _A = 0.5 [Fig. 6(G–I)] and more negative for I _A = −0.5 [Fig. 7(G–I)] within the accommodation region, in agreement with theory.

To evaluate the generality of this conclusion, we examined a total of 54 coiled‐coils with well‐defined insertion types. As expected, the minorhelical repeat [Fig. 8(A)] varied with the insertion length, as anticipated from Eq. (4). Furthermore, Figure 3(B) predicts that longer accommodation lengths are required for 1‐residue insertions to achieve a strain‐free conformation when compared to three‐ or four‐residue insertions; indeed the mean accommodation lengths for one‐residue insertions are approximately two‐fold greater than for the other two types [Fig. 8(B)]. It is particularly noteworthy that, for all three insertion types, there is significant variability in the accommodation lengths, even for the same structures seen in different signaling states (see later). Thus, insertions provide a means to generate conformational heterogeneity that appears ideal for signaling.

Figure 8.

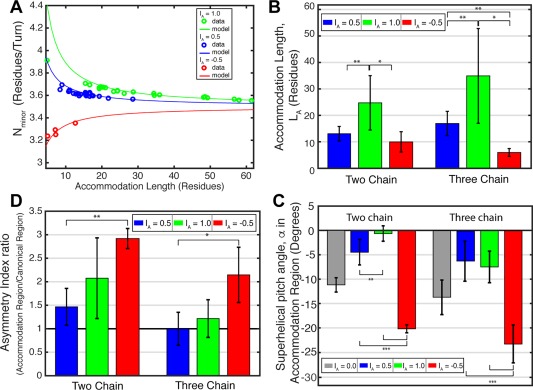
Comparison of the model with coiled‐coil structures. (A) The average value of N _minor from the accommodation region in coiled‐coils with I _A = 1.0 (green), 0.5 (blue), and −0.5 (red) insertion indexes versus the measured accommodation lengths, L _A. Data from coiled‐coil structures are plotted as circles. The lines represent the theoretical value of N _minor for coiled‐coils with given I _A and L _A, as determined by Eq. (4). (B) Bar graphs of the average accommodation length, L _A, within the accommodation region for two‐chain (left) and three‐chain (right) coiled‐coils with I _A = 0.5, 1.0, and −0.5. (C) The average superhelical pitch angle within the accommodation region for two‐ and three‐chain coiled‐coils. Average α from two‐chain and three‐chain canonical coiled‐coils, I _A = 0.0, are plotted for comparison. (D) Average coiled‐coil asymmetry index ratio for two‐chain and three‐chain coiled‐coils with I _A = 0.5, 1.0, −0.5. The ratio is the quotient of the maximum RMSD value in the accommodation region and the average RMSD value outside of the accommodation region; a ratio of 1 (black line) indicates equal bundle asymmetry within and outside of the accommodation region.

We also investigated the dependence of the superhelical pitch angle, α, on the accommodation length. The observed distribution was indeed within that expected from theory, assuming the chain adopted an α‐helical conformation [Fig. 8(C), Supporting Information Fig. S6]. In one interesting case (PDB ID: 3qhc), however, the accommodation length was so short that the chain could no longer adopt an α‐helical conformation. Instead, the chain locally deformed to a single turn of a π‐helix [Fig. 5(C)].

Asymmetric conformations are frequently observed in accommodation regions

We investigated the degree to which the helical bundles in our database deviate from C_n‐symmetry at various positions along the superhelical path. To quantify the asymmetry, we define the asymmetry index. For a homodimer, the index is computed by superposing both the backbone of chains A plus B onto chains B plus A, which is more sensitive to asymmetry than a simple superposition A onto B. For trimers, all three possible superpositions of the individual subunits are considered. The superpositions are conducted over consecutive overlapping 7‐residue windows and plotted as a profile to allow easy comparison with the AI profiles. Inspection of the profiles [Figs. 5, 6, 7(J–L), Supporting Information Figs. S2–S4] clearly show that the accommodation region is a hot spot for accumulation of asymmetric conformations. A similar conclusion is reached from an examination of the average values for each of the insertion types [Fig. 8(D)]. This finding reinforces our earlier suggestion that accommodation regions are particularly fertile ground for asymmetric conformational switching during signal transduction.

Histidine kinases show several different types of insertions depending on the type of domains being connected

Many of the binding and signaling domains of histidine kinases have seven‐residue hydrophobic repeats and structures characteristic of coiled‐coils. However, these domains tend to be more dynamic, less stable and shorter in length, presumably to allow multiconformational switching. Consecutive domains are generally connected by short helical linkers that accommodate either 1‐ (Fig. 1), 3‐, or 4‐residue insertions.78

VicK79 is an example of a dimeric protein with a domain structure: HAMP‐link1‐PAS‐link2‐DHp [in which link1 and link2 are coiled‐coil linkers; Fig. 9(A)], with each unit engaging in homomeric interactions along the dimer interface. The AI profile for the HAMP‐link1 connection in VicK clearly shows that the linker houses a four‐residue insertion (I _A = 0.5) [Fig. 9(A,B)]. Similarly, the AI profile for the link2‐DHp region indicates that link2 also hosts a four‐residue insertion (I _A = 0.5) [Fig. 9(A,C)]. The accommodation in link2 occurs with a short accommodation length (approximately six residues), centered near the catalytic histidine of the DHp, ideally localized for controlling autophosphorylation during signaling.

Figure 9.

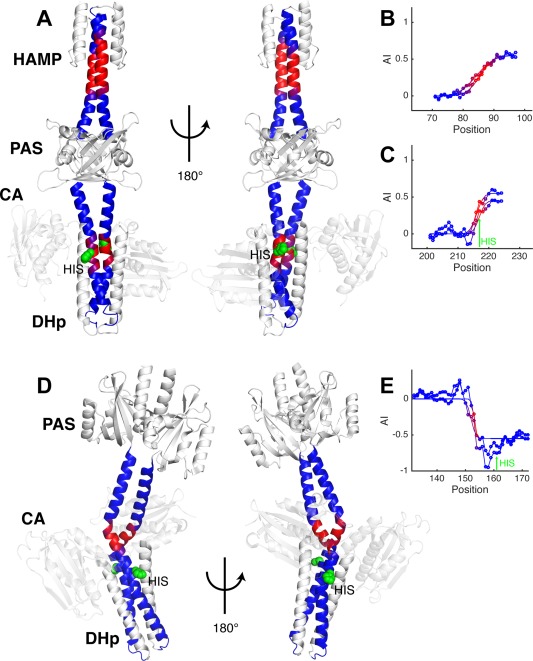
Coiled‐coils linking domains in histidine kinases have conserved insertions. (A) VicK histidine kinase with HAMP‐link1‐PAS‐link2‐DHp domain arrangement (PDB ID: 4i5s). (B) The accommodation index plot for the short coiled‐coil HAMP‐link1, indicating an I _A = 0.5 insertion. (C) The accommodation index plot for the link2‐DHp coiled‐coil. An I _A = 0.5 insertion is also observed. (D) Structure of the YF1 fusion histidine kinase (PDB ID: 4gcz). (E) The accommodation index plot for the coiled‐coil connecting the PAS and DHp in YF1 identifies an I _A = −0.5 insertion. Both chains are plotted (lines with circle markers) as well as their fits (lines only) in the AI profiles, and the vertical arrows show the location of the catalytic histidine. The dimerization backbones in the HK structures are colored to match their plots, and the histidine is shown in green as a space‐filling model. HK structures are shown in two different orientations to display differences in their coiled‐coil backbones.

As discussed by Moglich et al., there are two classes of PAS‐containing HKs, which differ in the connection between the last β‐sheet strand of the PAS domain and the N‐terminus of the helical linker78 that extends to the DHp. The HK YF116, 78 [Fig. 9(D)] is in a distinct class from VicK, which is reflected in a large difference in its accommodation index. The AI profile of YF1 indicates that the linker in this protein accommodates a three‐residue insertion (I _A = −0.5) [Fig. 9(E)], rather than the four‐residue insertion seen in VicK [Fig. 9(C)]. In YF1 the two helices are clearly asymmetric in the accommodation region over a short L _A = 2–3 residue accommodation length. Furthermore, the accommodation regions in both VicK and YF1 are proximal to the autophosphorylation site [Fig. 9(A,D)]. These results suggest that highly conserved insertions in the helices linking domains are important for facilitating the conformational changes in HKs.

The accommodation lengths in the coiled‐coil backbones of histidine kinases vary with signaling state

A third domain architecture, HAMP‐link‐DHp occurs in the cytoplasmic portions of a large class of sensor HKs. In this class, the helical linker is often referred to as a signaling helix or S‐helix.80 Constructs representing the HAMP‐link‐DHp‐catalytic domains from CpxA have been solved in multiple conformational states representing the Michaelis complex as well as the resting state (Figs. 10 and 11).81 A one‐residue insertion between the HAMP and DHp of CpxA had previously been inferred from sequence analysis [Fig. 1(A)]48, 81; AI profiles from both complexes clearly confirm this assignment as an I _A = 1.0 single‐residue insertion [Fig. 10(B,D)]. There are, however, large differences between the accommodation lengths and positions of the insertion in the Michaelis complex versus a resting state (Fig. 10). In the Michaelis complex, the accommodation occurs over L _A = 27 residues [Fig. 10(A,B)], which is significantly lengthened to L _A = 38 residues in the resting state [Fig. 10(C,D)]. Also, the accommodation is centered at residue Q239 in the Michaelis complex but shifts to L243 in the resting state. These changes localize precisely to a docking site for the catalytic domain (CA) of the protein (Fig. 11). In the resting state, the CA docks between the HAMP and DHp domains by making numerous contacts with the accommodation region, which spans these domains [Fig. 11(B)]. In the highly asymmetric Michaelis complex, one of the catalytic domains is released from the accommodation region to allow phosphorylation of a histidine sidechain in the DHp [Fig. 11(A)]. Thus, the AI profiles provide an accurate, unambiguous method to pinpoint how changes in the conformation of the helical bundle domains couple conformational changes in the kinase domain required for phosphorylation.

Figure 10.

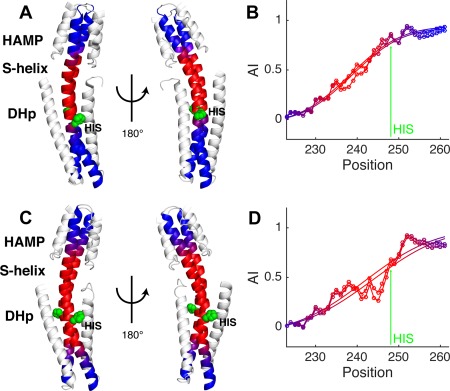
CpxA histidine kinase structures have I _A = 1.0 and different accommodation lengths. (A) Structure of the cytoplasmic region of CpxA in a Michaelis complex (PDB ID: 4biv). (B) The AI profiles for the two backbone chains of CpxA histidine kinase structure shown in A. Both chains are plotted (lines with circle markers) as well as their fits (lines only). (C) CpxA structure of the ADP‐bound resting state structure (PDB ID: 4biu chains c + d). (D) The corresponding AI profiles and fits. The arrow in both plots identifies the histidine at position 248. The dimerization backbone in the HK structures are colored to match their plots, and the histidine is shown in green as a space‐filling model. HK structures are shown in two different orientations to highlight structural differences in their coiled‐coil backbones.

Figure 11.

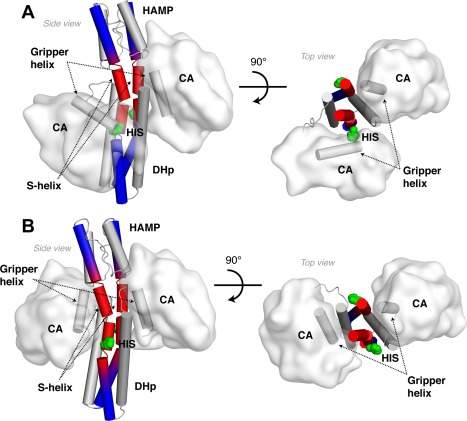
Variable accommodation lengths enable conformational switching in CpxA. (A) Kinase state structure of CpxA in a Michaelis complex shown from the side (left) and top (right) views. (B) ADP‐bound resting state structure of CpxA. Helices in the HAMP, S‐helix, and DHp are shown as cylinders, as is the “gripper helix” in the CA domain. The helical backbone extending from the top of the HAMP to the base of the DHp is colored to distinguish the region accommodating the I _A = 1.0 insertion (red) from areas with regular coiled‐coil geometry (blue).

An even larger difference in the conformational accommodation associated with different signaling states is seen in a protein consisting of the AF1503 HAMP fused to the DHp of the EnvZ HK (Fig. 12).47, 48 The protein with the WT HAMP domain is locked in a highly kinase‐on state [Fig. 12(A)], while the mutant A291F is locked in a resting conformation [Fig. 12(C)]. Interestingly, the accommodation in the WT HK occurs over a very short stretch [L _A = 11 residues, centered at residue V340, Fig. 12(A,B)] leading to a highly asymmetric bend just N‐terminal to the catalytic histidine, H342. The accommodation occurs over a 2.5‐fold longer stretch [L _A = 27 residues, centered at position L336, Fig. 12(C,D)] in A291F and the structure is significantly more symmetric. The same trend is also observed in the accommodation plots from the CpxA cytoplasmic structures, where the accommodation length is shorter in the kinase‐competent state [cf., Fig. 10(B,D)]. These results suggest that the different structural solutions used to accommodate insertions in the coiled‐coil backbones of histidine kinases are important for switching activation state.

Figure 12.

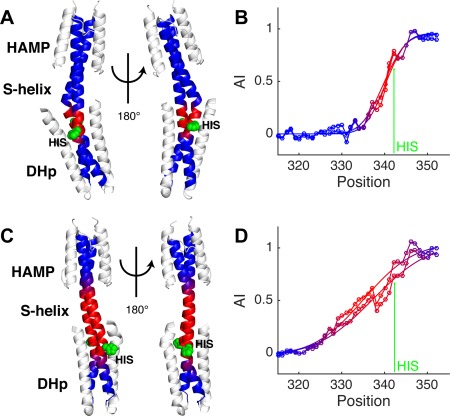
Distinct AF1503‐EnvZ fusion histidine kinase structures have different accommodation lengths. (A) Structure of the WT AF1503‐EnvZ histidine kinase (PDB ID: 3zrx). (B) Accommodation index plots for the kinase active WT AF1503‐EnvZ histidine kinase showing the measured AI profiles (lines with circle markers) and fits (lines only) for both coiled‐coil backbones in the structure. (C) Structure of the inactive A291F AF1503‐EnvZ histidine kinase (PDB ID: 3zrv), and (D) its AI profile. The arrow in the plots identifies the histidine at position 342. The dimerization backbone in the HK structures are colored to match their plots, and the histidine is shown in green as a space‐filling model. The HK structures are shown in two different orientations to display differences in their coiled‐coil backbones, which are striking.

Discussion

Relationship to earlier models for HK signaling

The variable accommodation lengths between phosphatase and kinase active structures suggest HKs may use a general mechanism to switch signaling states. Many earlier models for HK activation can now be seen as part of coupled transitions, associated with variable accommodation of insertions in different signaling states.

One recurring theme is symmetry/asymmetry transitions. Here, we show that shorter accommodation lengths lead to greater asymmetry than longer accommodation lengths. Thus a bistable system that adopts multiple accommodation lengths is well suited to generate the asymmetry that appears to accompany the kinase‐on state. A second proposed mechanism focuses on “cracking” of the first DHp helix at a conserved proline several residues C‐terminal to the catalytic histidine. This proline tends to demark the C‐terminal end of the accommodation region, where it acts as a hinge to facilitate bistable switching between structures with varying accommodation length.

A third model, which motivated this work, emphasizes changes in helical rotation between activation states. When the first structure of a HAMP domain was solved by Cole et al., they noticed that the helices were oriented in a somewhat unusual geometry, which could be related to a classical four‐helix coiled‐coil by approximately a 26° rotation about the helix axis.44, 47 This provided an attractive model, whereby the rotation of the HAMP helix 2 might propagate into the entire DHp, changing the exposure of the His sidechain to favor phosphorylation. However, when these workers solved the first functional HAMP‐DHp fusions, they noted that there was little difference in the helical rotation in the vicinity of the active site His.48 In fact, the structures showed that the helices had the same rotational angle near the top of the HAMP domain and the bottom of the DHp domain; the difference lies in the way the insertion is accommodated in between. Figure 13 illustrates a profile of the difference between the local helical rotation at various positions along the chain. At the top and bottom of the bundle, the structures are very similar but the helical rotations become strikingly different near the S‐helix region [Fig. 13(A)]. Thus, differences in accommodation position and length lead to local changes in the Z‐dependent helical twist [Fig. 13(B)] rather than a net rotation of the entire helices along the length of the bundle.

Figure 13.

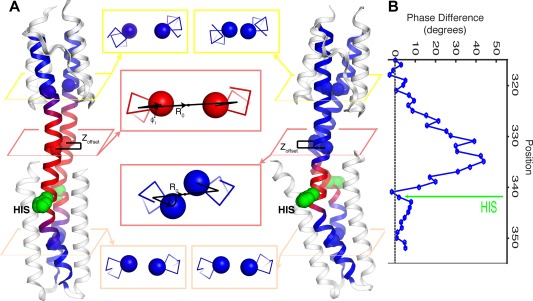
Variable accommodation lengths have multiple effects on HK structures. (A) Structures of the kinase inactive AF1503‐EnvZ histidine kinase (left) and kinase active WT AF1503‐EnvZ histidine kinase (right), along with core residues in different positions along their helical backbones (center). The different accommodation lengths in phosphatase and kinase active structures produce differences in superhelical radius, R ₀, helical phase, ϕ ₁, and vertical displacement, Z _offset, along the helical backbone, which are most pronounced within the accommodation region (pink boxes), as compared with places outside the accommodation region, including within the HAMP (yellow boxes) and DHp (peach boxes). (B) The difference in minor helical phase between the kinase active WT AF1503‐EnvZ HK and the kinase inactive A291F mutant HK.

Yet another model focuses on the diagonal displacement of helices within the interconnected four‐helix bundles,59, 60, 61 as well as changes in the interhelical distance of the intervening S‐helix. Figure 13(A) shows one example of a pair of sidechains located in the S‐helix at the same position in the two monomers, which are able to pack in a typical coiled‐coil geometry in one state, but are directed towards one another in a second conformation. The second conformation would lead to a potential clash, which is relieved by increasing the interhelical distance as well as displacing one helix axially relative to its neighbor. Thus, local changes in helical phase naturally transmit to changes in the shape of helical bundles, including switches from square‐shaped to diamond‐shaped cross‐sections in symmetrical four‐helix bundles48 or to kite‐like cross‐sections in less symmetrical four‐helix bundles.54

Finally, displacement of a given position of a helix along the superhelical axis, as originally postulated in the piston shift model is well established.56, 57 We refer to this model as a local Z‐displacement model, as the displacement of a helix, like its twist, might vary with the position along the central superhelical Z‐axis. While the shift is small—on the order of 1 to 2 Å—in the best‐characterized cases, this model is well established for chemotactic receptors that signal in arrays, such as the aspartate receptor.82 Changes in accommodation length also displace the helices along the Z‐axis because their Z‐position is directly related to the cosine of the superhelical pitch angle. A shift to a shorter accommodation length gives rise to a larger angle, which in turn gives rise to localized Z‐dependent displacements in the accommodation region. Furthermore, when insertions are accommodated over short lengths, in practice, the dimer becomes more asymmetric. This can give rise to localized axial displacement of one chain relative to another, as shown for the AFS1503‐ EnvZ HK structures in Figure 13.

Together, the distinct helical motions identified in models for HK signaling contribute to produce the conformational changes necessary to accommodate insertions over different lengths. Upon receiving an activating geometric input the HAMP undergoes a conformational change, which produces a local change in helical phase in the HAMP helices.44 This helical phase difference between phosphatase and kinase states is amplified along the coiled‐coil backbone by the conformational flexibility of the S‐helix [Fig. 13(B)], leading to local changes in coil geometry. Structurally this is observed as asymmetric buckling and local path changes in the helices forming the dimerization interface including a switch from left‐handed to right‐handed helical crossing angles [compare the HAMP–S‐helix–DHp helical paths in Fig. 12(A,C)]. These helical path changes restructure the four‐helix bundle of the DHp to promote autophosphorylation by releasing the “gripper” helix in the CA domain from the DHp, thereby freeing the CA domain to phosphorylate the conserved histidine (Fig. 11).54 In this way, a local change in helical phase within the HAMP can be amplified to produce dramatic structural changes necessary for signaling. In summary, the variable accommodation model represents a unification of earlier models, which now can be seen as part of a whole design.

Implications for protein design

Here, we have used the accommodation index in conjunction with an approximating functional form to quantify how insertions are accommodated structurally. The good correspondence between the accommodation index plots and the fit function indicates that the accommodation parameters, I _A and L _A, can describe the associated changes in helical phase. This raises the possibility of using the accommodation index to parametrically design coiled‐coils containing insertions. In this approach I _A, L _A, and the insertion position, μ, are used to generate an accommodation index function, AI (I _A, L _A, μ,; t), which can then be used to calculate the helical phase and associated minor helical frequency at every position in the chain. Using these parameters along with constraints for an α‐helix such as a constant rise per residue66 and coupling between the superhelical and minor helical frequencies [Eq. (1)–(3)],65 it may be possible to design coiled‐coil backbones where well‐defined insertions are accommodated structurally by smoothly varying Crick parameters. Furthermore, this method is hardly limited to left‐handed coiled‐coils or even highly regular regions of helical bundles. Rather, it can be used to generate conformations for any situation where morphing one helical bundle or beta barrel into a second conformational form, over a given chain length, is necessary.

Materials and Methods

Histidine kinase sequence analysis

We searched the SMART database (smart.embl‐heidelberg.de/) for histidine kinases from bacteria containing both HAMP and HISKA domains and retrieved 11,120 sequences.83, 84 These sequences were examined for HAMP domains that immediately precede DHp, using an in house Matlab code. The DHp domains were located by their highly conserved H‐box motif and protein sequences were aligned at the position of the catalytic histidine. HAMP domains were identified by sequences with >50% homology to the HAMP domain family alignment consensus sequence from the SMART database. Searches for HAMPs were limited to 150 residues N‐terminal of the catalytic histidine to avoid identifying HAMPs that are not adjacent to the DHp. (HAMPs range from 55 to 70 AA and the sizes of other domains commonly found in histidine kinases are comparable, PAS ∼80AA, or larger, GAF >100AA). Imposing this sequence constraint trimmed the set of histidine kinase sequences to 6044. The distance in residues, n, between the conserved N‐terminal acidic residue of the HAMPα2 and the catalytic histidine were tabulated for each sequence and a histogram of these values was constructed to show the sequence length distribution between HAMPs and DHps [Supporting Information Fig. S1(A)]. Plots of the average hydrophobicity of each residue position for HAMPα2‐DHpα1 sequences in Figure 1A are from the n = 31 case and were calculated using the Eisenberg consensus hydrophobicity scale for 3066 histidine kinases.85 This sequence set was also used to generate the logo plot in Figure 1B via the online WebLogo (weblogo.berkeley.edu).86

Selection of coiled structures

Most of the protein structures analyzed in this study were identified with the Coiled‐Coil Database (CC+).69 The database was searched using the dynamic interface by specifying structures that contained parallel two‐stranded and three‐stranded coiled‐coils containing canonical and non‐canonical (coils with insertions) heptad repeats. Homo‐oligomeric and hetero‐oligomeric coils were both considered. Unambiguous determination of an insertion in a coiled‐coil requires that the stretch of coiled structure is greater than the accommodation length. We therefore selected structures with coiled‐coils >14 residues for further analysis. Searches for non‐canonical coiled‐coils with more than three‐chains were conducted but we did not retrieve a sufficient number of structures (2 for four‐chain, and 1 five‐chain) for use in this study. Additional non‐canonical coiled‐coil structures were obtained by searching the PDB database through a coiled‐coil proteins SCOP browser query, and prior knowledge of interesting coiled‐coils. A total 243 two‐chain canonical coiled‐coils and 83 three‐chain canonical coiled‐coils were analyzed. Fewer noncanonical coiled‐coils were identified and we analyzed a total of 26 two‐chain (12 I _A = 0.5, 12 I _A = 1.0, 2 I _A = −0.5) and 28 three‐chain (13 I _A = 0.5, 12 I _A = 1.0, 2 I _A = −0.5) coiled‐coils.

Fits of coiled‐coils

Structures were fit with the Crick equations as implemented by the Crick Coiled‐coil Parameterization (CCCP) program. To examine how α‐helix and coil geometries vary as a function of position along a coiled‐coil we scanned structures with a seven residue moving window and fitted the structure in each window using CCCP. Other window sizes were considered but we found that seven residues provided the optimal performance for accurate fitting of the local structure while also minimizing “structural averaging.” For example, large windows give more reliable fit parameters than small windows, but they also provide lower resolution because the fit parameters are determined from a larger portion of the structure. Automated structure scanning was done using Matlab R2015A, with local windows fit to the Crick equations via the fcrick function from CCCP. To overall procedure, defined in a Matlab function fcoilscan, outputs a cell array of best‐fit Crick parameters with rows of data for each starting residue position and columns corresponding to fit parameters. The function also calculates the AI profile and minorhelical phases at every residue position in the coil. Both fcrick and fcoilscan are compatible with Matlab and GNU Octave, and are freely available for download at http://www.grigoryanlab.org/cccp/. The same URL also hosts a webserver for analyzing user‐specified structures with fcoilscan.

Calculation of the accommodation index

The accommodation index, AI(t), is computed by comparing the minorhelical phase at residue position t in a coiled‐coil structure with the minor helical phase predicted for a canonical coiled‐coil. The minor helical phase at position t in a structure ϕ ₁ (t) corresponds to the starting minor helical phase from the local window fits of the structure., or may be calculated from the fitted ω ₁ (t) from each local window since ${\varphi }_1\left(t\right)= {\varphi }_{1\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}+{\sum }_{i=1}^t{\omega }_1\left(i\right)$, where ϕ _1initial is the initial helical phase of a chain in the whole structure. Both approaches gave similar accommodation index curves. The predicted minorhelical phase at position t is given by ${\varphi }_1\left(t\right)={\varphi }_{1\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}+102.86°(t-1)$, where 102.86° is the average step size in phase between consecutive residue positions. These values are plugged into Eq. (5) to calculate the accommodation index at every position along the coil.

Quantifying the structural effects of residue insertions

Residue insertions, by definition, introduce discontinuities within heptad sequence repeats, and thereby alter the structure of a coiled‐coil in their vicinity. Places where the accommodation index plot exhibits the sharpest changes, ΔAI(t)/Δt ≠ 0, correspond to regions in the coiled‐coil where the structure deviates most from the canonical coiled‐coil structure. Three parameters are defined to characterize these regions: 1) The insertion index, I _A, where I _A = 1, 0.5, and −0.5 for one‐, four‐, and three‐residue insertions, respectively. 2) The residue position, μ, where the accommodation index has reached its halfway point, AI(μ) = ½I _A. This residue position assigns the structural location of the insertion in a coiled‐coil structure. 3) The accommodation length, L _A, of the insertion.

We fit the AI profiles from coiled‐coil structures with a cumulative distribution function (CDF) of the normal (Gaussian) distribution centered at $t-\mu$ with standard deviation $\sigma$:

$${AI}_{Fit}\left(I_A,\mu ,\sigma ;t\right)=\raisebox{1ex}{$I_A$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\left[1+Erf\left(\frac{t-\mu }{\sqrt{2} \sigma }\right)\right]$$ (Eqn. 6.)

t is the residue position, I _A and μ are defined above and Erf is the error function. The optimally fitting $\sigma$ is used to define L _A (see below). Equation (4) makes the simplification (convenient for our general analysis) that the accommodation index adjusts linearly in the accommodation region to make up for the total adjustment necessitated by the perturbation, that is, AI(t) = (I _A /L _A )(t –μ), for −L _A /2 ≤ t – μ ≤ L _A /2. Our fitting procedure here, however, does not make such an assumption and the local rate of change of helical phase is taken into account. Thus the gross rate $I_A/L_A$ in Eq. (4) is replaced with the local rate $d{AI}_{Fit}/dt$ here, giving the local minorhelical frequency:

$${\omega }_1\left(t\right)=102.86°\left(1-\frac{I_A}{\sqrt{2\pi {\sigma }^2}}\mathrm{e}\mathrm{x}\mathrm{p}\left[\raisebox{1ex}{$-{\left(t-\mu \right)}^2$}\!\left/ \!\raisebox{-1ex}{$2{\sigma }^2$}\right.\right]\right)$$ (Eqn. 7.)

where 102.86° is the average step size in phase between consecutive residue positions for a canonical coiled‐coil. Accommodation parameter can now be associated with familiar measures: I _A is the integrated area of the normalized Gaussian distribution, μ is the distribution mean, and σ is the standard deviation. Insertions with positive I _A decrease ω ₁ in the accommodation region, whereas ω ₁ increases for negative I _A values, as expected from theory. Other functional forms for AI_Fit(t) were considered but did not provide better overall fits to the accommodation index curves from analyzed coiled‐coil structures. Fits were carried out in Matlab and Octave using the built‐in non‐linear curve‐fitting function lsqcurvefit. For simplicity, I _A values were constrained to lie within ±0.05 of their ideal values.

Overall, the accommodation index plots were well‐described by AI_fit(t), with the standard errors of the mean for the accommodation parameters, Σ _I, Σ _μ, Σ _σ from each fit typically small. (The average of the standard errors for all fits of the accommodation plots are <Σ _I > = 0.03, <Σ _μ> = 0.53, and <Σ _σ > = 0.7, see Supporting Information Table S2 for parameter values and errors for every fit). To define the structural accommodation length, L _A, in terms of σ we use the relation $L_A=2\sqrt{2}\sigma$, which arises from a best‐fit approximation of a Gaussian with a rectangle function of equivalent area. The accommodation region μ ± L _A/2, therefore, is where the insertion most influences the structure of the coiled‐coil.

Analysis of coiled‐coil structures

Plots of the superhelical pitch angle, α, were generated from the α values extracted from CCCP fits to coiled‐coil structures. The asymmetry index is defined as the minimal rmsd from aligning the C _α atoms of the chains in the following manner: For a dimer chains A + B, onto chains B + A. For a trimer we averaged the three alignment permutations, that is, A + B+C onto C + A+B, C + A+B onto B + C+A, and A + B+C onto B + C+A. A 5 residue moving averaging filter was applied to the α(t) versus t, and asymmetry index versus t plots. In the α plots the average α values and twice the population standard deviation (<α > ± 2σ _α) for canonical coiled‐coils are represented by the dotted line and grey region, respectively. These values are calculated using a collection of 243 two‐chain coiled‐coils, and 83 three‐chain coiled‐coils from the Coiled‐Coil Database. Average values of N _minor and α in the accommodation region were calculated using the average ω₁ (since N _minor = 2π/ω₁) and average α from the region μ ± σ where σ is from the fits of the accommodation index plots. The asymmetry index ratio bar graphs are calculated by dividing the maximum RMSD value in the accommodation region by the average RMSD outside of the accommodation region. In all bar graphs the asterisks represent (*P < 0.05, **P < 0.01, and **P < 0.005) statistical significance for an unpaired t test.

Representation of protein structures

Images of the coiled‐coil structures were generated using PyMOL. The spectrum command with blue_red palette was used to distinguish the accommodation regions in coiled‐coil structures in red from the canonical regions in blue. Coloring was implemented by modifying the b‐factor values in pdb files according to a Gaussian function with a maximum value at μ and standard deviation σ, obtained from fits of the accommodation index plots.

Supporting information

Supporting Information