Abstract
In this letter, the authors propose a new entropy measure for analysis of time series. This measure is termed as the state space correlation entropy (SSCE). The state space reconstruction is used to evaluate the embedding vectors of a time series. The SSCE is computed from the probability of the correlations of the embedding vectors. The performance of SSCE measure is evaluated using both synthetic and real valued signals. The experimental results reveal that, the proposed SSCE measure along with SVM classifier have sensitivity value of 91.60%, which is higher than the performance of both sample entropy and permutation entropy features for detection of shockable ventricular arrhythmia.
Keywords: medical disorders, electrocardiography, electroencephalography, speech, medical signal processing, speech processing, entropy, state-space methods, correlation methods, time series, signal reconstruction, support vector machines, signal classification
Keywords: physiological signals, state space correlation entropy, time series, SSCE, state space reconstruction, synthetic valued signals, real valued signals, SVM classifier, support vector machine, sample entropy, permutation entropy, shockable ventricular arrhythmia, ECG, EEG, speech
1. Introduction
Entropy is a powerful tool to measure the dynamic characteristics of a signal or time series data [1]. The regularity of a time series data is assessed using entropy measures [2–4]. If the time series data is regular, then it has lower entropy value. The sample entropy (SE) and the permutation entropy (PE) measures have been widely used to assess irregularity in electrocardiogram (ECG), heart rate and electroencephalogram (EEG) signals [5–8]. These entropy measures are evaluated based on the state space reconstruction of time series data [2–4]. The SE and the PE measures have some limitations to quantify irregularity or randomness in a signal or time series data [1]. The SE is not suitable for longer duration signals, as it requires more computations for real time implementation. The PE is computationally faster than SE, but it does not consider the amplitude variations in a time series. Therefore, new entropy measures are required for time series by exploiting correlations and amplitude variations.
The information associated in a time series data is divided in the embedded vectors [2]. The regularity of the patterns in a time series can be exploited based on the correlation of the embedded vectors. In this letter, we introduce the state space correlation entropy (SSCE) as a new measure for analysis of time series data. The effectiveness of the proposed SSCE measure is verified using real valued signals and synthetic signals. The rest of this letter is organised as follows. In Section 2, the proposed SSCE measure is defined. The results and discussion are presented in Section 3. Finally, the conclusion of this letter is drawn in Section 4.
2. State space correlation entropy
The univariate signal or time series data, is given by
| (1) |
The algorithm for evaluation of SSCE measure includes five steps.
- (i) State space reconstruction: In this step, the () embedded vectors from the time series data (x) are evaluated. The embedded vector is given by
where , and m is the dimension of each embedded vector.(2) - (ii) State space covariance matrix evaluation: The () embedded vectors are arranged to form state space matrix. This matrix is defined by
(3)
The dimension of the state space matrix is . The state space covariance matrix is defined as
| (4) |
(iii) Correlation vector evaluation: The state space covariance matrix captures the correlations of the embedded vectors of time series. The upper triangular and the lower triangular elements of the matrix (C) are identical. The diagonal elements of ‘C’ matrix capture the autocorrelation of the embedded vectors. In this work, the upper triangular elements of the state space covariance matrix are extracted. The correlation vector (z) is formulated by using the upper triangular elements of the state space covariance matrix.
- (iv) Probability evaluation: The histogram of the correlation vector is evaluated using number of bins as K = 10. Then, the probability of each bin is evaluated based on the normalisation of the histogram of the correlation vector. The probability of bin is defined as
where is the number of elements in bin and . ‘n’ is the total number of elements in correlation vector.(5) - (v) SSCE Evaluation: The SSCE is defined as
(6)
The dimension of embedded vector is the important parameter for evaluation of SSCE. If m is small, then the number of embedded vectors of the time series are high. In such scenario, the temporal variations in the time series may not be perfectly detected [1]. In this study, m = 5 is considered for analysis of real valued and synthetic signals.
3. Results and discussion
The performance of the proposed SSCE measure is evaluated using ECG, EEG, speech and synthetic signals. The ECG signals from Creighton University ventricular tachy-arrhythmia and MIT-BIH malignant ventricular arrhythmia are used in this work [9, 10]. The sampling frequency of each ECG signal is 250 Hz. In this study, the ECG signals are segmented into frames using a window of size 8 s (2000 samples). The rapid ventricular tachycardia and ventricular fibrillation are considered as shockable ventricular arrhythmia (VA) class [6, 11]. Similarly, for non-shockable VA class, the ventricular ectopic beats, ventricular escape rhythm and normal sinus rhythm are considered [12]. The EEG signals from seizure and non-seizure classes are taken from a publicly available database [13]. The sampling frequency of each EEG signal is 173.61 Hz. Here, 512 samples of each EEG signal from seizure and non-seizure classes are considered. The speech signals for different emotion classes (anger, anxiety, boredom, disgusted, happiness and sadness) are taken from EMO-DB database [14]. The sampling frequency of each speech signal is 16 KHz. In this work, the speech signal for each sentence is divided into frames of size 20 ms ( samples). The synthetic signals such as white noise, pink noise, red noise, blue noise and violet noise data are considered [1].
The SSCE measure is evaluated for EEG, ECG, speech and synthetic signals. Fig. 1 shows the within-class variations (boxplot) of SSCE measure for synthetic, EEG, ECG and speech signals of different classes. It is observed that, the mean and the standard deviation values of SSCE for white noise, pink noise, red noise, blue noise and violet noise time series are , , , and . The white noise time series is regular than other noises [1]. This may be the reason for lower mean value of SSCE in white noise time series. The mean and the standard deviation values of SE, PE and SSCE measures for different emotion classes are shown in Table 1. It is evident that, the mean value of SSCE for anger class is higher than other classes of speech signal. The intensity of anger class is higher than those of the other emotional classes [15]. Since, the proposed entropy measure is related to the signal intensity (amplitude), the anger emotion have higher SSCE value than other emotion classes in speech signal. From Table 1, it is also observed that for seizure class the SSCE measure has higher mean value compared with non-seizure class. The PE and the SE have lower mean values for seizure class. The dynamic complexity of the neural activity is simpler in seizure class compared with non-seizure class [16, 17]. The SSCE measure only captures the correlations of the embedded vectors in the state space of time series. If the embedded vectors of a time series data are similar, then the correlation probability is high. For high correlation probability, the SSCE has less value. The probability density function (PDF) plot of SSCE for seizure and non-seizure classes are shown in Fig. 2. It is evident that, the PDF characteristics of SSCE measure is different for seizure and non-seizure cases. The probability value at fifth bin is higher for non-seizure class compared with seizure class. This may be the reason for higher mean value of SSCE measure for seizure class.
Fig. 1.
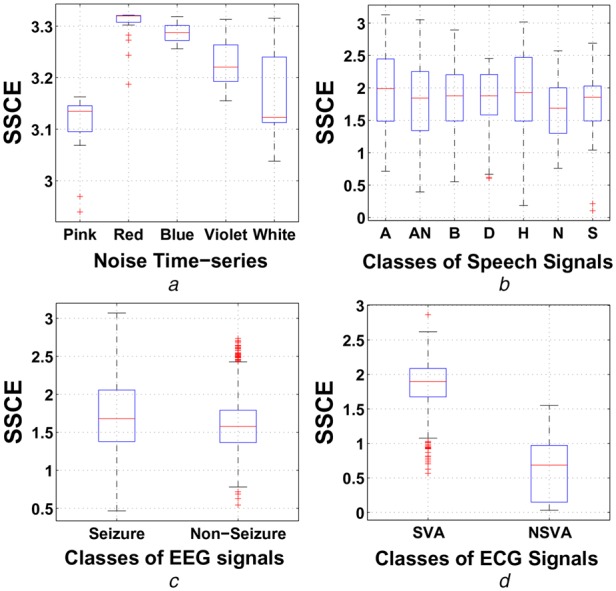
Within-class variations (boxplot) of SSCE measure for synthetic, EEG, ECG and speech signals of different classes
a Within-class variations of SSCE for different noise time series
b Within-class variations of SSCE for different emotion class in speech signals (A-Anger, AN-Anxiety, B-Boredom, D-Disgust, H- Happiness, N-Neutral and S-Sadness)
c Within-class variations of SSCE for seizure and non-seizure classes using EEG signals
d Within-class variations of SSCE for shockable ventricular arrhythmia (SVA) and non-shockable ventricular arrhythmia (NSVA) classes using ECG signals
Table 1.
μ ± σ values of SE, PE and SSCE for different classes
| Signals | Classes | SE | PE | SSCE | p-value |
|---|---|---|---|---|---|
| EEG | seizure | < 0.001 | |||
| non-seizure | |||||
| ECG | SVA | < 0.001 | |||
| NVA | |||||
| speech | neutral | < 0.001 | |||
| anger | |||||
| anxiety | |||||
| boredom | |||||
| disgust | |||||
| happiness | |||||
| sadness |
Fig. 2.
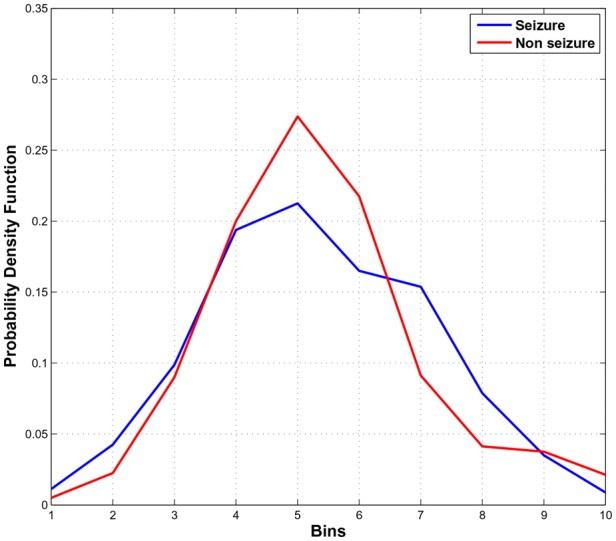
PDF plot of SSCE measure for seizure and non-seizure classes
The mean () and the standard deviation () values of SE, PE and proposed SSCE measures for shockable VA (SVA) and non-shockable VA (NSVA) classes are also shown in Table 1. It is observed that, the mean value of SSCE is higher in shockable VA class compared with non-shockable VA class. The PE has a lower mean value for the shockable VA class. The abnormal patterns (other than normal heart rhythm) are observed in shockable VA [6]. The beat-to-beat variations in ECG are higher for normal heart rhythm compared with shockable VA case [6]. Due to this reason, the mean value of SSCE measure is high for shockable VA class. The statistical significance of PE, SE and SSCE measures for classification of ECG signals are evaluated using t-test [1]. It is observed that, the p-values of PE, SE and SSCE are less than 0.001 and all these features are statistically significant for the detection of shockable VA from ECG. The support vector machine (SVM) model is used to classify the SSCE, the PE and the SE features of ECG episodes into shockable VA and non-shockable VA classes [11]. In this study, the SE, the PE and the SSCE features are evaluated from 526 shockable VA and 678 non-shockable VA ECG episodes. The 80% ECG instances are used for training of the SVM classifier and the remaining 20% (205 number of ECG feature instances) are considered for testing. The parameters of SVM used in this work are the regularisation parameter as C = 0.05 and the standard deviation of the radial basis function (RBF) kernel as . The accuracy, the sensitivity and the specificity values of the SVM classifier are shown in Table 2. It is observed that, the accuracy, the sensitivity and specificity values of SVM classifier with proposed SSCE features are 93.33, 91.60 and 95.87%, respectively. The accuracy and the sensitivity values of SVM classifier with proposed SSCE features is higher than the performance of PE and SE features. In this work, for SE features, the number of true positives (TPs), true negatives (TNs), false negatives (FNs) and false positives (FPs) are 88, 133, 2 and 17 using the SVM classifier and SSCE features with number of bins as K = 10. Similarly, for SVM classifier with SE features, the number of TPs, TNs, FNs and FPs are 93, 131, 4 and 12, respectively. The specificity is evaluated based on the number of TN and FP episodes [7]. The number of TNs for SE features are higher than SSCE features using SVM classifier. The variation of the number of bins (K) of SSCE measure with accuracy, sensitivity and specificity values for detection of shockable VA is shown in Table 3. For SSCE features with K = 14, the specificity value of SVM is higher than the performance of SE features. The number of bins equal to 14 is found to be the optimal parameter for SSCE for detection of shockable VA from ECG. The input parameter of both SSCE and SE measures is the dimension of embedded vector. The variations of SSCE and SE measures with the dimension of embedded vector (m) are shown in Figs. 3a and b, respectively. It is evident that, for shockable VA (SVA) and non-shockable VA (NVA) classes, the mean value of SSCE remains constant by varying the embedded dimension. For non-shockable VA case, there is not much variation in the mean values of SE with respect to the embedded dimension. However, for shockable VA case, the mean value of SE slightly degraded with an increase in the dimension of embedded vector. There is not much variation in the accuracy, sensitivity and specificity values of SVM by changing the dimension of the embedded vectors for SSCE and SE measures. The performance of SE, PE and SSCE measures is also evaluated using multiclass SVM classifier for classification of stress speech. It is observed that, the overall accuracy values for multiclass SVM using SE, PE and SSCE features are obtained as 57.32, 60.43 and 61.76%, respectively. For boredom and sadness classes, the accuracy values of SVM are high using SSCE features compared with SE and PE features. The proposed SSCE measure is implemented in MATLAB 2010 with a desktop computer of 4 GB RAM. The simulation times for evaluation of SE, PE and SSCE measures for an EEG signal with 512 samples are 0.04, 0.05 and 0.02 s, respectively. For an ECG signal with 2000 samples, the simulation times for evaluation of SE, PE and SSCE features are 0.32, 0.17 and 0.28 s, respectively. The above observations infer that, the proposed SSCE measure is effective for analysis of various physiological signals.
Table 2.
Performance of SVM classifier
| Features | Accuracy, % | Sensitivity, % | Specificity, % |
|---|---|---|---|
| SE | 92.08 | 88.66 | 97.77 |
| PE | 80.01 | 81.29 | 78.21 |
| SSCE | 93.75 | 91.09 | 97.87 |
Table 3.
Performance of SVM using SSCE features with different bins
| Bins | Accuracy, % | Sensitivity, % | Specificity, % |
|---|---|---|---|
| 8 | 92.08 | 90.80 | 93.87 |
| 10 | 93.33 | 91.60 | 95.87 |
| 12 | 90 | 88.27 | 92.63 |
| 14 | 93.75 | 91.09 | 97.87 |
Fig. 3.
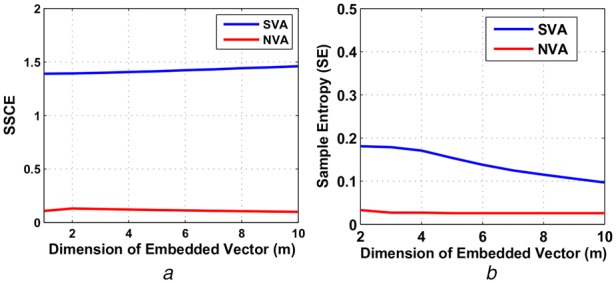
Variations of SSCE and SE measures with the dimension of embedded vector (m)
a Variation of SSCE with dimension of embedded vector
b Variation of SE with dimension of embedded vector
4. Conclusion
In this letter, a new entropy measure has been proposed to quantify regularity in a time-series data. The measure is defined as the SSCE. The effectiveness of the proposed entropy measure has been evaluated using ECG, EEG, speech and synthetic signals. The proposed SSCE measure has better performance for detection of shockable VA from ECG signal than SE and PE measures. In future, the SSCE measure may be used for detection of other cardiac ailments from ECG and for prediction of epileptic seizure from EEG.
5. Funding and declaration of interests
Conflict of interest: none declared.
6 References
- 1.Rostaghi M., Azami H.: ‘Dispersion entropy: A measure for time-series analysis’, IEEE Signal Process. Lett., 2016, 23, pp. 610–614 (doi: 10.1109/LSP.2016.2542881) [Google Scholar]
- 2.Richman J.S., Moorman J.R.: ‘Physiological time-series analysis using approximate entropy and sample entropy’, Am.J.Physiol.-Heart Circulatory Physiol., 2000, 278, pp. 2039–2049 [DOI] [PubMed] [Google Scholar]
- 3.Bandt C., Pompe B.: ‘Permutation entropy: a natural complexity measure for time series’, Phys. Rev. Lett., 2002, 88, p. 174102 (doi: 10.1103/PhysRevLett.88.174102) [DOI] [PubMed] [Google Scholar]
- 4.Li P., Liu C., Li K., et al. : ‘PAssessing the complexity of short-term heartbeat interval series by distribution entropy’, Med. Biol. Eng. Comput., 2015, 53, pp. 77–87 (doi: 10.1007/s11517-014-1216-0) [DOI] [PubMed] [Google Scholar]
- 5.Tripathy R.K., Sharma L.N., Dandapat S.: ‘A new way of quantifying diagnostic information from multilead electrocardiogram for cardiac disease classification’, IET Healthc. Technol. Lett., 2014, 1, pp. 98–103 (doi: 10.1049/htl.2014.0080) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tripathy R.K., Sharma L.N., Dandapat S.: ‘Detection of shockable ventricular arrhythmia using variational mode decomposition’, J. Med. Syst., 2016, 40, pp. 1–13 (doi: 10.1007/s10916-015-0365-5) [DOI] [PubMed] [Google Scholar]
- 7.Olofsen E., Sleigh J.W., Dahan A.: ‘Permutation entropy of the electroencephalogram: a measure of anaesthetic drug effect’, Br. J. Anaesth. , 2008, 101, pp. 810–821 (doi: 10.1093/bja/aen290) [DOI] [PubMed] [Google Scholar]
- 8.Acharya U.R., Joseph K.P., Kannathal N., et al. : ‘Heart rate variability: a review’, Med. Biol. Eng. Comput., 2006, 44, pp. 1031–1051 (doi: 10.1007/s11517-006-0119-0) [DOI] [PubMed] [Google Scholar]
- 9.Moody G.B., Mark R.G.: ‘The impact of the MIT-BIH arrhythmia database’, IEEE Eng. Med. Biol. Mag., 2001, 20, pp. 45–50 (doi: 10.1109/51.932724) [DOI] [PubMed] [Google Scholar]
- 10.Goldberger A.L., Amaral L.A., Glass L., et al. : ‘Physiobank, physiotoolkit, and physionet components of a new research resource for complex physiologic signals’, Circulation, 2000, 101, pp. e215–e220 (doi: 10.1161/01.CIR.101.23.e215) [DOI] [PubMed] [Google Scholar]
- 11.Li Q., Rajagopalan C., Clifford G.D. : ‘Ventricular fibrillation and tachycardia classification using a machine learning approach’, IEEE Trans. Biomed. Eng., 2014, 61, pp. 1607–1613 (doi: 10.1109/TBME.2013.2275000) [DOI] [PubMed] [Google Scholar]
- 12.Clifford G., Tarassenko L., Townsend N.: ‘One-pass training of optimal architecture auto-associative neural network for detecting ectopic beats’, IET Electron.Lett., 2001, 37, pp. 1126–1127 (doi: 10.1049/el:20010762) [Google Scholar]
- 13.Clifford G., Tarassenko L., Townsend N.: ‘Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state’, Phys.Rev.E, 2001, 64, p. 061907 (doi: 10.1103/PhysRevE.64.061907) [DOI] [PubMed] [Google Scholar]
- 14.Burkhardt F., Paeschke A., Rolfes M., et al. : ‘A database of German emotional speech’, Interspeech, 2005, 5, pp. 1517–1520 [Google Scholar]
- 15.Zao L., Cavalcante D., Coelho R.: ‘Time-frequency feature and AMS-GMM mask for acoustic emotion classification’, IEEE Signal Process. Lett., 2014, 21, pp. 620–624 (doi: 10.1109/LSP.2014.2311435) [Google Scholar]
- 16.Li X., Ouyang G., Richards D.A.: ‘Predictability analysis of absence seizures with permutation entropy’, Epilepsy Res., 2007, 77, pp. 70–74 (doi: 10.1016/j.eplepsyres.2007.08.002) [DOI] [PubMed] [Google Scholar]
- 17.Yusaf M., Nawaz R., Iqbal J.: ‘Robust seizure detection in EEG using 2D DWT of time-frequency distributions’, IET Electron.Lett., 2016, 52, pp. 902–903 (doi: 10.1049/el.2016.0630) [Google Scholar]


