Parametric Dose Standardization for Optimizing Two-Agent Combinations in a Phase I–II Trial with Ordinal Outcomes

Abstract

A Bayesian model and design are described for a phase I-II trial to jointly optimise the doses of a targeted agent and a chemotherapy agent for solid tumors. A challenge in designing the trial was that both the efficacy and toxicity outcomes were defined as four-level ordinal variables. To reflect possibly complex joint effects of the two doses on each of the two outcomes, for each marginal distribution a generalised continuation ratio model was assumed, with each agent’s dose parametrically standardised in the linear term. A copula was assumed to obtain a bivariate distribution. Elicited outcome probabilities were used to construct a prior, with variances calibrated to obtain small prior effective sample size. Elicited numerical utilities of the 16 elementary outcomes were used to compute posterior mean utilities as criteria for selecting dose pairs, with adaptive randomisation to reduce the risk of getting stuck at a suboptimal pair. A simulation study showed that parametric dose standardisation with additive dose effects provides a robust, reliable model for dose pair optimisation in this setting, and it compares favourably with designs based on alternative models that include dose-dose interaction terms. The proposed model and method are applicable generally to other clinical trial settings with similar dose and outcome structures.

1. Introduction

This paper was motivated by the problem of designing an early phase clinical trial of a three agent combination for treatment of cancer patients with advanced solid tumors. The first agent is a novel molecule (M) designed to inhibit the protein kinase complexes mTORC1 and mTORC2, and thus interfere with cancer cell proliferation and survival, among other cancer properties. M also has anti-angiogenic properties, through which it deprives the cancer of essential blood vessels that invest the tumors. The other two treatment components are the widely used chemotherapeutic agents carboplatin and paclitaxel. Paclitaxel, when given weekly, has been shown to act as an angiogenesis inhibitor as well. The property of antiangiogensis shared by M and weekly paclitaxel motivates this combination regimen, through which a more powerful antiangiogenic, and therefore anticancer effect is hypothesised. All three drugs also are expected to directly target the cancer cells through additional, different mechanisms, thereby complementing each other.

For the three-agent regimen in this trial, carboplatin is administered at a fixed dose based on the patient’s age, weight, and kidney function. The doses of the two agents that are varied are d_M = 4, 5, or 6 mg of M given orally each day, and d_P = 40, 60, or 80 mg/m² of paclitaxel given intravenously twice weekly. A total of nine (M, paclitaxel) dose pairs d = (d_M, d_P) are studied, with the goal to find the optimal d. Our proposed method will define “optimal” d by assigning joint utilities to Toxicity and Efficacy, assuming a Bayesian model, and identifying the d having largest posterior mean utility. Toxicity is defined as a four-level ordinal variable, Y_T, with possible levels y_T ∈ {Mild, Moderate, High, Severe}. As shown in Table 1, Y_T is defined in terms of the severity grades of many qualitatively different toxicities, with the level of Y_T determined by the highest level of any individual toxicity experienced by the patient. Reducing the many toxicities in Table 1 to the four-level ordinal outcome Y_T required many subjective decisions by the clinical oncologist planning the trial (the third author of this paper, RGZ). Efficacy is a four-level ordinal variable, Y_E, with possible values y_E ∈ {PD, SD1, SD2, PR/CR}, where PD = [progressive disease] = [> 20% increase in tumor size], SD1 = [stable disease level 1] = [0 to 20% increase in tumor size], SD2 = [stable disease level 2] = [0 to 30% reduction in tumor size], and PR/CR = [partial or complete response] = [> 30% reduction in tumor size]. This is a refinement of the commonly used 3-category definition where SD1 and SD2 are combined as SD = stable disease, sometimes with the 30% replaced by 20% so that SD is a change ≤ 20% in tumor size in either direction. In the trial, both Y_E and Y_T are scored within 42 days from the start of treatment. Thus, a criterion for determining an optimal dose pair must be defined in terms of the joint effect of d on Y = (Y_E, Y_T), which has 16 possible values.

Table 1.

Definitions of overall toxicity severity levels by grades of individual toxicities. Overall toxicity is scored as the maximum individual severity level. Grades are defined using NCI criteria.

	Overall Toxicity Severity Level (YT)
	Mild	Moderate	High	Severe
Fatigue	Grade 1	Grade 2	Grade 3	Grade 4
Nausea	Grade 1	Grade 2	Grade 3	–
Neuropathy	–	Grade 1	Grade 2	Grade ≥ 3
Hyperglycemia	Grade 2	Grade 3	Grade 4	–
Rash	Grade 1	Grade 2	Grade 3	Grade 4
Diarrhea	Grade 1	Grade 2	Grade 3	Grade 4
Stomatitis	Grade 1	Grade 2	Grade 3	Grade 4
Pneumonitis	Grade 1	Grade 2	Grade 3	Grade 4
Febrile neutropenia	–	–	Grade 3	Grade 4
Other Non-hematologic	Grade 1	Grade 2	Grade 3	Grade 4
Hyperlipidemia	Grade 1	Grade 2	Grade 3	Grade 4
Anemia	Grade 3	Grade 4	–	–
Thrombocytopenia	Grade 2	Grade 3	–	–
Neutropenia	Grade 3	Grade 4	–	–
AST/ALT	Grade 2	Grade 3	Grade 4	–
Blindness	–	–	–	Grade 4
Myocardioal Infarction	–	–	–	Grade 4
Stroke	–	–	–	Grade 4
Regimen-Related Death	–	–	–	Grade 5

An ordinal categorisation of solid tumor response is used commonly in oncology to compute descriptive statistics, but almost never is used for decision making by dose-finding designs. The most common practice is to define Y_T and Y_E as binary variables. In the present setting, this would be done by defining Y_E to indicate a “Response” event, which could be PR/CR, {PR/CR or SD2}, or {PR/CR, SD2, or SD1}. Most commonly, Y_T indicates a composite adverse event, “dose limiting toxicity (DLT).” These assumptions usually are made for phase I-II designs (cf. Braun 2002; Thall and Cook 2004; Bekele and Shen 2005; Zhang, Sargent, and Mandrekar 2006; Yin, Li, and Ji 2006). A further reduction is the conventional approach of ignoring efficacy and conducting a phase I trial based on the probability of DLT as a function of dose (cf. Storer, 1989; O’Quigley, Pepe, and Fisher, 1990; Babb, Rogatko, and Zacks, 1998). Curve-free dose-finding methods have been proposed by Gasparini and Eisele (2000) and Whitehead, et al. (2010) for phase I trials, and by Whitehead, et al. (2011) for phase I-II combination trials. Bekele and Shen (2005) and Zhou et al. (2006) proposed parametric model-based phase I-II methods to accommodate binary Y_T and continuous Y_E.

The utility-based two-agent phase I-II design of Houede et al. (2010) accounts for bivariate ordinal Y and models marginal dose-dose interactions by using a generalisation of the Aranda-Ordaz model (1981), given in the Appendix. Since this design deals with the same general problem as that addressed here, it is a natural comparator to our proposed methodology. The main differences between our methodology and that of Houede al. (2010) are that (i) we account for joint effects of two doses on each marginal outcome distribution using parametric dose standardisation, and (ii) we use adaptive randomisation to reduce the probability of getting stuck at a suboptimal dose pair. Additionally, our motivating application has an outcome of dimension (4,4) while that in the application of Houede et al. (2010) is (3,3) dimensional. Our simulations comparing the methods show that our proposal has more consistent performance across a range of dose-outcome scenarios, and in particular has better worst-case performance (Tables 5 and 6, Figure 5).

Table 5.

Comparison of design performance using three alternative generalised continuation ratio models for (4,4) dimensional bivariate ordinal outcomes. Scenarios 11 and 12 have no acceptable dose, so R_select values are less relevant and thus have a gray background.

	Scenario
	1	2	3	4	5	6	7	8	9	10	11	12
Parametric Dose Standardisation (PDS)
Rselect	76	77	80	78	78	78	81	78	80	89	93	94
Rtreat	65	63	61	72	70	67	70	70	65	85	79	67
% None	2	2	1	0	1	7	1	1	0	0	95	96
% Best	32	28	32	46	39	34	39	33	48	44	–	–
# Pats	59.4	59.4	59.6	59.9	59.8	57.9	59.7	59.8	59.9	59.9	26.5	27.7
# Eff	36.9	27.1	29.3	29.4	30.2	24.1	29.8	30.0	31.9	31.9	13.2	5.0
# Tox	28.6	25.2	23.6	19.2	22.9	20.8	22.1	22.1	19.8	22.6	18.1	7.7
Generalised Aranda-Ordaz Model (GAO)
Rselect	82	72	86	69	65	72	88	72	74	87	93	95
Rtreat	71	65	63	68	65	63	75	68	57	82	79	66
% None	2	3	1	0	1	6	1	1	1	0	94	94
% Best	49	25	64	31	8	19	67	22	47	54	–	–
# Pats	59.5	59.3	59.7	60.0	59.8	58.4	59.7	59.7	59.8	59.9	27.1	32.2
# Eff	36.2	25.8	28.1	27.9	28.3	23.3	29.2	28.7	30.9	30.5	13.5	5.7
# Tox	25.7	22.9	21.2	17.6	22.1	20.6	19.7	20.8	19.0	20.9	18.5	8.9
Conventional Multiplicative Interaction (CMI)
Rselect	83	66	85	66	62	69	87	68	86	92	95	97
Rtreat	69	60	61	67	62	64	73	68	65	85	80	68
% None	1	3	1	0	1	6	1	1	1	0	91	95
% Best	56	14	62	20	2	9	65	11	68	50	–	–
# Pats	59.7	59.3	59.7	59.9	59.7	58.3	59.7	59.7	59.8	60.0	29.3	29.0
# Eff	36.8	26.0	28.8	29.4	28.9	24.0	29.9	29.9	31.9	32.2	14.6	5.3
# Tox	26.9	24.8	23.1	19.6	24.2	21.6	22.0	23.0	19.7	22.9	19.9	8.1

Table 6.

Comparison of summary statistics for two-agent dose-finding designs, with (4,4), (3,3), or (2,2) dimensional bivariate outcomes.

		Scenario
		1	2	3	4	5	6	7	8	9	10	11	12
4 Eff, 4 Tox Levels PDS	Rselect	76	77	80	78	78	78	81	78	80	89	93	94
	Rtreat	65	63	61	72	70	67	70	70	65	85	79	67
	% None	2	2	1	0	1	7	1	1	0	0	95	96
	% Best	32	28	32	46	39	34	39	33	48	44	–	–
3 Eff, 3 Tox Levels PDS	Rselect	77	75	83	75	76	81	84	77	66	88	91	92
	Rtreat	66	63	63	70	69	67	71	69	59	85	79	67
	% None	2	2	1	0	1	6	1	1	1	0	94	95
	% Best	35	28	38	36	33	40	47	35	25	46	–	–
3 Eff, 3 Tox Levels GAO	Rselect	84	71	87	67	63	72	89	73	60	87	93	97
	Rtreat	72	64	64	67	64	63	76	68	51	81	77	67
	% None	2	3	1	0	1	4	1	1	0	1	94	93
	% Best	53	25	67	24	5	19	70	26	25	61	–	–
2 Eff, 2 Tox Levels PDS	Rselect	77	79	72	67	80	77	75	78	61	84	89	89
	Rtreat	67	67	60	69	72	67	67	70	58	83	79	66
	% None	3	2	1	0	1	7	1	1	1	0	95	96
	% Best	34	30	19	13	43	30	23	32	15	46	–	–
2 Eff, 2 Tox Levels Yuan-Yin (2011) Design	Rselect	81	77	67	65	75	72	71	73	57	86	91	51
	Rtreat	74	66	57	59	63	67	53	58	62	81	96	64
	% None	20	10	8	2	12	14	7	11	9	2	100	8
	% Best	31	29	20	8	26	22	23	21	18	48	–	–
2 Eff, 2 Tox Levels Wages-Conaway (2014) Design	Rselect	74	77	70	69	76	65	77	74	51	86	100	77
	Rtreat	73	69	60	66	68	58	64	62	47	79	97	61
	% None	0	2	1	0	2	5	0	2	0	0	71	63
	% Best	12	34	21	11	29	13	33	23	9	62	–	–
No Eff, 2 Tox Levels PO-CRM, Target 0.35	Rselect	79	73	55	64	71	64	60	61	61	90	100	81
	Rtreat	78	68	49	62	63	57	56	55	55	84	99	71
	% None	0	0	0	0	0	0	0	0	0	0	0	0
	% Best	27	28	21	3	20	17	13	15	19	65	–	–

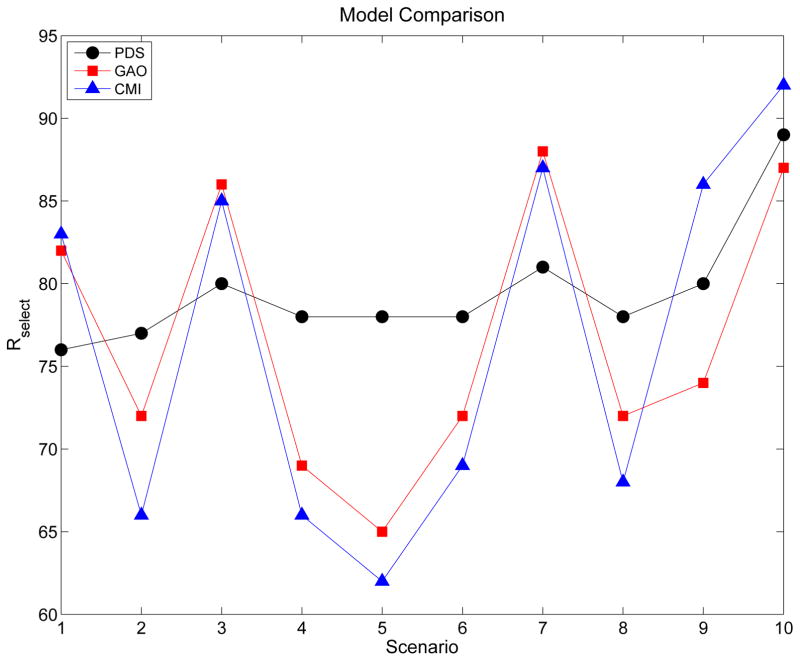
Figure 5.

R_select values for designs based on three different bivariate ordinal outcome models, PDS, GAO, and CMI, that account for dose-dose interactions differently. All three designs determine an optimal dose pair based on (4,4) dimensional bivariate ordinal outcomes under generalised continuation ratio models for the marginals.

Medically, the trial considered here is similar to the trial motivating the phase I-II design of Riviere, Yuan, Dubois, and Zohar (2015), in that both trials aim to find an optimal dose pair of a targeted agent and a chemotherapy agent. Key differences are that Riviere et al. address settings where toxicity is a binary variable and efficacy is a time-to-event variable and, assuming a proportional hazards model, the dose-efficacy curve may increase initially but then reach a plateau. The problem of optimising the doses of a two-agent combination based on bivariate binary (Y_E, Y_T) outcomes has been addressed in the phase I-II designs proposed by Yuan and Yin (2011) and Wages and Conaway (2014). Our computer simulations, reported in Section 4 and Table 6, show that defining efficacy and toxicity as ordinal variables with three or more levels is more informative than collapsing categories and defining two binary indicators, for example by dichotomising Y_E in one of the ways noted above and defining binary Y_T = I(High or Severe Toxicity).

Formulating a probability model and decision rules that use a (4,4) dimensional bivariate ordinal outcome to choose dose pairs in a sequentially adaptive phase I-II trial is challenging. In this trial, a maximum of 60 patients will be accrued, treated in 20 cohorts of size 3, starting at d = (4, 60). Denote an elementary outcome by y = (y_E, y_T), with the efficacy outcomes ordered from worst to best by y_E = 0, 1, ···, L_E, and the toxicity outcomes ordered from least to most severe by y_T = 0, 1, ···, L_T. Even if the trial’s 60 patients were distributed evenly among the 16 possible y pairs at completion, there would only be about four patients per outcome. This sample size allocation is an unrealistic ideal, however, because the elementary outcomes are not equally likely for any d, and moreover dose pairs are assigned in a sequentially adaptive manner. Unavoidably, in practice, the final distribution of patients among the 144 possible (d, y) combinations will be very unbalanced. Consequently, a dose-outcome model π(y, d, θ) = Pr(Y = y | d, θ), parameterised by θ, must borrow strength across many possible (d, y) values. We will take the common practical approach of modeling the marginal probabilities π_k(y_k, d, θ_k) = P(Y_k = y_k | d, θ_k) for k = E and T, and using a bivariate copula (Nelsen, 2006) to induce association between Y_E and Y_T and obtain π(y, d, θ).

Our goal in modeling the marginals is to obtain a dose-finding design with desirable properties. Each marginal model must account for four outcome level main effects, two dose effects on each outcome level, and possibly complex dose-dose interactions. The most difficult dose-outcome scenarios are those where the optimal pair d is located in a middle portion of the two-dimensional domain, rather than at one of its four corners. To address these issues in a practical way, we assume a generalisation of the continuation ratio (CR) model (Fienberg, 1980; Cox, 1988) for each marginal. Our main departure from conventional approaches to constructing a dose-finding model is that we standardise each agent’s dose parametrically in the linear term of each marginal. This gives a robust model that accounts for a wide variety of possible effects of d on π_E(y_E, d, θ_E) and π_T(y_T, d, θ_T).

Once the 16 possible elementary outcomes y = (y_E, y_T) were established, their numerical utilities U(y) were elicited from RGZ to quantify their relative desirability. These elicited utilities subsequently were reviewed by members of the Department of Investigational Cancer Therapeutics at M.D. Anderson Cancer Center, and a consensus was obtained without changing any of the numerical values. In practice, utility elicitation may be carried out more formally using the so-called “Delphi method” (Dalkey, 1969; Brook et al., 1986) or, for example, the methods described by Hunink, et al. (2014) or Swinburn et al. (2010). Our elicited utilities are given in Table 2. A general admissibility criterion for any utility function U(y_E, y_T) in this setting is that it should increase as either y_E or y_T becomes more desirable on its ordinal scale. That is, one should not use a utility function that does not make sense. These utilities are used during the trial as a basis for computing the posterior mean utility of each dose pair, which is the design’s optimality criterion. Adaptive randomisation (AR) among nearly optimal dose pairs is used to avoid getting stuck at a suboptimal pair (cf. Azriel, Mandel, and Rinott, 2011; Thall and Nguyen, 2012). Our simulations, given below in Section 4, show that parametrically standardising the two doses and including them additively in the model’s linear terms provides a robust basis for dose-finding for a wide variety of π_k(y|d) probability surfaces. In particular, our design’s performance compares favourably to what is obtained assuming a more conventional model with multiplicative dose-dose interaction terms.

Table 2.

Elicited numerical utilities of the 16 joint (Efficacy, Toxicity) outcomes.

Toxicity	Disease Status (Efficacy)
	PD	SD1	SD2	PR/CR
Mild	25	55	80	100
Moderate	20	35	70	90
High	10	25	50	70
Severe	0	10	25	40

The dose-outcome model is given in Section 2. Decision criteria and algorithms for trial conduct are presented in Section 3. The methodology is applied to the motivating trial in Section 4, including a simulation study. We close with a discussion in Section 5.

2. Dose-Response Models

2.1 Parametric Dose Standardisation

In phase I-II trials, a key issue is modeling the effects of intermediate doses on both π_E(y, d, θ_E) and π_T(y, d, θ_T). First, consider a single agent trial with lowest dose d₁, highest dose d_M, and mean dose d̄. For a given intermediate dose d_j between d₁ and d_M, and each k = E, T, the actual value of π_k(d_j, θ) may be, approximately, close to π_k(d₁, θ), midway between π_k(d₁, θ) and π_k(d_M, θ), or close to π_k(d_M, θ). If π_E and π_T both are defined using the same standardised dose, say x = d − d̄ or d/d̄, a problem arises from the facts that the shapes of the two curves π_E(x, θ) and π_T(x, θ) may be very different, and the desirabilities of an intermediate d_j in terms of π_E(x_j, θ) and π_T(x_j, θ) also may be very different. For example, d_j may have desirably low π_T(d_j, θ) close to π_T(d₁, θ), and low, intermediate, or high π_E(d_j, θ). An important case is one where π_T(d_j, θ) is close to π_T(d₁, θ) and π_E(d_j, θ) is close to π_E(d_M, θ), so d_j is optimal for any reasonable criterion. If the model does not accurately reflect the different shapes of π_T(d, θ) and π_E(d, θ) as functions of d, the utility-based method may not select d_j with sufficiently high probability.

Next, consider a phase I-II combination trial. For each agent, a = 1, 2, denote the dose vector by d_a = (d_a,1, ···, d_a,Ma) with mean d̄_a = (d_a,1 + ··· + d_a,Ma)/M_a. The modeling problem here is to characterise the joint effects of (d_1,j, d_2,r) on both Y_E and Y_T. An intermediate dose pair is any d = (d_1,j, d_2,r) not located at one of the four corners of the rectangular dose pair domain, i.e. 1 < j < M₁ and 1 < r < M₂. Standardising each dose as x_a,j = d_a,j − d̄_a or d_a,j/d̄_a, suffers from the same limitations described above for an individual agent. Consequently, the problems described above for a single agent are more complex in that they now are elaborated in terms of the two probability surfaces π_E(d_1,j, d_2,r) and π_T(d_1,j, d_2,r).

These problems motivate the use of two parametrically standardised versions of each dose, one with parameters corresponding to π_E and the other with parameters corresponding to π_T. For each outcome k = E, T and agent a, we define parametric dose standardisation (PDS) for d_a,j to be

$$d_{k,a,j}^{\lambda }=\frac{d_{a,1}}{{\overline{d}}_a}+{\left(\frac{d_{a,j}-d_{a,1}}{d_{a,M_a}-d_{a,1}}\right)}^{{\lambda }_{k,a}}\left(\frac{d_{a,M_a}-d_{a,1}}{{\overline{d}}_a}\right)$$ (1)

where all entries of the dose standardisation parameter vector λ = (λ_E,1, λ_E,2, λ_T,1, λ_T,2) are positive-valued. This construction gives two parametrically standardised versions of each dose of each agent, one for each outcome, mapping each d_1,j for agent 1 to ( $d_{E,1,j}^{\lambda },d_{T,1,j}^{\lambda }$), j = 1, ···, M₁ and each d_2,r for agent 2 to ( $d_{E,2,r}^{\lambda },d_{T,2,r}^{\lambda }$), r = 1, ···, M₂. The formula (1) is a two-agent version of that used by Thall et al. (2013) in the context of a design for optimising the dose and schedule of one agent.

For each agent a, the lowest and highest standardised doses in (1) are $d_{k,a,1}^{\lambda }=d_{a,1}/{\overline{d}}_a$ and $d_{k,a,M_a}^{\lambda }=d_{a,M_a}/{\overline{d}}_a$. Thus, the parametrically standardised doses at the lower and upper limits of the dose domain are usual standardised doses, and do not depend on either λ or the outcome k. These serve as anchors for the intermediate doses, 1 < j < M_a, where the PDS involves λ and k, and $d_{k,a,j}^{\lambda }$ is a parametric, outcome-specific modification of the commonly used form d_a,j/d̄_a, which corresponds to λ_k,a ≡ 1. Exponentiating the proportion (d_a,j − d_a,1)/(d_a,Ma − d_a,1) by the model parameter λ_k,a in (1) shifts each intermediate dose, d_a,j/d̄_a, either up toward d_a,Ma/d̄_a or down toward d_a,1/d̄_a. Since λ is updated along with the other model parameters in the posterior, the formulation (1) provides a data-driven refinement of dose effects on each outcome that is not obtained if one uses the usual standardised values d_a,j/d̄_a or d_a,j − d̄_a.

2.2 Generalised Continuation Ratio Models

Reviews of generalised continuation ratio (GCR) models, and of copulas used to obtain bivariate distributions having given marginals, are given in the Appendix. Given the PDS form (1), one may stabilise numerical computations by using either $x_{k,a,j}^{\lambda }=log(d_{k,a,j}^{\lambda })$ or $x_{k,a,j}^{\lambda }=d_{k,a,j}^{\lambda }-1$ in the model’s linear component. For a given dose pair (d_1,j, d_2,r), when no meaning is lost we will suppress the dose indices j = 1, ···, M₁ and r = 1, ···, M₂, and use the generic notation d = (d_1,j, d_2,r) and ${\mathit{x}}_k^{\lambda }=(x_{k,1,j}^{\lambda },x_{k,2,r}^{\lambda })$. Denote the conditional probabilities

$${\gamma }_k(y,\mathit{d},{\mathit{\theta }}_k)=P(Y_k\ge y\mid Y_k\ge y-1,\mathit{d},{\mathit{\theta }}_k),\text{for}k=E,T,y=0,\cdots ,L_k.$$ (2)

To construct the GCR model with PDS, we define the linear components

$${\eta }_k(y_k,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)={\alpha }_{k,y}+{\beta }_{k,y,1}{x}_{k,1,j}^{\lambda }+{\beta }_{k,y,2}{x}_{k,2,r}^{\lambda },\text{for}k=E,T,y_k=1,\cdots ,L_k.$$ (3)

To enhance robustness, we use the parametric link function of Aranda-Ordaz (AO) (1981), which defines a probability p in terms of a real-valued linear term η and parameter ϕ > 0 as

$$p=1-{(1+\varphi e^{\eta })}^{-1/\varphi }.$$ (4)

The AO link gives a very flexible model for p as a function of η, with ϕ = 1 corresponding to the logit link and the complementary log-log link obtained as the limiting case when ϕ → 0. For the GCR model with PDS, we define the marginal of [Y_k | d] by the equation

$${\gamma }_k(y,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)=1-{\{1+{\varphi }_k{e}^{{\eta }_k(y,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)}\}}^{-1/{\varphi }_k}\text{for}k=E,T,y=1,\cdots ,L_k.$$

That is, we assume an AO link with PDS in the linear terms. We define ${\eta }_k(0,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)=+\infty$, and ${\eta }_k(L_k+1,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)=-\infty$ to ensure that ${\gamma }_k(L_k+1,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)=0$. We require β_k,y,1, β_k,y,2 > 0 for each y ≥ 1 to ensure that ${\gamma }_k(y,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)$ increases with each dose. Writing α_k = {α_k,y, y = 1, 2, 3} and β_k = {β_k,y,a, y = 1, 2, 3, a = 1, 2}, the marginal parameter vector is θ_k = (α_k, β_k, λ_k,1, λ_k,2, ϕ_k). The key components of the marginal model are that the linear components (3) include the doses of the two agents additively using PDS (1), it has a GCR form (2), and it uses an AO link (4). In the sequel, for brevity we will abuse the notation slightly by identifying this model and the corresponding dose finding method using the acronym ‘PDS.’

Since each intermediate standardised dose $d_{k,a,j}^{\lambda }$ varies between the positive values d_a,1/d̄_a and d_a,Ma/d̄_a, we may consider 1 to be the middle numerical dose value. Mapping each $d_{k,a,j}^{\lambda }$ to either $x_{k,a,j}^{\lambda }=log(d_{k,a,j}^{\lambda })$ or $x_{k,a,j}^{\lambda }=d_{k,a,j}^{\lambda }-1$ has the same effect as centering the covariates at their means to reduce collinearity in conventional regression. Similarly, we define $x_{k,a,j}^{\lambda }$ so that it varies around 0 rather than 1 to improve numerical stability. If, instead, one were to transform $d_{k,a,j}^{\lambda }$ to maximise numerical stability at either the minimum or maximum of the dose domain, this would have the effect of destabilising computations at the other end. Consequently, it is very desirable to transform $d_{k,a,j}^{\lambda }$ to stabilise computations in the middle portion of the dose domain, and for values of ${\gamma }_k(y,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)$ near 1/2. For $x_{k,a,j}^{\lambda }=log(d_{k,a,j}^{\lambda })$, this implies that

$$e^{{\eta }_k(y,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)}=e^{{\alpha }_{k,y}}{(d_{k,1,j}^{\lambda })}^{{\beta }_{k,y,1}}{(d_{k,2,j}^{\lambda })}^{{\beta }_{k,y,2}},$$

with ${\gamma }_k(y,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)=1/2$ is obtained if ${\eta }_k(y,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)=0$ and ϕ_k = 1, corresponding to a logit link in (2). In this case, $e^{{\alpha }_{k,y}}{(d_{k,1,j}^{\lambda })}^{{\beta }_{k,y,1}}{(d_{k,2,j}^{\lambda })}^{{\beta }_{k,y,2}}=1$, and if $d_{k,1,j}^{\lambda }=d_{k,2,j}^{\lambda }=1$ then α_k,y = 0. Thus, numerical stability is greatest in this dose pair neighborhood, equivalently for $x_{k,1,j}^{\lambda }=x_{k,2,j}^{\lambda }=0$. Alternatively, one could use $x_{k,a,j}^{\lambda }=d_{k,a,j}^{\lambda }-1$.

Figure 1 illustrates possible shapes of the probability surface γ_E(1, d, θ_E) = Pr(Y_E ≥ 1|d, θ_E) as a function of the pair d = (d_M, d_P) = (Dose of Targeted Agent, Dose of Paclitaxel), for each of four different numerical dose standardisation parameter pairs (λ_E,1, λ_E,2). The surface in the upper left for λ_E,1 = λ_E,2 = 1 corresponds to the additive model with linear term

Figure 1.

Illustration of the probability surface γ_E(1, d, θ_E) as a function of dose pair d, for four different values of the dose standardisation parameters (λ_E,1, λ_E,2). The upper left plot is the surface corresponding to λ_E,1 = λ_E,2 =1, as a basis for comparison.

$${\eta }_E(1,(d_{1,j},d_{2,r}),{\mathit{\theta }}_k)={\alpha }_{E,1}+{\beta }_{E,1,1}\frac{d_{1,j}}{{\overline{d}}_1}+{\beta }_{E,1,2}\frac{d_{2,r}}{{\overline{d}}_2},$$

which may be used as a basis for visual comparison. Other probability surfaces as functions of d may be drawn similarly, such as γ_E(y, d, θ_E), γ_T(y, d, θ_T), π_E(y, d, θ_E), or π_T(y, d, θ_T), for integer y ≥ 1. Figure 1 shows that parametrically standardising the doses in this way give a very flexible model for the probabilities that are the basis for the dose-finding design.

Index patients by i = 1, ···, n for interim sample size n ≤ N, and denote the dose pair given to the i^th patient by d_[i]. The likelihood is the product

$$\mathcal{L}({\mathit{data}}_n\mid \mathit{\theta })=\prod _{i=1}^n\pi (Y_{i,E},Y_{i,T},{\mathit{d}}_{[i]},\mathit{\theta })$$

and the posterior is

$$p(\mathit{\theta }\mid {\mathit{data}}_n)\propto \mathcal{L}({\mathit{data}}_n\mid \mathit{\theta })p(\mathit{\theta }\mid \stackrel{\sim }{\mathit{\theta }}),$$

where p(θ | θ̃) denotes the prior with fixed hyperparameters θ̃. Collecting terms, for k = E, T, y = 1, 2, 3, and a = 1, 2, the model parameters are λ = {λ_k,a} for parametric dose standardisation, the intercepts α = {α_k,y}, the dose effects β = {β_k,y,a}, the AO link parameters ϕ = {ϕ_E, ϕ_T} and the copula’s association parameter ρ. Thus θ = (λ, α, β, ϕ, ρ).

2.3 Establishing Priors

Normal priors were assumed for the real-valued parameters {α_k,y}, the positive-valued dose main effect coefficients {β_k,y,a} were assumed to follow normal priors truncated below at 0, the copula association parameter was assumed to be uniform on [−1, +1], and each λ_k,a and the AO link parameter ϕ were assumed to follow lognormal priors. Prior means were estimated from the elicited probabilities given in Table 3 using the pseudo sampling method described in Thall, et al. (2011, Section 4.2) and Thall and Nguyen (2012, Section 4.3). Prior variances were calibrated to make the effective sample size (ESS), as defined by Morita, Thall, and Mueller (2008, 2010), of the prior of each marginal probability π_k(y, d, θ_k) suitably small, and to give a design with good operating characteristics over a diverse set of scenarios. The ESS of each prior was approximated by equating the prior mean and variance of π_k(y, d, θ_k) to the mean μ̃ = a/(a+b) and variance σ̃² = μ̃(1 − μ̃)/(a+ b + 1) of a Beta(a, b). Thus, a + b was used to approximate the ESS of the prior of π_k(y, d, θ_k). The overall mean of these ESS values was .09 for the selected prior standard deviation of 20. Detailed descriptions of the prior parameters are given in Supplementary Table S1.

Table 3.

Elicited prior mean marginal outcome probabilities, for each dose pair.

(dM, dP)	Efficacy				Toxicity
	PD	SD1	SD2	PR/CR	Mild	Mod	High	Severe
(4, 40)	.70	.10	.10	.10	.70	.20	.05	.05
(5, 40)	.50	.10	.20	.20	.60	.20	.10	.10
(6, 40)	.30	.20	.20	.30	.50	.20	.15	.15
(4, 60)	.50	.10	.20	.20	.60	.20	.10	.10
(5, 60)	.30	.20	.20	.30	.50	.20	.15	.15
(6, 60)	.20	.20	.20	.40	.30	.20	.30	.20
(4, 80)	.30	.20	.20	.30	.50	.20	.15	.15
(5, 80)	.20	.20	.20	.40	.30	.20	.30	.20
(6, 80)	.10	.20	.20	.50	.20	.20	.30	.30

3. Posterior Decision Criteria and Trial Design

3.1 Utility Based Decision Criteria

Given the Bayesian dose outcome model and elicited numerical utilities U(y) in Table 2, the trial is conducted using the following decision criteria. Given θ, the mean utility of dose pair d is

$$\overline{U}(\mathit{d},\mathit{\theta })=\sum _{\mathit{y}}U(\mathit{y})Pr(\mathit{Y}=\mathit{y}\mid \mathit{d},\mathit{\theta }),$$

where the sum is over all y pairs in the support of Y. Since θ is not known, we compute each dose pair’s posterior mean utility,

$$u(\mathit{d}\mid {\mathit{data}}_n)={\int }_{\mathit{\theta }}\overline{U}(\mathit{d},\mathit{\theta })p(\mathit{\theta }\mid {\mathit{data}}_n)$$ (5)

given the data on n patients available when an interim decision must be made. This integral is approximated by generating a posterior sample θ⁽¹⁾, ···, θ^(M) using Markov chain Monte Carlo (MCMC) (Robert and Cassella, 1999) and computing the sample mean of Ū(d, θ⁽¹⁾), ···, Ū(d, θ^(M)).

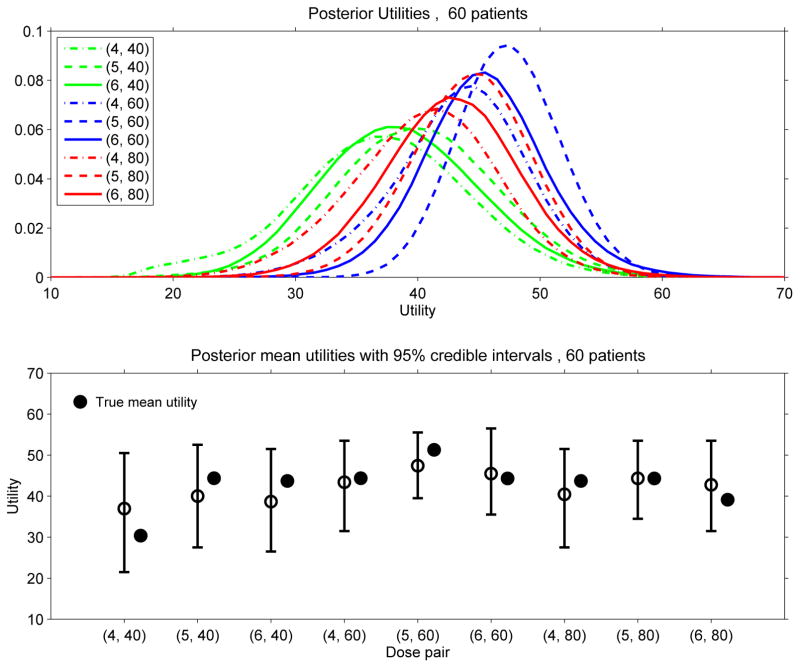
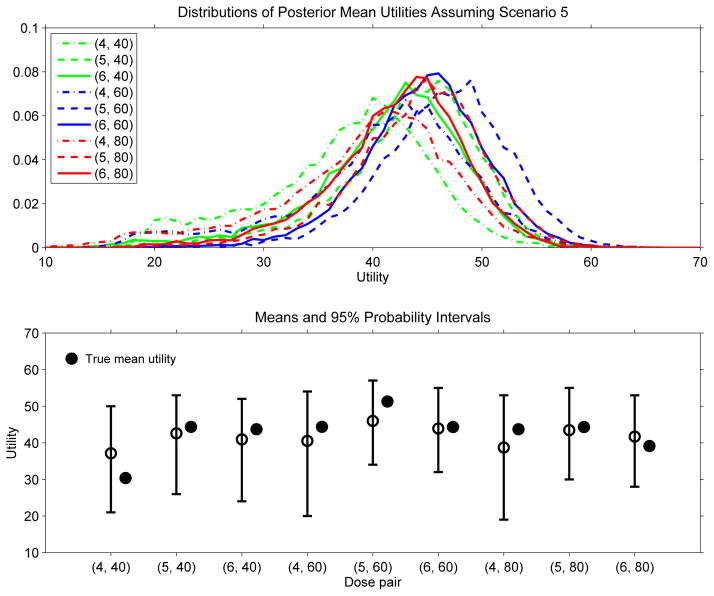
The posterior mean utilities given by (5) are the basis for the design’s sequential decision rules to select dose pairs during the trial. It is very important to bear in mind that each posterior mean utility is a statistic that can be quite variable. This is illustrated by Figure 2, which plots the distributions of u(d | data₆₀) and corresponding 95% probability intervals for each of the nine dose pairs, based on one 60-patient data set from a trial simulated under Scenario 5. To illustrate how such final utility distributions may vary across trials, Figure 3 provides similar plots based on a sample of 10,000 trials, each of size n = 60, with the data generated under Scenario 5. From a Bayesian perspective, the randomness of each distribution in Figure 2 is due to posterior uncertainty about θ, whereas the randomness of each distribution in Figure 3 is due to the random variation in the data. It is also is important to bear in mind that, for the smaller sample sizes that are the basis for interim decisions during the trial, the variability of u(d | data_n) for each d is greater than that shown by Figure 2 for the final data of n = 60 patients. In general, the substantial variability of each u(d | data_n) also would be the case for any statistic used as a decision criterion in this or similar small scale trial settings using any other adaptive design. These considerations motivate, in part, our use of adaptive randomisation between nearly optimal dose pairs in the trial design. The general point is that, in early phase trials, decision making must be done under great uncertainty.

Figure 2.

Posterior distributions of the mean utilities u(θ | data₆₀) for each of the nine dose pairs, based on a selected 60-patient data set obtained from one trial simulated under Scenario 5.

Figure 3.

Distributions of the final posterior mean utility u(θ | data₆₀) and 95% probability intervals for each of the nine dose pairs for the proposed PDS model-based method, based on a sample of 10,000 trials, each of size n = 60, with the data for each trial generated under Scenario 5.

3.2 Dose Acceptability Criteria and Adaptive Randomisation

To ensure that the trial is ethically acceptable, rather than simply choosing d from the nine pairs to maximise u(d | data_n), we impose additional constraints to ensure that any dose pair used to treat patients is both acceptably safe and acceptably efficacious. This follows the approach used by Thall and Cook (2004) and many others. We use the following two posterior acceptability criteria. For each k = E or T, denote π̄_k(y, d, θ_k) = Pr(Y_k ≥ y | d, θ_k). Indexing the toxicity levels by y = 0, 1, 2, 3 for mild, moderate, high, severe, π̄_T (2, d, θ) is the probability of high or severe toxicity with d. A dose pair d is considered unacceptably toxic if

$$Pr\{{\overline{\pi }}_T(2,\mathit{d},\mathit{\theta })>.45\mid {\mathit{data}}_n\}>\mathrm{.90.}$$ (6)

That is, d is not acceptable if, based on the current data, it is likely that d has a probability of high or severe toxicity that is above .45. For the efficacy rule, we similarly index the outcomes {PD, SD1, SD2, PR/CR} by 0, 1, 2, 3, so that π̄_E(2, d, θ) is the probability of SD2 or better with dose pair d. A dose pair d is considered unacceptably inefficacious if

$$Pr\{{\overline{\pi }}_E(2,\mathit{d},\mathit{\theta })<.40\mid {\mathit{data}}_n\}>\mathrm{.90.}$$ (7)

This says that d is not acceptable if, given the current data, it is likely that achieving SD2 or better occurs at a rate below 40%. A dose pair d is considered acceptable if it has both acceptable toxicity and acceptable efficacy, and we denote the set of acceptable dose pairs based on data_n by 𝒜_n. As data are acquired during the trial and the posterior becomes more reliable, 𝒜_n may change, so that a given d not in 𝒜_n may be in 𝒜_n+k, or conversely. The events used to define (6) and (7) and the corresponding numerical probabilities .45 and .40 are specific to the solid tumor trial. These particular values were determined by RGZ in collaboration with oncologist colleagues involved in planning the trial. In other trials, different toxicity and efficacy events and probability cut-offs should be chosen as appropriate.

Given the acceptability criteria, it may seem that one simply may choose the d ∈ 𝒜_n that maximises u(d | data_n). This may lead to a design with undesirable properties, in some cases, due to the well known “optimisation-versus-exploration” dilemma in sequential decision making (cf. Gittins, 1979; Sutton and Barto, 1998). The problem is that, given some optimality criterion, a “greedy” sequential decision rule that always takes the empirically optimal action based on the current data carries a risk of getting stuck at a truly suboptimal action. The problem that greedy sequential algorithms are “sticky” in this sense only recently has been discussed in the context of dose-finding trials, by Azriel, Mandel, and Rinott (2011), Thall and Nguyen (2012), Oron and Hoff (2013), Braun, Kang, and Taylor (2013), and Thall, et al. (2014).

We address the problem of stickiness by applying adaptive randomisation (AR) among d having u(d | data_n) close to the maximum, similarly to Thall and Nguyen (2012). Denote the acceptable dose pair maximising u(d | data_n) by ${\mathit{d}}_n^{\mathit{opt}}$. While nominally this dose pair is “optimal,” it is only empirically optimal based on the most recent data, and it may not be the truly optimal pair that would maximise Ū(d, θ) if θ were known. In practice the truly optimal dose pair cannot be known, but in a simulation study all assumed π^true(y | d) are specified, so the d^opt under this assumed state of nature is known, and design performance can be evaluated accordingly. While this distinction may seem obvious, the difference between an empirically optimal action and the truly optimal action is at the heart of the optimisation-versus-exploration dilemma. A general form for AR probabilities for dose pair d^* based on the posterior mean utilities of the acceptable dose pairs is

$$r_n({\mathit{d}}^{\ast })=\frac{u({\mathit{d}}^{\ast }\mid {\mathit{data}}_n)}{{\sum }_{\mathit{d}\in {\mathcal{A}}_n}u(\mathit{d}\mid {\mathit{data}}_n)}.$$

We studied several modified versions of AR, called AR(m), which is limited to randomising among only the best m dose pairs based on their current posterior mean utilities, for m = 1 (a greedy design with no AR), 2, 3, 4 and 9. The results are summarised in Supplementary Table S5. Additionally, we studied the required difference between the sub-sample sizes of the empirically best and other acceptable dose pairs, to ensure that an adequate number of patients have been treated at ${\mathit{d}}_n^{\mathit{opt}}$ before applying any AR rule. Based on this preliminary study, for the actual trial design, we used AR(2), with AR applied only if at least three or more patients have been treated at the current $d_n^{\mathit{opt}}$ than at any other acceptable d. Denote the empirically second best acceptable dose pair by ${\mathit{d}}_n^{\mathit{second}}$, that is, $u({\mathit{d}}_n^{\mathit{second}}\mid {\mathit{data}}_n)$ is the second largest posterior mean utility. For our implementation of AR(2), the next cohort of patients are treated with dose pair ${\mathit{d}}_n^{\mathit{opt}}$ with probability

$$r_n=\frac{u({\mathit{d}}_n^{\mathit{opt}}\mid {\mathit{data}}_n)}{u({\mathit{d}}_n^{\mathit{opt}}\mid {\mathit{data}}_n)+u({\mathit{d}}_n^{\mathit{second}}\mid {\mathit{data}}_n)},$$

and treated with dose pair ${\mathit{d}}_n^{\mathit{second}}$ with probability 1 − r_n.

3.3 Trial Conduct

Using the above decision criteria, the trial is conducted as follows. Recall that the maximum sample size is N = 60, and the cohort size is c = 3.

1. The first cohort is treated at d = (d_M, d_P) = (4, 60).

2. For each cohort after the first, the posterior decision criteria (5), (6), and (7) are computed based on the most current data.

3. When escalating, an untried dose of either agent may not be skipped.

4. If no d is acceptable, the trial is terminated with no d selected.

5. If exactly one d is acceptable, the next cohort is treated at that dose pair.

6. For cohort size c, if two or more d’s are acceptable and the number of patients treated at ${\mathit{d}}_n^{\mathit{opt}}$ minus the largest number of patients treated at any other acceptable dose is

   1. ≥ c, then apply AR(2) to choose randomly between ${\mathit{d}}_n^{\mathit{opt}}$ and ${\mathit{d}}_n^{\mathit{second}}$.

   2. < c, then treat the next cohort at ${\mathit{d}}_n^{\mathit{opt}}$.

4. Simulations

4.1 General Design Performance Evaluation

The trial design was simulated under each of 12 dose-outcome scenarios, given in Supplementary Table S2, assuming an accrual rate of 1.5 patients per month. Each scenario is specified in terms of fixed true four-level marginal efficacy and toxicity probabilities, which are not based on the design’s model or any other model. Association was induced by assuming a Gaussian copula with true association parameter 0.10. Additional simulations were conducted using alternative models, or different cohort size or maximum sample size. For each case studied, the trial was replicated 3000 times, and all posterior quantities were computed using MCMC with Gibbs sampling.

We use the following summary statistics, given by Thall and Nguyen (2012), to quantify overall design performance. For given d and assumed true outcome probabilities {π^true(y|d)}, we define the true mean utility of d to be

$${\overline{U}}^{\mathit{true}}(\mathit{d})=\sum _{\mathit{y}}U(\mathit{y}){\pi }^{\mathit{true}}(\mathit{y}\mid \mathit{d}).$$

Thus, Ū^true(d) is analogous to, but different from, the mean utility Ū(d, θ) based on the unknown parameter θ, and the posterior mean utility u(d | data_n), which is a statistic. Let ${\overline{U}}_{\mathit{max}}^{\mathit{true}}$ and ${\overline{U}}_{\mathit{min}}^{\mathit{true}}$ denote the largest and smallest possible true mean utilities among all dose pairs. To quantify the method’s reliability for selecting a dose pair with high true utility, which benefits future patients, denoting the final selected dose pair by d_select, we use the statistic

$$R_{\mathit{select}}=100\left\{\frac{{\overline{U}}^{\mathit{true}}({\mathit{d}}_{\mathit{select}})-{\overline{U}}_{\mathit{min}}^{\mathit{true}}}{{\overline{U}}_{\mathit{max}}^{\mathit{true}}-{\overline{U}}_{\mathit{min}}^{\mathit{true}}}\right\}.$$

To quantify benefit to the patients enrolled in the trial, we use the statistic

$$R_{\mathit{treat}}=100\left\{\frac{\frac{1}{N}{\sum }_{i=1}^N{\overline{U}}^{\mathit{true}}({\mathit{d}}_{[i]})-{\overline{U}}_{\mathit{min}}^{\mathit{true}}}{{\overline{U}}_{\mathit{max}}^{\mathit{true}}-{\overline{U}}_{\mathit{min}}^{\mathit{true}}}\right\},$$

where d_[i] is the dose pair given to the i^th patient, and N is the final sample size. For both statistics, a larger value in the domain [0, 100] corresponds to better performance. We also report the selection percentage of the best acceptable d, denoted by % Best.

Simulation results for six selected scenarios are summarised in Table 4. The results for all 12 scenarios are given in Supplementary Table S3 and Supplementary Figure S1. In terms of true utilities and selection percentages of the nine dose pairs, Table 4 shows that the design does a reliable job of selecting acceptable dose pairs having true mean utility at or near the maximum, while also reliably avoiding unacceptable dose pairs. Figure 4 illustrates how the utility function U(y) maps the eight assumed true outcome probability pairs ( ${\pi }_E^{\mathit{true}}(y_E,\mathit{d}),{\pi }_T^{\mathit{true}}(y_T,\mathit{d})$) for y_E = 0, 1, 2, 3 and y_T = 0, 1, 2, 3 to Ū^true(d) for each d, in Scenario 5. For each outcome, the assumed probabilities ${\pi }_k^{\mathit{true}}(y,\mathit{d})$ for y = 0, 1, 2, 3 are represented by successively darker shades of red for k = T and green for k = E. Figure 4 shows, for the PDS model based design, how the dose pair selection probabilities follow the magnitudes of the true mean utilities. A key point is that, if one wishes to compare dose pairs, inevitably a one-dimensional criterion is needed. The utility function provides this in a way that makes sense medically, provided that one accepts the particular numerical utilities given in Table 2.

Table 4.

Simulation results for the PDS-GCR-PO model based design. For each dose pair d = (d_M, d_P), Sel = selection percentage and Npat = number of patients treated. Utilities of unacceptable doses have a gray background. The highest utility among acceptable doses is given in boldface.

	Scenario 1	dP			Scenario 2	dP
	dM	40	60	80	dM	40	60	80
Ūtrue(d) Sel, Npat	4	56.0	51.8	48.3	4	43.2	44.4	37.9
		32, 9.4	25, 14.8	9, 8.4		8, 3.5	17, 12.2	3, 5.3
	5	51.8	47.2	44.7	5	49.7	46.8	38.9
		15, 7.4	7, 6.8	2, 3.2		28, 8.7	24, 10.5	2, 5.2
	6	48.3	44.7	39.4	6	45.5	39.7	33.6
		8, 6.0	2, 2.6	0, 0.9		10, 6.7	5, 5.6	0, 1.7
		Percent none selected = 2				Percent none selected = 2
	Scenario 3	dP			Scenario 5	dP
	dM	40	60	80	dM	40	60	80
Ūtrue(d) Sel, Npat	4	39.4	40.1	36.7	4	30.4	44.4	43.7
		1, 1.1	3, 8.6	1, 3.2		1, 1.2	15, 11.7	9, 6.3
	5	48.9	47.6	42.7	5	44.4	51.3	44.3
		12, 6.1	17, 9.1	3, 5.7		10, 4.4	39, 12.7	9, 8.5
	6	52.6	49.8	44.6	6	43.7	44.3	39.1
		32, 10.0	27, 11.2	3, 4.7		6, 4.0	10, 7.8	1, 3.4
		Percent none selected = 1				Percent none selected = 1
	Scenario 8	dP			Scenario 9	dP
	dM	40	60	80	dM	40	60	80
Ūtrue(d) Sel, Npat	4	33.8	45.4	48.2	4	43.8	50.8	52.6
		1, 0.8	9, 10.0	15, 7.6		1, 0.5	2, 8.3	4, 5.3
	5	37.2		48.953.2	5	50.8	52.6	58.4
		2, 2.6	21, 9.7	33, 12.6		1, 1.6	4, 5.9	17, 11.5
	6	41.3	45.9	45.6	6	52.6	58.4	64.0
		3, 2.5	9, 6.2	6, 7.9		4, 3.4	18, 8.6	48, 14.7
		Percent none selected = 1				Percent none selected = 0

Figure 4.

Illustration of true marginal outcome probabilities { ${\pi }_T^{\mathit{true}}(y,\mathit{d}),{\pi }_E^{\mathit{true}}(y,\mathit{d})$, y = 0, 1, 2, 3}, the resulting true mean utility Ū^true(d), and simulation results %Sel = percent selection and %Pat = percent of patients treated in the trial for each dose pair, using the proposed PDS model based method, under Scenario 5. ${\pi }_k^{\mathit{true}}(y,\mathit{d})$ for y = 0, 1, 2, 3 are represented by successively darker shades of red for k = T and green for k = E.

4.2 Comparison to Models with Qualitatively Different Dose-Dose Effects

The generalised Aranda-Ordaz (GAO) model used by the two-agent phase I–II design of Houede et al. (2010) to account for dose-dose interactions is given in the Appendix. As noted earlier, because this design addresses the same problem of choosing optimal d based on ordinal (Y_E, Y_T), it is a natural comparator to the PDS model based design proposed here. Another comparator may be obtained from the more conventional model formulation in which all λ_k,a = 1 in the PDS linear components and a multiplicative dose-dose interaction term is inclued in the linear term, using the usual standardised doses x_a,j = log(d_a,j/d̄_a). The linear components then would take the commonly assumed form

$${\eta }_k(y,\mathit{d},{\mathit{\theta }}_k)={\alpha }_{k,y}+{\beta }_{k,y,1}{x}_{1,j}+{\beta }_{k,y,2}{x}_{2,r}+{\beta }_{k,12}{x}_{1,j}{x}_{2,r},k=E,T.$$

The β_k,12’s are real-valued and assumed to have normal priors. The element β_k,12x_1,jx_2,r of this linear term is widely considered to be an “interaction” between two covariates in their joint effect on the outcome in a regression model. Here, the interaction is the joint effect of d₁ and d₂ on the marginal probability distribution of Y_k. We will refer to this as the conventional multiplicative interaction (CMI) model.

Table 5 summarises how well the design performs assuming each of these three alternative models, for (4,4) dimensional bivariate ordinal outcomes. All three designs reliably stop the trial early if no d pairs are acceptable, in Scenarios 11 and 12. For Scenarios 1 – 10, Figure 5 shows the comparative R_select results graphically. In the five scenarios {2, 4, 5, 6, 8} where d^opt is a middle dose pair, not located at one of the four corners of the 3 × 3 matrix of d pairs, the PDS model gives much larger R_select values than the other two designs. The differences R_select(PDS) - R_select(GAO) vary from 5 to 13 (7% to 20%), while R_select(PDS) - R_select(CMI) vary from 9 to 16 (13% to 26%). In the four scenarios {1, 3, 7, 9} where d^opt is located at one of the four corners of the matrix of d pairs, the GAO and the CMI model give R_select values that are larger than those of the PDS model by the smaller differences 5 to 7 (6% to 9%). The R_treat and % Best d selected values also follow these general patterns. Scenario 10 corresponds to the prior, and has three acceptable dose pairs all having the same maximum true utility. An important property of the PDS method is that it gives much more stable behavior across Scenarios 1 – 10, with R_select values in the range [76, 89], compared to ranges [65, 88] for the GAO method and [62, 92] for the CMI model. Similarly, the % Best d selected values have range [28, 48] for the PDS method versus ranges [8, 67] for the GAO model and [2, 68] for the CMI model. It thus appears that using parametrically standardised doses gives much more stable behavior across a range of scenarios, and provides insurance against very poor performance in some scenarios. The PDS model gives substantially larger R_select values in the harder cases where d^opt is a middle dose pair, with the price being smaller R_select values in the easier cases where d^opt is located at a corner of the rectangular dose pair domain.

4.3 Comparison to Designs that Reduce the Ordinal Outcomes

We next compare our proposed method, based on the (4,4) dimensional ordinal outcome Y = (Y_E, Y_T), to alternative designs that reduce this outcome by combining categories. The first two comparators are versions of the PDS and GAO designs based on (3,3) ordinal outcomes obtained by combining SD2 and CR/PR for Y_E and combining High and Severe for Y_T. We obtained a (2,2) outcome by also combining the Y_E events PD and SD1 so that Y_E became the binary indicator of [CR/PR or SD2], and combining the Y_T events Mild and Moderate so that Y_T became the binary indicator of [High or Severe]. For each of these (3,3) and (2,2) cases, in each scenario the outcome probabilities were obtained from those in Supplementary Table S2 by summing the corresponding elementary event probabilities. For the (2,2) case, in addition to the reduced version of the PDS design, we also included as comparators the phase I–II designs of Yuan and Yin (YY, 2011) and Wages and Conaway (WC, 2014), both of which rely on bivariate binary Y. A final comparator is the partial orders continual reassessment method (PO-CRM) of Wages, Conaway, and O’Quigley (2011), which uses only a binary version of Y_T to choose optimal d.

The YY design uses a copula to model the probability of toxicity as a function of d in phase I, and chooses a set of admissible d for subsequent efficacy evaluation in parallel treatment arms in phase II. The design applies AR based on the probability of a binary efficacy outcome in phase II, assuming a hierarchical binomial-beta-gamma model. At the end of phase II, the YY design selects the dose pair with acceptable toxicity that has highest posterior mean efficacy. Since the YY design allows one to vary the cohort size c and sub-sample sizes n_I and n_II in phases I and II, for comparison to the PDS model based design, we first simulated versions of the YY design with (c, n_I, n_II) = (3, 30, 30), (1, 30, 30), and (1, 20, 40), given in Supplementary Table S8. Since the YY design with (c, n_I, n_II) = (1, 30, 30) has slightly better overall performance than the other two, this version is used for comparison to the PDS design.

The WC design is based on partial orderings of d. Like the YY design, the WC design also chooses the dose pair d with acceptable toxicity that maximises the probability of efficacy. We simulated both the YY and WC designs using the same toxicity probability acceptability upper limit, .45, and efficacy probability lower limit, .40, as those used by the PDS design. Since the total number of possible partial orderings in the rectangle of d pairs is impractically large, a subset must be chosen. For comparison to the PDS model based design, we first simulated versions of the WC design with either six partial orderings, starting the trial at d = (1,2) as in our design, or 26 partial orderings, starting the trial at either d = (1,2) or (1,1), summarised in Supplementary Table S9. Since the version with 26 partial orderings, starting the trial at d = (1,2) had slightly better overall performance than the other two, it is included in Table 6.

An important point is that both the YY and WC designs choose d that has acceptably low toxicity and maximum efficacy, whereas the PDS design chooses d that has acceptably low toxicity, acceptably high efficacy, and maximum posterior mean utility. That is, the criteria are qualitatively different. The three designs have the same “best” d is scenarios 5, 6, 8, 9, and 10, and different “best” d in scenarios 1, 2, 3, 4, and 7. To compare the methods, we used the same utility-based criteria, namely R_select, R_treat, and true mean utility Ū^true(d) to define % Best d selected.

The results are given in Table 6. Comparing the PDS model based design with (4,4) versus (3,3) dimensional outcomes shows that the R_select values differ by at most ±3 for Scenarios 1 – 8 and 10, but in Scenario 9 using a (3,3) outcome greatly reduces R_select, from 80 to 66. A similar pattern is seen for R_treat and % Best d selected. Comparison of the PDS model, with either (4,4) or (3,3) outcomes, to the GAO model with (3,3) outcomes shows that the latter has much larger variability between scenarios in terms of R_select, R_treat, and % Best. Thus, as in Table 5, it appears that the PDS model provides a much more stable design, and in particular protects against very poor performance in some cases, as seen in Scenarios 4, 5, and 9 with the GAO model.

Simulation results for four designs in Table 6 are illustrated graphically for R_select in Figure 6, which shows that, in general, dichotomising the ordinal outcomes substantively decreases R_select values in some scenarios, regardless of the design used. Figure 6 also illustrates that the PDS model based design using the full (4,4) dimensional ordinal outcome is robust, in the sense that the R_select values stay consistently high across all scenarios. In the special case of Scenario 10, which corresponds to the prior, three of the nine d pairs are optimal, hence selecting an optimal d pair is much easier for all designs. Supplementary Table S10 shows that the PO-CRM has greatly inferior performance compared to the PDS based design. This may be attributed to the general fact that using binary toxicity alone for dose-finding may ignore useful efficacy information.

Figure 6.

R_select values of competing phase I-II designs to choose an optimal dose pair, given (4,4) dimensional ordinal (efficacy, toxicity) outcomes. ‘PDS 4 Levels’ denotes the proposed PDS model-based design. The other three designs all reduce both outcomes to binary variables, including the PDS design with dichotomised outcomes, YY = Yuan and Yin (2011) design, and WC = Wages and Conaway (2014) design.

4.4 Additional Sensitivity Analyses

Supplementary Table S6 shows that the PDS based design’s behavior is insensitive to cohort size c = 1, 2, or 3. Supplementary Table S4 summarises the PDS model-based design’s sensitivity to maximum sample sizes N = 30 to 300. The design’s operating characteristic improve greatly as N increases. For example, in Scenario 1, for N = 30, 60, 300, the corresponding R_select values are 67, 76, 95 and R_treat values are 61, 76, 78. The same pattern is seen for all other scenarios with acceptable dose pairs. In the two Scenarios 11 and 12, where there is no acceptable d, the simulated probability that no pair is selected is 1 for N ≥ 120. These results provide an empirical validation of the method’s consistency, in terms of both optimal dose pair selection and stopping the trial early for futility or safety in cases where this should be done. These numerical results also show that the maximum sample size 60 cannot reliably achieve R_select values of 80 or larger across the scenarios studied, in this particular setting, and that N ≥ 90 is needed to achieve R_select ≥ 80, and N roughly 200 to 240 is needed if R_select ≥ 90 is desired.

Supplementary Table S12 summarises the behavior of the PDS based design when the trial is conducted using each of three different numerical utilities. One is the elicited utility in Table 2, and two are hypothetical, given in Supplementary Table S11, constructed to place greater value on either lower toxicity or greater efficacy. The simulations show that, across the 12 scenarios, the three resulting designs behave differently, but with no general pattern favoring one utility over the others. The utility favoring higher efficacy gives a design that escalates more aggressively and thus has greater observed toxicity and efficacy. Analogously, the utility favoring lower toxicity results in less toxicity but also less efficacy. A general conclusion is that the design behaves in a way that reflects the numerical values of U(y), which is the intention.

Table 7 gives a patient-by-patient illustration of how the design may behave as the trial plays out, and what the interim estimates look like during the trial, for patients 1 – 12, 15, 30, 45, and 60. Since the maximum posterior mean utility after the first cohort is u(4, 80 | data₃) = 35.5, the pair d = (4,80) is used to treat cohort 2. Although u(6, 60 | data₆) = 34.0 is largest for n = 6, the constraint that an untried dose may not be skipped when escalating results in d = (5,60) being used to treat cohort 3. The trial continues similarly, applying the AR method as described in step 6 of the design in Section 3.3. For each d, the posterior variability of u(d | data_n) decreases with sample size n, but not monotonically. At the end of the trial, d = (6,60) is optimal with u(6, 60 | data₆₀) = 57.0, but d = (6,40) also is a good choice since it is nearly optimal with u(6, 40 | data₆₀) = 56.1.

Table 7.

Case-by-case example of a 60 patient trial. The largest current posterior mean utility is given in boldface.

Patient	Dose Pair		Outcomes		Posterior mean utility u(d | datan) and its (std dev) for each (d1, d2)
	d1	d2	YE	YT	(4,40)	(4,60)	(4,80)	(5,40)	(5,60)	(5,80)	(6,40)	(6,60)	(6,80)
(Prior)	–	–	–	–	34.8 (22.3)	37.3 (25.5)	38.0 (26.4)	36.3 (24.2)	39.0 (27.3)	39.7 (28.1)	36.8 (24.8)	39.5 (27.9)	40.2 (28.7)
1	4	60	1	0	49.2 (11.8)	54.2 (6.0)	54.8 (10.9)	51.0 (14.8)	55.9 (13.2)	56.5 (16.1)	51.6 (15.7)	56.4 (14.9)	56.9 (17.6)
2	4	60	1	0	49.8 (11.1)	54.7 (3.5)	55.2 (9.9)	51.5 (14.2)	56.3 (12.3)	56.7 (15.5)	52.0 (15.2)	56.7 (14.2)	57.1 (17.0)
3	4	60	0	2	33.6 (9.9)	35.5 (8.5)	35.5 (12.3)	33.8 (14.5)	34.9 (14.4)	34.9 (16.6)	33.3 (15.5)	34.0 (15.3)	34.1 (17.3)
4	4	80	1	1	35.2 (9.4)	37.2 (7.2)	37.4 (8.1)	37.9 (12.5)	39.6 (11.6)	39.7 (12.5)	38.7 (13.2)	40.2 (12.5)	40.3 (13.4)
5	4	80	0	1	31.7 (8.3)	33.7 (6.4)	31.8 (6.8)	35.3 (13.2)	37.4 (12.6)	35.5 (13.0)	36.3 (14.1)	38.3 (13.5)	36.5 (14.0)
6	4	80	0	1	30.4 (6.9)	31.4 (5.7)	29.6 (5.9)	32.5 (11.4)	33.6 (11.4)	32.3 (11.7)	32.9 (12.3)	34.0 (12.3)	33.0 (12.7)
7	5	60	1	1	30.4 (7.4)	31.8 (5.5)	30.0 (5.5)	34.2 (10.4)	35.5 (7.6)	34.8 (8.2)	34.6 (11.0)	36.0 (8.7)	35.4 (9.3)
8	5	60	1	0	30.4 (7.4)	32.9 (5.3)	31.7 (5.5)	37.8 (10.6)	40.0 (6.4)	38.7 (7.4)	37.6 (11.2)	39.4 (8.0)	38.3 (9.0)
9	5	60	0	2	31.5 (7.2)	31.6 (4.9)	30.7 (5.3)	32.3 (7.9)	31.9 (5.5)	31.1 (6.1)	34.5 (10.6)	33.8 (9.5)	33.0 (10.1)
10	6	40	2	2	30.9 (6.4)	31.9 (5.2)	30.4 (5.5)	31.3 (7.5)	32.3 (6.6)	31.1 (7.1)	48.4 (16.7)	50.2 (17.8)	49.6 (18.4)
11	6	40	2	2	31.7 (6.6)	32.2 (5.3)	29.5 (5.6)	30.9 (7.9)	31.4 (6.8)	29.0 (7.1)	52.7 (12.6)	54.7 (14.1)	53.3 (15.4)
12	6	40	3	2	31.3 (6.5)	31.8 (5.6)	29.6 (5.9)	30.8 (7.7)	31.4 (7.0)	29.4 (7.4)	57.0 (13.9)	62.9 (16.8)	62.7 (17.8)
15	6	60	1	2	32.0 (6.9)	32.6 (6.2)	30.4 (6.4)	32.1 (9.5)	32.8 (9.1)	31.2 (9.3)	56.0 (10.6)	56.9 (10.3)	57.3 (12.0)
30	6	80	2	1	35.8 (7.4)	36.2 (6.3)	36.1 (6.7)	38.9 (10.4)	39.1 (9.6)	39.1 (10.0)	53.7 (5.7)	53.6 (5.9)	53.9 (6.2)
45	6	40	1	0	33.6 (6.2)	33.6 (6.0)	28.2 (6.1)	34.6 (9.6)	34.3 (9.4)	28.5 (9.6)	55.5 (4.7)	55.4 (4.7)	48.7 (6.1)
60	6	60	3	1	36.7 (6.9)	37.9 (6.4)	31.5 (7.7)	37.2 (10.3)	38.2 (9.9)	32.1 (10.5)	56.1 (4.0)	57.0 (3.8)	50.4 (5.5)
Total number of patients assigned					0	3	3	0	3	0	21	24	6

5. Discussion

Because the generalised CR model given by (2) links the conditional probability ${\gamma }_k(y,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)$ to the linear term ${\eta }_k(y,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)$, it has the computational advantage that there are no order constraints on the intercept parameters α_k,1, ···, α_k,Lk. An alternative model may be defined by

$${\overline{\pi }}_k(y,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)=1-{\{1+{\varphi }_k{e}^{{\eta }_k(y,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)}\}}^{-1/{\varphi }_k}.$$

This generalises the proportional odds model (McCullagh, 1980) by replacing the logit link with the AO link. Because this model links the unconditional probability ${\overline{\pi }}_k(y,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)$ rather than the conditional probability ${\gamma }_k(y,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)$ to the linear term, it requires the order constraints α_k,1 > ··· > α_k,Lk for the probabilities to be well defined. Using this model for dose-finding, the need to impose these constraints on each parameter vector α_k = (α_k,1, ···, α_k,Lk), k = E, T makes the MCMC computations to obtain posteriors much more difficult, especially for small amounts of data. This is one important motivation for our use of the generalised CR model.

Various special cases or alternative formulations of the PDS model can be obtained by changing one or more of its components. A natural question is whether adding a multiplicative dose-dose interaction term to the model with parametric dose standardisation would improve the design’s behavior. This model would have linear components

$${\eta }_k(y,{\mathit{x}}_k^{\lambda },{\mathit{\theta }}_k)={\alpha }_{k,y}+{\beta }_{k,y,1}{x}_{k,1,j}^{\lambda }+{\beta }_{k,y,2}{x}_{k,2,r}^{\lambda }+{\beta }_{k,12}{x}_{k,1,j}^{\lambda }{x}_{k,2,r}^{\lambda }.$$

It may be considered a hybrid of the PDS and CMI model, in that it includes both parametric dose standardisation and a conventional multiplicative interaction term. Supplementary Table S7 shows that, compared to the PDS model, the hybrid model gives a design with R_select values 1 to 6 smaller in eight scenarios, 1 to 3 larger in two scenarios, and slightly larger incorrect early stopping probabilities. Thus, on average, this more complex hybrid model produces a design with slightly worse performance than the PDS model.

A computer program named “U2OET” for implementing this methodology is available from the website https://biostatistics.mdanderson.org/SoftwareDownload.

Appendix: Review of Generalised Continuation Ratio Models and Copulas

Recall that γ_k(y, d, θ_k) = P(Y_k ≥ y | Y_k ≥ y − 1, d, θ_k), for y = 0, ···, L_k. For given link function and linear term η(y, d, θ_k), a GCR model defines this conditional probability as

$${\gamma }_k(y,\mathit{d},{\mathit{\theta }}_k)=\mathit{link}\{\eta (y,\mathit{d},{\mathit{\theta }}_k)\}.$$

The marginal probabilities of a GCR model are given by

$$\begin{array}{lll}{\pi }_k(0,\mathit{d},{\mathit{\theta }}_k)\hfill & =\hfill & 1-{\gamma }_k(1,\mathit{d},{\mathit{\theta }}_k)\hfill \\ {\pi }_k(y,\mathit{d},{\mathit{\theta }}_k)\hfill & =\hfill & \{1-{\gamma }_k(y+1,\mathit{d},{\mathit{\theta }}_k)\}\prod _{r=1}^y{\gamma }_k(r,\mathit{d},{\mathit{\theta }}_k),y=1,\cdots ,L_k,\hfill \\ {\overline{\pi }}_k(y,\mathit{d},{\mathit{\theta }}_k)\hfill & =\hfill & \prod _{r=1}^y{\gamma }_k(r,\mathit{d},{\mathit{\theta }}_k),y=1,\cdots ,L_k.\hfill \end{array}$$

Since

$$P(Y_k\ge y\mid Y_k\ge y-1,\mathit{d},{\mathit{\theta }}_k)=1-\frac{P(Y_k=y-1\mid \mathit{d},{\mathit{\theta }}_k)}{P(Y_k\ge y-1\mid \mathit{d},{\mathit{\theta }}_k)},$$

the GCR model may be specified equivalently in the more commonly used form

$$\frac{Pr(Y_k=y\mid \mathit{d},{\mathit{\theta }}_k)}{Pr(Y_k\ge y\mid \mathit{d},{\mathit{\theta }}_k)}=1-{\gamma }_k(y+1,\mathit{d},{\mathit{\theta }}_k),y=0,\cdots ,L_k-1.$$

In general, the joint pmf of Y =(Y_E, Y_T) given by a copula (Nelsen, 2006) can be defined in terms of the marginal cdfs

$$F_k(y\mid \mathit{d},{\mathit{\theta }}_k)=Pr(Y_k\le y\mid \mathit{d},{\mathit{\theta }}_k)=1-{\overline{\pi }}_k(y+1,\mathit{d},{\mathit{\theta }}_k),\text{for}y=0,\dots ,L_k-1,k=E,T,$$

by applying the formula

$$Pr(Y_E=y_E,Y_T=y_T\mid \mathit{d},\mathit{\theta })=\sum _{a=1}^2\sum _{b=1}^2{(-1)}^{a+b}{C}_{\rho }(u_a,v_b)$$

where C_ρ(u_a, v_b) denotes the copula and u₁ = F_E(y_E|d, θ), v₁ = F_T(y_T|d, θ), u₂ = F_E(y_E − 1|d, θ) and v₂ = F_T(y_T − 1|d, θ). To obtain a bivariate distribution under the the PDS model, we assume a Farlie-Gumbel-Morgenstern (FGM) copula

$$C_{\rho }(u,v)=uv\{1+\rho (1-u)(1-v)\},\text{for}0\le u,v\le 1,-1\le \rho \le +1.$$

The GCR model given by Houede et al. (2010) accounts for the joint effects of the two doses on each ordinal outcome in a qualitatively different way. First, a conventional linear term for each agent a = 1, 2, level y of outcome Y_k for k = E, T, and dose d^(a) is defined as

$${\eta }_{k,y}^{(a)}={\alpha }_{k,y,0}^{(a)}+{\alpha }_{k,y,1}^{(a)}{d}^{(a)}.$$

A generalised Aranda-Ordaz (GAO) link is then defined as

$${\gamma }_k(y,\mathit{d},{\mathit{\theta }}_k)=1-{\{1+{\lambda }_k(e^{{\eta }_{k,y}^{(1)}}+e^{{\eta }_{k,y}^{(2)}}+\kappa e^{{\eta }_{k,y}^{(1)}+{\eta }_{k,y}^{(2)}})\}}^{-1/{\lambda }_k}$$

where κ > 0 is a dose-dose interaction parameter. Houede et al. (2010) obtain bivariate distributions by assuming a Gaussian copula,

$$C_{\rho }(u,v)={\mathrm{\Phi }}_{\rho }\{{\mathrm{\Phi }}^{-1}(u),{\mathrm{\Phi }}^{-1}(v)\}$$

where Φ_ρ denotes a bivariate normal cdf with correlation ρ and Φ denotes a N(0,1) cdf.