Abstract
Recent advances in the literature on mediation have extended from traditional linear structural equation modeling approach to causal mediation analysis using potential outcomes framework. Pearl proposed a mediation formula to calculate expected potential outcomes used in the natural direct and indirect effects definition under the key sequential ignorability assumptions. Current methods mainly focused on binary exposure variables, and in this article, this approach is further extended to settings in which continuous exposures may be of interest. Focusing on a dichotomous outcome, we give precise definitions of the natural direct and indirect effects on both the risk difference and odds ratio scales utilizing the empirical joint distribution of the exposure and baseline covariates from the whole sample analysis population. A mediation-formula based approach is proposed to estimate the corresponding causal quantities. Simulation study is conducted to assess the statistical properties of the proposed method and we illustrate our approach by applying it to the Jackson Heart Study to estimate the mediation effects of diabetes on the relation between obesity and chronic kidney disease. Sensitivity analysis is performed to assess the impact of violation of no unmeasured mediator-outcome confounder assumption.
Keywords: potential outcomes framework, mediation formula, natural direct effect, natural indirect effect, continuous exposure, sensitivity analysis
1. Introduction
Recently, research on the effects of exposure on health outcome has progressed from estimating the total effect of a given exposure to more complex explanatory questions. In particular, medical research has increasingly focused on identifying the mechanisms by which an exposure may exert its effects on health, particularly by decomposing the total effect into an indirect effect mediated through a specific mediator and the remaining direct effect. For example, obesity is known to be a risk factor for coronary heart disease and stroke, but the question remains as how much of the increased risk is through blood pressure, cholesterol and glucose, and how much is independent of these factors (Lu et al. 2014). This type of question could be addressed using data from cohort studies that include measurements of obesity as well as of possible mediators such as blood pressure, cholesterol, and glucose at baseline and also the outcome as time to incident coronary heart disease and stroke. A second example is the effect of the CHRNA5-A3 genetic locus on the risk of lung cancer. It is well documented that the CHRNA5-A3 region on chromosome 15q24-25.1 is strongly associated with an increased risk of lung cancer and nicotine dependence, and this effect seems to be at least partly mediated through smoking and chronic obstructive pulmonary disease (Wang et al. 2010).
The standard approach advanced by Baron and Kenny (1986) utilizes the linear structural equation modeling (LSEM) framework and involves a series of linear regression models. However, the popular product of coefficients approach used in the LSEM framework to estimate the indirect effects does not have a ‘causal’ interpretation when extended to non-linear models such as logistic regression (MacKinnon et al. 2007). More recently, causal mediation analysis approaches have been developed based on the potential outcomes framework (Robins and Greenland 1992; Albert 2008) and in one such approach, Pearl (2012) proposed a mediation formula, applicable to linear and non-linear models for the natural direct and indirect effects estimation. In this approach, the expected potential outcomes used in the definition of causal quantities are identified as the integration (or summation) of conditional means of the response variable over the probability density distribution of the mediators. There are necessary assumptions for the identifiability of the causal mediation effects using the mediation formula approach and the key assumption made is that of ‘sequential ignorability’ which consists of ignorable exposure and no mediator-outcome confounders (Imai et al. 2010a, 2010b). Sensitivity analysis approaches have been developed with different sensitivity parameters to formally quantify the robustness of conclusion regarding the mediation effects to the potential violation of untestable assumptions (Imai et al. 2010a, 2010b; Albert and Wang 2015). Building on the mediation formula, Imai et al. (2010a) provided a general approach to causal mediation analysis that accommodated linear and non-linear, parametric and non-parametric models, continuous or discrete mediators, and various types of outcome variables. The mediation formula approach is also extended to mediation analysis of complex causal models involving multiple mediators (Wang et al. 2013; VanderWeele and Vansteelandt 2013) and multiple-stage mediators (Albert and Nelson 2011; Wang and Albert 2012). To this date, mediation analysis methods have mainly focused on binary exposure variables. Although Imai et al. mentioned that the mediation formula approach can be extended to the case of non-binary exposure case at the cost of notational complexity, the corresponding population-wide average causal mediation effects involving the distribution of the observed exposure and baseline covariates are not clearly defined, specifically for a dichotomous outcome to identify the causal mediation effects on multiple scales (Imai et al. 2010a). In this paper, we give precise definitions of the natural direct and indirect effects utilizing the empirical joint distribution of the exposure and baseline covariates from the whole sample analysis population and propose a mediation formula based approach to estimate the corresponding causal quantities for a continuous exposure and a dichotomous outcome on both the risk difference (RD) and odds ratio (OR) scales. In addition, a sensitivity analysis method is extended to this setting.
The paper proceeds as follows. First of all, we introduce the model framework and give precise definitions of the population-wide natural direct and indirect effects for a continuous exposure and a dichotomous outcome on both risk difference and odds ratio scales. Next, a mediation formula approach is proposed to estimate the natural direct and indirect effects under given identification assumptions and we extend a previously proposed hybrid causal-observational sensitivity analysis approach to assess the robustness of estimated causal quantities. Then simulation studies are used to examine the statistical properties of the proposed mediation analysis method. The subsequent section illustrates our methods with a real data example and discussion follows.
2. Defining the natural direct and indirect effects
Assume that measurements have been made on a continuous exposure of interest X, a dichotomous outcome Y, a potential mediator M and a set of baseline covariates W not affected by the exposure. The relations among these variables are depicted in Figure 1. For example, X may denote Body Mass Index (BMI), a measure of obesity, binary M diabetes (yes or no) or continuous M fasting plasma glucose concentration (mg/dL), Y chronic kidney disease (CKD), and W baseline covariates, including age, gender and binary cigarette smoking (current smoker/non-current smoker). A question of interest may be the extent to which the effect of BMI on CKD is mediated through diabetes and the extent to which it is through other pathways (Maric-Bilkan 2013; Eknoyan 2007).
Figure 1.
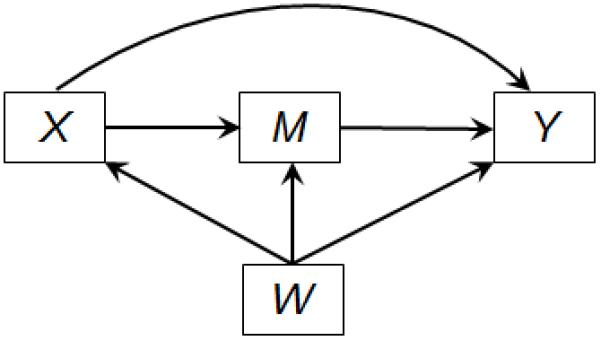
Mediation model with exposure X, mediator M, outcome Y and covariates W.
To model the causal effect of a continuous exposure, we use the potential outcomes framework (Robins and Greenland 1992; Albert 2008). We will let M(x) denote the potential value of the mediator under the exposure status x, Y(x, m) represent the potential outcome of Y when X = x and M = m and Y(x, M(x′)) indicates the counterfactual value of Y that would be observed if X was set to x and M was set to its potential outcome that would be observed if X was set to x′. For binary outcomes, we can define the natural direct and indirect effects of a continuous exposure on both the risk difference (Pearl 2001) and odds ratio scales (VanderWeele and Vansteelandt 2010).
On the risk difference scale, the natural indirect effect can be defined for any two levels of exposure,
| (1) |
where x1 ≠ x0. This equation can help understand the counterfactual question, what change would occur to the binary outcome if one changes the mediator from the value that would be realized under one condition M(x0), to the value that would be observed under another condition, M(x1), while holding the exposure status at x, which represents the indirect effect of the exposure on the outcome through the mediating variable. Equation (1) is equivalent to the definition in the binary exposure case when x1 = 1, x0 = 0 and x = 1 or 0. In our definition, we assume that x1 = x0 + 1 in order to provide the exposure effect and mediation effect estimates corresponding to ‘one’ unit increase of the continuous exposure variable, and we can rescale our original exposure variable in advance to assess the corresponding causal quantities for any unit increase of the exposure variable. In addition, we also define x = x0 or x1 by assuming the two manipulations x and x′ in the potential outcome Y(x, M(x′)) are consecutive or equal (consistent with the definition in the binary exposure case). We only consider x equals x0 in this article, and our definition and identification methodology, however, can be applied to both ‘x equals x0’ and ‘x equals x1’ and also cases with any arbitrary x value (neither x0 nor x1). Under these two restrictions, the natural indirect effect under exposure x is defined as,
| (2) |
On the risk difference scale, the natural indirect effect can be interpreted as the difference between two mean potential outcomes that would result under exposure x, but where the mediator takes values that would result under exposure statuses x + 1 and x respectively. Similarly, we can define the natural direct effect and total effect using the potential outcomes as,
| (3) |
| (4) |
The total effect decomposes into the natural direct and indirect effects,
| (5) |
and the proportion of exposure effect due to the mediator is defined as,
| (6) |
Similarly, we can define the natural indirect, natural direct and total effects on the odds ratio scale as following,
| (7) |
| (8) |
| (9) |
On the odds ratio scale, the decomposition still holds in which the total effect decomposes into a product of odds ratios for the natural direct and indirect effects, and we can define the corresponding mediation proportion using logarithm of odds ratio,
| (10) |
| (11) |
Of note, in this paper, the natural effects refer to the fact that we let the mediator take the value it would take naturally when the exposure is set to a specific value. This is in contrast to the controlled effects (Petersen et al. 2006; Goetgeluk et al. 2008), where the mediator is kept fixed at a controlled level. As the controlled effects do not allow an obvious definition of mediation effect, we will focus on the natural effects in this paper.
3. Estimation of the natural direct and indirect effects
3.1 Mediation formula (causal model) approach
Under a particular version of the sequential ignorability assumption, the natural direct and indirect effects for a continuous exposure can be nonparametrically identified with the observed data. We use the following version of this assumption proposed by Imai et al. (2010b): Assumption 1 (Sequential Ignorability)
| (12) |
| (13) |
Thus, the exposure is first assumed to be independent of subsequent potential mediators and potential outcomes given the baseline covariates (W), and then the mediator variable is assumed to be independent of potential outcomes given the observed exposure and baseline covariates. In addition, we also assume the technical assumption called ‘consistency’, that is, for any individual, the potential outcome of Y setting X = x is equal to the observed outcome if the exposure of this individual is x. This assumption provides the connection between potential and observed outcomes (VanderWeele 2009).
Under the sequential ignorability and consistency assumptions, the expected potential outcomes for Y used to define the natural direct and indirect effects can be written as follows,
| (14) |
where Fw(w) and FM | X=x′,W=w (m) represent the distribution function of W and the conditional distribution function of M given X and W, respectively. The above formula (proof is given by Imai et al. (2010b)), referred by Pearl as the mediation formula (Pearl 2012), provides identification of the natural direct and indirect effects when a continuous exposure is used. Instead of integrating over the unknown distribution of W as (14), an alternative approach is to average over the empirical distribution of W for the subjects in the chosen reference group and the integration of the mediator is replaced with summation in the case of discrete mediators. The estimation of causal quantities typically proceeds by fitting parametric models of Y and M to the data. We assume the following regression models for a dichotomous outcome Y and a binary or continuous mediator M,
| (15) |
| (16) |
The error term in the linear regression for continuous mediator M is assumed normally distributed with constant variance. In this paper, we focus on the identification and inference of the average causal effect using the whole sample analysis population as our reference group and the population-wide causal effects are defined as mean of the individual causal effect using the empirical joint distribution of the exposure and baseline covariates. If the assumptions of sequential ignorability (Assumption 1) hold and the regression models (15) and (16) are correctly specified, the average natural indirect effect on the risk difference scale is given by (continuous mediator case),
| (17) |
where N is the number of subjects in the total sample population, xi and wi are the exposure status and the baseline covariate for subject i respectively. Similarly, the average natural direct effect and total effect can be defined. On the odds ratio scale, the geometric mean of individual causal quantities is used for the average natural direct and indirect effects definition which is equivalent to arithmetic mean of logarithmic odds ratio. Variance estimates for causal quantities can be obtained via the delta method and integration of normally distributed mediators is approximated with a 40-point Gauss-Hermite quadrature (Lee et al. 2009; Lee et al. 2013).
3.2 Sensitivity analysis
For the identified mediation effect in our potential outcomes framework, the quantity cannot be given a causal interpretation without the particular sequential ignorability assumption. Specifically, the second no mediator-outcome confounder assumption (13) is nonrefutable in the sense that it cannot be directly tested with the observed data. Imai et al. argued that a mediation analysis is not complete without a sensitivity analysis (2010b). When the unmeasured mediator-outcome confounders exist, the expected potential outcomes E{Y(x + 1, M(x + 1))} and E{Y(x, M(x))} are identifiable but not E{Y(x, M(x + 1))}. We examine the effect of violation of assumption (13) on the estimation of the natural direct and indirect effects with the proposed hybrid causal-observational model approach (Albert and Wang 2015). In this approach, we consider a hybrid causal-observational model that extends the association model of the final outcome by incorporating both the causal and cohort effects, and this approach provides a novel sensitivity parameter presenting the proportion of the association effect due to the cohort effect. The model is specified as following,
| (18) |
where β1 represents the association effect of X on Y, and all β′s in (18) are estimable from the corresponding association model if we set x = x′. The weaker condition of sequential ignorability assumption ‘mediator comparability’ is satisfied if ϕ equals 0 indicating that the conditional expectation of the potential outcome Y(x, m) does not depend on the observed group x′, and therefore the related conditional expected potential used for the natural direct and indirect effects definition can be identified. So ϕ can be interpreted as the nonidentifiable proportion of the association effect due to the cohort effect and equivalently, (1 - ϕ) is the proportion of the association effect due to the causal effect of exposure. As the causal effect β1(1 - ϕ) and the cohort effect β1ϕ need not be in the same direction, it is possible for this ‘proportion’, ϕ, to be negative or greater than 1. For the more general hybrid model with x′ not equal to x, the natural direct and indirect effects can be estimated by varying ϕ to assess the effect of departure from mediator comparability.
4. Simulation study
We conducted a simulation study to examine the bias, efficiency and coverage of the confidence intervals for the natural indirect estimator from our proposed method on the risk difference and odds ratio scales when the outcome and mediator models were correctly specified or mis-specified. The outcome model (Y) includes a continuous exposure indicator (X) and a mediator variable M (either binary or continuous) and the mediator model (M) only includes the continuous exposure X. We considered eight different scenarios, classified into two groups as following (binary mediator case for scenarios 1 to 4 and continuous mediator case for scenarios 5 to 8),
-
(1)
Y | XM follows a logit model and M | X follows a logit model;
-
(2)
Y | XM follows a logit model and M | X follows a probit model;
-
(3)
Y | XM follows a probit model and M | X follows a logit model;
-
(4)
Y | XM follows a probit model and M | X follows a probit model;
-
(5)
Y | XM follows a logit model and M | X follows a linear regression model with normal errors;
-
(6)
Y | XM follows a logit model and M | X follows a Gaussian mixture model;
-
(7)
Y | XM follows a probit model and M | X follows a linear regression model with normal errors;
-
(8)
Y | XM follows a probit model and M | X follows a Gaussian mixture model;
For each of above scenarios, 1000 simulated datasets were generated with total sample size of 200.
The true natural indirect effect on risk difference scale is defined by the formula (17), assuming the true models for the mediator and the outcome are known with true coefficients in place of the estimates. The true natural indirect effect on odds ratio scale (presented as log(IE(x)OR)) can be calculated in a similar way. For each generated dataset of all eight scenarios, the proposed mediation formula approach was used to calculate the estimated IE (IE(x)RD or log(IE(x)OR)), consistently assuming a logit model for Y | XM and a logit model or a linear regression model for M | X. For IE(x)RD estimates on risk difference scale, we calculated the average estimate of IE(x)RD; the average percent error (PE = 100 × (Average Estimated IE(x)RD – True IE(x)RD)/true IE(x)RD), a measure of relative bias; the standard deviation (SD) of estimated IE(x)RD; the average estimated standard error (SE) of estimated IE(x)RD; the coverage probability (CP, percent of simulated datasets for which 95% confidence interval for IE(x)RD covered the true value). Similar summary statistics were calculated for log(IE(x)OR) estimates on odds ratio scale.
The simulation results are given in Table 1. For both the binary mediator and the continuous mediator cases, we see that the proposed approach produces a small relative bias (< 2.5%) in its estimation of IE(x)RD and log(IE(x)OR), and the coverage probabilities of 95% confidence intervals are within 4% of the nominal level when both the outcome model and the mediator model are correctly specified (scenario 1 and scenario 4). The average SEs are close to the SDs of the estimates, indicating that the proposed estimation and inference procedure work well for our finite samples. When either the outcome model or the mediator model is mis-specified (scenarios 2, 3, 4, 6, 7 and 8), the mediation formula approach using incorrect models is biased with relative bias up to 9%.
Table 1.
Simulation statistics of the estimated natural indirect effect for a continuous exposure and a dichotomous outcome, n = 200.
| Scenario | True Y Model | True M Model | Risk Difference, IE(x)RD (%) |
Odds Ratio, log(IE(x)OR) |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True IE | Ave Est IE | Ave PE (%) | SD of Est IE | AVE SE | CP (%) | True log(IE) | Ave Est log(IE) | Ave PE (%) | SD of Est log(IE) | AVE SE | CP (%) | |||
| Binary Mediator | ||||||||||||||
| 1 | Logit | Logit | 1.07 | 1.09 | 1.7 | 0.67 | 0.66 | 91.1 | 0.068 | 0.069 | 2.1 | 0.041 | 0.040 | 91.1 |
| 2 | Logit | Probit | 0.81 | 0.84 | 4.4 | 0.61 | 0.59 | 92.7 | 0.051 | 0.053 | 3.8 | 0.037 | 0.036 | 92.8 |
| 3 | Probit | Logit | 0.74 | 0.78 | 5.2 | 0.57 | 0.56 | 91.1 | 0.047 | 0.049 | 4.6 | 0.035 | 0.035 | 91.9 |
| 4 | Probit | Probit | 0.82 | 0.86 | 5.8 | 0.60 | 0.60 | 93.6 | 0.052 | 0.054 | 4.1 | 0.036 | 0.037 | 93.6 |
| Continuous Mediator | ||||||||||||||
| 5 | Logit | Lin† | 0.85 | 0.83 | −2.0 | 0.50 | 0.51 | 91.5 | 0.046 | 0.046 | −1.0 | 0.027 | 0.028 | 92.6 |
| 6 | Logit | Mix† | 0.71 | 0.64 | −9.1 | 0.53 | 0.52 | 92.5 | 0.038 | 0.034 | −8.8 | 0.028 | 0.027 | 92.9 |
| 7 | Probit | Lin† | 0.88 | 0.92 | 5.6 | 0.57 | 0.54 | 93.0 | 0.049 | 0.052 | 5.9 | 0.031 | 0.030 | 93.3 |
| 8 | Probit | Mix† | 0.87 | 0.81 | −7.4 | 0.64 | 0.64 | 93.1 | 0.042 | 0.039 | −7.4 | 0.030 | 0.030 | 93.7 |
Lin, a linear regression model for the continuous mediator M with normally distributed residuals; Mix, a Gaussian mixture model for the continuous mediator M with a weighted sum of two Gaussian component densities.
5. Illustration and data example
Our motivating example comes from the Jackson Heart Study (JHS) investigating the effect of obesity on CKD and its potential mediation effect through diabetes. The JHS is a single-site, prospective cohort study of the risk factors and causes of cardiovascular disease in adult African Americans (Sempos et al. 1999). The exposure variable for our example is the continuous variable BMI (kg/m2), and the outcome considered is the dichotomous CKD status (yes or no), with CKD defined as estimated glomerular filtration rate (eGFR) less than 60 ml/min/1.73 m2 or presence of albuminuria. We also considered, in separate models, the potential mediators, binary diabetes (yes or no) or continuous fasting plasma glucose (mg/dL), an accurate marker for diabetes. We considered diabetes or fasting plasma glucose individually in two different causal models to demonstrate the generality of our method. It is well known that obesity is a major cause of CKD and End Stage Renal Disease possibly through mediating effects of diabetes (Maric-Bilkan 2013). We aimed to test this hypothesis and quantify the proportion of the effect of obesity on CKD through diabetes in African Americans using the proposed methods discussed above. Of note, we only consider the standard two-stage causal model as Figure 1 in which obesity (exposure) leads to CKD (outcome) through diabetes (mediator) for illustrative purposes, other potential causal pathways, e.g. insulin therapy in patients with diabetes may induce weight gain (Russell-Jones ad Khan 2007), are not considered in our data example.
The JHS dataset used for the analysis included 2,285 subjects with complete data for all the variables specified in the models. We note that the average BMI (SD) was 33.1 (8.2) for participants with CKD (n = 326) and 31.3 (6.9) for participants without CKD (n = 1,959). In addition, the measured average BMI (SD) was 34.8 (7.6) for participants with diabetes (n = 361) and 31.0 (6.9) for participants without diabetes (n = 1,924), and the Pearson's correlation coefficient between BMI and fasting plasma glucose was 0.145 with 95% confidence interval (CI) [0.104, 0.184]. The models (15) and (16) were fitted and three baseline covariates (age, gender and smoking) were included in all three models, so that the parameters were α′ = (α2, α3, α4), β′ = (β3, β4, β5). Thus, the exposure BMI is first assumed to be ignorable given the pre-BMI covariates age, gender and smoking, and then the mediator variable (diabetes or fasting plasma glucose) is assumed to be ignorable given the observed value of the exposure BMI as well as the three covariates age, gender and smoking. We rescaled BMI by dividing the original BMI by 5 so that the resulting causal quantities correspond to 5 kg/m2 increase of BMI. Estimates of the natural direct, natural indirect, total effects and mediation proportion (%) for binary and continuous mediators are provided in Table 2 on the risk difference scale and odds ratio scale respectively. The 95% asymptotic CIs are constructed using the delta method.
Table 2.
Estimated causal quantities and 95% CIs from the delta method of diabetes/fasting plasma glucose on the relationship between BMI and CKD in the Jackson Heart Study based on the mediation formula approach.
| Binary Mediator Diabetes (yes or no) |
Continuous Mediator Fasting Plasma Glucose (mg/dL) |
|||||||
|---|---|---|---|---|---|---|---|---|
| Risk Difference (%) | Odds Ratio | Risk Difference (%) | Odds Ratio | |||||
| Est. | 95% CI | Est. | 95% CI | Est. | 95% CI | Est. | 95% CI | |
| Natural Indirect Effect IE(x) | 0.78 | 0.47, 1.09 | 1.06 | 1.04, 1.08 | 0.45 | 0.28, 0.62 | 1.04 | 1.03, 1.06 |
| Natural Direct Effect DE(x + 1) | 2.31 | 1.21, 3.41 | 1.21 | 1.11, 1.32 | 2.52 | 1.42, 3.62 | 1.23 | 1.13, 1.34 |
| Mediation Proportion (%) P(x) | 25.3 | 12.7, 37.9 | 23.6 | 11.5, 35.6 | 15.1 | 7.5, 22.8 | 16.1 | 8.3, 23.9 |
| Total Exposure Effect TE | 3.09 | 1.99, 4.18 | 1.28 | 1.17, 1.39 | 2.97 | 1.87, 4.07 | 1.28 | 1.17, 1.39 |
In the binary mediator case, the results indicate that the natural indirect effect through diabetes (yes or no) accounts for approximately 25% of the total effect of obesity on CKD. The effect estimates are interpreted as follows, 5 kg/m2 higher BMI increases the probability of CKD by 3.09% (95% CI: 1.99%, 4.18%), with an estimated 0.78% (95% CI: 0.47%, 1.09%) due to the indirect effect through diabetes (yes or no) and an estimated 2.31% (95% CI: 1.21%, 3.41%) due to the direct effect (or other unknown pathways). On the odds ratio scale, the results show that every 5 kg/m2 increase in BMI increases the odds of developing CKD by 28% (95% CI: 17%, 39%), and 23.6% (95% CI: 11.5%, 35.6%) of the excess risk of CKD is mediated through diabetes (yes or no). Similarly, when assessing causal quantities for the continuous mediator fasting plasma glucose (mg/dL), the magnitude of the total effect is comparable with that of the binary mediator, diabetes (yes or no), and a significant but lower proportion of the total effect (approximately 15%) is mediated through fasting plasma glucose (mg/dL).
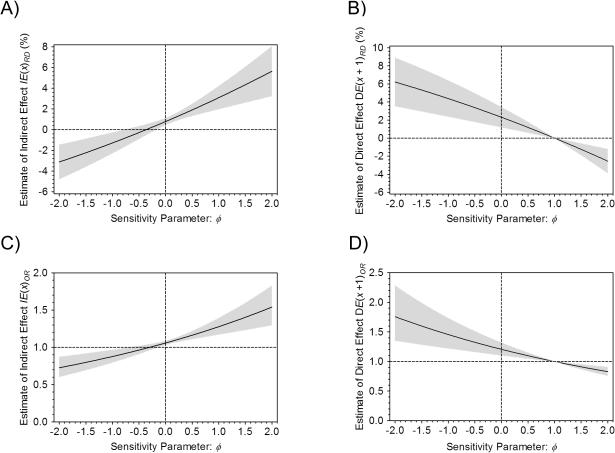
In addition, we conducted sensitivity analyses for the binary mediator case using the hybrid observational-causal model approach. It should be noted that we assume that the exposure BMI is independent of subsequent potential mediators and potential outcomes given age, gender and smoking in this sensitivity analysis and no further exposure-mediator or exposure-outcome confounders exist. The elicitation of plausible sensitivity parameter value ϕ for the present data example is described in the Appendix. In the sensitivity analysis, we examined the natural direct and indirect effect estimates of varying the assumed proportion ϕ, the association effect due to the cohort effect (from −2 to 2 in increments of 0.02). The change of IE(x)RD, DE(x + 1)RD, IE(x)OR and DE(x + 1)OR estimates over ϕ are shown in Figure 2. On the risk difference scale, IE(x)RD increases and DE(x + 1)RD decreases as ϕ increases (Figure 2A and 2B). The elicited value of ϕ = −0.02 provides an estimate for IE(x)RD of 0.74% (95% CI: 0.42%, 1.05%) and an estimate for DE(x + 1)RD of 2.35% (95% CI: 1.23%, 3.47%). The plausible range for ϕ of [−0.1, 0] provides a range for an estimate of IE(x)RD from 0.56% to 0.78% and for the estimate of DE(x + 1)RD from 2.52% to 2.31%, and neither the sign nor lack of statistical significance changes over the plausible range for ϕ. Figure 2C and 2D show similar results on the odds ratio scale and the only difference is that the change of DE(x + 1) over ϕ is concave down for the risk difference scale and concave up for the odds ratio scale. In summary, the sensitivity analysis results indicate that our original conclusion regarding the significant positive natural indirect effect through diabetes still holds if unmeasured mediator-outcome confounders (inducing a cohort effect proportion between −0.1 to 0) between the mediator and the outcome exist.
Figure 2.
Sensitivity analysis with the binary mediator diabetes (yes or no) for the Jackson Heart Study data. Figure 2A and 2B show the maximum likelihood estimates of the natural indirect effect IE(x)RD and the natural direct effect DE(x + 1)RD on the risk difference scale. Figure 2C and 2D show the maximum likelihood estimates of the natural indirect effect IE(x)OR and the natural direct effect DE(x + 1)OR on the odds ratio scale. The solid line represents the estimated natural direct and indirect effects, and the gray areas represent the 95% CIs from the delta method at each value of the sensitivity parameter ϕ.
6. Conclusions and discussion
In this article, we consider a two-stage mediation model with a continuous exposure variable and a binary outcome. We give precise definitions of the population-wide natural direct and indirect effects on both the risk difference and odds ratio scales utilizing empirical joint distribution of the exposure and baseline covariates from the whole sample analysis population. The natural direct and indirect effects are estimated with a mediation formula approach, and a sensitivity analysis method is proposed to assess the robustness of the estimated causal quantities.
To estimate the natural direct and indirect effects for a continuous mediator, we used 40-point Gauss-Hermite quadrature to evaluate the integration in formula (14). The integration results are very close with those using the ‘QUAD’ function in SAS/IML, which is a numerical integrator based on adaptive Romberg-type integration technique (data not shown). Gauss-Hermite quadrature is commonly used for low dimensional random effects models and a major disadvantage of the Gauss-Hermite quadrature is that the number of quadrature points increases as an exponential function of the number of dimensions. Alternatively, the quasi-Monte Carlo method which utilizes uniformly distributed deterministic sequences can be considered for mediation effect estimation involving multiple normally distributed mediators (Lee et al. 2009; Judd, 1998).
The variance of the estimated causal quantities was obtained using the delta method in this study. For the population-wide natural direct and indirect effects estimation on the odds ratio scale, the standard way is to first log-transform the ratio, calculate a confidence interval on the log scale using the delta method and assuming a normal distribution, then exponentiate it to give a 95% confidence interval for the desired causal quantities. Another approach is to obtain the variance estimates via the bootstrap resampling at the expense of higher computational cost (Efron and Tibshirani, 1993) which has the potential advantage of allowing the computation of the confidence intervals without requiring a normal distribution assumption for the estimator.
The two most common critiques with mediation analysis in epidemiological studies are 1) Mis-specification of parametric models for the mediator and outcome, for example, the outcome model and/or the mediator model can be mis-specified or an exposure-mediator interaction term is mistakenly excluded from the model, and 2) existence of possible mediator-outcome confounders. Either of them can cause biased results regarding mediation, resulting in invalid inference and possibly erroneous medical decisions. The simulation study in Section 4 suggests that our mediation formula approach is not robust and will be biased to estimate the mediation effect if either the outcome models or the mediator model is mis-specified. Standard model assessment techniques and selection procedures (e.g. likelihood ratio test, utilization of penalized model selection criteria as AIC or BIC) may be used to formulate reasonably correct association models. In our data example, the model selection criteria AIC in model (15) suggests excluding the exposure-mediator interaction term. However, the definition and the estimation method proposed in this paper can be extended to settings when interactions between the mediator of interest and the exposure are present. For the second critique, the researchers are recommended to collect all possible variables that may confound the mediator-outcome relationship and also perform sensitivity analysis to assess the robustness of conclusions regarding the mediation effect. For our data example, we consistently adjusted for age, gender and smoking as the minimum set of confounders, and our sensitivity analysis results indicate that the significant natural indirect effect of BMI on CKD through diabetes is robust even though other potential mediator-outcome confounders such as physical activity and alcohol usage exist. However, since the Jackson Heart Study is not a randomized experiment, it is possible that additional covariates other than age, gender and smoking could possibly confound the exposure-mediator or exposure-outcome relationship and invalidate the assumption (12).
In summary, this paper has described an estimating procedure of the natural direct and indirect effects for a continuous exposure and a dichotomous outcome on both risk difference and odds ratio scales. The procedure can be applied to any mediator type and definition of the natural direct and indirect effects for a continuous exposure can also be extended to other types of outcome. Mediation effects estimation method described in this paper has been encoded in a SAS macro, which is available for downloading from the webpage, https://github.com/souwwang/Continuous-Exposure-Mediation.
Acknowledgements
The author would like to thank Dr. Adolfo Correa and Dr. Yuan-I Min for editing the manuscript. Their valuable comments help greatly improve the manuscript.
Funding
This work is supported in part by the Jackson Heart Study contracts HHSN268201300046C, HHSN268201300047C, HHSN268201300048C, HHSN268201300049C, HHSN268201300050C from the National Heart, Lung, and Blood Institute and the National Institute on Minority Health and Health Disparities.
Appendix: Elicitation of Sensitivity Parameter ϕ
We follow the guidelines to elicitate the sensitivity parameters ϕ using the technique proposed by Albert and Wang (2015) which is a simple step-by-step approach involving effects of unobserved confounders. Simply, we consider the linear regression of Y on X, M, and W and denote the coefficient of X in this model as βY•X|M, W. In general, βY•X|M, W will not be the same as the true direct effect of X on Y, denoted as βY•X|M, W, U, which would be estimable if the unmeasured M-Y confounders (denoted by the vector U) were included in the above model. The ‘relative bias’, (βY•X|M, W - βY•X|M, W, U)/βY•X|M, W from the linear model provides a reasonable approximation of the sensitivity parameter ϕ for the assumed generalized linear model. The elicitation of the sensitivity parameter value for the JHS data analysis is specified as following,
From the fit of the linear model of CKD status (Y) regressed on BMI (X), diabetes (M) and baseline covariates (Ws: age, gender and smoking), we obtained the estimate, bY•X|M, W, (the ordinary least squares estimates of βY•X|M, W) = 0.02, and from the regression of diabetes on BMI and Ws we obtained bY•X|W (the ordinary least squares estimates of βY•X|W = 0.05.
Potential M-Y confounders considered (from ‘strongest’ to ‘weakest’) are physical activity (0 for non-ideal health and 1 for ideal health based on American Heart Association physical activity classification), and Alcohol drinking in the past 12 months (0 for No, and 1 for Yes).
- From prior substantive knowledge, we specify the regression coefficients for the two potential confounders as follows:
k Confounder bY·Uk|M, X, W bM·Uk|X, W 1 Physical Activity −0.06 −0.10 2 Alcohol Drinking 0.02 0.10 We compute the bias as B = −0.05 × {(−0.06) × (−0.10) + 0.02 × 0.10} = −0.0004, resulting in a specified sensitivity parameter value of ϕ = B/bY•X|M, W = −0.02.
For conservatism, we suppose a 5-fold increase in ϕ from our calculation, resulting in a value of around ϕ = −0.1. Thus, we consider a plausible range for ϕ to be −0.1 to 0 (including as an upper bound the most optimistic scenario of no M-Y confounding).
This approach supposes that the relative bias from the linear model transports reasonably well to a generalized linear model with a non-identity link function. In many applications it will be not essential that this approximation is very accurate, as only a rough idea of plausible values for the sensitivity parameter is needed. Albert and Wang (2015) shows that this approximation can be quite good using some simulation results.
Contributor Information
Wei Wang, Center of Biostatistics and Bioinformatics, New Guyton Research Building G562, University of Mississippi Medical Center, 2500 North State Street, Jackson, MS 39216.
Bo Zhang, Office of Surveillance and Biometrics, Center for Devices and Radiological Health, Food and Drug Administration, 10993 New Hampshire Avenue. Silver Spring, MD 20993, Phone: (240) 402-5253, Fax: (301) 847-8123, Bo.Zhang@fda.hhs.gov.
References
- Albert JM. Mediation analysis via potential outcomes models. Statistics in Medicine. 2008;27:1282–1304. doi: 10.1002/sim.3016. [DOI] [PubMed] [Google Scholar]
- Albert JM, Nelson S. Generalized causal mediation analysis. Biometrics. 2011;67:1028–1038. doi: 10.1111/j.1541-0420.2010.01547.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albert JM, Wang W. Sensitivity analyses for parametric causal mediation effect estimation. Biostatistics. 2015;16:339–351. doi: 10.1093/biostatistics/kxu048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baron RM, Kenny DA. The moderator-mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirani R. An introduction to the bootstrap. Chapman and Hall; New York: 1993. [Google Scholar]
- Eknoyan G. Obesity, diabetes, and chronic kidney disease. Current Diabetes Reports. 2007;7:449–453. doi: 10.1007/s11892-007-0076-5. [DOI] [PubMed] [Google Scholar]
- Goetgeluk S, Vansteelandt S, Goetghebeur E. Estimation of controlled direct effects. Journal of the Royal Statistical Society. Series B. 2008;70:1049–1066. [Google Scholar]
- Imai K, Keele L, Tingley D. A general approach to causal mediation analysis. Psychological Methods. 2010a;15:309–334. doi: 10.1037/a0020761. [DOI] [PubMed] [Google Scholar]
- Imai K, Keele L, Yamamoto T. Identification, inference and sensitivity analysis for causal mediation effects. Statistical Science. 2010b;25:51–71. [Google Scholar]
- Judd K. Numerical Methods in Economics. MIT Press; Boston: 1998. [Google Scholar]
- Lee K, Daniels MJ, Joo Y. Flexible marginalized models for bivariate longitudinal ordinal data. Biostatistics. 2013;14:462–476. doi: 10.1093/biostatistics/kxs058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K, Joo Y, Yoo JK, Lee J. Marginalized random effects models for multivariate longitudinal binary data. Statistics in Medicine. 2009;28:1284–1300. doi: 10.1002/sim.3534. [DOI] [PubMed] [Google Scholar]
- Lu Y, Hajifathalian K, Ezzati M, Woodward M, Rimm EB, Danaei G. Metabolic mediators of the effects of body-mass index, overweight, and obesity on coronary heart disease and stroke: a pooled analysis of 97 prospective cohorts with 1.8 million participants. Lancet. 2014;383:970–983. doi: 10.1016/S0140-6736(13)61836-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Brown CH, Wang W, Hoffman JM. The intermediate endpoint effect in logistic and probit regression. Clinical Trials. 2007;4:499–513. doi: 10.1177/1740774507083434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maric-Bilkan C. Obesity and diabetic kidney disease. Med. Clin. North. Am. 2013;97:59–74. doi: 10.1016/j.mcna.2012.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearl J. Proceedings of the Seventeenth Conference on Uncertainty and Artificial Intelligence. Morgan Kaufmann; San Francisco, CA: 2001. Direct and indirect effects. pp. 411–420. [Google Scholar]
- Pearl J. The causal mediation formula--a guide to the assessment of pathways and mechanisms. Prevention Science. 2012;13:426–436. doi: 10.1007/s11121-011-0270-1. [DOI] [PubMed] [Google Scholar]
- Petersen ML, Sinisi SE, van der Laan MJ. Estimation of direct causal effects. Epidemiology. 2006;17:276–284. doi: 10.1097/01.ede.0000208475.99429.2d. [DOI] [PubMed] [Google Scholar]
- Robins JM, Greenland S. Identifiability and exchangeability for direct and indirect effects. Epidemiology. 1992;3:143–155. doi: 10.1097/00001648-199203000-00013. [DOI] [PubMed] [Google Scholar]
- Russell-Jones D, Khan R. Insulin-associated weight gain in diabetes – causes, effects and coping strategies. Diabetes, Obesity and Metabolism. 2007;9:799–812. doi: 10.1111/j.1463-1326.2006.00686.x. [DOI] [PubMed] [Google Scholar]
- Sempos CT, Bild DE, Manolio TA. Overview of the Jackson Heart Study: a study of cardiovascular diseases in African American men and women. The American Journal of the Medical Sciences. 1999;317:142–146. doi: 10.1097/00000441-199903000-00002. [DOI] [PubMed] [Google Scholar]
- Vanderweele TJ, Vansteelandt S. Odds ratios for mediation analysis for a dichotomous outcome. American Journal of Epidemiology. 2010;172:1339–1348. doi: 10.1093/aje/kwq332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele T, Vansteelandt S. Mediation analysis with multiple mediators. Epidemiologic Methods. 2013;2:95–115. doi: 10.1515/em-2012-0010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Spitz MR, Amos CI, Wilkinson AV, Wu X, Shete S. Mediating effects of smoking and chronic obstructive pulmonary disease on the relation between the CHRNA5-A3 genetic locus and lung cancer risk. Cancer. 2010;116:3458–3462. doi: 10.1002/cncr.25085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W, Albert JM. Estimation of mediation effects for zero-inflated regression models 2012. Statistics in Medicine. 2012;31:3118–3132. doi: 10.1002/sim.5380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W, Nelson S, Albert JM. Estimation of causal mediation effects for a dichotomous outcome in multiple-mediator models using the mediation formula. Statistics in Medicine. 2013;32:4211–4228. doi: 10.1002/sim.5830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ. Concerning the consistency assumption in causal inference. Epidemiology. 2009;20:880–883. doi: 10.1097/EDE.0b013e3181bd5638. [DOI] [PubMed] [Google Scholar]