Abstract
The mechanical behavior of soft connective tissue is governed by a dense network of fibrillar proteins in the extracellular matrix. Characterization of this fibrous network requires the accurate extraction of descriptive structural parameters from imaging data, including fiber dispersion and mean fiber orientation. Common methods to quantify fiber parameters include fast Fourier transforms (FFT) and structure tensors, however, information is limited on the accuracy of these methods. In this study, we compared these two methods using test images of fiber networks with varying topology. The FFT method with a band-pass filter was the most accurate, with an error of 0.71 ± 0.43 degrees in measuring mean fiber orientation and an error of 7.4 ± 3.0% in measuring fiber dispersion in the test images. The accuracy of the structure tensor method was approximately 4 times worse than the FFT band-pass method when measuring fiber dispersion. A free software application, FiberFit, was then developed that utilizes an FFT band-pass filter to fit fiber orientations to a semicircular von Mises distribution. FiberFit was used to measure collagen fibril organization in confocal images of bovine ligament at magnifications of 63x and 20x. Grayscale conversion prior to FFT analysis gave the most accurate results, with errors of 3.3 ± 3.1 degrees for mean fiber orientation and 13.3 ± 8.2% for fiber dispersion when measuring confocal images at 63x. By developing and validating a software application that facilitates the automated analysis of fiber organization, this study can help advance a mechanistic understanding of collagen networks and help clarify the mechanobiology of soft tissue remodeling and repair.
Keywords: Collagen fibers, Confocal imaging, Ligament, Fiber orientation distribution, Fast Fourier transform (FFT), Structure tensor
1 Introduction
The mechanical function of biological tissue is primarily regulated by the underlying fibrillar architecture. In soft connective tissue, defects to the fibrillar collagen network are associated with acute and chronic disorders (Woo et al, 1989; Vogel et al, 1979; Makareeva et al, 2008). Therefore, an extensive amount of research has been devoted to characterizing collagen fiber organization in soft tissue (Polzer et al, 2013; Schriefl et al, 2012), and this requires the accurate extraction of descriptive structural parameters from imaging data (D’Amore et al, 2010). For tissues with multiaxial fiber networks, relevant structural parameters include fiber dispersion and mean fiber orientation, which are both properties of the fiber orientation distribution and are measures of material anisotropy. Accurate quantification of the fiber orientation distribution can advance a mechanistic understanding of collagen networks and clarify the mechanobiology of soft tissue remodeling and repair.
The measurement of the fiber orientation distribution has been advanced by the development of automated image analysis methods. A popular and robust method to analyze two-dimensional images of fiber networks is the fast Fourier transformation (FFT) (Polzer et al, 2013; Ayres et al, 2008; Sander and Barocas, 2009). The FFT method has been used to measure fiber orientation distributions in studies investigating electrospun tissue-engineered scaffolds (Ayres et al, 2008, 2006), corneal wound contraction (Petroll et al, 1993), and abdominal aortic aneurysms (Polzer et al, 2013). Another prevalent method is a gradient-based structure tensor (Jahne, 1993; Bigun et al, 2004), which has been used to analyze fiber orientation distributions in arterial adventitia (Rezakhaniha et al, 2012) and actin filaments in the lamellipodium (Weichsel et al, 2012). While both these image analysis methods are commonly used, the accuracy of the FFT and structure tensor methods have not been quantitatively compared, and there is limited knowledge on which method is superior for analyzing fibrillar networks.
Over the past decade, free software applications have been developed that enable researchers to use FFT and structure tensor methods to measure fiber organization. Researchers can now generate fiber orientation distributions based on FFT methods by using Oval Profile Plot and Directionality, which are plugins for Image J and Fiji, respectively (Schneider et al, 2012; O’Connell, 2012; Schindelin et al, 2012; Tienevez, 2010). Software applications are also available that use the structure tensor method, which includes the Directionality plug-in and OrientationJ (Rezakhaniha et al, 2012). Although these software applications have assisted the quantification of fiber dispersion and mean fiber orientation, the accuracy of these software applications has not been characterized with validation studies. Moreover, the sensitivity of these image analysis programs to variations in image topology and noise removal are not well understood. Therefore, uncertainty exists in the accuracy and physical meaning of the fiber organization parameters (D’Amore et al, 2010), when computed by these software applications.
The first objective of this study is to determine the accuracy of using FFT and structure tensors to measure fiber orientation distribution in two-dimensional images of fiber networks with variable fiber topology. The second objective is to develop and validate a free software application to accurately and automatically measure fiber orientation distribution in soft connective tissue.
2 Methods
2.1 Overview
The accuracy of using FFT and structure tensors to characterize fiber networks was determined using a three-stage process (Fig. 1). In stage I, test images with known fiber dispersion and mean fiber orientation were generated. In stage II, these test images were converted into fiber orientation distributions using formulations for FFT and structure tensor methods. Two established noise filtering techniques were investigated when using FFT analysis: band-pass and minimum. In stage III, mean fiber orientation and fiber dispersion were quantified by fitting the distribution data to an ellipse and semicircular von Mises distribution, respectively. Accuracy was determined by comparing the known parameter values used to generate the test images to the predicted parameter values measured using FFT or structure tensor analysis (Fig. 1). To determine the effect of image topology on accuracy, test images were generated with different fiber thickness, fiber dispersion, fiber aspect ratio and fiber network concentration. The FFT band-pass method was implemented into a new software application called FiberFit, which is now available as a free download (http://coen.boisestate.edu/ntm/fiberfit/). The FiberFit software was evaluated by measuring structural parameters of collagen fibril networks in confocal images of bovine ligament.
Fig. 1.
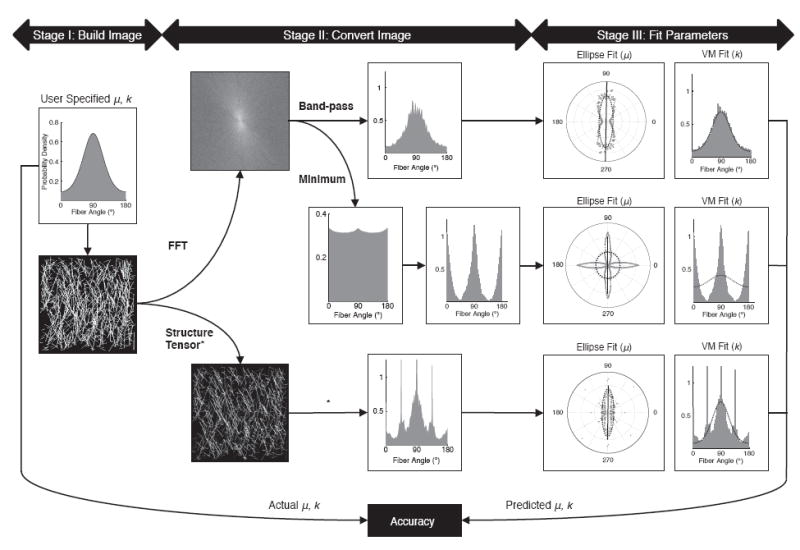
Experimental approach to calculate accuracy of FFT and structure tensor methods. In stage I, test images were generated from semicicular von Mises distributions. In Stage II, images were converted to a fiber orientation distribution using FFT or structure tensor methods. In Stage III, mean fiber orientation μ and fiber dispersion k were calculated by fitting the fiber orientation distribution data to an ellipse and a semicircular von Mises distribution, respectfully. Accuracy was determined by comparing the fitted parameter values (measured) with the user-specified parameter values (actual). All analysis was done using custom Matlab programs, unless otherwise noted (* = utilized OrientationJ software). The example image shown in this figure has a k = 1.0 and μ = 90°
2.2 Image Generation
Test images were automatically generated using a custom Matlab program (Fig. 2). Two assumptions about soft tissue were made when generating these test images: 1) fiber networks contain straight fibers and 2) the orientation distribution follows a perfect semicircular von Mises distribution. A binary image was populated with straight lines based on a semicircular von Mises probability density function (PDF), for user-specified values of μ and k.
Fig. 2.
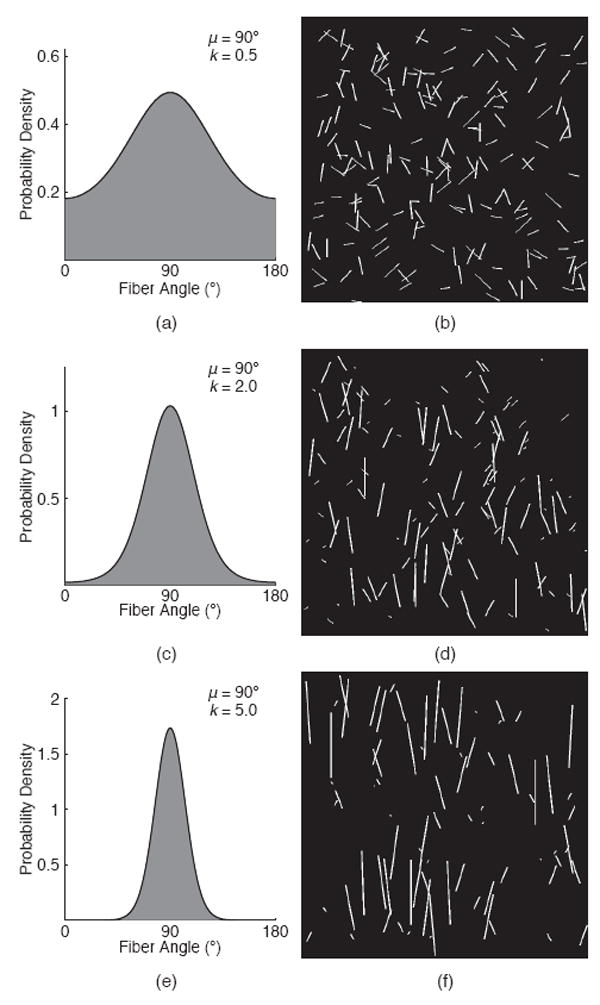
Generation of test images. Von Mises distributions (a, c, e) were converted into binary images (b, d, f) with known k and μ. Fiber alignment will increase with greater k values.
| (1) |
Where k is the dispersion parameter, μ is the mean fiber orientation parameter, and θ represents the angle orientation within the interval [0, π]. The dispersion parameter k is analogous to the reciprocal of variance, which is used to quantify the degree of fiber alignment (low k values = disordered networks, large k values = aligned networks). I0 (k) is the modified zero order Bessel function (Eq. 2).
| (2) |
The seed point for each line was randomized and the line was grown incrementally until the number of pixels matched the number of pixels defined at that angle by the von Mises PDF. Lines with a small length to thickness aspect ratio (≤ 1 to 1) were not included in the test patterns, since the desired orientation cannot be captured. If the endpoint landed outside of the designated image area, a new seed point was chosen and the process repeated until the entire fiber was in the desired image dimension. In total, thirty-nine 1074 × 1074 network images were generated with varying k values (0.2 - 5.0; Fig. 2) and a fixed μ value (90 degrees). The mean fiber orientation was fixed due to the nominal effect of image rotation on the measured structural parameters.
2.3 Image Conversion - FFT
Test images were converted to the frequency domain using Matlab’s fft2 function, which stems from the 2D discrete Fourier transform of an image (M × N pixels):
| (3) |
where x and y represent the spatial coordinates of the image, u and v are the frequency components in the x and y directions and . Frequencies are representative of changes in pixel intensity (Gonzalez and Woods, 2008). The transform is often complex and contains both real R(u,v) and imaginary I(u,v) parts, therefore we converted from the Fourier transform to a power spectrum with no imaginary parts (Eq. 4) (Sander and Barocas, 2009).
| (4) |
The two-dimensional power spectrum was rotated by 90 degrees to account for differences between power spectrum intensities and the physical orientation of the fibers. Power spectrum intensities were interpolated and a radial sum approach was used to define intensity at 1 degree increments to create a fiber orientation distribution of the fiber network (Ayres et al, 2008).
Due to inherent noise in FFT, two established noise filtering techniques were applied to modify the fiber orientation distribution. The first technique is the minimum method, which removes all data in the fiber orientation histogram below the minimum value (Ayres et al, 2006). This effectively creates a vertical shift in the histogram until the minimum histogram value is zero (Fig. 1). The second technique is to apply a band-pass filter to the power spectrum to attenuate frequencies corresponding to small entities or larger features in the image (Petroll et al, 1993; Sander and Barocas, 2009; Marquez, 2006). The frequency corresponding to a specific fiber diameter is given by:
| (5) |
where t is the fiber thickness in the 2D image and m is the image dimension (m x m pixels) (Marquez, 2006). For the band-pass method, preliminary tests were performed to determine the optimal radial band of cutoff frequencies to filter the power spectrum. These preliminary tests examined high cutoff frequencies that correspond to a t of 1-3, and low cutoff frequencies that correspond to a t of 10-100. For the images analyzed in this research, we determined that the accuracy of the FFT band-pass method was most sensitive to changes in the high cutoff frequency, and that an optimal radial band used a t of 32 (f = 17) and a t of 2 (f = 267) for the low and high cutoff frequency, respectively. This optimal radial band of t between 2-32 was used for all FFT band-pass results. All FFT noise filtering techniques were completed using a custom Matlab program, which generated a histogram of fiber orientations for each image.
2.4 Image Conversion - Structure Tensor
An ImageJ plugin, called OrientationJ (Rezakhaniha et al, 2012), was used to perform image analysis using the structure tensor method (Jahne, 1993; Bigun et al, 2004). In brief, the program calculates a structure tensor for each pixel in the spatial domain by computing the pixel intensity gradients in the x and y directions within a user-specified Gaussian-shaped window. The local fiber orientation at each pixel is defined by the eigenvector corresponding to the smallest eigenvalue of the structure tensor, and the fiber orientation distribution is built from pixel orientations that are weighted by coherency values, so that elongated structures are emphasized (Jahne, 1993; Rezakhaniha et al, 2012). For this study, we used a value of 1 for the standard deviation of the Gaussian local window, we used the Gaussian method to interpolate gradients, and we did not select coherency or energy thresholding values to remove areas of weak orientation (Sampo et al, 2014). OrientationJ generates a histogram of local fiber orientations, but does not fit the data to a specific statistical distribution (Rezakhaniha et al, 2012). We therefore only used OrientationJ to export a histogram of fiber orientations from each image (Fig. 1).
2.5 Parameter Fitting and Accuracy
Mean fiber orientation μ and fiber dispersion k were fit to the fiber orientation distributions determined from the FFT and structure tensor methods. The parameter μ was calculated using a direct least squares method (Fitzgibbon et al, 1999) to fit an ellipse to the fiber orientation distribution data, where μ was defined by the semi-major axis. The parameter k was then calculated by using the least squares method to fit a semicircular von Mises distribution to a histogram representation of the fiber orientation distribution data (Fig. 1). This two-step approach to parameter fitting was found to be more robust than fitting both parameters with a single von Mises fitting operation. These measured μ and k values were compared to the actual μ and k values that were used to generate the test images (Fig. 1). Accuracy in measuring μ was defined by the absolute mean difference (|μactual–μmeasured|), while accuracy in measuring k was defined by the absolute mean percentage error (|kactual–kmeasured| /kactual).
2.6 Sensitivity to Variation in Fiber Networks
The effect of fiber network topology on accuracy was tested by measuring μ and k in images with varying fiber thickness, fiber dispersion, fiber aspect ratio, and fiber concentration. These variables were selected based upon the diversity that exists in collagen networks of native and surrogate soft tissue (Polzer et al, 2013; Schriefl et al, 2012; D’Amore et al, 2010; Petroll et al, 1993; Sander and Barocas, 2009; Ayres et al, 2006). Images were created with fiber thicknesses of 1, 5, and 9 pixels, fiber dispersions of 1 and 5, and with fiber aspect ratios that were low (1 to 44), medium (1 to 89) and high (1 to 133). Three images were generated in each group for a total of 54 images. A second set of 200 images was generated to evaluate the effect of fiber concentration, or number of fibers per unit area. These images varied the number of fibers (Fig. 3), while holding fiber thickness and aspect ratio constant. Images were placed in incremental groups with fiber concentrations ranging from 2% to 60%. This sensitivity analysis was performed using the FFT band-pass method.
Fig. 3.

Representative test images showing variations in fiber concentration. (a) 8% fiber concentration and (b) 56% fiber concentration. Both images have a k = 1, fiber thickness of 5, and medium aspect ratio
2.7 Development of FiberFit Software
A portable software application, FiberFit, was developed in Python utilizing the FFT band-pass method. This software was designed to support fast and intuitive two-dimensional analysis of fiber networks. The image analysis code in FiberFit was created by using numpy and scipy libraries to port the FFT band-pass method we developed into Python (Jones et al, 2001). Testing was conducted to verify that FiberFit results were within 0.1 degrees for μ and within 0.01 for k compared to the results from the FFT band-pass code developed in Matlab. Therefore, the accuracy we report for the FFT band-pass method is applicable to FiberFit. Users can implement different cut-off frequencies for the band-pass filter and results can be exported for data storage.
2.8 Validation Experiment using FiberFit Software
The FiberFit software was evaluated using confocal images of ligament. Collagen fibril networks in five bovine ligament specimens were autofluoresced at 63x and 20x magnification, using a confocal microscope and ZEN imaging software (LSM 510 Meta; Carl Zeiss Inc., Thornwood NY). Z-stack images were acquired with a Diode laser source (405 nm), a 63x Plan-Apochromat oil-immersion (NA 1.4) or 20x Plan-Apochromat (NA 0.8) objective and an emission long-pass filter of 505 nm (Monici, 2005). The three-dimensional z-stack was then projected onto a two-dimensional surface (Fig. 4a,e).
Fig. 4.
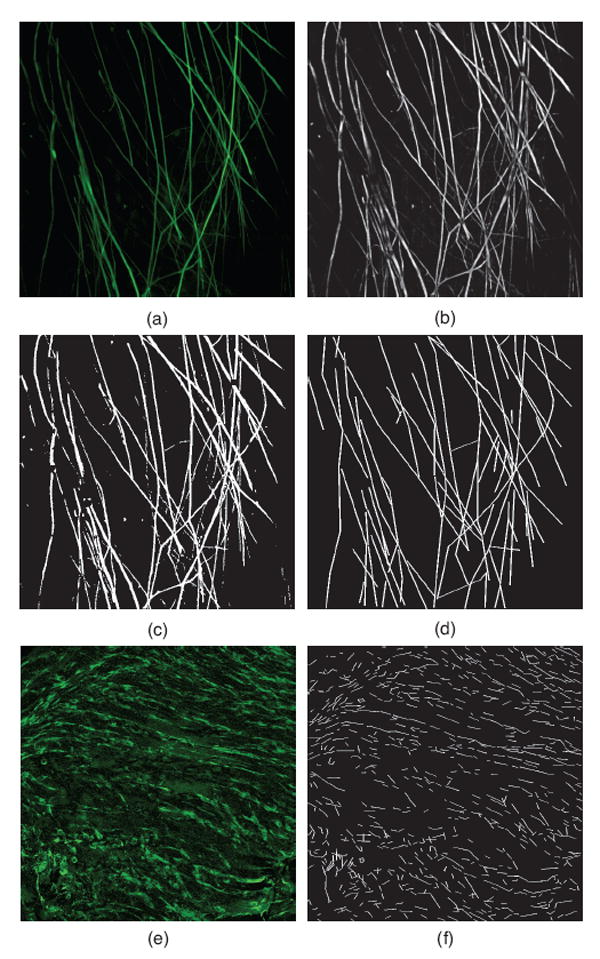
Images used for confocal validation. (a) Example confocal image at 63x, with corresponding (b) grayscale processing, (c) binary processing, and (d) manual tracing. (e) Example confocal image at 20x, with corresponding (f) manual tracing.
Prior to using FiberFit, image preprocessing methods were applied using ImageJ. The first steps in image preprocessing included sharpening (3×3 weighted average), filtering (rolling ball background subtraction), smoothing (3×3 mean filter), and normalizing the intensity values of all images. Each image was then converted into two formats: 8-bit grayscale (Fig. 4b) and binary (Fig. 4c). As a final noise removal step, a despeckle operation (3×3 median filter) was applied to all converted images. The grayscale and binary images were then analyzed using FiberFit to generate a fiber orientation distribution and calculate k and μ.
To determine the accuracy of using FiberFit to calculate k and μ, a third set of images was created by manually tracing the start and end points of the imaged fibrils (Fig. 4d,f.). This set of images replicated the linear fiber segments that we used in our binary test images to quantify accuracy (Fig. 2). A discrete fiber orientation distribution, f (θi), was built for each of these manually traced images by using the total number of pixels for lines orientated along each angle θi. The mean (μ) and standard deviation (σ) of the discrete fiber orientation distribution were calculated using the following equations (Mardia and Jupp, 2000):
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
A two-term exponential relationship between σ and k was developed (Eq. 11) by calculating σ (Eq. 10) for distributions with known k values (from 0 to 10, incrementing by 0.1) and fitting the data in Matlab using an exponential function (R2 = 1.0):
| (11) |
The k and μ parameters calculated from the discrete fiber orientation distributions (kdiscrete, μdiscrete) were then used as a gold standard to determine the accuracy of using FiberFit (kf ft, μf ft), where error in measuring μ was defined by the absolute mean difference (|μf ft–μdiscrete|), and error in measuring k was defined by the absolute mean percentage error (|kdiscrete–kf ft|/ kdiscrete). These same methods were applied to determine the accuracy of measuring μ and k with the FFT minimum (Matlab) and structure tensor (OrientationJ) methods.
To have confidence in using the manually traced images as a gold standard, these images had to pass a verification test. For this verification, we used FiberFit to directly calculate the k parameter of each manually traced image and compared this result with the k parameter calculated from the respective discrete distribution. If the k value determined from these two methods had a difference greater than 1.0, we excluded that manually traced image from further analysis. The ten manually traced images used in this study met the acceptance criteria and had a k value using FiberFit that was 0.28 ± 0.22 different than the k value using the discrete distribution method. Three additional images did not meet the acceptance criteria, and were rejected. Two of the rejected images had highly bimodal distributions. This verification test provided a baseline for using kdiscrete and μdiscrete to determine the accuracy of using FiberFit to analyze the preprocessed binary and grayscale confocal images.
2.9 Statistics
A MANOVA determined the effect of the image analysis method (FFT band-pass, FFT minimum, and structure tensor) on k and μ error. A MANOVA was also used to evaluate the effect of fiber thickness, dispersion, and aspect ratio on k and μ error when using the FFT band-pass method. Fiber concentration was evaluated separately using a MANOVA with four groups: k = 1, low aspect ratio; k = 1, high aspect ratio; k = 5, low aspect ratio; and k = 5, high aspect ratio. For all MANOVAs, pairwise differences were analyzed with a Bonferroni or Games-Howell post hoc test (depending on if equal variances could be assumed). The goodness of fit between the fiber orientation histogram and the semicircular von Mises distribution was quantified using the coefficient of determination (R2). The cofficient of determination was also used to compare k and μ between the grayscale and binary confocal images (FFT band-pass) and the manually traced confocal images (discrete).
3. Results
3.1 Accruacy of FFT and Structure Tensor Methods
The FFT band-pass method was the most accurate method for measuring the fiber dispersion parameter k (Fig. 5a.). The absolute mean percentage error in measuring k was 7.4 ± 3.0%, 72.4 ± 28.2%, and 47.4 ± 5.1%, for the FFT band-pass, FFT minimum, and structure tensor methods, respectively. The FFT band-pass method was also the most accurate method for measuring mean fiber orientation, μ (Fig. 5b.), but there was only a significant difference between the FFT band-pass and structure tensor methods (p <0.01). The absolute mean difference between actual μ and measured μ was 0.7 ± 0.4 deg, 3.2 ± 2.7 deg, and 4.8 ± 4.0 deg for the FFT band-pass, FFT minimum, and structure tensor methods, respectively. For all methods, the error in measuring k and μ was highest for disordered networks.
Fig. 5.
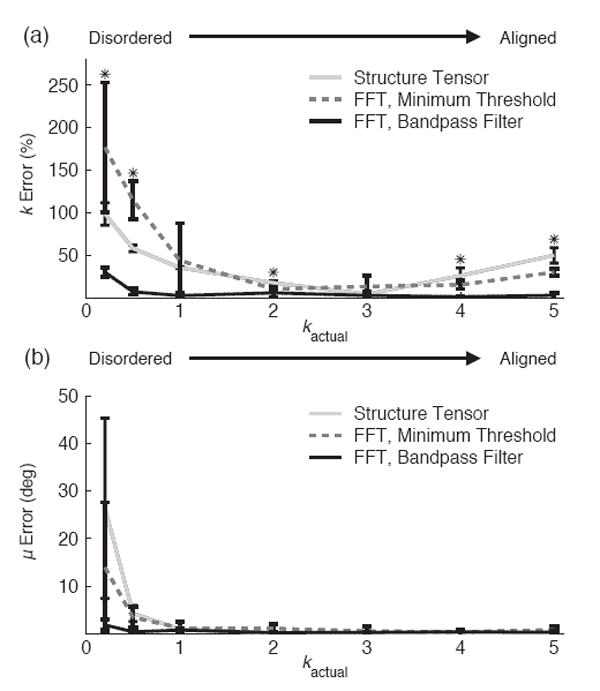
Comparison of image analysis methods. (a) Error in measuring k and (b) error in measuring μ when fiber networks vary from disordered to aligned. Bars represent standard deviation (*p < 0.05)
3.2 Sensitivity to Image Topology
When using the band-pass FFT method, the accuracy of measuring fiber dispersion k was affected by interactions between fiber dispersion and fiber thickness (Fig. 6a.; p < 0.001), but was not affected by interactions between fiber dispersion and fiber aspect ratio (Fig. 6a.; p = 0.22). As fiber thickness increased in aligned fiber networks, the accuracy of measuring k decreased by 5.3%. Conversely, as fiber thickness increased in disordered fiber networks, the accuracy of measuring k increased by 6.5%. The accuracy of measuring mean fiber orientation μ, when using the band-pass FFT method, was not affected by fiber dispersion (p = 0.407), but was dependent on both fiber thickness and fiber aspect ratio (Fig. 6b.; p = 0.002 and p = 0.008, respectively). Despite these significant differences, the average error was below 1 degree for all groups.
Fig. 6.
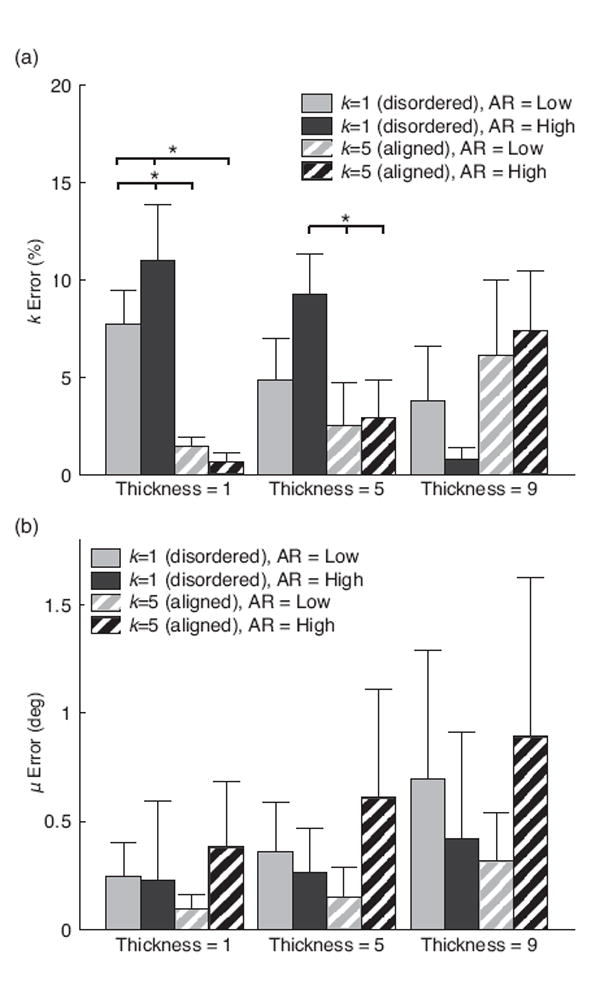
Sensitivity of FFT band-pass to fiber thickness and aspect ratio (AR). (a) Error in measuring k and (b) error in measuring μ. Bars represent standard deviation (*p < 0.05)
Variation in fiber concentration did affect the accuracy of measuring fiber dispersion k when using the FFT band-pass method for both disordered and aligned fiber networks (Fig. 7; p < 0.001 and p < 0.001, respectively). The accuracy of measuring the mean fiber orientation μ, was not affected by fiber concentration for both disordered (0.6 ± 0.4 degrees) and aligned (0.4 ± 0.3 degrees) fiber networks (p = 0.73 and p = 0.77, respectively).
Fig. 7.
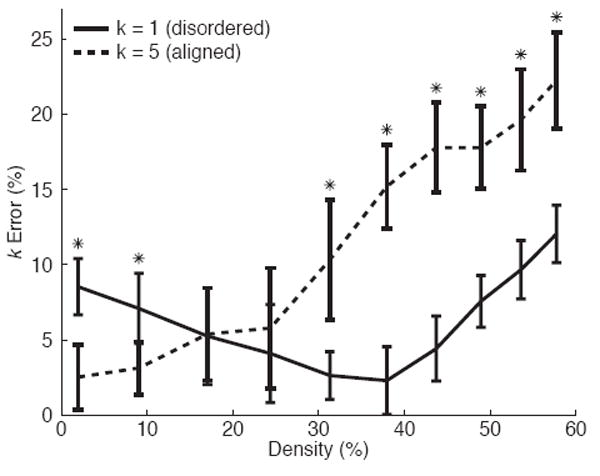
Sensitivity of FFT band-pass to fiber concentration. Bars represent standard deviation (*p < 0.05 between k = 1 and k = 5)
3.3 Validation Experiment using FiberFit Software
The FiberFit software quantified k and μ for all ligament confocal images with an average runtime of 2.4 ± 0.3 seconds on a 2.7 GHz processor. The measurement of k with FiberFit had the strongest correlation to the manual tracing method when analyzing grayscale images at 63x (Fig. 8a,c), while the measurement of μ with FiberFit had very strong correlations to the manual tracing method for both grayscale and binary images at 63x and 20x (Fig. 8b,d). A strong positive correlation existed between the k values that FiberFit calculated at 63x and 20x (R2 = 0.65); however, k values calculated at 20x had 22% greater error than k values calculated at 63x (Table 1, p=0.02). A very strong positive correlation existed between the μ values that FiberFit calculated at 63x and 20x (R2 = 0.98). The fiber orientation distributions generated by FiberFit had an average R2 fit to a von Mises distribution of 0.82 ± 0.10 (range from 0.6 to 0.95).
Fig. 8.
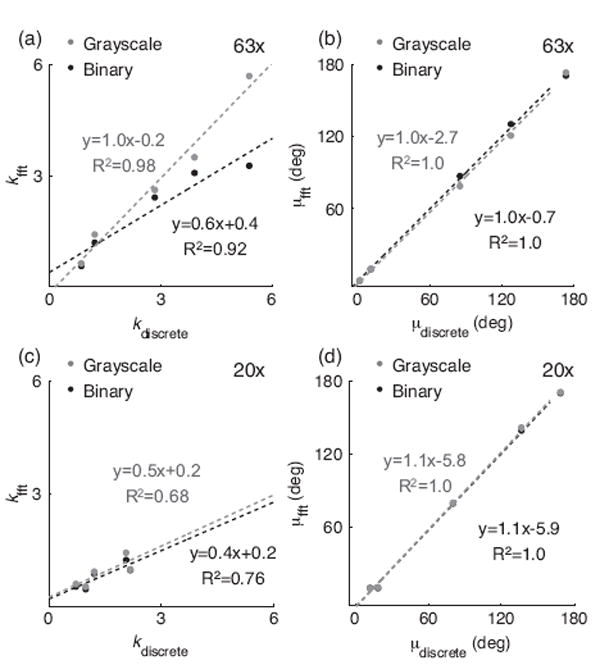
Correlation of FFT band-pass and corresponding discrete distribution analysis for grayscale and binary processing at (a,b) 63x and (c,d) 20x.
Table 1.
Comparison of image analysis methods using grayscale confocal images of bovine ligament at 63x and 20x.
| FFT, Band-pass (FiberFit) | FFT, Minimum (Matlab) | Structure Tensor (OrientationJ) | ||||
|---|---|---|---|---|---|---|
| 63x | 20x | 63x | 20x | 63x | 20x | |
| μ Error | 3.3 ± 3.1 deg | 3.8 ± 3.0 deg | 14.4 ± 16.3 deg | 16.2 ± 12.2 deg | 4.1 ± 5.3 deg | 2.4 ± 1.8 dega |
| k Error | 13.3 ± 8.2%b | 35.0 ± 15.5%a | 31.1 ± 23.1% | 83.8 ± 7.5% | 52.0 ± 23.4% | 48.1 ± 18.2%a |
= More accurate results than the FFT, minimum method (p <0.05)
= More accurate results than the structure tensor method (p <0.05)
Overall, the FFT band-pass method used by FiberFit had the best accuracy in measuring fiber dispersion k, compared to the FFT minimum and structure tensor methods (Table 1). The FFT band-pass method was 49% more accurate at measuring k than the FFT minimum method at 20x (p = 0.02), and was 39% more accurate at measuring k than the structure tensor method at 63x (p = 0.02). The FFT band-pass method and structure tensor method were both able to measure fiber orientation μ with an average error less than 5 degrees.
4. Discussion
This study has validated a computational methodology to measure structural parameters in fibrillar networks of soft connective tissue. We achieved our first objective by determining that FFT with a band-pass filter had the most accurate results, with an average error less than 8% in detecting fiber dispersion, and an average error less than 1 degree in detecting mean fiber orientation. We achieved our second objective by developing the software application, FiberFit, which uses FFT with a band-pass filter to automatically measure structural parameters in two-dimensional images of fibrillar networks. FiberFit was successfully used to measure collagen fibril networks in confocal images of bovine ligament.
Our findings clearly demonstrate that using a band-pass filter with FFT is more accurate than filtering noise with a minimum technique or using a structure tensor. In highly disordered networks (small k), the FFT band-pass method had marginal errors (<10%), while the FFT minimum and structure tensor methods had large errors (>50%). The large errors observed with the structure tensor method are potentially caused by noise from the bi-directional gradients at the fiber endpoints, which were more numerous in the disordered test images. Structure tensor accuracy may be improved by using coherency or energy thresholds (Rezakhaniha et al, 2012). The large errors observed with the FFT minimum method are related to this methods vertical shift of the fiber orientation distribution, which removed pertinent data in highly disorganized networks (Fig. 2a.), and resulted in false peaks at 90 degree offsets to the mean fiber orientation (Fig. 1). The FFT band-pass method directly filtered noise in the power spectrum and preserved pertinent data in the fiber orientation distribution (Fig. 1). In highly disordered networks (k = 0.2), the FFT band-pass method was the only method able to measure fiber dispersion k and mean fiber orientation μ within 0.06 and 1.9 degrees of the actual value, respectively. In addition, the FFT band-pass method gave the most accurate results when analyzing confocal images of ligament fibril networks (Table 1). These results indicate that the FFT band-pass method is an appropriate choice for analyzing disordered fiber networks.
Results from this study can support and advance previous research that has investigated the FFT method. The superior accuracy we found with the FFT band-pass method agrees with Sander et al., who reported that the FFT band-pass method was more accurate at calculating fiber dispersion than using the mean intercept length method or the line fraction deviation method (Sander and Barocas, 2009). Sander et al. also found that when the network dispersion increases (greater disorder), the error in measuring μ also increases. Our results support this finding, and we further determined that when the network dispersion increases, the error in measuring k also increases (Fig. 5a.). The error we calculated when measuring mean fiber orientation with the FFT band pass method (0.7 ± 0.4 degrees) is slightly better than reported by Sander et al. (2.9 ± 6.7 degrees), and is also better than the error acquired by the equation developed by Marquez (2.1 degrees; when using parameters n=13, l =44, and C =0.5) (Marquez, 2006). Other studies that examined the application of FFT toward fiber networks used a qualitative approach or a limited number of test images (< 5 total) (Sampo et al, 2014; Polzer et al, 2013; Schriefl et al, 2012), and therefore a direct comparison to our study is not feasible.
Our FFT sensitivity study revealed that the error in measuring fiber dispersion was also dependent on fiber thickness and fiber network concentration (Fig. 6,7). In general, increasing fiber thickness resulted in a decrease in the measured k value. As a consequence, increasing fiber thickness in aligned networks raised the fiber dispersion error, while increasing fiber thickness in disordered networks lowered the fiber dispersion error. This error may be decreased by modifying the band-pass cutoff frequencies (Sander and Barocas, 2009). A similar dependence on fiber anisotropy was observed when studying the effect of fiber concentration on accuracy. Aligned fiber networks with a high fiber concentration had large errors, while disordered fiber networks with a high fiber concentration had marginal errors. For aligned networks, the fiber dispersion error exceeded 10% once the fiber concentration reached 30%. The confocal images analyzed in this study had fiber concentrations safely below 20%, but studies that analyze images with very high fiber concentrations may consider modifying filter cutoff frequencies to improve error. Our findings on fiber concentration support previous work by Marquez. Although our study did not find an effect of aspect ratio on accuracy, it is recommended that aspect ratios should be greater than 10:1 to accurately measure the fiber orientation distribution using FFT (Marquez, 2006).
A novel aspect of this study was the computational generation of test images that resemble the collagen microstructure of soft connective tissue. Our study used a semicircular von Mises distribution to generate 293 binary test images with known structural parameters (k and μ) and variable fiber aspect ratios, thicknesses, and concentrations. This enabled us to investigate the sensitivity of FFT to the natural diversity of fibrillar networks observed in native and healing soft tissue (Chamberlain et al, 2011; Hurschler et al, 2003). Other groups have used different approaches to create test images of fiber networks (Polzer et al, 2013; Schriefl et al, 2012; Sander and Barocas, 2009; Sampo et al, 2014; Marquez, 2006). Marquez generated test images that were composed of a grid of geometric cells, where each cell constrained a single fiber with an orientation determined from a von Mises distribution. This approach allowed Marquez to analyze the effect of fiber thickness and fiber concentration on FFT accuracy; however, the images had limited fiber intersections and assumed all fibers were equal length. Sander et al. developed random test images with realistic fiber intersections and variable fiber lengths to examine the effect of orientation, anisotropy, and fiber concentration. An important difference between Sander et al. and the current study, is that we directly generated normalized test images from known structural parameters for comparison with FFT predicted parameters, while Sander et al. generated random test images and used length-weighted 2D tensors to measure the structural parameters for comparison with FFT predicted parameters. An advantage of our approach is that it ensures that no measurement error exists in the known structural parameters (kactual and μactual), but a disadvantage is that all of our test images have a normal distribution of fiber orientations. Therefore, our accuracy results do not account for fiber networks that exhibit bimodal distributions or have isotropic subpopulations of fibers (Gouget et al, 2012). A subset of our study’s test images are available for download (http://coen.boisestate.edu/ntm/fiberfit/), and may be useful to other research groups that are optimizing an image analysis technique.
The FiberFit software we developed for this study includes unique features that can support and expedite research in biomechanics and mechanobiology. A novel feature of FiberFit is the automated extraction of descriptive structural parameters (k and μ) based on the fitting of a semicircular von Mises distribution to the FFT generated fiber orientation distribution. The quantification of structural parameters from imaging data is a critical step to understanding the interrelations between biological processes, such as collagen remodeling, and the mechanical environment (Driessen et al, 2008; Grytz et al, 2011; Loerakker et al, 2014; Machyshyn et al, 2010). For example, the structural parameters acquired by FiberFit can be used to model the mechanical behavior of multi-axial fiber networks (Gasser et al, 2006; Holzapfel et al, 2000; Lanir, 1981). Constitutive models have been developed that use k and μ as material coefficients to describe a continuous fiber distribution (Girard et al, 2009), and these models are now available through the finite element solver FEBio (Maas et al, 2012; Gouget et al, 2012). Therefore, FiberFit can facilitate the development of models with realistic representations of fiber microstructure to study the mechanical effect of collagen organization, remodeling and repair. To our knowledge, FiberFit is the first free software to implement a band-pass filter for the FFT analysis of fiber networks. The band-pass cutoff frequencies are adjustable, and therefore users can optimize noise reduction for specific applications. To expedite the analysis of numerous 2D images, FiberFit can process a batch of images and will export summary tables and reports to make results easily accessible to the user. FiberFit is also a portable application, which allows users to run FiberFit without needing to install additional software.
Other software applications are also available that use FFT to characterize fiber networks, but these programs have not been validated and their accuracy is unclear. For example, the software application Directionality calculates a histogram of fiber orientations using either a Fourier method or a local gradient method to fit a Gaussian curve. The mean fiber direction, fiber dispersion, and goodness of fit are automatically calculated, however, the noise removal method for the Fourier transform is unknown. When we used Directionality with ten disordered test images (k = 1), we found that the mean fiber orientation results had a large error (5.8 ± 3.6 degrees) compared to results using FiberFit (0.7 ± 0.4 degrees). This finding highlights the importance of selecting an appropriate noise removal method and verifying accuracy using test images of known structure. The plugin Oval Profile Plot can automatically create a fiber orientation histogram from the FFT power spectrum using radial sums, however, it lacks options for noise removal and it does not quantify structural parameters by fitting a continuous probability distribution to the fiber orientation histogram.
This study has provided insight into the effect of image processing and image magnification on FFT accuracy. We determined that converting images to grayscale prior to using FiberFit (Schriefl et al, 2012; Sander and Barocas, 2009; Ayres et al, 2006) gave the most accurate results when quantifying fiber dispersion and mean fiber orientation in confocal images of ligament. Converting images directly to binary gave less accurate results for highly aligned fiber networks. Both these image processing techniques required background filtering to remove noise, otherwise mean fiber orientation error was almost two times greater (data not shown). We also determined that image magnification did not affect the accuracy of measuring mean fiber orientation, but did affect the accuracy of measuring fiber dispersion, k. The larger k errors we observed at lower magnifications may be caused by the presence of curvilinear fiber crimp, which is difficult to model using discrete fiber networks (Fig. 4f). In addition, at lower magnifications, the fibers become less distinct, and this naturally adds noise to the fiber orientation histogram, resulting in lower k values (less fiber alignment). Nevertheless, a strong positive correlation did exist when using FiberFit to measure the fiber dispersion of the same ligament specimens at different magnifications.
While this study only evaluated confocal images of ligament, FiberFit can also be used to analyze discrete fiber networks in other types of fibrous soft tissue and from other imaging modalities. For example, FFT has previously been used to analyze fiber networks from tendon, artery walls and tissue engineered scaffolds, when using imaging modalities that include scanning electron microscopy, standard light microscopy, and multiphoton microscopy (Frisch et al, 2012; Schriefl et al, 2012; Polzer et al, 2013; Ayres et al, 2006). Although FiberFit can analyze the fiber orientation distribution in any fiber network, it is important to note that image noise will be dependent on multiple factors (e.g. tissue type, magnification, operator), and therefore different image processing operations may be required prior to using FiberFit to ensure accurate analysis. In this study, we developed a validation strategy using discrete distributions from the manual tracing of images to assess FiberFit accuracy. This novel approach may be useful for evaluating and optimizing the use of FiberFit when new tissue types and imaging modalities are analyzed.
Further discussion is warranted on the methods used in FiberFt to fit a semicircular von Mises distribution to the fiber orientation data. In FiberFit, the parameters μ and k are sequentially fit to the fiber orientation distribution data, where μ is first calculated and then k. This two-step process proved to be more robust than fitting the parameters simultaneously using least squares or the Matlab Circular Statistics Toolbox (Berens, 2009). This strategy resulted in excellent fits of the semicircular von Mises distribution to the test images (R2 = 0.92 ± 0.07) and grayscale confocal images (R2= 0.77 ± 0.13). The R2 value of 0.77 indicates that a semicircular von Mises distribution was an appropriate probability distribution to describe the collagen fiber networks in the ligament specimens that we analyzed in this study.
Limitations exist in this study. We investigated two FFT noise removal methods, but other techniques exist that may provide superior performance (Polzer et al, 2013; Schriefl et al, 2012; Sampo et al, 2014). It is important to note that if an FFT noise removal method was not applied, the inherent noise in FFT would result in the calculation of k values less than 0.2 (nearly isotropic) for all test images, regardless of the actual fiber network alignment. Although we investigated the structure tensor method, we did not incorporate coherency or energy thresholds into the structure tensor algorithm. The application of these thresholds may improve the accuracy of the structure tensor and should be examined in future studies. Another limitation is that this study only analyzed two-dimensional images at a single size (1074 × 1074 pixels). However, our accuracy results should be valid to any image size, since the formulation of the band-pass filter used in FiberFit is automatically adjusted to image size (Eq. 5). In addition, the test images were generated with straight fibers, and therefore these results are not directly applicable to collagen networks that exhibit crimp or waviness. Images containing fiber crimp may exhibit a more disperse distribution of fiber orientations, as was observed in this study when confocal magnification was reduced from 63x to 20x. Finally, the confocal images used for validation covered a small field of view in relation to the entire specimen. In order to measure fiber organization at larger fields of view, other techniques may be more appropriate, such as quantitative polarized light imaging (Tower et al, 2002).
In conclusion, we found that using FFT with a band-pass filter gave accurate results when quantifying fiber orientation distributions in aligned and disordered fiber networks. A free software application, FiberFit, was developed that utilizes an FFT band-pass filter to fit fiber orientations to a semicircular von Mises distrution. FiberFit was able to quickly, automatically, and accurately extract fiber dispersion and mean fiber orientation from collagen fiber networks in ligament. We determined that converting images to grayscale prior to using FiberFit gave good results. This study provides guidelines, experimental methodologies and computational tools for researchers that are investigating the microstructure and mechanics of fibrillar networks in biological tissue.
Acknowledgments
This project was supported by Institutional Development Awards (IDeA) from the National Institute of General Medical Sciences of the National Institutes of Health under Grants No. P20GM103408 and P20GM109095. We also acknowledge support from The Biomolecular Research Center at Boise State with funding from the National Science Foundation, Grants No. 0619793 and 0923535; the MJ Murdock Charitable Trust; and the Idaho State Board of Education.
Contributor Information
Erica E. Morrill, Boise State University, Department of Mechnaical and Biomedical Engineering
Azamat N. Tulepbergenov, Boise State University, Department of Computer Science
Christina J. Stender, Boise State University, Department of Mechnaical and Biomedical Engineering
Roshani Lamichhane, Boise State University, Department of Computer Science.
Raquel J. Brown, Boise State University, Biomolecular Research Center
Trevor J. Lujan, Boise State University, Department of Mechanical and Biomedical Engineering
References
- Ayres C, Bowlin GL, Henderson SC, Taylor L, Shultz J, Alexander J, Telemeco Ta, Simpson DG. Modulation of anisotropy in electrospun tissue-engineering scaffolds: Analysis of fiber alignment by the fast Fourier transform. Biomaterials. 2006;27(32):5524–5534. doi: 10.1016/j.biomaterials.2006.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayres CE, Jha BS, Meredith H, Bowman JR, Bowlin GL, Henderson SC, Simpson DG. Measuring fiber alignment in electrospun scaffolds : a user s guide to the 2D fast Fourier transform approach. Journal of Biomaterials Science - Polymer Edition. 2008;19(5):603–621. doi: 10.1163/156856208784089643. [DOI] [PubMed] [Google Scholar]
- Berens P. CircStat: A MATLAB toolbox for circular statistics. Journal of Statistical Software. 2009;31(10):1–21. [Google Scholar]
- Bigun J, Bigun T, Nilsson K. Recognition by symmetry derivatives and the generalized structure tensor. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2004;26(12):1590–1605. doi: 10.1109/TPAMI.2004.126. [DOI] [PubMed] [Google Scholar]
- Chamberlain CS, Crowley EM, Kobayashi H, Eliceiri KW, Vanderby R. Quantification of Collagen Organization and Extracellular Matrix Factors within the Healing Ligament. Microscopy and Microanalysis. 2011;17(05):779–787. doi: 10.1017/S1431927611011925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Amore A, Stella JA, Wagner WR, Sacks MS. Characterization of the Complete Fiber Network Topology of Planar Fibrous Tissue and Scaffolds. Biomaterials. 2010;31(20):5345–5354. doi: 10.1016/j.biomaterials.2010.03.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Driessen NJB, Cox MaJ, Bouten CVC, Baaijens FPT. Remodelling of the angular collagen fiber distribution in cardiovascular tissues. Biomechanics and Modeling in Mechanobiology. 2008;7(2):93–103. doi: 10.1007/s10237-007-0078-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzgibbon A, Pilu M, Fisher RB. Direct least square fitting of ellipses. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1999;21(5):476–480. [Google Scholar]
- Frisch K, Duenwald-Kuehl S, Lakes R, Vanderby R. Quantification of Collagen Organization Using Fractal Dimensions and Fourier Transforms. Acta Histochem. 2012;114(2):140–144. doi: 10.1016/j.acthis.2011.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gasser TC, Ogden RW, Holzapfel Ga. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. Journal of the Royal Society, Interface / the Royal Society. 2006;3(6):15–35. doi: 10.1098/rsif.2005.0073. 0312002v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girard MJA, Downs JC, Burgoyne CF, Suh JKF. Peripapillary and posterior scleral mechanics–part I: development of an anisotropic hyperelastic constitutive model. Journal of biomechanical engineering. 2009;131(5) doi: 10.1115/1.3113682. 051,011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez R, Woods R. Digital Image Processing. 3. Pearson Prentice Hall; New Jersey: 2008. [Google Scholar]
- Gouget CLM, Girard MJ, Ethier CR. A constrained von Mises distribution to describe fiber organization in thin soft tissues. Biomechanics and Modeling in Mechanobiology. 2012;11(3-4):475–482. doi: 10.1007/s10237-011-0326-y. [DOI] [PubMed] [Google Scholar]
- Grytz R, Meschke G, Jonas JB. The collagen fibril architecture in the lamina cribrosa and peripapillary sclera predicted by a computational remodeling approach. Biomechanics and Modeling in Mechanobiology. 2011;10(3):371–382. doi: 10.1007/s10237-010-0240-8. [DOI] [PubMed] [Google Scholar]
- Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comperative study of material models. J Elasticity. 2000;61:1–48. [Google Scholar]
- Hurschler C, Provenzano PP, Vanderby R. Scanning electron microscopic characterization of healing and normal rat ligament microstructure under slack and loaded conditions. Connective tissue research. 2003;44(2):59–68. [PubMed] [Google Scholar]
- Jahne B. Theory and Scientific Applications. Springer; Berlin: 1993. Spatio-Temporal Image Processing. [Google Scholar]
- Jones E, Oliphant T, Peterson P, et al. SciPy: Open Source Scientific Tools for Python. 2001 URL http://www.scipy.org/
- Lanir Y. The fibrous structure of the skin and its relation to mechanical behaviour. In: Marks R, Payne P, editors. Bioengineering and the Skin. Springer Netherlands; 1981. pp. 93–95. [Google Scholar]
- Loerakker S, Obbink-Huizer C, Baaijens FPT. A physically motivated constitutive model for cell-mediated compaction and collagen remodeling in soft tissues. Biomechanics and modeling in mechanobiology. 2014;13(5):985–1001. doi: 10.1007/s10237-013-0549-1. [DOI] [PubMed] [Google Scholar]
- Maas SA, Ellis BJ, Ateshian GA, Weiss JA. FEBio: Finite Elements for Biomechanics. Journal of Biomechanical Engineering. 2012;134(1) doi: 10.1115/1.4005694. 011, 005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machyshyn IM, Bovendeerd PHM, van de Ven AAF, Rongen PMJ, van de Vosse FN. A model for arterial adaptation combining microstructural collagen remodeling and 3D tissue growth. Biomechanics and Modeling in Mechanobiology. 2010;9(6):671–687. doi: 10.1007/s10237-010-0204-z. [DOI] [PubMed] [Google Scholar]
- Makareeva E, Mertz EL, Kuznetsova NV, Sutter MB, DeRidder AM, Cabral Wa, Barnes AM, McBride DJ, Marini JC, Leikin S. Structural heterogeneity of type I collagen triple helix and its role in osteogenesis imperfecta. Journal of Biological Chemistry. 2008;283(8):4787–4798. doi: 10.1074/jbc.M705773200. [DOI] [PubMed] [Google Scholar]
- Mardia KV, Jupp PE. Directional Statistics. Wiley; New York: 2000. [Google Scholar]
- Marquez JP. Fourier analysis and automated measurement of cell and fiber angular orientation distributions. International Journal of Solids and Structures. 2006;43(21):6413–6423. [Google Scholar]
- Monici M. Cell and Tissue Autofluorescence Research and Diagnostic Applications. Biotechnology Annual Reveiw. 2005;11(11):227–56. doi: 10.1016/S1387-2656(05)11007-2. [DOI] [PubMed] [Google Scholar]
- O’Connell B. Oval Profile Plot plugin for ImageJ. 2012 URL rsb.info.nih.gov/ij/plugins/oval-profile.html.
- Petroll MW, Cavanagh DH, Barry P, Andrews P, Jester JV. Quantitative Analysis of Stress Fiber Orientation During Corneal Wound Contraction. Journal of Cell Science. 1993;104:353–63. doi: 10.1242/jcs.104.2.353. [DOI] [PubMed] [Google Scholar]
- Polzer S, Gasser TC, Forsell C, Druckmuüllerova H, Tichy M, Staffa R, Vlachovsky R, Bursa J. Automatic Identification and Validation of Planar Collagen Organization in the Aorta Wall with Application to Abdominal Aortic Aneurysm. Microscopy and Microanalysis. 2013;19:1395–1404. doi: 10.1017/S1431927613013251. [DOI] [PubMed] [Google Scholar]
- Rezakhaniha R, Agianniotis A, Schrauwen JTC, Griffa A, Sage D, Bouten CVC, Van De Vosse FN, Unser M, Stergiopulos N. Experimental investigation of collagen waviness and orientation in the arterial adventitia using confocal laser scanning microscopy. Biomechanics and Modeling in Mechanobiology. 2012;11(3-4):461–473. doi: 10.1007/s10237-011-0325-z. [DOI] [PubMed] [Google Scholar]
- Sampo J, Takalo J, Siltanen S, Miettinen A, Lassas M, Timonen J. Curvelet-based method for orientation estimation of particles from optical images. Optical Engineering. 2014;53(3) 033,109. [Google Scholar]
- Sander EA, Barocas VH. Comparison of 2D fiber network orientation measurement methods. Journal of Biomedical Materials Research - Part A. 2009;88(2):322–331. doi: 10.1002/jbm.a.31847. [DOI] [PubMed] [Google Scholar]
- Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B, Tinevez JY, White DJ, Hartenstein V, Eliceiri K, Tomancak P, Cardona A. Fiji: an open-source platform for biological-image analysis. Nature Methods. 2012;9(7):676–682. doi: 10.1038/nmeth.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider CA, Rasband WS, Eliceiri KW. NIH Image to ImageJ: 25 years of image analysis. Nature Methods. 2012;9(7):671–675. doi: 10.1038/nmeth.2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schriefl AJ, Reinisch AJ, Sankaran S, Pierce DM, Holzapfel GA. Quantitative assessment of collagen fibre orientations from two-dimensional images of soft biological tissues. Journal of The Royal Society Interface. 2012;9(76):3081–3093. doi: 10.1098/rsif.2012.0339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tienevez JY. Directionality plugin for ImageJ. 2010 URL http://fiji.sc/Directionality.
- Tower TT, Neidert MR, Tranquillo RT. Fiber alignment imaging during mechanical testing of soft tissues. Annals of Biomedical Engineering. 2002;30(10):1221–1233. doi: 10.1114/1.1527047. [DOI] [PubMed] [Google Scholar]
- Vogel A, Holbrook KA, Steinmann B, Gitzelmann R, Byres PH. Abnormal collagen fibrilstructure in the Gravis Form (Type I) of Ehlers-Danlos Syndrome. Laboratory Investigation. 1979;40(2):201–6. [PubMed] [Google Scholar]
- Weichsel J, Urban E, Small JV, Schwarz US. Reconstructing the orientation distribution of actin filaments in the lamellipodium of migrating keratocytes from electron microscopy tomography data. Cytometry Part A. 2012;81(A(6)):496–507. doi: 10.1002/cyto.a.22050. [DOI] [PubMed] [Google Scholar]
- Woo SLY, Buckwalter JA, Fung YC. Injury and Repair of the Musculoskeletal Soft Tissues. Journal of Biomechanical Engineering. 1989;111(1):95. [Google Scholar]


