PItcHPERFeCT: Primary Intracranial Hemorrhage Probability Estimation using Random Forests on CT

Abstract

Introduction

Intracerebral hemorrhage (ICH), where a blood vessel ruptures into areas of the brain, accounts for approximately 10–15% of all strokes. X-ray computed tomography (CT) scanning is largely used to assess the location and volume of these hemorrhages. Manual segmentation of the CT scan using planimetry by an expert reader is the gold standard for volume estimation, but is time-consuming and has within- and across-reader variability. We propose a fully automated segmentation approach using a random forest algorithm with features extracted from X-ray computed tomography (CT) scans.

Methods

The Minimally Invasive Surgery plus rt-PA in ICH Evacuation (MISTIE) trial was a multi-site Phase II clinical trial that tested the safety of hemorrhage removal using recombinant-tissue plasminogen activator (rt-PA). For this analysis, we use 112 baseline CT scans from patients enrolled in the MISTE trial, one CT scan per patient. ICH was manually segmented on these CT scans by expert readers. We derived a set of imaging predictors from each scan. Using 10 randomly-selected scans, we used a first-pass voxel selection procedure based on quantiles of a set of predictors and then built 4 models estimating the voxel-level probability of ICH. The models used were: 1) logistic regression, 2) logistic regression with a penalty on the model parameters using LASSO, 3) a generalized additive model (GAM) and 4) a random forest classifier. The remaining 102 scans were used for model validation.For each validation scan, the model predicted the probability of ICH at each voxel. These voxel-level probabilities were then thresholded to produce binary segmentations of the hemorrhage. These masks were compared to the manual segmentations using the Dice Similarity Index (DSI) and the correlation of hemorrhage volume of between the two segmentations. We tested equality of median DSI using the Kruskal-Wallis test across the 4 models. We tested equality of the median DSI from sets of 2 models using a Wilcoxon signed-rank test.

Results

All results presented are for the 102 scans in the validation set. The median DSI for each model was: 0.89 (logistic), 0.885 (LASSO), 0.88 (GAM), and 0.899 (random forest). Using the random forest results in a slightly higher median DSI compared to the other models. After Bonferroni correction, the hypothesis of equality of median DSI was rejected only when comparing the random forest DSI to the DSI from the logistic (p < 0.001), LASSO (p < 0.001), or GAM (p < 0.001) models. In practical terms the difference between the random forest and the logistic regression is quite small. The correlation (95% CI) between the volume from manual segmentation and the predicted volume was 0.93 (0.9,0.95) for the random forest model. These results indicate that random forest approach can achieve accurate segmentation of ICH in a population of patients from a variety of imaging centers. We provide an R package (https://github.com/muschellij2/ichseg) and a Shiny R application online (http://johnmuschelli.com/ich_segment_all.html) for implementing and testing the proposed approach.

Highlights

• •A hemorrhage segmentation algorithm from CT scans is proposed.
• •Validation using manual segmentation was done on 102 patients from multiple sites.
• •Software is provided as a website (http://johnmuschelli.com/ich_segment.html).
• •An R package (https://github.com/muschellij2/ichseg) is available.

1. Introduction

Intracerebral hemorrhage (ICH) is a neurological condition that results from a blood vessel rupturing into the tissue and possibly extending into the ventricles of the brain. The use of X-ray computed tomography (CT) scans allows clinicians and researchers to qualitatively and quantitatively describe the characteristics of a hemorrhage to guide interventions and treatments. CT scanning is widely available and is the most commonly used diagnostic tool in patients with ICH (Sahni and Weinberger, 2007). The volume of ICH has been consistently demonstrated to be an important diagnostic predictor of stroke severity, long-term functional outcome, and mortality (Broderick et al., 1993, Hemphill et al., 2001, Tuhrim et al., 1999). ICH volume change is also a common primary outcome (Anderson et al., 2010, Anderson et al., 2008, Mayer et al., 2005, Qureshi et al., 2011) and secondary outcome (Anderson et al., 2008, Morgan et al., 2008, Morgan et al., 2008) in clinical trials. Moreover, the location of the ICH has been shown to affect functional outcome in patients with stroke (Castellanos et al., 2005, Rost et al., 2008). Thus, quantitative measures of ICH (e.g. volume, location, and shape) are increasingly important for treatment and other clinical decision.

ICH volume can be estimated quickly, for example, using the ABC/2 method (Broderick et al., 1993). In this method, a reader chooses the slice with the largest area of hemorrhage. The length of the intersection between this first axis and the hemorrhage is denoted by A. The next step is to draw an orthogonal line at the middle of the segment of length A in the same plane that contains the largest hemorrhage area. The length of the intersection between this second orthogonal axis and the hemorrhage is denoted by B. The reader then counts the number of slices where hemorrhage is present (C). The volume estimate is $\frac{A\times B\times C}{2}$, which is an approximation of the volume under the assumption that the hemorrhage shape is well approximated by an ellipsoid (Kothari et al., 1996). As this method is relatively easy to implement in practice, it can be used to quickly produce rough estimates of hemorrhage volume (Webb et al., 2015).

Although ABC/2 is widely used, Divani et al. (2011) found that the measurement error associated with the ABC/2 method were significantly greater than those using planimetry, which requires slice-by-slice hemorrhage segmentation by trained readers. Planimetry is much more labor intensive and time consuming, but it more accurately estimates the true ICH volume compared to the ABC/2 approach, especially for irregularly shaped ICH and for smaller thickness (i.e. higher resolution) scans. Another problem that has not been discussed in the literature is that ICH may change over time. The shape of the ICH may initially be well approximated by an ellipsoid but the approximation may become increasingly inaccurate over time as the lesion changes shape, migrates through the surrounding tissues, or breaks down. Surgical interventions that target the removal of ICH may also change the shape of the ICH or cause additional bleeding. Moreover, the ABC/2 method has been shown to consistently over-estimate infarct volume (Pedraza et al., 2012) and may have significant inter-rater variability (Hussein et al., 2013). Therefore, a rapid, automated, and validated method for estimating hemorrhage location and its volume from CT scans is highly relevant in clinical trials and clinical care. Accuracy is accompanied by increase of both diagnostic and prognostic value.

Methods have been proposed for segmentation of ICH using magnetic resonance images (MRI) (Carhuapoma et al., 2003, Wang et al., 2013). However, in most clinical settings CT, not MRI, is the image of choice. Furthermore, MRI sequences and protocols may vary across sites and there is no general, standardized, agreed-upon MRI protocol for ICH standard-of-care. Thus, there is a need for ICH segmentation that relies only on CT scan information, is reliable, reproducible, available, and well validated against planimetry.

We propose an algorithm that can estimate the probability of ICH at the voxel level, produce a binary image of ICH location, and estimate ICH volume. We will compare our predicted ICH maps to the gold standard – manual segmentation. Several methods have been presented for automated methods for estimating ICH from CT scans (Gillebert et al., 2014, Loncaric et al., 1996, Loncaric et al., 1999, Pérez et al., 2007, Prakash et al., 2012). These methods include fuzzy clustering (Loncaric et al., 1996, Prakash et al., 2012), simulated annealing (Loncaric et al., 1999), 3-dimensional (3D) mathematical morphology operations (Pérez et al., 2007), and template-based comparisons (Gillebert et al., 2014). Unfortunately, no software for ICH segmentation is publicly available. We provide a completely automated pipeline of analysis from raw images to binary hemorrhage masks and volume estimates, and provide a public webpage to test the software.

2. Methods

2.1. Data

We used CT images from patients enrolled in the MISTIE II (Minimally Invasive Surgery plus recombinant-tissue plasminogen activator for Intracerebral Hemorrhage Evacuation) stroke trial (Morgan et al., 2008). We analyzed 112 scans taken prior to randomization and treatment, corresponding to the first scan acquired post-stroke for 112 unique patients. Inclusion criteria into the study included: 18 to 80 years of age and spontaneous supratentorial intracerebral hemorrhage above 20 milliliters (mL) in size (for full criteria, see Mould et al. (2013)). The population analyzed here had a mean (standard deviation (SD)) age of 60.7 (11.2) years, was 68.8% male, and was 53.6% Caucasian, 31.2% African American, 10.7% Hispanic, and 4.5% Asian or Pacific islander. CT data were collected as part of the Johns Hopkins Medicine IRB-approved MISTIE research studies with written consent from participants.

The study protocol was executed with minor, but important, differences across the 26 sites. Scans were acquired using 4 scanner manufacturers: GE (N = 46), Siemens (N = 38), Philips (N = 20), and Toshiba (N = 8). In head CT scanning, the gantry may be tilted for multiple purposes, for example, so that sensitive organs, such as the eyes, are not exposed to X-ray radiation. This causes scan slices to be acquired at an oblique angle with respect to the patient. Gantry tilt was observed in 88 scans. Slice thickness of the image varied within the scan for 14 scans. For example, a scan may have 10 millimeter (mm) slices at the top and bottom of the brain and 5 mm slices in the middle of the brain. Therefore, the original scans analyzed had different voxel (volume element) dimensions. These conditions are characteristic of how scan are presented in many diagnostic cases.

2.2. Hemorrhage segmentation and location identification

ICH was manually segmented on CT scans using the OsiriX imaging software by expert readers (OsiriX v. 4.1, Pixmeo; Geneva, Switzerland). After image quality review, continuous, non-overlapping slices of the entire hemorrhage were segmented. Readers employed a semiautomated threshold-based approach using a Hounsfield unit (HU) range of 40 to 80 to select potential regions of hemorrhage (Bergström et al., 1977, Smith et al., 2006); these regions were then further quality controlled and refined by readers using direct inspection of images. Binary hemorrhage masks were created by setting voxel intensity to 1 if the voxel was classified as hemorrhage, regardless of location, and 0 otherwise.

2.3. Image processing: brain extraction, registration

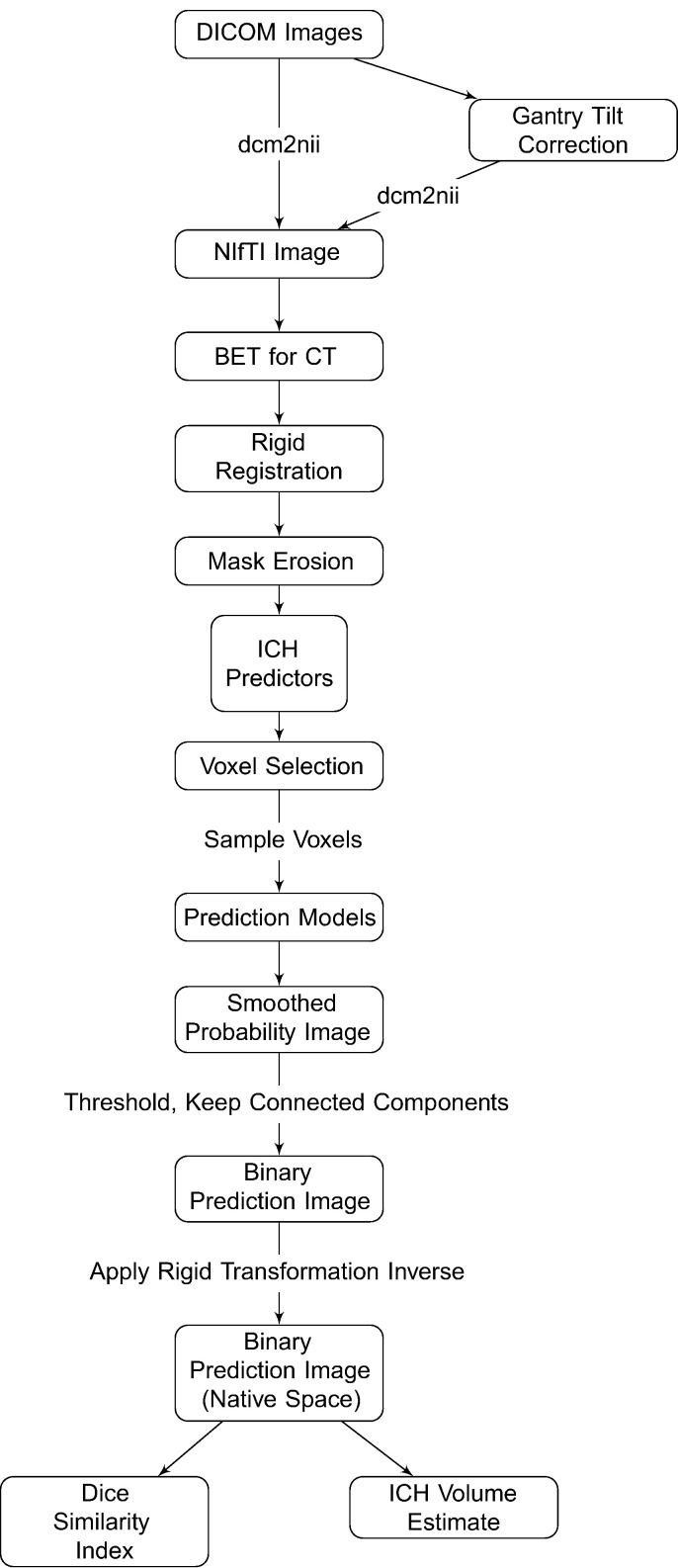
CT images and binary hemorrhage masks were exported from OsiriX to DICOM (Digital Imaging and Communications in Medicine) format. The image processing pipeline can be seen in Fig. 1. Images with gantry tilt were corrected using a customized MATLAB (The Mathworks, Natick, Massachusetts, USA) user-written script (http://bit.ly/1ltIM8c). Images were converted to the Neuroimaging Informatics Technology Initiative (NIfTI) data format using dcm2nii (provided with MRIcro (Rorden and Brett, 2000)). Images were constrained to values  −1024 and 3071 HU to remove potential image rescaling errors and artifacts. No interpolation was done for images with a variable slice thickness. Thickness was determined from the first converted slice and the NIfTI format assumes homogeneous thickness throughout the image. In a future release of dcm2nii, called dcm2niix, interpolation will be done for scans with variable slice thickness and gantry-tilt correction will be performed automatically.

Fig. 1.

Processing pipeline. Images in DICOM (Digital Imaging and Communications in Medicine) format were gantry tilt corrected if necessary and converted to NIfTI (Neuroimaging Informatics Technology Initiative) format using dcm2nii. After NIfTI conversion, the brain extraction tool (BET) was applied to the image using a previously published protocol. The image was registered to a brain CT template using a rigid-body transformation and was interpolated to template resolution. We estimated imaging predictors and used these predictors to estimate the probability of ICH in a prediction model. The probability of ICH was thresholded, connected component below 100 voxels (0.1 mL) were discarded, and the image was transformed back into original space of the patient. The ICH volume and the Dice Similarity Index, an overlap measure, were calculated compared to the true estimate from the manual segmentation.

All image analysis was done in the R statistical software (R Core Team, 2015), using the fslr (Muschelli et al., 2015) package to call functions from the FSL (Jenkinson et al., 2012) neuroimaging software (version 5.0.4), and the ANTsR package to call functions from the ANTs (Advanced Normalization Tools) neuroimaging software (Avants et al., 2011).

Brains were extracted to remove skull, eyes, facial and nasal features, extracranial skin, and non-human elements of the image captured by the CT scanner, such as the gantry, pillows, or medical devices. Removal of these elements was performed using the brain extraction tool (BET) (Smith, 2002), a function of FSL, using a previously published validated CT-specific brain extraction protocol (Muschelli et al., 2015).

2.4. Image registration

Rorden et al. (2012) introduced a CT template based on 35 individuals who presented with specific neurological deficits that were suspected to be caused by a stroke, but were later found to be due to a metabolic abnormality. This CT template is represented in MNI (Montreal Neurological Institute) space and brain-extraction was performed on the template. Prior to image processing, brain-extracted images were registered to this brain-extracted template using a rigid-body (6 degrees of freedom) and linearly interpolated to a 1 × 1 × 1 mm voxel resolution. After interpolation, transformed hemorrhage masks and brain masks are not binary. These transformed masks were re-thresholded using a value of 0.5 to preserve mask volume (Frequently asked questions for FLIRT, 2017). Using a nearest-neighbor interpolation for these binary images after registration could also be used as a simpler approach and should be relatively equivalent to the re-thresholding.

This rigid registration does not ensure brains are the same size or that voxels match across subjects. Having voxels registered across subjects is not necessary for our model, as we do not incorporate voxel-level spatial information into the model. Although brains with different shapes and sizes may map to different areas in the template space, the goals of this registration are to reorient the image, ensure isotropic voxel sizes for smoothing and other operations described below, and preserve the relative volume of the ICH. All image preprocessing and analysis are done in MNI space, described as template space, unless otherwise specified.

2.5. Brain mask erosion

After registration, each brain mask was eroded by a box kernel (3 × 3 × 1 mm). Though this erosion may exclude voxels from superficial bleeds towards the cortical surface, it excludes voxels with similar ranges as ICH voxels, caused by 1) incomplete skull stripping or 2) partial voluming effects with the skull. If any voxels from the hemorrhage mask were removed due to brain extraction or brain mask erosion, these voxels were included in estimating model performance but their predicted probability of ICH was set to 0. Therefore, these deleted ICH voxels will always be false negatives in our approach.

2.6. Imaging predictors

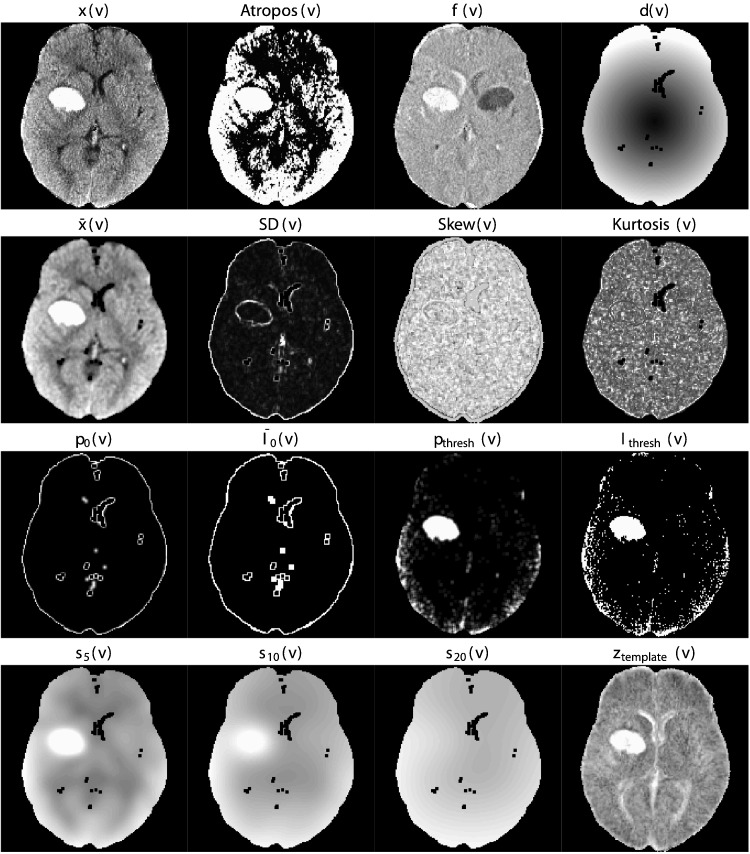
We derived a set of imaging predictors from each CT scan. We will describe each predictor together with the rationale for their use. These features make up the potential set of predictors (features) for image segmentation. Below we provide the definition of these predictors, while Fig. 2 displays them for one axial slice of one subject.

Fig. 2.

Predictor images. Here we display one axial slice of predictor images from one patient. The within-plane standardized and Winsorized predictor images were not shown as they are within-subject scaled versions of the image x(v) and appear very similar. Although they appear similar at a subject level, the distribution of these predictors is different across patients. Images that visually separate the areas of ICH compared to the rest of the images are likely to be better predictors.

2.6.1. CT voxel intensity information

The first predictor is the raw voxel intensity value in HU denoted by x(v). This is the main predictor used in visual inspection, with high HU values being indicative of hemorrhage. Based on the voxel intensity we have created an indicator for the HU intensity value to be between 40 and 80 (inclusive), to mimic the criterion used for screening in manual segmentation. Although all scans may not have the same intensity range overall or for the hemorrhage, the calibration of the CT scanner and how the Hounsfield unit is calculated generally gives similar ranges for similar tissues. Also, these thresholds have been used in previous ICH segmentation work (Prakash et al., 2012) and have been empirically shown to perform well. More precisely, we have introduced the predictor

$$I_{\text{thresh}}(v)=\left\{\begin{array}{ll}1& \text{if}40\le x(v)\le 80\\ 0& \text{otherwise}\end{array}\right)$$

2.6.2. Local moment information

For each voxel, we extracted a neighborhood of voxels: all adjacent voxels along the 3 dimensions together with the voxel itself, indexed by k: $k=1,\dots ,N(v)=27$, where N(v) is the number of voxels in the neighborhood. If x_k(v) denotes the voxel intensity in HU for voxel neighbor k, then the local mean intensity is defined as:

$$\bar{x}(v)=\frac{1}{N(v)}\sum _{k\in N(v)}{x}_k(v).$$ (1)

We also calculate statistics based on higher order moments and define the local SD, skew, and kurtosis as:

$$\begin{array}{ll}\hfill & \text{SD}(v)=\sqrt{\frac{1}{N(v)}\sum _{k\in N(v)}{\left\{x_k(v)-\bar{x}(v)\right\}}^2}\hfill \\ \hfill & \text{Skew}(v)=\frac{\frac{1}{N(v)}\sum _{k\in N(v)}{\left\{x_k(v)-\bar{x}(v)\right\}}^3}{{\left[\frac{1}{N(v)}\sum _{k\in N(v)}{\left\{x_k(v)-\bar{x}(v)\right\}}^2\right]}^{3/2}}=\frac{\frac{1}{N(v)}\sum _{k\in N(v)}{\left\{x_k(v)-\bar{x}(v)\right\}}^3}{SD{(v)}^3}\hfill \\ \hfill & \text{Kurtosis}(v)=\frac{\frac{1}{N(v)}\sum _{k\in N(v)}{\left\{x_k(v)-\bar{x}(v)\right\}}^4}{{\left[\frac{1}{N(v)}\sum _{k\in N(v)}{\left\{x_k(v)-\bar{x}(v)\right\}}^2\right]}^2}=\frac{\frac{1}{N(v)}\sum _{k\in N(v)}{\left\{x_k(v)-\overline{x}(v)\right\}}^4}{SD{(v)}^4}\hfill \end{array}$$

We did not divide by {N(v) − 1} in standard deviation and skew formula and did not subtract by 3 for kurtosis. As N(v) is the same at every voxel, these simplified choices will have no effect on modeling or prediction.

Voxels with a larger local mean have higher HU neighboring voxels, which increases their likelihood to be in or adjacent to the ICH. The higher order moments can provide information about how homogeneous the intensities in the neighborhood are and where edges may be located. We also introduce the variable of the percentage of voxels in each neighborhood that have HU values between 40 and 80:

$$p_{\text{thresh}}(v)=\frac{1}{N(v)}\sum _{k\in N(v)}I\left\{40,\le ,x_k,(,v,),\le ,80\right\}$$ (2)

which should be higher for ICH voxels as they are surrounded by neighbors with higher HU values.

Voxels that are on the surface or are surrounded by non-brain tissue are less likely to be in the ICH. Thus, voxels not in the eroded mask are set to 0. We also introduce the variable percentage of voxels that have neighbors of value of 0:

$$p_0(v)=\frac{1}{N(v)}\sum _{k\in N(v)}I\left\{x_k,(,v,),=,0\right\},$$ (3)

and an indicator of whether any voxels in the neighborhood had a value of 0:

$${\bar{I}}_0(v)=I\left\{p_0,(,v,),>,0\right\}.$$ (4)

The reason for introducing these predictors is that we expect that voxels that have neighbors with intensity zero are less likely to be ICH. Our approach will not assume that the probability of voxels with neighbors with HU intensity equal to zero are not in the ICH. Instead, we will model the probability of belonging to the ICH as a function of the predictors described in this section.

2.6.3. Within-plane standard scores

Some brain structures have high HU values but are not ICH, such as the falx cerebri, which lies largely on the mid-sagittal plane. Moreover, raw CT images may contain substantial inhomogeneity. For example, tissues closer to the top of the brain may have higher observed intensities (measured in HU) than those in the middle or bottom of the brain. Thus, if values are standardized within each plane (axial, sagittal, coronal), for each scan separately, the resulting plane-specific z-scores may discriminate better high relative values within the plane, which may attenuate the effect of HU intensity inhomogeneities. These transformations will also standardize the intensities so that shifts in intensities will be corrected across patients, such as those potentially due to shifts due to scanner.

Thus, for each voxel and slice (axial, sagittal, and coronal) planes, we defined

$$z_o(v)=\frac{x(v)-\bar{x}(v,o)}{\widehat{\sigma }(v,o)}$$ (5)

where o ∈{axial, sagittal, and coronal}, $\overline{x}(v,o)$ and $\widehat{\sigma }(v,o)$ denote the mean and standard deviation of the intensities of voxels in the plane o that contains the voxel v, excluding voxels outside the brain mask. In addition to the standardized images within each plane we have also calculated standardized scores based on the Winsorized mean and standard deviation. More precisely, we used the same formula as in Eq. (5), we set any HU values below the 20th percentile to the 20th percentile value and above the 80th percentile to the 80th percentile value within that slice and calculated the slice-specific mean and standard deviation,. This approach is expected to be more robust to small and moderate artifacts in the image.

2.6.4. Initial segmentation

A major advantage of our approach is that it can use the results of other segmentation algorithms as covariates in our model. Consider, for example, Atropos (Avants et al., 2011), a previously published, open source, general segmentation tool based on Markov random fields for image segmentation. Atropos combines an initial segmentation based on k-means with an expectation-maximization algorithm for a finite mixture model along with a Markov random field prior. We used Atropos to conduct a 4-tissue class segmentation which provides the probability for each class. We combined the top 2 probability classes into one class as Atropos orders the classes by the mean intensity and hemorrhages have higher HU values. This combined probability was then used as a predictor, denoted by Atropos(v). Although Atropos has been shown to perform well in other studies for tissue-class segmentation (Avants et al., 2011, Menze et al., 2015), the Atropos segmentation did not perform adequately in our ICH CT data. However, using the Atropos segmentation probabilities as predictors can be done seamlessly in our approach. Similarly, the results of any other segmentation approach can be incorporated in our approach and the relative performance of methods can be compared.

2.6.5. Contralateral difference images

As most hemorrhages are constrained to one side of the brain, the contralateral side tends to have lower HU values. In contrast, for non-hemorrhage voxels, the contralateral voxels tend to have similar HU values due to the quasi-symmetry of the brain and its adjacent tissues such as bone. To take advantage of this property, we right-left flipped the registered image, and computed a difference image

$$f(v)=x(v)-x(v^{*}),$$ (6)

where v^* is the contralateral voxel of v.

2.6.6. Global head information

Another potential predictor was the distance to the center of the brain, d(v), account for voxels that are far from the brain center but may contain artifacts. We also created 3 images by smoothing the original image using large Gaussian kernels (σ = 5 mm³, 10 mm³, 20 mm³) to account for potential heterogeneity in intensity. These smooth images we denoted by s₅(v), s₁₀(v) and s₂₀(v), respectively.

2.6.7. Standardized-to-template intensity

We have also incorporated predictors that contrast the scan HU intensities with those of an average brain obtained from healthy individuals. Using 30 CT images from non-stroke patients from Dr. Rorden (personal communication), we registered the brain-extracted scans to a CT template, and created a voxel-wise mean image M and voxel-wise standard deviation S image across registered images in template space. Each scan in our ICH study, we registered (using affine transformations followed by SyN (Avants et al., 2008)) it to the same CT template. We then created a standardized voxel intensity with respect to this population, z_template, using the following equation:

$$z_{\text{template}}(v)=\frac{x(v)-M(v)}{S(v)}$$

The image was then returned to the same as the other predictors. This predictor attempts to use the intensities of non-stroke patients that takes into account the spatial pattern of the mean and variability of intensities in CT scans. This predictor is similar to that used in Gillebert et al. (2014) and the authors have shown that this predictor can detect voxels outside of a standard range such as the hemorrhage.

2.7. Voxel selection procedure

We chose 10 scans from 10 patients to perform exploratory data analysis, model fitting, and estimation of model cutoffs; these data will be referred to as the training data. These scans were randomly selected. These selected patients had a mean (SD) hemorrhage volume of 37.8 (6) mL, had an average HU intensity of 58.8 HU and were scanned on the following scanners: GE (N = 6), Philips (N = 2), Siemens (N = 1), and Toshiba (N = 1). We used the 102 remaining scans as test data to evaluate the performance of the proposed approaches.

Using the training data, we estimated the 0.5% and 99.5% quantiles for all predictors across ICH voxels. The voxel selection procedure consisted of choosing all voxels that had all of predictors z_axial, z_coronal, and p_thresh within the corresponding 0.5 and 99.5 quantiles as well as values of HU intensity between 30 and 100. Voxels that did not meet these criteria were assigned a 0 probability of ICH. These cutoffs were found empirically to work well in the test scans. This approach excluded a mean of 63.6 (min: 37.1, max: 89.8) percentage of non-ICH voxels and included a mean of 97.9 (min: 91.6, max: 99.9) percentage of ICH voxels. We have found that this voxel selection procedure improves computational speed as well as the performance of the algorithms.

2.8. Models

Using the 10 training scans we obtained all voxels passing the voxel selection procedure described in Section 2.7. We then randomly sub-sampled 100,000 voxels, which were used for model fitting, model selection, and exploratory analysis, to reduce computational burden and increase speed of model fitting and exploratory analysis. The rest of the remaining voxels from the training data were used for model calibration. All models were fit with all the predictors described in Sections 2.6.

We fit several different models on the 100,000 sub-sampled voxels: 1) logistic regression with all covariates used as main effects (without interactions or nonlinear effects), 2) logistic regression model with a penalty on the model parameters to reduce the potential effect of high correlations between predictors, 3) generalized additive model (GAM) (Hastie and Tibshirani, 1986, Hastie and Tibshirani, 1990), which is similar to the logistic regression, but allows for non-linear effects on the linear predictor scale, and 4) random forest classifier (Breiman, 2001). All models were fit using R.

For the standard and penalized logistic regression model, we used all predictors. The penalized model was fit using the LASSO (Least Absolute Shrinkage and Selection Operator) penalty (Tibshirani, 1996) using the glmnet package (Friedman et al., 2010). The tuning parameter, λ, was chosen using 10-fold cross-validation on the training voxels; the cost function used was the misclassification rate. The parameter was chosen using the largest value of λ where that the misclassification rate is within 1 standard error of its minimum; this approach led to superior out-of-sample stability.

The generalized additive model (GAM) (Hastie and Tibshirani, 1986, Hastie and Tibshirani, 1990) was also fit using indicator variables for binary variables and thin-plate splines for all continuous measures. The model was fit using fast-estimation of the restricted maximum likelihood (fREML) implemented in the mgcv package (Wood, 2011, Wood et al., 2015). Detailed model specifications are provided in Section 5.2.

The random forest (Breiman, 2001) classification algorithm was implemented using the randomForest package in R (Liaw and Wiener, 2002) with the default pruning parameters and number of trees (ntree=500, mtry=4).

2.9. Estimating a cutoff for model probability

Each model described in Section 2.8 provides an estimate of the probability for each voxel to be in ICH.

To choose probability thresholds to create a binary segmentation, we chose the Dice Similarity Index (DSI) (Dice, 1945) as a measure of the quality of segmentation. The DSI is a measure of overlap that is insensitive to areas where neither the true nor the predicted segmentation were labeled ICH, and will be used as a performance measure when comparing models on the test data. DSI for scan i is calculated by

$$DS{I}_i=\frac{2\times TP}{2\times TP+FN+FP}$$

where TP denotes the number of “true positive” voxels, where the manual and predicted segmentation agree that the voxel is in ICH, FP denotes the number of “false positive” voxels, where the predicted segmentation indicates that there is no lesion when the manual segmentation indicates lesion, and FN denotes the number of “false negative” voxels, where the predicted segmentation indicates that there is lesion when the manual segmentation indicates that there is not. DSI ranges from 0 to 1, where 0 indicates no overlap and 1 denotes perfect overlap.

For each model, the probability image was smoothed by taking the average over the neighborhood voxels (1 voxel in every direction). For each threshold, we used the voxels in the training data that were not used for estimating the model, and found the threshold that maximized the DSI compared to the manual segmentation at those voxels. This threshold was applied to the smoothed probability maps to produce binary ICH images.

After thresholding the smoothed image using these DSI-optimized thresholds, we discarded regions with fewer than 100 (0.1 mL) connected voxels. This removal was done to eliminate speckling, which helped improve the false positive rate of images. For each model, the predicted ICH binary mask was transformed back to the original (i.e. native) space using the inverse of the rigid-body transformation. As the linear interpolation associated with this step results in a non-binary mask, we thresholded the image at 0.5 to preserve volume (Frequently asked questions for FLIRT, 2017), but could have similarly used a nearest-neighbor interpolation.

2.10. Testing ICH prediction and measuring model performance

For each of the remaining 102 scans in the test data, the voxel selection described in Section 2.7 was applied. Using the prediction process described in Section 2.8 an ICH probability map was estimated using each of the four models. Using the probability thresholds calculated on the training data, as described in Section 2.9, we obtained a binary ICH map for each of the four methods. For evaluation, all results are provided in the native space of the patient, not in the template space, as the manual segmentation was done in the native space.

Model performance was evaluated on the validation data using the DSI and the ICH volume. The ICH volume was estimated counting the number of ICH voxels multiplied by product of the voxel sizes, divided by 1000 (1000 mm³ per 1 mL), provided in mL. The large number of true negatives (non-ICH voxels) artificially inflates specificity and overall accuracy measures, which are not reported. The global equality median DSI across models was tested using the Kruskal-Wallis test. If a difference was present, we tested the null hypothesis of no difference in the medians for each combination of models (6 combinations) using a Wilcoxon signed-rank test, and corrected the p-value using a Bonferroni correction.

The performance of total ICH volume prediction was compared to the manual segmentation using the Pearson correlation and root mean squared errors (RMSE) between volumes measures. Similarly, we performed the Kruskal-Wallis test for the null hypothesis of equality of medians of the absolute value of the difference between the estimated volume from each model and the true volume. If the null hypothesis is rejected, pairwise tests were conducted as in the case of DSI. For DSI and correlation, higher values indicate better agreement with the manual segmentation. For RMSE, lower values indicate better agreement.

After choosing a single model, we explore the DSI over certain factors. First we will investigate the DSI by different scanner manufacturers and test median equality using the Kruskal-Wallis test, performing a similar pairwise Wilcoxon signed-rank test procedure with multiplicity correction. We similarly explore differences of DSI based on 3 categories of hemorrhage size (based on manual segmentation): using 0–30 mL, >30 to 60 mL, and >60 mL cutoffs, similar to Hemphill et al. (2001).

3. Results

3.1. Dice Similarity Index

In Fig. 3, we show the DSI distributions based on the test data for each model. DSI is high on average for all models, with a few scans having a very small DSI (i.e. failures). The median DSI for each model was: 0.89 (logistic), 0.885 (LASSO), 0.88 (GAM), and 0.899 (random forest). Using the random forest results in a slightly higher median DSI compared to the other models, and there was a statistically significant difference across medians (χ²(3) = 13.49, p < 0.05). Indeed, after Bonferroni correction, the hypothesis of equality of median DSI was rejected only when comparing the random forest DSI to the DSI from the logistic (p < 0.001), LASSO (p < 0.001), or GAM (p < 0.001) models. Based on visual inspection, the difference between the random forest and the logistic regression is quite small.

Fig. 3.

Distribution of Dice Similarity Index in test scans. Here we display the boxplot of the Dice Similarity Index (DSI), a measure of spatial overlap between the estimated hemorrhage mask and the manually delineated hemorrhage mask, in the 102 test scans. We present the DSI distribution for each model fit: a logistic regression, a logistic model penalized with the Least Absolute Shrinkage and Selection Operator penalty (LASSO), a generalized additive model (GAM), and a random forest algorithm. Overall, we see high agreement between the manual and estimated hemorrhage masks with the median of 0.89 for the logistic model, 0.885 for the LASSO, 0.88 for the GAM, and 0.899 for the random forest. The median DSI for the random forest was significantly higher than those of the other 3 models, after adjusting for multiplicity using a Bonferroni correction (all p < 0.05).

To better understand the DSI measurements in our data, Fig. 4 displays the CT scan of the patient in the test data that has the median DSI in the test scans. The image depicts the brain-extracted CT scan and the CT scan indicating different types of classification properties using overlaid colors. Green indicates a correct classification of ICH from the model (true positive), blue indicates a false negative, and red indicates a false positive. The image has a finer resolution along the axial plane (0.5 mm by 0.5 mm) than in the sagittal and coronal planes (5 mm), as is commonly used for radiological evaluation of hemorrhages. Patients with the lowest, 25th, 75th, and highest DSI are shown in Supplemental Figs. S1, S2, S3, and S4, respectively.

Fig. 4.

Patient with median Dice Similarity Index. We present the patient with the median Dice Similarity Index (DSI), a measure of spatial overlap, from the chosen predictor model fit with a random forest. The median DSI was 0.899, which indicates high spatial overlap. The green indicates a correct classification of ICH from the model, blue indicates a false negative, where the manual segmentation denoted the area to be ICH but the predicted one did not, and red indicates a false positive, where the predicted segmentation denoted the area to be ICH but the manual one did not.

3.2. ICH volume estimation

In Fig. 5, we show the estimated ICH volume versus that from the manual segmentation. The pink line represents the X = Y line, where the estimated and true volume are identical. The blue line represents the linear fit; the estimated linear regression equation and correlation are printed on the plot. The farther away the slope of the equation is from 1 the larger the bias with values larger than 1 representing over-estimated volumes. The correlation (95% confidence interval (CI)) between the true volume and the predicted volume were 0.92 (95% CI: 0.88,0.95) for the logistic model, 0.92 (0.88,0.94) for the LASSO, 0.91 (95% CI: 0.87,0.94) for the GAM, and 0.93 (95% CI: 0.9,0.95) for the random forest. The RMSE for logistic (RMSE: 10.7 mL), LASSO (10.8 mL), and random forest (10.3 mL) models were relatively close, but was slightly higher for the GAM model (11.4 mL). The Kruskal-Wallis test indicated no significant difference in the median absolute value of the difference in estimated versus true volume over models (χ²(3) = 2.3, p = 0.51).

Fig. 5.

Comparison of estimated and manual intracerebral hemorrhage volume for each model. In each panel, we show the volume of intracerebral hemorrhage (ICH) estimated from each model (x-axis) versus that from the gold-standard manual segmentation (y-axis) in the 102 test scans. The pink line represents the X = Y line, which represents perfect agreement. The blue line represents a linear fit of the data, and the estimated slope equation is displayed along with the Pearson correlation. Panel A represents the volume from the logistic regression model, B represents that from logistic model penalized with the LASSO, C represents that from a generalized additive model (GAM), and D represents that from a random forest algorithm. Overall, we see high agreement between the estimated volumes from automated segmentation from each model as all correlations are above 0.9. The farther away the slope of the equation is from 1 represents a multiplicative bias, where values greater than 1 represents larger estimated volumes. The farther the intercept is from 0 represents and additive bias in the estimated volume, where values greater than 0 again represent larger estimated volumes.

3.3. Model choice

In Supplemental Table 1, we report the estimated coefficients, standard errors, and z-statistics from the logistic regression model. In Fig. S5, we present the variable importance plot, representing the mean decrease in the Gini coefficient for each variable. The standardized-to-template and neighborhood mean seem to be the strongest predictors in the random forest. To reduce complexity and decrease computation time, some predictors may be removed, but as the random forest algorithm is robust as it does not choose covariates that do not decrease prediction error in each decision tree.

Overall, all models perform well for ICH segmentation. A small percentage (1.0%) of failures were observed with DSI  <0.5 (N = 1 out of 102 scans), but the random forest algorithm had a slightly higher median DSI, slightly lower RMSE, and a higher slightly correlation than the other models. Therefore, when implementing the algorithm, we will use the random forest model.

3.4. DSI by scanner manufacturer, average HU, and hemorrhage size

In the following section, we will use the DSI from the random forest model. In the 102 test scans, the median DSI was 0.89 for patients scanned in a GE scanner, 0.9 for Philips, 0.9 for Toshiba, and 0.92 for Siemens (Supplemental Fig. S6). The patient with a failed segmentation was scanned using a GE scanner. The Kruskal-Wallis test indicated a difference in median DSI in patients from different scanners (χ²(3) = 11.6, p = 0.009). After Bonferroni correction, the difference of DSI of patients scanned with Siemens versus GE scanners was the only statistically significant comparison by the Wilcoxon signed-rank tests (W = 428, p = 0.008, corrected).

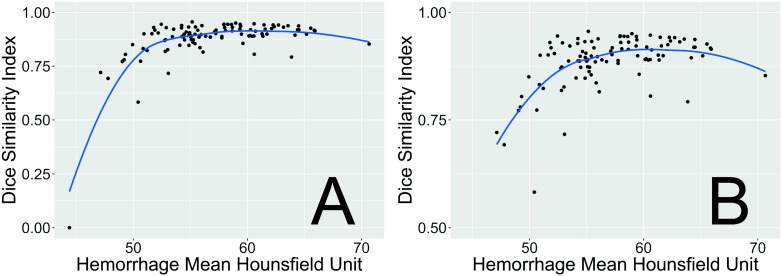
In Fig. 6, we see the effect of average HU over the hemorrhage versus DSI. We note the failed scan had a much lower average HU (44.4 HU) in the hemorrhage compared to the rest of the images (panel A). Overall, however, above 50 HU, there does not seem to be a strong effect on the average HU and DSI (panel B). We also note that the failed case was towards the cortical surface (Supplemental Fig. S1).

Fig. 6.

Dice Similarity Index (DSI) by average voxel HU in the hemorrhage. These values represent the mean Hounsfield Unit (HU) over all voxels in the manual hemorrhage mask for each patient in the test data set versus the DSI for that patient compared to automatic segmentation. The blue line represents a locally-weighted regression smoother (loess). We see that the case with the lowest DSI had a much lower average HU in the hemorrhage. Overall, however, above 50 HU, there does not seem to be a strong effect on the average HU and DSI.

After categorization of the hemorrhage volume, 34 (33.3%) patients had a volume of 0–30 mL (small), 46 (45.1%) had volumes  >30 to 60 mL (medium), and 22 (21.6%) had ¿60 mL (large). The median DSI for the small hemorrhages was 0.89, 0.91 for medium hemorrhages, and 0.9 for large hemorrhages.

The Kruskal-Wallis test indicated a difference in median DSI among the 3 groups (χ²(2) = 6.5, p = 0.04, see Supplemental Fig. S7). After Bonferroni correction, there was no statistically significant difference in median DSI, but the strongest comparison was for the small versus medium hemorrhage sizes (W = 537, p = 0.0502, corrected).

4. Discussion

We have presented a novel, fully automated method for segmentation of ICH from CT scans. Our method uses only CT scans from patients with acute ICH, from the MISTIE II trial. MRI was not used because MRI procedures for ICH have not been standardized and are not performed per the standard of care for the disease. We validated this method against manual segmentation. We used the Dice Similarity Index and correlation between the volume of ICH from manual and automatic segmentation as measures of algorithm performance.

We started by creating a rich set of predictors that are likely to capture the most discriminating features between ICH and non-ICH voxels and described the rationale for each predictor. Models of these predictors using logistic regression, logistic regression penalized with the LASSO, GAM, and random forests result in high values for the DSI and high correlations between the total ICH volume obtained from manual and automatic segmentations. Random forest was chosen as the algorithm, as it slightly outperformed the other approaches on the test data.

The approach failed on a very small subset of the validation set (N = 1 out of 102 with DSI below 0.5); the failed case had a much lower mean intensity inside the hemorrhage. In the successful cases, most discrepancies between the manual and automated segmentation observed occur at the edges of the hemorrhage. This “edge effect” may be due to the isotropic, non edge-preserving smoothing. Anisotropic smoothing, as proposed by Perona et al. (1994), may improve segmentation.

Although we have shown good performance in patients with ICH, intraventricular hemorrhage (IVH) and subarachnoid hemorrhages (SAH) are two other forms of hemorrhagic stroke that may occur clinically. As obstructive IVH requiring external ventricular drainage was in the exclusion criteria in MISTIE II (Mould et al., 2013), no cases with primary IVH were included. The 3 cases with the largest overall volume had some considerable IVH extensions, the largest being around 20 mL. This leads to an overall underestimation of the hemorrhage volume in our models. We believe the model may perform reasonably well with patients with IVH, yet may require a separate model, but not necessarily for SAH.

Intraventricular hemorrhages have similar HU ranges for large portions of the hemorrhage, but may have lower HU values of the hemorrhage which are less dense and surrounded by cerebrospinal fluid. Moreover, cases with larger IVH volumes may cause larger deformations than seen in cases with ICH only, which may negatively affect any registration process. In contrast, for SAH, the process of mask erosion may considerably remove voxels from the hemorrhage, which occurs largely on the cortical surface. This step is important to remove false positives, which may occur from partial volume effects with areas of the skull and voxels towards the cortical surface. If the methods for registration and erosion perform similarly to the cases with ICH, we can perform the same procedure and re-fit the model using additional cases of IVH and/or SAH.

Several other methods have been proposed for segmentation of ICH from CT scans (Gillebert et al., 2014, Loncaric et al., 1996, Loncaric et al., 1999, Pérez et al., 2007, Prakash et al., 2012). Loncaric et al. (1996) performed the analysis on only one 2-dimensional scan and could not be compared with our approach. The method proposed by Pérez et al. (2007) is semiautomated and was only validated by visual inspection. They reported segmentation failure in 6 out of 36 scans (16.7%) compared to 1 out of 102 scans (1.0%) for our method. Our reported median DSI (0.899) is much larger than the one reported by Gillebert et al. (2014) (approximately 0.62 and 0.78 for hemorrhagic strokes as read from their graphs). Our results were comparable to those reported by Prakash et al. (2012) (0.897, 0.858, and 0.9173 for different groups with hemorrhage). Loncaric et al. (1999) did not compare automatic and manual segmentation masks; instead they compared ICH volumes from 5 subjects measured at 3 time points. Their reported Pearson correlation was 0.917 for the 15 scans, similar to our results using the random forest (R = 0.93).

Only Gillebert et al. (2014) responded to our requests for segmentation software to perform the segmentation and we could not find any software online. Although the method of Gillebert et al. (2014) is comparable to ours, their approach has not been packaged for general use. We have released an open source package that can perform ICH segmentation (https://github.com/muschellij2/ichseg). Our software includes the models for prediction, the CT template from Rorden et al. (2012), template-level standardized mean and standard deviation images, as well as functions to register the images, create the predictors, predict from the models, and return a binary hemorrhage mask. Although an R package is ideal for prediction on a large number of images and for researchers who prefer scripting, releasing easy to use graphic user interfaces may increase the appeal of the methods proposed. Therefore, we have also released a Shiny (Chang et al., 2015) R application online (http://johnmuschelli.com/ich_segment_all.html) that takes an input CT scan and outputs ICH segmentation mask and provides a representation of each processing step.

A potential issue for CT images that contain ICH is image registration. Indeed, methods developed for registration of healthy brains can fail in brains exhibiting pathology. The only predictor that used non-linear registration was the standardized-to-template intensity. The potential problems associated with this transformation are mitigated by the transformation back to the native space. Thus, we use non-linear registration, but do not rely on a highly accurate image registration to template to compare voxels across patients; instead we use registration to obtain potentially noisy predictors in the native space.

Another potential concern could be that training data consisted of only 10 patient scans and using only 100,000 randomly sub-sampled voxels that passed the voxel selection procedure from these scans. Remarkably, the models have shown to have high out-of-sample accuracy. The training and test sets were kept unchanged to avoid overfitting the models to the test set. Validation of the method on additional data would be useful, while rater studies may provide more insight into the clinical differences between various segmentation approaches. However, we would like to note that our data was highly heterogeneous and contains test scans from multiple sites and scanners. Moreover, the location and size of hemorrhages is also highly heterogeneous. Thus, we expect our method to have a good out-of-sample accuracy in a heterogeneous population of CT images with ICH.

The proposed approach provides estimated binary hemorrhage masks, which can be used to automatically estimate quantitative measures of hemorrhage location (Muschelli et al., 2015). Our results would also allow automated shape analysis, which require a binary mask. The subject-specific hemorrhage masks can be used for other voxel-based analyses that could yield novel insights into the relationship between hemorrhage characteristics and patient outcomes.

4.1. Conclusions

We have implemented and validated a fully automated segmentation algorithm of ICH in CT scans and published the associated software both as an R package and as a GUI. The method relies on a series of processing steps and on creating a set of relevant predictors. This method has been shown to have very good agreement with the gold standard of manual delineation of hemorrhages. As an automated process, it is much faster, does not require extensive radiologic image experience, is scalable to thousands of images, and does not have inter-reader variability. As our methods and software produce binary hemorrhage masks that can be localized both in the native and template space (Muschelli et al., 2015), quantitative voxel- and region-level analyses could be conducted to assess the association between ICH characteristics and health outcomes. Methods also provide an estimator of the ICH volume, which can be used in standard statistical analyses, as it has been shown to be associated with long-term functional outcomes (Broderick et al., 1993, Jordan et al., 2009, Tuhrim et al., 1999).

Sources of funding

The project described was supported by the NIH grant R01EB012547 from the National Institute of Biomedical Imaging and Bioengineering, T32AG000247 from the National Institute on Aging, R01NS046309, R01NS060910, R01NS085211, R01NS046309, U01NS080824 and U01NS062851 from the National Institute of Neurological Disorders and Stroke, and R01MH095836 from the National Institute of Mental Health. Minimally Invasive Surgery and rt-PA in ICH Evacuation Phase II (MISTIE II) was supported by grants R01NS046309 and U01NS062851 awarded to Dr. Daniel Hanley from the National Institutes of Health (NIH)/National Institute of Neurological Disorders and Stroke (NINDS). Minimally Invasive Surgery and rt-PA in ICH Evacuation Phase III (MISTIE III) is supported by the grant U01 NS080824 awarded to Dr. Daniel Hanley from the National Institutes of Health (NIH)/National Institute of Neurological Disorders and Stroke (NINDS). Clot Lysis: Evaluating Accelerated Resolution of Intraventricular Hemorrhage Phase III (CLEAR III) is supported by the grant U01 NS062851 awarded to Dr. Daniel Hanley from the National Institutes of Health (NIH)/National Institute of Neurological Disorders and Stroke (NINDS).

Appendix A. Supplementary data

Supplementary methods, results, and model information.