Economic consequences of paratuberculosis control in dairy cattle: a stochastic modeling study

Abstract

The cost of paratuberculosis to dairy herds, through decreased milk production, early culling, and poor reproductive performance, has been well-studied. The benefit of control programs, however, has been debated. A recent stochastic compartmental model for paratuberculosis transmission in US dairy herds was modified to predict herd net present value (NPV) over 25 years in herds of 100 and 1000 dairy cattle with endemic paratuberculosis at initial prevalence of 10% and 20%. Control programs were designed by combining 5 tests (none, fecal culture, ELISA, PCR, or calf testing), 3 test-related culling strategies (all test-positive, high-positive, or repeated positive), 2 test frequencies (annual and biannual), 3 hygiene levels (standard, moderate, or improved), and 2 cessation decisions (testing ceased after 5 negative whole-herd tests or testing continued). Stochastic dominance was determined for each herd scenario; no control program was fully dominant for maximizing herd NPV in any scenario. Use of the ELISA test was generally preferred in all scenarios, but no paratuberculosis control was highly preferred for the small herd with 10% initial prevalence and was frequently preferred in other herd scenarios. Based on their effect on paratuberculosis alone, hygiene improvements were not found to be as cost-effective as test-and-cull strategies in most circumstances. Global sensitivity analysis found that economic parameters, such as the price of milk, had more influence on NPV than control program-related parameters. We conclude that paratuberculosis control can be cost effective, and multiple control programs can be applied for equivalent economic results.

Introduction

Paratuberculosis, or Johne’s Disease, is a disease of ruminants caused by intestinal infection with Mycobacterium avium subsp. paratuberculosis (MAP). Animals are chronically infected, usually at a young age, and are generally believed to undergo an extended latent period (Marcé et al., 2010). Infection is known to result in lower milk production (Aly et al., 2010; Gonda et al., 2007; Kudahl et al., 2004; Lombard et al., 2005; Nielsen et al., 2009; Raizman et al., 2007; Sorge et al., 2011), decreased reproductive performance (Kennedy et al., 2016; Marcé et al., 2009; Raizman et al., 2007; Smith et al., 2010; Vanleeuwen et al., 2010), and early culling (Lombard et al., 2005; Tiwari et al., 2005). Control of MAP in dairy herds has been difficult, partly due to the poor diagnostic sensitivity of many tests, the resistance of MAP in the environment, difficulties associated with use of available vaccines, and the long course of the disease (Garcia and Shalloo, 2015). Some analyses of the economic impacts of MAP control have found them to be cost-effective (Pillars et al., 2009; Radia et al., 2013), while others have found that MAP control is cost-effective only if testing is subsidized (Groenendaal and Wolf, 2008) or if MAP decreases milk production during latency (Wolf et al., 2014).

Simulation models attempting to identify the most cost-effective controls have produced equivocal results, indicating cost-effectiveness for quarterly serum enzyme-linked immunosorbent assay (ELISA) testing (Robins et al., 2015), quarterly milk ELISA testing (Kudahl et al., 2007), risk-based testing accompanied by infection control (Kudahl et al., 2008), vaccination or infection control (Groenendaal and Galligan, 2003), testing in series with ELISA and qPCR (Aly et al., 2012), and annual fecal culture accompanied by infection control (Cho et al., 2013). The lack of consensus is in part due to different model assumptions.

In particular, previous model-based economic analyses of MAP control programs were based on the assumption that all animals progressed to clinical disease over time (Aly et al., 2012; Cho et al., 2013; Groenendaal and Galligan, 2003; Kudahl et al., 2008, 2007; Robins et al., 2015). The findings of these analyses, therefore, were biased by the assumption that test-positive animals would eventually suffer from clinical disease, greatly decreased milk production, and decreased slaughter value. In addition, previous economic analyses (with one exception, (Robins et al., 2015)) have not considered adult infection, which molecular analysis has revealed to be a possibility (Pradhan et al., 2011) and which has been found to change simulation model outcomes (Smith et al., 2015). As hygiene programs are aimed at decreasing infectious pressure for calves, they are likely to be less effective than previously believed in the presence of adult infections.

Recent research indicates that while some animals (progressors) will progress to clinical disease, signified by wasting and diarrhea with large amounts of MAP shed in the feces, most animals (non-progressors) will remain in a latent or subclinical phase, intermittently shedding small amounts of MAP in their feces (Mitchell et al., 2015a, 2015b). The impact of paratuberculosis on milk production in dairy cattle differs significantly between these two groups of animals, with progressors demonstrating a continuous decrease in milk production (Smith et al., 2016). Non-progressors, by contrast, will experience a brief and limited decrease in milk production (Smith et al., 2016), from which their production levels will recover over time. This implies that the economic efficacy of test-and-cull programs will depend on their ability to distinguish between progressors and non-progressors. It has been found that repeated positive ELISA tests can identify progressive milk production decreases, which raises another option for MAP control, culling of cows after repeated ELISA positive results; this option was explored previously without the progression/non-progression dichotomy and found to be cost-effective if combined with improved hygiene (Kudahl et al., 2008). However, the cost-efficacy of this program and others has not previously been determined without the assumption that all animals will eventually progress to high-shedding, and this assumption could change the benefit estimated for control programs.

The goal of this research is to examine the economic consequences of paratuberculosis in US dairy herds by considering the new understanding of MAP infection dynamics, using a model that includes adult infection and non-progressing infections. The model considers age stratified MAP infection dynamics along with the economic efficacy of a variety of control programs. This will allow the estimation of the value of culling test-positive animals that may not progress to clinical disease by comparing control programs with varying ability to detect disease progression.

2. Methods

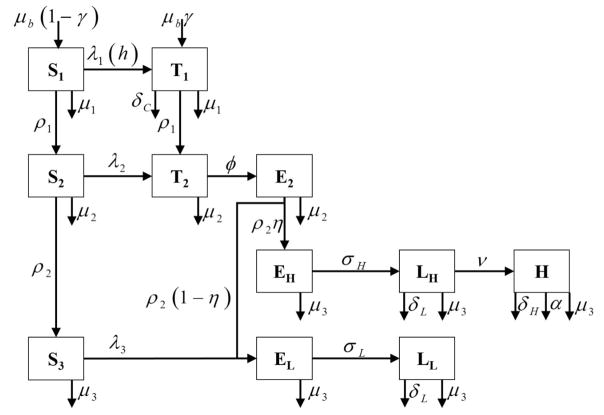
The infection and testing model (Figure 1) have been previously described (Smith et al., 2015). This is a continuous-time model, and was simulated over 25 years using values representative of US dairy herds. Results were calculated after 5 and 25 years.

Figure 1.

Schematic of model for Mycobacterium avium subsp. paratuberculosis in cattle herds. Animals exist in one of 11 states: susceptible calves (S₁), transiently shedding calves (T₁), susceptible heifers (S₂), transiently shedding heifers (T₂), latent heifers (E₂), susceptible adults (S₃), latent progressing adults (E_H), low-shedding progressing adults (L_H), high-shedding adults (H), latent non-progressing adults (E_L), and low-shedding non-progressing adults (L_L). All parameters are defined in Table 1.

2.1 Births and Vertical Infection

Briefly, cows are grouped by age (calf, heifer, and adult) and by infection status. Female calves are born at rate

$${\mu }_b=\frac{{\mu }_{b,\mathit{base}}\ast \left(S_3+E_H+E_L+L_H+L_L\right)+{\mu }_{b,H}H}{S_3+E_H+E_L+L_H+L_L+H}$$ (1)

where μ_b,base is the base birth rate in the herd and μ_b,H is the birth rate observed in high-shedding animals; male calves are not modeled. Animal categories consist of susceptible adults (S₃), latent adults (E_j), low-shedding adults (L_j), and high-shedding adults (H). Categories are further separated by path j, with a subscript H indicating a progressing (high-path) animal and a subscript L indicating a non-progressing (low-path) animal. Calves may be born susceptible S₁, but a proportion γ were born transiently shedding T₁. The proportion of calves born infected (probability of vertical transmission) was calculated as

$$\gamma ={\gamma }_E\left(E_L+E_H\right)+{\gamma }_L\left(L_L+L_H\right)+{\gamma }_{H}H$$ (2)

where γ_i is the probability that a cow in infection category i gives birth to a vertically infected calf. We assume that γ_L and γ_H are equal, as there is insufficient evidence to parameterize different values at this time.

2.2 Horizontal Infection

Susceptible calves (S₁) may be infected at rate λ₁ by direct contact with infected calves (T₁) or by indirect contact with shedding heifers or adults,

$${\lambda }_1\left(h\right)=\left(1-e_{\beta }\left(h\right)\right)\beta \left(T_1+T_2+L_L+L_H+H\right)$$ (3)

where β is the transmission coefficient of all contacts (direct and indirect) and e_β(h) is the proportional decrease in transmission due to improved hygiene. It is assumed that improved hygiene is focused on transmission to calves, as that is recommended by most control programs, and so does not impact transmission to heifers or adults. Susceptible heifers (S₂) may be infected at rate λ₂ by direct or indirect contact with transiently shedding heifers (T₂),

$${\lambda }_2={\beta }_a{T}_2$$ (4)

where β_a is the transmission coefficient for adults and heifers. Transiently shedding heifers became latent heifers (E₂) at rate φ. Susceptible adults (S₃) may be infected at rate λ₃ by direct or indirect contact with shedding adults,

$${\lambda }_3={\beta }_a\left(L_L+L_H+H\right).$$ (5)

We assumed no effective contact between heifers and cows and that heifers and cows have no exposure to calf feces sufficient for transmission.

Transmission parameters were calculated empirically, assuming that calves were twice as susceptible as adults (β_a = β/2). Briefly, 100 iterations of a disease-free herd were modeled for 200 years following introduction of a single latently infected adult. All iterations in which MAP persisted in the herd after 200 years were used to calculate an average endemic shedding prevalence, (L_L+ L_H + H)/(S₃ + E_L + E_H + L_L + L_H + H). The transmission parameters were adjusted to produce the desired average shedding prevalence (10% for well-managed herds and 20% for poorly-managed herds). The endemic herd populations produced by this process were used as initial populations for all further simulations.

2.3 Aging and Progression

Calves aged into heifers at rate ρ₁. Susceptible and latent heifers aged into adults at rate ρ₂. Transiently shedding heifers (T₂) transition to latency at rate φ. A proportion η of latent heifers entered the progressing path as latent (E_H), while the remainder entered the non-progressing path as latent (E_L). Animals infected as adults entered the non-progressing path as latent (E_L). Progressing adults became low-shedding (L_H) at rate σ_H and progress to high-shedding (H) at rate ν. Non-progressing adults became low-shedding (L_L) at rate σ_L. All age groups a had an age-specific death/culling rate, μ_a. High-shedding adults were subject to an additional death/culling rate due to clinical disease, α. The model was implemented stochastically using Gillespie’s direct algorithm (Gillespie, 2007), in which all potential events were used to determine the time of the next event and which event would occur. All possible events, with their corresponding changes and transition rates, are shown in Supplemental Table 1. Each scenario was simulated with 1,000 iterations.

2.4 Heifer Purchase and Sale

If the number of adults in the herd dropped below 90% of the optimal size (as determined by a disease-free model) at any time step, it was assumed that a heifer was purchased and immediately moved to the milking herd. The probability of a purchased heifer being infected was assumed prev, or the estimated true prevalence among US dairy cattle. Infected purchases were assumed to be latently infected and on the non-progressing path. When a heifer matured into a herd that is above 110% of the optimal adult herd size, the heifer was assumed to be sold during that time step, and was not added to the adult herd.

2.5 Testing

Testing and culling for MAP infection (represented by δ_C, δ_L, and δ_H in Figure 1) was assumed to take place at set intervals, either annually or biannually. When the testing interval has passed, it was assumed that a whole-herd test (WHT) was performed, in which all animals were tested. The number of test-positive animals in each category was determined by means of a binomial distribution, in which the probability of a positive result was the sensitivity Se_i for the shedding categories and the complement of the specificity, 1-Sp, for uninfected and latent animals. It was assumed, based on observation (Schukken et al., 2015), that non-progressing low-shedders would not test positive more than once. We assumed that test-positive animals were culled after no delay when tests were based on ELISA or polymerase chain reaction (PCR), while we assumed a delay of 3 months when tests were based on fecal culture (FC). Three possible actions were considered for culling of test-positive animals: culling all test-positive animals, culling only high-positive animals, or culling animals only after their second positive test. For ELISA and PCR, the sensitivity and specificity of the tests for identifying high-shedding animals were based on the kinetic ELISA (KELA) and quantitative PCR (qPCR) tests, respectively. For FC, it was assumed that the specificity for identifying high-shedding animals was 1. Culling after repeated test results required a modification in model compartments, not included in Figure 1 or equations for simplicity.

2.6 Economic calculations

Operating expenses and income were calculated after each action in the Gillespie model. Total cash flow at time t, κ(t), was calculated as the sum of income from milk produced (ι_milk(t)) and income from sales of culled adults (ι_cull(t)) and extra heifers (ι_sale(t)), minus the operating cost of raising the calves and heifers (ω_heifer(t)), the operating cost of milk production (ω_milk(t)), and the cost of purchasing replacement heifers (ω_purchase(t)). Thus,

$$\kappa \left(t\right)={\iota }_{\mathit{milk}}\left(t\right)+{\iota }_{\mathit{cull}}\left(t\right)+{\iota }_{\mathit{sale}}\left(t\right)-{\omega }_{\mathit{heifer}}\left(t\right)-{\omega }_{\mathit{milk}}\left(t\right)-{\omega }_{\mathit{purchase}}\left(t\right)-{\omega }_{\mathit{hygiene}}\left(t\right)-{\omega }_{\mathit{test}}\left(t\right)$$ (6)

where ω_heifer(t) is calculated in equation 9, ω_milk(t) is based on total milk production calculated in equation 10, ω_hygiene(t) is the cost of additional hygiene (Table 2), and ω_test(t) is the cost of testing. The cost of purchasing replacement heifers, ω_purchase(t), is the product of the number of heifers purchased and the sale price of a heifer, P_sale. The cost of testing, ω_testing(t), is calculated as the number of adult animals in the herd multiplied by the cost of the test per animal (Table 2).

Table 2.

Economic parameters and inter-quartile ranges (IQR) used in a model of Mycobacterium avium subsp. paratuberculosis control in dairy herds.

Cost	Description	Value (IQR)	Reference
prev	prevalence of MAP infection in purchased cows	0.094 (0.077–0.111)	(Adaska and Anderson, 2003)
CFC	cost of fecal culture test per animal	$36 ($25–$42)	(Besser, 2015; Collins and Manning, 2015; Cornell University Animal Health Diagnostic Center, 2015; “Tests and Fees,” 2015)
CE	cost of ELISA test per animal	$6 ($4–$8)	(Besser, 2015; Collins and Manning, 2015; Cornell University Animal Health Diagnostic Center, 2015; Indiana Animal Disease Diagnostic Laboratory, 2015; “Tests and Fees,” 2015)
CP	cost of PCR test per animal	$32 ($32–40)	(Besser, 2015; Collins and Manning, 2015; Cornell University Animal Health Diagnostic Center, 2015; Indiana Animal Disease Diagnostic Laboratory, 201 5; “Tests and Fees,” 2015)
ωhyg,mod	Annual cost of implementing moderate hygiene per adult (clean milk)	$35.54	(Wolf et al., 2014)
ωhyg,large	Annual cost of implementing improved hygiene per adult (clean milk, separate calving pens, separate housing)	$49.64	(Wolf et al., 2014)
Ccow	Daily operating cost per kg milk produced	$0.35 (0.33–0.37)	(USDA:ERS, 2010)
Cheifer	Daily operating cost of raising a calf/heifer	$2.995 (2.662–3.403)	(Karszes, 2014)
Pcow	Cull-cow price per kg	$1.9671 (1.7292–2.31)	(USDA:NASS, 2015)
Pmilk	Milk price per kg	$0.444 (0.394–0.482)	(USDA:NASS, 2015)
Psale	Sale price of replacement heifer	$2232 (2000–2500)	(Karszes, 2014)
Qcull	Average cull cow weight	680.4 kg (660–700)	(USDA, 2008)
Qmilk,X	Average daily milk production per uninfected cow	32.62 kg (25.45–42.73)	(Smith et al., 2016)
Qmilk,EL	Average daily milk production per latent cow (low path)	32.17 kg (24.09–42.73)	(Smith et al., 2016)
Qmilk,LL	Average daily milk production per low-shedding cow (low path)	30.94 kg (24.09–42.73)	(Smith et al., 2016)
Qmilk,EH	Average daily milk production per latent cow (high path)	33.12 kg (22.27–39.09)	(Smith et al., 2016)
Qmilk,LH	Average daily milk production per low-shedding cow (high path)	29.13 kg (22.27–39.09)	(Smith et al., 2016)
Qmilk,H	Average daily milk production per high-shedding cow	22.17 kg (12.27–32.27)	(Smith et al., 2016)
ψH	Proportional adjustment in cull weight for high-shedding cows	0.9 (0.75–1)	assumed
RPO	retention pay-off of a clinical animal	$1,351 ($0–$4,099)	(Groenendaal and Wolf, 2008b)
r	Discount rate	0.02 (0.01–0.08)	assumed

The income from sales of culled adults was calculated as

$${\iota }_{\mathit{cull}}\left(t\right)=n_{\mathit{cull};S,E,L}\left(t\right)\ast Q_{\mathit{cull}}\ast P_{\mathit{cull}}+n_{\mathit{cull};H}\left(t\right)\ast \left({\psi }_H\ast Q_{\mathit{cull}}\ast P_{\mathit{cull}}-\mathit{RPO}\right)$$ (7)

where, n_cull;i(t) is the number of culled adults in infection category i, Q_cull is the average cull cow weight, and P_cull is the cull cow price, ψ_H is the proportional adjustment in cull weight in high-shedding animals, and RPO is the retention pay-off, the value of the lost production from early culling of an animal due to disease. The number of culled susceptible and latent adults, n_cull;S,E(t), is calculated as the number of susceptible and latent adults multiplied by the complement of the specificity of the test, [S(t)+E(t)]*(1-Sp). The number of culled shedding animals, n_cull;L and n_cull;H, is calculated as the number of animals in that shedding category times the sensitivity of the test for that category, L(t)*Se_L and H(t)*Se_H. It is assumed that high-shedding animals will be slaughtered before becoming unsaleable, rather than removed from the herd with no economic value, and that they will not have a reduction in beef quality affecting their price beyond the reduced slaughter weight.

The income from sales of extra heifers was calculated as

$${\iota }_{\mathit{sale}}\left(t\right)=\left(n_{\mathit{adult}}\left(t\right)-n_{\mathit{adult}}^{\ast }\left(t\right)\right)\ast P_{\mathit{sale}}$$ (8)

where n_adult(t) is the number of adult animals, $n_{\mathit{adult}}^{\ast }\left(t\right)$ is the desired number of adult animals (maximum herd size), and P_sale is the sale price of a heifer. The operating cost of raising calves and heifers was calculated as

$${\omega }_{\mathit{heifer}}\left(t\right)=C_{\mathit{heifer}}\ast (S_1\left(t\right)+T_1\left(t\right)+S_2\left(t\right)+T_2\left(t\right)+E_2\left(t\right))$$ (9)

where, C_heifer is the daily operating cost to raise a calf or heifer and other values are the number of animals in each category as shown in Figure 1.

Income from milk produced was the product of the milk production in the previous time step, m(t), and the milk price, P_milk; likewise, operating cost of milk production was the product of the milk production, m(t), and the operating cost per unit of milk production, C_cow. Milk production was calculated as

$$m\left(t\right)=Q_{\mathit{milk},X}\ast S_3\left(t\right)+Q_{\mathit{milk},E}\ast \left(E_H\left(t\right)+E_L\left(t\right)\right)+Q_{\mathit{milk},L}\ast \left(L_H\left(t\right)+L_L\left(t\right)\right)+Q_{\mathit{milk},H}\ast H\left(t\right)$$ (10)

where, Q_milk,i is the average daily milk production of a cow in infection category i, with category x being uninfected. The values for Q_milk,i were taken from the results of the linear mixed model in Smith et al. (Smith et al., 2016), with all covariate values set to the mean (for continuous covariates) or the mode (for discrete covariates) of the data used to fit the model.

The net present value (NPV) of each scenario was calculated as

$$\mathit{NPV}=\sum _t\frac{\kappa \left(t\right)}{{\left(1+r\right)}^t}$$ (11)

where, t is time in years and r is the discount rate.

2.7 Control Programs

A total of 123 control programs were considered for each of 4 herd scenarios, generally broken down into test-and-cull (with different frequency and test choices) and hygiene. First, as optimal testing frequency is unknown, results were generated for annual and biannual whole-herd testing frequencies; if not specified, testing frequency is annual. Second, as testing might be expected to lapse after apparent disease elimination, two assumptions were considered: no testing after 5 negative tests, and continuous (continued testing); if not specified, testing ends after 5 negative whole-herd tests. Third, the four different testing scenarios were considered: no testing, FC, ELISA, or PCR. Fourth, four different culling scenarios were considered: cull all (culling all test-positive animals), cull high (culling only high-shedding animals), cull repeat (culling animals only after their second positive test), or test calves (testing and culling only calves, assumed to be based only on a single test option). For culling of only high-positive animals, it was assumed that the ELISA employed was the KELA (van Schaik et al., 2005), as it is the only ELISA for which application to culling of high-shedding animals has been provided in the literature. In all cases, the number of animals to be culled was calculated as

$$\mathit{culls}=\sum _i{Se}_{T,i}\ast N_i+\sum _j\left(1-{Sp}_T\right)\ast N_j$$ (12)

where Se_T,i is the sensitivity of test T for category i (being any target category for culling), N_i is the number of animals in category i, Sp_T,j is the specificity of test T for category j (being any non-target category) and N_j is the number of animals in category j. Fifth, three different levels of hygiene were considered: standard, moderate, or improved.

2.8 Herd Scenarios

Each of these control programs was implemented using the same set of initial population values, based on an endemically infected herd with no previous control as described above. Several scenarios were considered with each control program. As within-herd infection levels vary, two initial conditions were considered: 10% and 20% shedding prevalence. Finally, two herd sizes were considered: 100 head (small) and 1,000 head (large). Initial conditions were as described in 2.3, with the 1,000 head herd’s initial population structure being the 100 head herd’s initial population structure multiplied by 10.

2.9 Methods of Comparison

Resulting NPV distributions for each control strategy were analyzed within each scenario as follows. First, first- and second-order stochastic dominance (Levy, 1992) was calculated for all pairs of control strategies to determine overall stochastic dominance in maximizing NPV. First-order and second-order stochastic dominance are methods of determining preference for an activity with variable (stochastic) results; a dominant strategy by either method is to be preferred to its comparator. Briefly, if NPV_A is the cumulative distribution function of the NPV of control strategy A and NPV_B is the cumulative distribution function of the NPV of control strategy B, first-order dominance states that

$$P\left({\mathit{NPV}}_A\ge x\right)\ge P\left({\mathit{NPV}}_B\ge x\right)$$ (13)

for all possible values of x (the range of simulated NPV values for a farm in a given scenario) and

$$P\left({\mathit{NPV}}_A\ge x\right)>P\left({\mathit{NPV}}_B\ge x\right)$$ (14)

for at least one value of x, where P is probability. Likewise, second-order dominance states that

$$\mathit{AUC}\left({\mathit{NPV}}_A\right)\left[0:x\right]<\mathit{AUC}\left({\mathit{NPV}}_B\right)\left[0:x\right]$$ (15)

for all possible values of x (as in equation 12), where AUC(i)[0:x] is the area under the curve of the cumulative distribution function of i from 0 to x. For each control strategy, the dominance score was calculated as the number of control strategies over which it was either first- or second-order dominant, with a maximum score of 122 (all strategies except itself) and a minimum score of 0.

Second, results were compared across control strategies for each iteration, to compare results when starting from the same initial population. Third, dominance was determined within each scenario for each hygiene option, to determine the best testing strategy for maximizing NPV given a certain level of hygiene. Fourth, stochastic dominance in minimizing true prevalence in the adult herd, (E_L + E_H + L_L + L_H + H)/(S₃ + E_L + E_H + L_L + L_H + H) was determined for each scenario. Fifth, the probability of negative cash flow (κ<0) at any point during an iteration was calculated for each scenario. All simulations were run for 1,000 iterations.

2.10 Sensitivity Analysis

Global sensitivity analysis was performed using Latin Hypercube sampling with 500 sets of 100 iterations each, where iteration refers to the simulation of a single herd. For each iteration within each set, 100 and 1,000 head herds were simulated from the same initial population values under each of the generalized culling strategies (none, cull all positive, cull high positive, cull repeat positive, and test calves) with and without hygiene. Impact of parameters on NPV was determined using the Pearson’s rank correlation coefficient. All parameters used for the biological model are shown in Table 1, and all parameters for economic calculations are shown in Table 2. Where variability in parameters was not provided by the source, parameters were varied by ±10% for the sensitivity analysis. Where variability in parameters was available, parameters were varied over their interquartile ranges. Testing parameters were varied over the range of the interquartile ranges of all tests, and hygiene parameters were varied over the range of the possible additional hygiene levels. Parameters were considered significantly related to NPV at the level of α = 0.05 with Bonferroni’s correction.

Table 1.

Parameters and interquartile ranges (IQR) used in a model of Mycobacterium avium subsp. paratuberculosis infection in a dairy herd.

Par.	Description	Value (IQR)	Source
${Se}_H^E$	Sensitivity of ELISA for high-shedders	0.78 (0.68–0.86)	(Clark et al., 2008; Sweeney et al., 2006)
${Se}_H^K$	Sensitivity of KELA for high-shedders	0.31 (0.11–0.67)	(van Schaik et al., 2005)
${Se}_L^E$	Sensitivity of ELISA for low-shedders	0.24 (0.19–0.30)	(Clark et al., 2008; Sweeney et al., 2006)
${Se}_H^{FC}$	Sensitivity of FC for high-shedders	0.9 (0.75–1)	(Collins et al., 2006)
${Se}_L^{FC}$	Sensitivity of FC for low-shedders	0.5 (0.25–0.75)	(Whitlock et al., 2000)
${Se}_H^P$	Sensitivity of PCR for high-shedders	0.84 (0.77–0.90)	(Clark et al., 2008; Leite et al., 2013; Taddei et al., 2004)
${Se}_H^Q$	Sensitivity of qPCR for high-shedders	0.737 (0.49–0.90)	(Aly et al., 2012)
${Se}_L^P$	Sensitivity of PCR for low-shedders	0.47 (0.41–0.54)	(Clark et al., 2008; Leite et al., 2013; Taddei et al., 2004)
SpE	Specificity of ELISA	0.97 (0.91–0.99)	(Meens et al., 2014; Sweeney et al., 2014; Vitale et al., 2014; Whitlock et al., 2000)
${Sp}_H^K$	Specificity of KELA for high-shedders	0.997 (0.952–0.999)	(van Schaik et al., 2005)
SpF	Specificity of FC	0.98 (0.92–1)	(Sweeney et al., 2014; Vitale et al., 2014)
SpP	Specificity of PCR	0.94 (0.87–1)	(Taddei et al., 2004; Vitale et al., 2014)
${Sp}_H^Q$	Specificity of qPCR for high-shedders	0.943 (0.80–0.99)	(Aly et al., 2012)
SeC	Sensitivity of calf testing	0.5 (0.25–0.75)	assumed
SpC	Specificity of calf testing	0.98 (0.92–1)	assumed
δC	Culling rate of test-positive calves	SeCT1+(1-SpC)S1	calculated
δL	Culling rate of low-positive adults	SeL(LH+LL)+ (1-Sp)(EH+EL+S3)	calculated
δH	Culling rate of high-positive adults	SeHH+ (1-Sp)(EH+EL+S3)	calculated
μ1	removal rate of calves (/year)	0.09 (0.08–0.1)	(Mitchell et al., 2015b)
μ2	removal rate of heifers (/year)	0.01 (0.008–0.015)	(Mitchell et al., 2015b)
μ3	removal rate of adults (/year)	0.35 (0.3–0.4)	(Mitchell et al., 2015b)
μb,base	birth rate of female calves (/adult/year)	0.45 (0.4–0.5)	(Mitchell et al., 2015b)
μb,H	birth rate of high shedding dams (/adult/year)	0.15 (0.1–0.45)	(Smith et al., 2010)
γE	proportion of calves of latent animals infected at birth	0.01 (0–0.04)	(Mitchell et al., 2015b)
γL, γH	proportion of calves of shedding animals infected at birth	0.04 (0.01–0.08)	(Mitchell et al., 2015b)
ρ1, ρ2	aging rate (/year)	1 (0.8–1.2)	Assumed
η	proportion of infected heifers becoming progressing adults	0.335 (0.5–1)	(Mitchell et al., 2015b)
φ	transition rate from transient shedding to latent (/year)	2 (0.8–3)	(Mitchell et al., 2015b)
σL	transition rate from latent to low shedding, low path (/year)	0.53 (0.44–0.67)	(Smith et al., 2015)
σH	transition rate from latent to low shedding, high path (/year)	21.5 (1.75–40)	(Smith et al., 2015)
νH	transition rate from low to high shedding, high path (/year)	1.08 (0.75–1.94)	(Smith et al., 2015)
α	clinical disease-related culling rate (/year)	0.67 (0.5–0.8)	(Smith et al., 2010)
β	transmission coefficient for 10% and 20% initial prevalence (/year)	0.0115, 0.0225 (0.0225–0.0115)	calculated
βa	transmission coefficient to adults for 10% and 20% initial prevalence (/year)	0.00575, 0.01125 (0.00575–0.01125)	calculated
eβ	proportional transmission effect due to improved and moderately improved hygiene	0.6 0.98 (0.6–0.98)	(Benedictus et al., 2008; Collins et al., 2010) (Nielsen and Toft, 2011)

3. Results

Results varied by herd size and initial prevalence, but improved hygiene resulted in lower NPVs in all scenarios. The probability of negative cash flow at least one year during the 25 year observation period was low regardless of scenario or control program (never more than 6%), but was most likely to occur in a small herd with 20% initial prevalence instituting improved hygiene and calf testing and culling (6% probability each).

3.1 Stochastic Dominance

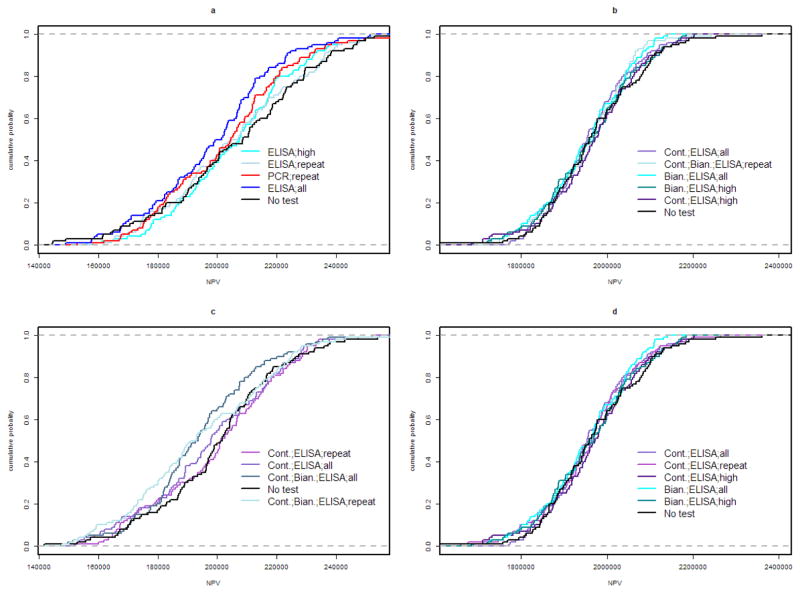
The 10 most dominant control programs and their relative dominance in maximizing NPV are shown in Table 3 for each scenario, and the dominance curves for the 5 most dominant control programs in each scenario are plotted in Figure 2. In the 100 head herd scenario with 10% prevalence, ELISA-based testing with cessation after 5 negative whole-herd tests was mostly dominant. In all other herds, continuous testing (no cessation of testing after 5 negative whole-herd tests) was preferred. For herds with 20% initial prevalence, ELISA was the test of the top 7 preferred control programs. In the herds with 10% initial prevalence, doing nothing was in the top 5 preferred programs.

Table 3.

Dominance rankings of the top 10 control programs for Mycobacterium avium subsp. paratuberculosis based on maximizing Net Present Value of dairy herds over 5 years, by herd size and initial prevalence. Score refers to the number of potential control programs (out of 122) for which a control program is either first or second order dominant. Unless otherwise stated, standard hygiene was used (as opposed to moderate or improved), animals were tested annually (as opposed to biannually), and testing was discontinued after 5 negative whole-herd tests (as opposed to continuous testing). Testing options are ELISA, PCR, or fecal culture (FC). Culling options are to cull all positive animals (cull all), cull only high-positive animals (cull high), or cull animals after their second positive test (cull repeat).

100 Head				1000 Head
10% Prevalence		20% Prevalence		10% Prevalence		20% Prevalence
Control	Score	Control	Score	Control	Score	Control	Score
ELISA, cull high	110	Continuous ELISA, cull all	116	Continuous ELISA, cull repeat	120	Continuous ELISA, cull all	115
ELISA, cull repeat	107	Continuous biannual ELISA, cull repeat	114	Continuous ELISA, cull all	117	Continuous ELISA, cull repeat	115
PCR, cull repeat	103	Biannual ELISA, cull all	113	Continuous biannual ELISA, cull all	114	Continuous ELISA, cull high	114
ELISA, cull all	97	Biannual ELISA, cull high	113	Nothing	113	Biannual ELISA, cull repeat	113
Nothing	82	Continuous ELISA, cull high	113	Continuous biannual ELISA, cull repeat	112	Biannual ELISA, cull high	112
Biannual ELISA, cull all	80	Continuous biannual ELISA, cull high	113	Biannual ELISA, cull repeat	109	Continuous biannual ELISA, cull repeat	112
FC, cull repeat	79	Continuous biannual ELISA, cull all	112	Continuous PCR, cull high	106	Continuous biannual ELISA, cull all	109
Biannual ELISA, cull repeat	78	Continuous ELISA, cull repeat	109	Continuous ELISA, cull high	105	Continuous FC, cull high	107
ELISA, cull all, moderate hygiene	75	Biannual ELISA, cull repeat	108	ELISA, cull high	104	Continuous PCR, cull high	106
ELISA, cull high, moderate hygiene	75	Continuous PCR, cull high	106	Moderate hygiene	104	Continuous PCR, cull repeat	106

Figure 2.

Cumulative distribution function of net present value (NPV) over 25 years in a herd endemically infected with Mycobacterium avium subsp. paratuberculosis, for the top 5 control programs and doing nothing under each herd scenario (a: 100 head, 10% initial shedding prevalence; b: 1,000 head, 10% initial shedding prevalence; c: 100 head, 20% initial shedding prevalence; d: 1,000 head, 20% initial shedding prevalence).

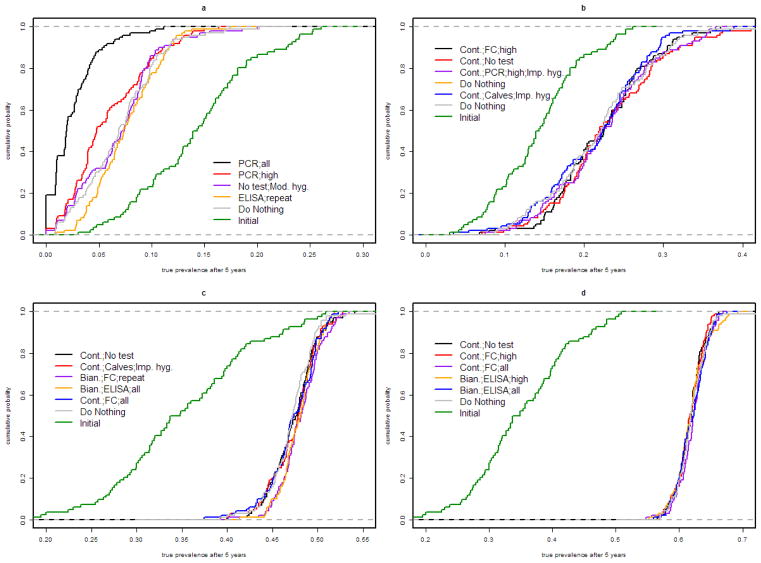
As there is no clear dominance for control programs economically, Figure 3 shows the dominance curves for total prevalence after 5 years of the 5 control programs most dominant by NPV for each herd scenario. Of the economically preferred programs, there was no dominance for decreasing prevalence in large herds or small herds with high initial prevalence. In small herds with 10% initial prevalence, culling animals with positive PCR results reduced prevalence most.

Figure 3.

Cumulative distribution function of total prevalence after 25 years in a herd endemically infected with Mycobacterium avium subsp. paratuberculosis, for the top 5 control programs (based on Net Present Value dominance) and doing nothing (gray) under each herd scenario (a: 100 head, 10% initial shedding prevalence; b: 1,000 head, 10% initial shedding prevalence; c: 100 head, 20% initial shedding prevalence; d: 1,000 head, 20% initial shedding prevalence), compared to the distribution of initial prevalence (green). In the 100 head herd with 10% initial shedding prevalence, elimination occurred in 19% of herds with culling of all PCR positive, 3% of herds with culling of PCR high-positives, and 2% of herds with moderately improved hygiene; elimination did not occur in any of the other herd scenarios.

The 10 most dominant control programs and their relative dominance in minimizing true prevalence is shown in Supplemental Table 2 for each scenario. In the 100 head herds, culling of all positives based on PCR was fully dominant. In the 1,000-head herds with 20% initial prevalence, culling of FC positives was fully dominant. In the 1,000-head herds with 10% initial prevalence, PCR and FC with culling of all positives were co-dominant.

The 5 most dominant testing programs and their relative dominance in maximizing NPV are shown for each combination of herd scenario and hygiene program in Supplemental Table 3. Continuous ELISA testing is mostly dominant regardless of hygiene standard, although the large, well-managed herd had higher dominance for no testing.

3.2 Preference by Iteration

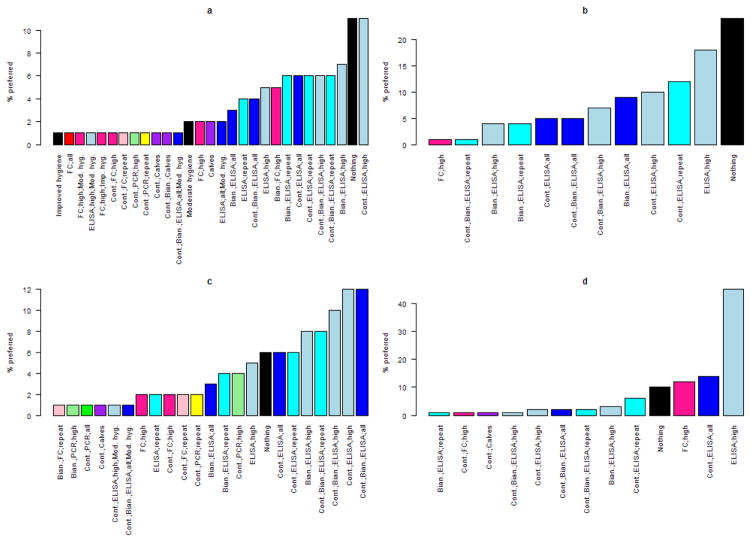
Figure 4 shows the number of individual iterations in which each control program had the highest NPV, based on identical starting values, for each herd scenario. While doing nothing was the preferred program in 6–24% of iterations, a wide variety of control programs were preferred at least once, with ELISA testing especially common. Fewer control programs were preferred at least once in the large herd than in the small herd. In herds with 10% initial prevalence, doing nothing was preferred at least as often as any other control program.

Figure 4.

Probability that one iteration of the simulation preferred a strategy for maximizing net present value while controlling Mycobacterium avium subsp. paratuberculosis in a dairy herd, given the same initial population distribution, for each herd scenario (a: 100 head, 10% initial shedding prevalence; b: 1,000 head, 10% initial shedding prevalence; c: 100 head, 20% initial shedding prevalence; d: 1,000 head, 20% initial shedding prevalence). Black colors indicate no testing; shades of blue are different ELISA-based control methods; shades of red are different fecal culture-based control methods; shades of green and yellow are different PCR-based control methods.

3.3 Sensitivity Analysis

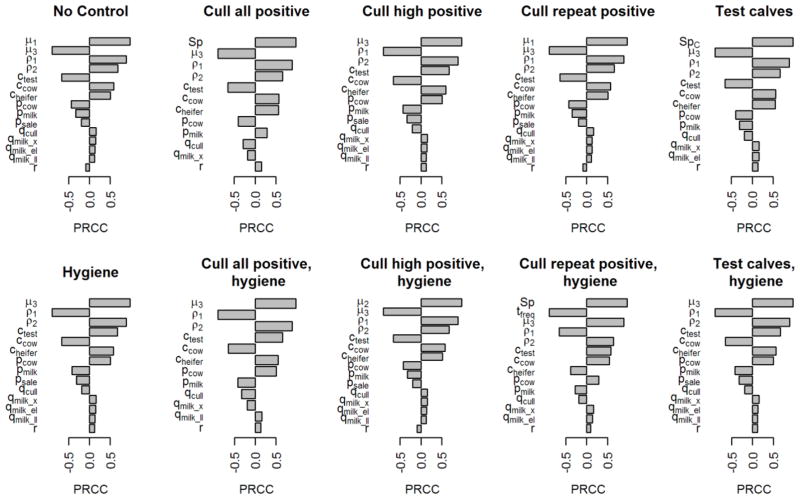
The partial rank correlation coefficients against mean NPV for all significant parameters found in the sensitivity analysis are shown in Figure 5 and in Supplemental Table 4. For most control scenarios, the most important parameters were the mortality rates and the aging rates of heifers and calves. Most economic parameters (costs of testing, raising heifers, producing milk; prices for cull cows, milk, and heifers; amount of milk produced; weight of cull cows; and the discount rate) were also significantly related to NPV. Parameters related to the control of MAP were rarely significantly associated with NPV; the main exception was specificity, which was positively correlated with NPV if all test-positive cows were culled, if only calves were tested, and if repeated positive cows were culled and advanced hygiene was used.

Figure 5.

Partial rank correlation coefficients (PRCC) of all significant parameters (after Bonferroni correction) from a global sensitivity analysis of the mean net present value over 25 years from a model for paratuberculosis in a 100-head dairy herd with 10% initial prevalence, by testing strategy.

Discussion

This study found that the economically best control for MAP in dairy herds is not the same as the best control for reducing prevalence over a 5 year period, and that the economics of control change with herd size and initial prevalence. In this study, initial prevalence was a proxy for herd management factors, as higher transmission rates were required to produce the higher average prevalence. Thus, we can say that the most cost-effective control for MAP depends on the herd’s size and existing management quality. While the effect of size is likely related to stochastic effects, as we have not accounted for economies of scale, the effect of management quality is most likely related to existing hygiene management.

Despite the differences between herd scenarios, some generalizations of the results could be made. In order to maximize NPV, the use of ELISA testing seems to be preferred (Table 3). This agrees with a number of studies finding that ELISA testing is cost-effective over a 10-year period (Kudahl et al., 2008, 2007; Robins et al., 2015). In contrast, this study found that PCR or FC testing was preferred for decreasing prevalence (Supplemental Table 2). While specificity is similar between these tests, PCR and FC tests are assumed to be more sensitive for low-shedding animals (Clark et al., 2008). However, ELISA is much less expensive, which would lead to its preferred status from an economic viewpoint. While PCR is similar to FC in terms of sensitivity and cost and has a faster turn-around time, we assumed that it has a lower specificity, which would limit its economic usefulness due to the culling of false-positives that is likely to happen. The specificity of FC would be lower if we considered the possibility of passive shedding, but analysis of these data found that most FC positive animals were truly infected based on tissue culture at slaughter (Whitlock et al., 2009). Aly et al. (2012) suggested that ELISA and PCR together, interpreted serially, would be most cost-effective. While that scenario was not considered in this study, our results would support the finding that screening with ELISA would be more cost-effective than PCR on all animals.

We considered the effect of improved hygiene (at 2 levels) on economic and prevalence outcomes, but found that such improved hygiene was rarely preferred from either point of view. This could be due to the small impact that has been observed in studies, combined with a high cost. In comparison, a simulation study that assumed high efficacy for improved hygiene found that such hygiene improvements were the most cost-effective (Groenendaal and Galligan, 2003). A recent study has found that herd hygiene is strongly associated with the probability of being high versus low prevalence, based on environmental sampling, but it did not consider the cost of the hygiene measures taken in low-prevalence herds (Wolf et al., 2016). When considering testing strategies within improved hygiene situations (Supplemental Table 3), little change was noted, indicating that a cost-efficient testing program will remain cost-efficient regardless of the hygiene measures. To our knowledge, only one other modeling study has considered the impact of hygiene and testing at the same time, and that study also found that ELISA testing is cost-effective even with improved hygiene (Cho et al., 2013). Our finding may be related to the assumption that hygiene changes only produce limited effects on prevalence in the short-term.

Looking at results for only small herds, the well-managed herds are predicted to maintain good economic control with no MAP-specific intervention, although test-and-cull strategies were also cost-effective (Table 3, Figure 4). In these small, well-managed herds, it appears that a broad range of control programs would be nearly equivalent. Figure 4 shows that no single program produced the highest NPV in more than 11% of well-managed individual small herds, or 12% of poorly-managed small herds. Thus, these herds may comfortably choose a control program that fits within their herd management plan from a long list of possibilities.

A larger herd, however, does not benefit from the stochastic effect caused by the small herd size, and is more likely to require active control of MAP. Although doing nothing produced the highest NPV in 10% of individual poorly-managed herds (compared to 24% of individual well-managed herds), it was dominant over only 18 of the 122 other control programs due to a greater skew to its distribution of NPV; in other words, when doing nothing did not work, the results were very bad indeed. Fewer control programs were co-dominant in the large herds, providing a shorter list of possibilities for these herds, but no clear dominance was shown.

The sensitivity analysis showed that the uncertainty around control-related parameters (test cost, sensitivity, or specificity, or hygiene cost or efficacy) would not significantly affect mean NPV compared with the uncertainty around milk production and heifer rearing costs. This indicates that these results should be robust to changes in test costs or performance.

Several assumptions were made, out of necessity, which could impact the results of this study. First, we assumed that animals were culled without delay; some farmers may delay culling for reasons of pregnancy or (currently) high milk production. Adding such a delay would likely decrease the cost-effectiveness of our test-based culling strategies, as the impact on infection pressure would be delayed. Second, we assumed that our parameters for progression and spread of MAP are representative of the biology of MAP in typical herds. Although changes to these biological parameters are likely to impact results in terms of prevalence, our global sensitivity analysis found that they were not significantly related to NPV and therefore should not affect economic conclusions. Third, we assumed that hygiene changes were expensive but limited in effectiveness. Despite many studies looking at hygiene changes associated with MAP risk, the majority are cross-sectional and cannot predict change over time (Doré et al., 2012); the literature surrounding long-term efficacy of improved hygiene is limited, and so limits our ability to model hygiene efficacy appropriately. Fourth, for simplicity we assumed that all replacement animals (purchased heifers) were non-progressing. Although the prevalence of progressing infections is low, it is indeed possible for a farm to import progressing animals. Relaxation of this assumption may make programs that rely heavily on replacement animals (due to extensive culling) less attractive for disease control. Fifth, as no reliable estimates are available for testing of calves, we were forced to assume a broad range of sensitivity and a specificity similar to other testing methods. If the sensitivity or specificity of calf testing is lower than we assumed, which is highly likely, the economic value of calf testing would be much lower. However, we did not find calf testing to be a preferred strategy even assuming reasonably good diagnostic performance, so this assumption is unlikely to affect our overall findings.

We can conclude from the results presented here that general MAP control policies can be cost-effective, especially in larger and higher prevalence herds. However, we cannot distinguish between the cost-effectiveness of several general policies. An individual-based model may be able to improve the results, as it would allow control policies to consider the age, milk production, and reproductive status of the test-positive cows.