Abstract
The free energies of adsorption of the monomer or dimer of the cationic β-hairpin antimicrobial peptide protegrin-1 (PG1) in a specific binding orientation on a lipid bilayer are determined using molecular dynamics (MD) simulations and Poisson-Boltzmann calculations. The bilayer is composed of anionic palmitoyl-oleoyl-phosphatidylglycerol (POPG) and palmitoyl-oleoyl-phosphatidylethanolamine (POPE) with ratio 1:3 (POPG:POPE). PG1 is believed to kill bacteria by binding on their membranes. There it forms pores that lyse the bacteria. Herein we focus on the thermodynamics of binding. In particular, we explore the role of counterion release from the lipid bilayer upon adsorption of either the monomeric or the dimeric form of PG1. Twenty two 4ns-long MD trajectories of equilibrated systems are generated to determine the free energy profiles for the monomer and dimer as a function of the distance between the peptide(s) and the membrane surface. The MD simulations are conducted at eleven different separations from the membrane for each of the two systems, one with PG1, the second with PG1 dimer only of a specific orientation of the monomer and dimer without taking into account the change of entropy for the peptide. To calculate the potential of mean force for each peptide/membrane system, a variant of constrained MD and thermodynamic integration is used. We observed that PG1 dimer binds more favorably to the POPG:POPE membrane. A simple method for relating the free energy profile to the PG1-membrane binding constant is employed to predict a free energy of adsorption of −2.4 ± 0.8 kcal/mol. A corresponding PG1-dimer-membrane binding constant is calculated as −3.5 ± 1.1 kcal/mol. Free energy profiles from MD simulation were extensively analyzed and compared with results of Poisson-Boltzmann theory. We find the peptide-membrane attraction to be dominated by the entropy increase due to the release of counterions in a POPG:POPE lipid bilayer.
Graphical Abstract
INTRODUCTION
A large number of antimicrobial peptides (AMP) are known to act against bacteria by binding and permeabilizing their membrane, but some of these AMPs are also toxic to human cells.1,2 It is thought that the difference in macromolecular composition and charge distribution of prokaryotic and eukaryotic membranes plays a critical role in the selectivity of most antimicrobial peptides.3 More specifically, an important hypothesis is that the high concentration of negatively charged lipids on the bacterial cytoplasmic membrane plays an important role in the selectivity of an AMP for bacterial cells over eukaryotic cells.4 How exactly this role is played out is not clear though. Understanding the mechanism of interaction between AMPs and membranes is therefore an important step in explaining their action.
In this paper we investigate the interaction of a cationic antimicrobial peptide protegrin-1, (PG1), with a mixed anionic POPG and POPE lipid bilayer. PG1 is a well studied antimicrobial peptide.5–12 It is a 18-residue cationic β-hairpin peptide (RGGRL CYCRR RFCVC VGR-NH2) with two disulfide crosslinks, and is highly enriched with basic amino acids (six positively charged arginine).12 PG1 is known to form stable dimers in a parallel β-sheet arrangement.13 Four or five of those dimers can then form an octameric or decameric protegrin pore in lipid bilayers, which, in turn, facilitates the transport of water, ions and electrolytes in and out of the cell.13 PG1 is admitted to form higher aggregates at the interface and inside the core of lipid bilayers.8,13,14 These aggregates disrupt the structural integrity of the membrane and form pores that permeabilize the bacteria. What is not known is how exactly PG1 recognizes and adsorbs to membranes of bacteria before it forms the pores that kill the microbes. Understanding the molecular details of how PG1 first absorbs onto membranes provides insight into the first steps that confer PG1 with antimicrobial character. Herein we use atomistic simulations to determine how a PG1 monomer and a PG1 dimer adsorb on a mixed anionic POPG and POPE lipid bilayer with ratio 1:3 (POPG:POPE). Such a lipid bilayer mimics the bacterial inner membrane. We use a variant of constrained molecular dynamics (MD) and of the thermodynamic integration method to determine the potential of mean force (PMF), and calculate the equilibrium binding constant and related adsorption free energy. Sec. II contains computational details, the MD protocol used for the PG1 and PG1 dimer simulation and the algorithm to calculate the PMFs for the peptide-membrane systems. Although the configuration of peptide does not change considerably during the course of the molecular simulation (because of the two cysteine - cysteine bonds that keep the structure fairly inflexible), the rotational degrees of freedom may not be insignificant. On the other hand, results from previous work15 indicate that the loss of rotational entropy upon binding does not contribute as significantly as ion release. We decided then to only study one orientational configuration, because of the considerable computational cost. In Results we examine the effect of the peptide proximity on the number of Na+ counterions in our model membrane. Counterion release upon binding of PG1 and PG1 dimer results in substantial entropy increase in the system and plays a key role in the mechanism of peptide membrane adsorption. To analyze further the nature of peptide-membrane interactions and to determine the contribution of the counterion release to the PG1 peptide adsorption, we decompose the adsorption free energy profile into enthalpic and entropic components. The importance of counterion release has been discussed before,16,17 and studied for the interaction of lactoffericin AMP with a POPG membrane.15 We also numerically solve the PB equation to describe the electrostatic interactions in the system. We employ this theory to further examine the electrostatic entropic and enthalpic contributions to the free energy from the double-layer in between the peptides and membrane. Finaly, we compare the MD results for the PMF with results obtained from the PB theory.
Methods
Microscopic models for PG1 peptide, PG1 dimer and POPG:POPE membrane
The system simulated with one PG1 peptide above a well-mixed membrane of 128 lipids (i.e., 64 lipids in each leaflet) containing 96 POPE lipids, 32 POPG lipids. The system is solvated with nearly 8900 TIP3P water molecules, 31 chlorine ions, and 56 sodium ions. Chlorine and sodium ions are added to create a 0.15 M physiological salt solution and to neutralize the charge of the peptide and POPG head groups. The monomer solution structure of the β-hairpin PG112 is obtained from the protein data bank (PDB code 1PG1). The initial PG1 peptide orientation has the peptide backbone parallel to the membrane along the y axis, and residues Cys6, Cys8, and Cys15 lying in the xy-plane.
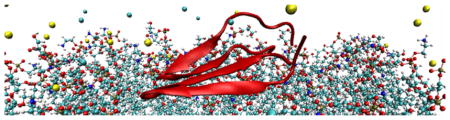
For the PG1 dimer we simulate the same solvated lipid bilayer system of 128 lipids, but with 38 chlorine ions, and 56 sodium ions, as we have to neutralize two identical PG1 peptides (Figure 1). The coordinates of the membrane-bound dimer NMR structure in an NCCN (N and C stand for the peptide’s N- and C- termini, respectively) packing mode13 are downloaded from the protein data bank (PDB code 1ZY6). Both peptides in the dimer are oriented parallel to the membrane so that one of the PG1 peptide backbones is parallel to the membrane along y, and residues Cys6, Cys8, and Cys15 reside in the xy-plane, (Figure 1).
Figure 1.
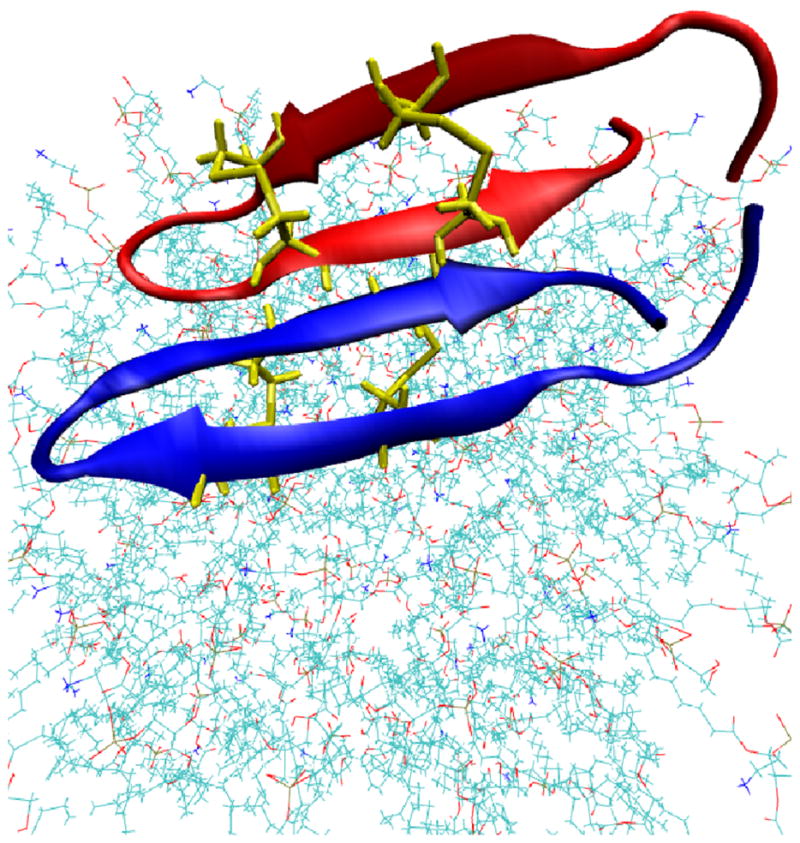
(Color online) Structure of the PG1 dimer in the parallel β-sheet arrangement and in an NCCN packing mode at the membrane surface (N and C stand for the peptide’s N- and C- termini). The peptide residues Cys (i.e. 4 Cys (in yellow)) are also indicated.
Herein, we restrict our attention to the parallel NCCN packing organization for the PG1 dimer, based on the NMR coordinates in a POPC bilayer. It will certainly be interesting to investigate other dimeric packing organizations for PG1. Experimentally, different dimeric structures have been observed depending on the environment: antiparallel in micelle environments and parallel in POPC bilayers.13,18 We are currently investigating these different dimeric structures. Preliminary results of simulations involving a mixed POPE/POPG membrane indicate a stronger binding affinity for the peptide in the parallel structure versus the antiparallel organization on the membrane surface and in the transmembrane region. The present study is a useful starting point for farther simulations of thermodynamic properties for parallel and antiparallel dimer structures of the peptide. These additional studies will give additional insight into the mechanisms leading to peptide-induced membrane disruption and membrane-peptide selectivity.
A set of 11 simulations for different distances for PG1 with respect to the membrane and a set of 11 simulations for different distances for PG1 dimer to the membrane are carried out. All systems were constructed in a rectangular cell with the z-axis perpendicular to the membrane using the program CHARMM19 and CHARMM-GUI Solvent Modeler.20 The CHARMM-27 force field21 with CMAP corrections22 is employed. All structures of the β-hairpin PG1 were generated with two disulfide bonds, amidated C-terminus, and six positevly charged arginines (ARG) reflecting the typical protonation states at neutral pH in water. The monomer and dimer of the PG1 are positioned at a fixed distance from the membrane surface and at a fixed orientation. After 5000 steps of energy minimization the 22 systems are equilibrated for 8 ns in the NPT ensemble using the NAMD software package23 employing the Nose-Hoover-Langevin pressure controller.24,25 The pressure is set to 1 atmosphere with a piston period set to 200 fs and piston decay of 100 fs. The system is heated to 310 K, which is above the gel-liquid crystal experimental phase transition of the mixed membrane in increments of 30 K, minimizing for 5000 steps at each temperature. The phase transition temperature of the POPG:POPE (1:3) membrane is about 291 K.26 The water molecules are simulated using the TIP3P water model.27 The van der Waals interactions are smoothly switched off over a distance of 4 Å, between 8 and 12 Å. The electrostatic interactions are simulated using the particle mesh Ewald summation with a grid of approximately 1 point per 1 apart in each direction with no truncation.28 During equilibration, the area per lipid remained constant to the mixed (1:3) POPG:POPE system average value, 63.1 ± 1.5 Å2, indicating all of our simulation boxes with periodic boundary condition are stable. The average dimensions of the equilibrated simulation box are 63.57 × 63.57 × 100.89 Å. Finally, for data collection, all of our 24 systems are simulated for 4 ns in the NVT ensemble with a time-step of 2 fs.
Construction of PMF for PG1 monomer and PG1 dimer in a specific binding orientation interacting with a lipid bilayer
We use a simple methodology for the calculation of the position PMF, W(z), and the binding free energy for peptide adsorption on a lipid membrane. In29 and15 the position, PMF, W(z), was evaluated from the orientational PMF, W(z,Ω), where Ω is the vector of rotational degrees of freedom. It was found that the orientational PMF, has no strong dependence on the rotation around space-fixed axes y with the origin at the peptide center of mass. Moreover, the PMF exhibited a minimum energy, when the peptide backbone is parallel to the membrane. On the other hand the PMF exhibited a maximum energy for the peptide orientation in which the peptide backbone is perpendicular to the lipid bilayer. Therefore, herein we restrict ourselves only to one orientational mode, in which the peptide backbone remains parallel to the membrane and and we did not take into account positive contribution (which could be different between monomer and dimer) due to entropy loss upon the peptide binding.
The positional PMF, W(z), has been evaluated for a set of 11 simulations for different distances D between the PG1 monomer or PG1 dimer surfaces and the membrane surface. Distance D is introduced as the reaction coordinate and is related to distance z by D = z – a, where a is an “effective” size of the peptide. This effective peptide size is used in the solution of the Poisson-Boltzmann equation. We use D in both the PB solution and the MD simulations, so that we can compare the results from both methods. In MD simulations, the peptides surface - membrane surface separation, D, ranges from 0 Å to 20 Å in increments of 2 Å (Fig. 2). The simulation procedure is broken down into several stages:
Figure 2.
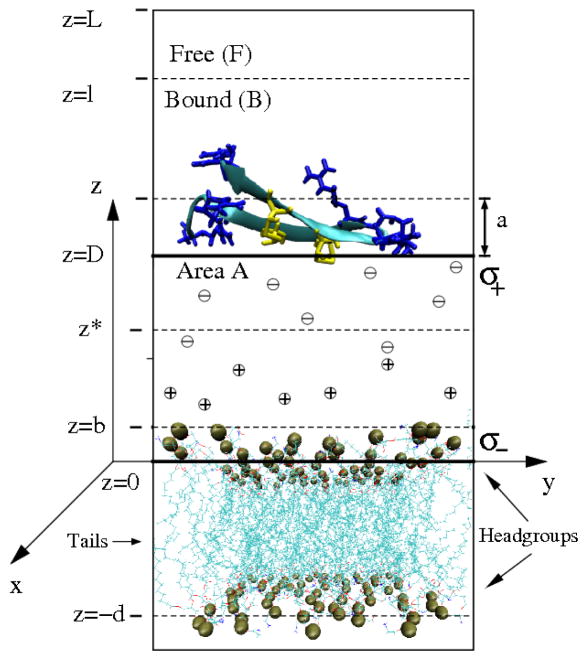
(Color online) Schematic binding geometry of the peptide PG1 at the membrane surface, and simplified geometry for Poisson-Boltzmann (PB) analysis. The peptide configuration is defined by a center of mass z-coordinate z. There are N = NF + NB peptides in volume V ≃ LA = VF +VB, where z = l divides the free (F) and bound (B) volumes. The thickness of the lipid head group region is 2b ≈ 8 Å. The peptide PG1 can be represented by spheres with “effective” radius a ≈ 8.9 Å. The P-P distance d ≈ 36 Å is the mean distance between the headgroup phosphorus atoms in the two membrane leaflets. For the PB analysis a simplify a plane-plane geometry, representing two oppositely charged planar surfaces, with charge densities σ+ and σ−, separated by distance D with counterions between them is used. z* is the running coordinate between the two surfaces for the reduced electrical potential ϕ(z*), will be explained below in the text. The origin z = 0 (z* = 0) is chosen at the membrane surface (average position of the upper leaflet phosphorus atoms). The lipid phosphorus atoms are shown as gold spheres. The peptide residues Arg and Cys (i.e. 6 Arg (in blue) and 4 Cys (in yellow)) are also indicated.
To create 11 simulation boxes for 11 different positions for a given orientation the PG1 monomer (dimer) peptide is first separated from the membrane to a distance of D and harmonic restraint forces are applied to all the peptide backbone atoms. The membrane center of mass is harmonically restrained with a spring with a force constant 20 (kcal/mol)/Å2. The system is equilibrated over 4 ns in the NPT ensemble.
After creating the 11 initial equilibrated systems, each of them is used for data collection during another 4 ns in the NVT ensemble. The (1:3) POPG:POPE membrane center of mass and the PG1 monomer (dimer) are harmonically restrained. To restrain the peptides and their orientation we use harmonic springs coupled to the three carbon CB backbone atoms of Arg1, Arg10 and Cys15. In the case of PG1 dimer we also apply three harmonic springs coupled to the two carbon CB backbone atoms of Arg1, Arg10 of one of the two PG1 peptides and one harmonic spring coupled to the carbon CB backbone atom of Cys15 of the other PG1 peptide. All spring constants are 20 (kcal/mol)/Å2.
The instantaneous restraint forces are computed during 4 ns trajectories for each of the 11 system configurations for single PG1 and for each of the 11 system configurations for PG1 dimer with sampling interval of 0.2 ps, and averaged to obtain the mean force F̄(D) = −F̄res(D) for each mean position. The PMF, W(D), is calculated using equation (1), presented in the following section.
Calculation of potential of mean force from MD simulations
To find the PMF, W(D), from the simulation, we apply the force method which was developed for the PMF calculation of a peptide in the vicinity of a neutral POPC membrane29 and charged POPG membrane;15 it is a variant of constrained MD and thermodynamic integration.30–35 More specifically, we use the relation F̄(D) = −∂W(D)/∂D, where F̄(D) is the mean force (which is in z-direction by symmetry) on the peptide for fixed D. In our studies both the PG1 peptide, or PG1 dimer and the membrane are restrained in space and the forces exerted on peptides and membrane harmonic restraint springs F̄res(D′) are monitored and averaged. Therefore we can obtain W(D) as
| (1) |
with F̄(D′) = −F̄res(D′). The integration over the D coordinate is performed using the trapezoidal rule.
For the calculation of the equilibrium binding constant K = ρB/ρF and related adsorption free energy ΔG0 we use29
| (2) |
where β = 1/kBT with kB Boltzmann’s constant and the standard relation
| (3) |
The free energy profile W(D) can be decomposed into enthalpic [ΔH(D)] and entropic [−TΔS(D)] components using
| (4) |
where
| (5) |
| (6) |
The entropic and enthalpic contributions from MD simulation can be determined in a finite difference approximation which is based on a simulation temperatures differences for the PMF W(D,T), W(D,T +ΔT), and W(D,T −ΔT).30
Calculation of potential of mean force from PB calculations
We also analyze our system with the help of Poisson-Boltzmann theory. In a similar manner to the analysis of the MD results, we compute the electrostatic PMF, WPB(z), and the enthalpic and entropic contributions to the computed free energy. A simplified geometry is implemented for the PB calculations. A schematic drawing of this binding-site geometry for the peptide (shown as a β-hairpin) and flexible membrane in water with Na+ and Cl− ions is illustrated in Figure 2. We consider a dilute solution of N identical peptides in a solution of Na+, Cl− ions at temperature T and volume V ≃ AL. The coordinate z is the normal coordinate of the center of mass of a peptide, with z = 0 chosen as the average position of the upper leaflet phosphorus atoms of the membrane lipids. Peptides are considered to be bound (B) if z < l and free (F) if z > l where the choice of l is discussed in section.
The membrane is then modeled as a uniformly negatively charged plane, and the peptide is considered as a positively charged sphere and, in an even more simplified model, as a positively charged plane. For our geometry it will be useful to introduce the distance D, as a reaction coordinate. This, as discussed previously, is the separation between the membrane surface and the “peptide” surface. Distance D is related to distance z by D = z – a, where a is an “effective” radius of the peptide. In addition we introduce the minimum separation surface-surface distance D0 which is the closest distance the peptide reaches during its binding to the membrane. In our study we restrict ourselves to surface (or adsorption) interactions. In other words, we investigate the behavior of PMFs for D ≥ D0. The densities of bound and free peptide are ρB = NB/VB and ρF = NF /VF, respectively, where VB = Al and VF = A(L – l) ≈ AL ≃ V, since l ≪ L. The choice of specific values for a and l are discussed in the Results section.
The cationic PG1 peptide or PG dimer and anionic membrane system can be represented by a simplified system that consists of two oppositely charged parallel planes, separated by a distance D, (see Figure 2). The two surfaces bear two different fixed surface charge densities σ+ > 0 and σ−< 0, respectively, in an aqueous solution with a uniform dielectric constant ε and with ions treated as continuous charge distributions. The PB equation can be used to describe the electrostatic interactions in this system. We assume that the electrolyte between the surfaces is in thermodynamic equilibrium with a solution bulk, and the mean electric potential in the spaces between the two charged planes satisfies a nonlinear one-dimensional PB equation36
| (7) |
where z* is the running coordinate, with z* = 0 chosen at the negatively charged plane; ϕ(z*) ≡ eψ(z*)/kBT is the dimensionless electrostatic potential; ψ(z*) is the actual potential; e is the proton charge; ϕ′(z*) ≡ dϕ(z*)/dz*, and (in esu) is the inverse Debye-Hückel screening length, which depends on the electrolyte concentration c0 and DB the Bjerrum length, DB = e2/εkBT. The boundary conditions relate the electric field − ϕ′ at each of the two planes, separated by a distance D, to the charge densities:
| (8) |
| (9) |
where the Gouy-Chapman lengths and for the corresponding surfaces are given by . The solution of (7) allows evaluation of the difference in pressure, ΔP(D) = Pin(D) − Pout, between that in the region between the surfaces (Pin(D)) and that of the reservoir (Pout). This pressure can be represented as the sum of an osmotic pressure that includes the entropic contribution of the ions and the Maxwell electrostatic pressure,36,37
| (10) |
We can now express the electrostatic free energy change Wpb(D) per area AP as a reversible work of the mean force F̄(D) = ΔP(D)AP. This is expressed as the integral over the pressure:
| (11) |
where D′ is the separation between the two planes. The arbitrary surface area, AP, is the area of an “effective” peptide surface opened to the membrane surface. This is the area of a planar surface roughly equivalent to the “effective” peptide surface, calculated as AP = πa2. In particular, for our single PG1 peptide we have , and for PG1 dimer we have . If we take into account that the average area per one charged lipid is 256 Å2 we have for our membrane-single PG1 peptide system σ−= − (1/256) e/Å2= −0.06 C/m2, and σ+ = (1/249) e/Å2 = +0.06 C/m2. The Bjerrum length for the TIP3P water with dielectric constant ε ≈ 95 at T = 310 K25,38 is DB = 5.7 Å. The corresponding Gouy-Chapman lengths are and , respectively. These values are close to the Debye-Hückel screening length DDH = 8.2 Å at c0 = 10.5 × 10−5 Å−3 ≈ 0.15 M at 310 K. For the membrane-PG1 dimer system we have σ− = − (1/256) e/Å2 = −0.06 C/m2, and σ+ = (1/388) e/Å2 = +0.04 C/m2. The corresponding Gouy-Chapman lengths are and , respectively.
Note, that in15 the contribution from counterion release was analytically estimated based on asymptotic limits for the potential of mean force, which are valid only for either a distance of separation between membrane and peptide D, that is smaller than the Gouy-Chapman length, D < DGC, or for a distance D that is larger than the Debye-Huckel distance, D > DDH. In,15 the Debye-Huckel distance was set at DDH = 10.0 Å and the Gouy-Chapman length was DGC = 3.0 or 4.0 Å. The implicit assumption underlying this analytical calculation is that counterion release does not play any role in the distances in between these two limiting cases, DGC < D < DDH. This may not be true, and indeed the comparison in15 between the potential of mean force computed from the molecular dynamics simulations and the one computed from Poisson-Boltzmann was not very favorable. In contrast, in the present study we solved the Poisson-Boltzmann equation numerically, without any such constraining assumptions. As discussed in the Results section, the numerical solution converges to the solution generated from the molecular simulations, within the accuracy limits of the two methods.
Results
Counterion release from POPG:POPE membrane
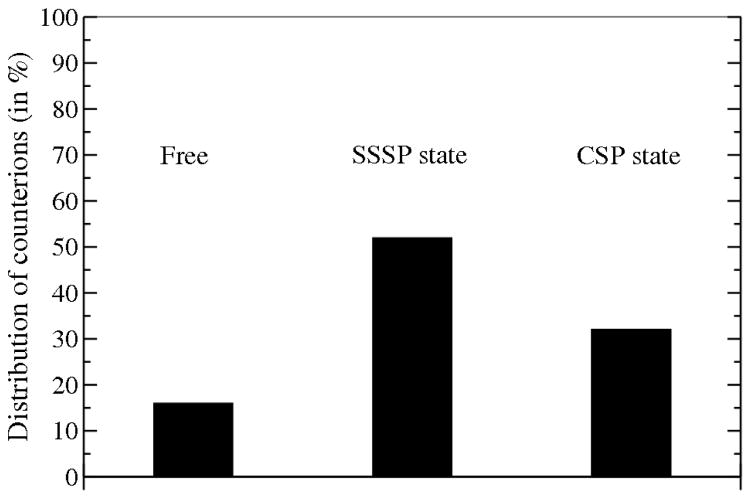
Here we investigate the effect of proximity between the monomer or dimer of PG1 and lipid bi-layers on the release of Na+ counterions from the membrane. These ions are initially involved in Na+-lipid and lipid-Na+-lipid complexes, known as “ion bonds” and “salt bridges” respectively.15,39,40 These bridges stabilize the mixed (1:3) POPG:POPE membrane by reducing charged lipid repulsion. It was found for a POPG membrane15 that solvent-separated ion-lipid pair states (SSSP), where a water molecule is shared between two ions, are more stable than the contact solute pairs (CSP). By analogy we determine the existence of an “ion bond” when any lipid head group oxygen is found within 3.5 Å of a Na+ ion (the CSP state) or within 6.0 Å of Na+ (the SSSP state). When the distance D between the PG1 peptide and the phosphate plane is considered to be large enough to neglect any influence of the peptide on the membrane (D > 18 Å), we find, on average, that 84% (±10%) of the 32 Na+ counterions are involved in “ion bond” and “salt bridges” formation with 54% (of 32 ions) in the SSSP states and only 30% (of 32 ions) in the CSP states. This is illustrated in (Figure 3). The percentage of the counterions “binding” to only one lipid, forming ions bonds is 33%. On the other hand, the percentage of the counterions “binding” to two or three lipids, forming “salt bridges”, are 31%, and 20%, respectively.
Figure 3.
Distribution of the average number of Na+ counterions involved in the formation of Na+-lipid complexes, known as “ion bonds” in the (1:3) mixed POPG:POPE membrane, averaged over a 4 ns simulation without peptide. SSSP state is the solvent-separated solute pair state, where a water molecule is shared between counterion and any lipid head group oxygen and CSP is the contact solute pairs state. For our system we define the existence of an “ion bond” when any lipid head group oxygen is found within 3.5 Å of a Na+ ion (the CSP state) or within 6.0 Å of Na+ (the SSSP state).
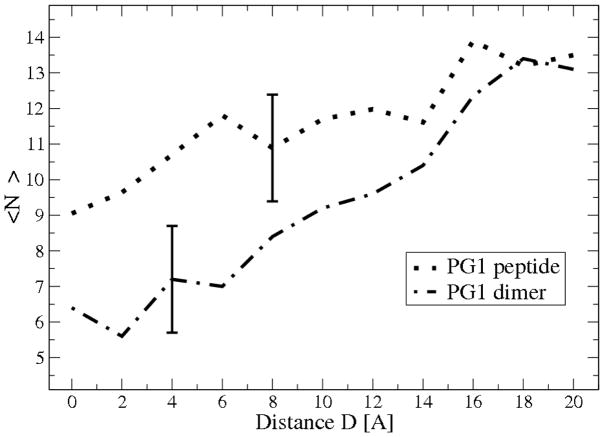
For POPG lipids there are four types of relevant oxygens: (1) OH oxygens, (2) phosphate oxygens, (3) ester oxygens, and (4) carbonyl oxygens. We find that almost all ions of the CSP state (more than 80 %) form “ion bonds” with the phosphate oxygen type. On the other hand the distribution of SSSP “ion bonds” is approximately uniform between all oxygen types. The release of Na+ ions from “bound” states with lipids upon peptide-membrane binding, is illustrated in Figure 4. The total number of CSP and SSSP bound counterions, < NB >, near the upper leaflet of the mixed (1:3) POPG:POPE membrane has been averaged over 4 ns of MD simulations. PG1 displaces 4.1 ± 1.5 Na+ ions when it adsorbs on the lipid bilayer. On the other hand, the PG1 dimer displaces an average 7.2 ± 1.5 Na+ ions when it binds on the membrane. It is notable that most of the released Na+ ions belong to the SSSP state.
Figure 4.
The average number < NB > of sodium counterions binding to the upper leaflet of the 1:3 mixture of POPG:POPE lipid bilayer averaged over a 4 ns simulation for the peptide PG1 and for the PG1 dimer. D is the separation distance between the PG1 or PG1 dimer surface and the phosphate plane of the upper leaflet of the membrane.
Binding affinity of PG1 or PG1 dimer to mixed (1:3) POPG:POPE membrane
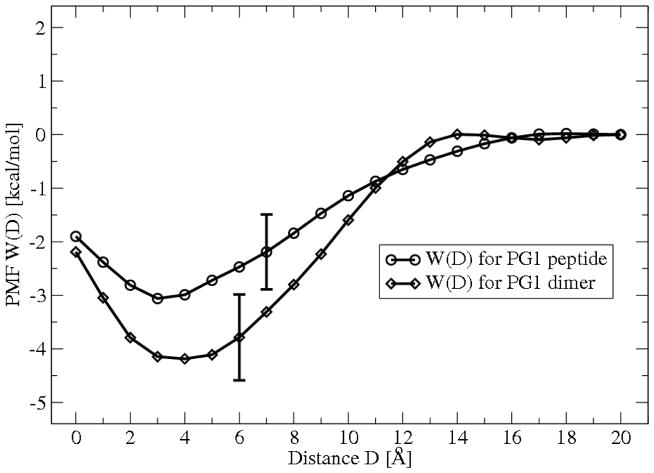
Figure 5 shows the PMF values for the PG1 and PG1 dimer in close proximity to the mixed (1:3) POPG:POPE membrane, as calculated with MD simulation. We find that the PMF minimum is approximately −3.1 kcal/mol for the PG1-membrane complex at a separation distance D=1Å. The minimum is −4.2 kcal/mol deep for the PG1-dimer-membrane at D= 2 Å. Thus the PG1-dimer forms a relatively stronger complex with mixed POPG:POPE membrane compared to a single PG1 peptide. Here we can clarify the choice of binding and geometry parameters for the system, D0, a and l. Again, we choose them so that MD and PB results are comparable. The latter are discussed in the next subsection. Analysis of the dimensions of the components of the system shows that the peptide PG1 can be represented by a spherical macroion with effective radius a ≈ 8.9 Å and a PG1 dimer with effective radius a ≈ 11.1 Å. These are the numbers we use in both PB and MD calculations. The minimum separation distance between the membrane surface and the peptide surface is chosen as D0 = 0. When analyzing the restraint forces Fres(z), we find that F̄(z) ≈ 0 for D > 18 Å, for both the PG1 and the PG1 dimer. Therefore the peptide is considered to be bound within l = D +a = 26.9Å, and the PG1 dimer within l = 29.1Å. We set the “zero” value for PMF at D=20 Å. We think this is a reasonable choice, because we find from MD simulations that the absolute value of mean forces F̄(z) for D =14 Å and D=16 Å is less than 0.25 (kcal/mol)/Å for PG1 and PG1 dimer. This is small than the statistical error in the calculation of the mean force, found to be 0.35 (kcal/mol)/Å using a block-averaging method.41
Figure 5.
The total free energy profile (PMF) W(D) for PG1 peptide and PG1 dimer obtained from MD simulation. Each data point for W(D) represents the mean of eight 0.5 ns simulations, and the error bar represent the standard deviation obtained from the dispersion among the eight. D is the separation distance between the PG1 surface and the phosphate plane of the upper leaflet of the membrane.
Using (3) we find an adsorption free energy for a PG1 monomer of ΔG0 = −2.4 ± 0.8 kcal/mol and an adsorption free energy for a PG1 dimer of ΔG0 = −3.5 ± 1.1 kcal/mol. Again then, the PG1 dimer binding is found to be relatively stronger, compared to the adsorption free energy of a monomer PG1 peptide.
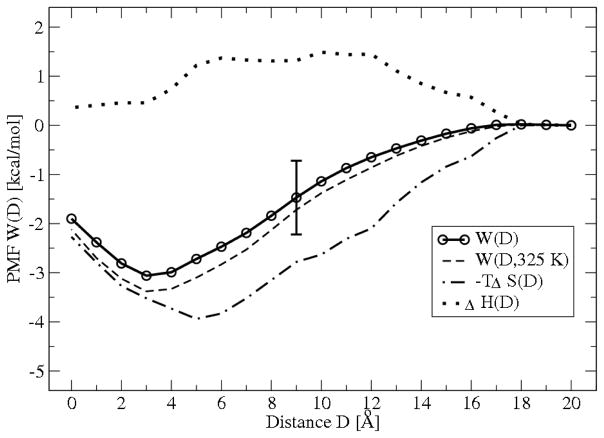
To analyze the nature of PG1-(1:3) POPG:POPE membrane interaction and to determine the contribution of the release of “bound” counterions to the peptide adsorption using MD simulation we decompose the adsorption free energy profile W(D) into enthalpic [ΔH(D)] and entropic [−TΔS(D)] components obtained from three different series of MD simulations using (5) and (6). The simulations were conducted at a temperature 310 K and ΔT = 15K. The results are shown in Figure 6. For comparison purposes, the free energy profile at the temperature of 325 K, W(D, 325K), is shown only for PG1-(1:3) POPG:POPE membrane interaction. For PG1-(1:3) POPG:POPE membrane, the adsorption free energy is dominated by the entropic contributions due to the counterion release from the membrane, while for the neutral membrane, the binding process is enthalpically driven.29
Figure 6.
The total free energy profile (PMF) W(D) for PG1 peptide interacting with a (1:3) POPG:POPE lipid bilayer and decomposition of W(D) into entropy −T ΔS(D) and enthalpy ΔH(D) contributions obtained from three different series of MD simulation using (5), (6) at the temperature 310 K and Δ T =15 K. For comparison purposes, the free energy profile at the temperature 325 K W(D,325K), are shown. D is the separation distance between the PG1 surface and the phosphate plane of the upper leaflet of the membrane.
PG1 - POPG:POPE PMF from Poisson-Boltzmann theory
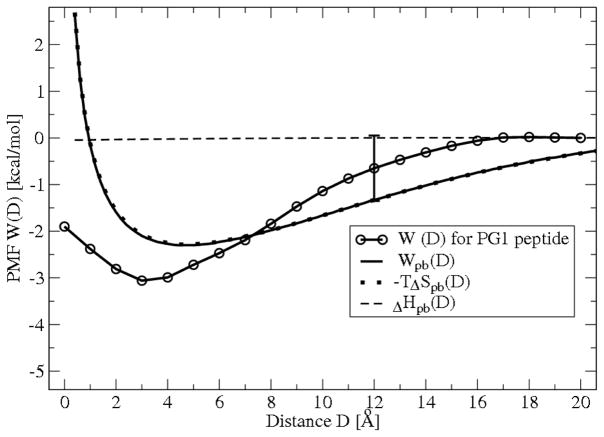
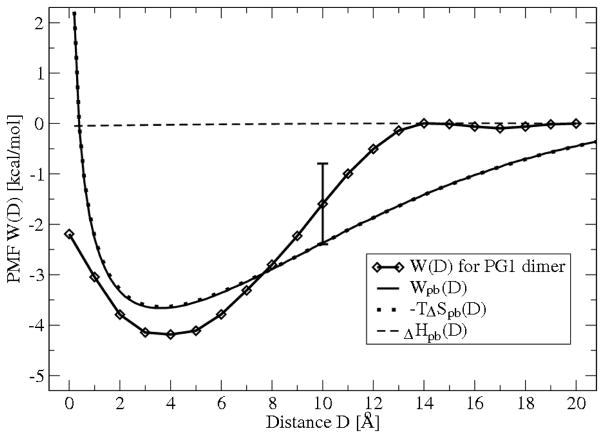
A numerical solution for the PB equation (7) with boundary conditions (8), (9) and osmotic pressure (10) can be calculated with MATLAB 7.7.0 (R2008b). The electrostatic PB PMF, Wpb(D), calculated using (11) together with the averaged PMF, W(D), obtained from MD simulation of the mixed membrane interacting with single PG1 peptide and with PG1 dimer are plotted in Figure 7 and Figure 8, respectively. The two curves for Wpb(D) and for W (D) from MD simulation on both figures are in relatively good agreement. Although the level of agreement between the two curves is high, it is not perfect since Wpb(D) does not include attractive van der Waals interactions29 Furthermore, the peptide and membrane charge distribution is assumed to be uniform. Despite these discrepancies, the simplified PB approach predicts a relatively good value of the PMF well-depth well enough to estimate the binding energy with reasonable accuracy.
Figure 7.
The total free energy profile (PMF) W(D) for PG1 peptide obtained from MD simulation and the theoretical electrostatic free energy profile from Poisson-Boltzmann theory, Wpb(D), are shown. Wpb(D) is calculated numerically from PB theory using (7), (10), (11). Decomposition of Wpb(D) into entropy −T ΔSpb(D) and enthalpy ΔHpb(D) contributions for the 1:3 mixture of POPG:POPE lipid bilayer interacting with a charged sphere representing the PG1 peptide we obtained from three different series of numerical solutions for Wpb(z), as explained in the text.
Figure 8.
The total free energy profile (PMF) W(D) for PG1 dimer obtained from MD simulation and the theoretical electrostatic free energy profile from Poisson-Boltzmann theory, Wpb(D), are shown. Each data point for W(D) represents the mean of eight 0.5 ns simulations, and the error bar represent the standard deviation obtained from the dispersion among the eight. Wpb(D) is calculated numerically from PB theory using (7), (10), (11). Decomposition of Wpb(D) into entropy −TΔSpb(D) and enthalpy ΔHpb(D) contributions for the 1:3 mixture of POPG:POPE lipid bilayer interacting with a charged sphere representing the PG1 dimer we obtained from three different series of numerical solutions for Wpb(z).
To decompose the PB PMF Wpb(D) (11) into entropic [−TΔSpb(D)] and enthalpic [ΔHpb(D)] (or internal energy ΔUpb(D)) contributions we take into account the temperature dependence of the water dielectric constant ε. An expression for the dielectric constant for TIP3P water was obtained using calculation of dipole moment fluctuations in the system as (eq.(76) in42):
| (12) |
where the choice of constants α and β depends on the type of water model and boundary conditions of the system, as discussed in.42 For the TIP3 water, dielectric constants calculated from (12) are ε=95 at T=310 K, ε=99 at T=295 K, and ε=90 at T=325 K. These values are employed in the decomposition of Wpb(D) into entropy, −T ΔSpb(D), and enthalpy, ΔHpb(D), contributions. These are obtained from three different series of numerical solutions for Wpb(z) using (5), (6) at T=310 K with Δ T =15 K. The entropic contribution [−TΔSpb(z)] together with Wpb(z) and ΔHpb(z) calculated for a single PG1 peptide and a PG1 dimer are shown in Figure 7 and Figure 8, respectively. We see that the PB electrostatic free energy profile essentially coincides with its entropy component in both cases. In other words, we find that the attraction of PG1 peptide or PG1 dimer to the membrane is of an almost entirely entropic nature. The enthalpic (or the electrostatic attraction) contribution, ΔHpb(z), to the PB PMF is negative (i.e. attractive), but rather small when compared to the entropic attraction −TΔSpb(z) induced by released ions from the ouble layer. Thus, for the mixed charged (1:3) POPG:POPE membrane interacting with a positively charged peptide, we can claim that the binding process is entropically driven due to counterion release from the screening ion layers.
Conclusions
The purpose of this paper is to explain the physical origin of the attractive forces between protegrin-1 and a (1:3) POPG:POPE membrane. We use MD simulations to analyze counterion release upon binding of either the monomeric or the dimeric form of PG1. We calculate the adsorption free energy for PG1 monomer to be ΔG0 = −2.4 ± 0.8 kcal/mol and the adsorption free energy for PG1 dimer to be ΔG0 = −3.5 ± 1.1 kcal/mol. To analyze the nature of the peptide membrane interaction and to determine the contribution of the release of “bound” counterions to the peptide adsorption using MD simulation we decompose the free energy profile W(D) for a single PG1 peptide interacting with (1:3) POPG:POPE membrane into enthalpic and entropic components obtained from three different series of MD simulation at different temperatures. Using this approach we predict that for PG1-(1:3) POPG:POPE membrane interaction the adsorption free energy is dominated by the entropic contributions due to the counterion release from the membrane. These results are in good agreement with theoretical predictions based on numerical solution of the nonlinear Poisson-Boltzmann equation for all separations between membrane and peptides. We decompose the adsorption PB free energy profile Wpb(D) into enthalpic and entropic contributions and find good qualitative agreement with MD results. The counterion release from the electric double layer appears as the physical origin of the strong attraction between the charged membrane and peptides. As we show, the PG1-dimer forms a relatively stronger binding complex with mixed POPG:POPE membrane compared to that with a single PG1 peptide. Further simulations of PMF for PG1 dimers and there complexes, particularly in the water and inside the membrane, will be useful, because they will shed light on the steps that take peptides from solution to a pore in the membrane.
Acknowledgments
This study utilized the high-performance computational resources of the National Computational Science Alliance under MCA04T033. Computational support from the Minnesota Supercomputing Institute (MSI) is gratefully acknowledged. The project was funded by a grant from NIH (GM 070989).
References
- 1.Zasloff M. Nature (London) 2002;415:389–395. doi: 10.1038/415389a. [DOI] [PubMed] [Google Scholar]
- 2.Devine DA, Hancock REW, editors. Mammalian Host Defense Peptides. Cambridge University Press; Cambridge, England: 2004. [Google Scholar]
- 3.Hancock RE. Lancet. 1997;349:418–422. doi: 10.1016/S0140-6736(97)80051-7. [DOI] [PubMed] [Google Scholar]
- 4.Matsuzaki K. Biochim Biophys Acta. 1999;1462:1–10. doi: 10.1016/s0005-2736(99)00197-2. [DOI] [PubMed] [Google Scholar]
- 5.Qu XD, Harwig SS, Shafer WM, Lehrer RI. Infect Immun. 1997;65:636–639. doi: 10.1128/iai.65.2.636-639.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yang L, Weiss TM, Lehrer RI, Huang H. Biophys J. 2000;79:2002–2009. doi: 10.1016/S0006-3495(00)76448-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Langham AA, Khandelia H, Schuster B, Waring AJ, Lehrer RI, Kaznessis YN. Peptides. 2008;29:1085–1093. doi: 10.1016/j.peptides.2008.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Langham AA, Sayyed-Ahmad A, Kaznessis YN. J Am Chem Soc. 2008;130:4338–4346. doi: 10.1021/ja0780380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bolintineanu DS, Sayyed-Ahmad A, Davis HT, Kaznessis YN. PLoS Computational Biology. 2009;5:e1000277. doi: 10.1371/journal.pcbi.1000277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Khandelia H, Kaznessis YN. BBA Biomembranes. 2007;1768:509–520. doi: 10.1016/j.bbamem.2006.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jang H, Ma B, Woolf TB, Nussinov R. Biophys J. 2006;91:2848–2859. doi: 10.1529/biophysj.106.084046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fahrner RL, Dieckmann T, Harwig SS, Lehrer RI, Eisenberg D, Feigon J. Chem Biol. 1996;3:543–550. doi: 10.1016/s1074-5521(96)90145-3. [DOI] [PubMed] [Google Scholar]
- 13.Mani R, Tang M, Wu X, Buffy IJ, Waring AJ, Sherman MA, Hong M. Biochemistry. 2006;45:8341–8349. doi: 10.1021/bi060305b. [DOI] [PubMed] [Google Scholar]
- 14.Jang H, Ma B, Lal R, Nussinov R. Biophys J. 2008;95:4631–4642. doi: 10.1529/biophysj.108.134551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tolokh I, Vivcharuk V, Tomberli B, Gray CG. Phys Rev E. 2009;80:031911. doi: 10.1103/PhysRevE.80.031911. [DOI] [PubMed] [Google Scholar]
- 16.Meier-Koll AA, Fleck CC, von Grunberg HH. J Phys: Condens Matter. 2004;16:6041–6052. [Google Scholar]
- 17.Ben-Yaakov D, Burak Y, Andelman D, Safran SA. Europhys Lett. 2007;79:48002. [Google Scholar]
- 18.Roumestand C, Louis V, Aumelas A, Grasi G, Calas B, Chavanieu A. FEBS Lett. 1998;421:263–267. doi: 10.1016/s0014-5793(97)01579-2. [DOI] [PubMed] [Google Scholar]
- 19.Brooks BR, Brucolleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. J Comp Chem. 1983;4:187–217. [Google Scholar]
- 20.Kim SJT, Iyer VG, Im W. J Comput Chem. 2008;29:1859–1865. doi: 10.1002/jcc.20945. [DOI] [PubMed] [Google Scholar]
- 21.MacKerell AD, Bashford D, Bellot M, Dunbrack RL, Evanseek J. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 22.MacKerell AD, Feig M, Brooks CL. J Chem Soc Soc. 2004;126:698–699. doi: 10.1021/ja036959e. [DOI] [PubMed] [Google Scholar]
- 23.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kalle L, Schulten K. J Comp Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Martyna GJ, Tobias DJ, Klein ML. J Chem Phys. 1994;101:4177–4189. [Google Scholar]
- 25.Feller SE, Zhang Y, Pastor RW, Brooks BR. J Chem Phys. 1995;103:4613–4621. [Google Scholar]
- 26.Tang M, Waring J, Hong M. ChemBioChem. 2008;9:1487–1482. doi: 10.1002/cbic.200800005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 28.Darden T, Perera L, Li L, Pedersen L. Structure. 1999;7:R55–R60. doi: 10.1016/s0969-2126(99)80033-1. [DOI] [PubMed] [Google Scholar]
- 29.Vivcharuk V, Tomberli B, Tolokh IS, Gray CG. Phys Rev E. 2008;77:031913. doi: 10.1103/PhysRevE.77.031913. [DOI] [PubMed] [Google Scholar]
- 30.Chipot C, Pohorille A, editors. Free Energy Calculations. Springer; Berlin: 2007. [Google Scholar]
- 31.Tobias DJ, Brooks CL., III Chem Phys Lett. 1987;142:472–476. [Google Scholar]
- 32.Roux B, Karplus M. Biophys J. 1991;59:961–981. doi: 10.1016/S0006-3495(91)82311-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ciccotti G, Ferrario M, Hynes JT, Kapral R. Chem Phys. 1989;129:241–251. [Google Scholar]
- 34.Shinto H, Morisada S, Miyahara M, Higashitani K. J Chem Eng Jap. 2003;36:57–65. [Google Scholar]
- 35.Darve E. In: Free Energy Calculations. Chipot C, Pohorille A, editors. Springer; Berlin: 2007. p. 119. [Google Scholar]
- 36.Russel W, Saville DA, Schowalter WR. Colloidal Dispersions. Cambridge University Press; Cambridge: 1989. [Google Scholar]
- 37.Andelman D. In: Handbook of Physics of Biological Systems. Lipowsky R, Sackman E, editors. Vol. 1. Elsevier Science; Amsterdam: 1995. p. 603. Chap 12. [Google Scholar]
- 38.Hochtl P, Boresch S, Bitomsky W, Steinhauser O. J Chem Phys. 1998;109:4927–4937. [Google Scholar]
- 39.Pandit SA, Bostick D, Berkovitz ML. Biophys J. 2003;85:3120–3131. doi: 10.1016/S0006-3495(03)74730-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhao W, Rog T, Gurtovenko A, Vattulainen I, Karttunen M. Biophys J. 2007;92:1114–1124. doi: 10.1529/biophysj.106.086272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Flyvbjerg H, Petersen HG. J Chem Phys. 1989;91:461–466. [Google Scholar]
- 42.Stern HA, Feller SE. J Chem Phys. 2003;118:3401–3412. [Google Scholar]