Non-Uniform Object-Space Pixelation (NUOP) for Penalized Maximum-Likelihood Image Reconstruction for a Single Photon Emission Microscope System

Abstract

This paper presents a non-uniform object-space pixelation (NUOP) approach for image reconstruction using the penalized maximum likelihood methods. This method was developed for use with a single photon emission microscope (SPEM) system that offers an ultrahigh spatial resolution for a targeted local region inside mouse brain. In this approach, the object-space is divided with non-uniform pixel sizes, which are chosen adaptively based on object-dependent criteria. These include (a) some known characteristics of a target-region, (b) the associated Fisher Information that measures the weighted correlation between the responses of the system to gamma ray emissions occurred at different spatial locations, and (c) the linear distance from a given location to the target-region. In order to quantify the impact of this non-uniform pixelation approach on image quality, we used the Modified Uniform Cramer-Rao bound (MUCRB) to evaluate the local resolution-variance and bias-variance tradeoffs achievable with different pixelation strategies. As demonstrated in this paper, an efficient object-space pixelation could improve the speed of computation by 1–2 orders of magnitude, whilst maintaining an excellent reconstruction for the target-region. This improvement is crucial for making the SPEM system a practical imaging tool for mouse brain studies. The proposed method also allows rapid computation of the first and second order statistics of reconstructed images using analytical approximations, which is the key for the evaluation of several analytical system performance indices for system design and optimization.

I. Introduction

SINGLE photon emission computed tomography (SPECT) is a widely used imaging modality for mapping the distribution of radiolabeled molecules [1]. One of the recent trends in SPECT instrumentations is to achieve an ultrahigh resolution for imaging small lab animals. Several recent developments include the SemiSPECT reported by Kastis et al. [2], the SiliSPECT under development by Peterson et al.. [3], the MediSPECT proposed (and evaluated) by Accorsi et al.. [4] and the U-SPECT-III proposed by Beekman et al.. [5], a low-cost ultra-high resolution imager based on the second-generation image intensifier [6] and the use of a pre-existing SPECT camera, arranged in an extreme focusing geometry for ultra-high resolution small animal SPECT imaging applications [7]. We have recently developed a prototype single photon emission microscope (SPEM) system for mouse brain studies [8], [9]. This system was based on the intensified EMCCD cameras that offer an excellent intrinsic resolution for low energy gamma rays [10]. It was demonstrated that the current dual-headed SPEM system is capable of visualizing a very small number (< 1000) of radiolabeled T cells in mouse brain [11].

In the work presented in this paper, we have developed an adaptive and non-uniform object pixelation (NUOP) strategy for image reconstruction using SPEM data. For most of reconstruction problems, image functions are typically represented with equally sized square pixels or cubic voxels throughout the object space. Despite its simplicity, the uniform sampling provided by the square pixels could be less efficient for the SPEM application. First, to fully utilize its excellent resolution capability, the reconstruction of SPEM images requires the use of very small pixel sizes, say 50 μm or below. If such pixel sizes were used uniformly throughout the entire object-space, the reconstruction would involve a tremendous amount of computation. Despite the extensive effort in adapting the reconstruction task in parallel computing environment, a single SPEM reconstruction typically requires tens of hours to a few days to complete. Secondly, since the primary task of the SPEM system is to reveal the microscopic structure inside a target-region, one could tolerate lower spatial resolutions in areas outside the target-region. Therefore, larger pixels could be used outside the target-region for an improved computation efficiency. Thirdly, given the fixed amount of imaging information carried by projection data, reducing the overall number of unknowns may help to improve the condition of the inverse problem and (in certain cases) to reduce noise in reconstructed images of the target-region.

The development of the NUOP scheme carries a similar spirit as several previous or on-going research efforts in the search for adaptive and sparse image representation schemes. These methods, in general, help to combat the ill-posed nature of reconstruction problems and to reduce the computational effort involved in medical image reconstruction. Several authors, such as Maltz et al. [12] and Zhang et al.. [13], have proposed and evaluated the use of nonuniform resolution grids in 3-D image reconstruction. Brankov et al.. have proposed the use of several content-adaptive mesh models that provide an efficient image representation based on adaptive sampling and linear interpolation [14], [15]. Similar to the previous approach, this method allows the density of sample points to vary according to the degrees of spatial details presented in different areas inside the object. Sitek et al.. have proposed the use of an adaptive tetrahedral mesh model defined by a point cloud [16]. In addition, the efforts by Reutter et al. of using spatial-segmentation and temporal B-spline basis functions for rapid kinetic parameter estimation from SPECT data could also fall into this category [17], [18].

Unlike these previous approaches [12]–[18], the NUOP approach proposed in this paper does not require any a priori information of the object to be imaged. Instead, it is determined adaptively according to (a) the imaging information being acquired by the detection system, (b) the known system response function and (c) the user-defined target-region. This approach offers a significant reduction of computation-effort without sacrificing the imaging quality in the target-region. This makes it particularly useful for the SPEM application. In addition, this development also allows rapid evaluation of the first and second order statistics of reconstruction images using analytical approximations. This provides crucial information for the derivation of several statistical system performance indices that could be used in system design and optimization [19]–[26].

In this study, we proposed and evaluated several systematic approaches for choosing NUOP for given objects. In order to study the effect of NUOP on reconstruction, we used the modified Uniform Cramer-Rao Bound (MUCRB) [25], [26] to evaluate the tradeoffs between spatial resolution and variance achieved in reconstructed images. Results from a Monte Carlo (MC) study of the NUOP methods are also presented in this paper.

II. Material and Methods

A. The SPEM System and Potential Challenges

We have previously reported the design and development of a single photon emission microscope system [8]–[11]. This system is based on the I-EMCCD detector that offers an intrinsic resolution of around 50 μm and a large imaging area of around 80 mm in diameter. These detectors are used with highly focusing multiple-pinhole collimators for imaging local target-regions, which are identified in scout images acquired with a separate low-resolution system or with the same detection system but using a low-resolution and high-sensitivity aperture.

Despite the feasibility demonstrated in previous studies, there exist several aspects of the SPEM system that require further improvements. First, image reconstruction with SPEM data is very time-consuming. Even with appropriate exploitation of the sparseness associated with multiple pinhole geometry, the total number of non-zero elements in a system response function (SRF) could reach the order of 10¹⁴. With the use of an eight-PC cluster that we assembled for this application, a single reconstruction typically takes a few days to complete. An improved reconstruction speed is crucial for practical applications of the SPEM system. Secondly, since the SPEM system is optimized for microscopic imaging of T-Rs, an ideal imaging scenario should consist of multiple iterations of studies using adaptive hardware, as proposed by Barrett et al. [27], and Freed et al. [28]. The information acquired through previous iterations could be used to refine the system configurations in real time. This adaptive imaging process would allow for an improved efficiency for collecting information regarding the target-region. A rapid and accurate image reconstruction process is crucial for implementing this adaptive imaging scheme.

B. Image Reconstruction

Let x = [x₁, x₂, … , x_N]^T denote the set of unknown deterministic parameters, e.g., the object intensities underlying the projection data y = [y₁, y₂, … , y_M]^T, the mapping from x to y is governed by a conditional probability density function, p(y∣x). For emission tomography, y can be approximated as a collection of independent random Poisson variables, whose expectations are given by

$$\overline{\mathbf{y}}\equiv E\left[\mathbf{y}\right]=\int p\left(\mathbf{y}\mid \mathbf{x}\right)\cdot d\mathbf{y}$$ (1)

or by the following discrete transform:

$$\overline{\mathbf{y}}=\mathbf{A}\cdot \mathbf{x}$$ (2)

where A is a M × N matrix that represents the discretized system-response function (SRF). Here we assumed that all systematic errors are corrected in the projection data. For linear Poisson variables y, the log-likelihood function is given by

$$L\left(\mathbf{y}\mid \mathbf{x}\right)\equiv \log p\left(\mathbf{y}\mid \mathbf{x}\right)=\sum y_i\log {\overline{y}}_i-{\overline{y}}_i$$ (3)

and

$${\overline{y}}_i=\sum _j{a}_{\mathit{ij}}{x}_j$$ (4)

where a_ij, gives the probability of a gamma-ray emitted from the j′th source voxel and being detected by the i′th detector pixel. The underlying image function may be reconstructed as

$$\{\begin{array}{c}{\widehat{\mathbf{x}}}_{\mathbf{P}\mathit{ML}}={\text{arg max}}_{\mathbf{x}}[L\left(\mathbf{y}\mid \mathbf{x}\right)-\beta R\left(\mathbf{x}\right)]\hfill \\ \text{and then}\hfill \\ {\widehat{\mathbf{x}}}_{\mathbf{PF}-\mathit{PML}}=\mathbf{F}\cdot {\widehat{\mathbf{x}}}_{\mathit{PML}}\left(\mathbf{y}\right)\hfill \end{array}\phantom{\}}$$ (5)

where R(x) is a scalar function that selectively penalizes certain undesired features in reconstructed images. F is an N × N matrix that represents the post-filtering operator. In this study, we used a quadratic roughness penalty function as defined by [29]

$$R\left(\mathbf{x}\right)=\sum _j\frac{1}{2}\sum _k{w}_{\mathit{jk}}\varphi \left(x_j-x_k\right)$$ (6)

where w_jk’s are the weighting factors that are non-zero for the pairs of immediate neighbours, and

$$\varphi \left(t\right)=\frac{t^2}{2}.$$ (7)

We have previously developed a parallel computation scheme for reconstructions using (5), which is implemented on a cluster of eight PCs with 24 processors. Images reconstructed with this setup were reported in [11].

C. Non-Uniform Object-Space Pixelation

If the final goal of a SPEM study is to obtain focused microscopic images of a local target-region (T-R), it is possible to speed up the reconstruction with a non-uniform object-space pixelation approach as detailed below:

• Step 1: Full system modeling. In this process, the object is divided into sufficiently small and uniform pixels. For example, one could use pixel-sizes smaller than or equal to 1/2 of the expected system resolution. This step results in a large and comprehensive system response function (SRF #1).

• Step 2: Define the pixelation density function (PDF). In the proposed NUOP approach, the pixelation density is represented by a vector D of N elements. Each element is an integer number ranging from 0 to (N_D – 1) that indicates the pixelation density designated for a corresponding source pixel. N_D is the maximum number of density levels chosen by the user. Several systematic approaches for defining PDFs will be discussed later in Section II-D. Here, we describe a simple algorithm for the actual rebinning process with a given PDF. For a given source pixel j, the corresponding D-value (D_j) equal to 0 indicates that the pixel does not need rebinning. D_j = 1 indicates that one would put 2 × 2 × 2 adjacent pixels into a larger pixel, D_j = 2 indicates binning 4 × 4 × 4 pixels together and so on. The rebinning process is started by looping through pixels having the maximum D-value (N_D – 1 according to the current definition). For a given pixel k, the nearby pixels to be combined are determined by a pre-defined look-up table. Within these pixels, only those with the same D-value and have not been grouped with any other pixel will be combined with pixel k and the rest pixels are ignored. Once the rebinning process for the current pixel (k) is completed, the algorithm goes on to find the next pixel with the same D-value and then combines it with its neighbors in the same way. After all pixels with the same D-value have been processed, the algorithm will then move on to those pixels with a smaller D-value and keep doing so until all pixels with D-values greater than 0 have been processed. The pixel numbers after rebinning are given based on the order, by which they are formed in the rebinning process. In practice, the user has complete freedom in defining the rebinning parameters, such as N_D and the subset of pixels to be combined with each target pixel, in response to the specific imaging task.

• Step 3: Rebin the SRF. Given SRF #1 and a PDF (D), a new SRF is derived by binning the entries of SRF #1 accordingly. For pixels to be combined into a larger pixel, the corresponding SRF elements are extracted from SRF #1. This process is equivalent to forward projecting from these pixels using SRF #1 and then combining the projections of individual pixels into a single projection. This gives the probability of a gamma ray emitted from the combined source pixel to be detected by each detector pixel in the system. For each target pixel, the subset of pixels to be combined are determined with the procedure described in Step 2. The SRF derived with this rebinning process is referred to as SRF #2, which is typically much smaller than SRF #1. Another operation in this step is to determine and record the neighboring pixels for each pixel-of-interest in the rebinned object-space. This information will be used later in reconstruction for defining the regularization (or penalty) function. This rebinning process, in effect, transforms the original mapping (2) into a new form

  $$\overline{\mathbf{y}}={\mathbf{A}}_{\mathit{RB}}\cdot {\mathbf{x}}_{\mathit{RB}}+\mathbf{r}$$ (8)

  where matrix A_RB denotes the rebinned SRF (SRF #2). Source function, x_RB, represents the concentrations of radioactivity contained in each pixel in the rebinned object-space. In the following text, we will refer to the object spaces, before and after the rebinning, as S₁ and S₂.
• Step 4: Reconstruction based on the original projection data y and SRF #2.

  $${\left({\widehat{\mathbf{x}}}_{\mathbf{P}\mathit{ML}}\right)}_{\mathit{RB}}=\text{arg}\underset{{\mathbf{x}}_{\mathit{RB}}}{\text{max}}[L\left(\mathbf{y}\mid {\mathbf{x}}_{\mathit{RB}}\right)-\beta R_{\mathit{RB}}\left({\mathbf{x}}_{\mathit{RB}}\right)].$$ (9)

  In this study, the penalty function R_RB(x_RB) is defined similarly as in (7) and (8) and all non-zero weighting factors, w_ij’s, were set to 1 for simplicity. Neighboring pixels were previously determined in Step 3.

• Step 5: Restore the resultant image, ${\left({\widehat{\mathbf{x}}}_{\mathbf{P}\mathit{ML}}\right)}_{\mathit{RB}}$, to produce an image representation in S₁. Based on the PDF defined in Step 2, the value of a given pixel j in S₂ is uniformly assigned back to those pixels in S₁ that was originally combined according to the rebinning process described in Steps 2 and 3. Similar processes are repeated until all pixels in S₂ are restored. The resultant image is referred to as ${\widehat{\mathbf{x}}}_2$ in the following text.

• Step 6: Post-filtering ${\widehat{\mathbf{x}}}_2$ with desired filter functions.

D. Fisher Information Matrix and Non-Uniform Object-Space Pixelation

The key to this proposed pixelation scheme is to find meaningful PDFs. In order to reduce the amount of computation involved, one would use as less source pixels as possible. However, a discrete image representation with a sufficiently fine sampling is necessary to ensure that the subtle details in the target-region are retained in reconstruction. This is particularly important for SPEM studies. In this section, we propose an adaptive procedure for defining the spatially variant PDFs. This approach is based on the corresponding Fisher Information matrix (FIM) [19]. For the imaging problem as outlined in (1)–(5), the associated FIM is given as,

$$\mathbf{J}=-E\left\{\left[\frac{\partial \log p\left(\mathbf{y}\mid \mathbf{x}\right)}{\partial \mathbf{x}}\right]\cdot {\left[\frac{\partial \log p\left(\mathbf{y}\mid \mathbf{x}\right)}{\partial \mathbf{x}}\right]}^T\right\}.$$ (10)

When the measured projection is characterized by a set of independent Poisson variables, FIM is given by

$$J_{\mathit{jk}}=-E\left[\frac{{\partial }^2}{\partial x_j\partial x_k}\log p\left(\mathbf{y}\mid \mathbf{x}\right)\right]\approx \sum _m\frac{a_{\mathit{mj}}\cdot a_{\mathit{mk}}}{\sum _n{a}_{\mathit{mn}}{x}_n}.$$ (11)

In practice, the source vector x is generally unknown. One may replace x with an estimated source distribution $\widehat{\mathit{x}}$ from a scout measurement and ignore the expectation operator in (11). This leads to the so-called observed Fisher Information matrix [30]

$$\mathbf{J}={\mathbf{A}}^T\text{diag}\left[\frac{1}{y}\right]\mathbf{A}.$$ (12)

It is easily seen that each column of J measures the weighted correlation between the responses of the system to gamma ray emission at a given pixel of interest and at all other pixels in object-space. As previously demonstrated by Qi et al. [21], [22], for spatially-invariant imaging systems, the reconstructed image property (such as impulse response function and local covariance structure) at or around a given pixel is affected mostly by those pixels that have relatively large (weighted) correlation with the pixel-of-interest. Therefore, one could use a finer pixelation for the target region and other correlated regions and use a coarser pixelation for regions less correlated to the target-region. This should not lead to significant degradation in reconstructed images of the target-region.

Based on this concept, the pixelation density function (PDF) could be chosen using the following procedures. First, one reconstructs the source distribution with a relatively coarse pixelation. For example, the pixel size could be chosen to be the smallest one that still provides an acceptably fast reconstruction. In practice, we found that representing a 3-D object with 32 × 32 × 32 pixels is usually adequate. The image obtained is used to identify a target-region and to provide a rough estimate of the underlying source function. For a given target-region ($\Re$), the columns of J corresponding to the pixels inside the region are derived using (12) and then combined into a single vector

$$\mathbf{Q}=\sum _{k\in \Re }\mathbf{J}\cdot e_k$$ (13)

where e_k is the k′th unit vector. Note that column vectors of J derived with (13) will be evaluated based on SRF #1.

As previously discussed, vector Q reveals the “relative importance” of each source pixel for the reconstruction of the target-region. The corresponding PDF (D) is therefore defined as a function of Q,

$$D_j=f\left(Q_j\right),$$ (14)

where f(·) is a pre-defined function that converts Q_j into the corresponding D-value that is an integer number ranging from 0 to (N_D – 1).

In this study, we evaluated three different functions for defining D. In the first approach, D_j is defined as

$$\begin{array}{cc}\hfill D_1{\mid }_j& =f\left(Q_j\right)\hfill \\ \hfill & =\{\begin{array}{cc}\mathrm{int}\left\{{\log }_s\frac{\max [Q_j,j=1,\dots ,N]}{Q_j}\right\},\hfill & \text{when}j\notin \Re ,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (15)

where int[u] returns the maximum integer that is smaller or equal to u. Constant s in (15) controls the rate, by which D_j changes with Q_j. In this work, we used an identical value s = 2 for all studies. This procedure assigns the ranking of each source pixel according its correlations to pixels inside the target-region.

We have also evaluated a more aggressive way of reducing the number of pixels in object-space, in which the PDF is defined as

$$\begin{array}{cc}\hfill D_2{\mid }_j& =f\left(Q_j\right)\hfill \\ \hfill & =\{\begin{array}{cc}\mathrm{int}\left\{{\log }_s\frac{\max \left[Q_j\cdot \left(\frac{1}{r_j^t}\right),j=1,\dots ,N\right]}{Q_j\cdot \left(\frac{1}{r_j^t}\right)}\right\},\hfill & \text{when}j\notin \Re ,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (16)

where r_j is the distance between the j′th pixel to the center of the target-region. The PDF given by (16) depends on both the FIM and how far a given location is from the center of the target-region. Factor t controls the degree of the distance-dependency. For comparison, the results obtained with (15) and (16) were evaluated against the results derived using the following simple PDF

$$\begin{array}{cc}\hfill D_3{\mid }_j& =f\left(Q_j\right)\hfill \\ \hfill & =\{\begin{array}{cc}\mathrm{int}\left\{{\log }_s\frac{\max [1{\mathit{overr}}_j^t,j=1,\dots ,N]}{\frac{1}{r_j^t}}\right\},\hfill & \text{when}j\notin \Re ,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (17)

which depends only on the linear distance r_j. The above definitions of PDFs are summarized in Table I.

TABLE I.

Summary of the Pixelation Density Functions Compared

PDF	Formulations	Note
D 1	$D_1{\mid }_j=\{\begin{array}{ccc}\hfill \mathrm{int}\left\{{\log }_s\frac{\max \left[Q_j,j=1,\dots ,N\right]}{Q_j}\right\},\hfill & \hfill \mathit{when}\hfill & \hfill j\notin \Re \hfill \\ \hfill 0,\hfill & \hfill \mathit{otherwise}\hfill & \hfill \hfill \end{array}\phantom{\}}$	PDF depends on the weighted correlation between the responses of the system to gamma ray emissions in the target-region and in other regions. Defined based on FIM.
D 2	$D_2{\mid }_j=\{\begin{array}{ccc}\hfill \mathrm{int}\left\{{\log }_s\frac{\max \left[Q_j\cdot \left(1∕r_j^t\right),j=1,\dots ,N\right]}{Q_{\mathit{ij}}\cdot \left(1∕r_j^t\right)}\right\},\hfill & \hfill \mathit{when}\hfill & \hfill j\notin \Re \hfill \\ \hfill 0,\hfill & \hfill \mathit{otherwise}\hfill & \hfill \hfill \end{array}\phantom{\}}$	PDF depends on both FIM and how far a pixel is from the center of a target-region. More aggressive in reducing the number of pixels in object space.
D 3	$D_3{\mid }_j=\{\begin{array}{ccc}\hfill \mathrm{int}\left\{{\log }_s\frac{\max \left[1∕r_j^t\right],j=1,\dots ,N}{1∕r_j^t}\right\},\hfill & \hfill \mathit{when}\hfill & \hfill j\notin \Re \hfill \\ \hfill 0,\hfill & \hfill \mathit{otherwise}\hfill & \hfill \hfill \end{array}\phantom{\}}$	PDF depends on the linear distance r only. Emphasize the importance of the target-region only, without considering the correlation with other regions in the object-space.

E. Modified UCRB

The impact of the proposed NUOP scheme on image quality was evaluated based on the Modified Uniform Cramer-Rao bound (MUCRB) that we previously developed for comparing different imaging system designs [25], [26]. Using this method, one can derive and compare the local resolution-variance tradeoffs in reconstructed images achievable with different PDFs. The spatial resolution property of an estimator can be quantified using the linearized local-impulse response (LIR) function [29]. Suppose is an estimator of the underlying image function derived based on a given measurement y, the mean of the estimator is defined as

$$\mu \left(\mathbf{x}\right)=E_{\mathbf{x}}\left[\widehat{\mathbf{x}}\left(\mathbf{y}\right)\right]=\int \widehat{\mathbf{x}}\left(\mathbf{y}\right)\cdot p\left(\mathbf{y}\mid \mathbf{x}\right)\cdot d\mathbf{y}$$ (18)

where E[·] denotes the expectation operator. The linearized LIR for the j′th pixel is given by [22]

$$\begin{array}{cc}\hfill {\mathbf{l}}_j\left(\mathbf{x}\right)=& \underset{\delta \to 0}{\lim }\frac{\mu \left(\mathbf{x}+\delta e_j\right)-\mu \left(\mathbf{x}\right)}{\delta }=\frac{\partial \mu \left(\mathbf{x}\right)}{\partial x_j}\hfill \\ \hfill =& [\frac{\partial E_{\mathbf{x}}\left({\widehat{x}}_1\right)}{\partial x_j},\frac{\partial E_{\mathbf{x}}\left({\widehat{x}}_2\right)}{\partial x_j},\dots ,\frac{\partial E_{\mathbf{x}}\left({\widehat{x}}_N\right)}{\partial x_j},\dots ,\hfill \\ \hfill & {\frac{\partial E_{\mathbf{x}}\left({\widehat{x}}_N\right)}{\partial x_j}]}^T.\hfill \end{array}$$ (19)

The mean gradient vector corresponding to the j′th pixel is given by

$$\begin{array}{cc}\hfill {\mathbf{g}}_j& ={\nabla }_{\mathbf{x}}\left[E_{\mathbf{x}}\left({\widehat{x}}_j\right)\right]\hfill \\ \hfill & ={\left[\frac{\partial E_{\mathbf{x}}\left({\widehat{x}}_j\right)}{\partial x_1},\frac{\partial E_{\mathbf{x}}\left({\widehat{x}}_j\right)}{\partial x_2},\dots ,\frac{\partial E_{\mathbf{x}}\left({\widehat{x}}_j\right)}{\partial x_2},\dots ,\frac{\partial E_{\mathbf{x}}\left({\widehat{x}}_j\right)}{\partial x_N}\right]}^T.\hfill \end{array}$$ (20)

It is easily seen that l_j and g_j defined in (19) and (20) are closely related. To use the MUCRB approach, we first define a class of estimators that produce similar resolution properties by satisfying the following constraint

$${\Vert {\mathbf{g}}_j-{\mathbf{f}}_j\Vert }_{\mathbf{C}}\le \gamma$$ (21)

where f_j is the desired point-spread function (or the mean gradient vector) at the j′th voxel. γ is a threshold that governs the degree of similarity between f_j and g_j. C is a symmetric and positive definite weighting matrix defined by the user. ∥·∥ is the Euclidean norm of a vector, so that

$${\Vert {\mathbf{g}}_j-{\mathbf{f}}_j\Vert }_{\mathbf{C}}^2={({\mathbf{g}}_j-{\mathbf{f}}_j)}^T\cdot \mathbf{C}\cdot \left({\mathbf{g}}_j-{\mathbf{f}}_j\right).$$ (22)

Since g_j is closely related to the local impulse response function, all estimators that satisfy constraint (21) with a small γ should produce very similar spatial resolution properties, regardless the physical system configuration and the estimation method used. With this constraint in place, the minimum attainable image variance at the j′th pixel is given by the so-called MUCRB,

$$\begin{array}{cc}\hfill \mathit{Var}\left({\widehat{x}}_j\right)& \ge \hfill \\ \hfill {\mathbf{f}}_j^T\cdot & {[\mathbf{J}+{(\lambda \cdot \mathbf{C})}^{-1}]}^{-1}\cdot \mathbf{J}\cdot {[\mathbf{J}+{(\lambda \cdot \mathbf{C})}^{-1}]}^{-1}\cdot {\mathbf{f}}_j.\hfill \end{array}$$ (23)

where λ is a scalar constant. The optimum mean-gradient vector that achieves this bound is given by

$${\mathbf{g}}_{\mathit{optimum}}=\mathbf{J}\cdot {[\mathbf{J}+{(\lambda \cdot \mathbf{C})}^{-1}]}^{-1}\cdot {\mathbf{f}}_j,$$ (24)

where J is the Fisher information matrix as defined in (11) and (12). Note that an efficient estimator that achieves the bound (23) is the post-filtered penalized maximum-likelihood (PF-PML) estimator, in which the post-filtering is performed using the desired point-spread function f_j as the filter [25], [26]. Using (23) and (24), one can derive the optimum tradeoffs between resolution and variance by varying the width of the filter function f_j.

To further evaluate the impact of different PDFs on image quality, we also compared the bias-variance tradeoff curves for region-of-interest (ROI) quantitation. The total activity uptake inside a ROI is given by

$$t\left(\widehat{\mathbf{x}}\right)=\sum _{i\in \mathit{ROI}}{\widehat{x}}_i=w^T\cdot \widehat{\mathbf{x}}$$ (25)

where w is an indicator vector defined as

$$w={\left\{w_j\right\}}^T,w_j=\{\begin{array}{cc}1\hfill & j\in \mathit{ROI}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$ (26)

For PF-PML estimators, the mean bias for ROI quantitation is given approximately by [26]

$$\text{bias}\left[t\left(\widehat{\mathbf{x}}\right)\right]\approx w^T\cdot {\mathbf{F}}^T\cdot {\left\{\right[\mathbf{J}+{(\lambda \cdot \mathbf{C})}^{-1}\left]\right\}}^{-1}\cdot \mathbf{J}\cdot \mathbf{x}-w^T\cdot \mathbf{x}$$ (27)

where F is a shift-invariant filtering matrix with each of its rows a spatially shifted version of f_j. With the same estimators, the variance associated with the activity in the ROI is given by

$$\begin{array}{cc}\hfill & V_{\mathit{ROI}}=\hfill \\ \hfill & w^T\cdot \mathbf{F}\cdot {\left[\mathbf{J}+{\left(\lambda \mathbf{C}\right)}^{-1}\right]}^{-1}\cdot \mathbf{J}\cdot {\left[\mathbf{J}+{\left(\lambda \mathbf{C}\right)}^{-1}\right]}^{-1}\cdot \mathbf{F}\cdot w.\hfill \end{array}$$ (28)

Again, by varying the width of the desired PSF (f_j), one achieves different tradeoffs between the mean bias and the corresponding variance for ROI quantitation. Detailed derivation of the MUCRB methods and the computation approach for evaluating the MUCRB can be found in [25], [26]. In the following text, resolution-variance tradeoffs will be referred to as R-V tradeoffs and bias-variance tradeoffs will be referred to as B-V tradeoffs.

F. Monte Carlo Simulations

To evaluate the proposed NUOP approach, a series of Monte Carlo simulations were performed. The simulated SPECT system consists of six pixelated detectors of 4.4 cm × 4.4 cm in size. The detectors are arranged in a stationary hexagonal ring. Each detector has 128 × 128 square pixels of 350 μm × 350 μm. It is coupled to a collimation aperture with 25 (5 × 5) pinholes of 200 μm diameter. The axes of all pinholes are perpendicular to the aperture surface. The pinhole-spacing was roughly 4.2 mm. All pinholes have sharp knife-edges and an acceptance angle of 45 degrees on both sides. The detector-to-aperture and aperture-to-center distances are 2.2 cm and 2 cm. The object-space was divided into 128 × 128 × 128 cubic voxels of 64 μm × 64 μm × 64 μm in size. This simulation study was carried out using a Monte Carlo package that we developed for the various SPECT applications [9], [11], [31], [32]. With this package, pinhole response is modeled with the analytical formula given in [33]. The depth-of-interaction effect in detectors is accounted for by treating the detector as multiple independent layers. In this study, both the photon attenuation in the object and the effect of Compton scattering were ignored.

Two simulated phantoms were used in this study. The first one (resolution phantom) has a spherical volume of 8 mm in diameter placed at the center of the ring-shaped SPECT system. It has a uniform background activity concentration of A_B1. The central spherical volume of 3 mm diameter has a background activity concentration of A_B2. This volume is divided into three sections, of 1.2 mm, 0.6 mm and 1.2 mm in height, along the x-axis (the axis of the ring-SPECT system). The top section contains seven hot rods of 250 μm diameter, superimposed on the continuous background (A_B2). These hot rods are parallel to the x-axis and are separated by 500 μm between adjacent rods. The bottom section has a similar configuration, except that the hot rods are replaced by cold rods of 400 μm diameter, which are separated by 800 μm spacing. The middle section has the uniform background (A_B2) only. The hot rods and cold-rods have activity concentrations of A_HR and A_CR respectively. The ratios of the activity concentrations within different regions in the simulated phantom are A_B1 : A_B2 : A_CR = 1:6:60:0. The entire 8 mm diameter sphere contains a total activity of 250μCi.

The second phantom (brain phantom) also has a spherical volume of 8 mm diameter. It consists of two hot spheres of 1 mm in diameter and two hot ellipsoidal volumes that have half-axes of 0.8 mm, 0.4 mm and 1.0 mm respectively. These features are superimposed on a uniform background and the feature-to-background ratio is 6:1. In addition, several small hot and cold spheres were inserted into the ellipsoidal volumes. The relative tracer concentrations in these small spheres are 12:1 or 1:1 in respect to the continuous background. The phantom contains a total activity of 100 μCi. The cross-sections of the phantom will be shown later along with reconstructed images.

III. Results

A. Image Reconstruction With Non-Uniform Object-Space Pixelation

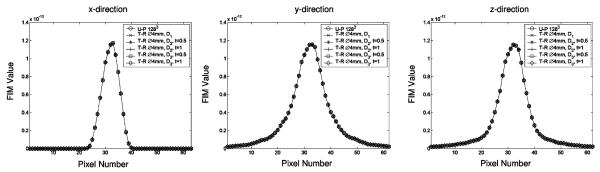
In this study, we used the resolution phantom and defined the central spherical region of 4 mm in diameter as the target-region. Five different PDFs, derived using (15)–(17), were implemented and compared. Since FIM plays an important role in determining image property, we first compared the FIMs resultant from the use of these PDFs. For each FIM, we computed a single column (J · e_j) corresponding to the central pixel. As previously discussed, each element of this vector represents the weighted correlation between the system responses to gamma ray emissions in the given pixel and in other pixels inside the object-space. The elements of J · e_j were then rearranged into 3-D format with the same order as for positioning corresponding source pixels in spatial domain. This procedure produces a 3-D “image” of the column vector, J · e_j, which is referred to as a FIM image.

In Fig. 1, we compared 1-D cross-sections of several FIM images derived using different PDFs. Since the resultant FIMs have different overall dimensions, this comparison was limited to the FIM elements that are corresponding to those source pixels inside the spherical target-region only. The rebinning processes resulted in virtually unchanged FIM values for these pixels. The comparison between the cross-sections along different directions also highlighted the effect of the non-isotropic sampling due to the specific system geometry. Despite this similarity, the rebinning process reduces the overall number of unknowns in reconstruction and helps to improve the condition of the inverse problem. Given the same amount of imaging information carried in projection data, this process could offer an improved image quality, as for the examples shown later in Figs. 6 and 7.

Fig. 1.

Cross-sections of several FIM images derived with different PDFs. Note that these FIMs were evaluated using the system-response functions after rebinning. The profiles shown are corresponding to the source pixels inside a 4 mm diameter target-region. The NUOP process has virtually no effect on the values of the FIM elements compared. x-axis is the axis of the SPECt system as defined in Section II-F.

Fig. 6.

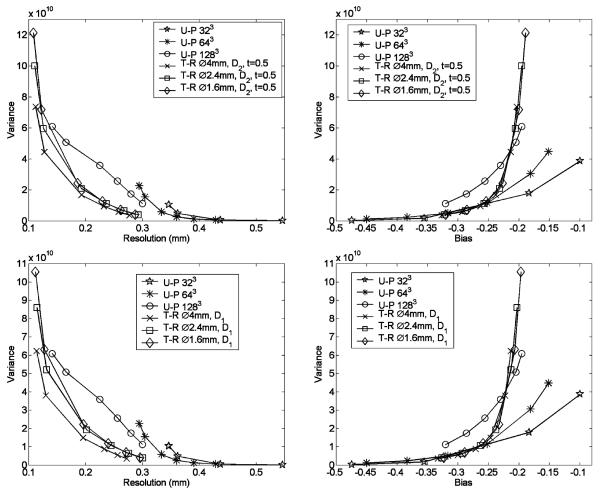
Comparison between resolution-variance (R-V) and bias-variance (B–V) curves achieved with different PDFs. The target-region was defined as the central spherical volume of 4 mm diameter. The pixel of interest, for which the R–V curves were evaluated, is located at the center of the object. Parameters used in PDFs are shown in the figure. Several R–V and B–V curves achieved with uniform-pixelation (U-P) with 32³ × 256 μm pixels, 64³ × 128 μm pixels and 128³ × 64 μm pixels are also compared.

Fig. 7.

Comparison between resolution-variance and bias-variance curves achieved with differently sized target-region. The simulated brain phantom was used in this study.

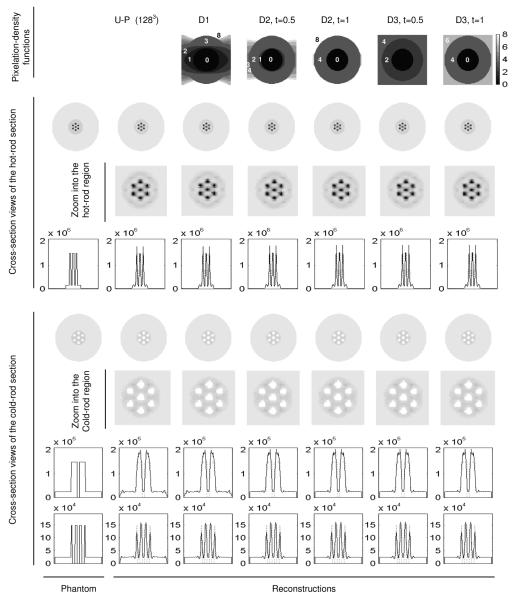
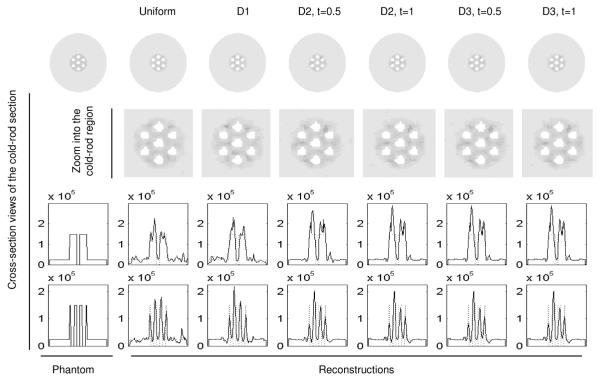
Several PDFs derived using (15)–(17) are shown in Fig. 2. Images reconstructed with the NUOP approach and noise-free projection data are also shown in Fig. 2. All images were reconstructed with 500 iterations to ensure convergence. The use of different PDFs produced virtually identical images. A similar comparison using noisy projection data is shown in Fig. 3, in which the different pixilation strategies resulted in comparable reconstructions. Note that due to the regularization used in the PF-PML reconstruction, the resultant images had appreciable overshot around the sharp features.

Fig. 2.

Comparing reconstructed images with different object-space pixelation schemes and noise-free projection data. The pixelation-density functions used are indicated in the top row and the parameters used for each PDF are indicated. U-P: Uniform-pixelation. The 2-D slices shown are perpendicular to the common axis and 1 mm from the center. The reconstructions were performed with 500 iterations a β was set to 0 for all cases.

Fig. 3.

Comparing reconstructed images with different object-space pixelation schemes and noisy projection data. The entire phantom contains 250 μCi activity. All images were reconstructed using PML algorithm with 500 iterations. The penalization factor β was 10⁻¹⁴ for all reconstructions.

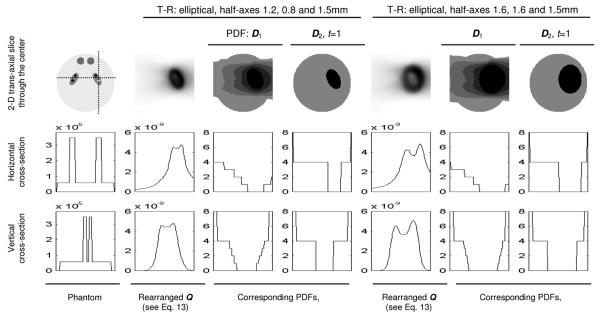
We further evaluated the NUOP scheme with the brain phantom and randomly generated noisy projections. A rapid reconstruction, with the object divided into 32 × 32 × 32 pixels, was performed to provide an overview of the object. Based on the resultant image, we defined two different target-regions (T-Rs) around the elliptical feature on the right-hand side (as shown in Fig. 4). Both T-Rs are elliptical and had the same orientations as the corresponding elliptical source features themselves. Their half-axes were 1.2 mm, 0.8 mm, 1.5 mm (1.5, 2 and 1.5 times the corresponding half-axes of the elliptical source feature) for the first one and 1.6 mm, 1.6 mm and 1.5 mm for the second one. Several PDFs derived for this series of studies are shown in Fig. 4 and the reconstructed images are shown in Fig. 5.

Fig. 4.

PDFs derived for differently sized target-regions.

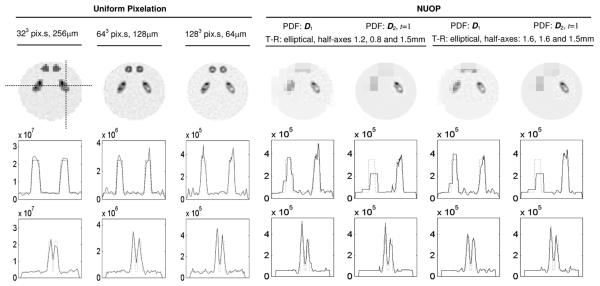
Fig. 5.

Reconstructed images of the brain phantom with different PDFs as shown in Fig. 4 and with uniform pixelation (U-P).

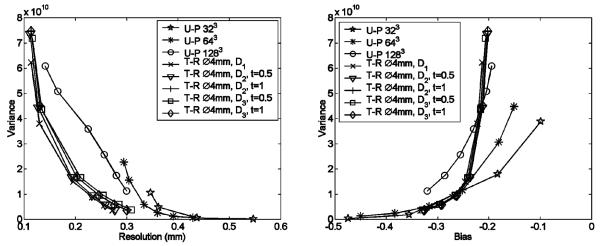
B. MUCRB Studies

To further evaluate the impact of the NUOP process on image quality, we derived the optimum resolution-variance (R-V) and bias-variance (B-V) tradeoffs achievable with the use of different pixelation strategies. This study was based on the use of the resolution phantom detailed in Section II-F. In order to derive the bias-variance curves, a ROI was defined as a spherical volume, of roughly 1 mm diameter, located at the center of the object. It contains an activity concentration two times that of the surrounding region. The R-V and B-V tradeoffs attainable with different pixelation schemes are compared in Fig. 6. In this comparison, the NUOP approach not only offered a much faster reconstruction (see Table II), but also produced lower variances at similar resolutions. As detailed in Section II-F, the simulated SPECT system uses detectors with 350 μm pixels and pinholes of 200 μm in diameter. We expect that the practical spatial resolution of the system is 200 μm −350 μm FWHM. Within this region, the NUOP schemes also offered a clear advantage over the uniform pixleation schemes (with identical pixel size for the target-region) in terms of B-V tradeoffs. In this study, we derived several B–V and R–V curves using different pixel sizes (such as 64 μm, 128 μm and 256 μm) inside the target-region.

TABLE II.

The Sizes of SRFs and Reconstruction Times With Different Pixelation Schemes

	Pixelation Schemes		No. of source pixels	Size of SRF (MB)	Recon. time1 (100 iteration)
Resolution Phantom Studies	U-P, 1283 pixels,		2097152	3950	632 mins
	T-R: Ø4mm	D1	228961	509	26 mins
		D2, t=0.5	132333	283	13 mins
		D2, t=1.0	130297	274	14 mins
		D3, t=0.5	142072	322	15 mins
		D3, t=1.0	130304	275	15 mins
	T-R: Ø2.4mm	D1	46681	117	6 mins
		D2, t=0.5	30525	74.8	4 mins
	T-R: Ø1.6mm	D1	15589	48.5	3 mins
		D2, t=0.5	10853	35	2 mins
Brain Phantom Studies	T-R, half-axes: 1.6mm, 0.8mm and 1.5mm	D1	85846	202	13 mins
		D2, t=1.0	46488	98.9	5 mins
	T-R, half-axes: 1.6mm, 1.6mm and 1.5mm	D1	194985	435	24 mins
		D2, t=1.0	123073	253	13 mins
	Uniform pixelation, 323 pixels		32768	63.3	4 mins

¹The reconstruction times with NUOP are corresponding to the use of a single CPU only. The reconstruction with uniform pixelation was performed in parallel on a single PC equipped with 4 CPUs.

For implementing the NUOP approach, it is natural to question about “how large a target-region should be for a given local feature?” In this study, this question is briefly explored with a few examples as shown below. We used the resolution phantom and assumed that the ROI is a small local region at the center. The size of a spherical target-region (T-R) was varied from 1.6 mm, 2.4 mm, 4 mm, to 8 mm in diameter (covering the entire object). To make the results more representative, we used two different PDFs in this comparison. Since the definition of PDF enforces the highest pixelation density within the T-R, its dimension would have a significant influence on image reconstruction. This was confirmed by the results shown in Fig. 7. For the spherical object of 8 mm in diameter, a target-region of 4 mm diameter appeared to be the favorable choice for optimized R-V tradeoffs. Smaller (1.6 mm and 2.4 mm diameter) T-Rs produced greater variances at similar resolutions. The use of differently sized target-regions did not have appreciable effect on B-V tradeoffs, and all results with NUOP are significantly better than those achieved with uniform object-pixelation.

The sizes of SRFs for all the imaging scenarios studied are summarized in Table II, along with the corresponding reconstruction times. It is demonstrated that the use of the NUOP offers a greatly improved computation speed, whilst providing an excellent reconstruction for the T-R. Note that the computation times (for NUOP case) are corresponding to reconstructions with a single CPU only. With the rapid advances in parallel computing, images of the T-R could be updated in real time during an imaging study. This feature helps to maximize the efficiency for collecting imaging information on given features, which is crucial for SPEM studies.

Based on the results presented in this section, several observations and discussions are given below:

• If the target-region and the desired pixel-size (for the region) are fixed, the use of NUOP could offer a much-reduced computation-effort. Furthermore, with the same amount of imaging information carried in projection data, the use of NUOP reduces the overall number of unknowns in the inverse (reconstruction) problem. This could lead to a lowered imaging noise in reconstructions. The degree of the noise reduction with NUOP is task- or application-specific, which deserves some future studies.

• As demonstrated in Fig. 6, the use of pixel sizes smaller than the “common” choice (½ of the desired system resolution) could provide improved resolution-variance tradeoffs. A pixel size of 64 μm (around 1/4 of the system resolution of 200–300 μm) appears to be an appropriate choice for the specific example.

• The pixel size that delivers the best R-V curves is not necessarily optimal for ROI quantitation or other imaging tasks. To derive the tracer uptake in a ROI of 4 mm diameter, the use of 256 μm pixel size (32 × 32 × 32 pixels) produced the lowest variance at the same bias. Clearly, the choice of pixel size should depend on the specific imaging task. Although the study of the “optimum” pixel size is beyond the scope of this paper, the NUOP formulation developed in this work provides a computationally efficient approach for future explorations on this topic.

• All three NUOP strategies led to similar resolution-variance and bias-variance tradeoffs. This result can be explained by a closer examination of the corresponding FIMs. Given a target pixel, the corresponding FIM column reveals the weighted correlations between the system responses to the target pixel and to other pixels in object space. For the SPECT systems simulated, their geometries are so designed that most of source pixels strongly correlated to the target pixel are physically located close to the target. Therefore, both FIM- and distance-based criteria allow most of these “important” pixels to be retained without rebinning. This leads to the similarity in selected FIM elements shown in Fig. 1 and also the comparable R-V and B-V performances shown in Figs. 6 and 7. The key advantage of the FIM-based approach over the distance-based one is that the former can be adapted to any object geometry with target-regions of any shape and size, whilst the latter does not offer the same degree of flexibility.

• In the comparison between the bias-variance (B–V) curves for the uniform and non-uniform pixelation cases (both having the same pixel-size of 64 μm for the target-region), the uniform pixelation scheme provided lower variances at relatively small biases (for example, when the absolute value of the relative bias is < 0.2 in Figs. 6 and 7). However, within this operating region, the resultant imaging resolutions are close to the physically permitable limit for the given system design. Therefore the corresponding reconstructions suffer from excessive noise amplification as indicated in the resolution-variance (R-V) curves shown in Figs. 6 and 7. For the simulated SPECT systems that are based on detectors with 350 μm pixels and pinholes of 200 μm diameter, we would expect the system resolution to be above 200 μm. If one considers only the data points that are associated with “practical” spatial resolutions (> 200 μm), the use of NUOP schemes offered superior B-V tradeoffs.

IV. Conclusions and Discussions

We proposed and evaluated a non-uniform object-space pixelation (NUOP) method for image reconstructions using SPEM data. Several approaches for defining the pixelation-density function were discussed and evaluated using Monte Carlo simulations. The impact of using the NUOP method was also studied based on the optimum resolution-variance and bias-variance tradeoffs achievable with different pixelation strategies. If the imaging task is to achieve an excellent reconstruction of a local target-region, the use of NUOP provides a greatly improved reconstruction speed. When combined with efficient parallel computers equipped having adequate memory space, practical SPEM images could be reconstructed within several minutes, rather than a few days as in our current practice.

This development also benefits the SPEM work in a different way. We are currently developing a four-head SPEM system that offers a variable system configuration. Depending on the specific imaging tasks, apertures with different pinhole configurations may be interchanged during an imaging study. In this system, the object is supported by a precise translation table that allows different sub-regions in the object to be brought into the focal region. These variable hardware components offer a large number of degrees of freedom that could be fine-tuned to offer an optimum imaging performance. In practice, since the object is generally unknown, choosing the optimum configuration in advance could be problematic even for experienced users. Instead, an imaging study could be started by using a “generic” aperture that offers a modest resolution and a wide angular coverage. Imaging information collected with this aperture can be used to refine the imaging task and help to optimize the system configuration in the real time based on several statistical approaches that predict the performance of the system for the specific imaging task. To ensure a meaningful decision on the “optimum” system configuration, many performance measures developed so far require the mean and covariance of reconstructed images. The evaluation of these quantities typically involves the inversion of Fisher Information matrix (FIM). With the regular uniform object pixelation scheme, this procedure is normally too computation-intensive to use in the adaptive imaging method. The non-uniform and adaptive pixelation schemes developed in this paper allow for rapid evaluations of the mean and covariance of reconstructed images, which could be an important step towards a fully adaptive SPEM system.