Modeling Self-Regulation as a Process Using a Multiple Time-Scale Multiphase Latent Basis Growth Model

Abstract

Measurement burst designs, wherein individuals are measured intensively during multiple periods (i.e., ‘bursts’), have created new opportunities for studying change at multiple time-scales. This paper develops a model that may be useful in situations where the functional form of short-term change is unknown, may consist of multiple phases, and may change over the long-term. Specifically, we combine measurement of intraindividual entropy, a latent basis growth model, a multiphase growth model, and a growth model with covariates into a unified framework that may help accommodate the complexity of patterns that emerge in multiple time-scale categorical data streams. Empirical data from a longitudinal study of young children's behavior during laboratory tasks designed to induce frustration are used to illustrate the utility of the proposed model for simultaneously describing intratask (short-term) change in self-regulation and developmental (long-term) shifts in intratask change.

In the study of development, we are often faced with the challenge of simultaneously considering and modeling change at multiple time-scales (Ram et al., 2013; Ram & Diehl, 2015). Three difficulties that are emerging are (a) how to operationalize a focal construct that is indicated by multivariate categorical time-series, (b) how to summarize the complex array of individual-specific trajectories that manifest at faster time-scales, and (c) how to examine shifts in those trajectories that manifest at slower time-scales. Several literatures contain examples of multiple time-scale data and these challenges (Diehl, Hooker, & Sliwinksi, 2015). For example, Ram and colleagues (2005) measured and modeled how consistency in cognitive performance across trials (faster time-scale) changed across 36 weekly measurement bursts (slower time-scale); Sliwinski and colleagues (2009) examined change in daily stress-reactivity across five biannual measurement bursts; and Carstensen and colleagues (2011) investigated change in moment-to-moment variability of emotional states across three 5-year measurement bursts. The methods used for analyzing phenomena across multiple time-scales were built to handle the third challenge mentioned above, but do not yet provide clear solutions for the first two. Therefore, this paper seeks to extend the modeling efforts – wrestling with how measures and models of intraindividual variability and change might be adapted to accommodate the three difficulties noted above.

Our work is motivated through the study of the development of self-regulation. More specifically, we are working to model data obtained in studies wherein children's emotions and behaviors during multiple laboratory visits (bursts) are coded into second-by-second multivariate categorical time-series, thereby producing multiple time-scale data (i.e., four measurement bursts). Questions that arise include: How to succinctly represent the variety of behaviors (and emotions) individuals display at any given moment (i.e., across 10 seconds); How to describe the complex behavioral changes that emerge during a challenging task (i.e., across 2.5 minutes); and How to examine whether these patterns change across childhood (across 3 years)? In attempting to answer these questions, this paper introduces a generic analytical strategy for simultaneously describing and modeling developmental (long-term) change in (short-term) regulation processes. The analytic strategy combines (1) an intraindividual variability-based measurement function that collapses multivariate categorical time-series data into a continuous univariate time series, and (2) a multiple time-scale multiphase latent basis growth model that articulates both long-term and short-term changes.

Motivating Problem

Self-regulation can be conceptualized as the set of processes that enable an individual to engage executive processes to delay, minimize or desist a prepotent response (Baumeister & Vohs, 2007; Carver & Scheier, 1998; Kopp, 1982). Prepotent responses are automatic reactions that are either learned or biologically prepared, and executive processes are those involving higher order psychological processes such as cognition and language. Although, self-regulation is often studied as an individual differences characteristic that develops across the lifespan (i.e., over years), self-regulation manifests in the interplay between prepotent responses and executive processes that emerges during a situation (e.g., within seconds or minutes). During the third year of life, children begin to autonomously initiate effortful strategic behavior, which calls upon their cognitive and linguistic skills, to modulate their emotions and impulses (Kopp, 1982; 1989). It is implied that self-regulation improves with age, although there are no studies that actually demonstrate how young children's moment-to-moment regulation develops with age. The investigation of static measures links between-person differences in a trait-like self-regulation construct to other between-person differences, but does not characterize self-regulation as a within-person process that unfolds over the course of a situation. Hence, examination of children's moment-to-moment dynamics (i.e. how children react and adapt to challenges in real time) across multiple time-scales may provide keen insights into both the moment-to-moment manifestation of self-regulation, and how those manifestations change with age.

Studies of young children's self-regulation rely on laboratory observations in which children are required to modulate reactions to challenging task conditions, such as delays of gratification or blocked goals. One task designed to elicit both anger and children's strategies for modulating anger is the Transparent Locked Box task (Goldsmith & Reilly, 1993). In this task, a desirable toy is placed in a clear, locked acrylic box. The child is left alone to open the box with the wrong set of keys that will not work. As in many adult studies, effective self-regulation in this task requires persisting despite frustration, (Corno, 1986; Corno & Rohrkemper, 1985; Baumeister & Heatherton, 1996; Baumeister & Vohs, 2007). In contrast, ineffective self-regulation can be characterized by increasing fragmentation of behavior, such as the manifestation of multiple emotions (e.g. anger, sadness) or off-task behaviors (e.g., distraction). In sum, one way to capture the self-regulatory process is by the manifestation of changes in fragmentation across task time. Fragmentation may manifest in many ways. One child may first engage the task, look out the window after an initial failure, re-engage in the task, become frustrated, but keep persisting. Another child, however, may engage, get frustrated, look out the door, try again briefly, then express sadness, and wander around the room.

The heterogeneity through which fragmentation manifests poses a measurement problem; the method of analysis must contain enough flexibility to capture different prevalence rates and transition patterns of behaviors/emotions. Further, the pattern of change in fragmentation may evolve in phases, with different children changing in different ways at the beginning, middle, and end of the task. As such, intratask change in fragmentation may show complexity – increases that are followed by recovery at different times for different children. As well, the pattern of intratask changes in fragmentation may also change as children develop - gains in the efficiency and capacity to regulate frustration and maintain persistence will, over the long-term, change how and when their behavior fragments (Kopp, 1982). Therefore, the method of analysis must also contain enough flexibility to capture both complex intratask (short-term) changes and developmental (long-term) shifts in the pattern of intratask change.

Growth Models

Several growth models currently exist to examine change of a focal construct across repeated measures (see Ram & Grimm, 2015 for an overview). In brief, a mathematical function, summarized as a set of basis functions and person-specific coefficients, is used to describe individual differences in how observed (or latent) scores change across a sequence of observations obtained at specific times (Laird & Ware, 1982). For example, polynomial functions may be used to describe specific aspects of change (e.g. linear, quadratic), and differences across persons are captured using an ensemble of person-specific coefficients (e.g., individual-specific rates of change). Complex patterns of change are accommodated by expanding the configuration and/or number of underlying functions (Ram & Grimm, 2007). When the functional form of change for the focal construct is unknown, for instance, the underlying change function may be estimated directly from the data as a set of factor loadings (basis functions) and factor scores (person-specific coefficients) – the latent basis growth model (McArdle & Epstein, 1987; Meredith & Tisak, 1990). Other types of complexity can be accommodated by separating the repeated measures into different phases, and using an a priori specified basis function to characterize change within each phase – the multiphase growth model (Cudeck & Klebe, 2002; Ram & Grimm, 2007). When the location of the phases is unknown prior to analysis, then the regime switching growth model (Dolan, Schmittmann, Lubke, & Neale, 2005) may be used to identify latent phases that are defined by different patterns of change (basis functions). In sum, growth models allow for description of many types of change, and the interindividual differences therein.

Interestingly, most growth model formulations are matched to change phenomena that manifest on single time-scale (e.g., across minutes, across days, or across years). Rarely are growth models explicitly formulated for description of multiple time-scale phenomena. A key counter-example surfaces in the study of cohort differences, where repeated measures are obtained from persons who belong (or are assigned) to different historical epochs (Bowles, Grimm, & McArdle, 2005; Hülür, Ram, & Gerstorf, 2015; Schaie, Willis, & Pennak, 2005). In such situations, the long (historical) time-scale is introduced as a between-person covariate (predictor or grouping variable), along with (regression or group-difference) parameters that describe cohort-related differences in the pattern of change (i.e., basis functions, factor loadings) or extent of change (i.e., person-specific coefficients, factor scores). Simply, the long-term changes across historical epochs are accommodated through inclusion of additional predictors – the growth model with covariates (Singer & Willet, 2003).

In this paper we illustrate how a variety of growth models can be combined to flexibly accommodate and describe multiple time-scale phenomena (see also Ram & Diehl, 2015, for methods used in other research disciplines). Specifically, we develop a model that may be useful in situations where the functional form of short-term change is unknown (as in a latent basis growth model), may consist of multiple phases (as in the multiphase growth model), and may change over the long-term (as in a cohort differences model). Specifically, we combine three types of growth models (latent basis, multiphase, growth model with covariates) into a unified framework that may help accommodate the complexity of patterns that can emerge in multiple time-scale data.

Multiple Time-Scale Multiphase Latent Basis Growth Model

In this section we discuss a proposed model motivated by our empirical application. More specifically, we describe how we implement an entropy function to transform each individual's multivariate categorical time-series into a univariate time-series of behavioral/emotional fragmentation. Then, we analyze the set of fragmentation scores measured within all individuals using a multiple time-scale multiphase latent basis growth model, which simultaneously estimates the pattern of intratask change (i.e., change on a fast time-scale) and long-term shifts of intratask change (i.e., change on a slow time-scale).

Using Entropy to Quantify Fragmentation

Conceptually, fragmentation corresponds to the degree of variability of behaviors and emotions that are exhibited within a very brief period of time (i.e., 10 seconds). Practically, the behaviors and emotions are coded into categories. A variety of indices provide a succinct description of within-entity variability across a set of nominal or ordinal categories (Shannon, 1948; Teachman, 1990; McDonald & Dimmick, 2003; Hollenstein, 2013; Ram & Gerstorf, 2009). In particular, entropy indices have been used to measure a wide variety of constructs, including biological diversity within an ecosystem (Magurran, 2004), ethnic variety within a community (Budescu & Budescu, 2012), social diversity of an individual's interaction partners (Ram et al., 2012), diversity of an individual's stessors (Brose et al., 2013; Koffer et al., in press) or emotions (Quoidbach, et al., 2014), behavioral disorganization of mother-child dyads (Dishion, Nelson, Winter, & Bullock, 2004; Lichtwarck-Aschoff, Hasselman, Cox, Pepler, & Granic, 2012), and cognitive uncertainty within an individual (Hirsh, Mar, & Peterson, 2012). Following this work, we use Shannon's (1948) entropy metric to quantify the extent of fragmentation in children's task behavior. Formally, we split the categorical time-series into a series of small windows (i.e., epochs) and calculate entropy of behavior for each epoch, e, at each age, a, for each individual, i, as

$$fragmentatio{n}_{iae}=-\left(\sum _{j=1}^m\left(p_{j_{iae}}\right){\log }_2\left(p_{j_{iae}}\right)\right)$$ (1)

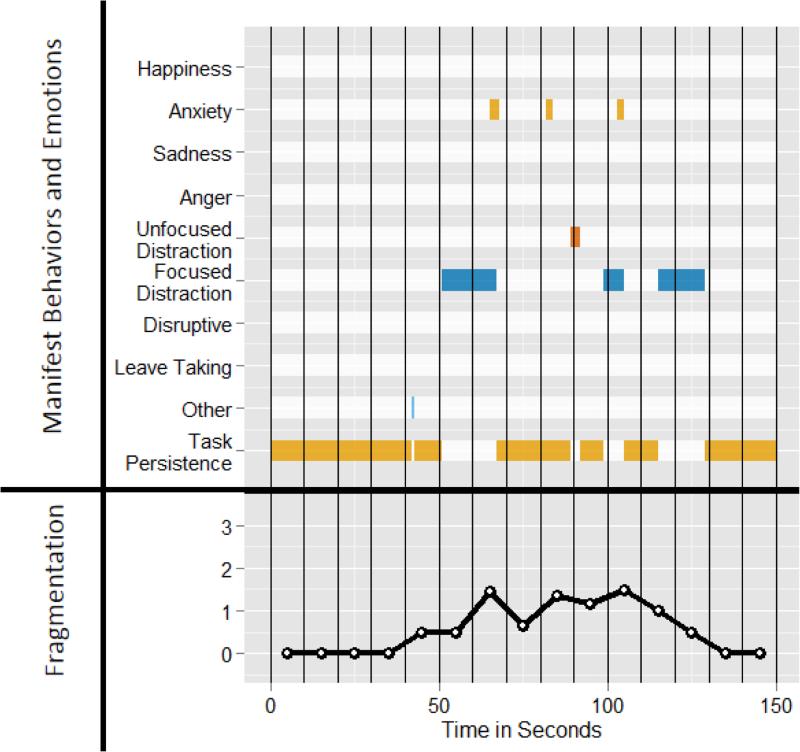
where p_jiae is the probability of observing behavior or emotion j (for a total of j = {1,2,...,m} behaviors/emotions) within a specific epoch of time (in our case, 10 seconds). Of note, consolidation into epochs facilitates observation and calculation of fragmentation scores by allowing enough time for multiple behaviors to manifest, and by accumulating enough total observations to calculate a probability for each category. When a single behavior is observed over the entire epoch, entropy equals 0, indicating the absence of fragmentation. When multiple behaviors are observed during an epoch, entropy increases, with higher values indicating greater fragmentation (i.e., more variability). Figure 1 demonstrates these properties by portraying a multivariate time series of 10 behaviors and emotions (color indicates presence of the behavior/emotion), thin vertical lines to denote epochs, and the corresponding value of fragmentation for each epoch (black dots in the bottom panel). Within Figure 1, the first four epochs contain only a single behavior and are summarized with fragmentation scores = 0, whereas epochs 5 to 7 contain multiple behaviors and emotions and are summarized with fragmentation scores > 0. As can be seen, this intraindividual variability-based metric consolidates the observed multivariate (10-variate) categorical time-series of length 150 in the upper portion of the figure into a continuous univariate time-series of length 15.

Figure 1.

In the upper panel is a 10-variate, categorical time series depicting a child's behavior and emotion during each of 150 seconds during the Transparent Locked Box task. Color indicates presence/absence of behavior/emotion. Within each 10-second epoch (indicated by thin vertical lines) the multivariate description is summarized in the lower panel as a fragmentation score (higher scores indicate greater dispersion of behavior/emotion across categories).

It is important to note that, for the current example, entropy outperforms many common summary metrics. Sums or averages of the categorical responses summarize the quantity of different responses within an epoch (i.e. more behaviors/emotions indicates more fragmentation), whereas metrics of variability (e.g., standard deviation) represent the evenness of responses by (i.e. the degree of dispersion of the responses). Entropy provides a nuanced measure of fragmentation by incorporating both quantity and evenness of responses (Hill, 1973). For example, visual inspection of epochs 5 and 12 within Figure 1 indicates that epoch 12 contains more fragmentation because the behaviors are more evenly spread (i.e. more variable). Yet, sums, averages, and standard deviations are equivalent between these two epochs; both epochs contain (have a sum of) two behaviors, have an average of 0.083 responses (i.e. 10 responses out of 120 possible), and a standard deviation of 0.278. Alternatively, entropy is greater for epoch 12 (1.0) than for epoch 5 (0.467), matching the initial visual inspection. Hence, entropy provides a finer-grained distinction for fragmentation as compared to more conventional forms of aggregation, and thus enables a more nuanced examination of intratask changes in fragmentation.

Multiple Time-scale Multiphase Latent Basis Growth Model

To simultaneously capture changes in fragmentation across multiple time-scales, we propose a growth model that summarizes intraindividual change through a series of phase-specific latent basis coefficients (factor loadings). More specifically, we combine the multiphase and latent basis growth models to describe complex patterns of change that manifest on the fast time-scale, across epochs. The model is generally written as

$$y_{iae}=\sum _{p=1}^P{\lambda }_{ep}Phas{e}_{iap}+{\theta }_{iae},{ϵ}_{iae}\sim N(0,{\sigma }_{\theta }^2)$$ (2)

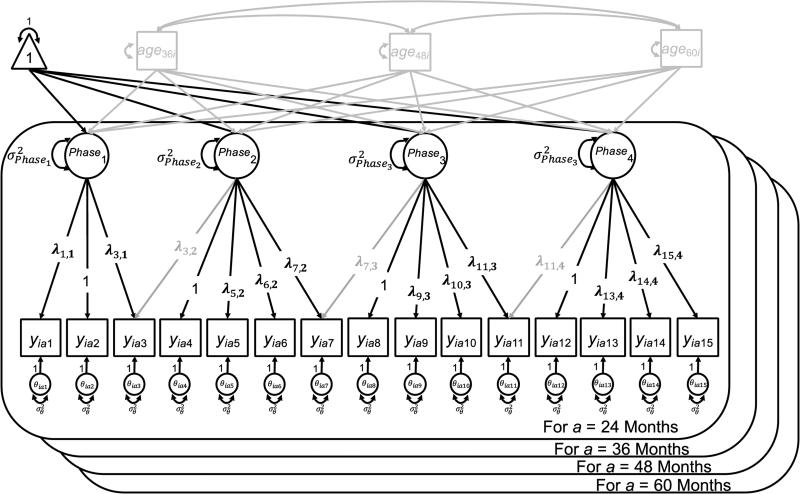
where y_iae is the entropy score that indicates level of fragmentation (computed using Equation 1) for individual i at age a within epoch e; λ_ep is an age-invariant basis coefficient for epoch e within phases p = 1 to P; Phase_iap is a latent growth factor score for individual i at age a within phase p; and θ_iae is the remaining portion of y_iae unaccounted for by the P growth factors. A depiction of the model with four phases (optimal number of phases found in our empirical application) is shown in Figure 2 (inside the large rectangular box; phase-specific growth factors span epochs 1 to 3, 4 to 7, 8 to 11, and 12 to 15, respectively). Thus, phases are constructed by specifying the phase-specific growth factors, Phase_iap, with loadings matched to specific subsets of the repeated measures (i.e. potentially non-zero factor loadings for epochs within the phase, and zero factor loadings for epochs outside the phase). Allowing the factor loadings to be estimated (rather than constrained to specific functional form, e.g., linear) offers substantial flexibility for accommodation of many possible trajectories of change. For example, if the phenomenon of interest is expected to be a relatively smooth transition between phases, with the trajectory of one phase beginning while the previous phase ends, then phases may have small overlaps for two consecutive phases (e.g., see the gray “cross-loadings” in Figure 2). Alternatively, if the phases are expected to have very distinct change trajectories and possibly with discontinuous jumps between phases, then each manifest variable would only be mapped to one growth factor, with no overlap of phases (i.e., the gray cross-loadings in Figure 2 should be set to zero). Here, we use Akaike Information Criterion (AIC; Akaike, 1973), Bayesian Information Criterion (BIC; Schwarz, 1978), and adjusted Bayesian Information Criterion (aBIC; Sclove, 1987) to inform the number of phase-specific growth factors and locations of “transitions” between phases of growth.

Figure 2.

Depiction of the multiple time scale multiphase latent basis growth model. Covariance between latent phases (σ_p1,p2, σ_p1,p3, etc.) and the labels for coefficients {γ₀₁, γ₁₁, ... , γ₃₄} are not depicted for visual simplicity.

Briefly, it is important to note that the inputted data structure for the multiple time-scale multiphase latent basis model growth model deviates from the wide-format structure of the latent growth model fitted within a structural equation modeling framework (i.e. one row for each individual, one column for each measurement occasion). The wide-format structure will be impractical for data from multiple time-scales because there will be many columns, creating a data matrix that is much wider than it is long. For example, the current empirical example contains 60 observations (15 epochs at each of 4 ages) for 128 participants, which yields a high-dimensional model-implied covariance matrix that will be difficult to invert during the estimation process. Therefore, we adopt the pseudo-maximum likelihood approach for structural equation models proposed by Asparouhov and colleagues (2005, 2006; Asparouhov & Muthén, 2005). In this approach, the data are structured to have multiple rows of data for each individual, (i.e. one row per measurement burst). Then, the pseudo-maximum likelihood estimator accounts for the row dependence by calculating and averaging the degree of within individual dependence (i.e., the design effect; Snijders & Bosker, 1999, p. 16), and then adjusting parameter estimates and standard errors according to that dependence (via robust maximum likelihood; Yuan & Bentler, 1998). The pseudo-maximum likelihood estimator facilitates model fitting by reshaping the model-implied covariance matrix to a manageable size during estimation, and also accounting for the row dependence introduced by that reshaping.

Returning to the construction of the multiple time-scale multiphase latent basis growth model, developmental differences may be quantified by allowing individual differences in Phase_iap to be explained (i.e. predicted) by a set of dummy-coded variables that indicate age. Therefore, we merge the initial combination of the multiphase and latent basis growth models with a growth curve that contains covariates. In particular, each individual's score on Phase_iap during a particular epoch at each developmental age is represented as

$$Phas{e}_{iap}={\gamma }_{0p}+{\gamma }_{1p}ag{e}_{1i}+{\gamma }_{2p}ag{e}_{2i}+\cdots +{\epsilon }_{iap},{\epsilon }_{iap}\sim N(0,{\sigma }_{Phas{e}_p}^2)$$ (3)

where γ_0p is the intercept (or predicted phase-p score) for the reference age (i.e., age 24-months in the present study), {age_1i, age_2i,...} are dummy variables indicating whether individual i is in a specific age group at measurement occasions {1,2,...}, {γ_1p, γ_2p,...} is the amount of deviation in the intercept of Phase_iap for age a relative to the reference age, and ε_iap is the residual for Phase_iap. The ε_iap values may covary across phases (denoted as σ_p1,p2 for covariance between the first two phases, σ_p1,p3 for the first and third phases, etc.). Equation 3 is depicted in Figure 2 as the manifest variables outside the large rectangular boxes that predict into the Phase_iap (labels for {γ_1p, γ_2p,...} are excluded for visual clarity). Accordingly, significant {γ_1p, γ_2p,...} indicates a non-negligible shift in the predicted factor scores for participants across different ages, and therefore provides evidence that the pattern of short-term change differs over the long-term. For example, if the basis coefficients for phase p show a positive linear change pattern, and γ_0p is also positive, then the reference age-group tends to manifest steady increases in fragmentation during phase p. If γ_1p is significant and negative, when children are in age group age_1a (i.e. the age when age_1a = 1) they tend to manifest smaller increases in fragmentation compared to the reference group. Therefore, the multiple time-scale multiphase latent basis growth model interweaves changes on a fast time-scale (i.e., Equation 2) with changes on a slow time-scale (i.e., Equation 3) to facilitate simultaneous examination of changes across both time-scales. Next, we present an empirical application that demonstrates the the empirical decisions we made in simultaneously representing children's changes in self-regulation across multiple time-scales, and the utility of the proposed model.

Empirical Illustration

Data are drawn from a longitudinal study of children and their families who lived in rural and semi-rural communities within central Pennsylvania (Cole et al., 2011). The 120 families who participated in the full longitudinal study were recruited from census tracks with high densities of young children and of households that were economically strained. Average family annual income at Time 1 (child age 18 months) was $40,655 (SD = $14,996). Most children (97.6%) came from a two-parent home, and were identified by their mothers as white (94.4%; with 5.6% as biracial). The majority of mothers (67.3%) had at least some college education and approximately half of fathers (44.8%) also had at least some college education. Mothers described themselves as unemployed or homemakers (28%), as working part-time (32%), and working full-time (39%). Almost all fathers (92%) described themselves as working full-time. Attrition across age was not significantly related to income (t₁₁₈ = .35, p =.73), child gender (χ² = 0, df = 1, p = 1.0), child race (χ² = 0, df = 4, p = 1.0), mother's level of education (χ² = 8.03, df = 6, p = .24), father's level of education (χ² = 4.47, df = 6, p = .61), mother's employment type (χ² = 3.58, df = 2, p = .17), or father's employment type (χ² = 2.91, df = 2, p = .23). Families in the full longitudinal study participated in 9 visits: 4 home visits (child ages 18, 30, 36, and 42 months) and 5 lab visits (child ages 18, 24, 36, 48 months, and 5 years). The present study used data from the Transparent Locked Box procedure administered during lab visits at age 24 months (N = 119), 36 months (N = 128), 48 months (N = 119) and 5 years (N = 99).

Procedure and Measures

The Transparent Locked Box task (Goldsmith & Reilly, 1993) was used to observe children's prepotent responses (desire for the object, anger at not being able to get the box open) and their engagement of executive processes (putative strategies). Each child selected from a small assortment, a toy to take home. The RA placed it in the box, locked the box, and then taught the child to open the box with a key. The RA then told the child that she needed to leave to do some other work. The child was given a key ring with the wrong keys and left to try to open the box for 2.5 minutes at ages 24 and 36 months, and 3 minutes at ages 48 and 5 years. At age 24 months, the mother stayed in the room but did not interact with the child while she completed a questionnaire (at this age separation distress often precludes the opportunity to study self-regulation of frustration). At each successive age, children were asked if they remembered the box and none did. However, by age 5 years, it was assumed that children might remember the box and so a parallel situation was used in which a knotted sack was substituted for a locked box. At the end of the designated time, the RA returned, explained that the child was mistakenly given the wrong keys, gave the child the correct keys, and helped the child open the box to get the toy. To keep the analytical frame consistent across ages, we use only the first 2.5 minutes (150 seconds) of observation.

Following the usual methods of classifying children's behavior with these tasks, two independent teams of undergraduates coded (1) the presence or absence of four emotions (Cole, Zahn-Waxler, & Smith, 1994) and (2) eight behaviors (Dennis et al., 2009). Coders indicated presence of four emotions: happiness, anger, sadness, and tension; and eight specific behaviors: attempting to open the box, focusing attention on the box, self-soothing, focused distraction (shifting attention away from the box and actively engaging in another activity), unfocused distraction (shifting attention away from the box, but not actively engaging in another activity), support-seeking (verbally bidding for adult help), attempting to leave the room, and any disruptive behavior (e.g., tearing the wall poster). Three of these behaviors (attempting to open the box, focusing attention on the box, and self-soothing) were collapsed into a single task-focused behavior category, and, to fulfill the condition that the j = 1 to m behavioral categories (in Equation 1) are exhaustive (Shannon, 1948; Budescu & Budescu; 2012), a catch-all “other” code was created to accommodate seconds in which the child was not engaged in any of the 12 coded behaviors and emotions (18.7% of seconds at 24 months, 9.8% at 36 months, 7.4% at 48 months, and 6.2% at 60 months).

Children's behavioral/emotional fragmentation was conceptualized as the extent of (cross-category) variability in behavior/emotion within 10-second epochs, and calculated as Shannon's (1948) entropy (Equation 1; Figure 1). Of note, the choice of epoch length is, from a mathematical perspective, arbitrary. However, the epoch length controls the smoothing of the time series; longer (i.e. fewer) epochs smooth over larger subsets of the original time series. At one extreme, implementation of a single epoch aggregates the entire time series and precludes examination of intratask change. At the other extreme, use of short epochs reduces the amount of variability that can be quantified within each epoch. Thus, the researcher should balance these extremes by selecting an epoch length that is long enough to capture the focal construct of interest (e.g., behavioral/emotional fragmentation), but short enough to allow for intratask change. Here, a team of developmental psychologists reviewed several video recordings of children completing the task, and jointly determined that a window of 10 seconds was needed to observe multiple behaviors/emotions (i.e., fragmented behavior).

Model Specification

The specific set-up of the multiple time-scale multiphase latent basis growth model used for the empirical example was determined using both practical and empirical criteria. The number of growth factors/phases was informed by the minimum number of variables needed to identify a factor, and heuristics regarding the number of meaningful factors that could be extracted from the observed data. In practice, although growth (and other) factors can be identified with a minimum of two repeated measures (with some constraints), growth factors based on at least three or more variables provide for more stable solutions (Kline, 2005, p. 172). Accordingly, to examine tradeoff between the flexibility in trajectories afforded by inclusion of more factors and the parsimony provided by fewer factors, we fit models with two, three, and four growth factors (2-, 3-, and 4-phase models). Also, as a comparison, we fitted the latent basis model that may be viewed as analogous to a 1-phase model specification.

Within each model, factor loading patterns were set so that each growth factor/phase captured approximately equivalent portions of the task span (15 epochs), with overlaps at the beginning and the end of interior spans. Across models, factors were identified by fixing the second loading (“peak” within a phase) equal to 1. Thus, factor loadings are interpreted as proportions of change to the within-phase “peak”, and factor scores interpreted as the total amount of change to that “peak” (see Ram & Grimm, 2007). Age was included as a predictor of the growth factors using three dummy variables (labeled as age_36i, age_48i, age_60i). Then, in Equation 3, parameter γ_0p represents the expected score for Phase_iap for a child at 24 months, γ_1p, to γ_3p represent differences between that score and the respective 36-, 48-, and 60-month scores. Differences between specific ages were tested using post-hoc comparisons of γ_p1 to γ_p3.

All models were estimated using Mplus with pseudo-maximum likelihood (Asparouhov & Muthén, 2005; Muthén & Muthén, 2015), and with missing data (3.64%) assumed to be missing at random (Little & Rubin, 1989).

Empirical Results

Behavioral Fragmentation

Age-specific descriptive statistics for fragmentation are given in Table 1. Descriptively, at age 24 months average fragmentation appears relatively stable across the task at about 0.5, indicating that children tend to show between 1 and 3 behaviors during each epoch. Alternatively, at 36, 48, and 60 months average fragmentation increases over the first eight epochs, and then stabilizes for the remainder of the task. A collection of age-specific observed trajectories from three randomly selected children are depicted in Figure 3 (solid-black lines; analogous to the trajectories shown in the lower portion of Figure 1). Notably, these individual-level trajectories look quite different from the average trajectory described by the means in Table 1. Therefore, we make use of the flexibility provided by the multiple time-scale multiphase latent basis growth model – in particular the allowance for individual (and age) differences in phase-specific growth factors – to allow for greater accommodation of complex patterns of individual deviance from the sample-level means.

Table 1.

Means and Standard Deviations of Fragmentation

Epoch	24 Months		36 Months		48 Months		60 Months
	Mean	SD	Mean	SD	Mean	SD	Mean	SD
1	0.53	0.49	0.32	0.43	0.23	0.42	0.25	0.45
2	0.36	0.48	0.30	0.42	0.20	0.40	0.26	0.48
3	0.42	0.50	0.31	0.47	0.27	0.44	0.29	0.44
4	0.45	0.54	0.38	0.50	0.25	0.42	0.26	0.45
5	0.48	0.54	0.37	0.52	0.31	0.46	0.23	0.41
6	0.50	0.56	0.48	0.53	0.29	0.44	0.35	0.49
7	0.45	0.53	0.46	0.56	0.38	0.47	0.44	0.51
8	0.56	0.50	0.38	0.49	0.38	0.49	0.38	0.50
9	0.49	0.54	0.51	0.56	0.41	0.48	0.36	0.52
10	0.47	0.54	0.50	0.54	0.39	0.50	0.35	0.47
11	0.47	0.57	0.43	0.53	0.40	0.49	0.29	0.47
12	0.48	0.54	0.53	0.57	0.34	0.45	0.38	0.49
13	0.48	0.54	0.46	0.55	0.41	0.53	0.43	0.55
14	0.48	0.52	0.36	0.47	0.42	0.52	0.43	0.47
15	0.50	0.56	0.41	0.52	0.45	0.55	0.35	0.50

Note: 24-Month N = 119, 36-Month N = 128, 48-Month N = 119, 60-Month N = 99. SD = standard deviation.

Figure 3.

Each row of panels depicts a different individual's observed (solid-black line) and model predicted (dashed-grey line) behavior during the Transparent Locked Box Task at age 24, 36, 48, and 60 months.

Intratask Change in Behavioral Fragmentation

Multiple time-scale multiphase latent basis growth models with 2, 3 and 4 phase-specific growth factors were fitted to the 15-occasion fragmentation data. The 2-phase model had two factors with basis coefficients for epochs 1-8 and 8-15; the 3-phase model had three factors with basis coefficients for epochs 1-5, 5-10, 10-15; and the 4-phase model had four factors with basis coefficients for epochs 1-3, 3-7, 7-11, and 11-15. As well, a latent basis model (i.e. a 1-phase model with an intercept) was fitted to the fragmentation data as a basis of model comparison. Both the AIC and aBIC indicated that the 4-phase model fitted the data best, whereas the BIC suggested the 2-phase model (1-phase model: AIC = 9041.164, BIC = 9144.062, aBIC = 9064.720; 2-phase model: AIC = 9028.160, BIC = 9135.173, aBIC = 9052.658; 3-phase model: AIC = 9033.719, BIC = 9169.544, aBIC = 9064.813; 4-phase Model: AIC = 9007.073, BIC = 9175.825, aBIC = 9045.705). Given the convergence between the AIC and the sample-size adjusted BIC, and that the BIC does not account for the large (multiple records per person) sample size within the current empirical example, we selected the 4-phase model as the best representation of the data. Model parameters are shown in Table 2. Examining the factor loadings, we see that each growth factor/phase is characterized by a “hump” that covers a specific portion of the task (beginning, early-middle, late-middle, and end). Moreover, the empirical example illustrates that the pattern of intratask change cannot be adequately summarized by the (1-phase) latent basis model, and requires the multiple time-scale multiphase latent basis growth model for a more complete characterization.

Table 2.

Summary of the Parameter Estimates for the Four-Phase Multiple Time Scale Multiphase Latent Basis Growth Model

Parameter	Estimate	se	z	p
Factor Loadings
λ 1,1	1.17	0.11	10.62	<.01
λ 2,1	=1.00	--	--	--
λ 3,1	1.21	0.42	2.86	<.01
λ 3,2	−0.08	0.36	−0.21	.83
λ 4,2	=1.00	--	--	--
λ 5,2	1.09	0.10	11.05	<.01
λ 6,2	1.27	0.12	10.94	<.01
λ 7,2	0.76	0.24	3.24	<.01
λ 7,3	0.44	0.17	2.53	.01
λ 8,3	=1.00	--	--	--
λ 9,3	1.07	0.08	13.34	<.01
λ 10,3	1.03	0.08	12.39	<.01
λ 11,3	0.87	0.23	3.86	<.01
λ 11,4	0.13	0.21	0.64	.52
λ 12,4	=1.00	--	--	--
λ 13,4	1.06	0.08	12.81	<.01
λ 14,4	0.98	0.07	13.77	<.01
λ 15,4	1.00	0.08	12.05	<.01
Age Differences
γ 0,1	0.40	0.04	10.89	<.01
γ 1,1	−0.12	0.04	−3.14	<.01
γ 2,1	−0.18	0.04	−4.57	<.01
γ 3,1	−0.16	0.04	−3.79	<.01
γ 0,2	0.41	0.04	9.74	<.01
γ 1,2	−0.05	0.05	−1.03	0.30
γ 2,2	−0.16	0.04	−3.78	<.01
γ 3,2	−0.14	0.05	−3.21	<.01
γ 0,3	0.48	0.04	11.03	<.01
γ 1,3	−0.03	0.05	−0.66	.51
γ 2,3	−0.09	0.04	−2.13	.03
γ 3,3	−0.13	0.05	−2.57	.01
γ 0,4	0.48	0.04	12.17	<.01
γ 1,4	−0.04	0.04	−0.98	.33
γ 2,4	−0.08	0.05	−1.86	.06
γ 3,4	−0.09	0.05	−1.94	.05
Factor Residual Variances/Covariances
${\sigma }_{p1}^2$	0.03	0.01	4.28	<.01
${\sigma }_{p2}^2$	0.06	0.01	6.06	<.01
${\sigma }_{p3}^2$	0.07	0.01	7.89	<.01
${\sigma }_{p4}^2$	0.07	0.01	6.56	<.01
σ p1,p2	0.04	0.01	6.11	<.01
σ p1,p3	0.03	0.01	4.12	<.01
σ p2,p3	0.03	0.01	5.23	<.01
σ p1,p4	0.02	0.01	2.62	.01
σ p2,p4	0.03	0.01	4.76	<.01
σ p3,p4	0.05	0.01	7.13	<.01
Manifest Variable Residual Variance
${\sigma }_{\theta }^2$	0.18	0.01	30.26	<.01

Note: Model configuration shown in Figure 2. N = 453. se = standard error, z = z-value, p = two-ailed p-value at α = .05. Overall Model fit: AIC = 9007.073, BIC = 9175.825, aBIC = 9045.705.

Seeing that the latent basis coefficients for the 4-phase model were all very close to 1, we also compared the fit of the 4-phase model to one where all of the basis coefficients where constrained to 1, analogous to a traditional RMANOVA-type model. We removed the phase-overlapping basis coefficients to ensure model identification (“stability factors” for epochs 1-3, 4-7, 8-11, and 12-15). The constrained version of the 4-phase model viably describes change as discontinuous jumps/steps in fragmentation between phases, but did not fit the data as well as the more flexible 4-phase model (χ² = 27.3, df = 14, p = .018).

The 4-phase model captured interindividual differences in intratask change (the variances for the factor scores all differed significantly from zero; ${\sigma }_{p_1}^2=.03$, ${\sigma }_{p_2}^2=.06$, ${\sigma }_{p_3}^2=.07$, ${\sigma }_{p_4}^2=.07$; all p < .01), and accounted for significant proportions of variability at each epoch (average R² = .27, range = [.18, .34], all p < .01). In sum, the model provides, through the combination of multiple latent growth factors and estimated factor loadings, for substantial flexibility in how individuals’ fragmentation changes in the short-term across the task. The range of differences is highlighted by the nonlinear person-specific observed (solid-black lines) and model-predicted trajectories (dashed-grey lines) shown in Figure 3.

Developmental Change in the Pattern of Intratask Change

The 4-phase model was configured to examine long-term (i.e. developmental) change in the short-term intratask change of fragmentation. Specifically, age differences are described by the relations between the dummy coded age variables and the four phase-specific growth factors (Equation 4; the γ parameters in Table 2). The age variables accounted for a significant proportion of the factor variance for the first phase (R² = .13, p = .01). Children at 24 months showed the largest hump of fragmentation (γ₀₁ = .40, p < .01), and at older ages they showed significantly smaller hump (γ₁₁ = −.12; γ₂₁ = −.18; γ₃₁ = −.16; all p < .01). Post-hoc analyses showed that children at 36-months had a larger hump than at 48-months (γ₁₁ – γ₂₁ = .07, p = .04), but did not differ significantly by 60-months (γ₁₁ – γ₃₁ = .04, p = .31). Fragmentation for children at 48 months did not significantly differ compared to children at 60 months (γ₂₁ – γ₃₁ = −.03, p = .45). The pattern of results for the first phase indicated that the youngest children showed the highest hump of fragmentation, and as they aged they tended to show lower humps of fragmentation. Age differences in extent of change during the beginning of the task were most salient between 24 and 36 months, with smaller or negligible differences after 36 months.

Age also accounted for a significant proportion of variability of the second (early-middle) growth factor (R² = .07, p = .02). Children at age 24 months showed the largest fragmentation hump (γ₀₂ = .41, p < .01), they did not significantly differ by 36 months (γ₁₂ = −.05, p = .30), but showed significantly lower humps of fragmentation by 48- and 60-months (γ₂₂ = −.16, p < .01; γ₃₂ = −0.15, p < .01). Post-hoc analyses indicated that children showed a larger hump at 36-months compared to 48-months (γ₁₂ – γ₂₂ = .11, p < .01) and 60-months (γ₁₂ – γ₃₂ = .10, p = .04). Yet, the size of the hump did not differ significantly from 48-months to 60-months (γ₂₂ – γ₃₂ = −.01, p = .75). In sum, age differences in the extent of change during the early-middle phase indicated that children tended to show larger humps of fragmentation at 24 and 36 months compared to 48 and 60 months.

Results from the third phase were mixed. Age variables did not account for a significant proportion of variance in the factor scores describing change during the late-middle of the task (R² = .04, p = .14), but significant differences between ages emerged from the model coefficients. Children showed the largest fragmentation hump at 24 months (γ₀₃ = .48, p < .01), did not differ significantly by 36-months (γ₁₃ = −.03, p = .51), but showed lower humps of fragmentation at 48- and 60-months (γ₂₃ = −.09, p = .03; γ₃₃ = −.13, p = .01). The size of children's fragmentation hump did not significantly differ from 36- to 48-months, (γ₁₃ – γ₂₃ = .06, p = .10) nor did the hump from 48- to 60-months (γ₂₃ – γ₃₃ = .40 p = .40). However, children at 36-months exhibited a significantly higher fragmentation than at 60-months (γ₁₃ – γ₃₃ = .10, p = .04). Though the results from the third phase partially indicate that the hump of fragmentation increases as children age, the results are not consistent across the different statistical tests, and therefore there is not strong evidence to support the conclusion that the pattern of fragmentation reliably differs across ages.

Significant age differences did not emerge for the fourth phase (R² = .02, p = .24). Twenty-four month-olds exhibited the most fragmentation during the fourth phase (γ₀₄ = .48, p < .01), but pattern of fragmentation did not significantly differ by 36 (γ₁₄ = −0.04, p = .33), 48 (γ₂₄ = −0.08, p = .06), or 60 months (γ₁₄ = −0.09, p = .05). Furthermore, children did not significantly differ in their fragmentation hump at 36-, 48-, or 60-months (γ₁₄ – γ₂₄ = .04, p = .39; γ₁₄ – γ₃₄ = .05, p = .29; γ₂₄ – γ₃₄ = .01, p = .90). Thus, the results from the fourth phase indicate that the pattern of fragmentation did not significantly differ across the different ages.

Integrating across the results from all phases, the long-term change of intratask change in fragmentation appears more prominently at beginning of the task. Within the first phase (0-30 seconds), children at older ages show lower hump of fragmentation. By the second phase (20 – 70 seconds), the humps do not reliably differ between 24 and 36 months, but by 48 months show lower hump of fragmentation. Within the third phase (60 – 110 seconds), small - but not significant - differences in the hump of fragmentation occur as children become older. Then, during the last phase (100 - 150 seconds) children show similar degrees of fragmentation across all ages. Figure 4 contains depictions of the expected age-specific trajectories. As seen within Figure 4, during the first phase children show the highest fragmentation at 24-months (gray dashed line). During the second phase, children's 36-month fragmentation pattern is much closer to their 24-month pattern, but separate from the patterns at 48- and 60-months. In the final two phases children's pattern of fragmentation at different ages tend to converge.

Figure 4.

Expected intratask change in fragmentation for prototypical individual at ages 24, 36, 48, and 60 months, as implied by the multiple time scale, 4-phase latent basis growth model.

Discussion

This paper aimed to extend multiple time-scale modeling efforts by combining an intraindivdual variability-based measurement tool, a latent basis growth model, a multiphase growth model, and a growth model with covariates in a way that allows for examination of long-term (developmental) change in a short-term (intratask regulation) process. In particular, we used an entropy metric to consolidate 10-variate categorical time-series data from a multiple burst study design into univariate time-series that could be described using a highly flexible growth modeling framework. We demonstrated the utility of a multiple time-scale multiphase latent basis growth model for describing interindividual differences in intratask change and testing for long-term (developmental) change of the short-term intratask change. Empirical results were used to characterize self-regulation as a process wherein children's behavior becomes more and less fragmented as they respond and deal with task-related challenges. By combining a multiphase growth model with a latent basis growth model, intratask (short-term) change was modeled using four phase-specific growth factors that described “humps” of increasing and decreasing fragmentation during the beginning, early-middle, late-middle, and end of the task. Integrating a growth model with covariates, developmental (long-term) change in the short-term changes was modeled using a set of age variables as predictors of the phase-specific growth factors. Results indicated that children showed the largest humps of fragmentation at younger ages (24 months); that, by the second phase, the pattern of fragmentation at 36-months matched the pattern from 24-months; and that, by the third or fourth phase, the pattern from 48- and 60-months matched the patterns from 24- and 36-months.

Entropy as a Measurement Model

Categorical time-series require specific modeling approaches. Within the current paper, we used the calculation of entropy as a measurement model to compress a multivariate categorical time-series into a univariate time-series. Our goal was to quantify the “simultaneous” activation of multiple behaviors and emotions (within 10 second epochs) into a single fragmentation score. This contrasts with other examinations of categorical time-series, which tend to focus on extracting common features (i.e., a common latent variable) from a set of categorical responses. For example, the hidden Markov model (Visser, Raijmakers, & Molenaar, 2002) extracts latent states from a set of categorical indicators, and estimates transitions between those states. Similarly, growth models can be used to examine changes in latent factors jointly indicated by multiple categorical variables (Muthén & Asparouhov, 2002). A clear distinction can be drawn between the entropy-based measurement model and the hidden Markov or growth model. If the manifest categorical responses are not assumed to have a common source of variability and the aim is to measure the degree of heterogeneity of responses, then the entropy-based measurement model provides a useful quantification. However, if categorical responses are assumed to share variance, and the goal is to extract that shared variance, the hidden Markov or growth models facilitate the measurement of those common sources. Thus, the entropy-based method is appropriate for applications that seek to quantify dispersion among categorical responses, rather than for applications that seek to extract variance that is shared across categorical responses.

Multiple Time-scale Multiphase Latent Basis Growth Model

The current paper introduced the multiple time-scale multiphase latent basis growth model as a new method for examining repeated measures. We place this model within an ordered taxonomy of different models for change, and emphasize the model's utility for capturing complexity of interindividual differences in intraindividual change. Models for change can be ordered based on the degree of a priori constraints. Repeated measures analysis of variance (RMANOVA with an unstructured residual error matrix) imposes the least constraints, whereas the latent growth model (such as the linear or quadratic growth model) imposes relatively severe constraints. The RMANOVA accommodates each individual's pattern of change by allowing for person-specific differences from a mean at each measurement occasion, whereas the latent growth model extracts factors of change that are defined (a priori) from a particular basis function. The multiple time-scale multiphase latent basis growth model outlined here sits between these two extremes, but somewhat closer to the RMANOVA. The latent basis functions within each phase (phase-specific factor loadings) enable the data to define the model-implied trajectory of change, but still imposes some structure through the predefined location of the phases. Accordingly, multiple time-scale multiphase latent basis growth model allows for rich idiosyncratic change across the repeated measures (analogous to the RMANOVA), and offers parsimony through use of factors of change (analogous to linear and quadratic growth models). As observed within the fragmentation data, the mean trajectory appeared flat at age 24 months but the observed and model-implied trajectories of individual change within Figure 3 are more nuanced. Hence, the person-specific deviations around the mean trajectory are captured via the estimated basis coefficients (in concert with the idiosyncratic factor scores); facilitating an individual-specific, semi-exploratory approach for investigating change.

A close examination of the taxonomy would show that the multiple time-scale multiphase latent basis growth model has, by definition, features of both the multiphase growth model and the latent basis growth model. The multiphase model (Cudeck & Klebe, 2002; Ram & Grimm 2007), separates change into a series of consecutive phases, but identifies a priori functional forms of change (e.g., polynomials) within each of those phases. The latent basis growth model typically estimates the functional form of the change trajectory using a set of factor loadings (basis function) that are estimated from the empirical data, but does not separate those loadings into functions that apply during different phases. By combing these features, the multiple time-scale multiphase latent basis growth model allows for data-based derivation of different functional forms for each of many phases. Each model is appropriate for different types of applications. The multiphase growth model is built for situations where the mathematical functions describing within-phase change are known (e.g. linear, quadratic). The latent basis growth model is built for situations where the individual differences in change manifest in a single nonlinear function of unknown shape. Combining these two, the multiple time-scale multiphase latent basis growth model is built for applications where the individual differences in change manifest differently across time. Selection among these three models may be driven by theory, relative fit to the data, or a combination of the two. The main conclusion here is that the multiple time-scale multiphase latent basis growth model extends the flexibility offered by either the multiphase or latent basis growth model; providing a flexible framework for articulation of change across multiple time-scales.

Examination of Self-Regulation as a Process

Self-regulation should be conceptualized as a dynamic process but is rarely studied as such in the developmental literature. With adult participants, prior work has conceptualized individuals’ ability to regulate as a finite resource that becomes exhausted in the face of repeated challenge (Carver & Scheier, 1998; Corno, 1986; Corno & Rhorkemper, 1985; Baumeister & Heatherton, 1996) and that improves with practice and experience (Baumeister & Vohs, 2007). If self-regulation is a process by which one efficiently and effectively recruits strategies to control action, then entropy reflects the fragmentation of the self-regulatory process. The results of this application of the multiple time-scale multiphase latent basis growth model suggests that there are age-related changes in how long it takes before young children show such fragmentation. Specifically, the longitudinal data indicate that, prior to age 36 months, children tended to manifest large humps of fragmented behavior throughout a task that challenged their ability to engage in self-regulation (i.e., persist despite frustration). As they got older, children's initial humps of fragmentation decreased. Hence, with age, children show an increased ability to remain on task – better self-regulation.

Importantly, the results of this study emerged from an examination of the dynamics of behavior and emotion across fast (epoch-by-epoch) and slow (year-to-year) time-scales. Studies that examine a more ‘trait-like’ feature of self-regulation, and do not examine the dynamics, may not be able directly to inform hypotheses of self-regulation that predict specific moment-to-moment changes of behaviors and emotions. Therefore, the implementation of the multiple time-scale multiphase latent basis growth model offers an opportunity to examine self-regulation as a process, the dynamics therein, and the developmental changes of those dynamics; providing complementary information to the wider literature that informs a more ‘trait-like’ characterization of self-regulation.

Note that while our model development was motivated by study of self-regulation, the model may be useful for examining a wide variety of multiple time-scale phenomena (see Ram & Gerstorf, 2009). For example, the model could be used to examine how short-term patterns of change evolve over the long-term across multiple bursts of task performance (i.e., reaction time during a cognitive task; Tamnes, Fjell, Westlye, Ostby, Walhovd, 2012), behavioral flexibility (i.e., the degree of behavioral consistency across different contexts; Erickson, Newman, Pincus, 2009), and the cortisol awakening response (i.e., the daily increase of cortisol after the first hour of awakening; Almeida, Piazza, Stawski, 2009). In other fields, examples include long-term changes in seasonal patterns of plant growth, product sales, and work productivity. Generally, the model will be useful when behavior is multiply determined by processes that evolve on both slow and fast time-scales.

Limitations and Future Directions

A few limitations must be considered. First, the model used in the empirical example specified the location of the measurement bursts (long time-scale) and intra-task phase transitions (short time-scale) a priori. That is, we “lumped” together sets of observations in particular ways – four measurement bursts with four phases – based on the study design (assessment at 12 month intervals) and knowledge about the phenomenon (fragmentation during laboratory task). In other applications, however, a priori definitions of the bursts and/or phases may not be available. For instance, we might have conceptualized intra-task change as having three phases rather than four phases. Our selection for the pattern of factor loadings (e.g., gray cross-loadings in Figure 2) was calibrated using fit criteria (i.e., AIC, BIC, aBIC). Alternatively, the locations of the phase transitions might be constructed differently (three-phase model reveals similar are-related change) or included within the model as parameters (or person-specific coefficients). For example, the regime-switching state-space model allows an individual to transition in and out of phases that are defined by their dynamics or pattern of change (Chow & Zhang, 2013). Future work should compare the two approaches to better understand the types of situations and phenomena that are best described by each approach.

Second, the implementation used here used a two-stage approach. First, fragmentation scores were calculated from the multivariate categorical data, and then those scores were modeled using the multiple time-scale multiphase latent basis growth model. In principle, the measurement and change models could be combined into a single model, and all the parameters could be estimated simultaneously. It may be possible to estimate the combined model using Bayesian software (e.g. JAGS, WinBUGS; Plummer, 2003; Spiegelhalter, Thomas, Best, & Lunn, 2002). Future work should pursue an integrated flexible measurement + flexible change model to better understand the degree of precision that is lost (or unintentionally gained) in the multi-step calculation-estimation approach used here.

Conclusion

Measurement burst designs, wherein individuals are measured intensively at multiple waves have gained substantial traction among developmental researchers (Nesselroade, 1991; Ram & Gerstorf, 2009). The data obtained from them is facilitating examination of behavioral change at multiple time-scales. The current paper developed and illustrated how a common intraindividual variability-based measurement paradigm and three types of growth models can be combined to examine long-term developmental change in a self-regulatory process that unfolds of the short-term. We hope that the methods and model presented may stimulate further collection of multiple time-scale data, creative analysis of those data, and further our understanding of how processes that unfold at different cadences contribute to behavioral change.