Influence of wave-front sampling in adaptive optics retinal imaging

Abstract

A wide range of sampling densities of the wave-front has been used in retinal adaptive optics (AO) instruments, compared to the number of corrector elements. We developed a model in order to characterize the link between number of actuators, number of wave-front sampling points and AO correction performance. Based on available data from aberration measurements in the human eye, 1000 wave-fronts were generated for the simulations. The AO correction performance in the presence of these representative aberrations was simulated for different deformable mirror and Shack Hartmann wave-front sensor combinations. Predictions of the model were experimentally tested through in vivo measurements in 10 eyes including retinal imaging with an AO scanning laser ophthalmoscope. According to our study, a ratio between wavefront sampling points and actuator elements of 2 is sufficient to achieve high resolution in vivo images of photoreceptors.

1. Introduction

Ocular aberrations not only limit the vision performance, but they also limit the possibility to examine the eye [1]. As the eye presents time-variable wave-front deformation [2], adaptive optics (AO) techniques can be applied to provide efficient wave-front control during the examination, enhancing the quality and increasing the resolution of retinal imaging [3, 4]. AO has enabled the examination of single cells in the eye, it provides the ability to see microscopic structures such as cone and rod photoreceptors or leukocytes in vivo and non invasively [5]. Thus, it is now possible to monitor retinal functions, retinal diseases and therapy effects on a cellular level. Since the first implementation of AO to correct for high order ocular aberrations [6], most of the ophthalmic imaging techniques have incorporated AO: flood illumination fundus imaging (FI) [6], scanning laser ophthalmoscopy (SLO) [7], optical coherence tomography (OCT) [8], fluorescence imaging [9] and two photon excitation imaging [10].

The correcting device of an AO loop is typically a deformable mirror (DM). It is compensating for wave-front distortions measured by a wave-front sensor, typically a Shack-Hartmann sensor (SH) [11, 12]. The link between wave-front measurement and wave-front correction is done through a computer using corresponding software. The AO loop characteristics depend on the number of actuators in the DM, the number of lenslets in the SH and the frequency of correction. One of the challenges of AO-imaging of the retina is that the aberrations to be corrected can significantly vary (in shape and amplitude) from one eye to another [13–15]. Thus, it is important to design robust systems, which are able to compensate for a large range of wave-front errors. This constraint mainly drives the choice of the DM: it should have enough actuators to compensate for high-order aberrations and it should present a significant stroke. The sampling density of the SH (number of lenslets) then needs to be chosen in order to be able to measure accurately all deformation modes generated by the DM. Moreover, ocular aberrations present high temporal fluctuations, around 30 Hz, so the correcting loop should operate at higher frequency to reach optimal imaging performance [16, 17]. The limiting factor for the loop speed is the wave-front measurement [18].

A survey of the literature of AO-ophthalmic instruments shows a large variety for the sampling density of the wave-front (WF) in comparison to the number of corrector elements: the ratio lenslets/actuators (RLA) varies from 2 to 30, the latest corresponding to a considerable oversampling [7,17,19–22]. As the beam power incident on the SH is divided by the number of lenslets, a high sampling density of the WF requires high light power to achieve sufficient signal to noise ratio (SNR). On the other hand, fewer lenslets require less power or shorter exposure times for the WF measurement. This can be translated into faster correction speed.

Given the considerable range of RLA commonly used in AO-ophthalmic systems, it remains unclear which configuration represents the best option in terms of sensitivity, AO loop speed and AO correction. In a previous study, the number of lenslets required across each actuator of two given DMs was determined by minimizing condition number (a measure for the stability of an AO system) and mean wave-front variance of the AO systems [23].

In this paper we extend this work and present a model that allows determining the WF correction ability in dependence on the SH and DM sampling densities. The model is used to assess the performance of several DMs (with different number of actuators and different mechanical properties), in combination with several SHs (with different sampling density of the wave-front). One thousand wave-fronts are generated from measured aberrations in human eyes to provide a broad database for the simulations. The model is tested in vivo in 10 eyes using a DM in combination with SHs presenting 4 different sampling densities. Finally, AO-SLO imaging is demonstrated using a low over-sampling of the WF.

2. Methods

2.1. Simulation of the AO correction loop

In order to analyze the relationship between number of actuators of a deformable mirror and number of lenslets of the associated Shack-Hartmann wave-front sensor, a simple model of an adaptive optics system is developed using the programming software Python.

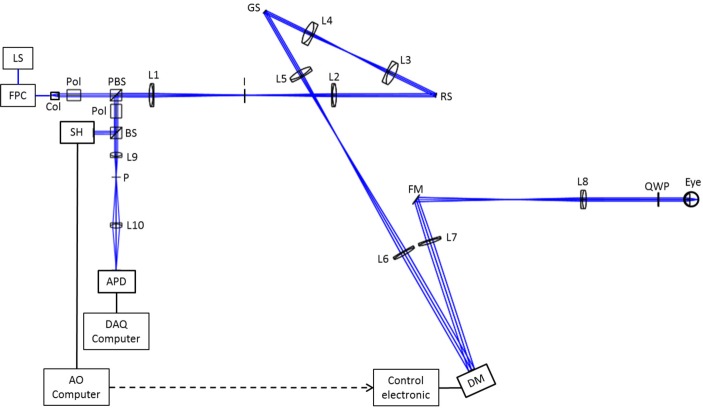
The considered optical system is shown in Fig. 1. A collimated beam is sent to a deformable mirror (DM) and 2 wave-front sensors are measuring the output WF. One of these sensors, denoted SH, is a Shack-Hartmann. It measures the slopes of the WF, which are used to drive the shape of the DM. The other sensor, denoted WFS, is used to assess the optical quality of the system. It measures directly the phase of the WF, with high sampling. Such a set-up corresponds to a 4f system, the DM and both sensors are located in conjugated pupil planes and have the same diameter. As such, the WF is considered identical in these 3 planes. In most AO systems, DM and SH do not have the same diameter. In this case, the focal lengths of the telescope lenses are chosen to accommodate the different diameters. However, this does not affect the phase of the WF in the pupil planes. The considered wavelength is 800 nm, a commonly used wavelength region in ophthalmic imaging.

Fig. 1.

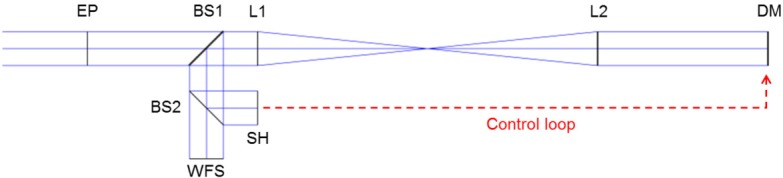
Modeled AO loop. EP: entrance pupil, BS1 and BS2: beam splitters, L1 and L2: telescope lenses, DM: deformable mirror, SH: Shack Hartmann sensor (measures the slopes of the WF), WFS: wave-front sensor (reference sensor, measures the phase of the WF).

The WF at the beam entrance can be arbitrarily set and the performance of correction is characterized for different loop configurations (number of actuators and SH sampling).

2.1.1. Elements of the simulation

The DM is modeled with a square array of actuators, regularly spaced along the x and y directions (z being the optical axis). The pupil diameter is defined so that one ring of actuators lies outside the pupil (actuators at each corner are removed). Two configurations are studied here, corresponding to commercialized electromagnetic DMs, commonly used for retinal imaging applications [5, 10, 22, 24–28]. The characteristics of both DMs, denoted DM52 and DM97, are presented in Table 1. The main difference is the density of actuators: the first one has 52 elements, and the second one has 97.

Table 1.

Characteristics of the two studied deformable mirrors.

	DM52	DM97
Manufacturer	Imagine Eyes	Alpao
Number of actuators	52	97
Pupil diameter	15 mm	13.5 mm

The method to assess the correction performance of a DM is based on its influence functions. An influence function is defined as the WF change resulting from the unit command on one actuator, the others being unactuated. In the model, the influence function f_i of each actuator is approximated by a Gaussian function [11]:

$$f_i(x,y)=K{e}^{-{(x-x_{act,i})}^2/(2s^2)}{e}^{-{(y-y_{act,i})}^2/(2s^2)},$$ (1)

with i the number of the considered actuator, (x_act,i, y_act,i) the coordinate of its center, K the amplitude of the Gaussian (actuator command) and s the standard deviation of the Gaussian. s is a parameter that considers the coupling factor between two neighboring actuators. A coupling factor of 15% means that when one element of the DM is actuated, the amplitude of the deformation below the neighbor actuator corresponds to 15% of the command given to the actuated element. The manufacturers of magnetic DMs indicate nominal coupling factors between 30% and 60%. In literature, coupling factors of 10% to 20% are used to model other types of DMs, including those with mechanical actuators [11, 29]. In order to quantify the impact of this actuator coupling factor, the 2 DMs are modeled with 3 different coupling factors: 15%, 30% and 60%.

The SH is modeled as a square array of lenslets. It generates the slopes of the WF at the location of the lenslets, in the x and y directions [30]. At first, the DM and the SH are supposed to be perfectly aligned (same center). The sampling density of the SH will be modified in the simulation. It is modeled by setting of the coordinates (x, y) of the center of each lenslet. The slopes of the WF are computed at these coordinates. It should be noted here that the lenslet array is arranged in a square grid, thus not all the lenslets are located inside the circular pupil, and are used for the WF simulation. Moreover, in reality, each lenslet focuses a part of the WF onto a detector and the spot displacement, compared to a reference position, gives the slopes (together with the focal length of the micro-lenses and the pixel size) [31]. In the model, analytic functions are used to describe the WF, and the derivatives of these functions at the position of each lenslet center are used to compute the slopes. The DM’s influence functions measured by the SH are then defined as the derivatives of the function defined in Eq. (1):

$$\frac{\partial f_i(x,y)}{\partial x}=-\frac{K}{s^2}(x-x_{act,i})e^{-{(x-x_{act,i})}^2/(2s^2)}{e}^{-{(y-y_{act,i})}^2/(2s^2)},$$ (2)

$$\frac{\partial f_i(x,y)}{\partial y}=-\frac{K}{s^2}(y-y_{act,i})e^{-{(x-x_{act,i})}^2/(2s^2)}{e}^{-{(y-y_{act,i})}^2/(2s^2)}.$$ (3)

As an example, Fig. 2(a) shows the influence function of one actuator of DM52, as computed for a SH with a lenslet array of 12×12 micro-lenses.

Fig. 2.

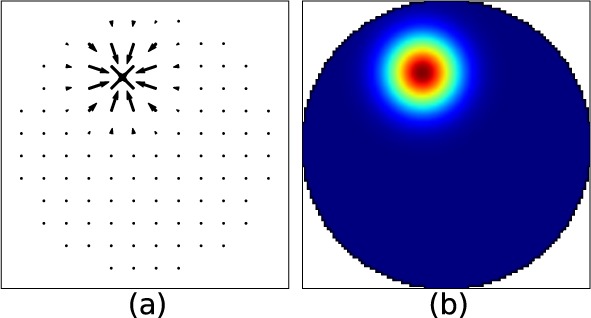
(a) Modeled influence function of one actuator of the DM52 as seen by a SH with a 12×12 lenslet array. The arrows represent the direction of the slopes of the WF at the lenslets location (arbitrary unit). (b) Same influence function as seen by WFS (μm).

The WFS is modeled as a square array of measurement points. The phase of the WF at each location is calculated. In order to characterize the WF accurately, the sampling of the WFS grid is high: 101×101 measurement points. This number of points was chosen arbitrarily and is high enough to capture high spatial frequency fluctuations in the WF. The WFS is used as the reference sensor of the model, that assesses the final optical performance. It is considered to be perfectly aligned with the DM.

Figure 2(b) shows a representative influence function of DM52, as computed for the WFS. In this case the WF is directly given as a phase map, with a high sampling, whereas the SH gives the slopes of the WF, with a lower sampling.

2.1.2. Wave-front definition

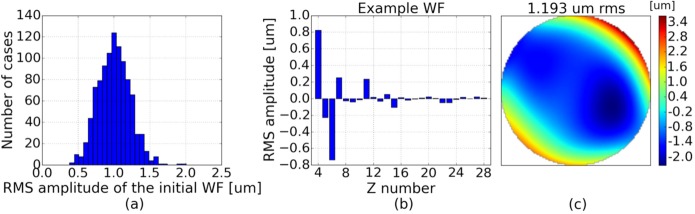
To define the incoming WF in the simulation, a combination of Zernike polynomials is used. The analytic formulas of the Zernike modes are well known, both for the phase and its derivatives. So, any WF can be easily introduced in the model. Zernike modes up to the sixth order are considered here (the 28 first modes according to the Noll definition [32], except piston, tip and tilt). The correction performance of aberrations introduced by different eyes will be studied for different AO-loop configurations (different RLAs). Based on the work of Thibos et al. [33], we have generated a set of 1000 WFs that are representative of aberrations introduced by healthy eyes. Each generated WF P is a combination of 25 Zernike modes (from 2nd to 6th order): $P={\displaystyle {\sum }_{i=4}^{28}{c}_i{Z}_i}$. The Zernike coefficients c_i were randomly drawn using a Gaussian distribution and certain boundaries (see Table 2). The range of amplitudes for the 2nd, 3rd and 4th order modes were deduced from the statistics on the Zernike coefficients given in [33] (for a 6 mm pupil diameter). 5th and 6th order aberrations were added to make the analysis more general. Figure 3(a) shows the distribution of the RMS amplitudes of the considered WFs. Fig. 3(b) presents the Zernike coefficients for one WF of this set and Fig. 3(c) shows the phase reconstruction of this WF on the WFS grid.

Table 2.

Boundary amplitudes of the Zernike modes for the generation of the studied set of WFs (based on data from [33]).

	Zernike mode	Coefficient min [nm]	Coefficient max [nm]
2nd order	Z4 (Focus)	−600	1000
	Z5 (Astm x)	−700	700
	Z6 (Astm y)	−1000	500
3rd order	Z7&8 (Comas)	−400	400
	Z9&10 (Trefoils)	−200	200
4th order	Z11 (Spherical), Z12&13, Z14&15	−100	100
5th order	Z16&17, Z18&19, Z20&21	−70	70
6th order	Z22, Z23&24, Z25&26, Z27&28	−70	70

Fig. 3.

(a) Distribution of the RMS amplitude of the 1000 WFs that will be considered in the model. (b) Zernike decomposition of one representative WF that was generated for the simulation (numbering as defined in [32]). (c) Phase reconstruction of the WF shown in (b), as computed for the WFS in the simulation.

2.1.3. AO control and performance

The SH measures the slopes S of the WF P, in the x and y directions. The measurement is then a vector of length twice the number of lenslets inside the pupil: $S_{SH}=(\frac{\partial P(x_{SH},y_{SH})}{\partial x},\frac{\partial P(x_{SH},y_{SH})}{\partial y})$. This vector is used to control the DM. S_SH can be decomposed onto the influence functions of the system [4]:

$$S_{SH}=M_{SH}\alpha +{\mathit{ϵ}}_{SH}.$$ (4)

M_SH is the interaction matrix of the system, it contains all influence functions, as measured by the SH (see Eq. (2) and (3)). α is a vector containing the commands of the DM allowing to correct the WF and ϵ_SH is the residual slope of the WF, measured after the mirror actuation.

In order to compute the DM commands, the interaction matrix must be inverted. A singular value decomposition is used for this purpose (see Eq. (5)) [34, 35]. The pseudo inverse of the interaction matrix is called control matrix and is denoted C_SH.

$$M_{SH}=u\mathrm{\Lambda }{v}^T=>C_{SH}=v{\mathrm{\Lambda }}^{-1}{u}^T,$$ (5)

where u and v are unitary matrix and Λ is a diagonal matrix containing the system’s eigen values λ_i. The condition number of the system is defined as the ratio between the largest eigen value and the smallest one. This number is an important characteristic, assessing the stability of the control loop: a low condition number ensures the convergence of the system [23]. Thus, to avoid divergence of the AO loop, some eigen values can be removed from the analysis. This improves the conditioning of the system and results in the filtering of some eigen modes. Thus, the generation of problematic mirror shapes is prevented. The number of filtered modes needs to be optimized during the system calibration. Figures 4(a) and (c) present the eigen values of AO systems composed of the DM97 (coupling factors of 15% and 60%) and 2 different SH sensors, with 16×16 and 30×30 lenslet arrays. We can see that the condition number is larger for the DM with 60% coupling factor, indicating that this system is less well conditioned. Figures 4(b) and (d) show the evolution of the condition number when eigen modes are filtered (starting from the last one: when 2 modes are filtered, the 2 smallest eigen values are not considered).

Fig. 4.

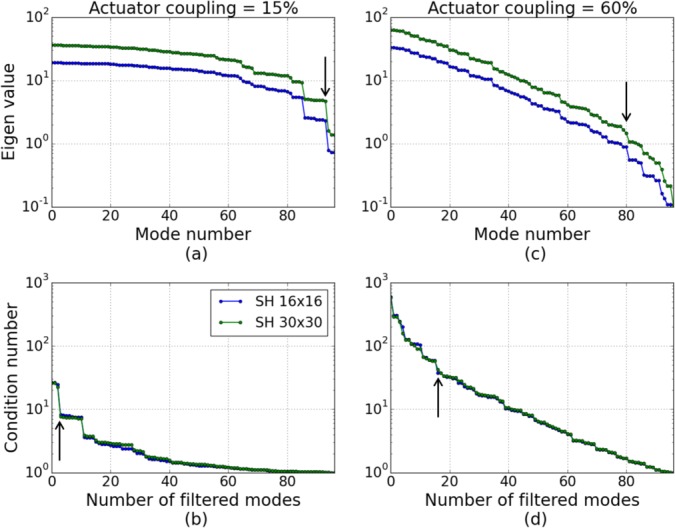
(a) Eigen values of AO systems composed of the DM97, modeled with an actuator coupling of 15%, and 2 SH sensors with different lenslet arrays. (b) Evolution of the condition number of the systems studied in (a), with respect to the number of filtered modes. (c) Same than (a) but for an actuator coupling of 60% (d) Same than (b) but for the system studied in (c). The arrows indicate the point where eigen values were filtered in our analysis.

For a given DM, we can see that the condition number is similar for the different lenslet array sizes. Thus, the main contribution to the stability of the system comes from the DM, not the SH. As can be seen in Fig. 4(b) and (d), the condition number is reduced through filtering of modes. Thereby, filtering of some modes results in large drops in the condition number (cf steps in Fig. 4(b) and (d)). As a criterion for choosing a reasonable number of modes to be filtered, we determined the location with the largest drop in the condition number. These locations are indicated with arrows in Fig. 4 and correspond to 3 modes in the case of low coupling and 16 modes in the case of high coupling of the actuators. The corresponding eigen values are set to 0 for the computation of the control matrix. The same analysis was performed for all the studied DM configurations and Table 3 summarizes the characteristics chosen in each case.

Table 3.

Number of filtered modes and condition number for each studied DM configuration.

	DM52			DM97
Actuator coupling	15%	30%	60%	15%	30%	60%
Nb of filtered modes	3	7	9	3	7	16
Condition number	7	7	50	8	9	40

Once the control matrix is determined, the commands of the DM, α, can be calculated:

$$\alpha =C_{SH}{S}_{SH}.$$ (6)

Finally, to characterize the performance of correction, the generated WFs are used as initial WFs in the simulation. The initial WF, before correction, is P_WFS = P(x_WFS, y_WFS). By combining the commands α computed with the SH measurement (Eq. (6)) and the influence functions as measured by the WFS (in phase, as defined in Eq. (1)), the residual WF, after correction, measured by the WFS can be deduced:

$$P_{Res,WFS}=P_{WFS}-M_{WFS}\alpha ,$$ (7)

with M_WFS the interaction matrix, containing all the influence functions measured by WFS.

The root mean square (RMS) amplitude of this residual WF is used to characterize the system performance. It corresponds to the standard deviation of the phase map P_Res,WFS. According to the Marechal criterion, the system will be considered diffraction limited when the RMS amplitude of the WF is lower than λ/14 [36]. The modeled wavelength (λ) is 800 nm, so the target correction performance is below 60 nm RMS.

2.2. Experimental SLO configuration

In order to validate the conclusions from the model an AO loop is introduced into a scanning laser ophthalmoscope set-up (AO-SLO) and the correction performance is characterized for four different SH samplings, that are alternatively used to control a DM.

2.2.1. AO elements

The correcting device is the Alpao DM97-15, as modeled in the previous section. It has 97 actuators, an actuator coupling factor of ~30% and a pupil diameter of 13.5 mm.

Two SHs will be used. The first one, denoted SH1, is custom-made, it consists of a lenslet array with 32×32 micro-lenses (Adaptive Optics Associates C-0300-16-S) in front of a CMOS camera (Pixelink PL-A741 m). The second one, denoted SH2, consists of a 66×57 lenslet array in front of a CMOS sensor (Optocraft SHSCam SHL-S-150-CL). The characteristics of both sensors are summarized in Table 4. For the same pupil diameter, the sampling in SH2 will be twice the sampling of SH1, this allows studying two different loop configurations without additional relay optics. The pupil diameter on the SH planes is defined by the smallest sensor dimension: 6.6 mm.

Table 4.

Characteristics of the two Shack Hartmann wave-front sensors.

	SH 1	SH 2
Pixel size of the detector	6.7 μm	8 μm
Dimensions of the detector	1280 × 1024 pixels	1248 × 1082 pixels
Lenslet focal length	16 mm	4.3 mm
Lenslet size (square)	300 μm	150 μm
Lenslet array (seen by the detector)	28 × 22	66 × 57
Lenslet array (considered in the experiment)	22 × 22	44 × 44
Number of micro-lenses in the studied pupil	368	1433

These two configurations provide RLAs of 3.8 and 14.8. In order to study smaller RLAs, SH1 is used in association with a telescope that decreases the beam size on the lenslet array. Thus, less lenslets are used. A reduction of the beam diameter by a factor 2 leads to a RLA of 1. And a magnification of 0.75 provides a RLA of 2.4. Table 5 summarizes the different studied configurations. The exposure time of each SH was set to have a spot intensity of ~30% of the detector range. The configuration with the fewest lenslets allows using the lowest exposure time.

Table 5.

SH configuration for the different studied RLAs.

RLA	1	2.4	3.8	14.8
SH used	SH1	SH1	SH1	SH2
Telescope magnification	0.5	0.75	NA	NA
Lenslet array	11 × 11	17 × 17	22 × 22	44 × 44
Exposure time (ms)	10	15	20	60

2.2.2. AO-SLO optical configuration

The principle of the set-up is based on a lens-based AO-SLO, as developed by Felberer et al [37]. The optical design is presented in Fig. 5.

Fig. 5.

Sketch of the AO-SLO instrument. LS: Light Source (804 nm); FPC: fiber polarization controller; Col: collimator; Pol: polarizer; PBS: polarizing beam splitter; L1–L2: lenses (200 mm focal length); I: variable aperture iris (focal plane); RS: resonant scanner (pupil plane); L3–L4: lenses (100 mm focal length); GS: galvanometer scanner (pupil plane); L5: lens (150 mm focal length); L6: lens (300 mm focal length); DM: deformable mirror (pupil plane); L7: lens (300 mm focal length); FM: folding mirror; L8: lens (160 mm focal length); QWP: quarter wave plate; BS: cube beam splitter; L9–L10: lenses (50mm focal length); P: Pinhole (focal plane); APD: avalanche photo-diode (focal plane); SH: Shack Hartmann wave-front sensor (pupil plane).

A broadband fiber light source (Exalos ESX8420-2411) is used, it has a center wavelength at 804 nm and a bandwidth of 40 nm. The light is collimated, and the resulting 8 mm diameter beam traverses a Glan-Thompson polarizer and a polarizing beam splitter. The linearly polarized light traverses the first telescope, composed of two achromatic lenses, and is reflected by the resonant scanner, which provides the horizontal scanning (GSI Lumonics, resonant frequency of 4 kHz). The beam then traverses a second telescope and is reflected by the galvanometer scanner, providing the vertical scanning (6230H, Cambridge Technology). The beam diameter is then doubled by the third telescope which relays the pupil to the deformable mirror (DM97). The light reflected by the DM passes through the fourth telescope, reducing the beam diameter to the size of a dilated eye (7 mm). Before entering the eye, the light traverses a quarter wave plate oriented at 45° to the input linear polarization plane, so the eye is illuminated with circular polarized light. The light is then back-scattered by the retina and traverses the system. The second passage through the quarter wave-plate changes the polarization state to linear and perpendicular to the initial state, so the returning beam is reflected by the polarizing beam splitter. After this reflection, it passes through a second Glan-Thompson polarizer, oriented perpendicularly to the first one, in order to filter any light components with incident polarization state (such as back-reflections from lenses). In addition a variable aperture iris located at the focal plane between the two lenses of the first telescope blocks residual back reflections. The beam is finally separated in 2 paths by a 50/50 cube beam splitter. The reflected beam is sent to the Shack-Hartmann sensor (SH1 or SH2), located in a pupil plane, conjugated to the DM and the eye pupil. Note that the Fig. 5 represents the nominal set-up for a RLA of 3.8 or 14.8. For RLAs of 1 and 2.4, an additional telescope is inserted before the SH, in order to reduce the beam size on the SH (see Sec. 2.2.1). The transmitted beam is focused by an achromatic lens onto a pinhole. The pinhole diameter is 15 μm, corresponding to one Airy disk diameter of the system. The beam is finally re-imaged by a last achromatic lens onto an avalanche photo-diode (APD: C10508, Hamamatsu). The signal of the APD is recorded with a data acquisition board with 10 MHz sampling rate.

The scanning angles of the mirrors were set in order to have a 1.2° × 1.2° field of view. The power entering the eye was set to 650 μW, which is well below the permissible limits for safe illumination of the eye given in the European Laser Safety Standard for a scanning beam at the studied wavelength [38].

2.2.3. Wave-front sensing and control

A commercial adaptive optics software, Alpao Core Engine (ACE), is used to interface the SH and the DM. It analyzes the measured WF slopes and controls the DM actuators in order to reach a target WF. The method to drive the DM is similar to the one described in Sec. 2.1.3. The influence functions are measured during the calibration phase, with a flat mirror at the eye’s pupil location, and with the scanning mirrors off. Then a control matrix is computed. As in the simulation, the last 7 modes are filtered out, minimizing the impact of noise in the system and ensuring AO loop convergence.

The loop is closed with a gain of 0.2 and a frequency of actuation of 3 Hz (the correction rate is the same for the 4 tested RLAs). Tip and tilt modes are not considered in the measurements: the average slopes in x and y directions are automatically subtracted. Although the control loop is performed using the slopes of the WF, a WF reconstruction is performed at each step, to characterize the WF amplitude. The reconstruction method is modal and is considering the first 28 Zernike polynomials (modes up to the 6th order, except piston, tip and tilt). The final WF is characterized by averaging 10 measurements. Under these conditions, the precision of the measurement is 2 nm.

2.2.4. In vivo imaging and post-processing

In order to evaluate the in-vivo performance of the system, the eyes of 5 healthy volunteers were measured. Prior to imaging, the nature and possible risks of the measurement have been explained and an informed consent was obtained. The evaluation was performed under a protocol approved by the local ethics committee (Medical University of Vienna), which adheres to the tenets of the Declaration of Helsinki. A routine clinical eye examination including eye length measurements was performed before the AO-SLO measurement. The subject interface of the instrument was a standard head rest and no bite bars were used.

The ability to measure and correct the WF was studied for both eyes of each volunteer, with the 4 studied RLAs. The imaging performance of the AO-SLO was also characterized in all cases, by recording images at the fovea. The volunteers were chosen with a natural diameter of the pupil in the dark environment larger than 6 mm, so that no artificial dilation was needed. However, the eyes of volunteer V2 were artificially dilated once, in order to perform rod imaging, with a RLA of 3.8.

Table 6 presents the volunteers’ characteristics. As accommodation was not prevented (through administration of special drugs) during the measurements, the RMS amplitude of the WF of each eye was varying by ~± 100 nm for the different configurations. Thus, an average of the measured WF amplitudes is indicated here. The measured WFs are well within the range of those studied in the model (see Fig. 3). However, the pupils’ diameters in our measurements are slightly larger than in [33]. Our WF measurements are in accordance with reports of other groups [13–15].

Table 6.

Characteristics of healthy volunteers that were included in the study.

Volunteer	V1	V2	V3	V4	V5
Age [year]	27	28	30	29	59
Gender	Male	Male	Female	Male	Male
Pupil diameter [mm]	7	6.8	6.5	6.2	6
Error right eye
Diopters (Sphe Astm)	−0.25 +0.50	+0.00 +0.25	−0.50 +0.25	−1.25 +0.25	−1.50 +0.50
WF [nm RMS]	856	1040	819	744	771
Error left eye
Diopters (Sphe Astm)	+0.00 +0.75	−0.25 +0.25	−0.25 +0.25	−1.25 +0.25	−1.75 +0.50
WF left eye [nm RMS]	747	1021	906	745	610

For the imaging part, one measurement corresponds to the recording of 50 AO-SLO frames (one frame has 494 lines, each consisting of 1250 pixels) within ~3 seconds. The AO loop was closed during imaging. The post-processing consists of several steps which includes averaging the recorded frames to improve the SNR. The applied method corrects for the sinusoidal motion of the resonant scanner and performs a frame registration to correct for lateral motion. Details are described by Felberer et al. [37].

3. Results

3.1. Simulation of the correction of 1000 WFs representative of healthy eyes

The AO-correction performance is evaluated for the DM52 and DM97, as explained in Sec. 2.1. Each DM was coupled to SHs with different sampling densities, in order to have RLA varying from ~0.6 to 20. For the DM52, the lenslet array was varying from 8×8 to 36×36. And from 10×10 to 50×50 for the DM97. Moreover, each DM was simulated with 3 different actuator coupling factors.

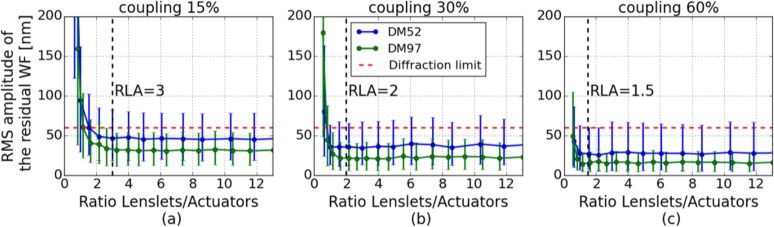
The AO-correction performance of the 1000 WFs presented in Fig. 3 was simulated with the different AO configurations and statistics on the RMS amplitude of the residual WFs were deduced. On Fig. 6, the average RMS amplitude of the residual WFs is plotted as a function of the RLA, for the different DMs. The error bars represent the range of the obtained residual amplitudes, in the considered cases (computed minimum and maximum). We can observe the benefit of a higher actuator density: for a given coupling factor, the performance of correction of the DM97 is overall better. In addition, we can see that the higher the actuator coupling, the better the correction performance. For a given coupling factor, a similar trend of the correction performance depending on the RLA can be observed for both DMs. The residual amplitude is first decreased by increasing the SH sampling density but it quickly reaches a plateau. After this point, higher sampling densities of the SH do not result in a better correction efficiency. In the following we define the optimal RLA as the lowest RLA that allows reaching the best correction with the considered system: there is no improvement in the performance of correction obtained with a RLA higher than this optimal value. For DMs with an actuator coupling of 15%, the optimal RLA is ~3. The optimal RLA decreases while the actuator coupling factor increases: it is ~2 for a coupling of 30% and ~1.5 for a coupling of 60%.

Fig. 6.

Simulation of the AO correction performance of 1000 WFs representative of aberrations introduced by healthy eyes, with DM52 and DM97, in combination with different SH sampling densities. (a) DMs modeled with an actuator coupling of 15%. (b) Actuator coupling of 30%. (c) Actuator coupling of 60%. The error bars show the minimum and maximum residual WF errors. The vertical dashed lines indicate the deduced optimal RLAs. RLAs up to 20 have been simulated, only RLAs up to 12 are shown for better visibility.

The evolution of the DM commands (required strokes to correct for aberrations) have also been studied: only small variations with the number of lenslets were observed (~10% of the maximum required command).

3.2. In vivo WF correction

WF measurement and correction was performed on the AO-SLO system, for 10 eyes, successively with RLAs of 14.8, 4.8, 2.4 and 1. Figure 7 presents the amplitude of the residual WF measured for each eye and each RLA, in comparison with the results from Sec. 3.1, for the model of the DM97 with a coupling factor of 30%. First, we can see that for RLAs larger than 2, the measured performance of correction is equivalent, and below diffraction limit. The residual errors obtained with the RLA of 1 are above diffraction limit in half of the eyes. We can note here that only V1, V2 and V3 were measured with the RLA of 1, the pupil diameter of V4 and V5 was smaller and too many spots were missing on the SH to allow convergence of the AO loop. The trend of the experimental curve follows the trend of the model but there is an offset of ~12 nm between RMS values of the experiment and the simulation.

Fig. 7.

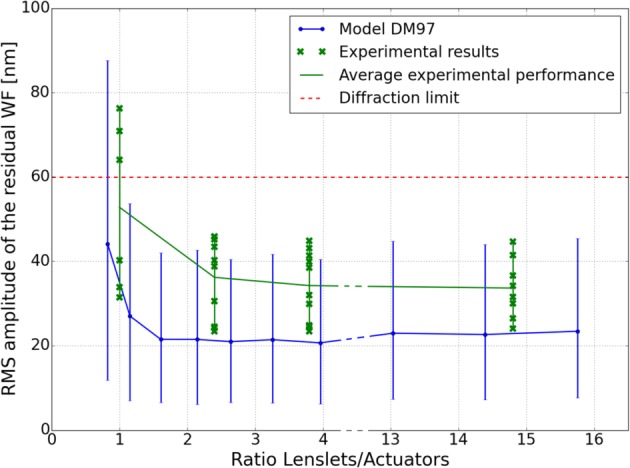
Comparison between the in-vivo AO-correction performance for the 10 healthy eyes and the simulated performance of the considered AO configurations (the blue error bars show the minimum and maximum residual WF errors).

To push further the comparison between model and experiment, the correction results were analyzed in details for V2. This subject was very stable and always fixating at infinity, so the WF from his eyes were similar in all configurations, allowing a fair comparison. The Zernike modes measured on the initial WF of the left eye of V2 were introduced in our model and the expected residual WF was computed for the four studied RLAs. Figure 8 presents the initial and corrected WFs, measured in the 4 configurations, together with the expected residual WFs, deduced from the model. Once again, the measured residual RMS of the WF is slightly larger than the modeled ones. The important outcome of this experiment is the measured difference of performance between the different RLAs, which is in accordance with the simulations. The model was predicting less than 2 nm of difference between the RMS amplitudes of the corrected WFs for RLAs larger than 2. The measured residual RMS amplitudes are within 1 nm. The model was also predicting a 10 nm increase between the RMS amplitude of the WF corrected with a RLA of 2.4 and 1, which is in good agreement with the 13 nm difference that was measured. Finally, the sets of commands that are sent to the DM to perform the correction can also be compared. With a maximum difference of 15%, the commands are similar for the 3 configurations with a RLA larger than 2. This indicates that the DM is driven in the same way.

Fig. 8.

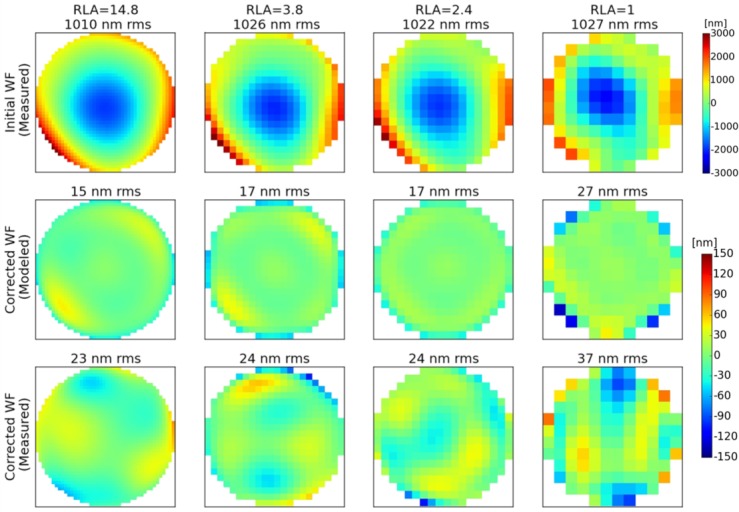
WF measurements and corresponding residual WFs after AO-correction of the left eye of V2 for different RLA configurations. 1st row: WFs measured before correction. 2nd row: Simulated residual WFs after correction of the measured WF. 3rd row: Measured residual WFs, after AO-correction with the instrument.

3.3. AO-SLO imaging

Imaging of the fovea of each subject was performed for all studied configurations, with a field of view of 1.2°. In order to perform a comparison between the images we qualitatively assessed the sharpness of the images and we determined if foveal cones can be resolved in the images. The obtained image quality was equivalent for RLAs larger than 2. Individual cone photoreceptors were visible within the image. For RLA of 1, the image quality was degraded and it was not possible to identify foveal cones. However photoreceptors could be resolved in the periphery of the fovea, for eccentricities from the fovea larger than 0.3°.

In order, to demonstrate the possibility to image cone and rod photoreceptors, the pupils of V2 were artificially dilated. The dilation was necessary to prevent accommodation, as the stability of focus is essential for rod imaging [5].

Figure 9(a) shows an average of 32 frames recorded in the fovea of the subject, with a field of view of 1.2°. Individual cone photoreceptors can be seen within the image. The images were recorded with a RLA of 3.8 (nominal set-up configuration) but similar images were obtained for RLAs of 2.4 and 14.8.

Fig. 9.

(a) Average of 32 AO-SLO images recorded at the fovea of V2, with a scanning angle of 1.2° × 1.2°. (b) Average of 37 AO-SLO images recorded at at an eccentricity of 14° temporal from the fovea, with a scanning angle of 1.2° × 1.2°.

Figure 9(b) shows an average of 37 frames recorded at an eccentricity of 14° temporal to the fovea. In order to image both cones and rods, a defocus of 100 nm RMS is added using the deformable mirror [5, 22]. In the image, the larger cones are surrounded by the smaller rods. At the measured eccentricity, the rod density is close to its highest value [39, 40] and the rod mosaic is not well observed over the entire image. But, at some locations, individual rods can clearly be identified.

4. Discussion

A method has been developed in order to characterize the influence of RLA on the AO-correction performance. It has been shown that for an ideal system (without any error) a SH providing a relatively low oversampling of the WF, compared to the number of actuators, is sufficient to provide an AO correction that is equivalent to systems with higher oversampling (cf Fig. 6). The actuator coupling factor of the DM is an important parameter that influences both the correction efficiency and the required RLA. The higher the coupling, the better the correction performance and the lower RLA can be used. For a DM with a coupling factor of 60%, the simulations show that a RLA of ~1.5 is sufficient. This value is in accordance with the work of Dubra [23]. For a DM with a coupling factor of 30%, a RLA of ~2 is needed.

Our model has been experimentally validated with in-vivo measurements of 10 eyes of 5 healthy volunteers in an AO-SLO set-up. A DM with 97 actuators and a coupling factor of ~30% was used. The AO-loop was driven by different SHs presenting different sampling densities. RLAs of 1, 2.4, 3.8 and 14.8 were tested. For RLAs larger than 2, all the measured WFs were corrected with the same performance and below diffraction limit. Moreover, foveal cones could be resolved on a field of view of 1.2°. This is in excellent agreement with our simulations and validates the main outcome of the analysis: a RLA of ~2 is sufficient for the control of our DM97. There seems to be no benefit for the AO correction using a larger oversampling of the WF (although this was not verified for pathological eyes).

The advantages of minimizing the number of lenslets are numerous for retinal AO-imaging. First, the signal to noise ratio of the WF measurement is increased, because the light is distributed over fewer elements. This could be used to dedicate more light to the imaging part (by changing the splitting ratio of the last beam splitter of the AO-SLO set up). On the other hand, the increased sensitivity of the SH could also be used to speed up the correction loop, by reducing the computational effort and the exposure time of the SH detector. This would allow correcting for high frequency fluctuations of the aberrations of the eye, thus improving the image quality. High speed AO retinal imaging has been realized with magnetic DMs and a RLA of ~2 [17]. Our model shows that such RLA should be sufficient to achieve diffraction limited performance in most eyes. Finally, with a lenslet array with fewer elements, each individual micro-lens can be larger. This increases the measurable WF amplitude range. Thus, the AO system would be more robust to large amplitude WF distortion that may occur in patients, assuming that the DM has sufficient stroke to correct for the measured amplitude.

4.1. Differences between simulated and experimental results

The comparison between simulations and experiments in Sec. 3.2 showed a difference of ~12 nm in the amplitude of the residual WFs. Three possible contributions to this difference are discussed below.

Rapid changes in the eye (motion, accommodation and higher order aberrations) cannot be compensated by the AO system due to a relatively low correction frequency (~3 Hz). These effects are not simulated and are likely to reduce the experimental correction efficiency. In this context, a faster correction, allowed by a smaller RLA, should improve the system performance.

Moreover, the influence of each actuator is simulated as a Gaussian function, but this approximation is not perfectly valid for the experimental influence functions. In addition, the DM is normal to the optical axis in the model but slightly tilted (6 °) in the AO-SLO set-up, thus the pupil on the DM is not perfectly circular. The effect of the shapes of the influence functions can be characterized by using the measured influence functions in our model, instead of the Gaussian functions. This was done for the 4 considered RLAs and the new simulated RMS amplitudes of the residual WFs were increased by ~4 nm. So, roughly one third of the difference between simulations and experiments seems to come from the DM model.

Finally, part of this difference might originate from influences on the WF sensing that were not modeled. Thus, we evaluated the potential impact of noise and misalignment of the SH by introducing these errors in our simulations.

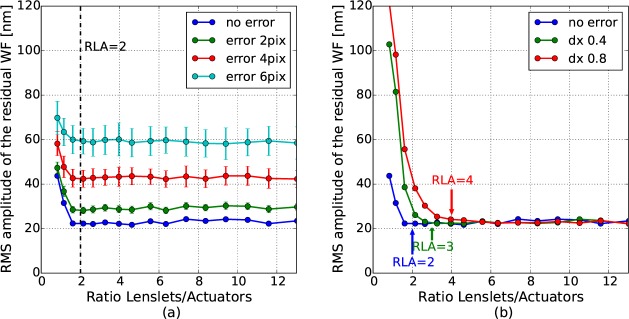
Different sources of noise in the system (detector, background, electronic, etc.) induce errors in the computation of the SH spot positions and thus in the WF measurement [31]. Moreover, the performance of the algorithm determining the centroids of the SH spots might also impact the WF slopes computation [41]. In a first approximation, all error sources can be modeled by adding random components (in number of pixels) to all the computed slopes. As the WF reconstruction from the slopes depends on the lenslet pitch and on the ratio between focal length and pixel size [42], this analysis is performed for a specific SH sensor (SH1: 0.3 mm pitch, 16 mm focal length and 6.7 μm pixel size). We can note here that keeping the detector characteristics fixed results in a varying ratio between detector pixel size and lenslet size: the larger the RLA, the fewer pixels are available for each lenslet. The simulated system performance at different levels of noise is presented on Fig. 10(a), for the AO correction of a focus aberration with an RMS amplitude of 1 μm. An error defined as 1 pixel means that values between −1 and +1 are randomly added to each component of the WF slopes (i.e. subpixel errors are considered). The error of each slope is independent from other slope errors and a uniform law is used to generate its value. For each noise level, the AO correction of the WF was performed 100 times and was statistically analyzed. As can be seen in the figure, the implementation of the noise decreases the performance of the AO-correction. Nevertheless, the best correction performance for a given noise level is still reached for the same RLA, around 2. This analysis confirms that part of the difference between simulated and experimental performance is due to the noise: if we assume that the noise can induce an error up to 2 pixels in the spots computations, then the performance of correction is degraded by ~10 nm. It is important to note here that our noise analysis strongly depends on the SH design including the detector’s pixel size and the focal length of the lenslet array. In addition, averaging or other wavefront reconstruction methods (such as modal reconstruction) have not been considered although these will greatly influence the outcome of the noise analysis.

Fig. 10.

(a) Impact of noise on the performance of the AO correction of an error of 1 μm RMS of focus. The simulation was performed with DM97 (coupling of 30%) and different SH sampling densities. (b) Impact of SH misalignment for the same correction case (the misalignment level is given in fraction of the lenslet size).

The effect of an optical misalignment of the SH, compared to the DM, was also modeled. Such error is simulated by translating the pupil mask in the SH plane. As the WF is defined in the DM coordinates space, a misaligned SH does not see the entire pupil and the number of measurement points is slightly reduced. Fig. 10(b) shows the simulated residual WF after the AO correction of 1 μm RMS of a focus mode, with the DM97 (coupling factor of 30%) and different SH sampling densities, in dependence of different levels of misalignment. Here, a translation along the x axis is studied but similar results are obtained for any orientations. Moreover, we only consider misalignments that are a fraction of the extension of one lenslet, because a larger misalignment is easily detectable with the SH. Up to a RLA of ~4, the RMS amplitude of the residual is larger in case of misalignment. For finer sampling, the misalignment does not have significant influence. The minimum required RLA for sufficient AO-performance slowly increases with the level of misalignment. For instance, a misalignment of 0.4 in lenslet dimension requires a RLA of 3, and the optimal RLA for a misalignment of 0.8 in lenslet dimension is increased to 4. Thus, a higher SH sampling reduces the need for a precise SH alignment.

4.2. Model parameters

The presented model assumes that the influence functions of the DM are known. The number of actuators and shape of the DM’s influence functions impact both performance of AO-correction and optimal RLA. The configuration of the SH will also impact the AO performance. For instance, the pixel size and focal length of the lenslets need to be chosen according to the required amplitude range and sensitivity. In this manuscript, we only studied the case of square array of lenslets, but other arrangements could be considered as well (diamond shaped or sparsely encoded lenslet arrays). Finally, there are several methods for the WF reconstruction and the control loop that might impact the AO performance [43]. An extensive parametric study could be performed with the method developed in this paper in order to identify the effects of these different characteristics.

The methodology developed in this paper was directly applied to ophthalmology, but it can also be useful for other fields of application of AO, such as microscopy, high energy laser or astronomy. In all cases, the AO system must be conceived to meet a specified performance. The developed model allows characterizing the AO correction, in dependence of the WF to be corrected and of the characteristics of the DM and the SH.

5. Conclusion

The simulation of an AO loop allowed determining the performance of AO-correction depending on the oversampling of the wave-front, compared to the number of corrector elements, for AO retinal imaging. The AO-correction performance of 1000 generated wave-fronts that are representative of aberrations of healthy eyes was analyzed with different AO loop configurations. Thereby, deformable mirrors with different number of actuators and different actuator coupling factors were simulated. The influence of the sampling of the wave-front on the AO-performance was investigated by modeling Shack Hartmann wave-front sensors with different number of lenslets. For a DM with an actuator coupling of 30%, a ratio lenslets/actuators of 2 is sufficient for an efficient AO correction.

The outcome of the simulations were validated in-vivo with an AO-SLO system, on 10 healthy eyes. Wave-front sensing and control was performed for 4 RLAs between 1 and 15 and the same correction performance was measured for RLAs larger than 2. Finally, high resolution AO-SLO-images of the retina of healthy eyes were successfully obtained with the different RLA configurations.

Funding

This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 701859. The Austrian Science Fund also contributed under the FWF project P22329-N20. Finally, Matthias Salas acknowledges funding from the macula vision research foundation (MVRF, USA).