Abstract
The hematocrit dependence of flow signal (split-spectrum amplitude decorrelation angiography-SSADA decorrelation value) was investigated in this paper. Based on the normalized field temporal correlation function and concentration dependent particle scattering properties, the relationship between hematocrit and flow signal was analytically derived. Experimental verification of the relationship was performed with custom-designed microfluidic chips and human blood with 45%, 40% and 32% hematocrit. It was found that, in large flow channels and blood vessels, the normal hematocrit is near the decorrelation saturation point and therefore a change in hematocrit has little effect on the SSADA decorrelation value (flow signal). However, in narrow channels in the capillary size range, the effective hematocrit (adjusted for the overlap between OCT beam and channel) is in the range of 6.7-9.5% and therefore variation in hematocrit does significantly affect the flow signal.
OCIS codes: (110.4500) Optical coherence tomography, (170.4460) Ophthalmic optics and devices, (170.3880) Medical and biological imaging
1. Introduction
In recent years, optical coherence tomography angiography (OCTA) has been used as a clinic tool to identify and diagnose ocular diseases such as glaucoma [1], age-related macular degeneration [2], and diabetic retinopathy [3]. Compared with conventional fluorescein angiography (FA) and indocyanine green angiography (ICGA), OCTA provides high-resolution 3-dimensional vasculature in a fast and noninvasive way [4].
Several OCTA algorithms have been developed and they could be based on phase [5–8], intensity [9–12], and complex value [13]. Among the OCTA algorithms, we developed an algorithm named split-spectrum amplitude-decorrelation angiography (SSADA) [12], which splits the spectrum into several spectral bands and calculates the decorrelation between two successive B-scans at the same position for each band. Then the flow signal is represented by the averaged decorrelation value of all the spectral bands. This method has been shown to greatly improve the signal-to-noise ratio of OCTA [15] and been employed to identify vascular and blood flow changes in different aspects of ophthalmology [1–4, 16, 17].
Quantitative characterization of the blood flows in retinal vasculature using OCTA is of great interest for early diagnosis of ocular diseases. A few groups including ours have demonstrated the application of quantitative OCTA for the evaluation of ocular blood flow. However, accurate determination of quantitative information from OCTA images obtained in-vivo may be challenging because too many factors/parameters are involved for in-vivo measurements. In vitro phantom experiments have usually been used to investigate the quantitative nature of the OCTA. Liu et al. used a solid scattering phantom to analyzed and removed bulk motions [18]. Tokayer et al. employed human blood phantom through a glass capillary with a diameter of 200 μm to study the OCTA signal under different A-line intervals and flow speeds [19]. Ruminski et al. used a 280-μm silicon capillary filled with 2% intralipid to investigate the contrast-to-noise ratio for the angiographic images derived from different OCTA algorithms [14]. Very recently, Choi et al. [20] as well as our group [21] have investigated the relationship between OCTA and flow speed in channels with different size using microfluidic chips.
In this paper, the hematocrit (HCT) dependence of flow signal (SSADA decorrelation value) will be investigated. Human blood with the HCT of 45%, 40% and 32% were used in this study to simulate the blood of a normal man, a normal woman, and an anemia people, respectively. Microchannels with widths ranging from 8 μm to 96 μm were used to mimic vessels down to a capillary level. Both the theoretical calculation and the experiments will be performed. The results show that the HCT dependence of flow signal varies for different microchannel width or vessel diameter.
2. Hematocrit dependent, normalized amplitude temporal decorrelation
SSADA detects flow based on the OCT signal scattered or reflected by red blood cells (RBCs). The temporal decorrelation of the OCT signal amplitude is used for the calculation of the flow. Based on the normalized field temporal correlation function and concentration dependent particle scattering properties, we will derive the relationship between the amplitude temporal decorrelation and the HCT, time interval as well as flow speed.
Assuming a Gaussian-shaped speed distribution [22] for the scattering particles, where is the average flow velocity, and an ensemble of scatters moving in a channel (vessel) with an otherwise static medium, the normalized field temporal correlation function g by the scattering particles can be described as [23]
| (1) |
where and are the electric fields at time t and , f is the frequency of the incident light and is the mean square particle displacement in time interval . can be described as . is the difference between the incident and scattered beam wave-vector. The expression of temporal correlation of scattering particles used here has been well established and verified in the laser speckle imaging field for imaging blood flow [24], where a Gaussian velocity distribution is assumed [25, 26]. The flow velocity inside a blood vessel is not a constant value even for a single OCT voxel. Typically, RBC flow velocity is highest in the center of the vessel and decreases at the vessel edges. A parabolic function can be used to describe the velocity distribution. In addition, due to pulsatile nature of the blood flow, the RBC velocity will not be constant. Recently, similar expressions has been used by other groups for quantitative description of OCTA [20, 27]. So this model is suitable for modeling hematocrit dependence of flow signal in OCTA.
Neglecting the phase term in the temporal correlation function as Eq. (1), the amplitude correlation function can be written as
| (2) |
Assuming the scattering is elastic, the can then be expressed as [28]
| (3) |
where and are the scattered and incident wave-vectors, respectively. is the norm of the probe light. is the angle between and . The angle is related to the absorption and scattering coefficients of the particles and can be expressed as [28]:
| (4) |
where is absorption coefficient and is scattering coefficient. is reduced scattering coefficient and is anisotropy. These optical properties of scattering particles are functions of incident wavelength and particle concentration ( in this study). Substituting Eqs. (3) and (4) into Eq. (2), we have:
| (5) |
The amplitude decorrelation value D as a function of the HCT thus can be written as
| (6) |
In OCT system, the OCT signal is a mix of scattering signal from both static and moving particles [29]. To take this into consideration, two parameters and are introduced to represent the signals from both static and the moving particles. Where is the portion of signal from static particles and is the portion of the signal from the moving particles. The decorrelation value can be further expressed as
| (7) |
The scattering property of a particle is also related to the particle concentration. Twersky's formula is usually used describe the relationship between the RBC scattering coefficient and the HCT for human blood [30, 31]
| (8) |
where is mean corpuscular volume and is scattering cross-section. Meinke et al. have measured the optical parameters of the human blood with different HCTs [32]. Based on their results, the following empirical model functions describing the , and can be obtained (for the wavelengths 825 nm-875 nm):
| (9) |
| (10) |
| (11) |
where , , and , are the standard reference values of the , and , respectively.
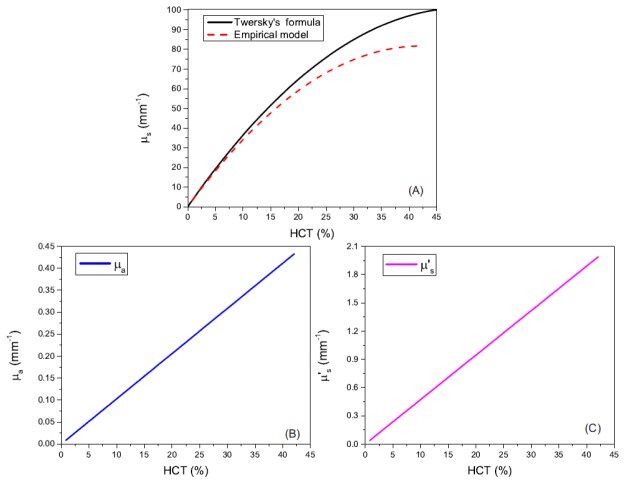
From Eqs. (8)-(11), the relationships between these optical parameters and the HCT at a wavelength of 840 nm (the central wavelength of the OCT system) are plotted in Fig. 1. Figure 1(A) shows the scattering coefficient as a function of the HCT at 840 nm. The black solid line is based on Twersky's formula [30] and the red dash line is based on the empirical model function in [32]. As illustrated in the figure, the scattering coefficients increase with the increase of the HCT. The two models match quite well at a low HCT (<5%). The relationship is linear for low HCT and become nonlinear for higher HCT (>10% for the empirical model and >~15% for the Twersky's formula). The become saturated at ~45% HCT for the empirical model and at ~50% HCT for the Twersky's formula. Figures 1(B) and 1(C) are the absorption coefficient and the effective scattering coefficient as functions of the HCT, respectively. Based on the empirical function models, they keep linearly increase as the HCT increase in the range of 0.84%-42.1%.
Fig. 1.
Optical parameters of the human blood at 840 nm as functions of the HCT. (A) Scattering coefficient. The black solid line is based on Twersky's formula [30] and the red dash line is based on the empirical model function in [32]. (B) Absorption coefficient. (C) Effective scattering coefficient. (B) and (C) are both based on the empirical model functions in [32].
Based on the optical parameters of the human blood and the analytic expression of the decorrelation value as a function of the HCT, a quantitative illustration of their relations can be provided. Before demonstrating the comparison between the model and the experimental data, we first illustrated the general characteristics of the decorrelation value as a function of the HCT under different flow speeds.
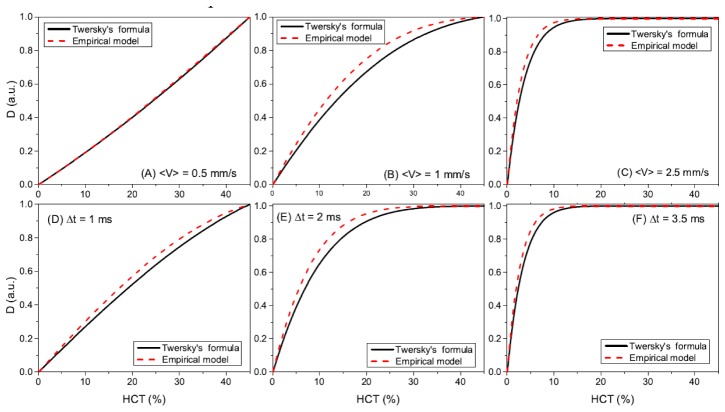
Figure 2 shows the dependence of the decorrelation value D on the HCT for different flow speed, time interval and scattering coefficients based on the two models. Figures 2(A), 2(B) and 2(C) show the decorrelation value as a function of HCT at the speed of, respectively, 〈v〉 = 0.5 mm/s, 〈v〉 = 1 mm/s and 〈v〉 = 2.5 mm/s with a time interval of 5 ms. Figures 2(D), 2(E) and 2(F) show the decorrelation value as a function of HCT with the time interval of, respectively, Δt = 1 ms, Δt = 2 ms, and Δt = 3.5 ms at a fixed flow speed of 3 mm/s. The black solid lines are based on Twersky’s formula and the red dashed lines are based on the empirical model. At a flow speed of 0.5 mm/s, the dependence of the decorrelation value on the HCT is linear in the range of HCTs we are interested and the results based on two models are very similar. At a flow speed of 1 mm/s, the dependence becomes more nonlinear and the decorrelation value saturates at an HCT of ~45%. At a flow speed of 2.5 mm/s, the decorrelation value saturates at an HCT of ~15%. At these two higher flow speeds, the two models show different results and the decorrelation value predicted by the empirical model are always a little higher than those obtained from the Twersky's formula before the decorrelation values become totally saturated. The decorrelation value as a function of the HCT for different B-scan time intervals shows the very similar trend as those for different speeds. At a time interval of 1 ms, the dependence of the decorrelation value on the HCT is almost linear in the range of HCTs we are interested and the results based on two scattering models are very similar. At a time interval of 2 ms, the decorrelation values became more nonlinear and saturated at an HCT of ~35%. At a time interval of 3.5 ms, the decorrelation value fast saturates at an HCT of ~10%.
Fig. 2.
The theoretical HCT dependence of the decorrelation value for different flow speeds, time intervals and scattering coefficients based on the normalized field temporal correlation function and concentration dependent particle scattering properties. The relationship between decorrelation value and HCT are shown at different flow speeds of (A) mm/s, (B) mm/s, (C), mm/s with a fixed time interval of 5 ms. The relationships are also shown with different time intervals of (D) ms, (E) ms, (F), ms at a fixed flow speed of 3 mm/s. The black solid lines are based on Twersky’s formula and the red dashed lines are based on the empirical model.
3. Materials and methods
3.1 Blood sample
Human RBC sample (SER-PRBC, ZenBio Inc, Research Triangle Park, NC) was used in this study. Anticoagulant has been pre-added. Phosphate buffered saline (PBS) was used to dilute the RBC sample to the different concentrations (45%, 40%, and 32% HCT, respectively). It was found that the blood could easily block the microfluidic chips even though anticoagulant was used. In order to reduce the chance of channel blocking by the blood, PBS and deionized water was used to hydrate and clean the microchannels before and after each experiment period. In addition, the duration of the blood stayed in the channels was less than half an hour for all the experiments.
3.2 Characterization of microfluidic chips
Two kinds of the microfluidic chips with different channel size were used in this study. One chip has channels with widths of 8, 16, 32 and 64 μm. The other has channel widths of 12, 24, 48 and 96 μm. All the channels have a height of 17 μm. The design of the microfluidic chips was based on flux equilibrium principle. So the total cross-section area for all channels with the same size is equivalent to the total area for the channels with other sizes. This design guarantees the same flow speeds for different regions of the chip. Although channels blocking may still happen, the flow speed difference for different regions of the chip is less than 10%, which has been validated in our previous study [21].
3.3 OCT system and scanning protocol
A commercial 70-kHz spectral-domain OCT system with a central wavelength of 840 nm (RTVue-XR, Optovue, Fremont, CA) was used in this study. The system has a full width at half maximum (FWHM) bandwidth of 45 nm. The axial resolution is 5 μm in tissue. For OCTA scans, two consecutive B-scans at the same position were employed to calculation the decorrelation values and each B-scan contained 304 A-scans. A total of 304 repeated B-scans was used to obtain a 3-dimensional (3D) volume. A scanning area of 3.5 × 3.5 mm was used throughout this study. It should be noted that the sampling rate is under Nyquist (~12μm spacing, Nyquist would be 7.3μm). We have investigated this issue in our previous publication [21]. It was found that the decorrelation value was affected by system sampling density (scan step size) and the decorrelation value was lower if the sampling density was lower. Generally, the image contrast will be lower in an under-sampling situation. In this study, the same scan pattern (the highest sampling density provided by the system) was used for all of the data and we would expect all the decorrelation value will be lower than the actual value. However, the trend and general conclusion will not be affected by the under-sampling. In addition, the system we used is an FDA 510(K) cleared device, the results will be more representative for real clinical data.
3.4 Experimental setup
The experimental setup for this study is shown in Fig. 3(A). A 60D lens corresponding to a focal length of 16.7 mm was mounted in front of the objective lens of the OCT system to simulate the focusing effect of the human eye. The measured lateral resolution of the system is 14.6 μm [21]. The laser light was focused on the microfluidic chip, which was mounted on a manual stage to fit the height of the objective lens. The chip was tilted (~8 degrees) to avoid strong surface reflection. Two polymer pipes with flat-end needles were inserted into two the inlet and outlet of the microfluidic chip. The inlet pipe was connected to a syringe, which was pumped by a mechanical syringe pump (70-2208, Harvard Apparatus, Holliston, MA). A flow speed of ~1 mm/s was adopted throughout this study. To guarantee a stable flow speed, the imaging and data acquisition started after the syringe pump operated for ~5 minutes.
Fig. 3.

(A) Photograph of the experimental setup. (B) Cross-sectional OCT image of the microchannels. (C) En face intensity image of the microfluidic channels. (D) En face SSADA image of the microfluidic channels.
The biologically relevant flow speed is between a few micrometers per second in capillaries to tens of millimeters per second in large vessels. However, OCTA decorrelation curve saturates. This saturation is dependent on both flow speed and the B-scan time interval. Other groups and we have investigated this [21, 28]. In this manuscript, we have shown that multiplication of these two parameters finally decides the saturation of the decorrelation curve. So for a specific system, the range of biologically relevant flow speeds (or speed below saturation point) is also related the B-scan time interval. For the current system setting used in this study, this range is below 5 mm/s as demonstrated in our previous publication [21]. The speed of 1mm/s was carefully selected based on the results in [21]. The speed would ensure the decorrelation values in all the channels will not be saturated and can be used for characterizing the effect of hematocrit. In [21], we discussed the effect of different flow speeds and channel widths on the OCTA signal. It was found that, with the current OCT system setting, the decorrelation saturation speed was around 5 mm/s. To keep a linear relationship between the flow speed and the decorrelation value, the flow speed should be less than 2.5 mm/s.
3.5 Data processing
The acquired three-dimensional volumetric data exported from the system was processed with a custom Matlab code. A manual segmentation software was used to segment the channels. Then maximum projection structure and OCTA images were obtained as shown in Fig. 3(C) and Fig. 3(D), respectively.
To improve the accuracy of the analysis, careful selection of the channel regions to be analyzed is important. As shown in Figs. 3(C) and 3(D), the channel widths in these images are 48, 24 and 12 μm from top to bottom. The regions showing strong normal reflection were excluded from the analysis. The channels that were blocked were also excluded from the analysis. Those blocked channels usually do not show flow in the OCTA image. The decorrelation values in a channel that was higher than a threshold (half of the maximum decorrelation values in a channel) were used for the analysis.
4. Results
4.1 Channel width dependency of decorrelation value at different HCTs
The channel width (or vessel diameter) plays an important role for quantitative analysis of the OCTA images. In a previous publication [21], it has been shown that at the same flow speed, decorrelation values in channels with different width are different. A model to relate the saturated decorrelation values with the channel width has also been proposed to describe the relationship [21]. This model is based on the fact that the decorrelation value is related to vessel (channel)-beam overlapped at saturation decorrelation region. This model can be extended to the situation where the decorrelation value is not saturated (the flow speed is less than saturated velocity). The relationship between the decorrelation value D and the channel width w at a flow velocity slower than the saturated velocity can be similarly expressed as
| (12) |
where is the saturation decorrelation and is the decorrelation value when the blood in hydrostatic equilibrium and only the Brownian motion involved. is related to the difference of the reflectance between the blood flow and static background. This value will be closer to zero if the difference is larger.
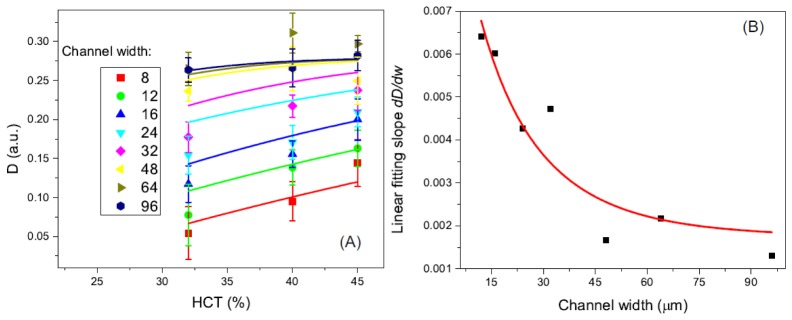
Figure 4 shows the decorrelation values in the channels with different channel width at a flow speed of 1mm/s. Three different HCTs of 32%, 40%, and 45% are shown as red, green, and blue columns, respectively. The model described in Eq. (12) was used to fit the results obtained at different HCTs. The corresponding fitted results are shown as the solid lines in Fig. 4. The parameters from the fitting results are shown in Table 1.
Fig. 4.
The relationship between the decorrelation value and the channel width for different HCTs. Solid lines are the fitting results of the experimental data with the model described in Eq. (12).
Table 1. Fitting results of the decorrelation value as a function of channel width at different HCTs.
| HCT (%) | R-Square | B | |
|---|---|---|---|
| 32 | 0.954 | 0.281 | 0.892 |
| 40 | 0.929 | 0.293 | 0.556 |
| 45 | 0.938 | 0.298 | 0.333 |
As shown in Fig. 4, the decorrelation value increases as the channel width increases from 8 to 36 μm and these values become saturated for larger channel width in the range of 48 to 96 μm. These results are consistent with the findings in our previous publication, where a relationship between the saturated decorrelation value and the channel width were obtained [21].
The proposed model showing in Eq. (12) fits well to the experimental data as quantitatively demonstrated by the “R-Square” values (coefficient of determination) in Table 1. As can be seen from the table, the saturated decorrelation value values become larger and the B becomes smaller as the HCT increases. This shows a higher HCT could increase the saturated decorrelation value (until the decorrelation value reach a maximum) and a higher HCT will also increase the reflectance difference between the flow and the static background.
4.2 Hematocrit dependency of decorrelation values at different channel width
It could be seen from Fig. 4 that the relationship between the decorrelation value and the HCT is also related to the channel width. To further investigate the relationship between the decorrelation value and the HCT, the experimental results in Fig. 4 are re-expressed in Fig. 5, where the decorrelation values are shown as a function of HCT. We further include the effect of the vessel diameter (or channel width for the microfluidic chips) into our theoretical model described in Section 2. If the diameter of the vessel is comparable to or smaller than the beam spot of the system, the diameter of the vessel may affect the ratio of static and moving particles in the imaging voxel. Based on a simple model [21], the ratio between the vessel-beam overlapped area and the beam-covered area can be expressed as
| (13) |
where is error function, is the size of the OCT probe beam and is the channel width. For small vessels (or small channels) with diameter less than OCT beam spot size, F is much less than 1. This will lead to a lower decorrelation value compared to a larger vessel with the same other parameters (flow speed, time interval, HCT et al.). If we assume the RBC is uniformly distributed among the imaging voxel, the effective HCT in the smaller vessels will be lower. Thus an effective can be expressed as
Fig. 5.
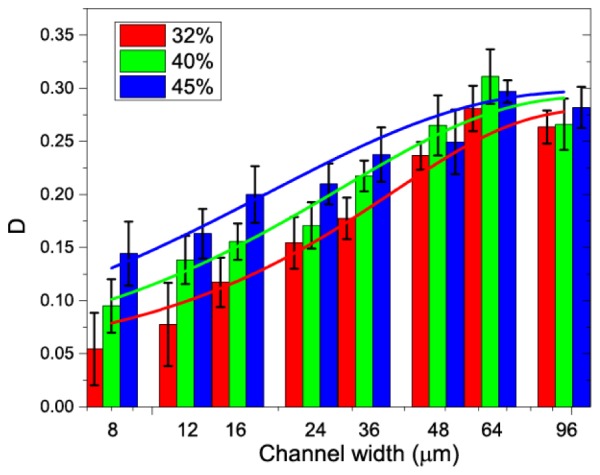
(A) Decorrelation value as a function of the HCT for all the channel widths ranging from 8 μm to 96 μm. Solid lines are theoretical model fitting results for different channel width. (B) Linear fitting slope value of the experimental data as a function of the channel width. Red solid line is the theoretical model (Eq. (16)) fitting result.
| (14) |
The decorrelation value as a function of the HCT thus can be deduced as
| (15) |
As shown in Fig. 5(A), the decorrelation values increase with the increase of HCTs from 32% to 45%. However, the amounts of increase are different for channels with different width. For the 8 μm channels, the decorrelation value increase from 0.05 to ~0.11 while the HCT changes from 32% to 45%. For the 96 μm channel, the decorrelation value does not change much when the HCT increase to 45% from 32%. The HCT in the blood will change the scattering property of the RBC and also the relative ratio between static scatters and dynamic scatters in the imaging voxel. Eventually, the decorrelation value will change accordingly if the decorrelation value is not saturated. For the larger channels/vessels, the decorrelation value is close to saturated value so the change is smaller or there is no change at all. For smaller channels/vessels, the decorrelation value has a strong dependence on the HCT. The effect of channel width on decorrelation value can be described by the overlap volume between the OCT beam spot and the channel [21]. When the channel width is larger than the beam spot, the imaging voxel could be fully occupied by the flow and decorrelation value will be higher and closer to the saturated value than the channel with the same flow speed and HCT. We fitted the experimental data of the relationship between decorrelation and HCT with the theoretical model described above by using an effective HCT for different channel width. For 8 μm channel width and 32%~45% HCT, the effective HCT is 6.73~9.46% for the current setup. The solid color lines in Fig. 5(A) show the results. The fitting between the experimental data and the theory are generally matched very well.
Figure 5(B) shows the slope of the linear fit with a relationship to the channel width. Based on Eq. (12), which is the theoretical model of the decorrelation value as a function of the channel width, we can derive the first-order derivative (equivalent the slope of the linear fit):
| (16) |
Thus we can use this equation to fit the slope data point and the result is demonstrated by the solid red line in Fig. 5(B). We achieved an “R-square” of 0.868. The corresponding and B are 0.04 and 0.39, respectively. It is clear that slope first decreases as the channel widths increasing from 8 to 36 μm and finally become saturated to around zero at channel width of 96 μm. This decrease of the slope has a turning point at the channel width of ~36 μm where the slope starts to be saturated. For the channels widths larger than 36 μm, the slope (~0.0015) is close zero which means the decorrelation value become saturated. These results suggest the effect of the channel width on the decorrelation measurement can be neglected when the channel width larger than 36 μm for the OCT system used.
5. Discussion
It is interesting to compare our works with the intralipid phantom study [20] which also employed similar microfluidic chip. The primary difference between these two studies is the different scattering media used. Choi et al. employed 1% to 4% intralipid while we used human blood with the HCTs of 32%, 40%, and 45%. Intralipid has been widely used as a scattering medium for phantoms that mimic turbid tissues when conducting optical experiments. However, the difference in other characteristics such as anisotropy, viscosity and absorption may lead to different results/conclusion when using intralipid to simulate red blood cell.
The analytic expression of the decorrelation as a function of the HCT can also be extended to the case of the intralipid by substituting the optical properties of the RBCs with those of the intralipid. To compare the results from the intralipid to those from the real blood, we simulate the relationship between decorrelation value and the root mean square particle displacement () for intralipid and blood. Because the flow speed and time interval have similar effect on the decorrelation value as demonstrated in Fig. 2, the mean scattering particle displacement instead of velocity or time interval was used for the simulation. The optical properties of intralipid are based the results from [33, 34]. The simulation results are shown in Fig. 6. It can be seen that the decorrelation value of the 10% intralipid saturates at a of ~400 μm while the saturated decorrelation value of the human blood with three different HCTs saturates are ~2500 μm. The difference originates from the factor as shown Eq. (5) and the factor from the intralipid is an order of magnitude larger than that of the blood. Because for both the blood and intralipid and , the factor can be simplified as , which means the decorrelation value is directly related to the anisotropy of the scattering particle. For an incident light centered at 840 nm, the anisotropy values are, respectively, ~0.98 [32] for the blood with 32%~45% HCT and ~0.6 [33, 34] for the 10% intralipid. The difference in the anisotropy values causes the different dynamic behavior of these two kinds of scattering media. The results show the optical properties of the scattering particle are important for the quantitative analysis of OCTA. Intralipid has different scattering property from real blood and therefore does not model blood well in the flow phantom studies.
Fig. 6.
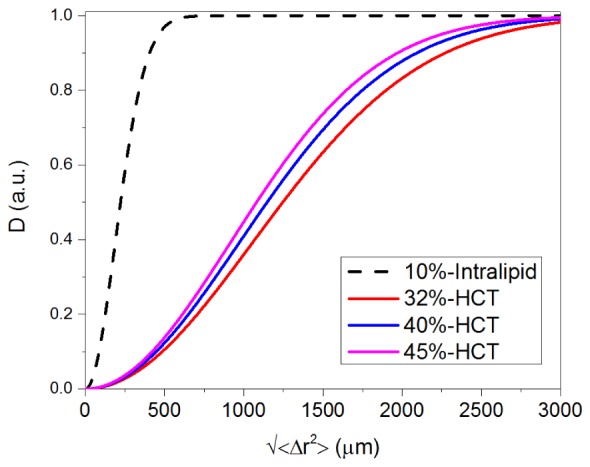
Comparisons of the decorrelation value (D) as functions of root mean square particle displacement () for 10% intralipid and 32%, 40%, 45% HCT.
Because the OCT amplitude decorrelation angiography is used here, phase term is neglected in Eq. (1). In the model by Choi et al., the phase term was taken into consideration when a complex OCT value based OCTA was used [20]. In a previous publication [13], it has been shown that OCT amplitude based OCTA and OCT complex value based OCTA show very similar trends although the unnormalized OCTA values from these methods are different. We used the same parameters of intralipid in our model and got very similar results as theirs (as demonstrated in Fig. 6). So we don’t expect much difference in our conclusions.
In a cylindrical channel or biological blood vessel, the flow velocity profile follows a curve of parabolic distribution. In the case of a rectangular channel used in our experiment, the flow profile would be different. Flow velocity profile in a rectangular channel has been investigated in the microfluidic research field [35]. The velocity distribution in the cross-section ( plane) of the channel can be described in terms of a Fourier series [36]:
| (17) |
where is the viscosity of the fluid, Δp is the pressure difference, L is channel length, h is the height of the channel and w is the width of the channel. In the shorter dimension of the channel cross-section, the velocity distribution is very close to parabolic. In the longer dimension, the velocity profile is largely affected by the aspect ratio (width/height ratio w/h) of the channel. At an aspect ratio close to 1, the velocity profile is close to parabolic. For a higher aspect ratio (>2), the velocity profile would be flatter in the center of the channel. Our analysis was performed one the en-face maximum intensity projection OCTA images. The velocity profile is still close to parabolic for narrower channels. However, because of the limitation of the lateral resolution and scanning density, it would be hard to tell the profile in the small channels from the OCTA images. For wider channels, the velocity profile would be flatter in the center of the channel, so the change across the large channels will be small. Because the flatter velocity profile, the maximum velocity in the wider rectangle channels will be lower than that in a situation where a velocity profile is parabolic. This may contribute to the drop in the decorrelation values in the wider channels as shown in Fig. 4 and the larger deviation from theoretical prediction for the data in the wider channels in Fig. 5.
6. Conclusion
We investigated the HCT dependence of flow signal (SSADA decorrelation value). OCT amplitude decorrelation was analytically derived from normalized field temporal correlation function and concentration dependent particle scattering properties. Different sizes of microchannels (ranging from 8 to 96 μm) were used to mimic large and capillary blood vessels in the experiment study. Human blood with 45%, 40%, 32% concentrations of red blood cell (RBC) was adopted to model the HCTs of a normal man, a normal woman, and an anemia people, respectively. The experimental and theoretical results gave the dependence of the decorrelation value on the HCT for different channel size. The dependency is related to the channel width as well as the beam spot size. In large flow channels and blood vessels, the normal HCT is near the saturation point and therefore changes in HCT has little effect on the SSADA decorrelation value (signal). However, in narrow channels in the capillary size range, the effective HCT is in the 6.73~9.46% range and therefore variation in HCT does significantly affect the flow signal.
Financial disclosures
Drs. Yali Jia and David Huang have a significant financial interest in Optovue, Inc., a company that may have a commercial interest in the results of this research and technology. David Huang also has a financial interest in Carl Zeiss Meditec, Inc. These potential conflicts of interest have been reviewed and managed by OHSU. Other authors do not have a financial interest in the subject of this article.
Funding
This research was funded by Oregon Health & Science Foundation, National Institutes of Health Grants DP3 DK104397, R01 EY024544, R01 EY023285 and R01 EY018184, unrestricted departmental funding from Research to Prevent Blindness (New York, NY), and P30 EY010572 from the National Institutes of Health (Bethesda, MD).
References and links
- 1.Liu L., Jia Y., Takusagawa H. L., Pechauer A. D., Edmunds B., Lombardi L., Davis E., Morrison J. C., Huang D., “Optical coherence tomography angiography of the peripapillary retina in glaucoma,” JAMA Ophthalmol. 133(9), 1045–1052 (2015). 10.1001/jamaophthalmol.2015.2225 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.de Carlo T. E., Romano A., Waheed N. K., Duker J. S., “A review of optical coherence tomography angiography (OCTA),” Int. J. Retina Vitreous 1(1), 5 (2015). 10.1186/s40942-015-0005-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ishibazawa A., Nagaoka T., Takahashi A., Omae T., Tani T., Sogawa K., Yokota H., Yoshida A., “Optical coherence tomography angiography in diabetic retinopathy: a prospective pilot study,” Am. J. Ophthalmol. 160(1), 35–44 (2015). 10.1016/j.ajo.2015.04.021 [DOI] [PubMed] [Google Scholar]
- 4.Spaide R. F., Klancnik J. M., Jr, Cooney M. J., “Retinal vascular layers imaged by fluorescein angiography and optical coherence tomography angiography,” JAMA Ophthalmol. 133(1), 45–50 (2015). 10.1001/jamaophthalmol.2014.3616 [DOI] [PubMed] [Google Scholar]
- 5.Zhao Y., Chen Z., Saxer C., Xiang S., de Boer J. F., Nelson J. S., “Phase-resolved optical coherence tomography and optical Doppler tomography for imaging blood flow in human skin with fast scanning speed and high velocity sensitivity,” Opt. Lett. 25(2), 114–116 (2000). 10.1364/OL.25.000114 [DOI] [PubMed] [Google Scholar]
- 6.Leitgeb R. A., Schmetterer L., Hitzenberger C. K., Fercher A. F., Berisha F., Wojtkowski M., Bajraszewski T., “Real-time measurement of in vitro flow by Fourier-domain color Doppler optical coherence tomography,” Opt. Lett. 29(2), 171–173 (2004). 10.1364/OL.29.000171 [DOI] [PubMed] [Google Scholar]
- 7.Makita S., Hong Y., Yamanari M., Yatagai T., Yasuno Y., “Optical coherence angiography,” Opt. Express 14(17), 7821–7840 (2006). 10.1364/OE.14.007821 [DOI] [PubMed] [Google Scholar]
- 8.Fingler J., Zawadzki R. J., Werner J. S., Schwartz D., Fraser S. E., “Volumetric microvascular imaging of human retina using optical coherence tomography with a novel motion contrast technique,” Opt. Express 17(24), 22190–22200 (2009). 10.1364/OE.17.022190 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Barton J., Stromski S., “Flow measurement without phase information in optical coherence tomography images,” Opt. Express 13(14), 5234–5239 (2005). 10.1364/OPEX.13.005234 [DOI] [PubMed] [Google Scholar]
- 10.Wang R. K., Jacques S. L., Ma Z., Hurst S., Hanson S. R., Gruber A., “Three dimensional optical angiography,” Opt. Express 15(7), 4083–4097 (2007). 10.1364/OE.15.004083 [DOI] [PubMed] [Google Scholar]
- 11.Mariampillai A., Standish B. A., Moriyama E. H., Khurana M., Munce N. R., Leung M. K. K., Jiang J., Cable A., Wilson B. C., Vitkin I. A., Yang V. X. D., “Speckle variance detection of microvasculature using swept-source optical coherence tomography,” Opt. Lett. 33(13), 1530–1532 (2008). 10.1364/OL.33.001530 [DOI] [PubMed] [Google Scholar]
- 12.Jia Y., Tan O., Tokayer J., Potsaid B., Wang Y., Liu J. J., Kraus M. F., Subhash H., Fujimoto J. G., Hornegger J., Huang D., “Split-spectrum amplitude-decorrelation angiography with optical coherence tomography,” Opt. Express 20(4), 4710–4725 (2012). 10.1364/OE.20.004710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Liu G., Lin A. J., Tromberg B. J., Chen Z., “A comparison of Doppler optical coherence tomography methods,” Biomed. Opt. Express 3(10), 2669–2680 (2012). 10.1364/BOE.3.002669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ruminski D., Sikorski B. L., Bukowska D., Szkulmowski M., Krawiec K., Malukiewicz G., Bieganowski L., Wojtkowski M., “OCT angiography by absolute intensity difference applied to normal and diseased human retinas,” Biomed. Opt. Express 6(8), 2738–2754 (2015). 10.1364/BOE.6.002738 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gao S. S., Liu G., Huang D., Jia Y., “Optimization of the split-spectrum amplitude-decorrelation angiography algorithm on a spectral optical coherence tomography system,” Opt. Lett. 40(10), 2305–2308 (2015). 10.1364/OL.40.002305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang X., Jia Y., Spain R., Potsaid B., Liu J. J., Baumann B., Hornegger J., Fujimoto J. G., Wu Q., Huang D., “Optical coherence tomography angiography of optic nerve head and parafovea in multiple sclerosis,” Br. J. Ophthalmol. 98(10), 1368–1373 (2014). 10.1136/bjophthalmol-2013-304547 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Jia Y., Bailey S. T., Hwang T. S., McClintic S. M., Gao S. S., Pennesi M. E., Flaxel C. J., Lauer A. K., Wilson D. J., Hornegger J., Fujimoto J. G., Huang D., “Quantitative optical coherence tomography angiography of vascular abnormalities in the living human eye,” Proc. Natl. Acad. Sci. U.S.A. 112(18), E2395–E2402 (2015). 10.1073/pnas.1500185112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liu X., Kirby M., Zhao F., “Motion analysis and removal in intensity variation based OCT angiography,” Biomed. Opt. Express 5(11), 3833–3847 (2014). 10.1364/BOE.5.003833 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tokayer J., Jia Y., Dhalla A. H., Huang D., “Blood flow velocity quantification using split-spectrum amplitude-decorrelation angiography with optical coherence tomography,” Biomed. Opt. Express 4(10), 1909–1924 (2013). 10.1364/BOE.4.001909 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Choi W. J., Qin W., Chen C. L., Wang J., Zhang Q., Yang X., Gao B. Z., Wang R. K., “Characterizing relationship between optical microangiography signals and capillary flow using microfluidic channels,” Biomed. Opt. Express 7(7), 2709–2728 (2016). 10.1364/BOE.7.002709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Su J. P., Chandwani R., Gao S. S., Pechauer A. D., Zhang M., Wang J., Jia Y., Huang D., Liu G., “Calibration of optical coherence tomography angiography with a microfluidic chip,” J. Biomed. Opt. 21(8), 086015 (2016). 10.1117/1.JBO.21.8.086015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bonner R., Nossal R., “Model for laser Doppler measurements of blood flow in tissue,” Appl. Opt. 20(12), 2097–2107 (1981). 10.1364/AO.20.002097 [DOI] [PubMed] [Google Scholar]
- 23.Durduran T., Choe R., Baker W. B., Yodh A. G., “Diffuse optics for tissue monitoring and tomography,” Rep. Prog. Phys. 73(7), 076701 (2010). 10.1088/0034-4885/73/7/076701 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Boas D. A., Dunn A. K., “Laser speckle contrast imaging in biomedical optics,” J. Biomed. Opt. 15(1), 011109 (2010). 10.1117/1.3285504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Berne B. J., Pecora R., Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics (New York: Courier Dover Publications, 2000). [Google Scholar]
- 26.Nadort A., Kalkman K., van Leeuwen T. G., Faber D. J., “Quantitative blood flow velocity imaging using laser speckle flowmetry,” Sci. Rep. 6, 25258 (2016). 10.1038/srep25258 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Choi W. J., Li Y., Qin W., Wang R. K., “Cerebral capillary velocimetry based on temporal OCT speckle contrast,” Biomed. Opt. Express 7(12), 4859–4873 (2016). 10.1364/BOE.7.004859 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tuchin V., Tissue Optics, Light Scattering Methods and Instruments for Medical Diagnostics, 2nd ed. (SPIE Press, 2007). [Google Scholar]
- 29.Lee J., Wu W., Jiang J. Y., Zhu B., Boas D. A., “Dynamic light scattering optical coherence tomography,” Opt. Express 20(20), 22262–22277 (2012). 10.1364/OE.20.022262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Twersky V., “Absorption and multiple scattering by biological suspensions,” J. Opt. Soc. Am. 60(8), 1084–1093 (1970). 10.1364/JOSA.60.001084 [DOI] [PubMed] [Google Scholar]
- 31.Bosschaart N., Edelman G. J., Aalders M. C. G., van Leeuwen T. G., Faber D. J., “A literature review and novel theoretical approach on the optical properties of whole blood,” Lasers Med. Sci. 29(2), 453–479 (2014). 10.1007/s10103-013-1446-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Meinke M., Müller G., Helfmann J., Friebel M., “Empirical model functions to calculate hematocrit-dependent optical properties of human blood,” Appl. Opt. 46(10), 1742–1753 (2007). 10.1364/AO.46.001742 [DOI] [PubMed] [Google Scholar]
- 33.Michels R., Foschum F., Kienle A., “Optical properties of fat emulsions,” Opt. Express 16(8), 5907–5925 (2008). 10.1364/OE.16.005907 [DOI] [PubMed] [Google Scholar]
- 34.van Staveren H. J., Moes C. J. M., van Marie J., Prahl S. A., van Gemert M. J. C., “Light scattering in Intralipid-10% in the wavelength range of 400-1100 nm,” Appl. Opt. 30(31), 4507–4514 (1991). 10.1364/AO.30.004507 [DOI] [PubMed] [Google Scholar]
- 35.Stone H. A., “Introduction to fluid dynamics for microfluidic flows,” in CMOS Biotechnology, Lee H., Westervelt R. M., Ham D., eds. (Springer; 2007). [Google Scholar]
- 36.Zheng X., Silber-Li Z., “Measurement of velocity profiles in a rectangular microchannel with aspect ratio α = 0.35,” Exp. Fluids 44(6), 951–959 (2008). 10.1007/s00348-007-0454-4 [DOI] [Google Scholar]