Abstract.
The glomerulus is the blood filtering unit of the kidney. Each human kidney contains glomeruli. Several renal conditions originate from structural damage to glomerular microcompartments, such as proteinuria, the excessive loss of blood proteins into urine. The gold standard for evaluating structural damage in renal pathology is histopathological and immunofluorescence examination of needle biopsies under a light microscope. This method is limited by qualitative or semiquantitative manual scoring approaches to the evaluation of glomerular structural features. Computational quantification of equivalent features promises to improve the precision of glomerular structural analysis. One large obstacle to the computational quantification of renal tissue is the identification of complex glomerular boundaries automatically. To mitigate this issue, we developed a computational pipeline capable of extracting and exactly defining glomerular boundaries. Our method, composed of Gabor filtering, Gaussian blurring, statistical -testing, and distance transform, is able to accurately identify glomerular boundaries with mean sensitivity/specificity of and accuracy of 0.92, on glomeruli images stained with standard renal histological stains. Our method will simplify computational partitioning of glomerular microcompartments hidden within dense textural boundaries. Automatic quantification of glomeruli will streamline structural analysis in clinic and can pioneer real-time diagnoses and interventions for renal care.
Keywords: glomerulus, digital pathology, Gabor filtering, texture analysis, F-test
1. Introduction
The kidney is the organ of the body that filters blood to make urine. This essential regulatory role in invertebrates is performed by the nephron, and adult humans have on average 900,000 to 1 million in each kidney.1 Each nephron is spearheaded by a glomerulus, a complex bundle of capillaries surrounded by numerous cell types and filtration membranes, compacted into a sphere of diameter.2 Proteinuria, excessive loss of blood serum proteins into the urine, is a symptom of kidney disease, indicating structural damage to one or more of these glomerular compartments.3,4 Quantifying the number and distribution of glomerular structures is exceedingly tedious to perform by manual inspection under light microscopy (the standard clinical approach). This has two consequences: (1) the time taken to accurately provide a diagnosis to patients may be long and (2) prediction of disease trajectory in an early proteinuric disease, where structural damage is not yet blatant, is challenging and not precise. This is a clinical obstacle, as proteinuria can lead to kidney failure and death. Each year Medicare spends to care for over 525,000 U.S. patients with end stage kidney failure,5 many of whom display proteinuria as a component of their renal failure progression.
If a computational model that quantitatively characterizes a histologically stained tissue could be developed, then global distributions of important renal structures could be rapidly extracted by diagnostic pathologists, thus improving diagnostic efficiency. To our knowledge, there exists no method that is unsupervised, robust, and capable of extracting glomerular regions under a diverse set of conditions from a diverse population of histology images. However, there have been some works on the topic, one using a combination of edge detection, fitting curves, and a genetic algorithm;6 a second work using edge detection followed by edge patching using a genetic algorithm;7 a third work using segmental histogram of orientated gradients (S-HOG);8 and one work combining two software packages, Icy9,10 and Cytomine.11–13 The methods presented in Refs. 8 and 12 are supervised methods, both of which can claim great performance. However, these methods may have clinical limitation, where pathologists do not have time to gather and annotate the large datasets required for training supervised methods. S-HOG reported high precision and recall with their method on 993 images of glomeruli. We objectively compare our results with S-HOG in Sec. 2.6. The methods in Refs. 6 and 7 utilize edge detection to define glomerular boundaries. These methods have not demonstrated their performance in a diverse population of samples and are constrained by the prominence of the renal capsule to define the glomerular edge, which is not prominent in some stain types, such as hematoxylin and eosin (H&E). Additionally, both of the methods in Refs. 6 and 7 are sensitive to selection of the deviation of the Gaussian filter, which is difficult to optimize under a variety of microscopy imaging conditions. Furthermore, disease conditions change the distribution and/or presence of glomerular structures dramatically, and none of the above works have demonstrated application to disease data. We will briefly demonstrate proof-of-concept of our method applied to animal model disease data in Sec. 2.5. Demonstration of application to animal disease models is highly important because the flexibility of proteinuric animal models allows control over the pathological symptoms observed in an image. Control over the corresponding pathological structural changes allows the modeling of important diagnostic biomarkers with high predictive power on the trajectory of renal disease, which can be translated to human analysis. To our knowledge, this is the first report of computational segmentation of the glomerular boundary in a diseased renal tissue.
Renal architecture is exceptionally diverse and heterogeneous, thereby making computational analysis difficult to encompass within a single model, while being easily observable by eye. Gabor filtering is ideal to tackle such a system as it has been shown to reflect the way mammalian vision systems interpret spatial and frequency stimuli.14,15 The utility of Gabor textural segmentation to analyze histopathological images has been referenced in the literature.16–18 One work successfully implemented Gabor filters as textural descriptors used to classify histopathological images of oral submucous fibrosis (OSF) as OSF with dysplasia and OSF without dysplasia.17 Another work uses Gabor filters as textural descriptors to distinguish between epithelium and stoma in tumor tissue microarrays.18 However, we were unable to find literature that utilizes Gabor filters to automatically detect textural difference within renal tissue architecture. We will demonstrate that Gabor filtering can produce highly precise and accurate structural boundaries as compared to human visual annotation for both mouse and rat glomeruli, and we expect that the method is generalizable to other species as well.
In the past, we have reported using Gabor filters to detect glomeruli.19 Here, we propose an improved method, a pipeline of image processing and statistical tools working in complement to discriminate dense glomerular textural density from sparse extraglomerular textural density. Our method first uses a form of hotspot analysis for glomerular nuclear clustering to select candidate glomerular regions for a more detailed analysis. Hotspot detection is commonly used to identify regions of dense features of interest in images and has been applied to extensive imaging modalities, such as positron emission tomography,20 magnetic resonance imaging,21 and thermography.22 Hotspot detection is also popular in histological applications. Two works use clustered Ki-67 positive nuclei to detect cancerous regions.23,24 Another work proposes a strong method for detection of cancerous hotspots in breast cancer by multiplexing Getis–Ord25 statistical analyses of multiple classified nuclei types to find colocalized density of specific cells.26 Our work is similar to these analyses in that clustered hematoxylin nuclear pixels form dense clusters, which are the regions of interest. However, we were unable to find literature that reports the use of hotspot analysis for hematoxylin stained pixels in normal, healthy renal tissue.
After hotspot extraction, the glomerular boundary is further refined through a combination of Gabor textural segmentation,27 Gaussian blurring,28 -testing29 for intraglomerular space, and a spatial weighting map emphasizing glomerular concentricity. Gaussian blurring is an effective noise removal and signal approximation tool.28 -testing is used to refute or reinforce the pixels segmented by Gabor textural segmentation on the basis of variance. A spatial weighting map is used to connect any gaps between both segmentations in a smooth, continuous manner. We can accurately identify glomeruli in five common histopathology stains: H&E, periodic acid-Schiff (PAS), Gömöri’s trichrome, Congo red (CR), and Jones silver. When compared to human annotation of the glomerular boundary, our method localizes the exact boundary with mean sensitivity/specificity of and accuracy of 0.92 on 1000 rat renal tissue images.
By enabling the boundary of the glomerulus to be segmented, we have opened a gateway that will allow streamlined analysis of standard intraglomerular structures, which promise high clinical impact if computationally quantified. A comprehensive clinical analysis of such structures includes quantification of glomerular volumes, podocyte effacement and death, changes in mesangial cellularity and matrix volume, and lumen content.30 These benchmark indicators are already clinically known to provide informative power on the source and trajectory of renal disease but cannot be quantified if glomerular regions are not identified from tubular regions. We envision our method to be part of a semisupervised pipeline for digital pathology workflow, where pathologists accept or reject proper segmentations to speed data collection and accurate feature extraction. This approach will provide a faster statistical sampling in clinical pathology than the current practice and will ensure accuracy in diagnosis. The ultimate aim of our approach is to further facilitate the development of digital protocols that quantify glomerular features and motivate the shift of renal pathology to a computational era.
2. Results
2.1. Single Glomerular Location Estimation from Biopsies
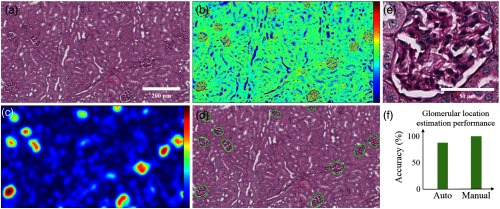
Figure 1 shows the process by which images of single glomeruli can automatically be extracted from large fields of view. Biopsy sized sections of tissue are cropped from whole-slide images of rat or mouse kidneys and are stain normalized with histogram specification28 to a well-stained image [Fig. 1(a)]. Converting the true color image to grayscale intensity and inverting all pixel values reveals that glomerular regions demonstrate higher nuclei density than surrounding regions [Fig. 1(b)]. Smoothing the image in Fig. 1(b) with a Gaussian blur generates an approximate nuclei heat map; see Fig. 1(c). Thresholding the image in Fig. 1(c) produces approximate estimates of glomerular boundaries; see Fig. 1(d). Cropping a squared block centering around an estimated boundary yields singular glomerular images; see Fig. 1(e). This method accurately extracts 87% of the glomeruli identified by a manual annotator in each biopsy mimicking image [Fig. 1(f)].
Fig. 1.
Estimation of glomerular locations from renal biopsies. (a) A renal biopsy mimic image, (b) the inverse grayscale intensity of a depicting higher signals in the nuclei locations, (c) Gaussian blurring of the high intensity nuclei in b, (d) approximated glomerular regions obtained from c, (e) singly extracted glomerulus, and (f) the above method detects 87% of the glomeruli that a manual examination discovers.
2.2. Glomerular Boundary Segmentation
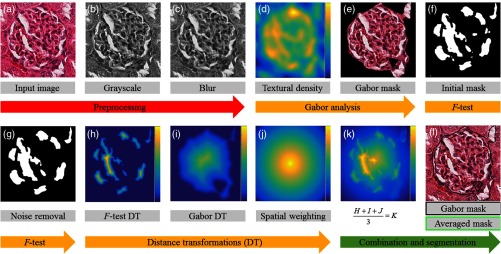
Figure 2 depicts the pipeline to derive accurate individual glomerular boundaries. Figures 2(a) and 2(b) depict a glomerulus image and its grayscale intensity image, respectively. The grayscale image is blurred with a Gaussian filter [Fig. 2(c)], which improves the detection of textural density by Gabor filtering. The filtering image shown in Fig. 2(c) with a Gabor filter bank produces one image output for each Gabor filter. Figure 2(d) depicts the projection along the first principal component of these images, delineating the intraglomerular space. Clustering images at the output of Gabor filter bank into two classes yields a binary mask [Fig. 2(e)] corresponding to the glomerular foreground. These foreground pixels are compared with the background using a statistical -test29 to obtain a secondary binary mask; see Fig. 2(f). Morphological operation28 removes the structural noise and results in an image shown in Fig. 2(g). Next, a distance transform operation is applied to binary masks derived from Gabor and -testing, generating intensity images shown in Figs. 2(h) and 2(i), respectively. Moving to Fig. 2(j), a spatial weighting map has utility in filling in small gaps between Gabor and -testing distance transforms. Normalizing and averaging the images in Figs. 2(h)–2(j) yields the output shown in Fig. 2(k). This object is then fixed value thresholded to yield the segmented boundary [shown using dashed black line, see Fig. 2(l)]. A comparison with the original boundary identified by Gabor [shown using black line, see Fig. 2(l)] demonstrates that -testing and spatial weighting improve accuracy of the segmentation boundary.
Fig. 2.
Computational pipeline for segmenting the glomerular boundary. (a) H&E stained glomerular tissue image, (b) grayscale version of the image shown in a, (c) Gaussian blurred image of b, (d) intensity image of the first principal component of the Gabor filter bank outputs using as input the image shown in c, and (e) -means clustering was used to find final Gabor boundary. (f) -testing examines the entire image for similarity with e, and outputs 0 or 1 for each pixel, (g) morphological noise removal for the image in f, (h, i) respective binary masks obtained from -testing and Gabor filter bank were distance transformed, (j) intensity image of a spatial weighting intensity map obtained from a, (k) heatmap of an average of intensity images in h–j, and (l) final segmentation after thresholding is shown using dashed black line. The segmentation obtained from initial Gabor [see (e)] is shown using black. The dashed black boundary depicts improved detection of glomerulus.
2.3. Parameter Performance Analysis
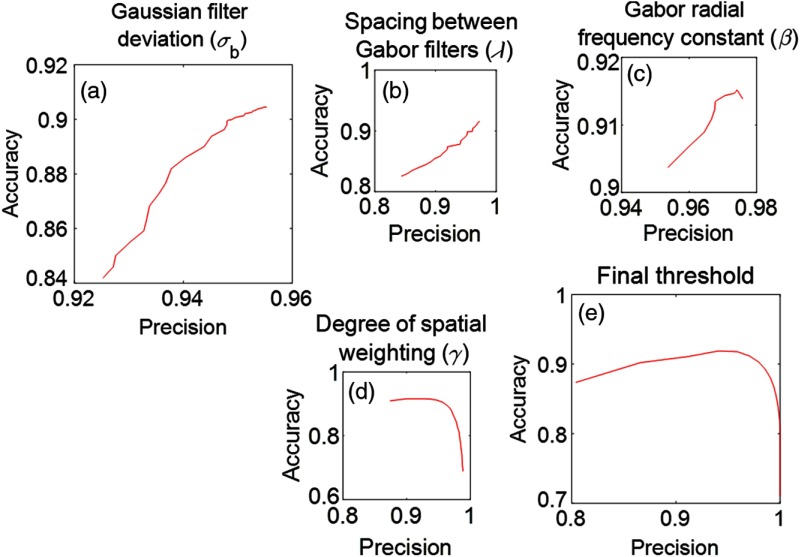
Gaussian blurring was found to be a positive influential factor as a preprocessor step to the segmentation of individual glomerular boundaries. The single mandatory parameter for this step is the standard deviation of the Gaussian function to blur with and was tested in the range . Maximum radial frequency31 used in the Gabor filtering is found to be another influential factor in glomerular segmentation. A scalar multiplier was used to vary the maximum radial frequency; see Sec. 3.4.1. The Gabor orientation parameter, tested for , defines how evenly the angles of the filters should be spaced,31 and this parameter value shows optimal segmentation at spacing. The degree of spatial weighting controls the weight that the spatial map [Fig. 2(j)] has when averaged with the Gabor and -test distance transform [Figs. 2(h) and 2(i)]. Average threshold refers to the threshold used to define the final glomerular boundary, segmenting the image seen in Fig. 2(k), and has bounds [0,0.3].
Figure 3 shows the influence of the parameters specified above on the mean precision and accuracy32 of all 1000 tested rat renal glomerular images. Figure 3(a) shows the deviation of Gaussian filter, , which achieves optimal performance at . Figure 3(b) shows the spacing between orientations of the Gabor filters, , with optimal performance at spacing between orientations. Figure 3(c) shows the restriction of the radial frequency of Gabor filters, , optimized at . Figure 3(d) demonstrates that the percent of spatial weighting is optimized at . Finally, Fig. 3(e) shows that performance is optimized at a final threshold value of 0.15. For the cases shown in Figs. 3(a)–3(c), we defined optimality at a parameter value where both precision and accuracy become maximum. For the other two cases, we defined optimality at a parameter value where the combined precision and accuracy score becomes maximum.
Fig. 3.
Evaluation of parameter tuning. All scores reported precision versus accuracy: (a) amount of blurring with Gaussian filter, (b) spacing between Gabor filter orientations, (c) restriction on the maximum frequency size of the Gabor filter bank, (d) overall weighting of the spatial weighting map, and (e) value of the final threshold, which defines the glomerular boundary. Optimal parameter values are presented in Sec. 2.3.
The remaining parameters did not require tuning for optimal segmentation. Resize amount defines the fraction to shrink the image to increase computational speed. We defined this fraction to be 0.25. The significance level used for the -test was 0.05. Window size defines a square window of size used to compute the background variance for -testing; see also Sec. 3.4.2. Area threshold defines the maximum size of objects to be removed from the binary mask obtained at the output of the -test, and we defined this threshold to be 600 pixels. A final morphological disk is used to smooth the glomerular boundary, and its radius was fixed at 25 pixels. A summary of all the parameters used for this method can be found in Sec. 3.5.
2.4. Glomerular Segmentation Performance Analysis
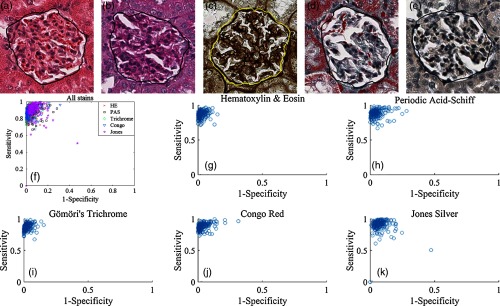
We evaluated the glomerular segmentation performance using rat glomeruli images, composed of five sets of 200 images stained with different histological reagents. To demonstrate the proof-of-concept, we manually cropped the glomerular regions [e.g., Fig. 2(a)] from all images. Glomerular locations can also be estimated using the method and analysis as described in Secs. 2.1 and 3.3. Figure 4 shows the performance of the glomerular segmentation. Figures 4(a)–4(e) demonstrate exemplar final segmentation for each of the five tested stain types. Figures 4(f)–4(k) show sensitivity and specificity of segmentations as scatters (see Sec. 3.4 for the method.) Overall, our method localizes the exact glomerular boundary with mean sensitivity/specificity of and accuracy of 0.92 on 1000 images. The H&E and trichrome images showed the most specific performance as compared to manual annotation, with a mean sensitivity/specificity of . Jones silver staining was least specific but also most sensitive, with mean sensitivity/specificity of . CR and PAS staining fall between the other contenders, with sensitivity/specificity of each. H&E and trichrome images showed the lowest variance of performance metrics; Jones silver and PAS showed the highest.
Fig. 4.
Glomerular segmentation performance for five different stains. (a–e) Automatic segmentations of glomeruli stained by H&E, PAS, Gömöri’s trichrome, CR, and Jones silver, respectively. (f) Scatter of sensitivity versus specificity for all 1000 glomerular images. (g–k) Scatter of sensitivity versus specificity for individual stains. Overall, H&E showed the highest performance with the lowest variation between samples.
2.5. Application to Focal Segmental Glomerulosclerosis
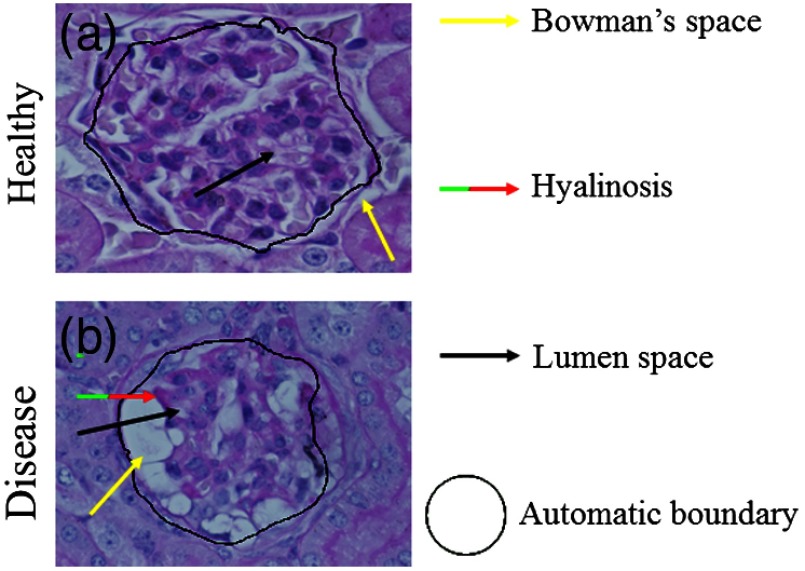
For proof-of-concept, Fig. 5 shows automatic segmentation of glomerular boundaries in both a healthy model and a mouse model of focal segmental glomerulosclerosis (FSGS).33 The glomerulus in the bottom row shows pathological changes, such as hyalinosis, marked with a red-green arrow, expansion of the Bowman’s space, marked with a yellow arrow, and change in lumen space, marked with a black arrow. Despite the pathological differences, our method is able to identify both glomeruli.
Fig. 5.
Segmentation of a disease glomerulus. (a) A healthy glomerulus and (b) glomerulus from mouse model of FSGS. Bowman’s space is marked with a yellow arrow, hyalinosis with a red-green arrow, lumen space with a black arrow, and automatic boundary with a black line.
2.6. Comparison with the Segmental Histogram of Orientated Gradients Method Developed by Kato et al.
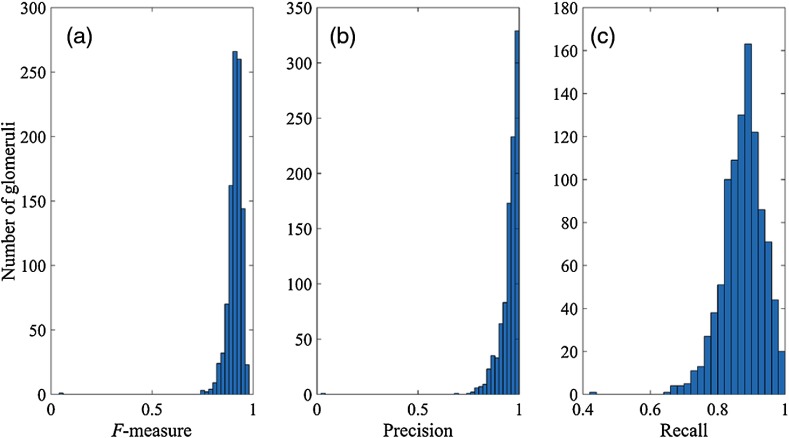
To objectively compare the performance of our method with S-HOG, we generated histograms of our precision, recall, and -measure for 1000 rat glomeruli images and presented the results in Fig. 6. Kato et al.8 generated similar metrics to report the performance of the S-HOG method. They reported that 90.1% of the glomeruli from a large sample had an -measure of 0.8 or greater using their method. We found that 99.1% of glomeruli scored an -measure of 0.8 or greater using our method.
Fig. 6.
Histogram representations of the performance of our method. (a) Distribution of -measure for 1000 images, (b) distribution of precision for 1000 images, and (c) distribution of recall for 1000 images. Using similar performance metrics Kato et al.8 reported 90.1% of the glomeruli from a large sample had an -measure of 0.8 or greater using their method. We found that 99.1% of glomeruli scored an -measure of 0.8 or greater using our method.
3. Methods
3.1. Overview of Computational Pipeline
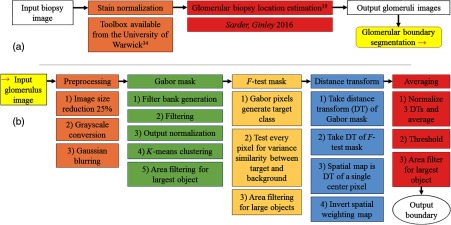
Figure 7 shows an overview of the entire computational pipeline. Figure 7(a) shows a brief overview of the method for glomerular location estimation from renal biopsies. Stain normalization is recommended with the open source toolbox available from the University of Warwick.34 Glomerular location estimation methodology is explicated briefly in Sec. 2.1 and more extensively in our recent work.19 Figure 7(b) shows the pipeline to localize individual glomeruli boundaries. Individual glomeruli images are preprocessed for Gabor filtering, and each image is filtered with a bank of Gabor filters for textural discrimination, which creates an initial mask of glomerular area. A second mask is generated by statistically -testing every pixel from the Gabor segmentation within a local window. Both masks are distance transformed and averaged along with a spatial weighting map. The averaged image is thresholded to determine the output segmentation boundary.
Fig. 7.
Computational pipeline overview. (a) Glomerular location estimation outline. Biopsy sized images are recommended to be stain normalized; a free MATLAB® toolbox is available from the University of Warwick.34 Glomerular biopsy location estimation is extensively discussed in Ref. 19. Each candidate region is sent to the boundary estimation method. (b) Images are preprocessed, and an initial mask is segmented by Gabor textural segmentation. Next, the Gabor textural segmentation output is -tested locally at every pixel. The results of these steps are distance transformed and averaged with a spatial weighting map. Thresholding the average of all three sources yields the final glomerular boundary.
3.2. Renal Tissue Slicing, Slide Preparation, and Digital Imaging
Intact kidney tissues from normal healthy untreated rats (generously provided by Dr. Tracey Ignatowski, Pathology and Anatomical Sciences, University at Buffalo) and normal healthy untreated mice were collected and euthanized under an institutionally approved laboratory protocol. Tissues were formalin fixed, processed in a standard fashion, and embedded in paraffin blocks. Microtome tissue slices from those paraffin blocks were cut using an Olympus CUT 4060 microtome at thickness along the sagittal plane and stained with Jones silver; slices with thickness were cut and stained with Gömöri’s trichrome, H&E, and PAS; and slices with thickness were cut and stained with CR. These thicknesses mimic clinical practice. Imaging was conducted using a whole-slide bright-field microscope (Aperio, Leica, Buffalo Grove, Illinois), using a objective with 0.75 NA. Resolution of the acquired image was . Disease data described in Sec. 2.5 were provided by Dr. Feng Chen, Washington University School of Medicine at St. Louis and prepared under the protocol described in Ref. 33. Results presented in Figs. 5, 8, and 9 were conducted using murine tissue, and all other results were obtained using rat tissue.
Fig. 8.
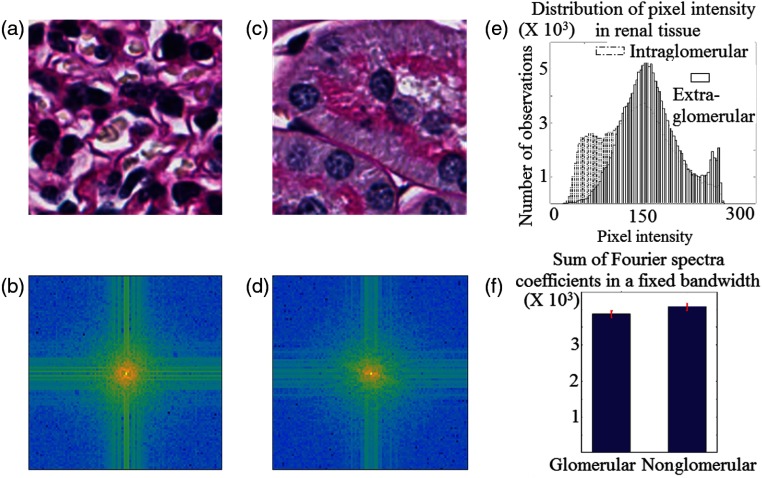
Motivation of using Gabor analysis and -testing. (a) Patch of intraglomerular region, (b) Fourier transform of a, (c) patch of extraglomerular region, (d) Fourier transform of c, (e) representative intensity histograms for 16 regions similar to a and c, respectively, and (f) sum of Fourier spectra coefficients for intra- and extraglomerular regions. Error-bars represent standard deviations of the sum metrics computed using data from four different mice.
Fig. 9.
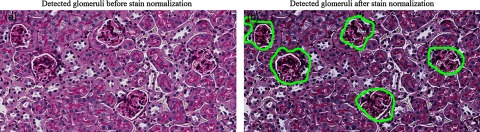
Influence of stain normalization. (a) Performance of glomerular location estimation before stain normalization for an image with low contrast between glomerular nuclei and tubular nuclei. (b) Drastic improvement in detected glomeruli after being normalized to a well-stained image.
3.3. Single Glomerular Location Estimation from Biopsies
To identify candidate glomerular regions, we apply an image filtering method, which is similar to hotspot analysis for histological images. In this application, the pixels, which stain intensely for hematoxylin, are the points to be clustered into hotspots. For computational speed, each full size, full resolution image was compressed to 10% of its original size using MATLAB® command “imresize.”35 Rat renal biopsy mimic images [Fig. 1(a)] were grayscale transformed, normalized, and then subtracted from 1, to obtain high intensity, dense clusters of nuclei corresponding to glomerular regions. Transformation to grayscale was performed using the weighted sum inbuilt with MATLAB® “rgb2gray” command and is shown in Fig. 1(b).35 Next, Gaussian blurring was used to smooth high intensity regions with close proximity together, seen in Fig. 1(c). Thresholding at a fixed value yields approximate locations of glomeruli, and an area opening eliminates outlier regions [Fig. 1(d)]. The value of this area opening was calculated based on estimated rat glomerular size, reported in Sec. 3.2 and Table 2. To extract each individual glomerulus from the biopsy mimic images, a width box was used, centered on the centroid of each object. The box size was chosen to reflect the average glomerular size reported in Table 2. Note that the method described here may not work for silver stains because nuclei are not prominently stained under this method. For tissue sections cut serially and stained with differing dyes, we expect that a mask automatically extracted from an adjacent serial slice of different stain will also accurately segment glomerular regions in the next silver slice.
Table 2.
Mean glomerular diameter and equivalent approximated area assuming circularity.
| Species | Mean glomerular diameter () | Approximate glomerular area () |
|---|---|---|
| Mouse | ||
| Rat |
3.4. Glomerular Boundary Segmentation
We review Gabor textural segmentation, statistical -testing, and distance transform, which are key methods for glomerular boundary segmentation.
3.4.1. Gabor textural segmentation
Simple cells in the visual cortex of mammalian brains can be modeled by Gabor functions. It is then intuitive that processing digital image information with Gabor filtering is an effective tool to render frequency and spatial signals into objects in a manner similar to the human visual system.
Here, we have implemented the unsupervised texture segmentation method using Gabor filter banks.27 A two-dimensional (2-D) Gabor function is defined as a sinusoidal plane wave at a specific frequency and orientation modulated by a 2-D Gaussian envelope. This function is given by
| (1) |
where and are the standard deviation of the Gaussian envelope along - and -axes, respectively, and and are the frequency and phase of the sinusoidal plane wave along the axis with orientation, respectively. A Gabor filter at any other orientation can be obtained by rigid rotation of the plane. In the frequency domain, with , the Gabor function is given by
| (2) |
where , , and . The width of the filter in the spatial domain is inversely related to the bandwidth in the frequency domain. To resolve fine texture, smaller bandwidths are required, and to localize textural boundaries, the magnitude of the filter in the spatial domain must match that of the structure of interest.
MathWorks has developed an algorithm to implement textural segmentation using an array of filters generated from Eq. (1). This method uses a set of filter banks at multiple orientations and radial frequencies to filter an image into its Gabor components. For images of size , the filter bank orientations were spaced at in an interval of , and the radial frequencies were up to , where . Values for , were dictated by MATLAB® inbuilt default and can be found in MATLAB® documentation for “imgaborfilt.”35 To normalize the Gabor filters’ outputs, pixel-wise mean and standard deviation of these filters’ outputs were computed. Each pixel value of each Gabor filter output was reduced by its respective mean and divided by its respective standard deviation to compute the normalized outputs. The resulting matrices were then clustered into two classes using -means clustering, repeated five times to avoid local minima.36
3.4.2. -test based segmentation
To perform the -test based segmentation, first, the independent measurements and were collected from independent random variables and with variances and . For 2-D image analysis, is formed by the pixels labeled by Gabor output based on the method described in Sec. 3.4.1, and is formed by the pixels in a moveable window of predefined size, which was iteratively centered on each pixel in the image. The testing problem is given by
| (3) |
The test statistic is given by
| (4) |
which is -distributed with and degrees of freedom, and , are sample variances of and , respectively. The null hypothesis is rejected when , where is the critical value of the -distribution with and degrees of freedom and a significance level .29 The above test was performed at every pixel of the image, iteratively centering the movable window onto every pixel. For each local window of every pixel in the image, 0 was assigned for a rejected -test and 1 for passing -test, which labeled a secondary binary mask.
3.4.3. Distance transforms
Distance transforms are performed on binary images, and they reassign each foreground pixel with its Euclidean distance to the closest background pixel.37 We applied distance transforms on the binary Gabor segmentation and -test segmentation. We employed a slightly different distance transform to generate a spatial weighting map corresponding to the glomerulus. Here, every pixel was assigned its Euclidean distance to the center of the image to be segmented, and the resulting image was inverted by subtracting it from 1, so the highest value pixels were in the center and the lowest were at edges of the image. The spatial weighting map aided in filling in disjointed gaps between -test and Gabor segmentations and de-emphasizing objects near the image border. To derive the glomerular boundary, an average of all normalized distance transformed images was computed. Note that the spatial weighting can be weighted anywhere between 0% and 100% while averaging, but we found optimality around 80%. Thresholding this averaged image yields the final segmentation.
3.5. Parameter Values
Table 1 summarizes the required parameters of the method, the range of values tested, if optimized, and our reported optimal value for each parameter. These parameters were optimized for the resolution of the rat renal tissue histology image, details of which are briefed in Sec. 3.2. However, in Figs. 5, 8, and 9, we use mouse tissue to demonstrate several proof-of-concepts. Readers should note that the selection of parameters , , area threshold, and morphological disk radius are sensitive to glomerulus size and, thus, take on different optimal values in different species. However, each of these parameters can be estimated for tissue coming from another species by first estimating the approximate size of glomeruli and then scaling the parameters relative to the observed structure size. Table 2 reports our typical measured sizes of mouse and rat glomeruli as well as the estimated area, assuming each glomerulus to be circular.
Table 1.
Parameter values used for the proposed method. Of the listed nine parameters, only two were dynamic over the production of the results presented above. These parameters are the standard deviation of the Gaussian blur and the scale parameter of the maximum radial frequency of the Gabor filters.
| Parameter | Use | Description | Value range | Optimized value |
|---|---|---|---|---|
| Preprocessing | Deviation of Gaussian filter | 0 to 3 | 1.1 | |
| Gabor filtering | Restricts max radial frequency of the Gabor filter | 0 to 1 | 0.35 | |
| Resize amount | Gabor filtering | Compress image to boost speed | 0.25 | No optimization |
| Gabor filtering | Spacing between Gabor filter orientations | 0 deg to 90 deg | 1 deg | |
| -testing | Significance level of the -test | 0.05 | No optimization | |
| Window size | -testing | Local window to select the background for the -testing | No optimization | |
| Area threshold | Intermediate processing | Eliminates noisy structures from -test output | 600 pixels | No optimization |
| Percent spatial weighting | Intermediate processing | Binds Gabor and -test segmentations together | 0 to 1 | 0.8 |
| Average threshold | Final processing | Defines glomerular boundary | 0 to 0.3 | 0.15 |
| Morphological disk radius | Final processing | Smoothens small imperfections in the segmented glomerular boundary | 25 pixels | No optimization |
4. Discussion
In this work, we presented a robust pipeline for automatically extracting glomerular regions without supervision. Intuitively, the detection of glomeruli via texture is supported by the contrast of dense glomerular nuclear packing juxtaposed with sparse, repetitive tubular nuclei. Furthermore, these two distributions are demarcated by a prominent edge between them and manifested in the Bowman’s space. In this section, we will provide more rigorous motivation for the use of Gabor filters and statistical testing. We will also discuss the advantages, drawbacks, and obstacles of the presented method.
To motivate the use of Gabor filtering for glomerular segmentation, we performed a two-sample -test,29 to determine if intra- and extraglomerular regions had different responses in the frequency domain. First, 16 patches, each containing , were extracted from intraglomerular regions, and then, a second identical set was taken from extraglomerular regions. Patches were selected randomly from four different mice. The Fourier transform of each image was computed, and each transform was cropped to a fixed space–frequency bandwidth. Within this bandwidth, the sum total of the respective Fourier coefficients was measured. Such sum metrics from four different mice were used for the -test. We found that at the 5% significance level, we can reject the null hypothesis with value 0.0022 that the Fourier spectra of intra- and extraglomerular regions are similar. Figure 8(a) shows a sample patch of glomerular region, and Fig. 8(b) shows the respective Fourier spectra. Similarly, Fig. 8(c) shows a patch of extraglomerular region, and Fig. 8(d) shows the respective Fourier spectra. Comparing Figs. 8(b) with 8(d), the difference in spectra is readily apparent. Figure 8(f) shows the difference in means of the respective sum metrics as computed from the Fourier spectra, where the respective error bars describe the standard deviation along the mice. In addition to sharp contrast between frequencies (textures) in intra- and extraglomerular regions, a spatial difference in edge patterns between these two regions is also expected. One expects the edge features in spatial domain of an intraglomerular region [e.g., Fig. 1(e)] to be circularly patterned, while the edge features outside the glomerulus to be more linearly patterned. This has been demonstrated in the literature by Kato et al.;8 hence, we omit a pictorial proof here for brevity. Due to this, the renal glomerulus is a unique object recognition problem with both spatial and frequency domain contrast from its background in renal histology images. The Gabor filter uniquely discriminates an object from its background by exploiting both spatial and frequency information, while balancing the trade-off between space–frequency duality. Thus, we conclude the motivation for the use of Gabor filters.
Similarly, to motivate and support the use of -testing to segment glomerular regions, intensity distributions of intra- and extraglomerular regions obtained from 16 patches of murine renal tissue images are shown in Fig. 8(e). The difference in distributions is readily apparent. We found that the intensity variation of intraglomerular region is higher than that of extraglomerular region using a right tailed chi-squared test29 at 5% significance level. This finding justifies the use of -testing.
On a different note, digital histopathology images suffer from uneven contrast due to the imaging scanner, staining variation, chemical reactivity from different manufacturer batches, staining protocol, variable tissue thickness, and human errors.38–40 A common solution is stain normalization. To quantify staining variation and its influence on our method, we first examined four biopsy sized images, each from a different mouse and each containing 5 to 8 glomeruli. Specifically, we examined the hit ratio of detected glomeruli with our method before and after stain normalization. Before stain normalization, between the four images, the ratio of detected glomeruli to true varied by 0.222. After stain normalization by RGB histogram specification, the variance decreased to 0.020. The stain normalization toolbox available at the University at Warwick was used.34 Although it is not always required to normalize images if they are stained well, poorly stained images significantly benefit from normalization. For example, Fig. 1(a) shows an example of an image that does not require staining normalization. In contrast, Fig. 9(a) shows an example of a sample where glomerular nuclei have low contrast as compared with tubular nuclei. No glomeruli were detected in this sample before normalization [Fig. 9(a)], and all glomeruli were detected after normalization [Fig. 9(b)]. In contrast to this, in Fig. 1(a), nearly all glomeruli were discovered without normalization. We also stain normalized all 1000 individual rat glomeruli images used for the study presented in Fig. 4 to that of a well-stained glomerulus for each stain type, to quantify staining variation on our glomerular boundary labeling method. We noticed no significant statistical difference on the performance before and after. We believe this is likely because our glomerular boundary segmentation method is local, and staining is piece-wise invariant in the field of view of a single glomerulus.
Although Gabor filter bank-based segmentation is known in the literature for texture segmentation, we report for the first time the use of statistical -testing to boost the segmentation performance of the Gabor method. There are several advantages that support using the proposed pipeline. First, it is unsupervised, meaning large numbers of annotated training data are not required to be gathered. Second, we have shown that it is reproducible and robust for a variety of staining conditions and demonstrated proof-of-concept in disease murine renal tissue image with FSGS. Our method is also efficient; it requires between 6 and 10 s to extract all glomerular boundaries from a biopsy sized image with between 5 and 15 glomeruli. Drawbacks of this method include high parameterization, and the -means clustering step in Gabor filter bank-based analysis can be time-consuming as the size of the image increases.
Although we have validated our method for healthy rat tissues, we have only shown a proof-of-concept example using an FSGS diseased glomerulus. Future obstacles will likely develop as we progress to validate our model in diseased rat or murine tissues.41–43 Diseased renal tissues display a wide range of structural changes; glomeruli shapes might be different than expected, completely intact, partially intact, absent, and may have abnormal ratios of glomerular compartments, all of which would likely affect intraglomerular texture and require adaptations to our method to ensure continued robustness. Additionally, quite often, there are slight anatomical differences between species. Because we aim for our method to be clinically impactful, future extensions will also involve application to human data. Human glomeruli will likely be slightly different than rat or murine glomeruli in terms of both scale and structure. This would call for further modifications to our method. However, all in all, we believe that the results described in this article are promising and have a high potential for further clinical and academic research on the automated quantification of renal microenvironment.
5. Conclusions
Our method is the first to open the gateway to unsupervised, automated glomerular structural analysis. By removing the obstacle of automated glomerular identification, future studies will be able to computationally quantify intraglomerular structures much more easily than in times prior. The most important result of our work is the discovery that textural discrimination is highly effective in identifying glomerular boundaries, over a wide range of staining types. Our proposed textural segmentation pipeline was able to efficiently discriminate glomerular regions, with an average sensitivity and specificity of over 1000 rat renal glomeruli images. We hope our method will expedite future studies in automated, computational quantification of renal structures, to bring about more rapid diagnosis and intervention at early stages of proteinuric renal disease.
Acknowledgments
We thank Dr. Tracey Ignatowski (Pathology and Anatomical Sciences, University at Buffalo) for providing us the rat renal tissues for this work. We thank the Histology Core Facility (Pathology and Anatomical Sciences, University at Buffalo) for performing histopathological staining of tissues. This project was supported by the Faculty Start-up Funds from the Pathology and Anatomical Sciences Department, Jacobs School of Medicine and Biomedical Sciences, University at Buffalo. F.C. was supported in part by grants from Department of Defense Grant PC130118 and National Institute of Health Grant DK087960.
Biographies
Brandon Ginley is a PhD student at the Pathology and Anatomical Sciences Department at the University at Buffalo, the State University at New York (SUNY). He received his BS degree in biomedical engineering from the University at Buffalo in 2016. His research focuses on the development of computational image quantification techniques that have translational impact by providing quantitative statistics holding high predictive power on the trajectory and management of diseases.
John E. Tomaszewski is the chairmen of the Pathology and Anatomical Sciences Department at SUNY Buffalo. He received his BA degree from LaSalle College in 1973 and his MD degree from the University of Pennsylvania, School of Medicine in 1977. His research interests focus on development of translational strategies that combine quantitative image analysis with multidimensional molecular data to predict trajectory of disease and its response to treatment with higher precision and accuracy than the current paradigm.
Rabi Yacoub is an assistant professor at the Department of Medicine at SUNY Buffalo. He is an expert in nephrology. He received his MD degree in medicine from Aleppo University in 2002. His research focuses on human and animal studies that explore the relationship between gut microbiota and renal diseases. In addition to his research, he also sees patients in Buffalo General Medical Center renal clinics and teaches renal fellows, medicine residents, and medical students in the renal clinic.
Feng Chen is an associate professor of medicine at the Division of Nephrology, Washington University School of Medicine. He received his BS degree in biology from Sudan University, Shanghai, and his PhD in human genetics from the University of Utah, Salt Lake City. His research currently focuses on studying the genetic determinants and pathogenic mechanisms of urogenital diseases. Through this, he aims to improve diagnostic and therapeutic strategies targeting urogenital disease.
Pinaki Sarder is an assistant professor of pathology and anatomical sciences, biomedical engineering, and biostatistics at SUNY Buffalo. He obtained his MSc and PhD degrees in electrical engineering from Washington University, St. Louis, in 2010. He is trained in quantitative biomedical imaging, biomedical signal and image processing, and fluorescence microscopy. In his current research, he is focusing on computational quantification of microcompartmental structures with pathological relevance in large tissue images.
Disclosures
The authors have no financial interests or potential conflicts of interest to disclose.
References
- 1.Bertram J. F., et al. , “Human nephron number: implications for health and disease,” Pediatr. Nephrol. 26(9), 1529–1533 (2011). 10.1007/s00467-011-1843-8 [DOI] [PubMed] [Google Scholar]
- 2.Hall T. J., et al. , “Ultrasonic measurement of glomerular diameters in normal adult humans,” Ultrasound Med. Biol. 22(8), 987–997 (1996). 10.1016/S0301-5629(96)00142-1 [DOI] [PubMed] [Google Scholar]
- 3.Gorriz J. L., Martinez-Castelao A., “Proteinuria: detection and role in native renal disease progression,” Transplant. Rev. 26(1), 3–13 (2012). 10.1016/j.trre.2011.10.002 [DOI] [PubMed] [Google Scholar]
- 4.Gross J. L., et al. , “Diabetic nephropathy: diagnosis, prevention, and treatment,” Diabetes Care 28(1), 164–176 (2005). 10.2337/diacare.28.1.164 [DOI] [PubMed] [Google Scholar]
- 5.“Chronic kidney disease and kidney failure,” http://report.nih.gov/nIHfactsheets/ViewFactSheet.aspx?csid=34&key=C (28 December 2016).
- 6.Zhang J., Hu J. L., “Glomerulus extraction by optimizing the fitting curve,” in Proc. of the 2008 Int. Symp. on Computational Intelligence and Design, Vol. 2, pp. 169–172 (2008). 10.1109/Iscid.2008.223 [DOI] [Google Scholar]
- 7.Ma J. X., Zhang J., Hu J. L., “Glomerulus extraction by using genetic algorithm for edge patching,” in IEEE Congress on Evolutionary Computation, Vols. 1–5, pp. 2474–2479 (2009). 10.1109/Cec.2009.4983251 [DOI] [Google Scholar]
- 8.Kato T., et al. , “Segmental HOG: new descriptor for glomerulus detection in kidney microscopy image,” BMC Bioinf. 16, 1–18 (2015). 10.1186/s12859-015-0739-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.de Chaumont F., et al. , “ICY: an open bioimage informatics platform for extended reproducible research,” Nat. Methods 9(7), 690–696 (2012). 10.1038/nmeth.2075 [DOI] [PubMed] [Google Scholar]
- 10.ICY, http://icy.bioimageanalysis.org/.
- 11.Maree R., et al. , “Collaborative analysis of multi-gigapixel imaging data using Cytomine,” Bioinformatics 32(9), 1395–1401 (2016). 10.1093/bioinformatics/btw013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mar R., et al. , “An approach for detection of glomeruli in multisite digital pathology,” in IEEE 13th Int. Symp. on Biomedical Imaging (ISBI) (2016). 10.1109/ISBI.2016.7493442 [DOI] [Google Scholar]
- 13.Cytomine, http://www.cytomine.be/.
- 14.Daugman J. G., “Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters,” J. Opt. Soc. Am. A 2(7), 1160–1169 (1985). 10.1364/JOSAA.2.001160 [DOI] [PubMed] [Google Scholar]
- 15.Marcelja S., “Mathematical description of the responses of simple cortical cells,” J. Opt. Soc. Am. 70(11), 1297–1300 (1980). 10.1364/JOSA.70.001297 [DOI] [PubMed] [Google Scholar]
- 16.Khan A. M., et al. , “HyMaP: a hybrid magnitude-phase approach to unsupervised segmentation of tumor areas in breast cancer histology images,” J. Pathol. Inf. 4(Suppl.), S1 (2013). 10.4103/2153-3539.109802 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Krishnan M. M., et al. , “Automated oral cancer identification using histopathological images: a hybrid feature extraction paradigm,” Micron 43(2–3), 352–364 (2012). 10.1016/j.micron.2011.09.016 [DOI] [PubMed] [Google Scholar]
- 18.Linder N., et al. , “Identification of tumor epithelium and stroma in tissue microarrays using texture analysis,” Diagn. Pathol. 7, 22 (2012). 10.1186/1746-1596-7-22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sarder P., Ginley B., Tomaszewski J. E., “Automated renal histopathology: digital extraction and quantification of renal pathology,” Proc. SPIE 9791, 97910F (2016). 10.1117/12.2217329 [DOI] [Google Scholar]
- 20.Guan H., et al. , “Automatic hot spot detection and segmentation in whole body FDG-PET images,” in 2006 Int. Conf. on Image Processing (2008). 10.1109/ICIP.2006.312368 [DOI] [Google Scholar]
- 21.Vos P. C., et al. , “Automatic computer-aided detection of prostate cancer based on multiparametric magnetic resonance image analysis,” Phys. Med. Biol. 57(6), 1527–1542 (2012). 10.1088/0031-9155/57/6/1527 [DOI] [PubMed] [Google Scholar]
- 22.Wronkowicz A., “Approach to automated hot spot detection using image processing for thermographic inspections of power transmission lines,” Diagnostyka 17(2), 81–86 (2016). [Google Scholar]
- 23.Niazi M. K. K., et al. , “Hotspot detection in pancreatic neuroendocrine tumors: density approximation by α-shape maps,” Proc. SPIE 9791, 97910B (2016). 10.1117/12.2217687 [DOI] [Google Scholar]
- 24.Niazi M. K. K., et al. , “Hot spot detection for breast cancer in Ki-67 stained slides: image dependent filtering approach,” Proc. SPIE 9041, 904106 (2014). 10.1117/12.2045586 [DOI] [Google Scholar]
- 25.Getis A., Ord J. K., “The analysis of spatial association by use of distance statistics,” Geogr. Anal. 24(3), 189–206 (1992). 10.1111/j.1538-4632.1992.tb00261.x [DOI] [Google Scholar]
- 26.Nawaz S., et al. , “Beyond immune density: critical role of spatial heterogeneity in estrogen receptor-negative breast cancer,” Mod. Pathol. 28(12), 1621 (2015). 10.1038/modpathol.2015.133 [DOI] [PubMed] [Google Scholar]
- 27.Jain A., Farrokhnia F., “Unsupervised texture segmentation using Gabor filters,” Pattern Recognit. 24(12), 1167–1186 (1991). [Google Scholar]
- 28.Gonzalez R. C., Woods R. E., Digital Image Processing, 3rd ed., Prentice Hall, Upper Saddle River, New Jersey: (2007). [Google Scholar]
- 29.Hogg R. V., Craig A., McKean J. W., Introduction to Mathematical Statistics, 6th ed., Prentice Hall, Upper Saddle River, New Jersey: (2004). [Google Scholar]
- 30.D’Amico G., Bazzi C., “Pathophysiology of proteinuria,” Kidney Int. 63(3), 809–825 (2003). 10.1046/j.1523-1755.2003.00840.x [DOI] [PubMed] [Google Scholar]
- 31.Jain A. K., Farrokhnia F., “Unsupervised texture segmentation using Gabor filters,” Pattern Recognit. 24(12), 1167–1186 (1991). 10.1016/0031-3203(91)90143-S [DOI] [Google Scholar]
- 32.Fletcher R. H., Fletcher S. W., Clinical Epidemiology: The Essentials, 4th ed., Lippincott Williams & Wilkins, Baltimore, Maryland: (2005). [Google Scholar]
- 33.Wang Y., et al. , “Activation of NFAT signaling in podocytes causes glomerulosclerosis,” J. Am. Soc. Nephrol. 21(10), 1657–1666 (2010). 10.1681/ASN.2009121253 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.“Stain normalisation toolbox,” https://www2.warwick.ac.uk/fac/sci/dcs/research/combi/research/bic/software/sntoolbox/ (28 December 2016).
- 35.MathWorks, https://www.mathworks.com/.
- 36.“Texture segmentation using Gabor filters,” http://www.mathworks.com/help/images/texturesegmentation-using-Gabor-filters.html (28 December 2016).
- 37.Maurer C., “A linear time algorithm for computing exact Euclidean distance transforms of binary images in arbitrary dimensions,” IEEE Trans. Pattern Anal. Mach. Intell. 25(2), 265–270 (2003). [Google Scholar]
- 38.Khan A. M., et al. , “A nonlinear mapping approach to stain normalization in digital histopathology images using image-specific color deconvolution,” IEEE Trans. Biomed. Eng. 61(6), 1729–1738 (2014). 10.1109/Tbme.2014.2303294 [DOI] [PubMed] [Google Scholar]
- 39.Reinhard E., et al. , “Color transfer between images,” IEEE Comput. Graphics 21(5), 34–41 (2001). 10.1109/38.946629 [DOI] [Google Scholar]
- 40.Lyon H. O., et al. , “Standardization of reagents and methods used in cytological and histological practice with emphasis on dyes, stains and chromogenic reagents,” Histochem. J. 26(7), 533–544 (1994). 10.1007/Bf00158587 [DOI] [PubMed] [Google Scholar]
- 41.Lowenborg E. K., Jaremko G., Berg U. B., “Glomerular function and morphology in puromycin aminonucleoside nephropathy in rats,” Nephrol. Dial. Transplant. 15(10), 1547–1555 (2000). [DOI] [PubMed] [Google Scholar]
- 42.Tesch G. H., Allen T. J., “Rodent models of streptozotocin-induced diabetic nephropathy,” Nephrology 12(3), 261–266 (2007). 10.1111/j.1440-1797.2007.00796.x [DOI] [PubMed] [Google Scholar]
- 43.Shankland S. J., “The podocyte’s response to injury: role in proteinuria and glomerulosclerosis,” Kidney Int. 69(12), 2131–2147 (2006). 10.1038/sj.ki.5000410 [DOI] [PubMed] [Google Scholar]