Macroscopic singlet oxygen modeling for dosimetry of Photofrin-mediated photodynamic therapy: an in-vivo study

Abstract.

Although photodynamic therapy (PDT) is an established modality for cancer treatment, current dosimetric quantities, such as light fluence and PDT dose, do not account for the differences in PDT oxygen consumption for different fluence rates ($\varphi$). A macroscopic model was adopted to evaluate using calculated reacted singlet oxygen concentration (${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$) to predict Photofrin-PDT outcome in mice bearing radiation-induced fibrosarcoma tumors, as singlet oxygen is the primary cytotoxic species responsible for cell death in type II PDT. Using a combination of fluences (50, 135, 200, and $250\mathrm{J}/{\mathrm{cm}}^2$) and $\varphi$ (50, 75, and $150\mathrm{mW}/{\mathrm{cm}}^2$), tumor regrowth rate, $k$, was determined for each condition. A tumor cure index, $\mathrm{CI}=1-k/k_{\text{control}}$, was calculated based on the $k$ between PDT-treated groups and that of the control, $k_{\text{control}}$. The measured Photofrin concentration and light dose for each mouse were used to calculate PDT dose and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$, while mean optical properties (${\mu }_{\mathrm{a}}=0.9{\mathrm{cm}}^{-1}$, ${\mu }_{\mathrm{s}}^{\prime }=8.4{\mathrm{cm}}^{-1}$) were used to calculate $\varphi$ for all mice. CI was correlated to the fluence, PDT dose, and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ with $R^2=0.35$, 0.79, and 0.93, respectively. These results suggest that ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ serves as a better dosimetric quantity for predicting PDT outcome.

1. Introduction

As an established methodology for cancer treatment, photodynamic therapy (PDT) has been approved by the US Food and Drug Administration for the treatment of some cancers and precancers, such as Photofrin-PDT for esophageal cancer, nonsmall cell lung cancer, Barrett’s esophagus,^1–3 and 5-aminolevulinic acid (ALA)-PDT for actinic keratosis.⁴ Furthermore, off-label PDT applications as well as clinical trials have been performed.^5–7 PDT is a photochemical process combining the interactions among photosensitizer, light, and oxygen. During this process, the ground-state photosensitizer (${\mathrm{S}}_0$) is excited by light and converted to an excited state (${\mathrm{S}}_1$). The ${\mathrm{S}}_1$ state is a short-lived state and the photosensitizer will lose its energy and return to the ground state by either emitting a fluorescent photon or decaying to the ground state nonradiatively, or it will undergo a process known as intersystem crossing and converted to a triplet state (${\mathrm{T}}_1$). While in the ${\mathrm{T}}_1$ state, the photosensitizer can be involved in two types of processes called type I and type II. In type I photodynamic interactions, the excited triplet can transfer an electron to ground-state molecular oxygen (${}^3{\mathrm{O}}_2$) to form a charged superoxide anion, which in turn, form reactive oxygen species (ROS) via secondary chemical reactions. ROS interact with substrates to cause biological damage.^8–10 The photosensitizer triplet may react directly with a biological substrate under hypoxic conditions. In type II interactions, the excited triplet will transfer energy to ${}^3{\mathrm{O}}_2$ to produce excited-state singlet oxygen (${}^1{\mathrm{O}}_2$), the major cytotoxic species causing biological damage.⁸ Although the precise mechanisms of PDT are not yet fully understood, it is generally accepted that ${}^1{\mathrm{O}}_2$ is primarily responsible for cell death and PDT outcome for type II photosensitizers.¹¹ Although the clinical use and indications of PDT are increasing slowly, an ideal dosimetric predictor for PDT efficacy is still elusive, which to some extent, has hindered the clinical application of PDT. In most clinical protocols, dosimetry is still based on the administered photosensitizer dosage and the delivered light fluence under a range of fluence rates ($\varphi$). This method of clinical dosimetry does not take into account the absorption and scattering of light or the uptake of the photosensitizer in the target tissue.¹² This might be responsible for the unpredictable response and variability between clinical dosimetry and PDT outcome.^13,14

To find a better solution for PDT dosimetry, explicit PDT dosimetry has been introduced. Unlike using the given photosensitizer dosage and light fluence as PDT metrics, in explicit PDT dosimetry, the light dose absorbed by the photosensitizer in tissue is measured and defined as PDT dose, which is determined by the product of photosensitizer concentration and light fluence. PDT dose may serve as a good predictor of outcome in ${}^3{\mathrm{O}}_2$ enriched conditions.¹² However, in hypoxic conditions, it becomes less accurate for predicting the PDT efficacy since it does not consider the rate of PDT consumption of ${}^3{\mathrm{O}}_2$ for different $\varphi$.^15,16 With integration of the variation of ${}^3{\mathrm{O}}_2$ concentration ($[{}^3{\mathrm{O}}_2]$) into explicit dosimetry, a so-called singlet oxygen explicit dosimetry method based on mathematical modeling to calculate the ${}^1{\mathrm{O}}_2$ has made it possible to predict the PDT outcome.¹⁷ For this purpose, an empirical four-parameter macroscopic ${}^1{\mathrm{O}}_2$ model was developed, and the reacted singlet oxygen (${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$) was proposed as a dosimetry quantity for the accumulated concentration of ${}^1{\mathrm{O}}_2$ that is responsible for cellular killing and clinical outcomes.¹⁸ In this study, this model was adopted to evaluate the potential of using calculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ as a dosimetric predictor for Photofrin-mediated PDT on tumor growth in a mouse tumor model.

2. Materials and Methods

2.1. Mouse Tumor Model

Radiation-induced fibrosarcoma (RIF) cells of logarithmic growth phase ($30\mu \mathrm{l}$ of $1\times {10}^7\text{\hspace{0.17em}\hspace{0.17em}cells}/\mathrm{ml}$) were injected subcutaneously in the right shoulders of 6- to 8-week-old female C3H mice (NCI-Frederick, Frederick, Maryland). The fur of the tumor region was clipped prior to cell inoculation. PDT was carried out around 5 to 10 days after inoculation when tumors reached 3 to 4 mm in length and in height. A few days before PDT, the tumor and the surrounding area was depilated with Nair (Church & Dwight Co., Inc., Ewing, New Jersey). All procedures were approved by the University of Pennsylvania Institutional Animal Care and Use Committee. Animal husbandry was provided by the University of Pennsylvania Laboratory Animal Resources in association with Assessment and Accreditation of Laboratory Animal Care.

2.2. Photodynamic Therapy Protocol

Photofrin (Pinnacle Biologics, Chicago, Illinois) at a dosage of $5\mathrm{mg}/\mathrm{kg}$ was injected through the mouse tail vein as described previously.^19,20 At a 24-h drug–light interval, superficial irradiation of the tumor was performed with a 630-nm laser (Biolitec AG., A-1030, Vienna). A microlens fiber was coupled to the laser to irradiate the tumor uniformly. Animals were assigned to four light dose groups, and each group was comprised of 2 to 3 subgroups with different $\varphi$. There were a total of 11 treatment groups: $50\mathrm{J}/{\mathrm{cm}}^2$ at 50, 75, and $150\mathrm{mW}/{\mathrm{cm}}^2$, $135\mathrm{J}/{\mathrm{cm}}^2$ at 50, 75, and $150\mathrm{mW}/{\mathrm{cm}}^2$, $200\mathrm{J}/{\mathrm{cm}}^2$ at 50 and $150\mathrm{mW}/{\mathrm{cm}}^2$, and $250\mathrm{J}/{\mathrm{cm}}^2$ at 50, 75, and $150\mathrm{mW}/{\mathrm{cm}}^2$. Tumor-bearing mice that received neither light irradiation nor Photofrin were used as controls.

2.3. Photodynamic Therapy Efficiency Assessment

Mouse tumors were measured daily using a sliding caliper for up to 14 days post-PDT. The tumor volume ($V$) was calculated by the formula $V=\pi /6\times a^2\times b$; where $a$ and $b$ refer to the width and length of the tumor, respectively.²¹ Since initial tumor volumes at the time of treatment were not identical among mice, daily tracked tumor volumes were scaled according to the initial volume; the treatment day volume is normalized to be $\sim 12{\mathrm{mm}}^3$ for all mice. Tumors were selected for various treatment groups randomly. By fitting the tumor volumes to an exponential growth equation, $V=A{\mathrm{e}}^{kd}$ the tumor regrowth rate ($k$) was obtained, where $A$ is the amplitude and $d$ represents the number of the days after PDT. $k$ was not allowed to be negative in the fit. The tumor cure index (CI) was calculated by the following expression:^22–24

$$\mathrm{CI}=1-\frac{k}{k_{\text{control}}},$$ (1)

where $k_{\text{control}}$ is the tumor regrowth rate for the control mice without PDT.

2.4. Determination of the Light Distribution in Tumors with Different Optical Properties

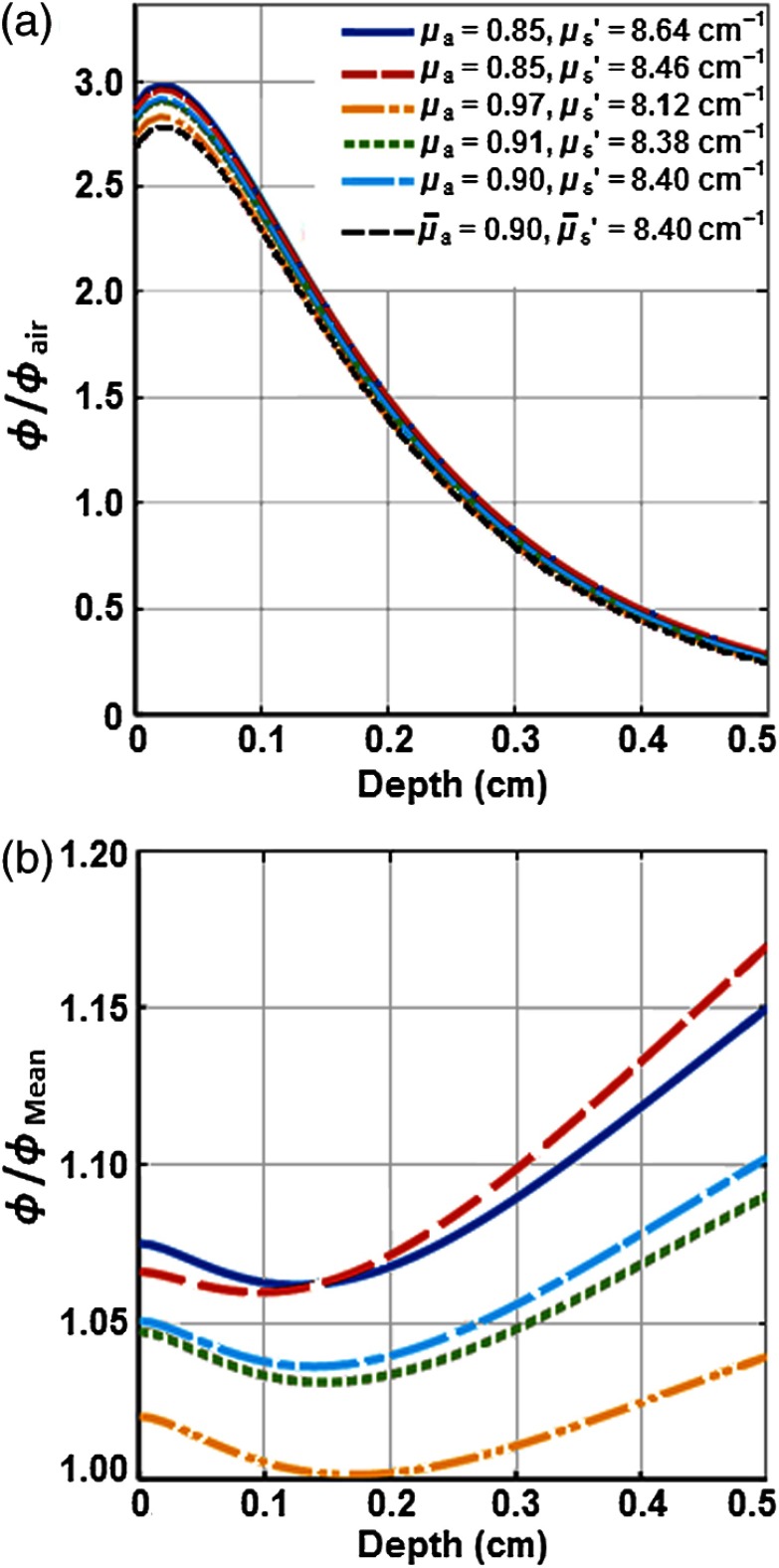
In-vivo measurements of the tissue optical properties were performed in another set of mice administered with $5\mathrm{mg}/\mathrm{kg}$ Photofrin with a two-catheter method described in detail elsewhere.¹⁸ Two parallel catheters were inserted into the tumor with one centrally positioned and the other a fixed distance away. A 2-mm point source fiber was coupled to the 630-nm diode laser, and light fluence profiles were obtained along the length of the second catheter using an isotropic detector. Profiles were then fit to a diffusion equation to extract the absorption coefficient (${\mu }_{\mathrm{a}}$) and reduced scattering coefficient (${\mu }_{\mathrm{s}}^{\prime }$) of the tumor tissue for the mice.²⁵ An analytical functional fitting to Monte Carlo (MC) simulation was used to calculate the spatial distribution of $\varphi$ in the tumors with different ${\mu }_{\mathrm{a}}$ and ${\mu }_{\mathrm{s}}^{\prime }$ using a method that has been published previously.²⁶ Figure 1(a) shows the spatial distribution of the ratio of fluence rate and in-air fluence rate ($\varphi /{\varphi }_{\text{air}}$). The deviation of $\varphi$ due to the effect of various ${\mu }_{\mathrm{a}}$ and ${\mu }_{\mathrm{s}}^{\prime }$ has been shown in Fig. 1(b). In-air fluence rate was measured on the surface of the tumors for each individual mouse that was used for this study. This independent verification indicated that calculation using the mean optical properties is accurate to within 10%.

Fig. 1.

MC simulation of the spatial distribution of light fluence rate ($\varphi$) in RIF tumors with different optical properties (${\mu }_{\mathrm{a}}$ and ${\mu }_{\mathrm{s}}^{\prime }$). (a) The ratio of light fluence rate and in-air fluence rate ($\varphi /{\varphi }_{\text{air}}$) versus tumor depth and (b) the ratio of light fluence rate for each condition and the mean fluence rate ($\varphi /{\varphi }_{\text{Mean}}$) versus tumor depth. ${\varphi }_{\text{Mean}}$ was calculated from the mean optical properties of ${\stackrel{-}{\mu }}_{\mathrm{a}}=0.9{\mathrm{cm}}^{-1}$ and ${\stackrel{-}{\mu }}_{\mathrm{s}}^{\prime }=8.4{\mathrm{cm}}^{-1}$.

2.5. Measurement of the Photofrin Concentration in Tumors

A custom-designed multifiber probe connected to a CCD camera (InSpectrum 150, Roper Scientific, Princeton, New Jersey) was used to collect surface fluorescence of Photofrin at the tumor site. A 405-nm laser was used as an excitation light to obtain the fluorescence signals. The fluorescence measurement was conducted immediately before and after PDT. The raw fluorescence spectrum was fit to the basis spectrum of Photofrin and autofluorescence in the absence of the photosensitizer using a singular value decomposition (SVD) method described by Finlay et al.^27,28 The attenuation of Photofrin fluorescence signal due to the light absorption and scattering by tissue was corrected by applying an empirical correction factor (CF)

$$\mathrm{CF}=\frac{C_{01}+C_{02}{\mu }_{\mathrm{s}}^{\prime }}{{\mu }_{\mathrm{s}}^{\prime }}·\exp [(b_1+b_2{\mu }_{\mathrm{s}}^{\prime }).\sqrt{3{\mu }_{\mathrm{a}}{\mu }_{\mathrm{s}}^{\prime }}],$$ (2)

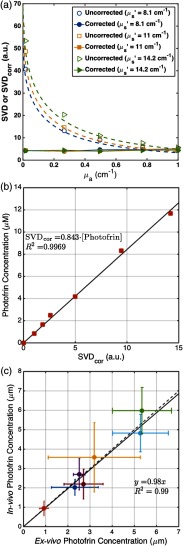
where constants $C_{01}=0.30\pm 0.11$, $C_{02}=0.035\pm 0.019$, $b_1=0.78\pm 0.11$, and $b_2=-0.026\pm 0.014$ were determined from fitting the fluorescence SVD for phantoms with different ${\mu }_{\mathrm{a}}$ and ${\mu }_{\mathrm{s}}^{\prime }$. The correction factor is specific to the probe and the semi-infinite geometry set-up used for the measurements. To obtain the values of the parameters in the expression for CF, a set of liquid phantoms were prepared with various optical properties (${\mu }_{\mathrm{a}}=0$ to $0.9{\mathrm{cm}}^{-1}$, ${\mu }_{\mathrm{s}}^{\prime }=5$ to $15{\mathrm{cm}}^{-1}$) and a constant Photofrin concentration of $2\mathrm{mg}/\mathrm{kg}$ ($3.3\mu \mathrm{M}$) using Intralipid (Fresenius Kabi, Uppsala, Sweden) as the scatterer and ink (Parker^® Quink^®) as the absorber. Optical properties of each phantom were measured and fluorescence spectra were obtained. The corrected SVD (${\mathrm{SVD}}_{\mathrm{cor}}=\mathrm{SVD}\times \mathrm{CF}$) with the appropriate CF should have the same magnitude for phantoms with the same Photofrin concentration. Fitting the raw SVD to this enabled for fitting and determining the parameters necessary in CF. Furthermore, a calibration curve was determined between ${\mathrm{SVD}}_{\mathrm{cor}}$ and various Photofrin concentrations ranging from 0 to $7\mathrm{mg}/\mathrm{kg}$ (0 to $11.7\mu \mathrm{M}$). Raw fluorescence SVD measurements performed in vivo could then be corrected using Eq. (6), and absolute Photofrin concentration could be determined using the calibration curve from ${\mathrm{SVD}}_{\mathrm{cor}}$ values in vivo [see Figs. 2(a) and 2(b)].

Fig. 2.

(a) Fluorescence singular decomposition (SVD) amplitude for phantom experiments with different optical properties with the same Photofrin concentration. (b) Photofrin concentration (in $\mathrm{mg}/\mathrm{kg}$) versus corrected fluorescence SVD (${\mathrm{SVD}}_{\mathrm{cor}}$). (c) The in-vivo measured photosensitizer concentration using the contact probe (based on fluorescence spectroscopy) versus ex-vivo measured Photofrin concentration.

Using a method described by Penjweini et al.,¹⁶ ex-vivo measurements of the Photofrin concentration were performed in another set of mice administered with the photosensitizer at the same concentration as the PDT-treated mice. After the 24-h drug–light interval, interstitial measurements were performed using the same fluorescence method as that of the PDT-treated mice. The tumors were then immediately excised and frozen. Homogenized solutions of the tumors were prepared using Soluble (PerkinElmer, Waltham, Massachusetts) and fluorescence of the homogenized sample was measured by a spectrofluorometer (FluoroMax-3; Jobin Yvon, Inc.) with an excitation at 405 nm and an emission range from 590 to 740 nm with an emission maximum at 630 nm. The photosensitizer concentration in the tissue was calculated based on the change in fluorescence peak magnitude resulting from the addition of a known amount of Photofrin to each sample after its initial reading. As shown in Fig. 2(c), the ex-vivo measurements of Photofrin concentration were compared to those obtained in vivo using the interstitial method to evaluate the in-vivo acquired Photofrin concentrations; the linear fit, $y=0.98x$, to the data (shown as a solid line) with the fitting goodness of $R^2=0.99$ shows their reasonable agreement, validating the in-vivo measurements. The dashed line represents the line for $y=x$, if the two measurements were completely in agreement.

For actual application of CF [Eq. (2)], the mean tissue optical properties (${\mu }_{\mathrm{a}}=0.9{\mathrm{cm}}^{-1}$, ${\mu }_{\mathrm{s}}^{\prime }=8.4{\mathrm{cm}}^{-1}$) were used for all mice. This may introduce an additional maximum CF variation of $\pm 4\%$ due to the variation of tissue optical properties as shown in Fig. 1.

2.6. Macroscopic Singlet Oxygen Model for Photodynamic Therapy

An empirical macroscopic ${}^1{\mathrm{O}}_2$ model derived from reaction rate equations for a type II PDT mechanism was adopted in this study.¹⁸ The complete set of the reaction rate equations and their derivations have been described in detail elsewhere.^18,29–31 In this model, the reaction rate equations are simplified as the following, which incorporates a set of PDT kinetic equations:

$$\frac{\mathrm{d}[S_0]}{\mathrm{d}t}+\left(\xi \sigma \frac{\varphi ([S_0]+\delta )[{}^3{\mathrm{O}}_2]}{[{}^3{\mathrm{O}}_2]+\beta }\right)[S_0]=0,$$ (3)

$$\frac{\mathrm{d}[{}^3{\mathrm{O}}_2]}{\mathrm{d}t}+\left(\xi \frac{\varphi [S_0]}{[{}^3{\mathrm{O}}_2]+\beta }\right)[{}^3{\mathrm{O}}_2]-g(1-\frac{[{}^3{\mathrm{O}}_2]}{[{}^3{\mathrm{O}}_2](t=0)})=0,$$ (4)

$$\frac{\mathrm{d}{[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}}{\mathrm{d}t}+\left(\xi \frac{\varphi [S_0][{}^3{\mathrm{O}}_2]}{[{}^3{\mathrm{O}}_2]+\beta }\right)=0,$$ (5)

where $S$ represents the light source power. $\xi$, $\sigma$, $\delta$, $\beta$, and $g$ are specific PDT photochemical parameters with definitions and magnitudes listed in Table 1.

Table 1.

Model parameters used in the macroscopic kinetics equations for Photofrin.

Parameter	Definition	Value	References
$ϵ$ (${\mathrm{cm}}^{-1}\mu {\mathrm{M}}^{-1}$)	Photofrin extinction coefficient	0.0035	18
$\xi$ (${\mathrm{cm}}^2{\mathrm{s}}^{-1}{\mathrm{mW}}^{-1}$)	Specific oxygen consumption rate	$3.7\times {10}^{-3}$	18,32,33
$\sigma$ ($\mu {\mathrm{M}}^{-1}$)	Specific photobleaching ratio	$7.6\times {10}^{-5}$	18,32
$\beta$ ($\mu \mathrm{M}$)	Oxygen quenching threshold concentration	11.9	18,32
$\delta$ ($\mu \mathrm{M}$)	Low-concentration correction	33	18,34
$g$ ($\mu \mathrm{M}/\mathrm{s}$)	Macroscopic oxygen maximum perfusion rate	0.76	18
${[{}^3{\mathrm{O}}_2]}_0$ ($\mu \mathrm{M}$)	Initial ground-state oxygen concentration	40	35,36

The calculation of the equations was performed using MATLAB^® R2015b (Natick, Massachusetts).

2.7. Statistical Analysis

The tumor regrowth rate ($k$) and CI of each condition have been expressed as the $\text{mean}\pm \text{standard deviation}$. Differences in the tumor regrowth rate and CI between each PDT group and control group were analyzed by Mann–Whitney test. Analyses were carried out using SPSS 22.0 software. For all tests, $p<0.05$ level (95% confidence level) was considered statistically significant.

3. Results

3.1. Tumor Regrowth Curves

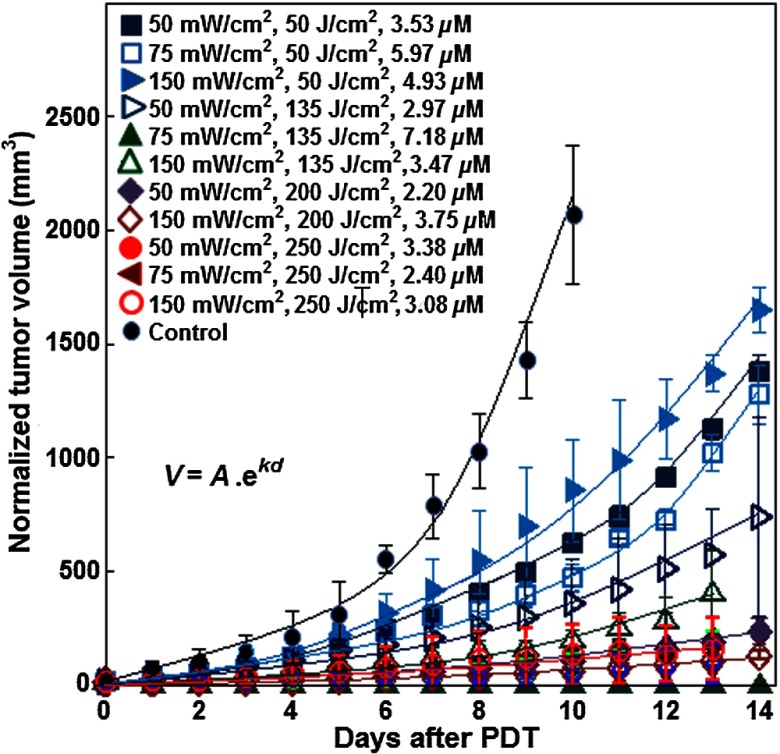
To compare the regrowth rate between different tumors, volumes were normalized so that the initial volumes on day 0 were matched to be the same among all tumors, $\sim 12{\mathrm{mm}}^3$. Figure 3 shows the normalized tumor volume versus time (in days) for the 11 treatment groups and the control group along with the fits to the data with an exponential growth equation. These exponential fits to the data determine the value of $k$ for each treatment group of mice. The statistical analyses showed a reduction of tumor regrowth rate for all treated groups compared to the control (all with $p<0.05$). Some mice within the same group had different CIs. For the group with a total fluence of $135\mathrm{J}/{\mathrm{cm}}^2$ and $\varphi =50\mathrm{mW}/{\mathrm{cm}}^2$, one out of four (25%) mice showed a complete response (no tumor regrowth for 14 days post-PDT). This is reflected in Table 2 under the column labeled CI variation count. At the same total fluence, all mice (100%) for the group treated at $\varphi =75\mathrm{mW}/{\mathrm{cm}}^2$ and no mice (0%) for the group treated at $\varphi =150\mathrm{mW}/{\mathrm{cm}}^2$ exhibited a complete response. At $200\mathrm{J}/{\mathrm{cm}}^2$, no tumors showed a complete response with either 50 or $150\mathrm{mW}/{\mathrm{cm}}^2$. At $250\mathrm{J}/{\mathrm{cm}}^2$, three out of five (60%) tumors showed a complete response at $50\mathrm{mW}/{\mathrm{cm}}^2$, two out of four (50%) had a complete response at $75\mathrm{mW}/{\mathrm{cm}}^2$, and two out of nine (22.2%) had a complete response with $150\mathrm{mW}/{\mathrm{cm}}^2$ (Table 2).

Fig. 3.

Exponential fitting of the change in normalized tumor volume over time after PDT. Before PDT, all the tumor volumes in each group had no significant difference between each other ($p>0.05$). After PDT, comparing with the control group, each PDT group could effectively inhibit the regrowth of tumor ($p<0.05$).

Table 2.

The drug concentration, tumor regrowth rate, CI, and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ of each PDT group.

Groups	Fluence rate ($\mathrm{mW}/{\mathrm{cm}}^2$)	Fluence ($\mathrm{J}/{\mathrm{cm}}^2$)	PDT dose ($\mu \mathrm{M}\mathrm{J}/{\mathrm{cm}}^2$)	Mean Photofrin ($\mu \mathrm{M}$)	Photofrin variationc ($\mu \mathrm{M}$)	Mean ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$b (mM)	${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ variationc (mM)	$k$ (${\text{days}}^{-1}$)	CI variation countd	CI
1	50	50	$126.5\pm 27.6$	$3.5\pm 0.9$	—	$0.35\pm 0.06$	—	$0.31\pm 0.02$	$0/4$	$0.24\pm 0.05$
2	75	50	$235.5\pm 55.8$	$6.0\pm 1.3$	—	$0.40\pm 0.03$	—	$0.30\pm 0.07$	$0/5$	$0.28\pm 0.17$
3	150	50	$199.9\pm 112.8$	$4.9\pm 2.6$	—	$0.24\pm 0.02$	—	$0.32\pm 0.01$	$0/4$	$0.23\pm 0.02$
4	50	135	$229.7\pm 38.8$	$3.0\pm 1.0$	$2.5/4.3$a	$0.66\pm 0.19$	$0.57/0.91$e	$0.19\pm 0.13$	$1/4$	$0.54\pm 0.21$
5	75	135	$661.9\pm 327.1$	$7.2\pm 3.2$	—	$1.05\pm 0.21$	—	0	$5/5$	1
6	150	135	$322.3\pm 42.0$	$3.5\pm 0.4$	—	$0.53\pm 0.03$	—	$0.23\pm 0.04$	$0/4$	$0.45\pm 0.09$
7	50	200	$204.8\pm 37.1$	$2.2\pm 1.1$	—	$0.63\pm 0.29$	—	$0.21\pm 0.01$	$0/5$	$0.49\pm 0.02$
8	150	200	$417.8\pm 137.9$	$3.8\pm 1.0$	—	$0.76\pm 0.09$	—	$0.17\pm 0.02$	$0/5$	$0.59\pm 0.04$
9	50	250	$362.1\pm 124.0$	$3.4\pm 1.1$	$3.2/3.7$	$1.03\pm 0.35$	$0.97/1.09$	$0.21\pm 0.18$	$3/5$	$0.77\pm 0.31$
10	75	250	$263.0\pm 51.9$	$2.4\pm 0.4$	$2.1/2.7$	$0.74\pm 0.11$	$0.65/0.81$	$0.18\pm 0.11$	$2/4$	$0.57\pm 0.31$
11	150	250	$393.0\pm 188.2$	$3.1\pm 1.8$	$2.5/5.3$a	$0.81\pm 0.27$	$0.69/1.04$e	$0.20\pm 0.10$	$2/9$	$0.52\pm 0.23$
Control	0	0	0	0	—	0	—	$0.42\pm 0.07$	—	0

Note: In group 4, 9, 10 and 11, cured and not cured tumors coexisted in the same PDT group.

^aPhotofrin concentration in tumors with complete and partial response is significantly different, $p<0.05$.

^bThe average value of reacted singlet oxygen concentration at 3-mm depth of the tumor among mice used.

^cVariation is shown for (tumors with complete response)/(tumors with partial response).

^dCI variation is shown as (tumors with a complete response)/(total number of tumors in the group).

^e${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ concentration in tumors with complete and partial response is significantly different, $p<0.05$.

3.2. Variation in Photofrin Concentration

With the same administered Photofrin dose of $5\mathrm{mg}/\mathrm{kg}$, the uptake of photosensitizer in tumors varied from 0.95 to $10.53\mu \mathrm{M}$; the mean concentration was $3.93\pm 2.15\mu \mathrm{M}$; and the median value was $3.54\mu \mathrm{M}$. As shown in Table 2, the mean uptake of Photofrin in tumors of each treatment group ranged from 2 to $7\mu \mathrm{M}$. Treatment groups with mixed tumor control results (complete and partial responses) reflected this difference in Photofrin concentration as well. To evaluate the in-vivo measurements, ex-vivo measurements of the Photofrin concentration were performed in another set of mice administered the same amounts of the photosensitizer. As shown in Fig. 2(c), the in-vivo measured concentrations have been compared with those obtained ex-vivo; each individual data point represents the average value of three measurements with the standard error of the mean. A linear fit of $y=0.98x$ (solid black line) with $R^2=0.99$ shows a good correlation of the in-vivo and ex-vivo data.

3.3. Variation in Calculated [¹O₂]_rx

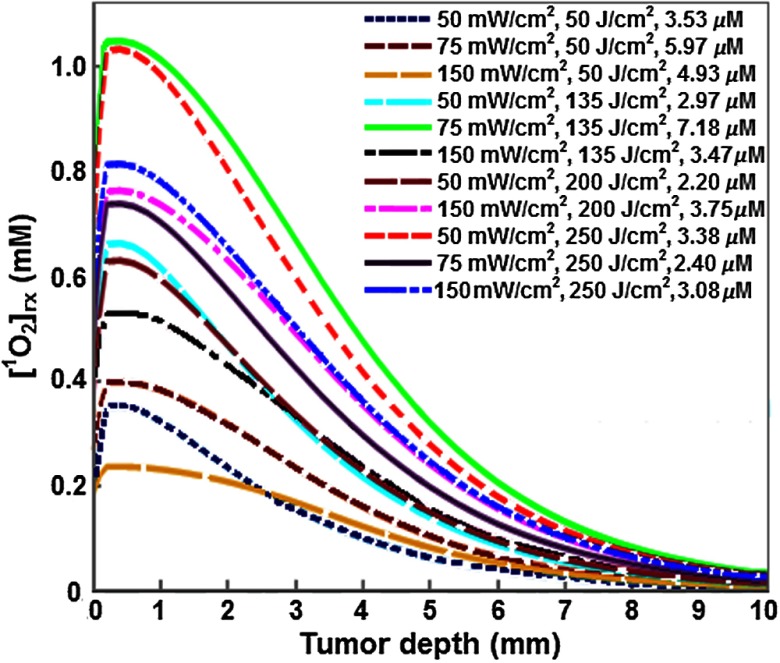
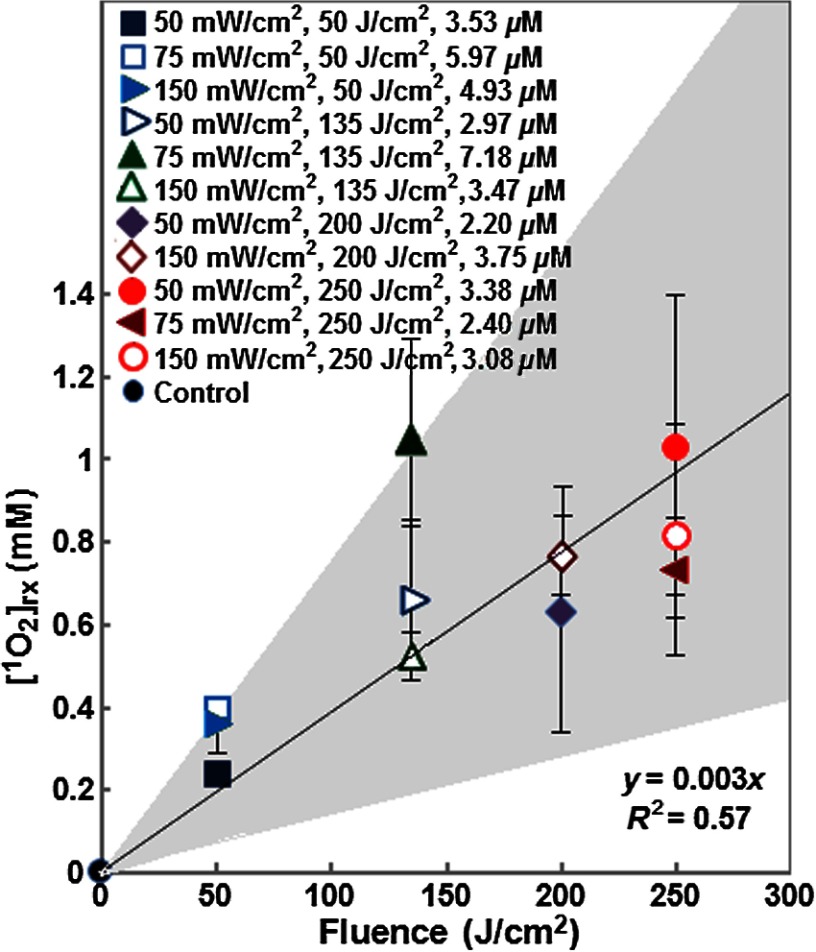
Figure 4 shows that the spatial distribution of calculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ along the tumor depth. With increasing tumor depth, ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ is decreased due to the distribution of treatment light inside the tumor. Figure 5 shows the impact of fluence on mean ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$, which is the mean reacted singlet oxygen produced at 3-mm depth inside the tumor based on a previous study.¹⁶ Although the amount of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ is increased with an increase in fluence, the generation of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ varied with $\varphi$. For example, at the lowest fluence of $50\mathrm{J}/{\mathrm{cm}}^2$, the ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ calculated for groups treated with 50, 75, and $150\mathrm{mW}/{\mathrm{cm}}^2$ was 0.35, 0.40, and 0.24, respectively. In all 11 PDT treatment groups, the highest amount of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ was found in the group treated with $75\mathrm{mW}/{\mathrm{cm}}^2$ to a fluence of $135\mathrm{J}/{\mathrm{cm}}^2$, while the lowest ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ was found in the group treated with $150\mathrm{mW}/{\mathrm{cm}}^2$ to a fluence of $50\mathrm{J}/{\mathrm{cm}}^2$. Table 2 shows the variation of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ within PDT treatment groups with a mix of tumors that exhibited complete and partial treatment response (group 4, 9, 10, and 11). The mean calculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ between the tumors that showed complete response and partial response was significantly different in groups 4 and 11 ($p<0.05$), whereas there was no significant difference ($p>0.05$) in groups 9 and 10.

Fig. 4.

Spatial distribution of reacted singlet oxygen (${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$) in tumors of each PDT group. Here, the Photofrin concentration was the mean calculated concentration of each PDT condition.

Fig. 5.

The impact of PDT fluence on reacted singlet oxygen generation at a 3-mm tumor depth. The black solid line shows the best-fit to the data using functional form, $y=0.003x$ with a goodness of fit of $R^2=0.57$. The gray area shows the upper and lower bounds of the fit with their 95% confidence level.

3.4. Correlation Between Three Photodynamic Therapy Metrics and Cure Index

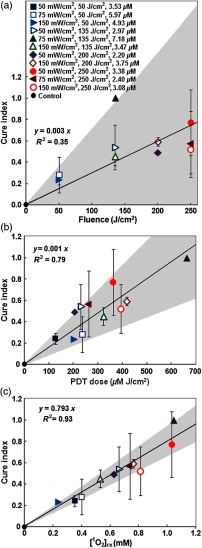
The relationship between CI and three PDT dose metrics, i.e., fluence, PDT dose, and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$, was further investigated. Figures 6(a)–6(c) show their correlations. The solid lines show the best linear fit to the data using functional forms $y=0.003x$ for (a), $y=0.001x$ for (b), and $y=0.795x$ for (c) with a goodness of fit of $R^2=0.35$, 0.79, and 0.93 for (a), (b), and (c), respectively. The gray area shows the upper and lower bounds of the fit with their 95% confidence levels. As shown in Fig. 6(a), the relationship between fluence and CI was poor with $R^2=0.35$. At the same fluence, CI varied greatly with $\varphi$.

Fig. 6.

Linear fitting of tumor CI versus (a) fluence, (b) PDT dose, and (c) mean ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ at a 3-mm tumor depth in each group. The gray area in each figure shows the upper and lower bounds of the fit with 95% confidence level. The solid lines show the best-fit to the data using functional forms, $y=0.003x$ for (a), $y=0.001x$ for (b), and $y=0.795x$ for (c) with goodness of fit of $R^2=0.35$, 0.79, and 0.93 for (a), (b), and (c), respectively.

The relationship of CI and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ could be fit with a linear function of the form $y=0.795x$ with a goodness of fit of $R^2=0.93$ [see Fig. 6(c)]. With increasing amounts of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$, CI was also improved. Among the 11 PDT treatment conditions, $135\mathrm{J}/{\mathrm{cm}}^2$ at $75\mathrm{mW}/{\mathrm{cm}}^2$ resulted in the highest calculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ concentration as well as the best control of tumor regrowth. However, there was one PDT treatment condition ($150\mathrm{mW}/{\mathrm{cm}}^2$, $250\mathrm{J}/{\mathrm{cm}}^2$) that did not follow this trend. While the amount of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ of this condition was higher than that of groups treated with $135\mathrm{J}/{\mathrm{cm}}^2$ at $50\mathrm{mW}/{\mathrm{cm}}^2$, $250\mathrm{J}/{\mathrm{cm}}^2$ at $75\mathrm{mW}/{\mathrm{cm}}^2$, and $200\mathrm{J}/{\mathrm{cm}}^2$ at $150\mathrm{mW}/{\mathrm{cm}}^2$, the CI was lower. Details of the results are listed in Table 2. Upon further investigation of the tumor CI and the mean calculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ for individual tumors that are a part of treatment groups where tumors exhibited both complete and partial response from treatment (Table 2), the results show that when the calculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ was larger than 1 mM, tumors resulted in a complete response.

4. Discussion

The three elements of PDT (light, drug, and ${}^3{\mathrm{O}}_2$) are dynamically changing and interacting with each other during PDT, which makes PDT dosimetry very complex and challenging. As the primary cause of cell damage during PDT, ${}^1{\mathrm{O}}_2$ has gained special attention as the dosimetric index both by direct experimental methods as well as indirect mathematical modeling methods, but it is still difficult for direct measurements in in-vivo PDT studies.^37,38 Here, the predictive potential of calculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ using an indirect method for PDT outcome was evaluated.

Based on four different PDT light doses, plus a series of $\varphi$, the effectiveness of Photofrin-PDT on tumor regrowth inhibition was investigated. Although the results showed that all of these PDT conditions were effective in controlling the regrowth of tumors, CI varied with changes in total fluence and $\varphi$. Furthermore, unlike treatment with the monomeric photosensitizers, benzoporphyrin derivative monoacid ring A- or 2-(1-Hexyloxyethyl)-2-devinylpyropheophorbide-mediated PDT,^22,23 Photofrin-mediated PDT-treated tumors exhibited both complete and partial response in the same treatment group at certain PDT conditions.

In this study, tumors with complete response and partial response coexisted in the group treated with $135\mathrm{J}/{\mathrm{cm}}^2$ at $50\mathrm{mW}/{\mathrm{cm}}^2$ (group 4) as well as $250\mathrm{J}/{\mathrm{cm}}^2$ at 50, 75, and $150\mathrm{mW}/{\mathrm{cm}}^2$ (groups 9, 10, and 11). Varying results for the same PDT condition were also reported by Sitnik and Henderson³⁹ and Wang et al.¹⁹ for a wide range of $\varphi$ from 10 to $200\mathrm{mW}/{\mathrm{cm}}^2$. Furthermore, in this study, the linear fitting of fluence with CI showed that the relationship between them was very poor with $R^2=0.35$. All these data suggest the inaccuracy of the fluence alone for the prediction of PDT outcome.

PDT dose is a metric that incorporates the light dose absorbed by the photosensitizer in tumors.¹² As indicated in this study, PDT dose was more correlated to CI than fluence with a goodness of fit of $R^2=0.79$. However, CI was not always improved with increasing PDT dose. For instance, a PDT dose of $204.84\mu \mathrm{M}\mathrm{J}/{\mathrm{cm}}^2$ resulted a higher CI ($0.49\pm 0.02$) than that of 235.47 and $322.21\mu \mathrm{M}\mathrm{J}/{\mathrm{cm}}^2$, which resulted in a CI of $0.28\pm 0.17$ and $0.45\pm 0.09$, respectively. A PDT dose of $362.13\mu \mathrm{M}\mathrm{J}/{\mathrm{cm}}^2$ also resulted in a higher CI ($0.77\pm 0.31$) than that of 417.76 and $392.98\mu \mathrm{M}\mathrm{J}/{\mathrm{cm}}^2$, which resulted in a CI of $0.59\pm 0.31$ and $0.52\pm 0.23$, respectively. To some extent, the differences of the in-vivo photosensitizer concentration from the administrated dose could explain the different predictive ability between PDT dose and fluence. As demonstrated in this study, at a given Photofrin dose of $5\mathrm{mg}/\mathrm{kg}$, the uptake of Photofrin varied from tumor to tumor. In PDT conditions of $135\mathrm{J}/{\mathrm{cm}}^2$ at $50\mathrm{mW}/{\mathrm{cm}}^2$ (group 4) and $250\mathrm{J}/{\mathrm{cm}}^2$ at $150\mathrm{mW}/{\mathrm{cm}}^2$ (group 11), the in-vivo Photofrin concentration within the same group between tumors with complete and partial response was significantly different ($p<0.05$). The tendency to have large variations in Photofrin uptake by the tumors is in agreement with the other studies.^18,40

The calculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ did not follow the trend of increasing light dose or $\varphi$. Among the 11 PDT treatment groups with light ranging from 50 to $250\mathrm{J}/{\mathrm{cm}}^2$, the highest amount of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ was found with the group treated to $135\mathrm{J}/{\mathrm{cm}}^2$ with $75\mathrm{mW}/{\mathrm{cm}}^2$. This is consistent with the $\varphi$ dependence of PDT oxygen consumption. Higher $\varphi$ tends to create hypoxic environments that limit the production of ${}^1{\mathrm{O}}_2$.⁴¹ Furthermore, this treatment group had the highest measured in-vivo Photofrin concentration at $7.2\pm 3.2\mu \mathrm{M}$. These results emphasize the importance of explicit dosimetry of light, ${}^3{\mathrm{O}}_2$, and photosensitizer concentration to utilize ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ as a predictive dosimetric quantity for outcome.

The potential of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ as a predictor for PDT efficiency was evaluated by analyzing the correlation between ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ and CI. In most PDT conditions, the amount of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ calculated was consistent with CI; CI improved with increasing ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$. The correlation of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ with CI in treatment groups 4, 9,10, and 11 was further analyzed due to the mixed response from tumors. The results indicated that when ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ was more than 0.81 mM, tumors exhibited a complete response in all PDT conditions except with a fluence of $250\mathrm{J}/{\mathrm{cm}}^2$ at $50\mathrm{mW}/{\mathrm{cm}}^2$. In the same condition, when the mean ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ concentration was of 0.97 mM, only partial tumor control was achieved. All these results indicated that the threshold dose of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ to induce tumor control was more than 1 mM. Previous studies demonstrated the threshold dose of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ to produce necrosis in the same RIF tumor model was about $0.74\pm 0.25\mathrm{mM}$ for Photofrin-PDT (Table 1).⁴² As for inducing a tumor cure for PDT, it is reasonable to believe that the mean values of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ are larger than that necessary to induce tumor necrosis. However, further studies with a wide range of PDT fluences and a larger sample size are needed to validate these results.

Among the three metrics, i.e., fluence, PDT dose, and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$, ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ had the best correlation with CI with a goodness of fit of $R^2=0.93$. These results indicated that ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ better predicts PDT outcome than fluence or PDT dose.

5. Conclusions

In this empirical macroscopic ${}^1{\mathrm{O}}_2$ model, a set of equations were used to simplify the energy transfer processes in type II PDT, and calculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ was proposed as a dosimetric quantity. These equations can be solved by inputting parameters including the light fluence (rate), tissue optical properties, photosensitizer concentration, and photochemical parameters. The predictive ability of calculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$, as a dosimetric quantity, was evaluated by analyzing the relationship between ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ and CI due to PDT. The relationship between CI with two other commonly used metrics, fluence, and PDT dose, was also investigated. Preliminary results showed that compared with fluence or PDT dose, ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ was the most accurate metric and could serve as a better dosimetric quantity. Further studies are required to validate these results and establish the threshold dose of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ to induce a complete response in this RIF tumor model. Furthermore, other factors, such as the photosensitizer photobleaching and the ${}^3{\mathrm{O}}_2$ variation during PDT should be considered to improve the predictive ability of this macroscopic model.

Biographies

Haixia Qiu received her MD in 2006 in laser medicine from the Medical College of Chinese People's Liberation Army. She is currently a visiting scholar in the Department of Radiation Oncology at the University of Pennsylvania. Her current research interests include PDT dosimetry, the underlying mechanism of PDT and the clinical application of PDT.

Michele M. Kim received her BA and MS degrees in physics from the University of Pennsylvania in 2012 and is currently a PhD candidate at the University of Pennsylvania in physics while pursuing a certificate in medical physics. Her research topics include preclinical and clinical PDT dosimetry.

Rozhin Penjweini received her PhD degree in 2012 in physics from the University of Vienna. She is currently a postdoctoral researcher in the Department of Radiation Oncology at the University of Pennsylvania. Her current research interest is in vivo explicit singlet oxygen dosimetry for PDT. She also has practical experience in various fluorescence microscopy techniques for studying the structure, transport, and stability of nanomedicines in living cells.

Timothy C. Zhu received his PhD degree in 1991 in physics from Brown University. He is currently a professor in the Department of Radiation Oncology at the University of Pennsylvania. His current research interests include in vivo explicit PDT dosimetry, singlet oxygen explicit dosimetry, integrated system for interstitial and intracavitory PDT, diffuse optical tomography, and external beam radiation transport.