Binding Pose Flip Explained via Enthalpic and Entropic Contributions

Abstract

The anomalous binding modes of five highly similar fragments of TIE2 inhibitors, showing three distinct binding poses, are investigated. We report a quantitative rationalization for the changes in binding pose based on molecular dynamics simulations. We investigated five fragments in complex with the transforming growth factor β receptor type 1 kinase domain. Analyses of these simulations using Grid Inhomogeneous Solvation Theory (GIST), pK_A calculations, and a tool to investigate enthalpic differences upon binding unraveled the various thermodynamic contributions to the different binding modes. While one binding mode flip can be rationalized by steric repulsion, the second binding pose flip revealed a different protonation state for one of the ligands, leading to different enthalpic and entropic contributions to the binding free energy. One binding pose is stabilized by the displacement of entropically unfavored water molecules (binding pose determined by solvation entropy), ligands in the other binding pose are stabilized by strong enthalpic interactions, overcompensating the unfavorable water entropy in this pose (binding pose determined by enthalpic interactions). This analysis elucidates unprecedented details determining the flipping of the binding modes, which can elegantly explain the experimental findings for this system.

Introduction

Structure-based drug design is used to guide drug discovery with the help of a known three-dimensional structure of a potential drug target. The correct prediction of small molecule binding to a target is essential for the success of structure-based drug design projects. The most common way to experimentally determine binding modes is by X-ray crystallography. As obtaining a crystal structure for every ligand modification is rather time-consuming, it is usually assumed that minor ligand modifications do not alter the binding pose and only a few ligands with major alterations are crystallized. However, it is rather intricate to predict which modification preserves the binding mode and which one leads to an alternate binding mode and may result in incorrect interpretations in structure-based design. Therefore, it is essential to know how often a structural revalidation of the binding modes by X-ray crystallography is required. Unfortunately, there is no simple answer to this question.¹ Small molecules, e.g. fragments, may readily change their binding modes upon larger modifications (for fragments already an absolute small modification can be large relative to the fragment size) but on the other hand may preserve key binding interactions when bound to binding site hot-spots.² Nonadditive behavior of substituents in structure–activity relationships can provide crucial hints on changes in binding modes even in absence of structural information.³ Additionally, binding site dynamics may give rise to an ensemble of receptor states that in turn allow different binding poses for small molecules.⁴ A detailed understanding of how and why different binding modes originate is crucial to improve methods to correctly predict binding poses⁵ and to rationalize structure–activity relationships.³

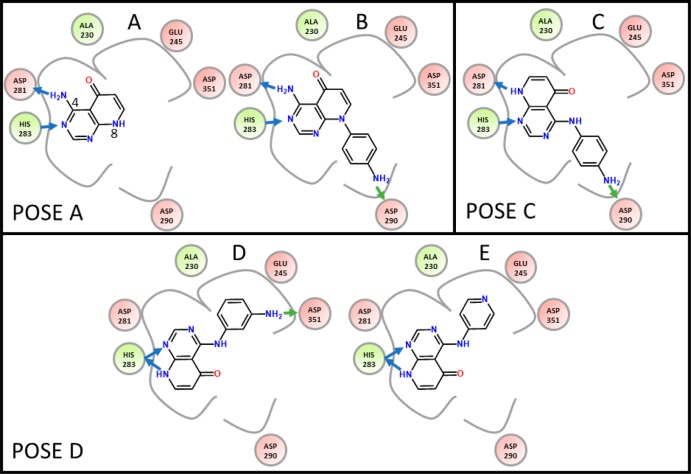
One of the studied potential drug targets is TIE2, an angiopoietin receptor, involved in the formation of new blood vessels. Fragments of a potential TIE2 inhibitor^6,7 were studied by Czodrowski et al. to determine the contributions of individual functional groups to ligand binding free energy.⁸ Five related compounds (Figure 1) were crystallized in complex with the transforming growth factor β receptor type 1 kinase domain (TGFBR1). Surprisingly, these five fragments differ in their binding modes. Figure 1A shows the core fragment with the hinge binding motif 4-amino-8H-pyrido[2,3-d]pyrimidin-5-one of the initial inhibitor, while Figures 1B–E show four molecules with different substitutions on the core fragment. Interestingly, the five compounds show three different hinge binding modes.

Figure 1.

Mini-library of the five compounds used by Czodrowski et al. Compound A shows the core 4-amino-8H-pyrido[2,3-d]pyrimidin-5-one fragment. Compound B has a p-anilino group as decoration on the “pyridine” position (position 8). It binds to the hinge binding region (backbone of ASP-281 and HIS-283) similarly as compound A. Compound C with the p-anilino substituent at the amino group in position 4 shows an alternative binding mode in comparison to compound A. Compound D with the m-anilino group and compound E with the pyridyl-substituent show a third binding mode, where the scaffold is flipped with respect to pose C by 180° along the hinge axis. Blue arrows indicate H-bonds to backbone atoms, whereas green arrows indicate H-bonds to side chains.

Compounds A and B (Figure 1) show the same binding mode (Pose A). As compounds C, D, and E each have substituents at the amino group in position 4, they must have an alternate binding mode due to steric repulsion. Unexpectedly, these three similar compounds show different binding poses. Compound C with a p-anilino group binds such that the substituent is solvent exposed (binding pose C, Figure 2: green ligand). Compound D with the m-anilino substitution and E with the p-pyridine moiety bind in an orientation, where the substituents point to the buried, less solvent exposed pocket (binding pose D, Figure 2: blue ligand). If only one of these five crystal structures were obtained, these changes in binding conformation would not have been predicted correctly, resulting in misinterpretation of structure–activity relationships.

Figure 2.

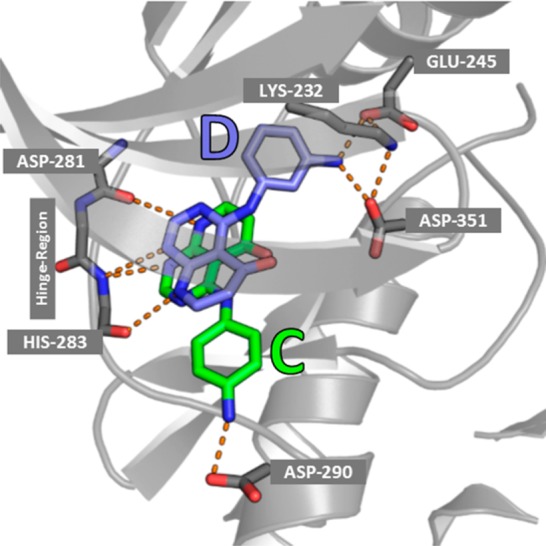
Binding region of the transforming growth factor β receptor type 1 kinase domain with two ligands bound. Compound D (blue ligand) occupies the less solvent exposed/buried pocket (kinase back-pocket) in the background, whereas compound C (green ligand) points its substituent to a more solvent exposed region. In the back-pocket GLU-245, LYS-232, and ASP-351 can be found, whereas ASP-290 is close to the amino group of the solvent exposed residues.

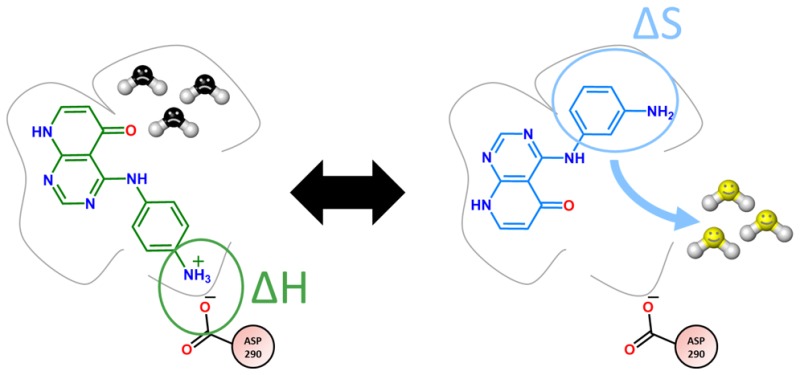
Czodrowski et al. attempted to rationalize the observed binding mode flips.⁸ They captured the thermodynamic behavior of the different ligands and binding poses by performing docking studies and analyzing solvent molecules around the protein using SZMAP⁹ and WaterMap.¹⁰ The thermodynamic interpretation originally presented is not unambiguous. It was claimed that binding pose D can be explained by the replacement of a “happy” (Watermap)/“hydrophilic” (SZMAP) water. However, replacement of “happy”/“hydrophilic” water molecules has usually a negative contribution to the free energy of binding because they have a lower free energy than bulk waters. Hence, the replacement of these water molecules is unfavorable in terms of binding free energy,^10,11 and therefore that interpretation is doubtful. In this study, we present a theoretical paper of the thermodynamics of these binding poses to clarify the unexpected behavior of the five ligands and to shed light on the question why compound C is not found in the same binding pose as compound D and vice versa.

To correctly describe the thermodynamics of ligand binding, it is necessary to study not only the direct enthalpic interactions of the ligand and the protein but also to account for differences in the solvation of the formed complexes. The (de)solvation of the protein binding site and the ligand can be an important driving force for the biomolecular recognition of a ligand and can be as important as the direct contact between protein and ligand.¹²⁻¹⁴ This versatile behavior of water in binding pockets attracted the attention of the scientific field, which resulted in an increasing number of publications concerning the analysis of water molecules in ligand-binding with a vast variety of different techniques,^9,10,15−17 making it one of the “hot topics” in medicinal chemistry.

Furthermore, it is also necessary to calculate both enthalpic and entropic contributions, because the free energy is generally not correlated to the enthalpy or the entropy alone.¹⁸ In this contribution, we analyze the different binding modes in terms of thermodynamics and decompose the (binding) free energy into entropic and enthalpic contributions of the complex and the solvent molecules.

We use Molecular Dynamics (MD) simulations in combination with Grid Inhomogeneous Solvation Theory^17,19 (GIST) and the Liner Interaction Energy (LIE)^20,21 module of AmberTools15 to analyze the thermodynamic properties of the ligand binding poses. To estimate the protonation of all ligands we perform pK_A calculations because results are expected to depend on the protonation state of the ligands. Only the combination of these computational methods allows us to explain the experimental observed binding pose changes in great detail.

Materials & Methods

To capture the complete thermodynamics of the ligand binding process—including the flip in the binding pose from compound C to D (Figure 1)—we have to use an amalgam of analyses tools.

Molecular Dynamics Simulations

The two ligand fragments (compound C and D) in their neutral and positively charged form were parametrized using the antechamber module of the Amber package²² with the AM1-BCC charge model^23,24 and the general Amber force field²⁵ (partial charges for all ligands are shown in Figures S1–S4). In addition to the crystal structures, structures of compounds C and D in the other possible binding pose were modeled. This was achieved by “in silico” modification of the ligands. The two ligands were simulated in both protonation states and in both binding poses in complex with the TGFBR1 kinase domain using experimental crystal structures (PDB: 4X2K, 4X2G) and as unbound ligands in solution. In total, eight simulations of the ligands in complex with the protein were performed plus four simulations of the unbound ligands. ff14SB²⁶ was chosen as protein force field. All ligand protein complexes were solvated with TIP4P²⁷ water molecules in an octahedral box. Periodic boundary conditions were applied and a minimum distance of 15 Å between the solute and the edge of the box was chosen. Equilibration of the systems was performed according to an established protocol previously developed in our group.²⁸ A Langevin thermostat was used to keep the temperature at 300 K. The pressure of 1 bar was kept by using an isotropic implementation of the Berendsen barostat. The time step was set to 2 fs and coordinates were saved every 10 ps for a 200 ns trajectory without restraints.

Five representative conformations were obtained by clustering a 200 ns trajectory of each ligand using a hierarchical agglomerative (bottom-up) approach implemented in cpptraj.²⁹ Five clusters were used as we had to find a compromise between calculation effort and accuracy. The 2000 water molecules closest to the complex of every representative conformer were retained, they were again solvated in an octahedral box and equilibrated. During equilibration and simulation of the five clusters we applied coordinate restraints to the whole protein and the ligand, as it is required for the GIST analysis.¹⁷ Every cluster was simulated for 100 ns and coordinates were saved every 100 ps.

Grid Inhomogeneous Solvation Theory

GIST allows for a thermodynamic analysis of water molecules around a solute. The method calculates the free energy of water molecules on a grid based approach for a single conformation of the solute. Recently published studies highlighted that GIST is a valid and useful approach to study biomolecular systems in combination with molecular dynamics simulations,^19,30 allowing one to differentiate between entropic and enthalpic contributions to the total free energy. For all calculated values, the references state, to which all values refer, is pure water. A detailed description of how entropic and enthalpic terms are calculated is given by Nguyen et al.¹⁷ In all our calculations, a temperature of 300 K was chosen.

In an approximated manner, the free energy of solvation of a solute ΔG_Solv can be written according to eq 1.

1

It is defined as the integral over the solvation free energies ΔG_Solv(q) of a solute determined for each of its conformations q times the probability p(q) to find the solute in this conformation. To calculate ΔG_Solv(q) for a particular conformation q, its coordinates are restrained to retain this conformation. In this paper we consider the occurrence of different relevant conformations by simulating an unrestraint complex system. The trajectory is subsequently clustered into five representative conformations. Those are simulated with coordinate restraints and analyzed using GIST. Equation 1 is used to calculate the solvation free energy ΔG_Solv from the solvation free energies of the five restrained solute conformers ΔG_Solv(q) (the integral is approximated with a discrete sum). The probabilities p(q) are the relative cluster sizes, i.e., the number of structures per cluster.

GIST analyses various thermodynamic properties of water with a grid based approach. We want to emphasize that GIST covers the thermodynamic properties of the water only and it does not cover the entropic and enthalpic differences of the ligand and the protein upon binding. The results of a GIST calculation are multiple grids. As continuous grids are difficult to visualize, we tried to enhance the visualization of our results by extracting the most abundant water positions from the grid values.

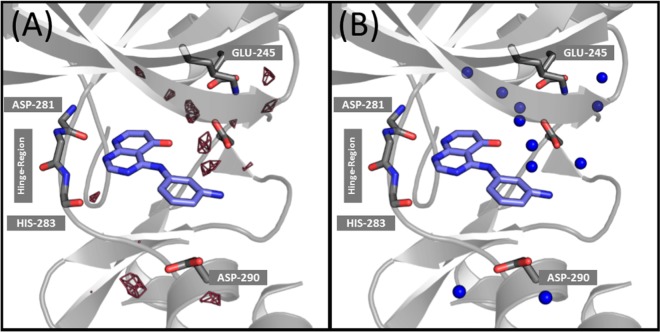
To find sensible water positions, a script was written to search for the grid point with the highest water density. From this grid point and the surrounding grid points the density of one water molecule is subtracted. Afterward, the next most abundant grid point is found by the program and again the density of one water molecule is subtracted. This is done for 99% of the water density. A 1% residual density is necessary due to boundary effects. To assign thermodynamic values to the refined water positions, the thermodynamic value (e.g., entropy, enthalpy, or free energy) of the analyzed grid points are averaged (density weighted). Figure 3 shows the results for the total entropy of the water molecules in a grid representation (A) and with representative water molecules (B). Each depicted water molecule has an entropy value larger than 3.5 kcal/mol. An analogous procedure can be applied to all other thermodynamic values of the GIST output; see ref (17). Aside from an easier visualization an additional advantage of this representation is that less abundant (less populated) grid points are weighted to a lesser extent and therefore points with high entropy due to low occupancy are not overinterpreted.

Figure 3.

Comparison of the grid visualization (A) and with representative water molecule representation (B). The grid points with a high entropic penalty (−TΔS > 3.5 kcal/mol, pink grid) and the refined water positions with a high entropic penalty (−TΔS > 3.5 kcal/mol, blue spheres) are shown for compound C. Results are very similar whether refined water positions or raw grid representation is used for analysis, but visualization clearly benefits from further processing of raw grid results.

In contrast to the visualization of single water molecules and their corresponding properties, we also aimed for a quantitative description of the binding thermodynamics. Therefore, we summed the thermodynamic value of interest (density-weighted) over all grid points of the ligand binding region to capture differences in the overall thermodynamics. To ensure that roughly the same volume is used to estimate the water properties of the pocket for every simulation, all grid points within 5 Å of the ligand, the ASP-290, or the GLU-245 residue (shown in Figure 3) are used to calculate the thermodynamic properties of the pocket.

Binding Enthalpies

As the GIST analysis omits the enthalpic interactions between the ligand and the protein, we choose a method explicitly including this interaction. Therefore, we used the LIE implementation of the AmberTools15 package to estimate the enthalpy of ligand binding.^20,21 In LIE, eq 2 is applied to estimate the free energy of solvation:

2

ΔU_l–s describes the difference in interaction energy between the unbound solvated ligand and the ligand in complex with the protein plus solvation. If we set the parameters α = β = 1 and γ = 0, we obtain the difference in interaction energy ΔU for the ligand in the bound and unbound state. In LIE usually the parameters α and β are fitted to obtain values for ΔG. In contrast, the method with the suggested parameters (α = β = 1 and γ = 0) is a measure for the change in interaction enthalpy between the ligand in the bound and in the unbound state. Therefore, this method includes the interaction of the ligand with the protein, which is not captured by the GIST analysis. This method was further used to analyze the difference in the binding enthalpy between a protonated and the neutral form of the ligands C and D.

pK_A Calculations

Implicit solvent calculations^31,32 can be employed for the calculation of pK_A values. We make use of the OpenEye software protein_pka which is based on their Poisson–Boltzmann solver ZAP.³³ The actual pK_A value is derived from a thermodynamic cycle: the solvation energy of the protonated and deprotonated form of the residue (amino acid or ligand) is computed by solving the Poisson–Boltzmann equation whereas the pK_A value of the residue in aqueous solution is taken from literature or experiment. Based on these contributions, the pK_A value can finally be computed. However, sampling of the different possibilities of the charge states (residue 1 protonated and residue 2 protonated, residue 1 protonated and residue 2 deprotonated, etc.) of the residues is necessary: protein_pka makes use of Monte Carlo sampling to simulate the effect of different charge states. The protein structures were prepared by protein_pka (addition of hydrogen atoms and rebuilding missing heavy atoms). AM1-BCC charges^23,24 were used for the protein and the ligand. The protonation states can be computed using the Henderson–Hasselbach equation. Several publications highlight a protonation effect upon ligand binding to a protein.³⁴⁻³⁷

Results and Discussion

As discussed in a previously published study by Czodrowski et al. the role of water molecules in the proximity of the binding pocket can play a significant role in explaining the two different binding modes.⁸ To simplify the complex process of solvation, we distinguish in a first approximation between water molecules with a negative and a positive free energy value compared with water molecules in bulk. If the free energy of the water molecule is more positive than in bulk water, we can gain free energy of binding when the water is removed from the protein and released into bulk. Water molecules with a positive free energy value in comparison to bulk water are either entropically constrained, i.e., restricted in their movement with no or too low enthalpic compensation (entropically unfavored water position, e.g., formation of a water wire or water polygons in an apolar environment), or have in general too low enthalpic interactions in comparison with bulk water (enthalpically unfavored water position, e.g., hydrophobic pocket).³⁸ Water molecules with a negative free energy value compared to bulk water often show strong enthalpic interactions. These strong enthalpic interactions lead to a highly favorable enthalpy of solvation. However, the phase space that these enthalpically strong bound water molecules can occupy (e.g., water near a charged residue) is usually restricted, resulting in a low entropy contribution. Therefore, the very favorable enthalpy of solvation is partially compensated by entropic restrictions. This phenomenon is called entropy-enthalpy compensation.³⁹⁻⁴¹ As neither enthalpy nor entropy is able to describe the differences in free energy completely,¹⁸ it is necessary to investigate both enthalpy and entropy to identify water molecules with a positive free energy contribution.

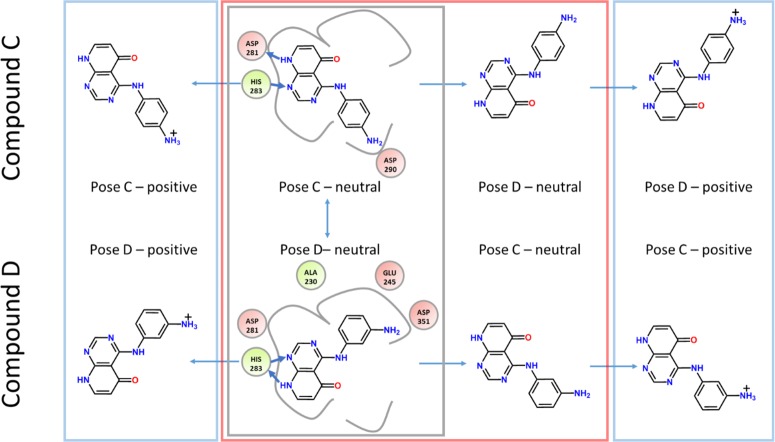
To explain why compound C is not found in pose D and vice versa, analyses of all possible binding poses and different protonation states were performed (summarized in Figure 4). Once more we would like to point out that the two ligands only differ in the position of the amino group, which is in para-position in compound C and in meta-position in D.

Figure 4.

Overview of all investigated structures. Compound C as crystallized (pose C) and compound D as found in the crystal structure (pose D) (gray box). To explain the surprising binding mode flip an analysis of compound D in pose C and vice versa (red box) is also required. To rationalize the complete binding behavior we also have to account for the possibility of different protonation states of the ligands within the binding pocket (blue boxes).

We start the thermodynamic analysis by investigating the free energy contributions of water molecules for the four uncharged states (red box of Figure 4). As already pointed out by Czodrowski et al.⁸ the differences between compound C and D in terms of physicochemical properties are very subtle at first glance. Redocking for both compounds was successful but when compound D was docked into the crystal structure of compound C binding pose C was obtained. The same result was obtained for the cross-docking of compound C into the crystal structure of compound D.

To rationalize the binding behavior we started with analyzing the solvent structure of the neutral ligands in the binding pose from the crystal structure and in the docked binding pose. The visualization of the GIST water entropies can be seen in Figure 5.

Figure 5.

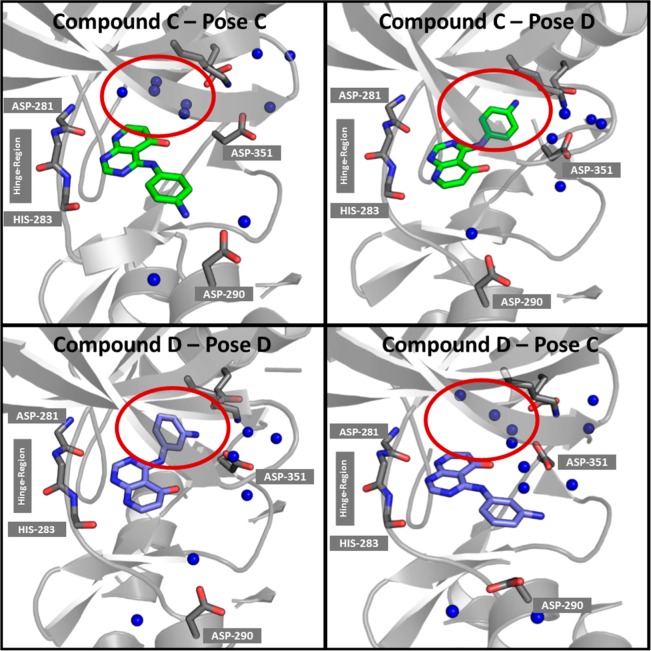
Visualization of water entropies from the GIST calculation for compounds C and D in both binding poses. Blue spheres indicate water molecules with a low/unfavorable entropy (−TΔS > 3.5 kcal/mol) in a radius of 5 Å around the ligands and the shown ASP-290 and GLU-245 residues. For both compounds binding pose C reveals more entropically disfavored water molecules in the back-pocket (highlighted with red ovals).

Entropically unfavorable water sites in respect to bulk water (−TΔS > 3.5 kcal/mol) are shown in Figure 5 as blue spheres. For compound D (Figure 5: bottom) we find that the binding pose D (left) has significantly fewer entropically unfavorable water molecules than binding pose C (right). Thus, for compound D the binding pose D is entropically favored over pose C. Some of these entropically unfavorable water molecules do not show strong enthalpic interactions with the ligand or the protein or other water molecules. The free energy of these water molecule is high in comparison to bulk water molecules. In the buried pocket (red oval in Figure 5) such water molecules with a positive contribution to the free energy are found, which can be replaced by a ligand, as found for compound D in pose D.

However, also for compound C binding pose D shows significantly fewer ordered water molecules (Figure 5: top), indicating that our analysis is missing important details for this ligand. To shed light on this behavior, enthalpic and entropic contributions to solvation as well as the resulting free energy of water molecules within the previously mentioned 5 Å radius to the binding pocket are studied and results listed in Table 1.

Table 1. Thermodynamic Values of Pocket Water Molecules from the GIST Calculations (kcal/mol).

compound	pose	charge	ΔH	–TΔS	ΔG
C	C	neutral	–156.0	74.1	–82.4
	D		–162.0	70.3	–91.7
D	C		–155.9	79.7	–76.0
	D		–151.0	69.5	–81.5
C	C	positive	–175.0	88.6	–86.4
	D		–155.1	72.4	–82.7
D	C		–166.1	82.9	–83.2
	D		–154.9	68.2	–86.7

The first four rows list the results of the GIST calculations for the uncharged ligands. For compound D we find that pose D is energetically favorable (ΔG_D(pose D) < ΔG_D(pose C)) and that this difference in free energy has its origin in the water entropy. This is in good agreement with the visualization and the results obtained earlier by Czodrowski et al.⁸ The solvent calculations with WaterMap and SZMAP also identified two to three “unhappy”/“hydrophobic” water molecules which are replaced by compound D in the buried pocket. As a reminder: “unhappy”/“hydrophilic water molecules correspond to water molecules with a positive free energy value compared with bulk water. This explains the binding mode of compound D but would also mean that compound C should be found in the crystal structure with binding pose D. The free energy for compound C in pose D is also lower than in pose C (ΔG_C(pose D) < ΔG_C(pose C). The previously published explanation that the displacement of an enthalpically strong bound water molecule is responsible for this change in the binding is doubtful, as this should lead to a decrease in binding affinity.

These results indicate that the binding pose of compound C cannot be explained by solvation analysis alone. Therefore, further investigation of the binding of the ligand C is required. A more detailed investigation of the binding site and the residues in close proximity to the ligand revealed that the binding site shows two negatively charged residues (ASP-351, GLU-245) in the buried pocket together with a positively charged lysine (LYS-232), forming salt bridges with each other. Furthermore, a negatively charged aspartate (ASP-290) is close to the amino group of the solvent exposed ligand. Hence, protonation of the aniline group and formation of a salt bridge with the deprotonated aspartate residue (shown in Figure 6) could occur as no other positively charged group is in close proximity.

Figure 6.

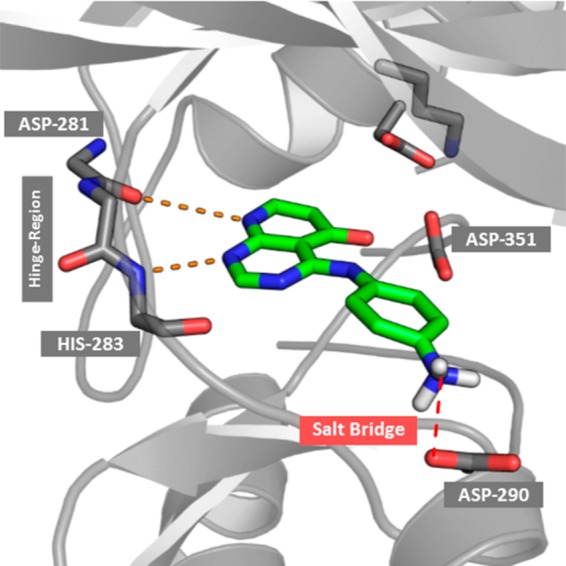
Possible salt bridge formed between the negatively charged aspartate (ASP-290) residue and the positively charged amino group of ligand C.

We therefore performed pK_A calculations for the compounds C and D for their native X-ray pose as well as their docking pose. Table 2 summarizes the results from the pK_A calculations.

Table 2. Results from the pK_A Calculations^a.

		ligand
pKA		C	D
pose	C	7.3	b
	D	b	b
free ligand		6.2	4.4

^aThe reported values correspond to the pK_A values of the amino group in compounds C and D.

^bAmino group is definitely not protonated at physiological pH: this can be concluded due to the pK_A value which is computed to be below 0.

The results of the pK_A calculations showed that indeed compound C in binding pose C is likely protonated, whereas for all other structures it is unlikely that the ligands are protonated at neutral pH.

Therefore, we performed the GIST calculations for the protonated form of the ligands C and D (Table 1; row 5–8). Again the entropy for binding pose D is higher than for pose C. In terms of free energy the compounds show the correct trend, but the difference between the different compounds and the different binding poses are smaller than for the neutral compounds. As the method’s error (max standard error of the mean for the GIST calculation: 3.1 kcal/mol) is in the same range, we have to further investigate the system to ensure the trend is correct. The enthalpic interactions between two charged residues (only present with a positively charged ligand) are significantly stronger than interactions between a charge and a dipole or two dipoles. Since GIST does not cover the interaction energy between ligand and protein this could further help to explain the binding mode. Therefore, we hypothesize that the strong enthalpic interaction of the salt bridge in the solvent exposed binding mode overcompensates the entropic unfavorable contributions of the ordered water molecules in the buried pocket.

To ensure that the pK_A calculations are correct, we present further evidence that the ligand is indeed protonated and this is responsible for the binding mode flip. Unfortunately, protonation states usually cannot be determined by X-ray crystallography for most biomolecular systems and techniques sensitive to proton location, like neutron scattering, are rarely used within drug design projects. However, by looking at pK_A values for related molecules it becomes evident that p-phenylenediamine is significantly more basic (pK_A = 6.2) than the m-phenylenediamine with a pK_A of 4.98,⁴² indicating that compound C is much easier to protonate than compound D at physiological pH. This is corroborated by the pK_A calculations of the protein-complex. In terms of biomolecular recognition the position of the amino group in para-position (N–O distance 2.8 Å) is closer to the carboxyl group of the aspartate than the amino group in the meta-position (N–O distance 3.5 Å). The difference in the pK_A values might also influence the solvation thermodynamics as the amount of the respective protonated species differ between the two compounds. However, the absolute number of protonated species is considered small and therefore these contributions are likely to be minor without a stabilizing functional group in vicinity. While at the first glance the change of the amino group from ortho- to meta-position does not seem to be significant, it fundamentally changed the properties of the molecule.

To further analyze the idea that the compound can be protonated we used the LIE tool of the AmberTools package.²⁹ We wanted to choose a method which explicitly includes the interaction of the protein and the ligand, as this kind of interaction is omitted by the GIST analysis.

To obtain the difference between the interaction energy of the ligand in complex and as free ligand two simulations were necessary. The enthalpic difference between the two states here is the value of interest. Further, we are interested in the change of binding energy between protonated and unprotonated state (shown in the last two columns of Table 3). As expected, the results show that the interaction between the ligand and the surrounding (protein and water) is enhanced when the ligand is protonated for both binding poses. Still, the gain in (more favorable) interaction energy for position C (−15.8 kcal/mol) is higher compared to the gain in pose D (−10.8 kcal/mol) for compound C. It is likely that this gain in enthalpy is responsible for the binding pose change. For binding pose C this enthalpic gain helps to compensate the entropic penalty of the water molecules in the buried pocket and therefore stabilizing the binding pose of compound C. For both binding poses of compound D, we see a gain in interaction energy similarly to compound C in position C (16.2 and 16.0 kcal/mol). In contrast to compound C, compound D is much more difficult to protonate and therefore the energy gain may not be enough to compensate for the energy necessary for the protonation.

Table 3. Results of the Linear Interaction Energy Calculations of Protein–Ligand Interactions ΔU (kcal/mol) for Compounds C and D.

		ligand
		neutral		positive		difference
ΔU		C	D	C	D	C	D
pose	C	–5.3	–6.7	–21.2	–22.9	–15.8	–16.2
	D	–3.4	–11.8	–14.2	–27.8	–10.8	–16.0

Looking at Table 3 from a different angle: Although we already see that in the neutral form compound C slightly prefers pose C (−1.9 kcal/mol), this could be in the range of the method’s error. The preference enhances for the positive form of compound C and is significantly larger (−7.0 kcal/mol) than the error of the method. For compound D, we found a preference for pose D over pose C (≈5.0 kcal/mol) for both the positive and neutral form.

Further evidence that the preference of the neutral compound C for pose C is not significant brought the application of the MM/PBSA method to this problem.⁴³⁻⁴⁵ With this method we found that compound C prefers pose D in the unprotonated state by 6 kcal/mol, whereas for the charged compound we could not find any preference (Δ < 1 kcal/mol) for one of the two binding poses. Similar results were obtained with MM/GBSA. This finding further supports our hypothesis that compound C has to be protonated, when it is found in pose C.

Enthalpy (LIE) calculations without solvent and further information about the MM/GB(PB)SA calculations are given in the SI.

To summarize: Binding pose D is favorable for compound D, not only but also due to entropic contributions from the water molecules being (the phase space water molecules can occupy) more favorable than in pose C. Hence, the binding pose of compound D is to a large extend determined by the entropic contribution of the water molecules. This explains how water can influence the affinity and specificity of ligand binding sites.⁴⁶ The importance of water for ligand binding is already well established.⁴⁷ In the presented case the replacement of entropically hindered water with respect to bulk results in a gain in free energy. In contrast, there are cases reported in literature where the enthalpy gain by formation of a water mediated hydrogen bond is larger than the entropic cost of restricting the phase space of the water molecules.¹³

For binding pose C, the entropy of the water molecules in the binding pocket is unfavorable in comparison to the water molecules in pose D, but compound C is protonated, leading to strong enthalpic interactions. These contributions overcompensate the entropic energy penalty. Therefore, pose C is dominated by the enthalpic contributions to the free energy. This highlights that entropy and enthalpy are both important for ligand binding. Our findings confirm once more that ligand binding depends on the balance between entropy and enthalpy. The relative importance of the enthalpic and entropic contribution might change dramatically upon subtle modifications in ligand chemistry. Our study also highlights the already known fact that enthalpy alone is not a good measurement for free energy,¹⁸ a fact often forgotten in medicinal chemistry when focusing solely on direct protein–ligand contacts.

Furthermore, the pH effect on binding affinities and binding modes is often neglected. Indeed, the protonation state and the binding affinity are linked together. The pK_A of a ligand influences the binding affinity and selectivity, but also the binding of a ligand affects the pK_A of the ligand and the protein,⁴⁸ as shown in this study.

Conclusion

Our analysis shows that the combination of in silico analysis tools can unravel the origin of different binding poses. The present study provides an explanation of binding modes and rationalizes, based on thermodynamics, the observed binding mode flips. We show how a minor change in the structure of a ligand leads to major structural changes, which could result in a misinterpretation of structure–activity relationships. The binding pose of compound D is by a large extend determined by releasing entropically unfavored (with respect to bulk water) water molecules from the binding pocket into bulk upon binding. For a second compound C, very similar to the first one, the binding mode is determined by the enthalpic contributions of ligand binding. The enthalpic interactions that play a key role in one of the binding poses are strongly related to the protonation of the amino group in this ligand. We encourage to carefully investigate protonation states, if functional groups are present which may or may not be protonated in the environment of another charged group with opposite sign. Seemingly subtle changes in the chemical structure can significantly alter the physicochemical properties of certain groups. As the obtained results go beyond the limit of chemical intuition, the computational methodology presented can be of value for medicinal chemistry programs.⁴⁹ The investigated TGFBR1 kinase domain binding mode flip is not an isolated case. Similar observations are reported in the literature but are usually discovered by serendipity.¹

The enhanced thermodynamic understanding of such binding flips can help to improve binding pose prediction of unknown ligands. While we have to admit that the extensive study presented here is most likely beyond the scope of typical drug design programs, the ligand binding poses analyzed here would most likely not have been correctly predicted by any state-of-the-art structure-based drug design methodology. Nevertheless, such challenging cases can be used to strengthen our ability to accurately predict binding modes and binding mode flips.

Glossary

Abbreviations

TGFBR1

Transforming Growth Factor Beta Receptor Type 1

LIE

Linear Interaction Energy

GIST

Grid Inhomogeneous Solvation Theory

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jcim.6b00483.

• Partial atomic charges of all parametrized ligands, additional enthalpy calculations without solvent, and further information about the MM/GB(PB)SA calculations (PDF)

Author Present Address

^⊥ C.K.: F. Hoffmann–La Roche AG, Pharma Research and Early Development, Therapeutic Modalities, Roche Innovation Center Basel, Grenzacherstrasse 124, 4070 Basel, Switzerland.

Author Present Address

^∥ J.E.F.: Boehringer Ingelheim RCV GmbH & Co KG, Doktor-Boehringer-Gasse 5-11, 1120 Vienna, Austria

The authors declare no competing financial interest.