Cell signaling as a cognitive process

Abstract

Cellular identity as defined through morphology and function emerges from intracellular signaling networks that communicate between cells. Based on recursive interactions within and among these intracellular networks, dynamical solutions in terms of biochemical behavior are generated that can differ from those in isolated cells. In this way, cellular heterogeneity in tissues can be established, implying that cell identity is not intrinsically predetermined by the genetic code but is rather dynamically maintained in a cognitive manner. We address how to experimentally measure the flow of information in intracellular biochemical networks and demonstrate that even simple causality motifs can give rise to rich, context‐dependent dynamic behavior. The concept how intercellular communication can result in novel dynamical solutions is applied to provide a contextual perspective on cell differentiation and tumorigenesis.

Introduction

Cells require encapsulation to spatially organize their chemical constituents such that the time and place of molecular interactions are a necessary determinant of their effect (Farnsworth et al, 2013). Under such confinement, they can control the flow of matter and energy, thereby maintaining themselves in entropy‐dissipating non‐equilibrium conditions (Schrödinger, 1944; Prigogine & Nicolis, 1967). This enables information to be concentrated in cells in a form of self‐organizing chemical activity patterns (Turing, 1952; Grecco et al, 2011). The cells continuously adjust these internal states to allow for robustness in identity under changing external conditions, especially to unfamiliar changes for which no regulatory program has been fixed in advance (Ibarra et al, 2002; Fong & Palsson, 2004; Kashiwagi et al, 2006; Stolovicki et al, 2006). Such flexible dynamics therefore implies that genes serve as repositories of dynamic control information regarding the combination of interacting proteins that define a stable phenotypic state. Distinct biochemical manifestations of this information pool reflect proteome plasticity: In multicellular organisms, all cells contain nearly identical copies of the genome but exhibit drastically different phenotypes. This principle also accounts for efficient adaptation on evolutionary as well as short timescales, and implicitly incorporates the “tinkering” aspect of biological systems (Jacob, 1977). Cells thereby define a wider dynamical domain in which they can interact with their environment to generate and maintain their identity, a process reminiscent to cognition (Box 1; Maturana & Varela, 1980). In a very general formulation, cognition can be defined as a set of processes that are in a structural coupling with the environment such that the system adapts to its environment or transforms the environment to adapt it to the “needs” of the system (Bourgine & Stewart, 2004). In terms of living systems, cognition is realized via recursive chemical communication of intracellular signaling networks between cells. Thus, processing external chemical cues on the level of intracellular networks, and at the same time emitting the information about their state to the neighboring cells, allows cellular entities in tissues to establish a collective behavior to maintain themselves. Depending on the conditions, the behavior of this network of signaling networks converges to one of multiple stable dynamical solutions that can differ from those in isolated cells.

Box 1: Cellular cognition.

In the 1980 book “Autopoiesis and Cognition—the realization of the living”, H. Maturana and F. Varela defined living systems as “… units of interactions, they exist in ambience. From a purely biological point of view, they can not be understood independently of the part of the ambience with which they interact: the niche; nor can the niche be defined independently of the living system that specifies it” (Maturana & Varela, 1980). On the basis of this concept, Maturana then defined cognition as a process driven by structural, bidirectional causal organism–environment relations that are necessary to understand coding and information transmission in living systems. In 1993, J. Stewart related the concept of cellular cognition to the characteristics of the immune system within a living organism in order to encompass its properties of recognition, learning, memory, and self/non‐self discrimination into one theoretical framework (Stewart, 1993). He discussed these properties in relation to neuronal systems and higher‐order cognition. Later on, Bourgine and Stewart proposed that living systems must be both autopoietic and cognitive, providing more refined definitions for these concepts. In their view, an autopoietic system is “a network of processes that produces the components that reproduce the network, and also regulates the boundary conditions necessary for its ongoing existence as a network”. Moreover, “A system is cognitive if and only if sensory inputs serve to trigger actions in a specific way, so as to satisfy a viability constraint” (Bourgine & Stewart, 2004).

Cells therefore necessitate both autopoiesis and cognition (Maturana & Varela, 1980) to generate and dynamically maintain heterogeneous cellular identities in tissues. Autopoiesis is a necessary characteristic of living systems to replicate the components and reproduce the architectures of biochemical networks, thereby maintaining themselves and the boundary conditions necessary for their own existence (Bourgine & Stewart, 2004). Cognition on the other hand is required to differentiate the replicated entities through the dynamics of the network of networks that is established through bidirectional intercellular communication (Fig 1). In this way, cognition is a property that emerges from recursive interactions between the signaling networks of cells.

Figure 1. Differentiating cellular identities in a multicellular population.

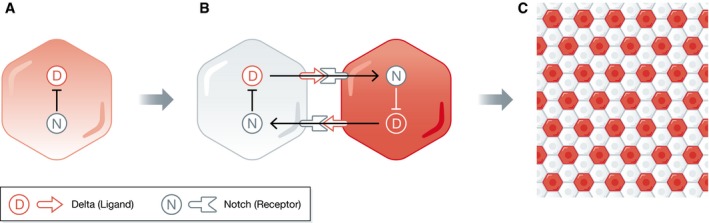
Schematic representation of the core Notch signaling architecture where identical cells adopt two different fates due to intercellular communication. The Notch protein (N) is a transmembrane receptor that binds to its ligands Delta (D) that are anchored on the membrane of neighboring cells. (A) On a single‐cell level, Notch activity inhibits Delta expression. (B) When cells interact via the Delta–Notch system, it becomes one network with an effective double‐negative feedback topology that generates bistability. Starting from a homogeneous population in terms of Delta expression, the lateral inhibition mode will drive the system to a new dynamical state where neighboring cells will adopt opposite fates of high and low Delta expression. (C) Due to this inhibitory bidirectional communication, a salt‐and‐pepper pattern is generated on the population level. The red intensity is related to the amount of ligand, whereas cells without a ligand are white.

Based on this framework, we discuss what determines the dynamics of signaling networks and how this information can be extracted experimentally. We start by considering undirected protein interaction networks derived from proteomic approaches. We argue that temporal behavior of the protein reactants is necessary to deduce the causality of intracellular networks and thereby their dynamical potential. From there, we describe how intercellular communication endows the system with cognitive properties, generating new dynamical behavior different than the one in the isolated cells. As an example, we elaborate on a Turing‐like principle that accounts for the emergence of diverse identities in a clonal cell population. In this context, we also discuss how the collective behavior in a normal tissue can be affected by changes in the cognitive abilities of cells induced upon oncogenic mutations. Thus, by considering cellular identity to be dynamically maintained by recursive interactions, we explore whether cells can learn to perceive their environment and thereby change their identity.

What protein interactions tell us about cellular states

Current proteomic approaches allow quantitative detection of protein abundances and protein reactions in terms of protein complexes and post‐translational modifications (PTMs) in ensemble of cells (Cox & Mann, 2011; Larance & Lamond, 2015) (Box 2). The protein abundances provide the composition of the proteome reflecting the gene expression in a particular cell population that is studied in a distinct experimental context. The detection of protein complexes and/or PTMs on the other hand gives access to the basic reactions—the currency of signal transduction—through which the cells process extracellular information. A major advantage of all proteomic approaches is that hundreds to thousands of protein complexes or PTMs can be simultaneously and rapidly analyzed. In case of protein interaction maps, the nodes of the obtained protein interaction networks represent the proteins under study and the links or the edges represent their physical interactions (Gavin et al, 2002; Völkel et al, 2010). These interactions can be both, direct or indirect, since there is no clear separation criterion in the case when several proteins are part of an isolated complex. However, even if all possible PTMs/interactions could be obtained experimentally, this single (static) proteomic snapshot does not provide sufficient information to identify how processing of distinct signals determines the cellular phenotype (Fig 2A). The temporal component is therefore a necessary experimental prerequisite to identify which proteins alter their interactions in response to external stimuli because signals propagate through changes in the reaction states of the network components (Von Kriegsheim et al, 2009; D'Souza et al, 2014; Francavilla et al, 2014; Humphrey et al, 2015).

Box 2: Proteomic approaches to derive protein interactions.

Three main proteomics‐based approaches allow for systematic, large‐scale identification of protein–protein interactions (Larance & Lamond, 2015): (i) methods based on affinity pull‐down where the protein of interest and its interacting partners are specifically isolated. The protein complexes are then eluted for subsequent analysis by digestion and liquid chromatography followed by tandem mass spectrometry (LC‐MS/MS). (ii) Proximity labeling methods in which cell lines are constructed that ectopically express a protein of interest fused to either a promiscuous biotin ligase or a peroxidase enzyme that can further covalently transfer biotin labels to potential interacting proteins in close proximity. LC‐MS/MS methods are further used to identify the corresponding protein interaction map. (iii) Protein interactions can also be identified by protein correlation profiling with chromatography and density gradient centrifugation, for example, to separate endogenous protein complexes according to size, density, charge, or hydrophobicity, assuming that interacting proteins will co‐elute.

The obtained interactions using proteomic approaches can represent both, direct and indirect connections, since it is not always clear whether an identified multiprotein complex is one complex or the summation of different sub‐complexes that contain the same building blocks. By extracting protein complexes from cell lysates, spatial constrains imposed by supramolecular assemblies (like membranes or cytoskeletal structures) on protein complexes are also obliterated. This might result in the loss of complexes that are dependent on the integrity of supramolecular structures as well as generate non‐physiological interactions due to mixing of all components. In addition, information on cell‐to‐cell variability in proteome composition and molecular reactions is lost.

Figure 2. Different perceptions of protein interaction networks.

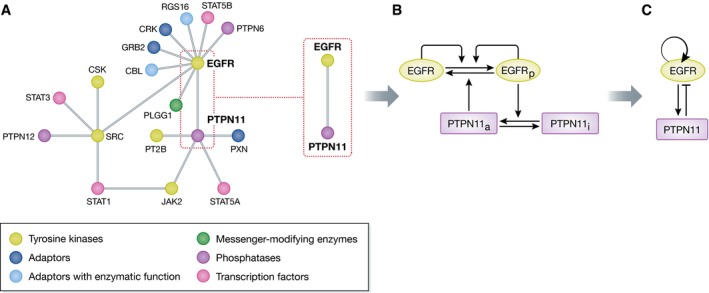
(A) Schematic representation of a subset of the epidermal growth factor receptor (EGFR) interaction network as obtained from proteomics approaches (adapted from Kiel et al, 2013). In this case, the edges represent any form of interaction and the nodes represent the proteins. This type of representation provides information, which proteins work together to generate cellular functionality, but do not allow to extract information on this functionality. (B) One interaction between EGFR and a protein tyrosine phosphatase PTPN11 (SHP2) is highlighted for which the complete details of the chemical conversions (horizontal arrows) and the causalities between the communicating chemical intermediates (vertical arrows) are depicted. (C) The causality alone is sufficient to identify all possible dynamical solutions of the two component network module and describe its functionality.

What is relevant to note here is that after killing the cells to extract protein complexes, the derived interaction maps reflect the state of the cell in equilibrium conditions. Even if the fixation of the cells would be so rapid that the proteome cannot relax to equilibrium, the obtained snapshots of the temporal evolution of the reaction states in the proteome represent only one of many possible dynamical solutions of the network. Therefore, no knowledge can be gained how information flows in the network to realize these states. To obtain this level of information, it is necessary to deduce the causal relationships between protein reactions in the proteome.

Causality determines the dynamics of biochemical networks

Causality in biochemical systems is generated when protein reaction states or complexes can affect the interaction or reaction of other proteins. In this manner, directional activatory or inhibitory effects on each other's chemical conversions are established (Fig 2B) (Sachs et al, 2005; Zamir & Bastiaens, 2008). The directionality of the interaction determines how the information flows through the system, processing and translating external cues into specific cellular behavior. This type of representation is referred to as “network topology”, where each node represents a chemical intermediate of a reaction and the directed edges the positive or negative influence of one node on another (Fig 2C).

To illuminate how the topology of molecular networks determines their dynamical behavior (Brandman et al, 2005; Santos et al, 2007; Ryu et al, 2015), we start with the autocatalytic phosphorylation cycle as it typically occurs in receptor tyrosine kinases (Lemmon & Schlessinger, 2010). This reaction cycle has only one stable dynamical solution, which is the phosphorylation steady state of all receptors. This state is dynamically maintained since a constant ATP input is required to sustain the phosphorylation at a certain level, when phosphatase‐mediated hydrolysis removes the phosphates from the tyrosine residues (Fig 3A) (Ostman & Bohmer, 2001). Things become more interesting if the activity of the phosphatase (PTP) is coupled to that of the RTK via Rac‐induced NOX complex activation, which in turn generates reactive oxygen species (ROS), thus inactivating the PTPs (Denu & Tanner, 1998; Finkel, 1998; Meng et al, 2002). This reaction scheme generates a toggle switch—or double‐negative feedback loop—that together with the autocatalytic RTK activity can give rise to bistable behavior (Reynolds et al, 2003) (Fig 3B). In this system, there are three solutions: two dynamically maintained low and high RTK phosphorylation states, both of which are stable and can coexist in a given parameter interval, and an unstable solution that acts as a threshold in the system. In which stable solution the system will end up is directly related to the initial conditions, that is, the initial phosphorylation level of the receptor. In a cellular context, this might be dependent on the history of the cell in terms of prior growth factor‐induced signaling states. When these simple networks interact in a recursive bidirectional way between cells, novel dynamical states can be generated and maintained, different than those of isolated cells. This principle that resembles a cognitive process is further elaborated in the section “Recursive communication between cells leads to cognition”.

Figure 3. Dynamical properties of biochemical networks are determined by their underlying causality.

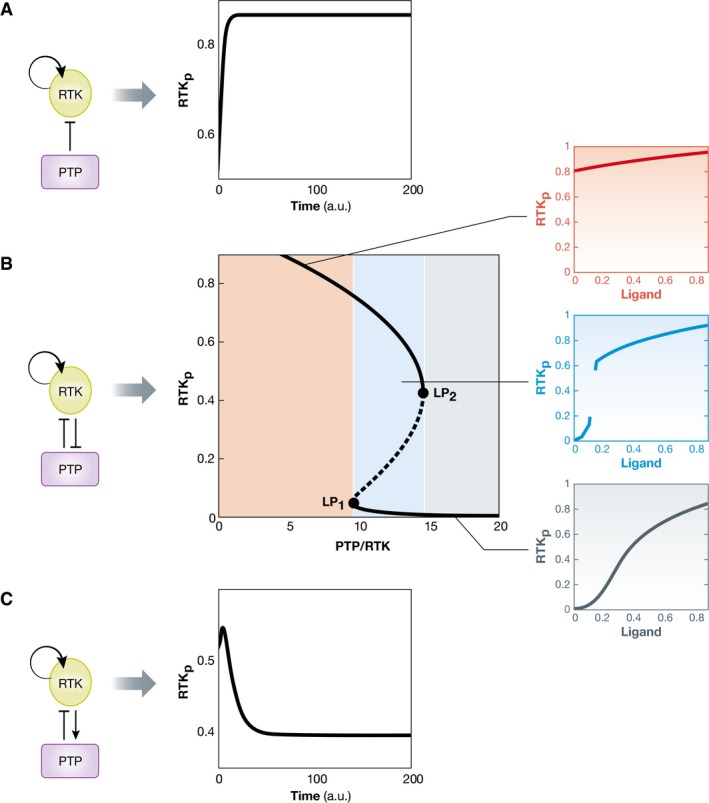
(A) Autocatalytic RTKs that are inactivated by protein tyrosine phosphatases have only one dynamically maintained steady‐state solution that is determined by the PTP activity. (B) If the activity of the phosphatase is coupled to that of the RTK in a double‐negative feedback manner, the RTK–PTP system can exhibit a rich behavior that depends on the PTP–RTK expression ratio. The bifurcation diagram (middle) shows the three possible solutions as a function of this ratio: two stable steady states (solid black lines) and an unstable steady state (dashed line). The parameter interval between the two bifurcation points (LP) denotes the bistability region. The activation dynamics of the receptor upon growth factor stimulus will be determined by the positioning of the system in parameter space (PTP–RTK ratio). At high PTP–RTK ratios, the system responds in an analog manner to growth factor stimulation. In the intermediate (bistability) interval, the system generates an all‐or‐none response with a threshold to growth factor. Upon RTK overexpression, the system is already switched on and responds in a shallow analog manner to growth factors. (C) A negative feedback RTK–PTP interaction results in a single dynamical solution that results in an adaptive response to growth factor.

On the other hand, if the interaction between the RTK and the PTP is defined by a negative feedback, the system will have a unique dynamical solution that maintains low levels of phosphorylation of the receptor (Fig 3C). Typical examples of phosphatases that could work in this way are the cytosolic phosphatases Shp1/2 that are activated by binding to phosphotyrosine residues via an SH2 domain (Barford & Neel, 1998; Keilhack et al, 1998).

The response of both systems (toggle switch and the negative feedback) to growth factor stimuli is thus uniquely determined by their respective topology. In case of the toggle switch coupled to an autocatalytic RTK activation, a small amount of the ligand will initially activate a small amount of receptors. This activated fraction however will suffice to push the system over the threshold and fully activate all other receptors (Reynolds et al, 2003). An irreversible situation is thereby generated in which all receptors remain active (Fig 3B). In the case of the negative feedback however, the system will tend to relax back to the original low phosphorylation state after stimulation and therefore lead to a pulse of receptor activity—an adaptive response (Fig 3C) (Tyson et al, 2003). Signal duration is therefore commonly regulated via negative feedback motifs.

The above examples show how intracellular network topology gives rise to differential dynamics in single cells, and even plasticity in signaling responses to growth factors. This description does not require the full details of the reactions that generate the communicating chemical intermediates, but only the directionality and type of interactions (Fig 2B and C). The relation between dynamics and causality (and vice versa) is however not a one‐to‐one mapping (Box 3). A given dynamical behavior can result from several different network topologies (Kirshna et al, 2009), but also a single network can display multiple stable dynamical solutions (Koseska et al, 2007). In the formulation of dynamical systems theory, these solutions are called attractors (Box 4) (Strogatz, 2001). Each attractor represents a distinct state of the system in phase space (Strogatz, 2001) that is stable within a given parameter range. This basin of stability reflects the robustness of the dynamical solution to external perturbations or stochastic fluctuations (Menck et al, 2013). Characteristic network topologies that display a rich phase space combine activatory and inhibitory interactions (Kirshna et al, 2009; Kaluza & Meyer‐Ortmanns, 2010). In particular, the ratio between the two types of causal interactions suggests whether the system can have multiple dynamical solutions (Kaluza & Meyer‐Ortmanns, 2010; Hong & Strogatz, 2011; Levnajić, 2012). Thus, cells use simple network motifs as building blocks to generate multiple attractors that enable flexibility in the responsiveness of the system. This implies that even genetically identical cells can respond differently to input signals because they are in different attractors, as dependent on initial conditions. For example, two completely identical cells that contain the RTK–PTP toggle switch discussed above can have two opposed states of the RTK: fully on or off (Fig 3B). Which of the two states is attained depends on the history of the cell as conditioned by previous stimuli. The same two states can be also observed in a population of genetically identical cells with different RTK–PTP expression levels due to the naturally occurring variance in protein abundances that results from gene expression noise. Thus, the multiple attractors that can arise from a fixed network configuration provide plasticity to the system.

Box 3: Network topology and dynamics.

The possible dynamical solutions of a given network are determined by the underlying topology (directed activatory or inhibitory links) and the dynamical behavior of the chemical intermediates that represent the nodes of the network. Let us consider a simple case of two interacting components: Protein X stimulates its own production (positive feedback) and that of protein Y, whereas Y inhibits X by transcriptional or translation regulation, or degradation. The positive feedback from X to itself generates bistable behavior that can be observed for different maximum rate production (Angeli et al, 2004; Mitrophanov & Groisman, 2008). Generating the negative feedback loop between X and Y on the other hand establishes the necessary preconditions for oscillations. For a particular dynamics of the nodes, for example, when the half‐life of the protein Y is smaller than that of X, oscillatory behavior will be observed (Kirshna et al, 2009).

Figure for Box 3. Relationship between network topology and dynamics.

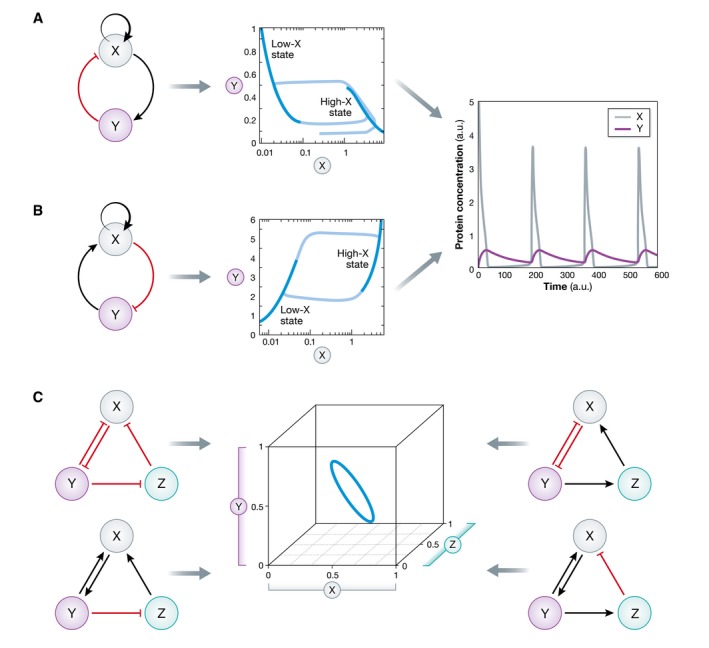
(A, B) Two distinct negative feedback network topologies give rise to the same dynamical behavior: oscillations. (C) Subset of three‐component network modules that give rise to the same limit cycle representation in phase space.

How does the dynamics of this system evolve? In the absence of the negative feedback loop, namely Y is held fixed and the system is bistable for a certain range of Y values. Thus, depending on the initial conditions, the system will be either in high‐ or low‐activity states of protein X (dark blue lines). When the regulation from X to Y is established, the system displays oscillatory behavior: When the underlying bistability pushes X toward the high activity state, more Y is produced leading to a decrease in X, and vice versa for the low state, enabling the oscillations to continue (light blue lines).

Different causal relations however can give rise to the same dynamical behavior like bistability and oscillations as shown in (B). The degeneracy of the problem further increases with increased number of nodes in the network (C).

Box 4: Concepts from dynamical systems theory.

Consider a cellular state that is specified in terms of the concentrations of the active protein states. For example, if upon a given stimulus, k signaling proteins are activated, the cellular response, and thereby its state is described by the concentrations of those proteins (x(t), y(t), z(t), …) over time. One state of the system, that is, one combination of these proteins represents a point in vector space that is called phase space. The dynamics of the system is then described by the dynamics of the corresponding phase space points in terms of their trajectories. With time, the phase variables reach a stable range of values. This bounded region of phase space is called attractor and represents dynamical solution of the system that is invariant with time. The attractors can be fixed points representing stationary states, limit cycles (periodic oscillations), and strange attractors (chaotic behavior). Different dynamical solutions that a system can reach depending on the initial values of the variables are represented as different attractors in phase space. Staring from a given set of initial values, the system will tend to evolve toward a particular attractor. The regions of such initial values, called basins of attraction or basins of stability, partition the phase space around the stable attractors. The system can therefore jump between different attractors if large enough perturbations are applied.

Figure for Box 4. Dynamical systems.

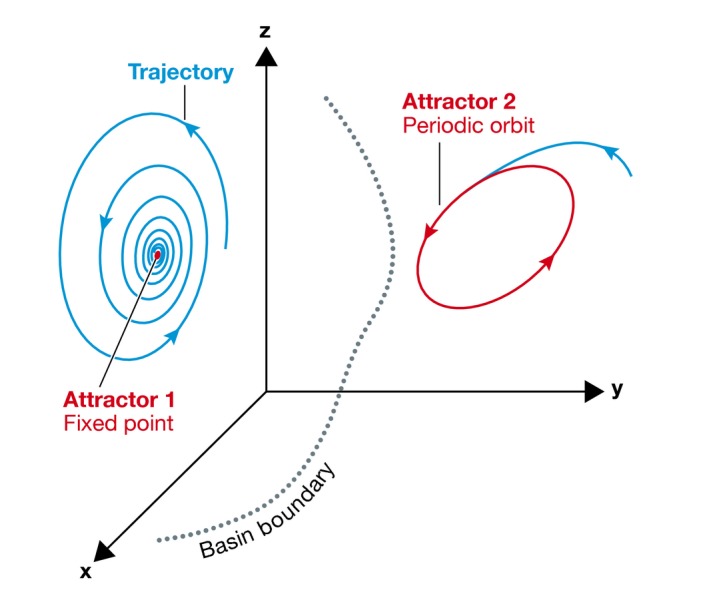
The dynamics of a cellular state that is specified in terms of concentration of three proteins (x, y, z) can be fully described through the evolution of the trajectories in phase space. Different stable dynamical solutions (attractors) are separated by their corresponding basins of attraction.

An additional level of plasticity is realized when causal connections are conditioned by other ones. The conditioning can be stimulus dependent, enabling diverse signals to be processed through the same cascade. An example is the mitogen‐activated protein kinase (MAPK) cascade of Raf, Mek, and Erk (Marshall, 1995; Lewis et al, 1998), where the phosphorylated active forms of the kinases represent the communicating intermediates of the nodes (Kholodenko et al, 2002). The positive feedback between Erk and Raf in this case is conditioned on nerve growth factor (NGF)‐dependent protein kinase C (PKCδ) phosphorylation of Raf kinase inhibitor protein (RKIP) that removes it from Raf (Santos et al, 2007). In network formalism, this directed link is not between the two nodes RKIP and RAF, but rather the interaction between PKCδ and RKIP enables the causal interaction between Erk and Raf to take place (Fig 4). This results in a sustained Erk activity profile. On the other hand, epidermal growth factor (EGF) stimulation does not lead to PKCδ activation and only the negative feedback between Erk and Raf manifests. This now results in a transient Erk activity profile. This NGF/EGF stimulus‐dependent conditioning of the causal interactions thus leads to different MAPK dynamics that cause cellular differentiation and proliferation, respectively. Recently, it has been postulated that this negative feedback is also conditioned on the activity of the epidermal growth factor receptor, which might further discriminate the two input signals by the MAPK module (Ryu et al, 2015).

Figure 4. Conditional causal interactions increase signaling plasticity.

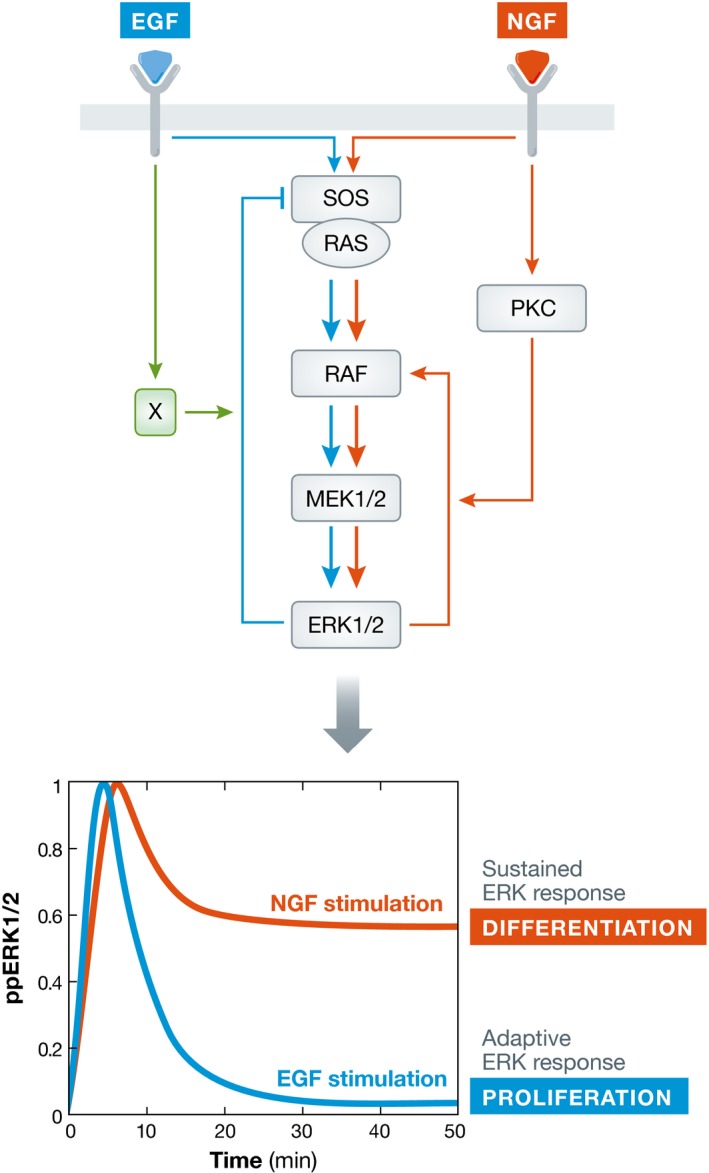
Signal‐dependent conditioning of causal interactions leads to difference in effective network topology that manifests by distinct Erk response profiles. This in turn leads to different cellular fates in PC12 cells: proliferation (EGF, adaptive Erk response) and differentiation (NGF, sustained Erk response).

Understanding how a given dynamical behavior arises necessitates network reconstruction to identify the underlying topology of the network. This information then allows to investigate the potential of cells in terms of dynamical solutions and thereby their plasticity in responses.

Deriving causality from dynamics

It is exactly the dynamical behavior of the system's components, that is, the active states of signaling molecules as a function of time, that is the subject of experimental observation (Santos et al, 2007; Ryu et al, 2015). Importantly, the observed dynamical responses of the nodes do not reflect the kinetic properties of the molecules in isolation, but rather the dynamics of the network in which they are embedded. A given measurement reveals only one dynamical solution that the protein interaction network can exhibit, which is dependent on the initial conditions of the nodes. To reconstruct a causal network from this dynamics of its constituents, it is necessary to exploit the property that coupled events have temporal order. One possibility is to impose a causal relation of a “driver component” and a “response component” on the nodes.

This is accomplished by combining experimental perturbations with observations of the chemical intermediates. The perturbations need to be small, to maintain the system in the same dynamical solution. Quantification of the corresponding changes in the nodes in terms of global response coefficients allows reconstructing the underlying causal relationships by computing the local response coefficients using Modular Response Analysis (MRA, Box 5A) (Bruggeman et al, 2002; Santos et al, 2007; Klinger et al, 2013). In reality, the dynamics of only a limited set of nodes is observed within the context of the complete proteome. MRA allows uncovering the causal interactions between the measured nodes, as conditioned by the unobserved components of the proteome. It is therefore necessary to consider whether chronic genetic perturbations alter the context of the hidden network by affecting gene expression. Genetic perturbation should be thus ideally complemented by acute perturbations using, for example, small molecule inhibitors, pharmaco‐ or optogenetic perturbations that maintain the same proteome context (Zamir & Bastiaens, 2008; Toettcher et al, 2013; Kim et al, 2014).

Box 5: Principles of network reconstruction.

Figure for Box 5. Methods for network reconstruction.

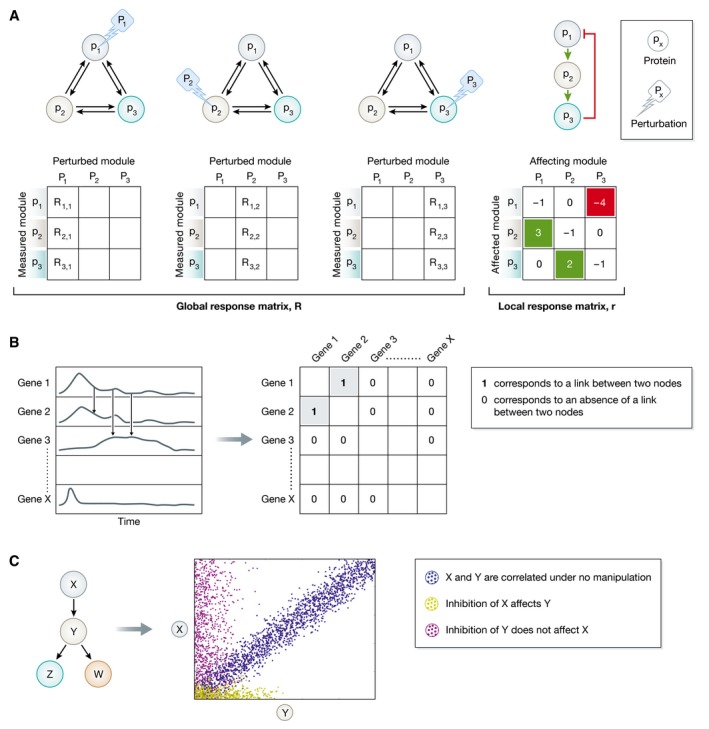
(A) Schematic representation of MRA (adapted from Zamir & Bastiaens, 2008). The upper left graphs depict a network of three proteins (p₁, p₂, p₃) for which network reconstruction is applied to uncover the strength and sign of the six possible causal connections. Perturbing (P_i) each of the nodes and measuring the corresponding response of all nodes in the network allows to obtain the nine global response coefficients from which the local response coefficients are computed. These indicate the causal connectivity strength in both directions between p₁, p₂, and p₃ (right graph). (B) Schematic representation of time series measurements as obtained from a transcriptomics experiments (left chart). To reconstruct the gene regulatory network, the pairwise similarity between the time series is calculated. This allows generating an association matrix (right table) from where the links between the nodes can be deduced. 1 corresponds to a link between gene 1 and gene 2, and 0 corresponds to an absence of an edge between the two nodes. (C) Simplified representation of how Bayesian network operates on a hypothetical network of four proteins, X, Y, Z, and W, as adapted from Sachs et al (2005). Each dot represents the amount of two phosphorylated proteins (X and Y) in a single cell. X and Y are correlated under no manipulation (blue dots). Inhibition of X affects Y (yellow dots), whereas the opposite is not true (magenta dots). This reveals the directionality of the interaction from X to Y.

A. To reconstruct a causal network from the dynamics of its constituents, the property that coupled events have temporal order is exploited. Modular Response Analysis (MRA) uses this principle by imposing causality on the system via sequential node perturbations (Bruggeman et al, 2002). The corresponding changes in the remaining components of the system are thereby quantified as a means to infer directional relationships between the nodes in the network. One can thus measure the response of protein p_i to the perturbation in protein p_j (P), as mediated by the entire network after reaching a steady state. From this global response coefficients (R_ij = ∂p_i/∂Ρ) matrix, the local response coefficients r_ij = ∂p_i/∂p_j indicating the causal connectivity between p_i and p_j can be derived according to ∑r _ik R _kj = 0. r_ij > 0 indicates activatory links, r_ij < 0 inhibitory links, and r_ij = 0 no direct links between the nodes p_i and p_j.

B. Stepwise network inference from time‐resolved data can be also accomplished using association measures. At a distinct time point after stimulus, the extent of modification of some property of the nodes, that is, gene expression or protein phosphorylation, is measured for all nodes simultaneously. Experimental acquisition of this information at n (non)uniformly distributed time points thereby reflects the dynamics of each of the nodes in the network. Since the temporal profiles of two nodes that regulate each other are similar, the regulatory links can be derived by thresholding the pairwise similarities in the association matrix. Measures operating on vectors, such as classical distance measures and dynamic time warping, random variables (correlations, permutation‐based and information‐theoretic measures), model‐based measures (Granger causality) and measures operating on symbolic dynamics can be used to derive the association matrix (Hempel et al, 2011a). Applying additionally partial variants of the measures to account for indirect regulations and scoring rules for the pairwise weighting of the interactions, the number of falsely identified links can be reduced (summary on the methods and scoring schemes is presented in Hempel et al, 2011a). Since the majority of these methods and scoring schemes are symmetric, it is necessary to apply time shifting or symmetry breaking schemes to infer the causality of the identified links.

C. Bayesian networks, a form of graphical models, have been also used to reconstruct causal signaling networks from multivariate datasets, for example, the phosphorylation state of multiple proteins in a same cell. They explicitly make use of the naturally occurring cell‐to‐cell variance, since Bayesian networks can represent probabilistic non‐linear dependence relationships among multiple interacting components. The analysis algorithm therefore approximates the network topology that closely predicts the made observations by traversing the space of possibilities via single‐link changes that improve the score of the model (Sachs et al, 2005). Although the obtained relationships are statistical in nature, causality of the interactions could be obtained when experimental perturbations are additionally applied.

Applying MRA to reconstruct large‐scale networks is however experimentally challenging, since the number of combinations between perturbations and node observations scales quadratic with the number of nodes (Box 5A). Therefore, other methods that uncover the asymmetry of causal interactions without necessarily using perturbations are required to deduce topology. This can be achieved by applying asymmetric measures to time‐resolved biochemical reaction data. In these approaches, the similarity between the activity profiles is quantified, while implicitly or explicitly accounting for time delays in the responses of the nodes (Box 5B). Similarly to the reconstruction of gene regulatory networks (Wang et al, 2008; Hempel et al, 2011a,b; Ma et al, 2014), it is possible to apply these methods to time‐resolved proteomics data to identify the flow of information in the system. Currently, all of the time series analysis methods have a limited accuracy in the number of identified links (~80/30% true/false positives). This strongly depends on the size of the network and the temporal resolution of the measured profiles (Hempel et al, 2011b). To compensate for the limited information contained in sparsely sampled time series, the activity states of several proteins have been simultaneously measured in single cells (Sachs et al, 2005; Kirshnaswamy et al, 2014). By having hundred individual cells, each providing a point of multidimensional data, cell‐to‐cell variability has been used to infer and quantify (non)linear relationships between proteins using different statistical approaches. For example, Bayesian analysis (Box 5C) has been applied to reconstruct protein interaction networks from primary human immune system single‐cell data obtained by flow cytometry (Sachs et al, 2005). The cell‐to‐cell variability in the measured activity state of multiple phosphorylated proteins and phospholipid components as obtained by node perturbations has been incorporated in a Bayesian model to derive probabilistic dependences among multiple components. In another study, conditional density‐based analysis of single‐cell mass cytometry data has been developed to identify and quantify the functional dependencies between proteins that participate in antigen recognition in cells of the immune system (Kirshnaswamy et al, 2014). The next challenge will be to combine the associations between multiple network components obtained at distinct time points in a single measure. This would provide a theoretical framework that combines the information contained in the cell‐to‐cell variance with the information that the temporal profiles encode, resulting most likely in more efficient methods for reconstruction of causal protein interaction networks.

Recursive communication between cells leads to cognition

In the previous examples of signaling network reconstruction, external growth factors were imposed, thereby enforcing a unidirectional information flow from the environment to the inside of the cell. However, the collective behavior of cells that leads to coordinated dynamical behavior, such as the behavior of cells in an organ or a tissue (Perbal, 2003; Harper et al, 2010), requires constant adjustment of the internal state by not only signal reception, but also emission of information about the internal state to neighboring cells. This iterative exchange of information that occurs via cell‐cell communication can therefore give rise to cooperative cellular behavior even under noisy conditions (Koseska et al, 2009; Box 6). For example, most physiological events in mammals are subjected to well‐controlled daily oscillations that are generated by an internal self‐sustained circadian oscillator located in individual neurons in the hypothalamic suprachiasmatic nucleus (SCN) (Welsh et al, 1995; Moore, 1997). In this case, a coherent and synchronous circadian output is produced as a result of intercellular recursive communication via neurotransmitters (Yamaguchi et al, 2003).

Box 6: Stabilizing cellular responses by intercellular communication.

Cooperative cellular responses are generally subject to fluctuations in intercellular signals that are themselves processed by biochemical networks in which the level of the components is also subject to stochasticity. In addition to the observations that transcriptional noise can be filtered out by cell‐intrinsic factors, that is, given topology of gene regulatory networks (Thattai & van Oudenaarden, 2000; Hooshangi et al, 2004), it has been also hypothesized that intercellular communication can enhance the reliability of cellular responses in noisy conditions (Koseska et al, 2009). In particular, it has been shown that cells reach a particular fate only when a specific size of the population is reached.

Figure for Box 6. Intercellular communication reduces noise and stabilizes cellular fate.

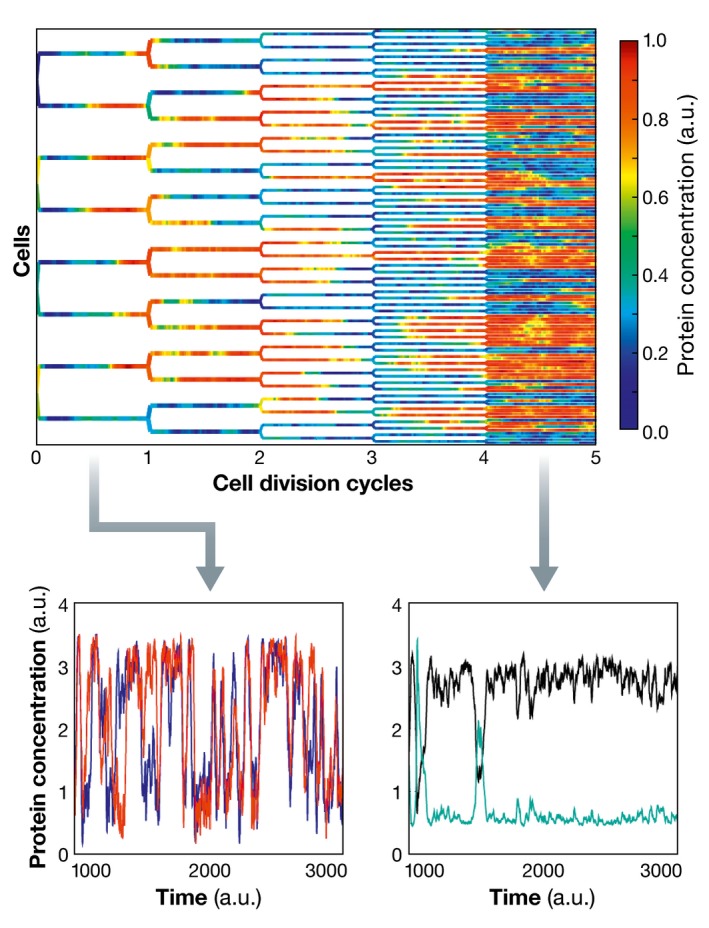
Population growth leads to effective reduction in the amplitude of the noise that decreases as the square root of the number of cells. The protein concentration in each cell is represented in color code. For low cell densities, cells display stochastic fluctuations in protein concentration (time series depicted in the lower left plot). Increasing the density of cells after four division cycles and thereby the communication between them effectively decreases the noise, and distinct cells commit to one of two different cell states (lower right plot).

A theoretical basis for this has been established in general non‐linear stochastic models, where noise is known to be tunable through the size of the system such that the amplitude of the noise is inversely proportional to the square root of number of cells (Pikovsky et al, 2002).

Even more, intercellular recursive communication can give rise to new attractors different than those of the isolated cells (Koseska et al, 2007; Ullner et al, 2008a,b), thereby displaying cognitive behavior. Analogous are the observations that individual hematopoietic stem cells acquire tissue‐like properties as a result of microenvironmental cues from the liver (Jang et al, 2004). Interestingly, specific communication‐induced dynamical solutions allow for heterogeneity to be established and maintained in a population (Koseska et al, 2010), resembling differentiated cellular entities in tissues. Theoretical studies have suggested that novel dynamical solutions can be generated in systems characterized with bidirectional inhibitory intercellular communication, rendering cognition a generic property of such multicellular systems (Koseska et al, 2007; Ullner et al, 2008a,b).

To demonstrate this idea, let us consider again the RTK–PTP toggle switch example described above. This network can exhibit one of two possible stable steady states in isolated cells, dependent on prior exposure to growth factor. This is a result of bistability that is generated due to the RTK‐induced PTP inhibition via ROS (Fig 5A). However, when ROS diffuses across the membrane, the short‐range bidirectional coupling between the networks in neighboring cells can theoretically generate a novel dynamical solution—an inhomogeneous steady state (IHSS, Fig 5B). This solution occurs due to symmetry breaking of the steady state via a pitchfork bifurcation and is characterized with two stable branches. Thus, even when the two communicating networks of the neighboring cells start from identical initial conditions, one of them must adopt the high branch, whereas the other cell must adopt the low branch. This will result in one cell having high and the other a low level of phosphorylated RTK. This IHSS solution coexists in parameter space with the bistability region (Fig 5B), but is a distinct dynamical solution of the coupled networks. Moreover, the IHSS (Koseska et al, 2007) is a generalized Turing instability (Turing, 1952; Challenger et al, 2015) that occurs via a communication‐induced Turing‐type bifurcation (Koseska et al, 2013). This solution has been theoretically linked to emergence of heterogeneous dynamical behavior in a homogeneous multicellular population as a way to establish asymmetric cell differentiation (Koseska et al, 2010). The IHSS solution has also been related to striped pattern formation that results from Delta–Notch signaling (Fig 1). In this case, the IHSS is driven by a primary signaling source and the addition of cis‐interactions (Formosa‐Jordan & Ibanes, 2014). Expanding the size of the population can further increase the number of dynamical solutions and thereby the differentiation potential in the system by means of clustering distinct manifestations of the same dynamical solution (Koseska et al, 2010).

Figure 5. Intercellular communication between RTK–PTP networks establishes cognitive behavior.

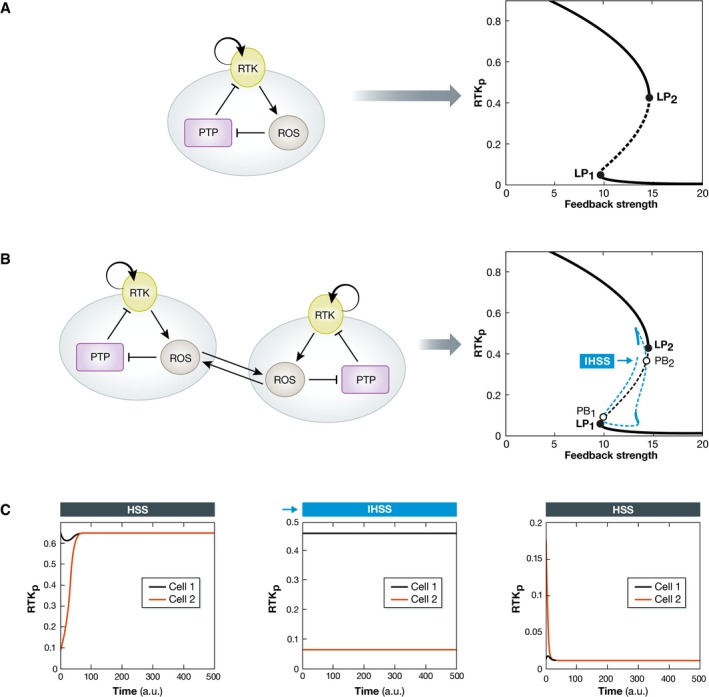
(A) A simple, ROS‐mediated double‐negative RTK–PTP interaction network generates a bistable system. The bistability region is denoted on the bifurcation diagram with the two bifurcations (LP₁, LP₂). (B) ROS‐induced communication between the networks of two neighboring cells generates a novel dynamical solution, an inhomogeneous steady state (IHSS) that coexists with the bistability region. This occurs through symmetry breaking of the homogeneous steady state via a pitchfork bifurcation (PB₁, PB₂). When the system is entrained in the IHSS, both cells must populate the two opposite stable branches (solid blue lines) characterized by low and high levels of RTK phosphorylation. The dashed blue lines denote unstable IHSS. (C) The corresponding time series of the three stable regimes, the high and the low homogeneous steady states, and the inhomogeneous steady state are shown. The mathematical model and the parameters used are shown in the Appendix.

The described principles are not specific for the RTK–PTP interaction network considered here, but is rather an inherent property of coupled systems, since it relies on the dynamics of the underlying networks as determined by their topology. For example, single cells that contain a three‐component genetic repressilator network motif (Elowitz & Leibler, 2000) can exhibit a single dynamical solution—autonomous oscillations with a defined period (Fig 6). Coupling these networks via a small signaling molecule however generates not only an IHSS, but also an inhomogeneous limit cycle solution, IHLC (Fig 6, Ullner et al, 2008b). This IHLC mimics the cellular potential to both proliferate and differentiate, and has been therefore related to asymmetric stem cell differentiation with self‐renewal (Suzuki et al, 2011).

Figure 6. New dynamical solutions emerging from network of intracellular networks differentiate cellular identities.

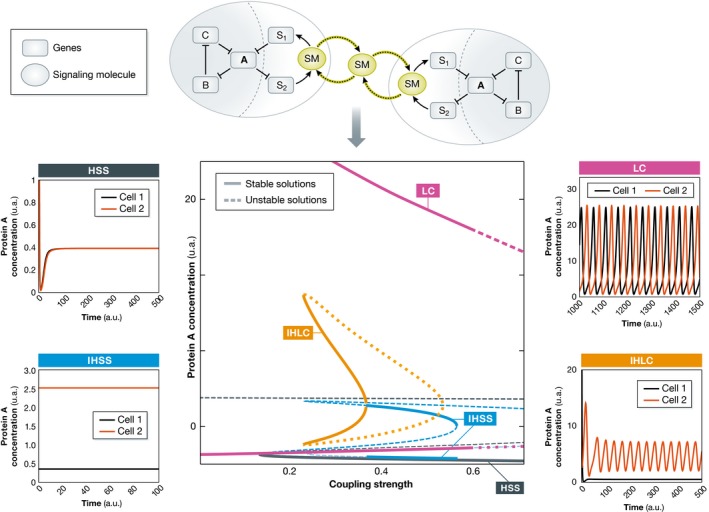
Schematic representation of paradigmatic gene regulatory networks that communicate among cells by small signaling molecules (SM). The network in isolated cells can exhibit only one dynamical solution: oscillations. Intercellular communication among identical cells generates novel dynamical solutions. The bifurcation diagram identifies the coupling strength for which different dynamical solutions can be observed. Solid lines denote stable and dashed/dotted lines unstable dynamical solutions. The corresponding time series of a homogeneous steady‐state (HSS), inhomogeneous steady‐state (IHSS), limit cycle (LC), and inhomogeneous limit cycle (IHLC) solutions are also depicted. The IHSS (also IHLC) is generated when the symmetry of the system is broken due to the intercellular communication (particular coupling strength). In this way, heterogeneity in a homogeneous cellular population is established and maintained: One of the cells exhibits high (dark orange line), whereas the other one exhibits low concentration (black line) of the protein A.

Thus, paracrine intercellular communication can generally result in collective dynamic behavior that is different from that of isolated cells, which might account for tissue‐specific cell functionalities. The above‐described hypotheses therefore state that cell identity is not purely determined by the manifestation of the genome but rather defined by recursive intercellular communication. The inherent multistability of multicellular systems defines the range in which cells can respond and adapt, while still maintaining their identity. In this description, stable attractors are associated with specific functional outputs, giving a mathematical formalism to cellular information processing. A further extension of the idea is the possibility for cells to modulate their dynamics on the proteome level and thereby acquire new functions. Making the parallel to neural networks and the concept of reservoir computing (Box 7), it is theoretically possible for recurrent networks that employ dynamic processes on different timescales to process information using transiently stable attractors (Maass et al, 2002). This significantly increases the network capabilities for information processing, especially of time‐varying inputs that can be further translated to novel cellular functions. If it can be realized on the level of the proteome, this could imply that the identity of cells can be altered by “teaching” them how to perceive the environment.

Box 7: Reservoir computing.

Reservoir computing is a machine‐learning concept referring to models that rely on mapping of stimuli on a high‐dimensional space in a non‐linear fashion. Such models include echo‐state and liquid‐state machines and state‐dependent networks (Buonomano & Maass, 2009). This concept for real‐time processing of time‐varying inputs requires recurrent networks whose components interact with each other via diverse processes with different timescales and transfer functions, for example, phosphorylation, enzymatic degradation, transcriptional, post‐transcriptional, and post‐translational regulation. In this view, each node in the network receives time‐varying input from external sources as well as from other nodes. The recurrent nature of the connections turns the time‐varying input into spatial–temporal patterns of activation in the network nodes, which are read out by linear discriminant units.

What determines the identity of cancer cells?

The collective behavior of cells on the level of tissues is generally stable against mutations that occur in single cells, allowing them to retain their identity (Bissel & Hines, 2011). The question therefore is how the cancer phenotype is stabilized under these conditions. When an oncogenic “gain‐of‐function” mutation occurs in single cells, it constitutively activates a certain protein. In terms of the intracellular signaling network, the continuous activity of this node “pushes” the complete network to a particular dynamical state. If we assume that the topology is not affected by the oncogene expression, then the number of attractors in these cells is reduced. However, comparative bioinformatics analysis of microarray datasets from multiple tumors and the non‐malignant tissues they were derived from has identified significantly increased number of interactions and multi‐edge node pairs in the regulatory networks of tumor cells (Schramm et al, 2010; Rahman et al, 2013). The formation of these new connections likely results from changes in gene expression that lead to an altered proteome composition (Schramm et al, 2010). Another possibility is that oncogene overexpression leads to new interactions with effectors by a simple mass action effect (Jones et al, 2006). Thus, a significant rewiring of the signaling networks in cells where oncogenic mutations occur will effectively modulate their dynamical possibilities by increasing the number of attractors. This would lead to an increased plasticity of cancer cells as compared to the tissue cells they are derived from. That this might be the case is evident from the fact that some cancer cells reversibly transit among states that differ in their competence, as a means to explore possibilities to contribute to tumor growth (Mani et al, 2008; Gupta et al, 2011).

This also allows cells to “jump” to a new “selfish” attractor that is intrinsically stabilized in single cells (Kaneko, 2011). Due to the acquired changes in dynamics, these cells loosen their collective behavior in the tissue and start to behave more as single entities. Since they represent an aberrant cell type, they are functionally unnecessary for the organism and therefore have not achieved robustness against noise and mutation during evolution (Kaneko, 2011). This leaves the dynamical state of these cells more changeable to somatic mutations, allowing them to continuously transit between different attractors (Capp, 2005). Selection pressure would eventually drive them in a state with a larger basin of attraction, giving rise to a stable cancer cell characterized by increased signaling entropy (Teschendorff et al, 2014; Box 8). The incidence of intercellular communication between cancer cells is now higher than that to the normal tissue, thereby stabilizing the tumor identity (Hamada et al, 1988). To which extent the dynamics of communicating signaling networks can be trained by environmental cues to maintain a specific behavior in a tissue context can be thus applied both, to understand how cancer cells acquire metastatic behavior, but also whether cancer cells can be “retrained” by the surrounding tissue to adapt their behavior. It has been demonstrated, for example, that transplantation of cancer cells into other tissues in which their interaction with other cells is modified, led to “reprogramming” of their oncogenic behavior (Mintz & Illmensee, 1975; Hochedlinger et al, 2004; Kasemeier‐Kulesa et al, 2008).

Box 8: Redundancy of signaling routes and signaling entropy.

The highly interconnected networks in transformed cells increase the redundancy in signaling paths that can be quantified through the concept of signaling entropy (West et al, 2012). Increasing the number of routes through which information can flow increases the signaling entropy. The high signaling entropy of cancer cells makes them robust to inhibition of protein interactions (Teschendorff et al, 2014), implying that pharmacological targeting of an oncogene product alone does not necessarily affect cell transformation. The topology of the transformed network, especially the positioning of negative feedbacks that can lead to homeostatic behavior against pharmacological perturbations, plays thereby a crucial role. For example, a negative feedback from Erk to EGFR has been shown to lead to AKT cross‐activation upon MEK inhibition in cells with oncogenic KRas or BRaf. A successful therapy for colon cancer therefore requires combined inhibition of MEK and EGFR to prevent AKT activation and tumor cell survival (Klinger et al, 2013).

Conclusion

Signaling cannot be perceived as a unidirectional process from the outside to the inside of the cell that is executed by hardwired cellular machinery. It is rather a dynamical manifestation of a highly adaptive network that is determined by the recursive interactions between the protein reaction states within the network as well as with the networks of other cells with which it communicates by extracellular chemical means. In this way, the processing of information becomes dependent on historical and extracellular context. We therefore like to think about signaling in cellular ensembles as a process reminiscent to cognition. In order to understand how this cognitive process works, inferring the topology of the network of signaling networks is a prerequisite to relate the observed biochemical behavior to the general principles of information processing between cells, and the thereby established cellular function. It is thus important to consider that new dynamical solutions can arise from intercellular communication and that cognition is not a property of single cells per se. This in turn opens the possibilities to manipulate cellular identity by changing its interaction with the environment: the multicellular context in which it is embedded.

Conflict of interest

The authors declare that they have no conflict of interest.

Supporting information

Appendix

The EMBO Journal (2017) 36: 568–582