Functionally Driven Brain Networks Using Multi-layer Graph Clustering

Abstract

Connectivity analysis of resting state brain has provided a novel means of investigating brain networks in the study of neurodevelopmental disorders. The study of functional networks, often represented by high dimensional graphs, predicates on the ability of methods in succinctly extracting meaningful representative connectivity information at the subject and population level. This need motivates the development of techniques that can extract underlying network modules that characterize the connectivity in a population, while capturing variations of these modules at the individual level. In this paper, we propose a multi-layer graph clustering technique that fuses the information from a collection of connectivity networks of a population to extract the underlying common network modules that serve as network hubs for the population. These hubs form a functional network atlas. In addition, our technique provides subject-specific factors designed to characterize and quantify the degree of intra- and inter- connectivity between hubs, thereby providing a representation that is amenable to group level statistical analyses. We demonstrate the utility of the technique by creating a population network atlas of connectivity by examining MEG based functional connectivity in typically developing children, and using this to describe the individualized variation in those diagnosed with autism spectrum disorder.

1 Introduction

Computational techniques applied to neuroimaging data have helped characterize brain connectivity anomalies in autism spectrum disorder (ASD) and schizophrenia. While structural connectivity is based on tractography using diffusion MRI [1], functional connectivity is investigated by using coherence measures between regions [2] using fMRI or magnetoencephalography (MEG) [3].

The study of brain connectivity networks has recently gained considerable attention. The high dimensionality of these networks as well as their variation at the subject level within the population calls for methods that can elucidate the underlying network structure while reducing dimensionality. In this paper, we present a novel approach that extracts the underlying network modules that describe the hubs of brain connectivity. Such modules are characterized by highly inter-connected regions within the module, in comparison to their connectivity to regions outside the module. This collection of network modules can serve as an atlas of network variation in a population. In addition to extracting these neurophysiological network hubs, our method provides representations of intra- and inter-connectivity strength of these network hubs for each subject, facilitating group-based statistical analysis.

The approach we take to extract these network hubs is based on multi-layer graph clustering. The advent of graph-based clustering techniques has led to recent growing interest in methods for clustering of multi-layer graphs in the area of mobile phone networks and document clustering [4–6]. However, such methods are mainly concerned with the approximation of graph Laplacian to feed the spectral clustering algorithm, and lack interpretability. In our approach, we present a framework for multi-layer graph clustering for analysis of connectivity in terms of splitting the brain network into hubs characteristic of a population and their low-dimensional interaction weights amenable to group-wise statistics. The connectivity network of each typically developing control (TDC) is represented as a graph, and all TDC graphs are stacked to form a multi-layer graph, each layer representing an individualized variation of the underlying network connectivity. A matrix factorization model is employed to decompose the set of healthy connectivity graphs into clusters of network modules (hubs) shared among all graph layers. These network hubs are learned by using a gradient descent approach minimizing the reconstruction error of decomposition in the healthy population network set. The network hubs obtained are then used adaptively to optimize hubs intra- and inter-connectivity weights for each subject.

While our method is generalizable to non-negative connectivity matrices obtained from DTI or fMRI, we demonstrate its applicability to resting-state MEG connectivity networks in alpha frequency-band for a population of ASD subjects.

2 Methods

Our framework is based on the premise that there are a few underlying subnetworks that describe a population with variation demonstrated between each subject. The method we present here determines the network hubs that characterize the commonality across all subjects within a population (e.g. default mode network), with the interaction within and between these hubs that captures the individualized variation in each subject. Therefore, we capture not only the dominant network hubs that describe a population, but also the subtle connectivity between these hubs that describes the variation in each subject either due to inherent heterogeneity or induced by pathology. This collection of network hubs will be referred to as the network atlas.

Given a population, we create this network atlas using the connectivity matrices from all the subjects. The connectivity is quantified by a non-negative similarity measure between n regions leading to a non-negative connectivity matrix of subject m, i.e. S^(m) ∈ ℝ^n×n, represented by a graph with n vertices. We then use a matrix factorization model S^(m) ≈ U Λ^(m)U^T where U = [u₁, u₂, …, u_k] ∈ ℝ^n×k is the common factor of the population characterizing the shared underlying connectivity modules of the population. ${\mathit{\Lambda }}^{(m)}=\left[{\lambda }_{ij}^{(m)}\right]\in {ℝ}^{k\times k}$ is also the symmetric subject-level factor capturing the weights of each subject’s network modules. k ≪ n is the number of network hubs (modules) to be identified. Due to the symmetry of Λ^(m), this decomposition model can be re-written as

$${\mathit{S}}^{(m)}\approx \mathit{U}{\mathit{\Lambda }}^{(m)}{\mathit{U}}^T=\sum _{i=1}^k{\lambda }_{ii}^{(m)}{\mathit{u}}_i{\mathit{u}}_i^T+\sum _{i=1}^k\sum _{\begin{array}{c}\hfill j=1\hfill \\ \hfill j>i\hfill \end{array}}^k{\lambda }_{ij}^{(m)}({\mathit{u}}_i{\mathit{u}}_j^T+{\mathit{u}}_j{\mathit{u}}_i^T).$$ (1)

In this model, each network hub is identified by the first term in (1), i.e. ${\mathit{u}}_i{\mathit{u}}_i^T$, whose subject-level intra-connectivity strength is represented by coefficients ${\lambda }_{ii}^{(m)}$. On the other hand, the subject-level inter-connectivity strength between hubs i and j is represented by ${\lambda }_{ij}^{(m)}$ where the inter-connectivity pattern is identified by ${\mathit{u}}_i{\mathit{u}}_j^T+{\mathit{u}}_j{\mathit{u}}_i^T$, i.e. the second term of (1). Elements of U are constrained to remain non-negative U_ij ≥ 0, thus retain the interpretation of its components (i.e. ${\mathit{u}}_i{\mathit{u}}_j^T$) as a connectivity matrix (i.e. hubs and their interconnectivity modules). Λ^(m) is constrained to be non-negative ${\lambda }_{ij}^{(m)}\ge 0$ and symmetric ${\lambda }_{ij}^{(m)}={\lambda }_{ji}^{(m)}$ due to the symmetry of connectivity matrices S^(m), but no constraints are imposed on it to be diagonal, because this lets our model capture the inter- connectivity weights on off-diagonal elements, and not overlook the interactions between network hubs in the study.

2.1 Objective Function

Since we would like to obtain the underlying network modules shared among all subjects in the population, we stack the connectivity graph of all subjects to form a multi-layer graph {S^(m)}. The network hubs shared by the population is then obtained by minimizing the reconstruction error of the decomposition across layers. This can be obtained by minimizing the following objective function with appropriate constraints on U and Λ^(m) as explained in equation (1),

$$J(\mathit{U},{\mathit{\Lambda }}^{(m)})=\sum _{m=1}^M{\Vert {\mathit{S}}^{(m)}-\mathit{U}{\mathit{\Lambda }}^{(m)}{\mathit{U}}^T\Vert }_F^2+\beta ({\Vert \mathit{U}\Vert }_F^2+\sum _{m=1}^M{\Vert {\mathit{\Lambda }}^{(m)}\Vert }_F^2),$$ (2)

$$\text{subject to }{U}_{ij}\ge 0,{\lambda }_{ij}^{(m)}\ge 0\text{ and }{\mathit{\Lambda }}^{(m)}={\mathit{\Lambda }}^{{(m)}^T}$$

where M is the number of subjects within the population, and ‖․‖_F denotes the Frobenius norm. The regularization term, as the sum of the squared norm of U and Λ^(m), is added to improve the numerical stability, and β is a tunable parameter balancing the two terms of reconstruction error norm and regularization.

2.2 Optimization Solution

Due to symmetry of S^(m) and Λ^(m), equation (2) can be rewritten as

$$J(\mathit{U},{\mathit{\Lambda }}^{(m)})=\sum _{m=1}^M\mathit{\text{trace }}\left\{{({\mathit{S}}^{(m)}-\mathit{U}{\mathit{\Lambda }}^{(m)}{\mathit{U}}^T)}^2\right\}+\beta \left(\mathit{\text{trace }}\right\{\mathit{U}{\mathit{U}}^T\}+\sum _{m=1}^M\mathit{\text{trace }}\{{\mathit{\Lambda }}^{{(m)}^2}\left\}\right),$$ (3)

$$\text{subject to }{U}_{ij}\ge 0,{\lambda }_{ij}^{(m)}\ge 0\text{ and }{\mathit{\Lambda }}^{(m)}={\mathit{\Lambda }}^{{(m)}^T}.$$

To minimize (3), we propose an iterative procedure in which U and Λ^(m) are alternately optimized by given multi-layer graph of the population {S^(m)}. We use the gradient decent approach, i.e. alternately updating $U_{ij}=U_{ij}-{\eta }_{ij}\frac{\partial J}{\partial U_{ij}}$ and ${\lambda }_{ij}^{(m)}={\lambda }_{ij}^{(m)}-{\zeta }_{ij}^{(m)}\frac{\partial J}{\partial {\lambda }_{ij}^{(m)}}$ with step-sizes η_ij ≥ 0 and ${\zeta }_{ij}^{(m)}\ge 0$, where

$$\frac{\partial J}{\partial \mathit{U}}=-4\sum _{m=1}^M\left[\right({\mathit{S}}^{(m)}-\mathit{U}{\mathit{\Lambda }}^{(m)}{\mathit{U}}^T\left)\mathit{U}{\mathit{\Lambda }}^{(m)}\right]+4\beta \mathit{U},$$ (4)

$$\frac{\partial J}{\partial {\mathit{\Lambda }}^{(m)}}=-2{\mathit{U}}^T({\mathit{S}}^{(m)}-\mathit{U}{\mathit{\Lambda }}^{(m)}{\mathit{U}}^T)\mathit{U}+2\beta {\mathit{\Lambda }}^{(m)}.$$ (5)

Due to non-negativity of S^(m), our non-negativity constraints will be guaranteed by positive initialization of U and (symmetric) Λ^(m), and applying the step sizes as ${\eta }_{ij}=\frac{\frac{1}{4}{U}_{ij}}{{(\beta \mathit{U}+{\sum }_{m=1}^M\mathit{U}{\mathit{\Lambda }}^{(m)}{\mathit{U}}^T\mathit{U}{\mathit{\Lambda }}^{(m)})}_{ij}},{\zeta }_{ij}^{(m)}=\frac{\frac{1}{2}{\lambda }_{ij}^{(m)}}{{(\beta {\mathit{\Lambda }}^{(m)}+{\mathit{U}}^T\mathit{U}{\mathit{\Lambda }}^{(m)}{\mathit{U}}^T\mathit{U})}_{ij}}$. This results in the following multiplicative updating solutions

$$U_{ij}=U_{ij}\frac{{\left({\sum }_{m=1}^M{\mathit{S}}^{(m)}\mathit{U}{\mathit{\Lambda }}^{(m)}\right)}_{ij}}{{(\beta \mathit{U}+{\sum }_{m=1}^M\mathit{U}{\mathit{\Lambda }}^{(m)}{\mathit{U}}^T\mathit{U}{\mathit{\Lambda }}^{(m)})}_{ij}},$$ (6)

$${\lambda }_{ij}^{(m)}={\lambda }_{ij}^{(m)}\frac{{\left({\mathit{U}}^T{\mathit{S}}^{(m)}\mathit{U}\right)}_{ij}}{{(\beta {\mathit{\Lambda }}^{(m)}+{\mathit{U}}^T\mathit{U}{\mathit{\Lambda }}^{(m)}{\mathit{U}}^T\mathit{U})}_{ij}},\text{ for }1\le m\le M.$$ (7)

Starting with initial random positive elements on U and (symmetric) Λ^(m), the iterative procedures (6) and (7) are performed alternately until convergence. Such initialization will guarantee non-negativity on U and Λ^(m) as well as the symmetry of Λ^(m), which can be verified from equations (6) and (7).

2.3 Optimizing Subject-Level Factors

The above procedure is performed on the multi-layer graph of a population to create an atlas of network hubs. The common factor U obtained from them is employed to optimize equation (2) to compute subject-level factors Λ^(m) from their connectivity matrices. Since the common factor U is given, (2) can be minimized by only performing the iterative procedure of (7) with random symmetric non-negative initialization of Λ^(m) for each subject, yielding the subject-specific intra- and inter-connectivity weight of network hubs. It is worth noting that, given U, equation (7) is iterated on both control and patient data so that both populations undergo the same procedure to be comparable in statistics.

2.4 Statistical Analysis and Interpretation

As explained at the beginning of section 2, elements of the subject-level factors Λ^(m) represent weights of network hubs in that subject. The intra-connectivity of network hubs is represented by the diagonal elements of Λ^(m), i.e. ${\lambda }_{ii}^{(m)}$, and their inter-connectivity is represented by the upper triangular elements (due to symmetry of it). Hence, a significant group difference at a diagonal element ${\lambda }_{ii}^{(m)}$ interprets as an alteration in the communication within the i^th network hub, characterized by ${\mathit{u}}_i{\mathit{u}}_i^T$, and a group difference at an off-diagonal element ${\lambda }_{ij}^{(m)}$ indicates changes in the interaction between the network hubs i and j, i.e. the inter-connectivity pattern ${\mathit{u}}_i{\mathit{u}}_j^T+{\mathit{u}}_j{\mathit{u}}_i^T$ has been affected by disease.

3 Results

The proposed method provides a means to extract common population level information while also capturing individual subject variation. We demonstrate the applicability of this methodology to the study of resting-state (RS) MEG functional connectivity in a population of ASD, in comparison to a network hub atlas that has been learned on a TDC population. The connectivity of the entire population is then represented in this more concise module representation.

In order to perform a preliminary test, we applied our method to a set of synthetic noisy networks with known common modules (hubs), which were successfully restored by the procedure explained in section 2.

Dataset Demographics

The dataset consisted of 77 male children, 37 ASD and 40 TDCs, aged 6–14 years (mean=10.2 years, SD=1.8 in ASD, and mean=10.3 years, SD=1.7 in TDC, no significant difference in age p > 0.6). RS MEG was acquired in a magnetically shielded room using a 306-channel Elekta scanner. Two minutes of recorded data were obtained after artifact removal, which were low-pass filtered before downsampling to 500 Hz to avoid aliasing.

Source Localization and Connectivity Measures

RS eyes-closed data were band-pass filtered to the alpha band activity (8–12 Hz). MEG data were divided into 2.5-second epochs with 50% overlap and transformed into the frequency domain. A 5mm isotropic source grid was obtained by sampling cortical gray-matter areas from the T1-weighted MRI of each subject. The sensor-space frequency-domain data were used by VESTAL [7] to obtain source amplitude at each source location. From this spatial distribution of source amplitudes, an inverse operator was determined [7] and applied to the MEG data yielding source time-courses at each location. 301 structurally meaningful regions of interest (ROIs) were determined using Freesurfer tools to subdivide the cortical surface of a template subject and to map these ROIs into each of the 77 subjects. Of the 301 ROIs, we identified 202 ROIs that have at least one source assigned to them. ROI dominant time-courses were then determined by using singular value decomposition. Connectivity matrices were computed for the 202 regions yielding 77 matrices of size 202 × 202. Synchronization likelihood (SL), a non-negative measure of synchronous activity between 0 (no connection) and 1 (completely synchronous), was used to quantify the connectivity between two regions [3].

Connectivity Network Analysis

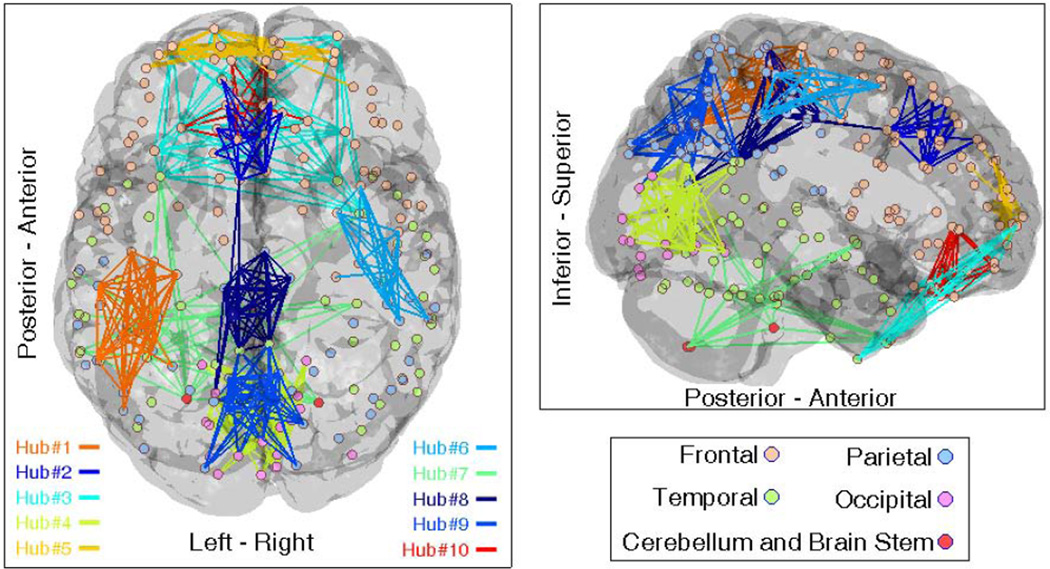
The SL connectivity matrices of 40 TDC subjects were used to compute the network hubs as well as their 40 subject-level weights. We set β = 0.1 and used k = 10 to obtain 10 network hubs. The iterative procedure of (6) and (7) was performed that converged to the network atlas U of size 202 × 10. The resulting ten network hubs (i.e. the first term in equation (1), ${\mathit{u}}_i{\mathit{u}}_i^T$ for 1 ≤ i ≤ 10) are shown together on a brain map in Fig. 1, thresholded for binary visualization of their dominant edges.

Fig. 1.

The k=10 functional network hubs of brain MEG alpha activity obtained from the 40 TDC connectivity matrices, displayed together with no specific order

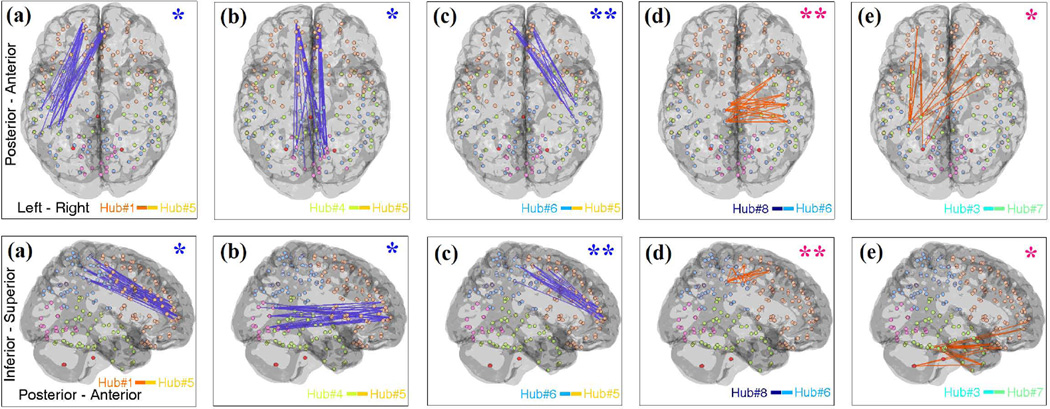
Given the network hubs computed for the TDC population, the subject-level weights Λ^(m), each of size 10 × 10, for the 40 TDC as well as 37 ASD connectivity matrices were obtained. These subject-level weights of the two groups were then used to perform statistical group comparison for each of 10 diagonal and 45 upper-triangular elements of Λ across subjects, out of which five of upper-triangular elements indicated significant group differences (p < 0.05). In Fig. 2, we show the five inter-connectivity patterns that correspond to the significant weights, by displaying their inter-connectivity maps generated by the second term of equation (1), i.e. ${\mathit{u}}_i{\mathit{u}}_j^T+{\mathit{u}}_j{\mathit{u}}_i^T$, as explained in section 2.4. The interconnectivity patterns which have larger weights in TDC are shown in blue (Fig. 2 (a) to (c)), while those larger in ASD are shown in orange (Fig. 2 (d) and (e)).

Fig. 2.

The five inter-connectivity (between-hub) patterns with significant group difference between ASD and TDC (axial and sagittal view). Blue and orange interconnectivity networks have higher weights in TDC and ASD, respectively. p < 0.05 and p < 0.01 are labelled with one and two stars, respectively.

It is observed from Fig. 1 that our method has extracted modular brain functional hubs that are spatially close but sparsely distributed on the cortex. The arrangement of these network hubs may also define the default functional network in MEG brain connectivity. As mentioned above, the statistical group comparison of ten diagonal elements of subject-level weights did not show significant difference (with p < 0.05) indicating that the contribution of network hubs does not substantially differ between ASD and TDCs. It is however worth noting that Hub#5 demonstrated the most different intra-connectivity among the ten hubs shown in Fig. 1. This network showed a group difference of p < 0.1 (with higher weights in ASD) indicating hyperconnectivity in short-range communications in the very frontal area of ASD brain, an observation consistent with the literature of ASD frontal lobe overconnectivity [8]. It is interesting to observe that such enhanced connectivity within this hub in ASD, coincides with underconnectivity in the interaction of this hub with bilateral hubs Hub#1 and Hub#6 (Fig. 2(a) and (c)) as well as the occipital hub Hub#4 (Fig. 2(b)). This may be an indication that the local overconnectivity in the front of ASD brain has led to long-distance underconnectivity, or vice versa.

Fig. 2 (a)–(c) shows that ASD brain has deficient long-range connectivity primarily in fronto-occipital communications (connectivity pattern between Hub#4 and Hub#5 shown in Fig. 2 (b)) as well as in fronto-parietal connections (between Hub#1 and Hub#5 as well as Hub#6 and Hub#5 shown respectively in Fig. 2 (a) and (c)), consistent with findings of fronto-posterior under-connectivity in autism [9]. In addition, Fig. 2(d) shows that ASD has enhanced short-range connectivity (between Hub#8 and Hub#6). Fig. 2(e) also shows increased interconnectivity between the frontal and temporal/subcortical regions in ASD (between Hub#3 and Hub#7).

The network hubs obtained here are clinically interpretable as they implicate the regions associated with the known default mode network (DMN) which is the network most commonly elucidated in functional resting state literature. We have also observed that the average weights of the intra-connectivity networks (i.e. hubs) are an order of magnitude larger than the inter-connectivity weights. Therefore, the inter-connectivity network modules do not substantially contribute to reconstructing subjects’ functional networks, but important in characterizing the effect of disease. Finally, we tested the method on subsets of healthy subjects and have obtained similar network hubs indicating the repeatability of the results.

4 Conclusion

We have presented a new analysis technique of connectivity matrices using a low-rank matrix factorization model that extracts a set of population specific network hubs shared by all the matrices in a multi-layer graph framework. Application to a dataset of TDC subjects provided a set of functional network hubs and their intra- and inter-connectivity weights. The network hubs obtained from TDC were used to compute the subject-level weights for ASD subjects. Group-wise analysis of intra- and inter-connectivity weights revealed significant long-range connectivity deficiencies as well as short-range overconnectivity in ASD. The proposed framework can be extended to any non-negative connectivity matrix, and the weights obtained in the process can be exploited for statistical analysis.