Route choice in pedestrians: determinants for initial choices and revising decisions

Abstract

In moving pedestrian crowds, the distribution of individuals over different available routes emerges from the decisions of individuals that may be influenced by the actions of others. Understanding this phenomenon not only is important for research into collective behaviour, but also has practical applications for building safety and event management. Here, we study the mechanisms underlying pedestrian route choice, focusing on how time-independent information, such as path lengths, and time-dependent information, such as queue lengths, affect both initial decisions and subsequent changes in route choices. We address these questions using experiments with nearly 140 volunteers and an individual-based model for route choice. Crucially, we consider a wide range of route choice scenarios. We find that initial route choices of pedestrians achieve a balanced usage of available routes. Our model suggests that pedestrians performing trade-offs between exit widths and predicted exit crowdedness can explain this emergent distribution in many contexts. Few pedestrians adjust their route choice in our experiments. Simulations suggest that these decisions could be explained by pedestrians comparing estimates of the time it would take them to reach their target using different routes. Route choice is complex, but our findings suggest that conceptually simple behaviours may explain many movement decisions.

1. Introduction

Most pedestrians are familiar with the situation of having to choose between different routes in busy places, such as selecting one of a number of exits from an underground station. Previous work has established that pedestrian crowds display collective behaviour, as the interactions between individuals give rise to the observed dynamics of the whole crowd [1]. It is likely that, when choosing routes, pedestrian crowds also display collective behaviour, as individual pedestrians may respond to the movement or behaviour of others [2]. The distribution of pedestrians over available routes would then emerge from individual-level route choices that may depend on what others do. Route usage is of direct relevance for building design, event planning and traffic control [3] and pedestrian crowds therefore provide one example for the importance of understanding collective behaviour, a widespread phenomenon in nature [4].

When moving, pedestrians seek to avoid collisions with others and steer around obstacles. They are also likely to have one overarching destination or goal they want to reach (e.g. to exit an underground station). These two types of movement decisions take place at different spatio-temporal scales and have been categorized as occurring at the ‘operational level’ and at the ‘strategic level’, respectively [5]. Here, we investigate movement decisions that can be found at an intermediate level, typically referred to as the ‘tactical level’ [5]. Typical decisions at this level include deciding between different exits from a room or deciding which path to follow at a junction.

At the operational level, pedestrians frequently update their movement direction in response to changing circumstances around them (e.g. to overtake slower pedestrians [6]). In contrast, decisions at the strategic level are unlikely to be updated frequently. For example, during an evacuation only extreme situations, such as a serious injury or losing sight of a relative [7,8], might alter the strategic goal of leaving the building. We propose that movement decisions at the tactical level may be adjusted systematically in response to changing situations. For example, pedestrians might move from a first-choice exit to another exit because of a long queue at the former. We seek to establish the mechanisms underlying such dynamic tactical-level route choices in humans using experiments that simulate low-pressure evacuations.

Human route choice has been investigated extensively in previous research. It has been suggested that pedestrians generally choose the route that coincides with their estimate of the quickest path [9]. Pedestrians could estimate the quickest path based on time-independent information such as exit width or path length [10]. For example, pedestrians may prefer nearer exits, as they could walk shorter distances to reach them, which may reduce their walking time [11]. Wider exits may be preferred over narrow ones, as they allow pedestrian crowds to pass more efficiently [12]. This implies that the layout of possible exit routes could be important [13] and could lead to pedestrians trading off the distance from exits against their width, for example.

When pedestrian densities are low, individuals may only need to consider time-independent information when making decisions. For example, at low crowd densities, the shortest path is typically also the quickest [14]. However, as already indicated above, at higher pedestrian densities, time-dependent information may inform human route choice [12]. Time-dependent information about exit routes can take different forms and can be communicated in different ways. Pedestrians might be unfamiliar with the location of exits [15] and try to obtain information from others [16]. Individuals in dense crowds could get stuck in queues, causing them to search for alternative routes [17], or, alternatively, their line of sight to alternative exits may even be occluded [18]. Taking time-dependent information into account could have the effect that pedestrians change their opinion on which path to use (e.g. based on estimating the quickest path). Experiments conducted with human participants in virtual environments support this proposition and additionally suggest that time-dependent information plays a more important role in route choices than time-independent information [12].

Previous work has focused particularly on developing efficient and realistic simulation models for human route choice [8–23]. In principle, these models are very useful, as they provide hypotheses for behavioural mechanisms underlying route choice and could in theory be used to predict crowd behaviour in real-life scenarios [23]. However, many of these models [9,10] have not been validated against empirical data, which makes it difficult to judge their appropriateness. Some models have been compared with experimental data, but only one route choice scenario was investigated (e.g. choice between two identical exits [21]), and it is therefore not clear whether the models also apply in different scenarios. While experiments in virtual environments have started to investigate what factors influence route choice in more detail [12,19,22], it is not clear to what extent these findings can be extrapolated to real-life human behaviour. In summary, only a very few experiments with pedestrian crowds have been conducted specifically to study human route choice [2].

Our work addresses these issues and uses both experiments and simulations of a novel model to explore the mechanism of dynamic route choice. In our experiments, we present crowds of almost 140 pedestrians with a choice of different exit routes from a room. In contrast to previous work, we study a wide range of route choice scenarios that differ in the arrangement of exit locations and in the initial positioning of participants in our experiments. We use this substantial dataset to address two main research questions. First, we investigate the initial choice of exit of pedestrians at the start of the experiment. In particular, we test if time-independent information (e.g. proximity to exits) is sufficient to explain these initial route choices. Second, we investigate the mechanisms underlying dynamic route choices (i.e. how route choices change over time). We propose a general, perception-based mechanism for human route choice that takes both time-independent and time-dependent information into account. With simulations of a model derived from this mechanism we test if this mechanism can reproduce the dynamic route choice observed in our experiments.

The remainder of this manuscript is structured as follows. First, we describe our experiments and use the experimental data to characterize exit usage and changes in route choice. These results provide initial insights into what affects human route choice. Subsequently, we present our route choice model. We compare simulations of this model with our experimental data and thereby investigate route choice mechanisms in more detail by suggesting a possible mechanism for route choice behaviour.

2. Experiments and data capture

2.1. Experimental set-up

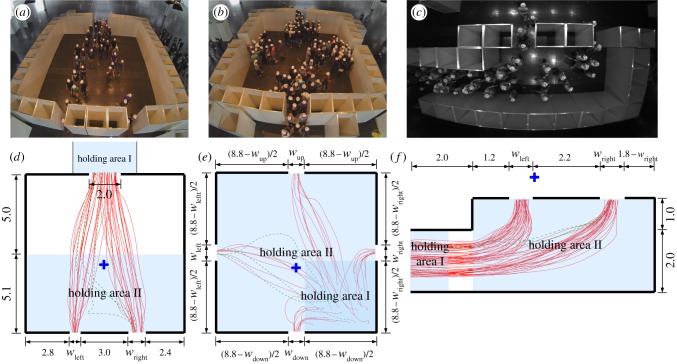
We conducted experiments at the Düsseldorf trade fair centre (Germany) in June 2013 with a total of 138 participants (54 female and 84 male). The average age was 24 years, with the youngest participant 18 and the oldest 62 years. The same group of participants completed experiments for three different route choice scenarios, which we subsequently refer to as experiments A, B and C. We used 2.5 m high barriers to construct different layouts of rooms with exits for each experiment. Snapshots and sketches of the experimental set-ups are shown in figure 1. Before the start of each run, participants were located in holding areas (indicated in figure 1). After an acoustic signal, they were asked to pass through the experimental set-up as quickly as possible, but without competing or pushing. In total, we conducted 19 experimental runs: 10 runs for experiment A, six runs for experiment B and three runs for experiment C. Each run is referred to in the format ‘experiment_run’ (e.g. ‘A_1’ represents the first run of experiment A). We varied the number of participants included in the experiment, the width of exits and the distribution of participants over the different holding areas between experimental runs. Details are described in figure 1 and in the electronic supplementary material, table S1.

Figure 1.

Experimental set-up. (a–c) Still images for experiments A_3, B_3 and C_2, respectively. These images provide an overview of the experiment and we did not use them to obtain the trajectories of pedestrians (see text). (d–f) The layout for the three experiments A, B and C and pedestrian trajectories for experiments A_3, B_3 and C_2, respectively. All units are in metres. The number of participants in holding areas I and II for each run is listed in the electronic supplementary material, table S1. Trajectories shown in red indicate pedestrians who walked directly to one exit. Trajectories of pedestrians who changed their route choice are shown as green dashed lines. The blue cross represents the coordinates of the origin (0, 0) in our trajectory data. (Online version in colour.)

We recorded the experiments from above using a camera grid of six by four cameras mounted 7.5 m above the floor. An additional camera to obtain an overview of the entire scene was used. Pedestrian trajectories of each run were automatically extracted from the video recordings using custom-made software (detailed information about this procedure can be found in [24]; data are available as electronic supplementary material). Sample trajectories for experiments A_3, B_3 and C_2 are presented in figure 1d,e,f, respectively. We carried out all subsequent analysis of the trajectories using the Python programming language [25].

2.2. Egress time

We recorded the time at which each participant had exited the experimental set-up after the start of the experiment, t_i, as the time when individuals crossed the line segment representing the exit. From this, we computed the overall egress time for an experimental run, T = max{t_i}, for each run, which is given in the electronic supplementary material, figure S1 and table S2. T was comparable in size across runs with the same initial conditions, which demonstrates that pedestrian groups showed consistent behaviour under unchanged conditions. As expected, T increased when the number of pedestrians, N, increased, in agreement with the results in [14,26]. These results suggest that, despite the fact that we used the same pool of participants for all our experimental runs, there is no immediately obvious evidence for an effect on the observed dynamics by participants habituating to the experimental set-up.

2.3. Exit usage

As explained in the Introduction, the observed distribution of pedestrians over different routes emerges from the route choices of individuals. This distribution can therefore provide an insight into what affects route choice. We obtained the distribution of participants over exits from our trajectory data for all experimental runs and show the results in figure 2a–c.

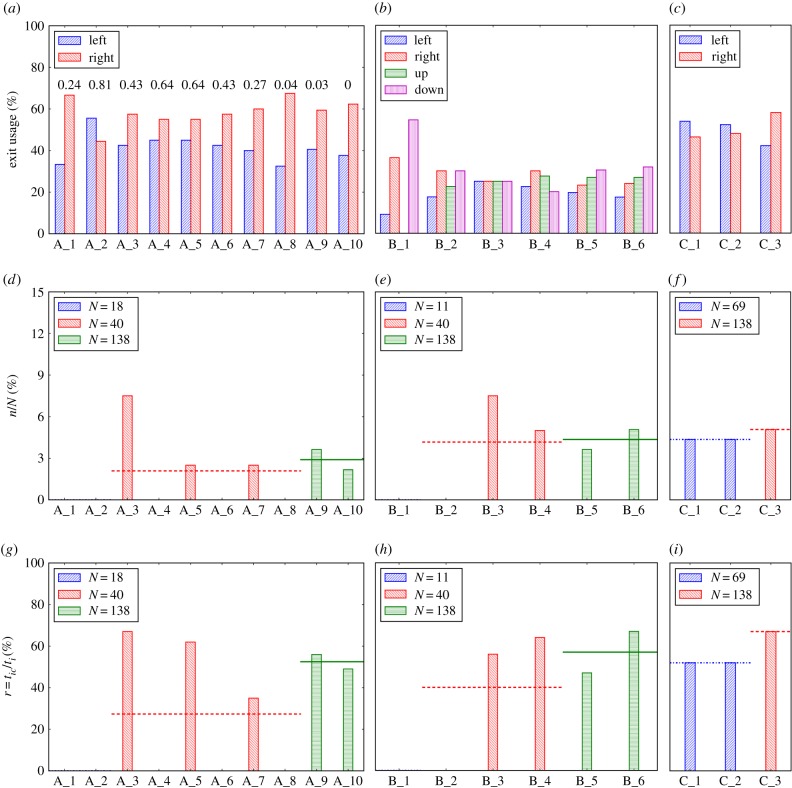
Figure 2.

Experimental results. (a–c) The exit usage for each run of experiments A, B and C, respectively. We show the percentage of the total number, N, of pedestrians for each exit in the experiments. Recall that in experiment A (a), the right exit was wider; in experiments B_5 and B_6, the top and bottom exits were wider; and in experiment C_3, the right exit was wider. In all other experiments, all exits had the same width. The numbers in panel (a) represent the p-value for each run from a binomial test with the hypothesis that pedestrians choose either exit with equal probability. For large pedestrian numbers (A_8, A_9 and A_10), the p-values are below 0.05, which means it is unlikely that the preference for the wider (the right) exit has arisen by chance. (d–f) The occurrence frequency of path re-planning behaviour, n/N, in each run of experiments A, B and C, respectively. Here, n represents the number of the pedestrians who changed their route choice. (g–i) The mean value of the ratio, r = t_ic/t_i, for each run of experiments A, B and C, respectively. t_i is the egress time of the individuals with path re-planning behaviour, and t_ic is the estimated time at which a change of route choice was displayed. The ratio r captures the time point during experiments at which changes in route choice occurred (0% implies at the start and 100% implies at the end of experiments). The horizontal lines denote the average value for runs with the same initial conditions. (Online version in colour.)

Our data provide evidence for some preferences in route choices. In experiment A, the path length to both exits was the same, and we observe a general tendency for the wider (the right) exit to be used by more pedestrians than the narrower (the left) one (figure 2a). However, only for large pedestrian numbers (runs A_8, A_9 and A_10) can we be sure that the differences in exit usage we observe are unlikely to have arisen by chance (see the binomial test in figure 2a). An exception to this trend was run A_2, where the exit usage for the wider exit was lower. A possible explanation for this exception could be that the influence of exit width on exit usage was less prominent when the density was below a certain value (i.e. when there was no queue [13]), but we do not have enough data to formally test this explanation. Exit usage in the other experimental runs that included exits of different widths (B_5, B_6 in figure 2b and C_3 in figure 2c) also suggested a preference of participants for wider exits (statistical analysis omitted because of lack of replicates).

In addition to preferring wider exits, pedestrians may prefer nearby exits [11]. Our results provide support for this suggestion but also indicate that such a preference is not always evident. In experimental runs B_1–B_4, the bottom and right-hand exits were closer to the participants who were positioned in holding area I. These two nearby exits were used by more participants in B_1 and B_2, whereas the tendency does not exist in B_3 and B_4 (figure 2b). Similarly, in experimental runs C_1 and C_2, pedestrians reached the left-hand exit first when leaving their holding position and this exit was used by slightly more participants (figure 2c).

These observations provide some limited support for the notion that pedestrians use time-independent information in their route choice. We now investigate the evidence for dynamic route choice (i.e. the use of time-dependent information by pedestrians).

2.4. Path re-planning behaviour

We manually examined the video recordings of our experiments for evidence of changes in route choice. Previous work has used algorithms based on changes in movement direction to detect changes in route choice [27]. However, such an approach was not feasible for the range of route choice scenarios we investigate here. For example, in experiment C, pedestrians did not have to change their movement direction substantially when deciding to use the right exit instead of the left one. To ensure that we identified route choice changes in a consistent and reproducible way, we devised a robust approach to distinguish three categories of pedestrian behaviour based on their movement direction, body orientation and head turns:

• — The first category of pedestrian moved towards one exit and kept their head turned towards this exit throughout the experiment.

• — The second category of pedestrian also moved towards one exit throughout the experiment. However, pedestrians in this category turned their head (but not their body) towards other exits and thus appeared to direct their attention towards alternative routes.

• — The third category of pedestrian showed an extension of the behaviour displayed by pedestrians in the second category. Pedestrians in this category initially turned their head and body towards one exit and started to move towards this exit. At some point, they turned their head from one exit to an alternative one in a clearly distinguishable way. Subsequently, they reverted to a behaviour similar to that of the pedestrians in the first category with aligned head direction, body orientation and movement indicating that they were moving towards one exit, different from their original choice. Figure 1 shows that pedestrians in this category typically followed trajectories that were clearly distinguishable from those of other pedestrians.

In our analysis, we labelled pedestrians in the third category as having changed their choice of exit route. We additionally estimated the time point at which pedestrians changed their mind on which route to use, t_ic. This time point was defined as the time when pedestrians first showed aligned head direction, body orientation and movement towards the alternative exit (different from the original one).

We plot the number of pedestrians who showed a change in route choice, n, for each run in the experiments in figure 2d–f. Although path re-planning behaviour did occur in all our experiments (but not in all runs), the number of pedestrians who showed this behaviour was generally only a small proportion of all pedestrians involved in the experimental run (0–7.5%). This suggests that pedestrians' initial choice of exit route was largely responsible for the observed exit usage. In addition, seeing that not all pedestrians opted for the same exit when one exit was much closer than others, it could be suggested that pedestrians took into account what others were or might have been doing and balanced this information or intuition against their own preferences. This proposition is supported in particular by experimental runs B_2–B_6, where the exit usage was relatively balanced (figure 2b) with participants arranged in different holding areas (figure 1e and electronic supplementary material, table S1). We re-visit these considerations when developing our model in the next section.

From the egress time of individuals, t_i, and the estimated time at which they displayed a change of mind in their route choice, t_ic (both reported in electronic supplementary material figure S2 and table S3), we compute the ratio r = t_ic/t_i. The mean value of the ratio r for each run is shown in figure 2g–i. The average value of r for the runs with the same initial conditions falls within the range of 30–60%. This illustrates that pedestrians tended to change their mind on which exit to use roughly half way through the time they spent inside the experiment. We confirm this result by investigating the distribution of r for all pedestrians across all experimental runs (electronic supplementary material, figure S3). We use a Kolmogorov–Smirnov test to verify that this distribution can be approximated by a normal distribution with mean and standard deviation of 55.56% and 16.51%, respectively (n = 43, D = 0.08, p = 0.95).

This finding on the distribution of timings for changes in exit route choice could be interpreted as follows. At the start of the experiments, changes in route choice occurred infrequently, because the situation around pedestrians did not change much. Over time, the distribution of the crowd could change substantially (e.g. queues formed and some queues moved faster) and pedestrians consequently were more likely to consider alternative routes. As experiments progressed, queues got shorter and shorter, making the situation for pedestrians more stable again.

3. Modelling and simulation

3.1. Modelling

We propose a general mechanism for route choice in pedestrians by extending a previous model [9]. Our model describes tactical-level route choice by suggesting how individuals select one route from a number of discrete routes, such as exit doors. We do not model strategic-level route choices, as these were fixed to leaving the experimental set-up and identical for all participants in our experiments. While we model operational-level movement decisions (e.g. avoiding collisions) using a recently released pedestrian simulation framework [28], our model is flexible and could be used with alternative models for operational-level movement (e.g. the reciprocal velocity obstacle [29] or the social force model [30]). At the start of our experiments, all participants were stationary and thus had to select a route. We separately model these initial route choices and subsequent route choices.

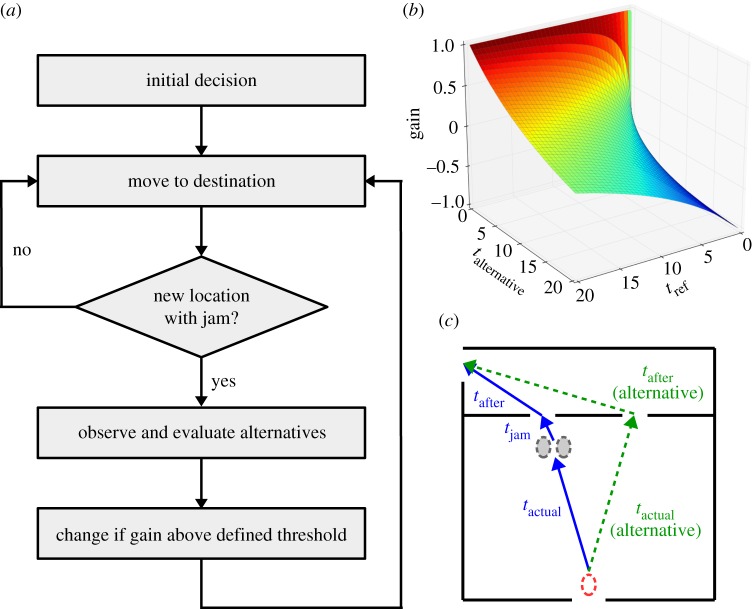
We first describe how simulated pedestrians adjust their route choice once they have made an initial decision. The key underlying assumption of our model is that individual pedestrians estimate how long it takes them to complete different exit routes and that they use these estimates as a basis for selecting a route. The algorithm of the model is described in figure 3a. We assume that individuals revise their initial decision if they have to wait in a queue (get caught in a pedestrian jam, defined below) or if they reach an intermediate target (e.g. once they have passed one exit on a route that includes multiple exits—this second scenario does not arise in the experiments we consider). When considering alternative routes, individuals use a ‘gain metric’ to compare their current choice with alternatives (defined below). A change in route choice only occurs if the gain for an alternative path is above a predefined threshold, θ. For each alternative, they estimate the time it would take them to reach their final goal if they followed the associated exit route. This time is computed as the sum of three components. The first component, t_actual, is the time it takes the pedestrian to reach the exit or the queue at the exit (estimated using the walking speed of the agent and the direct path to the exit or queue location). The second component, t_jam, is the time the pedestrian has to wait in the queue in front of the exit (calculated using the length of the queue and the speed of a reference pedestrian selected from the queue in front of the exit; details in [9] and in the electronic supplementary material). The third component, t_after, is the time it takes the pedestrian to reach their final target after passing through the exit (calculated using the walking speed of the pedestrian). In our experiments, pedestrians had reached their final target when they exited through any of the exits, and t_after = 0 in this case. For each route alternative, the sum (t_actual + t_jam + t_after) is then compared with t_ref (the sum of the three components for the currently selected exit), according to the following gain function:

3.1

Figure 3.

Route choice algorithm for individual pedestrians. (a) Outline of the route choice algorithm. An initial decision on a route can be revised later if individuals are in a queue or reach an intermediate target. Individuals assess their relative preference for different routes using a gain function (see equation (3.1)), which is zero for similar routes and tends to −1 or 1 when the difference between routes is large. Panel (b) shows this gain function plotted against estimated times to complete a reference and an alternative route (see text and equation (3.1) for details). (c) Example to illustrate travel time estimation of individuals. A pedestrian (shown as a dashed red oval at the bottom of the panel) has to choose between two routes. One exit is clear (dashed green lines) and the other is blocked by a short queue (solid blue lines). The estimated travel time is the sum of the time needed to reach a queue or exit location (t_actual), the expected time of waiting in a queue (t_jam) and the time needed to reach the final target after passing through an exit (t_after). Simulated pedestrians compare the relative merit of the alternative routes using the gain function shown in equation (3.1). (Online version in colour.)

The gain function takes values between −1 and 1 and converges to 1 when t_ref is much higher than the sum of the three components for an alternative exit (figure 3b). Figure 3c shows an example with two alternative routes. When deciding which alternative routes an individual considers, we take into account which exits the individual is likely to be able to see. We determine exits an individual can see as the ones where the direct line of sight from the individual to the exit location is uninterrupted by walls or other pedestrians (disregarding pedestrians who are queueing in front of the exit for which visibility is assessed, see electronic supplementary material). As pedestrians in our model walk in a straight line towards their next immediate target, picking a non-visible exit would lead to unrealistic behaviour, such as pedestrians attempting to walk through walls.

An individual is defined as having to wait in a queue or being in a jam when their current speed is less than half of their desired speed (each individual is assigned a desired speed in simulations, see electronic supplementary material). In addition to considering the route preferences of individuals based on equation (3.1) and visibility criteria, we also take psychological and physical constraints imposed by a pedestrian crowd into account. For example, it might be difficult to leave from the centre of a dense queue, while people on the periphery of the queue can walk away easily. In addition, pedestrians at the front of the queue have invested some time in waiting already and may therefore be less likely to change their exit choice. To take account of these considerations, we assume in our model that an individual can only leave from a queue if 80% of the queue is in front of them. This constraint implies that, if pedestrians leave a queue, they do so from the back, which results in queues starting to dissolve from the back. An alternative for determining individuals' ability to leave a queue would be to compute the local density of pedestrians around them. However, this is time consuming to compute and likely to result in a similar effect to the approach we adopt. In general, we found that such a constraint on where pedestrians left queues in front of exits was needed to ensure that the shape of pedestrian queues in front of exits was qualitatively similar to the queue shapes visible in the experimental data. Without such a constraint, many pedestrians would leave from the side of queues, something we rarely observe in our data. However, it should be noted that, while we included these constraints into our model for the above reasons, they do not change the fundamental principle of dynamic route choice based on estimated time to exit comparisons implemented in our model. For the low numbers of pedestrians who changed their exit route choice in our experiments, this implementation detail is unlikely to be important. It is only in simulations with much larger numbers of pedestrians that these constraints become important. Without empirical data on route choice in such large crowds, we leave checking the appropriateness of the above constraints for future work.

The initial exit route choice of individuals is treated separately in our model. We assume a sequential decision-making process in which the distance to exits, the number of the agents sharing the same choice and the exit widths are considered. In our model, we calculate the distances from each pedestrian to all available exits, and then compute the exit choices of pedestrians sequentially in order of increasing values of pedestrians' distance to their nearest exit. For simplicity, we assume that individuals know the decisions of others. In practice, these decisions could be communicated via head turns, body turns or other visual or acoustic cues. For a given pedestrian, the probability of choosing a route i, P_i, then depends on the distance to the investigated exit, d_i, the number of pedestrians who have already chosen that exit, n_i, and the width of exit, w_i, as follows:

3.2

Here, d_max is defined as the sum of all distances to exits, n_max is the total number of the agents included in the initial route choice process, and w_max is the sum of exit widths taken into consideration in the decision-making process. M is a normalization factor for the probabilities across all exits. α, β and δ are weighting factors for d_i, n_i and w_i, respectively.

As mentioned above, we implemented our model algorithms in the open-source pedestrian simulation framework JuPedSim [28]. This allowed us to focus on the tactical-level route choices we consider here, while using a JuPedSim implementation for operational-level movement (e.g. locomotion, collision avoidance [5]). At the operational level, we used a previously developed model that implements continuous space in two dimensions and is able to reproduce several important self-organized phenomena of pedestrian crowds, such as counter flows, lane formation or bottleneck flow, at a low computation cost [31]. The movement of pedestrians is simulated within a given topology (e.g. a room with exits) and an initial configuration. The initial configuration includes the desired destinations, preferred speeds and route choices for all agents. We used the default values for all individual-specific quantities (e.g. preferred speed). Simulations were performed using release 0.7 of JuPedSim. We provide more details about the framework in the electronic supplementary material.

3.2. Simulation and validation

We carried out simulations of our model in the same experimental set-ups and initial conditions as used in the experiments (figure 1 and electronic supplementary material, table S1). To investigate how well our model reproduced the experimental data, we considered different values of four model parameters: the threshold θ for selecting an alternative route, as well as α, β and δ that control the relative weighting of the distance to exits, the crowd density around exits and the widths of exits in initial route choices, respectively. We assessed the sensitivity of our simulations to different values of these parameters by conducting a broad scan of the four-dimensional (θ, δ, α, β) parameter space. Specifically, for each distinct experimental scenario, we ran 10 replicate simulations with different initial conditions for all possible combinations of the following parameter values: θ = (0, 0.05, 0.1, 0.15, 0.2, 0.3, 0.5, 0.7, 0.9, 1.0), δ = (−2, −1, −0.5, −0.2, −0.1, 0, 0.1, 0.2, 0.5, 1, 2), α = (0, 2, 4, 6, 8, 10), β = (0, 2, 4, 6, 8, 10). This approach resulted in a total of 39 600 simulations for each simulation scenario (e.g. for experiment A with 18 pedestrians). Recall that high positive values of θ imply that pedestrians are unlikely to change their route choice. High negative values of δ imply that pedestrians prefer wider exits, whereas δ = 0 implies that individuals do not take exit widths into consideration. High α values imply that individuals are likely to choose the nearest exit and α = 0 implies that individuals do not take into account how far away they are from an exit in their initial route choice. Similarly, β = 0 implies that individuals ignore the density around exits, and high values of β imply they choose less crowded exits.

To compare simulations and experimental data in a quantitative and efficient way, we defined a distance measure, dist, as follows

3.3

Here, 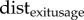and dist_n are the averaged differences between experiments and simulations in the number of pedestrians who used each exit and who changed their route choice, respectively. The lower the dist, the closer simulations were to the experimental data. We thus used dist to demonstrate the sensitivity of our simulations to different parameter values and we selected the set of parameter values producing the minimal value of dist for a more detailed comparison between simulations and data. To avoid over-fitting our model, we conducted this parameter calibration using the combined experimental data from all scenarios in experiments A, B and C. In this way, we obtained one set of parameter values that minimized the sum of dist across all 19 experimental runs.

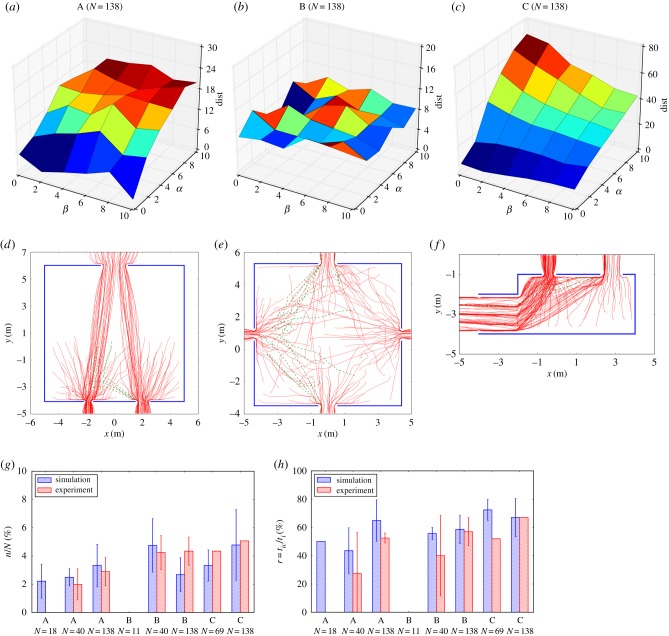
Our simulations produced substantial variation in dist and therefore in exit usage and changes in decisions for different parameter values (figure 4a–c and electronic supplementary material, figure S4). Examples for simulated trajectories are shown in figure 4d–f. The parameter values achieving the closest match to the experimental data were θ = 0.5, δ = −2, α = 0 and β = 2. This suggests that a trade-off between choosing wide exits (δ < 0) and avoiding crowded exits (β > 0) explained the observed route choices of pedestrians relatively well (with some exceptions, see below). As expected from our experimental results, we found high values of θ, suggesting that pedestrians in simulations did not change their exit route choice frequently. Our parameter calibration suggested that proximity to exits did not play a role in exit choice (α = 0). However, this result has to be interpreted with care, as our calibration does not consider how many pedestrians used the exit nearest to them (see equation (3.3)). It should therefore be clear that the calibration of our model is a starting point only. In the following, we discuss the scenarios for which our globally calibrated model does not perform well, but we also show that our global calibration does broadly capture exit decisions in many of the scenarios we tested experimentally.

Figure 4.

Simulation results. Panels (a–c) show part of our sensitivity analysis based on the quantity dist (see equation (3.3)) for experiments with a pedestrian number of 138 in scenarios A, B and C, respectively. The calibration of parameters was performed across all experimental runs in scenarios A, B and C. In (a–c), the simulations use θ = 0.5 and δ = −2 (see text and electronic supplementary material for additional information on sensitivity analysis). (d–f) Examples for simulated pedestrian trajectories for the same scenarios as in (a–c). Trajectories in red indicate pedestrians who walked directly towards one exit and dashed trajectories in green indicate simulated pedestrians who changed their mind on which route to use. Panels (g) and (h) show the occurrence frequency of path re-planning behaviour, n/N, and the mean value of the ratio r for all scenarios in experiments and simulations. n,N and r are defined as in figure 2. In (g,h), the simulations use the values of parameters listed in the electronic supplementary material, table S4. We report mean values and standard deviations (g and h only) obtained from 10 replicate simulations with simulated pedestrians initially randomly distributed in the corresponding holding areas in figure 1d–f. (Online version in colour.)

The variation in dist for changing parameter values in the different experimental scenarios provides more information on the success of our calibration (figure 4a–c and electronic supplementary material, figure S4). For low pedestrian numbers, in experiments A (N = 18) and B (N = 11), values of dist remained relatively flat, suggesting that the symmetry of the experiments led to a fairly even distribution of pedestrians over exits in simulations, regardless of specific parameter values (electronic supplementary material, figure S4a,c). Across other scenarios, the value of dist showed similar trends and its minimum value occurred around α = 0 and β = 2 (figure 4a,c and electronic supplementary material, figure S4b,d,e). One exception is experiment B for N = 138, in which no clear trend was observed but the minimum value of dist still occurred when α = 0 and β = 2 (figure 4b).

A closer look at exit usage further shows that the globally calibrated values of parameters did not produce a perfect match between simulations and experiments (electronic supplementary material, figures S5 and S6). This was the case in experiments A for N = 18, B for N = 11 and C for N = 69 (electronic supplementary material, figures S5a,d,g and S6a,d,g). Despite the broad range of scenarios tested, our global parameter calibration produced a good match in exit usage between simulations and experiments in all other experimental scenarios (electronic supplementary material, figures S5 and S6). Furthermore, our model captured the frequency and timing of changes in route choice well for all experimental scenarios (figure 4g,h). Based on these findings, we suggest that, while our globally calibrated model fails to accurately capture route choice in all scenarios we studied, it nevertheless performs well across a broad range of scenarios.

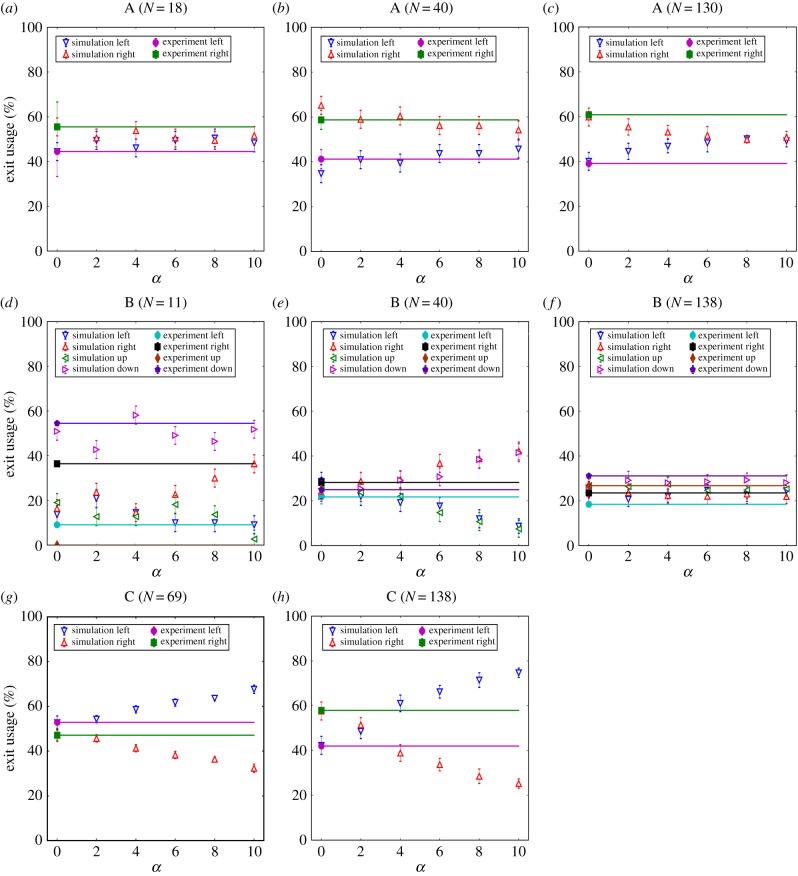
Pedestrians might adjust the relative importance they assign to different aspects of available routes, depending on the context. For example, proximity to exits may be more important in larger rooms, such as in experiment B. If this was the case, our model should be calibrated separately for different experimental scenarios. Unfortunately, we do not have a sufficient number of replicate experimental runs to perform a robust parameter calibration separately for experiments A, B and C. Nevertheless, it is instructive to perform such an analysis in an exploratory way (figure 5 and electronic supplementary material, figures S7 and S8). This analysis yielded eight separate parameter sets that minimized dist for experiment A (N = 18, 40 and 138), B (N = 11, 40 and 138) and C (N = 69 and 138), respectively, which are shown in the electronic supplementary material, table S4. The variation in dist for changing parameter values showed that, for some scenarios, there were distinctive trends in the value of dist, suggesting that optimal parameters can be found (electronic supplementary material, figure S7b–e,g,h). For other scenarios trends in dist were difficult to identify, which suggested that for these cases the experimental data provide inconclusive results in our calibration approach (electronic supplementary material, figure S7a,f). The large variation in optimal parameter values found in this calibration (electronic supplementary material, table S4) as well as the close match in exit usage between simulations and experiments (figure 5 and electronic supplementary material, figure S8) have to be interpreted in consideration of the exploratory nature of this analysis.

Figure 5.

Sensitivity analysis for the model parameter α which controls the relative weighting of a preference for nearer exits in the initial route choice of pedestrians. Parameter calibration was performed separately for each scenario A, B and C and number of pedestrians, respectively. The parameter sets that minimized dist for each scenario are listed in the electronic supplementary material, table S4. For each scenario, the simulation was conducted 10 times with pedestrians randomly distributed within their allocated starting positions (holding areas, figure 1d–f). We report mean values across replicates alongside 1 s.d. The experimental data are the average value for runs with the same initial conditions. (Online version in colour.)

4. Discussion

We report findings on pedestrian route choice based on extensive experiments and we use a simulation model, building on previous work [9], to illustrate that simple behavioural mechanisms are sufficient to describe many, but not all, of the observed dynamics. Importantly, we conduct experiments with a large number of participants (nearly 140) and we consider a variety of route choice scenarios by altering the topology of the experimental set-up and the initial positioning of pedestrians inside this set-up. We found evidence for pedestrians adjusting their route choice in all the scenarios we considered, but this dynamic route choice behaviour was comparatively rare. Overall, participants in our experiments achieved an efficient emergent distribution over the available exit routes based on their initial route choice at the start of the experiment.

While the precise details of our model for pedestrian route choice should certainly be scrutinized, it nevertheless suggests that simple behavioural rules could explain both the initial route choices as well as subsequent dynamic route choices. Our model suggests that, in their initial route choice, individuals trade off their preferences for routes (based on exit widths, in agreement with [10]) against how crowded they perceive routes to be. To keep our implementation simple, we assumed that pedestrians make their initial decision sequentially. In reality, this is unlikely to be the case ([27], see also discussion below), but it allows for an interesting comparison with previously established models for group decision-making in animals. These models suggest similar mechanisms for how individuals decide between a number of options with the crucial difference that individuals seek to maintain group cohesion and thus aim to achieve crowding rather than to avoid it [32,33]. It has previously been suggested that under certain circumstances pedestrians may switch to a behaviour similar to the one suggested by work on animals (e.g. ‘herding’ in stressful evacuations [30,34]). However, this is certainly not what we found in our experiments.

In the calibration of model parameters presented above, we did not require simulations to capture the number of pedestrians who used the exit closest to them (see equation (3.3)). Therefore, it is not unexpected that proximity to exits did not affect route choice in our calibrated model (α = 0). However, as proximity to exits could be an important factor in route choice [11], we performed an additional calibration study that considered the number of pedestrians who used the exit closest to their initial position (electronic supplementary material, figure S9). This analysis suggested that proximity to exits does play a role in route choice, but it also confirmed that it plays a less prominent role than the crowdedness of exits (α = 15 and β = 30 in electronic supplementary material, figure S9). Such calibration approaches that consider additional aspects of the route choice dynamics lead to simulations that capture our data more completely. However, the more criteria are included in the calibration, the more important it becomes to consider an appropriate weighting of their relative importance. For example, from a crowd safety perspective, it could be suggested that the distribution of pedestrians over exits is more important than the number of pedestrians who choose to use the exit closest to them. These considerations are important, but beyond the scope of this work. Our data are available in the electronic supplementary material, and it is therefore possible to perform such an extended analysis in the future.

Previous work has suggested that pedestrians prefer wider exits [10]. Our experiments showed a slightly higher usage of wider exits and we thus included such a preference into our model for initial route choice. We performed additional simulations to illustrate that our model is robust and can be extended to larger crowds (electronic supplementary material, figure S10). These simulations also showed that, in principle, higher usage of wider exits can occur in our model as a result of changes in route choice towards exits with fast-moving queues.

The analysis presented above demonstrates both the potential and the limitations of our model. We suggest that, with additional data (more replicates for experimental runs), a better calibration of model parameters could be achieved, taking context-dependent behaviours into account. We would also like to note that quantitative calibration of models for emergent phenomena, as attempted here, is inherently difficult and rarely attempted. As such, we suggest our approach provides a useful starting point for further study. In our opinion, there are two main issues that require additional attention. First, the calibration of models to data needs to be improved to ensure calibrated models capture all the key features in data. It may be possible to adapt established statistical techniques for this purpose [12]. Second, to fully capture mechanisms underlying route choice, it may be necessary to consider additional aspects, such as relative positions of pedestrians, decision timings and prior knowledge of available exit routes. Previous work on more limited scenarios could provide useful starting points [35].

Our model assumes that, once pedestrians have made their initial decision on which route to use, they then use their own assessment of how quickly they could reach their target by following different routes to decide if they should change the route they are using (building on previous work [9]). In our model, individuals' estimates are based on path lengths and the waiting time in a queue in front of exits. Experiments with human participants in virtual environments have also shown the importance of queue dynamics for route choice [12]. We found this mechanism to be sufficient for reproducing our experimental findings qualitatively. However, it is likely that additional behaviours affect the route choice decisions of pedestrians. Based on our findings and previous work, we suggest the following behaviours could all play a role, potentially at the same time, in determining pedestrian route choice (anecdotal observations for some of these behaviours in our experiments are discussed in the electronic supplementary material, figures S11 and S12):

• — Jam-avoidance behaviour. Queues or ‘jams’ are observed in front of exits when the number of the participants is large. Pedestrians have to wait in or near the jams for some time and their desire to avoid this delay may influence their route choices (as implemented in our model).

• — Time-estimating behaviour. One version of this behaviour is implemented in our model: pedestrians try to estimate how long it would take them to reach their target if they followed alternative routes and change their route choice if they identified a superior route. We have focused on path lengths and queue dynamics in our model, but additional factors, such as route characteristics (e.g. exit widths or the presence of obstacles [26]), could be relevant.

• — Following behaviour (‘herding’). Individuals might change their route choice because of a desire to follow other pedestrians (e.g. to stay with friends or family members or because they do not know the environment [30,34]). We do not implement following behaviour, but only consider the opposite, jam avoidance.

• — Route-comparing behaviour. Individuals could differ in the degree to which they compare route alternatives using the behaviours described above. For example, some individuals may compare routes more frequently or may be willing to change their route choice even if the potential gain is relatively small (in our model, this would result in individual-specific values for the parameter θ).

• — Alternative motivation. It is likely that in our experiments participants wanted to minimize the amount of time it took them to exit the experimental set-up. While this is a relevant scenario, it has been shown that in other situations alternative considerations affect the route choice of pedestrians (e.g. familiarity with routes, weather protection or pleasantness of routes [20]).

• — Emotional state. Our experiments simulated low-pressure pedestrian egress. However, increased pressure on individuals to reach their target quickly could affect their route choice. For example, based on experiments in virtual environments, it has been suggested that increased pressure could lead to individuals being less willing or able to adjust their route choice [19].

This non-exhaustive list shows that many factors could affect the route choice of pedestrians and that additional work is needed to establish their relative importance in different contexts. As discussed in the Introduction, an understanding of pedestrian route choice has many practical applications. From this perspective, we suggest that, despite the multitude of additional factors that could affect pedestrian route choice and the limitations of our model, it is encouraging to see the extent to which our comparatively simple route choice model reproduces our experimental findings.

Ethics

The experiments were approved by the German Federal Ministry of Education and Research and conducted under the supervision of Forschungszentrum Jülich GmbH. All participants provided informed consent in writing prior to the experiments.

Data accessibility

The data presented in this manuscript are available as electronic supplementary material.

Authors' contributions

W.L. carried out the data analysis, calibrated the model, conducted the simulations and drafted the manuscript; A.U.K.W. conceived the study, designed and conducted the experiments, built the model and helped draft the manuscript; N.W.F.B. helped draft the manuscript and revised the manuscript critically. All authors contributed to the design of the study and gave final approval for publication.

Competing interests

We have no competing interests.

Funding

This study was supported by the project BaSiGo, which is supported by the German Federal Ministry for Education and Research with grant no. 13N12045 and the Pillar ‘civil security’ of the programme High-Tech Strategy. N.W.F.B. is supported by a Leverhulme Early Career Fellowship.