Frogs use a viscoelastic tongue and non-Newtonian saliva to catch prey

Abstract

Frogs can capture insects, mice and even birds using only their tongue, with a speed and versatility unmatched in the world of synthetic materials. How can the frog tongue be so sticky? In this combined experimental and theoretical study, we perform a series of high-speed films, material tests on the tongue, and rheological tests of the frog saliva. We show that the tongue's unique stickiness results from a combination of a soft, viscoelastic tongue coupled with non-Newtonian saliva. The tongue acts like a car's shock absorber during insect capture, absorbing energy and so preventing separation from the insect. The shear-thinning saliva spreads over the insect during impact, grips it firmly during tongue retraction, and slides off during swallowing. This combination of properties gives the tongue 50 times greater work of adhesion than known synthetic polymer materials such as the sticky-hand toy. These principles may inspire the design of reversible adhesives for high-speed application.

1. Introduction

How can a frog grab a flying insect using just its tongue? There are over 4000 species of frog and toad that use a sticky, whip-like tongue to grab prey faster than a human can blink [1]. There is no known commercial mechanism that can match the grabbing speed of the frog tongue, let alone adhere to a highly textured surface like a fly. One may think that the frog tongue succeeds in capturing only lightweight prey; however, the frog tongue can pull up to 1.4 times the frog's body weight [2]. Little is known about the underlying physics that makes the tongue so sticky.

Frog studies date back to the 1800s, when Augustus Waller published a paper on the frog tongue nerves and papillae [3]. Even then, Waller was fascinated by the soft, sticky nature of the frog tongue: ‘The attention of physiologists was first directed by me to the peculiar advantages possessed by the tongue of the living frog … the extreme elasticity and transparency of this organ induced me to submit it to the microscope’ [3, p. 139]. Kleinteich & Gorb [2] were the first to measure the frog tongue retraction force in the horned frog Ceratophrys cranwelli; the average adhesive strength was 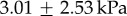with a maximum recorded adhesive strength of 17.7 kPa. In the animal kingdom, these values are not the highest: the leaf beetle and Tokay gecko have adhesive strengths of 16.5 kPa and 100 kPa, respectively [4,5]. We show here that adhesive strength alone is not the most accurate indicator of stickiness. In this investigation, we also make clear the tongue's mechanism of adhesion. Kleinteich postulated that the tongue acts like sticky tape or pressure-sensitive adhesive, a permanently tacky surface that adheres to substrates under light pressure [2,6]. We show that the frog tongue acts more like a car's shock absorber than a pressure-sensitive adhesive; its viscoelastic nature enables rapidly applied forces to be dissipated in the tongue tissue. The adhesivity of the tissue is due to the unique saliva, which is able to flow into textured surfaces and grip firmly during tongue retraction.

In this study, we elucidate the mechanism by which frog tongues stick. We begin with the high-speed videos of the tongue projection. We then present measurements of the rheological properties of the saliva and mechanical properties of tongue tissue. Lastly, we apply these measured properties in a mathematical model for the work of adhesion of the frog tongue.

2. Results

2.1. Kinematics

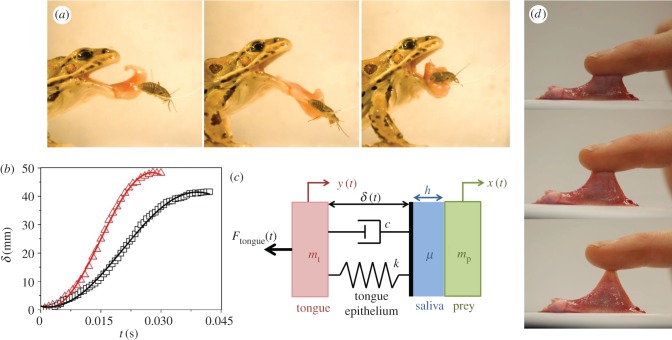
We performed high-speed videography of the common leopard frog Rana pipiens capturing crickets attached to a string, as shown in figure 1a. The frog's tongue is able to capture an insect in under 0.07 s, five times faster than a human eye blink. Figure 1b shows the corresponding tongue displacement during both successful and unsuccessful capture. Only the vertical position of the tongue is shown. The solid lines show sinusoidal fits to the tongue displacement, with further details given in the Experimental methods. Acceleration on the insect can reach 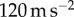, 12 times the acceleration of gravity. Consequently, a 0.5 g insect effectively feels over 5 g of force. These high forces necessitate a high adhesion force to the tongue, which we investigate in a series of tests.

Figure 1.

Frog tongue projection. (a) Prey capture by Rana pipiens. Photos are separated by 0.03 s. (b) Tongue displacement during insect retraction, measured from the tongue tip, for failed insect capture (red triangles) and successful insect capture (black squares). Solid lines represent a sinusoidal fit. (c) Model of tongue using a mass–spring–damper system. (d) Finger retracted from the tongue surface showing its strong adhesion.

Touching the frog tongue with a finger, as shown in figure 1d, indicates that the tongue is quite sticky, similar to marshmallow or chewing gum. Attempts to remove one's finger result in the tongue stretching rather than the bond breaking. The tongue also shines visibly from its coating of saliva. Later, we will use a floating spring–mass–damper system to model prey capture (figure 1c). To that end, we performed a series of tests on the tongue and its saliva layer to gather all parameters for our model.

2.2. Material properties and rheology

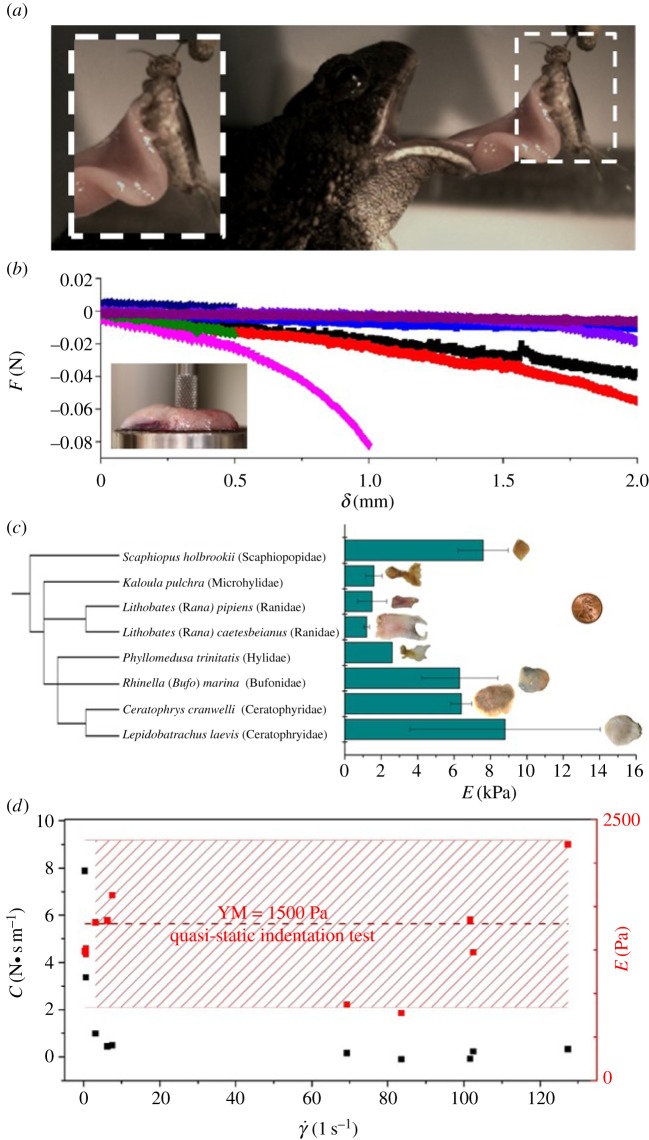
We collected the tongues of six frogs and two toads, which have been frozen over the last year at the Atlanta Botanical Garden, Atlanta, GA, USA. Species include Rana pipiens (Ranidae), Lithobates catebeianus (Ranidae), Ceratophrys cranwelli (Ceratophyridae), Rhinella marina (Bufonidae), Kaloula pulchra (Microhylidae), Lepidobatrachus laevis (Ceratophryidae), Scaphiopus holbrookii (Scaphiopodidae) and Phyllomedusa trinitatis (Phyllomedusinae; Hylidae). A phylogenetic analysis shows that the frog and toad species tested are distantly related (figure 2c).

Figure 2.

Tongue material properties. (a) Stretching of tongue epithelium during prey capture. The gaps indicate areas where prey has been released. (b) Relationship between force and displacement for indentation tests shown in the inset. (c) The phylogenetic tree of amphibian species in this study. Young's modulus for eight species, measured by quasi-static test. A penny is shown for reference. (d) Damping coefficients (black squares) and Young's modulus (red squares) for the frog tongue, measured in a dynamic tensile test. The average Young's modulus and error bars from part (c) is shown as red dotted line.

When the frog retracts its tongue, the insect's inertia pulls it in the opposite direction, as shown in figure 2a. Small filaments of the tongue thus stretch while other parts are clearly pulled off the tongue, as shown by the small gaps in the image. We measured the softness of the tongue epithelium in the perpendicular direction using microindentation. We slowly indented the tissue with a rigid cylinder and measured the relationship between stress and strain [7] (figure 2b). Softness of the tongue in the linear elastic regime is characterized by Young's modulus. The average Young's modulus is 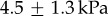, with the lowest value of 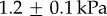for Lithobates catebeianus and the highest value of 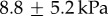for Lepidobatrachus laevis (figure 2c). Our model species for this study, the leopard frog Rana pipiens, has a tongue softness 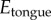of 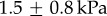, which is one-third the average softness across the species tested. Materials of such softness are exceedingly rare in Nature. When using indentation techniques, materials with similar Young's modulii include: muscle at 7 kPa [8], rat spinal cord at 3 kPa [9] and rat brain, which we tested, at 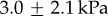. Human tongue, which we tested, had a stiffness of 15 kPa, 10 times greater than that of the leopard frog. The widespread softness of amphibian tongues suggests that evolution of a soft tongue was necessary for this mode of prey capture.

Our previous test can only describe the low-speed behaviour of the tongue. To understand high-speed behaviour, we performed a dynamic indentation test [10]. We model the tongue epithelium using the Kelvin–Voight model, as a linear spring of stiffness k and purely viscous damper in parallel, with the underlying assumption of tissue homogeneity. Using a leopard frog tongue sample, a rigid cylindrical indenter is pressed into the tissue surface at varying sinusoidal frequencies, and the corresponding damping coefficient c and stiffness coefficient k are measured (figure 2d). At frequencies above 1 Hz, the damping coefficient is 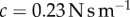. Young's modulus, calculated from the corresponding stiffness, matches the results of our quasi-static indentation test.

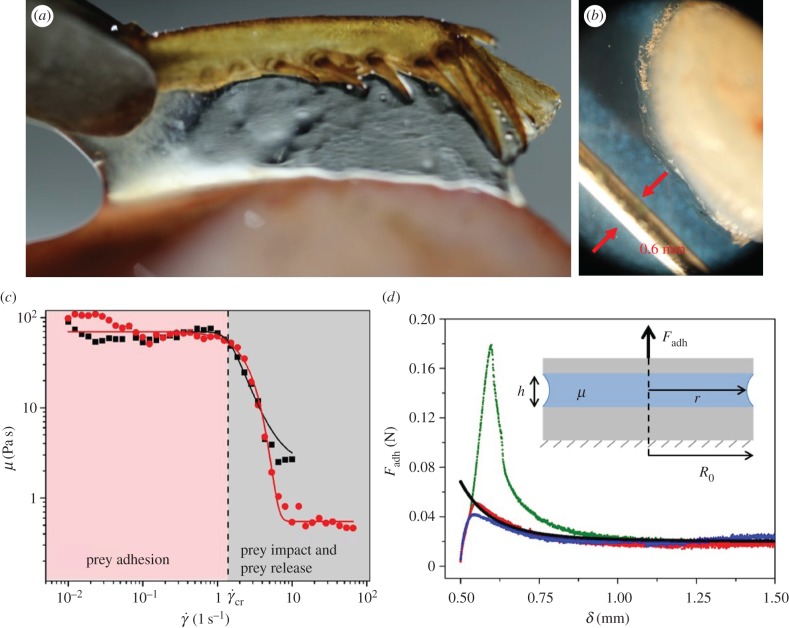
Saliva is known for being viscoelastic, having properties of both a fluid and a solid. Indeed, when pulling a cricket leg from the tongue surface, the saliva also displays excellent wetting properties (figure 3a). The microstructure of the frog tongue is known to vary across lineages [11]. The frog tongue is covered in fungiform and filiform papillae, which can reach 230 μm in height and 160 μm in diameter [12]. These papillae contain mucus glands, which secrete the saliva; the saliva penetrates between all papillae, saturating the epithelial tissue like a hydrogel. We measured the maximum possible thickness of the saliva layer by measuring the change in weight induced by wiping a tongue clean of saliva. 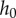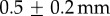The average layer height is , nearly seven times thicker than human saliva [13]. This is an overestimation since it is likely we are drawing saliva out from between the papillae stalks. To validate, we dipped a freshly severed frog tongue in liquid nitrogen then viewed the tissue cross section. The saliva was visualized as a semi-opaque layer, while the tissue was pink and opaque (figure 3b). The saliva layer ranged from 0.2 to 0.7 mm.

Figure 3.

Saliva properties. (a) A cricket leg is retracted from the frog tongue. (b) Tongue tissue cross-section showing the semi-opaque saliva layer. Reference pin is 0.6 mm wide. (c) Frequency sweep test of frog saliva. Black and red symbols denote experiments, solid lines the Carreau–Yasuda theoretical model. (d) Separation forces for frog saliva sandwiched between two parallel plates as shown in inset. Blue, red and green squares denote three experimental trials. The black line denotes the Stefan theory. (Online version in colour.).

We laboriously collected 0.3 ml of saliva from 15 leopard frogs and placed it into a cone-and-plate rheometer. We performed a frequency sweep test to determine the shear viscosity. The results closely match the Carreau–Yasuda model [14] for shear-thinning fluid (solid lines in figure 3c), where the viscosity μ is given by

2.1

where 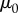and 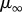are the asymptotic viscosities at zero and infinite shear rate, respectively, 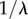is the critical shear rate when viscosity decreases, a is the width of transition, and 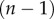is the power-law slope fitting the transition region. Our two trials with separate samples show the results are repeatable.

At low shear rates 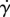, the saliva zero shear viscosity 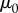plateaus at 70 Pa s, nearly 50 000 times more viscous than human saliva [15] (figure 3c). While this value may seem high, other shear-thinning biological mucus has similar values at low shear rates such as human lung mucus 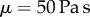[16] and sundew plants 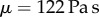[17], which also follows the Carreau–Yasuda model. For frog saliva, the critical shear rate 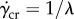ranges from 1.4 to 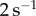. Shear rates above this value yield low viscosities in the range 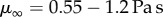. For frogs, a saliva with variable viscosity increases functionality in all phases of prey capture, as labelled in figure 3c. Low viscosity assists in prey impact and release; high viscosity assists in prey adhesion. We provide modelling and scaling arguments to support this claim in the following sections.

2.3. Prey impact and release

During prey impact, a low-viscosity saliva is better at penetrating rough surfaces and increasing contact area, much like paint on a wall. As we will see in later sections, a larger contact area results in better adhesion. Figure 3d shows the tongue and insect modelled by two circular flat plates. During impact, the plates are compressed with speed V. If the layer is thin, the corresponding shear rate is 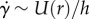, where 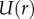is the fluid velocity in the radial direction. Since the saliva is incompressible, we may use conservation of volume to write the velocity 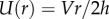and the radius of the saliva as 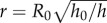. Together, the relationship between shear rate 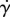and plate velocity V may be written

2.2

The leopard frog tongue can reach impact speeds up to 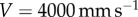. If we assume instantaneous impact, or fixed surface contact, this results in saliva shear rates of 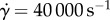, well above 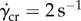, the limit at which frog saliva viscosity drops. This shear rate represents the highest shear-rate scenario between tongue and prey. For lightweight prey, shear rates may be lower. Nevertheless, high-speed impact takes advantage of the saliva's rheological properties to increase tongue adhesion while simultaneously overcoming the insect reaction time.

A soft tongue also helps to increase contact area during prey impact. Consider indentation of a rigid spherical insect of radius 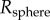into a frog tongue, represented as a semi-infinite elastic plane. From Hertz theory, the applied force scales nonlinearly with the displacement δ according to 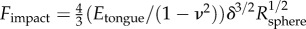, where 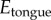and ν are Young's modulus and Poisson's ratio, respectively, of the tongue [7]. During indentation, the saliva fills the gap between the indenter and the surface at the tissue–indenter–air interface, allowing the contact area A to be approximated as the surface of a spherical cap: 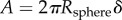. Eliminating 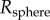and δ, we may rewrite the applied force as 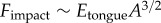. The softer the tongue, the larger the area of contact. In fact, replacing the frog tongue with a stiffer human tongue would result in an 80% decrease in contact area.

If the tongue is so sticky, how does the frog ultimately remove the insect? X-ray videography has shown that a frog retracts its eyeballs to push food down its throat [18]. A leopard frog retracts its eyeballs at speeds up to 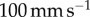. This motion provides a shearing force parallel to the tongue at shear rates around 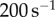, well above the limit at which saliva will flow. Much like pushing a hockey puck on ice, objects on the frog tongue are easy to shear, enabling effortless prey removal. The true strength of the saliva is in the direction perpendicular to the tongue surface, which we consider in the next section.

2.4. Prey adhesion

The most challenging part of catching prey is keeping the prey on the tongue [19]. How does the prey remain stuck to the tongue? Previous models of adhesion have considered soft surfaces (e.g. [20–22]). These models consider adhesion in the context of surface energy and cannot be applied here since our soft substrate is coated in a layer of viscous fluid. We present a series of adhesive models of increasing sophistication, incorporating saliva rheology in combination with tongue viscoelasticity. We first consider the adhesive ability of saliva between two rigid plates. We then consider adhesion with a soft frog tongue at low and high speed.

During retraction, adhesion force 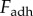consists of a surface tension force 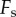and viscous force 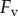: 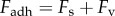. We consider normal separation of only frog saliva sandwiched between circular, rigid, flat plates. The surface tension force [23] scales with the product of the Laplace pressure 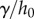and contact area 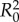, yielding 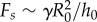, where 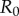is the plate radius, γ is the surface tension and 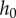is the initial saliva layer thickness. 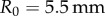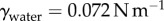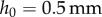Using , and , the surface tension force contributes less than 10% to the overall force required for insect adhesion and is neglected from consideration hereon.

The adhesive force 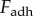is now equal to the viscous force 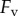. The viscous force holding the plates together is given by the Stefan equation [24],

2.3

where μ is the saliva viscosity and V is the separation velocity of the plates (figure 3d inset). The Stefan equation is valid if the saliva layer is thin, the fluid is an incompressible Newtonian fluid and the flat plates are rigid. Is it possible to use the Stefan equation to model adhesion on a soft, deformable frog tongue coated in a thin layer of viscoelastic saliva?

While the frog saliva is non-Newtonian, we may relax the incompressible Newtonian fluid assumption when operating in the low shear rate regime, where saliva has a viscosity 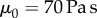across an order of magnitude in shear rates. We test the validity of the force law in equation (2.3) by separating frog saliva trapped between two flat aluminium plates of radius 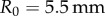. The plates are brought to a height 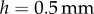then retracted at a rate of 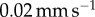. The corresponding force is shown for three separate trials of a single saliva sample in figure 3d. The discrepancy in the third trial (green data) comes from the evaporation of the saliva sample over an extended period of time, but still fits the Stefan equation trend assuming a thinner saliva height h. Since two of three trials compare well with the Stefan theory (solid black line), we will use the force law from equation (2.3), hereon. Other studies have used the Stefan equation to characterize the viscous force on the tongue, such as chameleon tongue adhesion [25].

Previous studies [2,4,5] have measured adhesion force 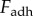, which only partially describes adhesive strength. A whole picture of the adhesion process is given by work of adhesion W, the energy expended to remove an adhesive from a solid surface. This measurement encompasses all sources of energy storage and dissipation during the full time of contact. The work of adhesion is defined as the area under the force–displacement curve, from initial displacement to failure. The resultant value is then divided by the initial contact area, 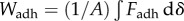. The average work of adhesion for the separation of frog saliva between two rigid plates is .

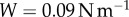We now consider the effect of tongue softness. We perform a quasi-static separation test of a frog tongue and a rigid, flat aluminium indenter (figure 4a,b). We conduct five tests with retraction velocity (V) ranging from 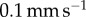to 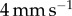. The relationship between force and displacement is shown as the scatter data in figure 4c. The tongue can be stretched by 8 mm, more than twice the thickness of the tongue, without breaking contact. We observe from figure 4a a negligible change in saliva layer height during indenter retraction. Therefore, we can relax the rigid plate assumption by assuming the saliva does not stretch during adhesion ().

Figure 4.

Adhesive force and work of adhesion of the frog tongue, measured in a quasi-static test. (a) Time sequence of an indenter pulling away from the frog tongue. The tongue deforms greatly before separating. (b) Schematic of the quasi-static test. (c) Relationship between force and displacement. Experiments denoted by points and mathematical model by solid lines. Various retraction speeds are shown including (black), (red), 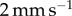(orange), 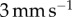(green) and 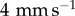(blue). Inset shows model predictions of the average contact radius. (d) Work of adhesion 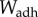for each retraction rate. Experiments are solid colours, with theory overlaid in hatched colour. (e) Tongue peeling as the indenter is displaced. The tongue is visualized through a transparent acrylic indenter. Graph shows that the average contact radius decreases linearly with displacement.

Theoretical predictions for force–displacement are shown as solid lines in figure 4c. Our model was created by combining equations (2.1)–(2.3) with the assumption that 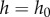, and solved using iteration,

2.4

Our iterative technique, as detailed in the Experimental methods section, captures the experimental force values well, across a range of applied indenter speeds. Physically, the peak force represents the point at which the saliva begins to flow, when the shear rate exceeds the critical shear rate. Our model also predicts the change in contact radius in figure 4c (inset). The linear change in contact radius is qualitatively similar to our experiments. We note the radius decreases quickly once the viscosity of the saliva drops. Physically, the model demonstrates two phases in the adhesion. In the first phase, the tongue is stretched progressively, which increases the force applied to the saliva. The saliva remains unchanged in both height and viscosity, because it is below its critical shear rate. In the second phase, the elastic force from the tongue is sufficiently high that the saliva begins to flow. The tongue contact area decreases and the adhesion force decreases accordingly. In both phases, the adhesion force arises from the stretching of the tongue. The maximum force obtained arises from the rheological properties of saliva, which drive the onset of peeling of the saliva layer.

The work of adhesion is 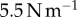and is relatively invariant across pulling speed, as shown in figure 4d. Our mathematical model (hatched colour) matches closely, over-predicting the work of adhesion by at most 25% of the experimental values. The work of adhesion of the tongue is 60 times greater than for rigid plates coated with saliva. Thus, softer materials have higher work of adhesion. Indeed, when comparing the frog tongue with other stiffer materials such as tree frog toe pads (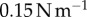) [26] and sticky hand toys (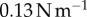), the frog tongue has more than 50 times higher work of adhesion.

Why does the frog tongue have such a high work of adhesion? The answer to this question elucidates why the frog tongue feels so sticky. When we separate tape from our fingers, a stiff glue from the tape prevents fracture, and increases the work necessary to dislodge the tape. However, the frog tongue has a reversible shear-thinning adhesive. To increase its work of adhesion, the frog instead relies on a soft tongue, similar to tape with a backing material made of jelly. When forces are applied, work is done to distend the frog tongue.

Figure 5 shows how a softer tongue can increase the work of adhesion. Consider a tensile test done on both a frog tongue with Young's modulus E and a human tongue, which is nearly 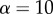times stiffer. Assume both tongues have the same adhesive coating, which sets the fracture force f of both materials. Because the frog tongue is 10 times softer, it can stretch to 10 times the deformation of the human tongue before fracture occurs. The work of adhesion for the frog tongue is 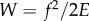, which is α times greater than the work of adhesion for the human tongue. Softer tongues have a higher work of adhesion.

Figure 5.

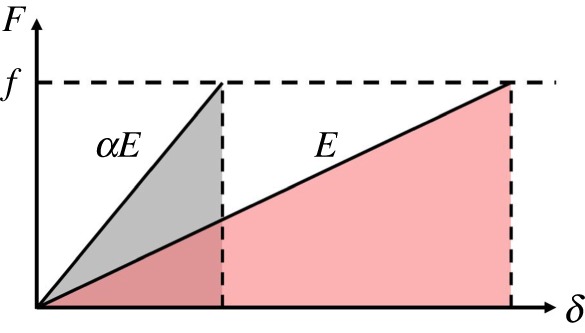
The relationship between force and displacement for a soft tongue and a stiff tongue. Both tongues have an adhesive fracture force f (dotted line). (Online version in colour.)

3. Dynamic simulation

The limits of modern technology preclude a high-speed test of the tongue. How does the tongue's damping alter adhesion in a real prey capture scenario? We use a dynamic simulation to investigate the importance of tongue damping. We use the floating spring–mass–damper system in figure 1c to simulate a frog capturing an insect of mass 0.5 g. The tongue epithelial tissue represents a spring–damper in parallel. The damping coefficient is given by the measured value 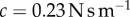. The spring stiffness (k) can be extrapolated from the measured Young's modulus 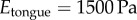and the contact radius of a cricket, 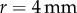. The applied force 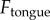is extrapolated from the high-speed video data in figure 1b. The saliva layer sits between the spring–damper and the prey; by examining the force exerted by the spring and damper, we can determine the force exerted on the saliva 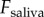. Our equation of motion is

3.1

where 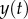is the acceleration of the tongue based on experimental data, spring constant 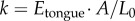and 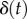is the epithelial displacement between tongue muscle and the prey. We solve this equation for the displacement 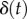using details in the Experimental methods section. We write the force exerted on the saliva as .

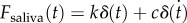As shown from equation (2.4), a larger applied force on saliva will generate higher shear rates, which can cause separation. For clarity, we will refer to 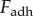as 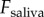for the dynamic simulation. The applied force 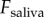should be minimized to keep the insect attached. Tongue elasticity stores energy in the tissue and damping absorbs the stored energy. If the tongue had no damping coefficient, the stored energy would be exerted back onto the insect, resulting in higher peak forces. Figure 6a shows how the saliva force changes with the addition of a damping coefficient. The black line is the force applied on the tongue, 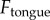. The black dashed line represents the minimum force at which saliva drops in viscosity from equation (2.4); this point is where rapid peeling occurs and should be avoided. The green line shows the predicted force using the damping coefficient of the frog tongue. The red line shows the force with no damping. As the damping increases, the peak force on saliva decreases, as desired. Peak force on the saliva can decrease by as much as 30% from the addition of a damping coefficient.

Figure 6.

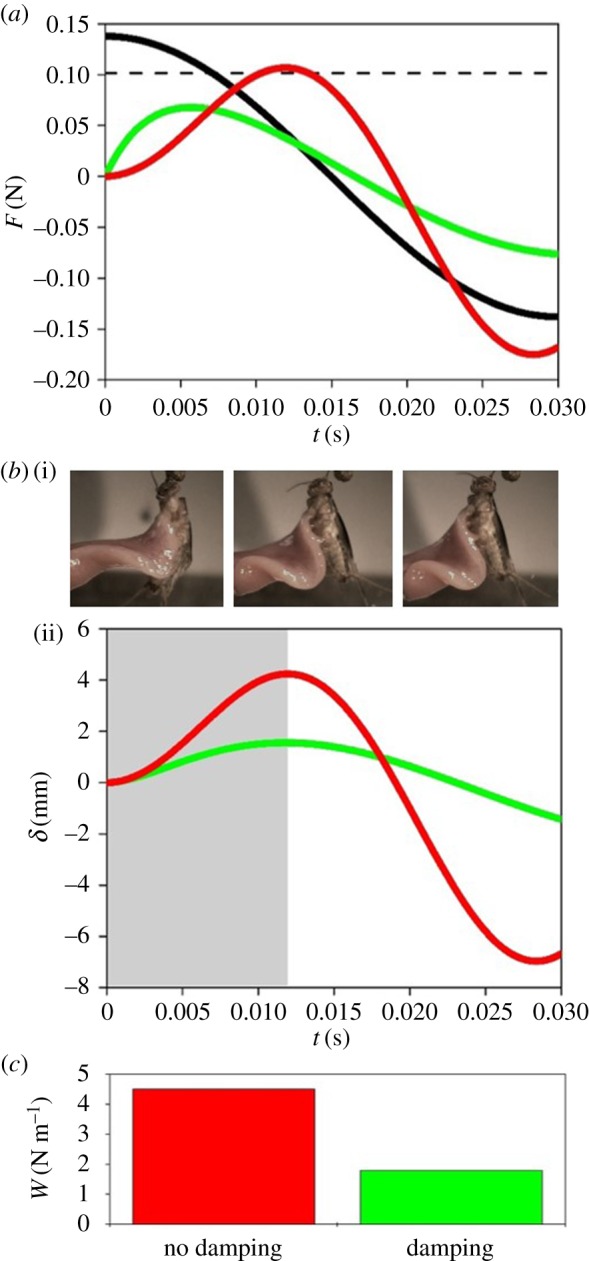
Dynamic simulation of frog tongue. (a) Time course of the applied force on tongue 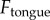(solid black line). The separation force on the saliva 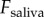is shown for two damping coefficients. Zero damping is in red, and realistic damping (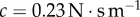) is in green. The dashed black line represents the force at which saliva flows and prey is released. (b) Time course of the stretch of the tongue epithelial tissue. Experimental video footage illustrates the stretch. (c) Work of adhesion for the two damping coefficients tested. (Online version in colour.)

Damping not only alters the peak force applied, but also the work that is done on the saliva. Figure 5b shows how epithelium displacement 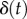changes with damping. The predicted value of 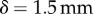for the measured damping is close to the displacement observed in experimental footage in figure 6b(i). Without damping, the tongue epithelium would stretch up to 4 mm, probably resulting in fracture. The total work for each case is summarized in the bar chart in figure 6c. The work performed on the saliva for the damped tongue is 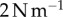, which is about a third of the work required to separate the saliva, found in §2.4. However, without damping, the work is 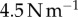and may result in the tongue separating from the insect. The damping of the tongue acts like the shock absorber of a car. Damping allows higher forces to be exerted on the prey before peeling occurs. The use of shocks has been shown to be important in reducing force and oscillation, such as in mammalian paws [27] and soft soles in running shoes [28].

4. Discussion

The study of adhesives has long been inspired by amphibians, reptiles and invertebrates. The gecko is the champion of dry adhesion, using van der Waals forces derived from its thousands of setae. The limpet Patella vulgata L. excretes thick mucus to adhere to wet, rough surfaces, using the viscous forces associated with Stefan adhesion [5,29]. Comparatively less work has been done on frog tongues, a wet bioadhesive. Previous investigators have speculated that the sticky saliva acts like a pressure-sensitive adhesive such as Scotch Tape. In our study, we found the tongue's adhesion is more subtle than that. The tongue's stickiness is a result of both material properties of the tongue and rheological properties of its coating. In comparison, modern sticky tapes are often made of stiff materials. Forces applied to the tape directly cause separation in the adhesive. In the frog, applied forces are either dissipated in the tongue's internal damping or stored in its stretchy tissue. A stiff tongue would result in reduced contact area during prey impact. The shear-thinning properties of saliva emulate paint, a well-known shear-thinning fluid. Paint is thrown onto a wall with a brush, flowing at high speeds to create an even coating. At low speeds, it clings to the wall. In the same way, the saliva coats the insect on impact, but sticks to the prey in retraction.

Our study shows that an even and thin coating of the saliva is critical to prey capture. This study points to the importance of the saliva in prey adhesion. During our adhesion testing, areas of the frog tongue would dry out and cause nearly instantaneous fracture from the indenter. Any non-uniformities in the layer will cause stress concentrations and areas where fracture can occur during prey retraction. The frog probably has several biological adaptations to protect its saliva. We observe that the frog prevents its tongue from desiccation by keeping its mouth shut. In addition, the densely packed papillae create a composite-like surface structure which may aid in continuous adhesion of saliva to tissue, much like a hydrogel [11].

5. Conclusion

Frog tongues have a number of properties that enable successful high-speed prey capture. First their tongue is one of the softest biological materials known, enabling the tongue to wrap around the prey during impact, facilitating a large contact area. Second, the tongue is highly damped like a car's shock absorber. As an insect is suddenly pulled at high speed, the insect's inertia induces large separation forces with the tongue. These forces are reduced by the internal damping in the tongue. We use mathematical modelling to show that, without the tongue's damping, the insect is in danger of breaking contact with the insect. Lastly, the tongue is coated with a thin layer of saliva with non-Newtonian properties like paint. The saliva flows upon impact with the prey, grips when the prey is retracted, and then flows again when the frog swallows. The combination of these favourable traits may be useful in designing reversible adhesives that stick at high speed.

6. Experimental methods

6.1. Kinematics

Five leopard frogs Rana pipiens (Sullivan Company) were used for high-speed videography of tongue projection. The frog was placed into a clear acrylic container and a 0.5 g cricket was suspended with fishing twine. Tongue projection was filmed from the side using a Phantom Miro M110 high-speed camera at 1400 fps. The video was analysed using Tracker to determine tongue kinematics. A sinusoidal fit is applied to the insect capture kinematics (black boxes) from figure 1b. The applied tongue force (figure 6a, black line) is determined to be 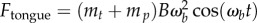, where 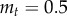g is the mass of the frog tongue, 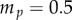g is the mass of the prey, 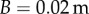is the amplitude of the tongue tip during prey capture and 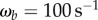is the tongue base frequency.

6.2. Tissue softness measurement

A Bose ElectroForce 3100 was used to perform quasi-static probe indentation tests on all frog tongue tissue samples. A leopard frog tongue was collected and tested within 1 h of death; tongues from all other frog and toad species were frozen post-mortem, then defrosted and tested. Each species was tested three times except for Phyllomedusa trinitatis, which was tested once. Each tongue was tested in the elastic solid regime, where stress is linear with strain. A rigid, flat-ended cylindrical indenter of diameter 2 mm was used to probe the tissue at a rate of 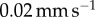. The force–displacement model for a cylindrical indenter is

6.1

where 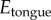is Young's modulus of the tongue, r is the indenter radius, δ is displacement and ν is Poisson's ratio. Poisson's ratio is assumed to be 0.5 for a perfectly elastic material [30]. Young's modulus was calculated from the force and displacement measured from the indenter.

6.3. Dynamic indentation

Using the same set-up from the quasi-static indentation test, the cylindrical indenter was sinusoidally pressed into the tongue tissue at various frequencies with an amplitude of 1 mm, and the force was recorded. The Kelvin–Voigt model is used to represent the tissue as an elastic spring and purely viscous damper in parallel. The system is described by the linear differential equation: 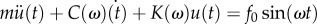, where m is the indenter mass, 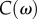is the damping coefficient, 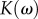is the stiffness coefficient and ω is the frequency. The sinusoidal-resistive force is given by 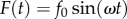, and the applied indenter displacement is given by 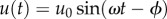, with a phase shift ϕ. 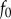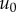The stiffness and damping coefficients for each frequency can be determined by measuring ϕ, and , and are given by the following solutions to the differential equation [10]:

6.2

and

6.3

Young's modulus can be determined by using equation (6.1), with .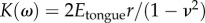

6.4. Rheometer tests

Saliva was collected by opening the mouth of a recently euthanized frog and rubbing its tongue on a plastic sheet. The thin layer of saliva was then swirled using tweezers until a saliva globule was formed. The globule was immediately placed in a sealed container. For one frog, this process took less than 30 s. We were able to collect saliva with minimal evaporation due to the unique seal of the frog mouth, which protects from water leakage. This process was repeated for all frog specimens. Care was taken to use an intact tongue so that blood did not contaminate the sample. The 0.3 ml saliva sample was placed in a cone-plate rheometer (Anton Parr MCR 501) and a frequency sweep test was performed from 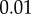to 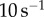to determine the shear viscosity. During the test, the sample was surrounded by a ring of water to reduce the saliva evaporation rate. Following the hour-long experiment, the saliva was intact, with only slight evaporation found at an edge.

6.5. Saliva Stefan adhesion

A Bose ElectroForce 3100 was used to perform Stefan adhesion tests on a leopard frog saliva sample. A rigid, flat-ended cylindrical indenter of radius 5.5 mm was brought into contact with a saliva sample of height 0.5 mm, then retracted at a speed of 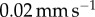to a total displacement of 1.5 mm. The force from three trials was recorded. The force sensor had a reading offset of 0.02 N. Between each trial, the saliva was scraped off the indenter and reapplied to the base platform to reduce air pockets in the sample. The duration of each trial was 75 s, with approximately 60 s between each trial. The third trial exhibited slight evaporation of the saliva sample, as evident in the data discrepancy.

6.6. Quasi-static adhesion

Using a Bose ElectroForce 3100, a 5.5 mm radius indenter was brought into contact with a freshly severed leopard frog tongue and then retracted at a rate of 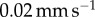. The force from 11 trials was recorded, then averaged for figure 4c. To reduce sliding of the frog tongue and the base plate, the bottom of the tongue was wiped dry prior to experimentation.

6.7. Quasi-static iterative model

Our theoretical prediction (equation (2.4)) combines saliva rheology, elastic force of the tongue and viscous resistance by Stefan adhesion. The solution is found by iteration. As the indenter retracts, the tongue stretches, applying an elastic force on the saliva layer

6.4

where r is the contact radius, 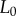is the thickness of the tongue sample and δ is the indenter displacement. In steady state, the elastic force of the tongue equals the adhesive force of the saliva 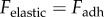. The internal damping of the tissue is disregarded for this quasi-static test. The variables that change as a function of displacement are the adhesion force , strain rate 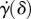and contact radius 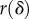. Initial conditions are 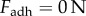, 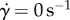and 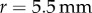. For each incremental change in δ, is calculated from equation (6.4) then substituted into equation (2.4) to find the corresponding shear rate 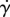. An increase in shear rate drives a shrinking of the contact radius. The incremental change in contact radius 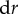may be written as 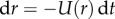, where 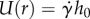, assuming a Couette flow profile in the saliva. Throughout the simulation, we assume the saliva thickness remains constant, in accordance with our observations.

When we ran the above version of the model, we found that the strain rate diverged, and the tongue broke contact prematurely. As an ansatz, we cap the strain rate from above based on our experimental observations. A transparent acrylic indenter is retracted at a fixed rate from the frog tongue surface, and the peeling area over time is measured (figure 4e). Specifically, we observe the average contact radius varies linearly with displacement, suggesting that strain rate has a maximum finite value. Based on conservation of mass, the largest strain rate that can be attained is 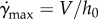, since the maximum velocity within the saliva is the indenter velocity, 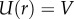. This cap is used in our computations, and results in the contact radius r shown in the inset of figure 4c.

6.8. Peeling visualization

A transparent acrylic indenter of radius 5.5 mm was used to visualize peeling during quasi-static adhesion. A Canon EOS 1D camera was used to film the progression of full contact to separation. The video was then analysed to find the total contact area between the tongue and the indenter over time.

6.9. Dynamic simulation

The frog tongue and prey is modelled as a mass–spring–damper system (figure 1c). Using the principle of superposition, the applied tongue force (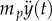) can be modelled as a summation of unit impulses over time. Using the convolution integral, we can combine the applied tongue force curve with the response for a unit impulse for our single degree-of-freedom system. The convolution integral provides the spring stretch δ over time.

Ethics

This study was approved by the Office of Research Integrity Assurance and conducted in accordance with all protocols filed under the Georgia Tech Institutional Animal Care and Use Committee. All leopard frog tongue tissue samples were donated post-mortem by Dr E. Behravesh following his undergraduate dissection class.

Competing interests

We declare we have no competing interests.

Funding

This material is based upon work supported by the National Science Foundation Graduate Research Fellowship (DGE-1148903), NSF career award (PHY-1255127), Georgia Tech School of Biology and the Elizabeth Smithgall Watts endowment.