Abstract
In this paper, the role of gradient micro-inertia terms and free micro-inertia terms is investigated to unveil their respective effects on the dynamic behaviour of band-gap metamaterials. We show that the term alone is only able to disclose relatively simplified dispersive behaviour. On the other hand, the term alone describes the full complex behaviour of band-gap metamaterials. A suitable mixing of the two micro-inertia terms allows us to describe a new feature of the relaxed-micromorphic model, i.e. the description of a second band-gap occurring for higher frequencies. We also show that a split of the gradient micro-inertia , in the sense of Cartan–Lie decomposition of matrices, allows us to flatten separately the longitudinal and transverse optic branches, thus giving us the possibility of a second band-gap. Finally, we investigate the effect of the gradient inertia on more classical enriched models such as the Mindlin–Eringen and the internal variable ones. We find that the addition of such a gradient micro-inertia allows for the onset of one band-gap in the Mindlin–Eringen model and three band-gaps in the internal variable model. In this last case, however, non-local effects cannot be accounted for, which is a too drastic simplification for most metamaterials. We conclude that, even when adding gradient micro-inertia terms, the relaxed micromorphic model remains the best performing one, among the considered enriched models, for the description of non-local band-gap metamaterials.
Keywords: gradient micro-inertia, free micro-inertia, complete band-gaps, non-local effects, relaxed micromorphic model, generalized continuum models
1. Introduction
The question of effectively studying the dynamic behaviour of microscopically heterogeneous materials in the simplified framework of continuum mechanics is a major challenge for engineering sciences.
Indeed, it is rather clear from the present state of knowledge that classical Cauchy continuum models are too simplified to describe the behaviour of a huge class of materials in the dynamic regime. As a matter of fact, almost all real materials show dispersive behaviour with respect to wave propagation, especially when considering waves with small wavelengths. More precisely, this means that the speed of propagation of waves is not a constant, as happens for Cauchy continua, but that it depends on the wavelength of the travelling wave. Such a phenomenon is comprehensible if one thinks of the fact that the mechanical properties of materials vary when going down to lower scales. It is then sensible that the speed of propagation of mechanical waves varies when considering waves with wavelengths which are small enough to be comparable to the characteristic size of the underlying heterogeneities.
If Cauchy continuum theories are not rich enough to catch these dispersive behaviours, generalized continuum theories offer the possibility of describing wave dispersion while still remaining in the framework of continuum mechanics. Although various generalized continuum models have been introduced to describe dispersion (see the pioneering works [1,2]; for a review of the use of enriched models in the dynamics of heterogeneous materials we refer to [3]), it is still not completely clear whether such dispersive properties can be attributed to the constitutive assumptions which are made on the strain energy density or to the choice of the micro-inertia terms which can be introduced.
The aforementioned considerations about the dispersive behaviour of materials can be reformulated with renewed awareness when talking about metamaterials.
Metamaterials are man-made artefacts which are conceived by assembling small structural elements in periodic or quasi-periodic patterns in such a way that novel mechanical behaviour emerges. Metamaterials are often studied from both a static (those with enhanced mechanical properties with respect to traditional materials) [4–6] and a dynamic (those exhibiting band-gaps, negative refraction, cloaking, focusing, etc.) point of view [7–14]. The characteristic size of microstructures in such metamaterials usually ranges from micrometres to centimetres, so that they show dispersive behaviours for wavelengths which are relatively large.
More than this, some metamaterials can exhibit dispersive behaviour, which gives rise to unorthodox mechanical properties that are not encountered in natural materials. For example, some metamaterials are able to inhibit wave propagation within certain frequency ranges due to the presence of an underlying microstructure which is able to resonate locally when excited at those frequencies or even to remain completely unperturbed. The energy of the incident wave remains trapped at the level of the microstructure and the macroscopic propagation results to be inhibited. Evidence of this type has been reported in the literature based on both theoretical studies [15,16] and experimental results [10,17].
To capture the complex behaviour exhibited by such metamaterials while remaining in the framework of continuum mechanics, generalized continuum models with enriched kinematics are needed. This means that extra degrees of freedom must be introduced in the spirit of micromorphic theories [1,2], which take into account micro-motions at the level of the microstructure. More particularly, the kinematic unknowns of such micromorphic models are usually the macro-displacements u and the micro-distortion tensor P. Well-adapted constitutive choices must then be introduced for the strain energy density in order to describe accurately the behaviour of the considered metamaterials in the static regime.
As a last point, appropriate inertia terms must be introduced to model the mechanical behaviour of metamaterials in the dynamic regime. It is exactly this point that will be the focus of the present paper: how to choose well-suited micro-inertia terms when dealing with enriched continuum models of the micromorphic type? How does each of these terms affect the dynamic behaviour of real band-gap metamaterials? Some hints on the role of micro-inertia in modelling dispersive behaviour are given in [18] but many fundamental questions remain open.
We will show in this paper that:1
— Gradient micro-inertia terms only allow us to describe dispersion either in classical or in enriched continuum models [18].
— Micro-inertia terms involving time derivatives of the extra kinematic degrees of freedom η∥P,t∥2 allow us to describe and control optic branches in the dispersion relations of classical and relaxed micromorphic continuum models [1,2,19–26].
— The relaxed micromorphic model with micro-inertia of the type η∥P,t∥2 is able to describe the onset of the first band-gaps in mechanical metamaterials [20–24].
— The relaxed micromorphic model with both micro-inertia terms η∥P,t∥2 and allows us to account for the first and also for the second band-gap which occurs for higher frequencies.
— Classical Mindlin–Eringen models with full micro-inertia η∥P,t∥2 and allow for the description of only the first band-gap.
— Internal variable models with full micro-inertia η∥P,t∥2 and allow for the description of three band-gaps, even if some peculiar phenomena related to non-locality cannot be accounted for and the resulting behaviour is thus not versatile enough to model realistic metamaterials.
For the first three points a clear treatise is present in the literature, while the last three points are discussed for the first time in this paper.
Finally, we show that a weighted gradient micro-inertia of the type allows us to flatten some optic curves independently for longitudinal and transverse waves. More precisely, if the parameter allows us to flatten one optic curve for longitudinal waves, the parameter has an analogous effect for transverse waves. Such improved control on the dispersion curves will allow for a more effective fitting procedure on real band-gap metamaterials, since the description of the second band-gap occurring at higher frequencies becomes accessible. The effects of analogous decompositions on the other terms of the energy densities have already been studied in [27].
We have already shown in [20] that the relaxed micromorphic model with free micro-inertia can be successfully used to describe the dynamic behaviour of actual band-gap metamaterials. In that case, we showed that the model is perfectly able to capture experimental results related to the transmission coefficient at an interface between a classical Cauchy material and a specific band-gap metamaterial. The proposed use of the relaxed micromorphic model for the description of that particular physical system is accurate enough to faithfully reproduce the transmission coefficient as a function of frequency, also capturing specific internal resonance phenomena that are characteristic of the targeted metamaterial.
Moreover, preliminary studies on other band-gap metamaterials, which will be reported in papers in preparation or already submitted to other journals, allow us to:
— confirm the effectiveness of the use of the relaxed micromorphic model for the description of actual band-gap metamaterials via a restricted number of constitutive parameters (such parameters are true material parameters, i.e. they are constants when fixing the metamaterial and independent of frequency; see [28]),
— perfectly fit the relaxed micromorphic model on both the dispersion curves of the targeted metamaterials and the reflection/transmission spectra at material surfaces embedded in such metamaterials,
— show the specific effect that both free micro-inertia and gradient micro-inertia have on the dispersion patterns of such specific metamaterials. Indeed, as will be shown in subsequent works, both types of micro-inertia are needed when one wants to describe, with sufficient precision, a wide class of realistic band-gap metamaterials.
This paper lays the foundations for the extensive use of enriched continuum models of the micromorphic type for the characterization of the behaviour of a huge class of actual metamaterials. The advantage of the use of such models will become evident when the mechanical behaviour of a consistent number of metamaterials is described with the simple introduction of a few material parameters which are true material constants, independent of frequency and not relying on the usual hypothesis of separation of scale.
2. The relaxed micromorphic model
Our novel relaxed micromorphic model endows the Mindlin–Eringen representation with the second-order dislocation density tensor α=−Curl P instead of the full gradient ∇P.2 In the isotropic case, the elastic energy reads
| 2.1 |
where the parameters and the elastic stress are analogous to the standard Mindlin–Eringen micromorphic model. The model is well posed in the static and dynamic cases, including when μc=0 (see [19,25]).
In our relaxed model, the complexity of the general micromorphic model has been decisively reduced and features basically only symmetric gradient micro-like variables and the Curl of the micro-distortion P. However, the relaxed model is still general enough to include the full micro-stretch as well as the full Cosserat micro-polar model (see [26]). Furthermore, well-posedness results for the static and dynamic cases have been provided in [26], making decisive use of recently established new coercive inequalities that generalize Korn’s inequality to incompatible tensor fields [29–33].
The relaxed micromorphic model counts six constitutive parameters in the isotropic case (μe, λe, μmicro, λmicro, μc, Lc). The characteristic length Lc is intrinsically related to non-local effects due to the fact that it weights a suitable combination of the first-order space derivatives in the strain energy density (2.1). For a general presentation of the features of the relaxed micromorphic model in the anisotropic setting, we refer to [34].
As for the kinetic energy, we consider in this paper that it takes the following form:3
| 2.2 |
where ρ is the value of the average macroscopic mass density of the considered metamaterial, η is the free micro-inertia density and the , are the gradient micro-inertia densities associated with the different terms of the Cartan–Lie decomposition of ∇u.
If the first two terms appearing in equation (2.2) can be directly related to those introduced by Mindlin [2], the last three terms of the gradient micro-inertia are considered here for the first time when dealing with enriched continua of the micromorphic type. In fact, gradient micro-inertia terms are currently used when dealing with second gradient continua [35,36], but never when considering micromorphic models. Nevertheless, based on our first comparisons with experimental results [20,28], we are persuaded that gradient micro-inertia is essential also when considering enriched models of the micromorphic type if the ultimate goal is that of describing the behaviour of actual physical systems.
The associated equations of motion in strong form, obtained by a classical least action principle, take the form [22–25]
| 2.3 |
where
| 2.4 |
The addition of a gradient micro-inertia to the kinetic energy (2.2) modifies the strong-form PDEs of the relaxed micromorphic model with the addition of the new term . Of course, boundary conditions would also be modified with respect to the ones presented in [20,24]. The study of the new boundary conditions induced by gradient micro-inertia will be the subject of a subsequent paper, in which the effect of such extra terms on the conservation of energy will also be analysed.
3. Plane-wave propagation
Sufficiently far from a source, dynamic wave solutions may be treated as planar waves. Therefore, we now want to study harmonic solutions travelling in an infinite domain for the differential system (2.3). We suppose that the space dependence of all introduced kinematic fields is limited to the scalar component X, which is also the direction of propagation of the wave. To do so, following [20–24,37], we define
| 3.1 |
With this decomposition, equations (2.3) can be rewritten as [22,23]
- — a set of three equations only involving longitudinal quantities:
3.2 - — two sets of three equations only involving transverse quantities in the ξth direction, with ξ=2,3:
3.3 - — one equation only involving the variable P(23):
3.4 - — one equation only involving the variable P[23]:
3.5 - — one equation only involving the variable PV:
3.6
Once this simplified system of PDEs is obtained, we look for a waveform solution of the type:
| 3.7 |
where we set for compactness
| 3.8 |
where , and are the unknown amplitudes of the considered waves,4 k is the wavenumber and ω is the wave frequency.
Replacing the waveform solution (3.7) in equations (3.2)–(3.6), it is possible to express the system as
| 3.9 |
where
Here, we have defined:
To have non-trivial solutions of the algebraic systems (3.9), one must impose that
| 3.10 |
The solutions ω=ω(k) of these algebraic equations are called the dispersion curves of the relaxed micromorphic model for longitudinal, transverse and uncoupled waves, respectively.
In what follows we will present the results obtained for the numerical values of the elastic coefficients shown in table 1 if not otherwise specified.
Table 1.
Values of the parameters used in the numerical simulations (top), and corresponding values of the Lamé parameters and of the Young modulus and Poisson ratio (bottom), for the formulas needed to calculate the homogenized macroscopic parameters starting from the microscopic ones (see [34]).
| parameter | value | unit |
|---|---|---|
| μe | 200 | MPa |
| λe=2μe | 400 | MPa |
| μc=5μe | 1000 | MPa |
| μmicro | 100 | MPa |
| λmicro | 100 | MPa |
| Lc | 1 | mm |
| ρ | 2000 | kg m−13 |
| λmacro | 82.5 | MPa |
| μmacro | 66.7 | MPa |
| Emacro | 170 | MPa |
| νmacro | 0.28 | — |
In the following sections, we will explicitly discuss the effect of each micro-inertia parameter on the dispersion curves of the relaxed micromorphic model. More particularly, we will focus on the following cases:
— vanishing free micro-inertia η=0 and non-vanishing gradient micro-inertia,
— both non-vanishing gradient micro-inertia and free micro-inertia.
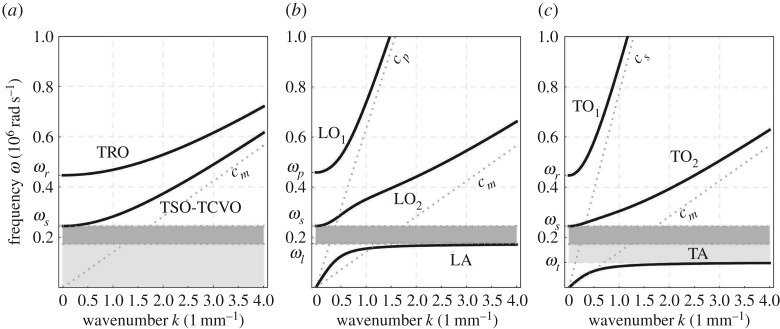
The remaining case (vanishing gradient micro-inertia and non-vanishing free micro-inertia η≠0) is the classical case treated for the relaxed micromorphic model in [20–24,37]. For the sake of completeness, we present in figure 1 the dispersion curves for this case when using the values of the parameters given in table 1.
Figure 1.
Dispersion relations ω=ω(k) for the uncoupled (a), longitudinal (b) and transverse (c) waves of the relaxed micromorphic model with free micro-inertia η= 10−2 kg m−1. TRO, transverse rotational optic; TSO, transverse shear optic; TCVO, transverse constant-volume optic; LA, longitudinal acoustic; LO1/LO2, first and second longitudinal optic; TA, transverse acoustic; TO1/TO2, first and second transverse optic.
It can be found that, when considering the free micro-inertia alone, the relaxed micromorphic model is able to predict the first band-gap, which usually occurs at relatively low frequencies. Moreover, the relaxed micromorphic model is, for the current state of the art, the only continuum model which is able to describe simultaneously band-gaps and non-local behaviour [20].
In the following sections, we will present the new results concerning the effect of the gradient micro-inertia terms on the dispersion curves of the relaxed micromorphic model, as well as the effect of such gradient micro-inertia terms on more classical enriched models (Mindlin, internal variable).
4. Case of vanishing free micro-inertia η and non-vanishing gradient micro-inertia
In this section, we discuss the effect on the dispersion curves of enriched continuum models of the gradient micro-inertia term alone. We will show that the fact of complementing the macro-inertia only with the gradient micro-inertia is a fundamental modelling limitation since the complexity of the dynamic behaviour of micromorphic models cannot be unveiled. Nevertheless, the gradient micro-inertia allows us to describe some dispersion which is not allowed by classical Cauchy models.
(a). Study of the dispersion curves
In the case in which we consider only the gradient micro-inertia to be non-vanishing, the matrix associated with the longitudinal dynamic system can be expressed as:5
| 4.1 |
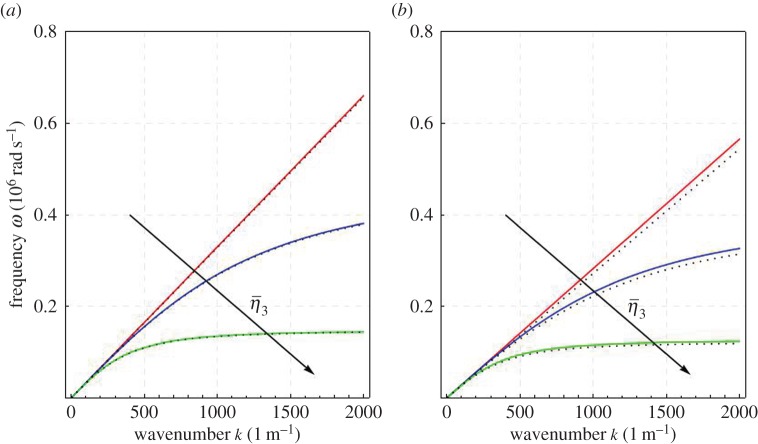
It is possible to remark that the polynomial det A1(ω,k) is of the second order in ω. This implies that we have a unique positive solution of the equation det A1(ω,k)=0 when considering positive k.6 In particular, when plotting such a solution in the (ω,k) plane only one acoustic branch can be detected (figure 2).7
Figure 2.
Dispersion relations ω=ω(k) for the longitudinal waves of the relaxed micromorphic model with gradient micro-inertia kg m−1 and η=0. Black dots indicate the dispersion relations for a first gradient model with Lamé parameters μmacro and λmacro and the same inertiae ρ and (a). The same picture obtained imposing λmicro=0 (b): a very slight variation with respect to the first gradient case can be detected. (Online version in colour.)
Comparing the results shown in figure 2 with those presented in figure 1, it can be immediately noticed that the fact of considering the gradient micro-inertia alone significantly constrains the behaviour of the considered enriched continuum. Even if the constitutive expression for the strain energy density W is the same in both figure 2 and figure 1 (see equation (2.1)), the fact of using a gradient micro-inertia instead of a free micro-inertia drastically simplifies the patterns which are found for the dispersion curves. With reference to figure 2, we can remark that a unique acoustic branch is found and that the presence of a non-vanishing micro-inertia parameter induces a dispersive behaviour. When the gradient micro-inertia parameters are all vanishing (), this means that only a macro-inertia is present and this corresponds to an almost constant speed of the travelling waves, which is what happens for the classical Cauchy case. It can be shown that, considering an adapted choice of the constitutive parameters for the relaxed micromorphic model with macro-inertia alone, the dispersion curve obtained is exactly the straight one obtained with the classical Cauchy model.
With a similar reasoning to the one made for longitudinal waves, considering the case for transverse waves, the matrix associated with the transverse dynamic system can be expressed as
| 4.2 |
It is possible to see that the new inertia terms play the same role for the transverse waves that was played by for the longitudinal waves. The results concerning the solutions ω=ω(k) of the characteristic equation det A2(ω,k)=0 are analogous to the case of longitudinal waves (figure 3).
Figure 3.
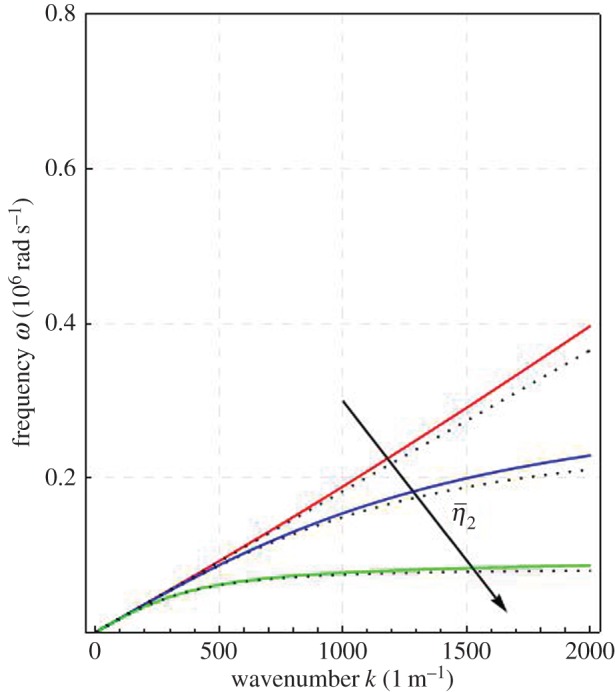
Dispersion relations ω=ω(k) for the transverse waves of the relaxed micromorphic model with gradient micro-inertia kg m−1 and η=0. Black dots indicate the dispersion relations for a first gradient model with Lamé parameters μmacro and λmacro and the same inertiae ρ and . (Online version in colour.)
If the particular case with non-null gradient micro-inertia and null free micro-inertia η=0 is considered, the matrix associated with the uncoupled waves reduces to
| 4.3 |
from which it is not possible to derive any dispersion curve, due to the absence of inertia terms.
(b). A first conclusion on the effect of gradient micro-inertia on enriched continuum models
— When considering a macro-inertia term alone, only one acoustic branch is present that has an almost constant speed of propagation. Such behaviour is strongly dictated by the macro-inertia term since the difference on the associated dispersion curves between a simple Cauchy energy W(∇u ) and an enriched model W=W(∇u ,P, Curl P) is small and vanishing considering an adapted choice of the constitutive parameters.
— When complementing the macro-inertia with a gradient micro-inertia the speed of propagation of waves is not constant anymore, but it depends on the wavelength of the travelling waves. Nevertheless, only an acoustic branch can be described, independently of the more or less complicated (standard or enriched) kinematics.
— Complementing the macro-inertia with a free micro-inertia allows us to disclose the full rich constitutive behaviour provided by considering an enriched model, as studied in [20–24,37] and reproduced in figure 1. Two optic branches are observed, for both longitudinal and transverse waves, in addition to the acoustic ones already discussed in the previous case (figure 1). The properties of such curves depend both on the constitutive parameters appearing in the expression of the energy (equation (2.1)) and on the free inertia parameter η. In this framework of inertia of the type , the relaxed micromorphic model is the only non-local, enriched continuum model allowing for the presence of band-gaps [21].
5. Case of both non-vanishing free micro-inertia η and gradient micro-inertia
In this section, we will discuss the effect of a full inertia on the dispersion curves of the relaxed micromorphic model. We will show that the complementation of the macro-inertia with both the gradient and free micro-inertia allows for the description of a new feature of the relaxed micromorphic model, i.e. the onset of a second band-gap occurring at higher frequencies than the first one.
(a). Dispersion relations
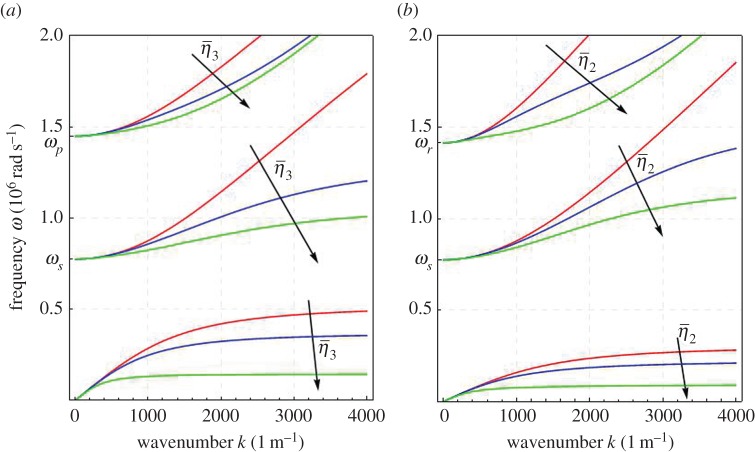
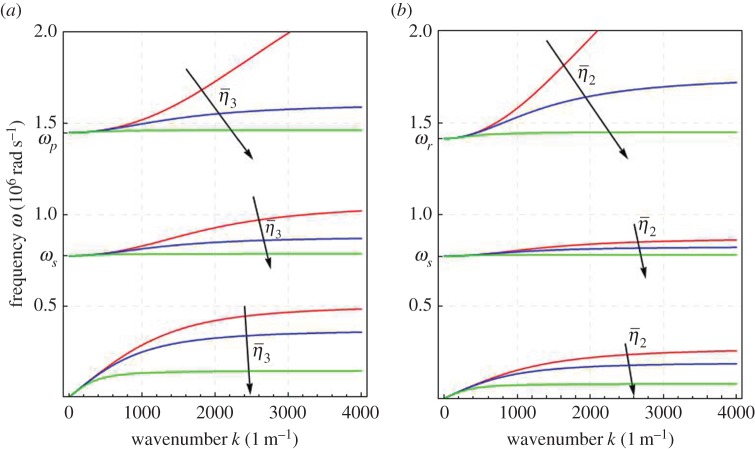
Now, we show in figure 4 the results obtained for non-null micro-inertia η≠0 with the addition of gradient micro-inertia . Surprisingly, the combined effect of the traditional micro-inertia η with the gradient micro-inertiae can lead to the onset of a second longitudinal and transverse band-gap. Indeed, the existence of a horizontal asymptote for the first optic branches in figure 4 could be shown. Nevertheless, an explicit computation of such asymptotes becomes over-burdening. For this reason, we limit ourselves to remark that, for all the metamaterials that we tested up to now, it is always possible to find , and that are large enough to have horizontal asymptotes appearing in graphics considering k ranging from 0 (infinite wavelength) to values of k corresponding to wavelengths smaller than the size of the unit cell. Moreover, it is possible to note that the addition of gradient micro-inertiae , and has no effect on the cut-off frequencies, which only depend on the free micro-inertia η (and of course on the constitutive parameters).
Figure 4.
Dispersion relations ω=ω(k) of the relaxed micromorphic model for the longitudinal waves with free micro-inertia η=10−3 and gradient micro-inertia kg m−1 (a) and transverse waves with micro-inertia η=10−3 and gradient micro-inertia kg m−1 (b). (Online version in colour.)
The uncoupled waves in the relaxed micromorphic model with generalized inertia behave in the same way as in the relaxed micromorphic model, as it is possible to see by analysing the matrix
| 5.1 |
The resulting dispersion curves are the same as those obtained with the classical relaxed micromorphic model (figure 1b).
(b). Cut-offs and asymptotic behaviour
To study the asymptotic behaviour of the dispersion curves for the relaxed micromorphic model with full inertia, let us introduce the following quantities:
As stated in the previous section, the cut-off frequencies are not modified by the insertion of a gradient micro-inertia term. Therefore, considering the longitudinal waves, we have one acoustic branch of the dispersion curve and two optic branches with cut-off frequencies:
| 5.2 |
On the other hand, the asymptotic behaviour changes in a radical fashion from the classical relaxed micromorphic model. The horizontal asymptote of the acoustic curve changes and we have the onset of a new horizontal asymptote for one of the optic branches, the values of which are, respectively,
| 5.3 |
No difference is found from the other optic branch that has an asymptote with slope cm, as in the classical relaxed micromorphic model.
Analogously, considering the transverse waves, we have one acoustic branch and two optic branches with cut-off frequencies,
| 5.4 |
Once again, the horizontal asymptote of the acoustic curve changes with respect to the classical relaxed case and we have an extra horizontal asymptote for one of the optic branches, the values of which are, respectively,
| 5.5 |
No difference is found from the other optic branch that has an asymptote with slope cm, as in the classical relaxed micromorphic model.
Finally, no change whatsoever is present in the uncoupled waves that keep having cut-off frequencies ωs and ωr and oblique asymptote of slope cm.
6. Combined effect of the free and gradient micro-inertiae on more classical enriched models (Mindlin–Eringen and internal variable)
In this section, we discuss the effect on the Mindlin–Eringen and the internal variable model of the addition of the gradient micro-inertia to the classical terms . We will show that the previously discussed effect of the parameters and is maintained for both the Mindlin–Eringen case and the internal variable case.
Figure 5 refers to the study of the effects of the parameters and on the dispersion curves of the classical Mindlin–Eringen micromorphic model. For the sake of completeness, we recall that the (simplified) strain energy density for this model in the isotropic case takes the form
| 6.1 |
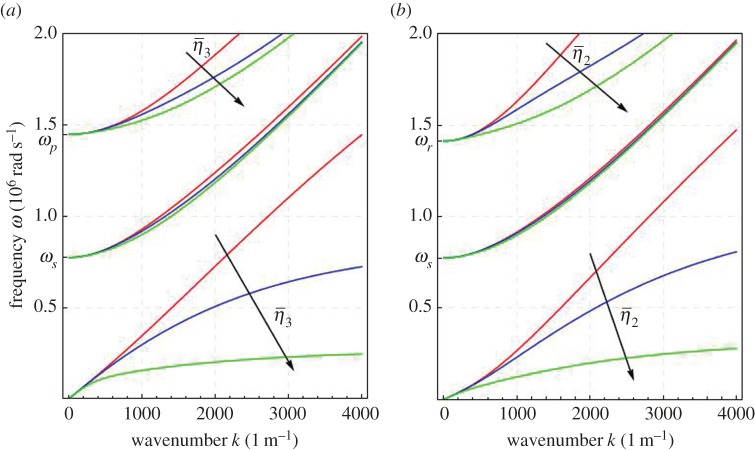
Figure 5.
Dispersion relations ω=ω(k) of the standard Mindlin–Eringen model for the longitudinal waves with free micro-inertia η=10−3 and gradient micro-inertia kg m−1 (a) and transverse waves with micro-inertia η=10−3 and gradient micro-inertia kg m−1 (b). (Online version in colour.)
Recalling the results of [22], we remark that when the gradient micro-inertia is vanishing () the Mindlin–Eringen model does not allow the description of band-gaps, due to the presence of a straight acoustic branch. On the other hand, when switching on the parameters and , the acoustic branches are flattened (they take a horizontal asymptote), so that the first band-gap can be described. The analogous case for the relaxed micromorphic model (figure 1) allowed instead for the description of two band-gaps.
Figure 6 shows the effect of the addition of the gradient micro-inertia on the behaviour of the internal variable model. We recall [26] that the energy for the internal variable model does not include higher space derivatives of the micro-distortion tensor P and, in the isotropic case, takes the form
| 6.2 |
Figure 6.
Dispersion relations ω=ω(k) of the internal variable model for the longitudinal waves with free micro-inertia η=10−3 and gradient micro-inertia kg m−1 (a) and transverse waves with micro-inertia η=10−3 and gradient micro-inertia kg m−1 (b). (Online version in colour.)
By direct observation of figure 6, we can note that, by suitably choosing the relative position of ωr and ωp, the internal variable model allows us to account for three band-gaps.
We thus have an extra band-gap with respect to the analogous case for the relaxed micromorphic model (figure 1), but we are not able to consider non-local effects. Excluding the possibility of describing non-local effects in metamaterials can be sometimes too restrictive. For example, flattening the curve which originates from ωr and which is associated with rotational modes of the microstructure is unphysical for the great majority of metamaterials.
7. Conclusion
In this paper, we have discussed the fundamental role of micro-inertia in enriched continuum models of the micromorphic type.
We show that if, on one hand, the free micro-inertia term is strictly necessary to disclose the full rich behaviour of micromorphic media in the dynamic regime, on the other hand the gradient micro-inertia has the macroscopic effect of flattening some of the dispersion curves, so allowing for the description of extra band-gaps. In particular, we have shown that:
— In the case of the relaxed micromorphic model, one band-gap can be described when introducing the free micro-inertia alone. When introducing a mixed micro-inertia two band-gaps can be accounted for by the same model.
— In the case of the Mindlin–Eringen model, no band-gaps are possible with the term alone, while the onset of a single band-gap can be granted by the addition of the extra term .
— In the internal variable model, two band-gaps are possible with the term alone, even if non-localities cannot be accounted for by such a model. When adding the extra term even three band-gaps becomes possible, but the behaviour of the dispersion curves becomes fairly unrealistic for a huge class of real metamaterials.
In conclusion, the results presented in this paper confirm the preceding findings according to which the relaxed micromorphic model is the most suitable enriched model for the simultaneous description of (i) band-gaps and (ii) non-localities in mechanical metamaterials.
Future work will be devoted to the application of the results obtained in this paper for the fitting of the proposed model with enriched micro-inertia on real metamaterials exhibiting multiple band-gaps.
Footnotes
In order to clarify the nomenclature used in this paper, we call ‘classical continua’ the classical continua of Cauchy for which the strain energy density depends on the first gradient of the displacement u. When we talk about ‘enriched continua’, we are referring to continua with enriched kinematics, i.e. continua whose motion is defined by the displacement ‘u’ and the micro-distortion P. Different sub-classes of enriched continua can be introduced depending on the constitutive choice of the strain energy density. For example, we talk about ‘classical micromorphic’ media when the strain energy depends on ∇u, P and ∇P, while we call ‘relaxed micromorphic media’ those for which the strain energy density is a function of ∇u, P and Curl P.
The dislocation tensor is defined as αij=−(Curl P)ij=−Pih,kϵjkh, where ϵ is the Levi–Civita tensor and the Einstein notation of sum over repeated indices is used.
The Cauchy inertia and free micro-inertia terms appearing in equation (2.2) are classical and already introduced by Mindlin [2] and Eringen and Suhubi [1], while the gradient micro-inertia terms are introduced here for the first time in a micromorphic framework. Indeed, Mindlin [2] recognized inertia terms which are similar to our gradient micro-inertia terms when considering the particular case of the long-wavelength limit of his micromorphic model. Expression (2.2) of the energy that we propose here is more general (i.e. not restricted to large wavelengths) and indeed the gradient micro-inertia will show its higher effect for relatively small wavelengths (high wavenumbers).
Here, we understand that having found the (in general, complex) solutions of (3.7) only the real or imaginary parts separately constitute actual wave solutions which can be observed in reality.
We can see from the form of A1(ω,k) that considering an additional micro-inertia is equivalent to defining an average macroscopic density depending on the wavelength as . The same can be found for the transverse waves.
It can be checked that, when considering elastic parameters which guarantee positive definiteness of the elastic energy, the solutions ω=ω(k) of the characteristic polynomials are always real [37].
Here and in the sequel, we will always set , since we could not isolate a characteristic effect of such parameters on the dispersion curves.
Authors' contributions
All the authors contributed equally to this work.
Competing interests
The authors have no conflict of interests to declare.
Funding
A.M. thanks INSA-Lyon for the funding of the BQR 2016 ‘Caractérisation mécanique inverse des métamatériaux: modélisation, identification expérimentale des paramtres et évolutions possibles’, as well as the CNRS-INSIS for the funding of the PEPS project.
References
- 1.Eringen AC, Suhubi ES. 1964. Nonlinear theory of simple micro-elastic solids I. Int. J. Eng. Sci. 2, 189–203. (doi:10.1016/0020-7225(64)90004-7) [Google Scholar]
- 2.Mindlin RD. 1964. Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 16, 51–78. (doi:10.1007/BF00248490) [Google Scholar]
- 3.Engelbrecht J, Berezovski A. 2012. Internal structures and internal variables in solids. J. Mech. Mater. Struct. 7, 983–996. (doi:10.2140/jomms.2012.7.983) [Google Scholar]
- 4.Lakes RS. 1987. Foam structures with a negative Poisson’s ratio. Science 235, 1038–1040. (doi:10.1126/science.235.4792.1038) [DOI] [PubMed] [Google Scholar]
- 5.Schaedler TA, Jacobsen AJ, Torrents A, Sorensen AE, Lian J, Greer JR, Valdevit L, Carter WB. 2011. Ultralight metallic microlattices. Science 334, 962–965. (doi:10.1126/science.1211649) [DOI] [PubMed] [Google Scholar]
- 6.Zheng X. et al. 2014. Ultralight, ultrastiff mechanical metamaterials. Science 344, 1373–1377. (doi:10.1126/science.1252291) [DOI] [PubMed] [Google Scholar]
- 7.Florescu M, Torquato S, Steinhardt PJ. 2009. Complete band gaps in two-dimensional photonic quasicrystals. Phys. Rev. B 80, 155112 (doi:10.1103/PhysRevB.80.155112) [Google Scholar]
- 8.Florescu M, Torquato S, Steinhardt PJ. 2009. Designer disordered materials with large, complete photonic band gaps. Proc. Natl Acad. Sci. USA 106, 20 658–20 663. (doi:10.1073/pnas.0907744106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lucklum R, Ke M, Zubtsov M. 2012. Two-dimensional phononic crystal sensor based on a cavity mode. Sensors Actuat. B Chem. 171–172, 271–277. (doi:10.1016/j.snb.2012.03.063) [Google Scholar]
- 10.Man W. et al. 2013. Photonic band gap in isotropic hyperuniform disordered solids with low dielectric contrast. Opt. Express 21, 19 972–19 981. (doi:10.1364/OE.21.019972) [DOI] [PubMed] [Google Scholar]
- 11.Miniaci M, Krushynska A, Bosia F, Pugno NM. 2016. Large scale mechanical metamaterials as seismic shields. New J. Phys. 18, 083041 (doi:10.1088/1367-2630/18/8/083041) [Google Scholar]
- 12.Miniaci M, Marzani A, Testoni N, De Marchi L. 2015. Complete band gaps in a polyvinyl chloride (PVC) phononic plate with cross-like holes: numerical design and experimental verification. Ultrasonics 56, 251–259. (doi:10.1016/j.ultras.2014.07.016) [DOI] [PubMed] [Google Scholar]
- 13.Pham K, Kouznetsova VG, Geers MGD. 2013. Transient computational homogenization for heterogeneous materials under dynamic excitation. J. Mech. Phys. Solids 61, 2125–2146. (doi:10.1016/j.jmps.2013.07.005) [Google Scholar]
- 14.Sridhar A, Kouznetsova VG, Geers MGD. 2016. Homogenization of locally resonant acoustic metamaterials towards an emergent enriched continuum. Comput. Mech. 57, 423–435. (doi:10.1007/s00466-015-1254-y) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Armenise MN, Campanella CE, Ciminelli C, Dell’Olio F, Passaro VMN. 2010. Phononic and photonic band gap structures: modelling and applications. Phys. Procedia 3, 357–364. (doi:10.1016/j.phpro.2010.01.047) [Google Scholar]
- 16.Spadoni A, Ruzzene M, Gonella S, Scarpa F. 2009. Phononic properties of hexagonal chiral lattices. Wave Motion 46, 435–450. (doi:10.1016/j.wavemoti.2009.04.002) [Google Scholar]
- 17.Steurer W, Sutter-Widmer D. 2007. Photonic and phononic quasicrystals. J. Phys. D Appl. Phys. 40, 229–247. (doi:10.1088/0022-3727/40/13/R01) [Google Scholar]
- 18.Askes H, Aifantis EC. 2011. Gradient elasticity in statics and dynamics: an overview of formulations, length scale identification procedures, finite element implementations and new results. Int. J. Solids Struct. 48, 1962–1990. (doi:10.1016/j.ijsolstr.2011.03.006) [Google Scholar]
- 19.Ghiba I-D, Neff P, Madeo A, Placidi L, Rosi G. 2014. The relaxed linear micromorphic continuum: existence, uniqueness and continuous dependence in dynamics. Math. Mech. Solids 20, 1171–1197. (doi:10.1177/1081286513516972) [Google Scholar]
- 20.Madeo A, Barbagallo G, d’Agostino MV, Placidi L, Neff P. 2016. First evidence of non-locality in real band-gap metamaterials: determining parameters in the relaxed micromorphic model. Proc. R. Soc. A 472, 20160169 (doi:10.1098/rspa.2016.0169) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Madeo A, Neff P, d’Agostino MV, Barbagallo G. 2016. Complete band gaps including non-local effects occur only in the relaxed micromorphic model. C. R. Mécanique 344, 784–796. (doi:10.1016/j.crme.2016.07.002) [Google Scholar]
- 22.Madeo A, Neff P, Ghiba I-D, Placidi L, Rosi G. 2014. Band gaps in the relaxed linear micromorphic continuum. Z. Angew. Math. Mech. 95, 880–887. (doi:10.1002/zamm.201400036) [Google Scholar]
- 23.Madeo A, Neff P, Ghiba I-D, Placidi L, Rosi G. 2015. Wave propagation in relaxed micromorphic continua: modeling metamaterials with frequency band-gaps. Cont. Mech. Thermodyn. 27, 551–570. (doi:10.1007/s00161-013-0329-2) [Google Scholar]
- 24.Madeo A, Neff P, Ghiba I-D, Rosi G. 2016. Reflection and transmission of elastic waves in non-local band-gap metamaterials: a comprehensive study via the relaxed micromorphic model. J. Mech. Phys. Solids 95, 441–479. (doi:10.1016/j.jmps.2016.05.003) [Google Scholar]
- 25.Neff P, Ghiba I-D, Lazar M, Madeo A. 2015. The relaxed linear micromorphic continuum: well-posedness of the static problem and relations to the gauge theory of dislocations. Q. J. Mech. Appl. Math. 68, 53–84. (doi:10.1093/qjmam/hbu027) [Google Scholar]
- 26.Neff P, Ghiba I-D, Madeo A, Placidi L, Rosi G. 2014. A unifying perspective: the relaxed linear micromorphic continuum. Cont. Mech. Thermodyn. 26, 639–681. (doi:10.1007/s00161-013-0322-9) [Google Scholar]
- 27.d’Agostino MV, Barbagallo G, Ghiba I-D, Madeo A, Neff P.2016. A panorama of dispersion curves for the weighted isotropic relaxed micromorphic model. (http://arxiv.org/abs/1610.03296. )
- 28.Madeo A, Collet M, Miniaci M, Billon K, Ouisse M, Neff P.2016. Modeling real phononic crystals via the weighted relaxed micromorphic model with free and gradient micro-inertia. (http://arxiv.org/abs/1610.03878. )
- 29.Bauer S, Neff P, Pauly D, Starke G. 2014. New Poincaré-type inequalities. C. R. Math. 352, 163–166. (doi:10.1016/j.crma.2013.11.017) [Google Scholar]
- 30.Bauer S, Neff P, Pauly D, Starke G. 2016. Dev-Div- and DevSym-DevCurl-inequalities for incompatible square tensor fields with mixed boundary conditions. ESAIM: Control Optimis. Calculus Variat. 22, 112–133. (doi:10.1051/cocv/2014068) [Google Scholar]
- 31.Neff P, Pauly D, Witsch K-J. 2011. A canonical extension of Korn’s first inequality to H(Curl) motivated by gradient plasticity with plastic spin. C. R. Math. 349, 1251–1254. (doi:10.1016/j.crma.2011.10.003) [Google Scholar]
- 32.Neff P, Pauly D, Witsch K-J. 2012. Maxwell meets Korn: a new coercive inequality for tensor fields in Rn×n with square-integrable exterior derivative. Math. Methods Appl. Sci. 35, 65–71. (doi:10.1002/mma.1534) [Google Scholar]
- 33.Neff P, Pauly D, Witsch K-J. 2015. Poincaré meets Korn via Maxwell: extending Korn’s first inequality to incompatible tensor fields. J. Differ. Equ. 258, 1267–1302. (doi:10.1016/j.jde.2014.10.019) [Google Scholar]
- 34.Barbagallo G, d’Agostino MV, Abreu R, Ghiba I-D, Madeo A, Neff P.2016. Transparent anisotropy for the relaxed micromorphic model: macroscopic consistency conditions and long wave length asymptotics. (http://arxiv.org/abs/1601.03667. ) [DOI] [PMC free article] [PubMed]
- 35.Berezovski A, Engelbrecht J, Berezovski M. 2011. Waves in microstructured solids: a unified viewpoint of modeling. Acta Mech. 220, 349–363. (doi:10.1007/s00707-011-0468-0) [Google Scholar]
- 36.Love AEH. 1944. A treatise on the mathematical theory of elasticity. New York, NY: Dover Publications, Inc. [Google Scholar]
- 37.Neff P, Madeo A, Barbagallo G, d’Agostino MV, Abreu R, Ghiba I-D.2016. Real wave propagation in the isotropic relaxed micromorphic model. (http://arxiv.org/abs/1605.07902. ) [DOI] [PMC free article] [PubMed]