Abstract
From a systematic study of the concentration driven diffusion of positive and negative ions across porous 2D membranes of graphene and hexagonal boron nitride (h-BN), we prove their cation selectivity. Using the current–voltage characteristics of graphene and h-BN monolayers separating reservoirs of different salt concentrations, we calculate the reversal potential as a measure of selectivity. We tune the Debye screening length by exchanging the salt concentrations and demonstrate that negative surface charge gives rise to cation selectivity. Surprisingly, h-BN and graphene membranes show similar characteristics, strongly suggesting a common origin of selectivity in aqueous solvents. For the first time, we demonstrate that the cation flux can be increased by using ozone to create additional pores in graphene while maintaining excellent selectivity. We discuss opportunities to exploit our scalable method to use 2D membranes for applications including osmotic power conversion.
Keywords: porous 2D materials, graphene, hexagonal boron nitride, charge selective, defects
Ion selective membranes are key targets for the advancement of separation-based technologies with the aim to reduce their flow resistance while maintaining high selectivity. In battery design, a low resistance separation membrane would reduce internal resistance1 with very similar aims for separators in fuel cells or supercapacitors.2,3 Likewise, ion selective membranes are attractive for applications in osmotic power generation based on salinity gradients.4 The prospect of using two-dimensional (2D) materials like graphene as selective membranes has generated considerable excitement, as an atomically thin material presents an obvious opportunity to reduce the flow resistance.5 All of these applications require a membrane with excellent selectivity for positive ions over negative ions while maximizing ionic transport.
Significant progress has been made in the scalable manufacture of 2D materials; in particular, chemical vapor deposited (CVD) mono- and few-layer films are ideally suited to address the technological needs for atomically thin, functional membranes.6 While single-crystal monolayer graphene has been shown to be intrinsically impermeable to gases,7 technologically relevant large-area (>few cm2) 2D CVD films typically exhibit a range of defects through which ions can pass in solution, indicating a pathway toward their use as ion selective membranes.8 Critical to membrane applications is the combination of high selectivity and high permeance.
A number of methods have been demonstrated to control perforation of graphene membranes including ion bombardment, ozone treatment, and oxidative etching.9−11 Atomic and molecular transport through the pores has been characterized by ionic current as well as optical and conductivity measurements.8,12,13 Despite these positive results, it remains unclear how selectivity arises, exemplified by the lack of established methods for controlling selective permeance.14 A fundamental understanding of selectivity is required for engineering new 2D materials into functional membranes.15
Furthermore, recent literature has attributed the selective flux to drilled or etched pores in graphene membranes without characterizing the contribution from the intrinsic defects present across all CVD graphene membranes. Consequently, it is hard to distinguish the contribution to selectivity and leakage currents from both the engineered pore and the defects.
Since the selectivity of extrinsic material systems like graphene could arise due to charges on the pores, their size or a combination of both16,17 highly controlled experiments are crucial. It was suggested that for desalination by size, physical control of the pore size is required down to the sub-angstrom level.16 Alternatively, high selectivity could be achieved by exploiting charge effects to exclude co-ions from the pore and only allow the passage of counterions.18−20
Here, we set out to understand transport and selectivity through CVD-grown 2D membranes in aqueous solutions, focusing first on the contribution of intrinsic defects to selectivity. These are unavoidable in industrially relevant large-area membranes, so their effect must be well characterized. By investigating the current–voltage (I–V) curves of graphene and hexagonal boron nitride (h-BN) membranes, we first prove selectivity to cations and confirm that it mainly arises due to charge selective pores. We propose a mechanism for how charge selectivity arises in these pores and demonstrate a pathway to maximize ion flux while maintaining excellent selectivity.
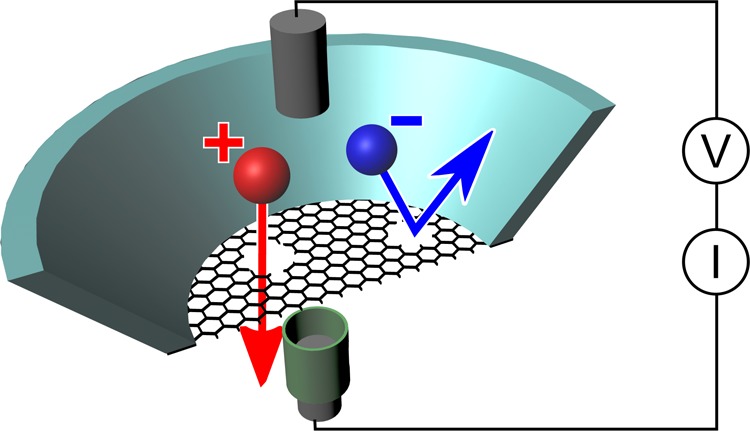
In order to acquire large data sets with minimal experimental overheads, we use our established setup based on glass capillaries.8,21 We measure the selectivity of 2D membranes by sealing the layers across the tips of glass nanocapillaries with typical diameters of 180 nm, unless otherwise stated. Using electrodes inside the reservoir and the capillary, we apply a voltage and measure the selective current. We have previously shown that the resistance is a direct measure of the defect density in graphene,8 and selectivity can be directly extracted from the I–V curves.21 In brief, when the concentration in the reservoir is lower than that in the capillary and the membrane allows positive ions to cross more easily than negative ions, then diffusion will cause a net current to flow even at V = 0 (green square in Figure 1a). The voltage needed to stop the diffusive flow is called the reversal potential (red circle in Figure 1a). The reversal potential (Vrev) depends on the concentration gradient and for a perfectly selective membrane is predicted by the Nernst equation22
| 1 |
where R denotes the gas constant, T the absolute temperature, z the ion valency, F is Faraday’s constant, and Co,i are the ion concentrations on either side of the membrane. We use concentrations rather than activities as most of our solutions are dilute, and this provides a conservative estimate of the selectivity. For z = 1 at 10× difference in concentration, one expects a reversal potential of 58 mV. All our results are benchmarked with control measurements using “bare” capillaries and Nafion as a positive control (see Supporting Information).23
Figure 1.
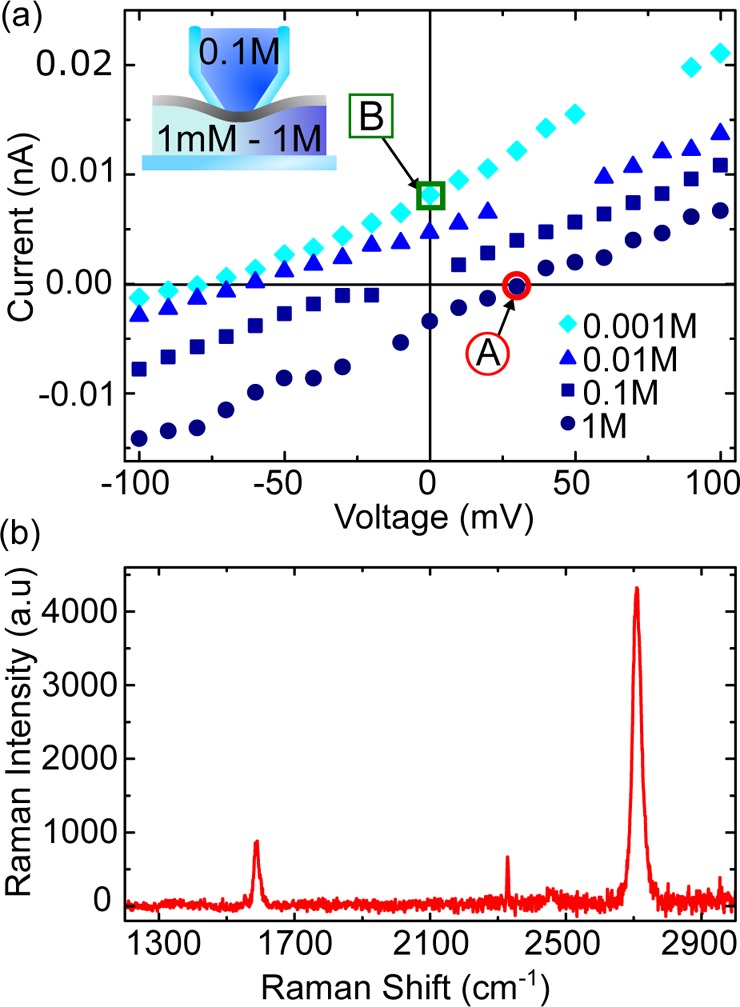
(a) Typical I–V curves for a capillary (180 nm) sealed with a monolayer CVD graphene membrane. The solution in the capillary is 0.1 M KCl, and the reservoir solution is varied from 0.001 to 1 M (all solutions at pH 6). When the concentration in the reservoir is lower, diffusion causes a positive current (B) to flow, indicating that the K+ ions cross the membrane more easily. The voltage to stop this current is indicated by red circles (A). (b) Representative Raman spectrum of the CVD graphene used in this work. Acquired after transfer onto SiO2. It indicates high-quality monolayer graphene.
While most work across the literature so far has focused on graphene, our study here extends to CVD-grown monolayer h-BN24−26 which, while isostructural to graphene, has distinctive properties. h-BN is a wide band gap semiconductor27 exhibiting polar bonding/edges. The differences between h-BN and graphene allow us to establish if selectivity is material-specific or dominated by external parameters.
Results
We first focus on the cation selectivity arising from the small number of defects inherently present in the 2D membranes we studied. The preferred monovalent system is KCl, as the hydration radii of K+ and Cl– and thus mobilities are similar for co- and counterions.28 A set of typical I–V curves for a graphene membrane separating a capillary containing 0.1 M KCl and reservoirs of different KCl concentrations is shown in Figure 1a. It is clear that the I–V curves shift and change as the concentration is varied, indicating selectivity; when there is a 10× difference in concentration across the membrane, the reversal potential is shifted by 48 mV, and at 100× difference, the shift is 74 mV. The extent of the selectivity can be quantified by plotting the value of the reversal potential (marked by a red circle) against the logarithm of the reservoir concentration (Figure 2a). In the range of 0.001 to 0.1 M, we observe a clear linear dependence on reservoir salt concentration for three concentrations in the capillary of 0.01, 0.1, and 1 M. For the lowest concentration in the capillary (0.01 M, light blue line in Figure 2a), we extract a gradient of 43.3 mV/log(M), approaching the theoretical limit. Increasing the capillary concentration to 0.1 M KCl reduces the gradient to 35.9 mV/log(M) (blue line Figure 2a) and even further to 32.0 mV/log(M) at 1 M (navy line Figure 2a). Our results prove that K+ passes through the membrane more easily than Cl–, and hence the graphene membranes are cation selective. However, the reversal potential is only one measure, and the diffusive current is actually more important in practice.
Figure 2.
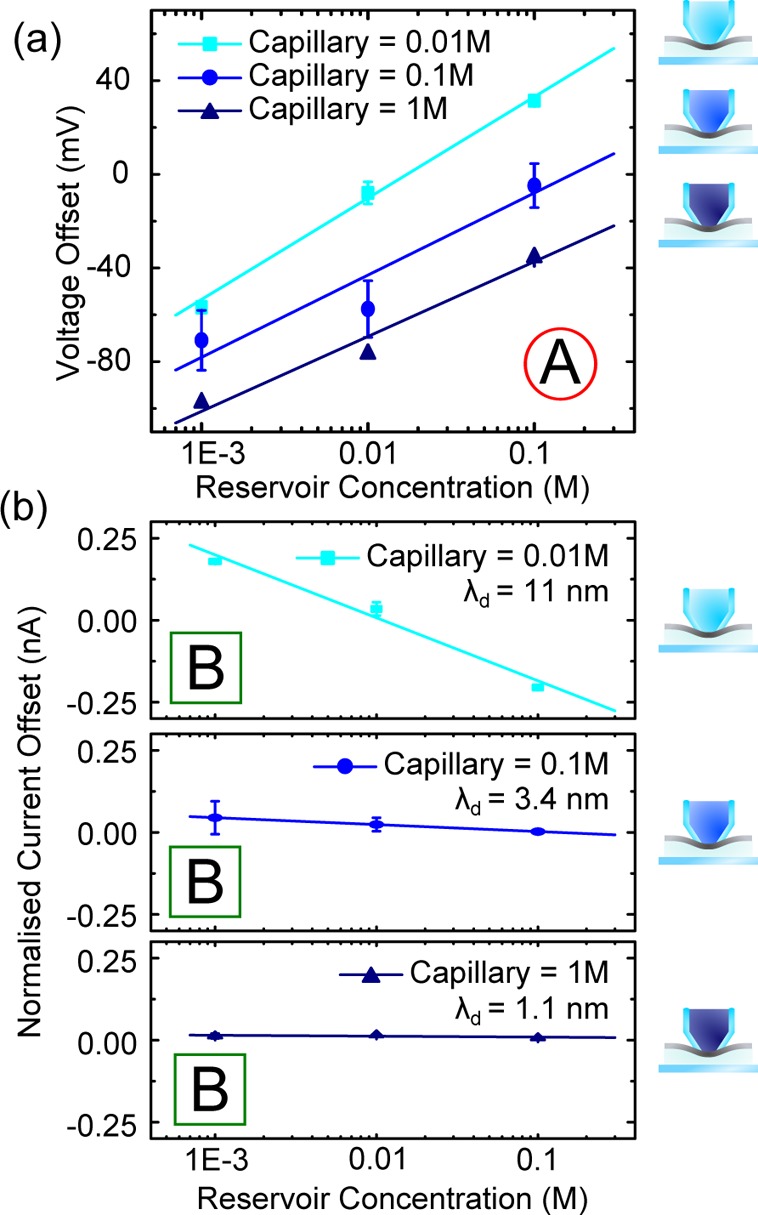
Measurements to determine the selectivity of monolayer CVD graphene to KCl. (a) Voltage offsets and (b) current offsets extracted from the I–V curves as the reservoir concentration is varied from 1 mM to 2 M KCl for experiments with 0.01, 0.1, and 1 M KCl in the capillary (all solutions unbuffered at pH 7). The legend indicates the Debye length in the capillary. To account for the different solution conductivities, the current offsets have been normalized to the conductivity for 0.1 M solution; for a non-normalized version, see Supporting Information. For 0.01 M in the capillary, from the gradient of the fitted line, the voltage offset is 43.3 mV/log(M) and the normalized current offset is −0.2 nA/log(M). The values for 0.1 M in the capillary are 35.1 mV/log(M) and −0.02 nA/log(M). For 1 M in the capillary, the values are 32.0 mV/log(M) and −0.003 nA/log(M).
In Figure 2b, we plot the diffusive current (green square, B, in Figure 1a). The obvious negative gradient provides more evidence for selectivity for a capillary concentration of 0.01 M. However, the selective current is greatly reduced for higher salt concentrations in the capillary (>0.1 M) (Figure 2b), strongly suggesting that the Debye screening length on the high concentration side plays an important role. The dependence on Debye screening length strongly points toward charge selectivity; that is, negatively charged pores in the graphene are the dominating cause.
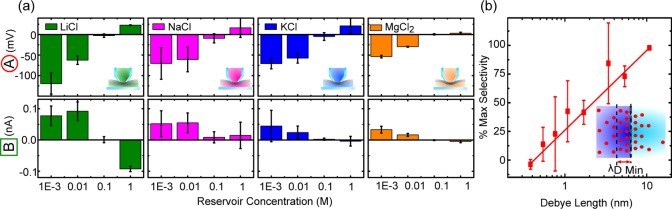
Ions have different diameters, and in aqueous solution, both the size of the hydration shell and the strength it is bound with need to be considered.28 These differences may influence selective transport.29 To determine if the type of ion affects the selectivity, we repeated our experiments with NaCl, LiCl, and MgCl2. Summarizing the reversal potential and diffusive current in Figure 3a, it can be seen that all three ions show significant selectivity for the positive ion over the Cl–. The Li+ was selected for most strongly, whereas for Mg2+, selectivity was much lower. This is surprising as Mg2+ is larger than Li+. With this result, we can exclude ion radii as the primary cause of selectivity. If charge selectivity is dominating, then Mg2+ as a divalent ion will more effectively screen the charge of the pore, leading to a shorter Debye screening length and thus reduce the charge selective effect, as observed. Our results indicate that selectivity arises primarily through charges on the graphene layers.
Figure 3.
Investigating the selectivity of monolayer graphene to different ions. (a) Voltage offsets (A) and current offsets (B) for a 0.1 M capillary and reservoir concentrations of 0.001 to 1 M for LiCl, NaCl, KCl, and MgCl2 (all solutions unbufffered at pH 7). All show evidence for selectivity. (b) Percent of the maximum selectivity for each condition plotted against the Debye length on the high concentration side of the membrane. The exponential dependence of selectivity on Debye length shows that selectivity is due to charge and is controlled by the highest ion concentration.
Our selectivity data indicate a fundamental difference of 2D membranes when compared to that of traditional materials like Nafion (see Supporting Information). Usually, one expects that selectivity is controlled by the lowest ion concentration. In contrast, for graphene, the decisive role of the shortest Debye screening length is shown by the exponential dependence of the selectivity (Figure 3b). Clearly, the higher ion concentration controls the selectivity, regardless of whether it is the reservoir or the capillary (see Supporting Information). We attribute this to the atomic thickness of the graphene; that is, the entrance to the pore is the dominating source of selectivity because the effective length of the selective channel is negligible.30
Having established that the selectivity depends on the Debye screening length, we can determine the pore size.19 For a 2 nm Debye layer, the selectivity is 50% whereas it increases to 100% at 10 nm (Figure 3b). Given that Debye overlap is essential for selectivity, we can conclude that the pores are probably between 0.4 and 3 nm in diameter, in line with previous literature.8,9,31−33 Because we see no significant selectivity due to ion size, this suggests that the precise diameter of the pores is not significant for controlling selectivity, and many intrinsic pores are larger than 1 nm. Individual defects in graphene membranes have been imaged using transmission electron microscopy (TEM),13,31,34 demonstrating that different atomic arrangements are found. However, our results suggest that the exact defect shape is not critical for selectivity as it arises from charge effects. This is in contrast to the transport of gases through graphene nanopores for which it has been suggested that small differences in the atomic structure of the pore can change the permeance.35 In our experiments in aqueous solution, the charge effects are much longer ranged than such steric effects and therefore dominate the behavior.
At first glance, it is surprising that CVD graphene is cation selective. For the development of full control over charge selectivity, it is important to determine its origin. A negatively charged graphene surface is the obvious explanation. We tested this hypothesis by changing the pH, maintaining the same pH in the capillary and the reservoir. As before, we identify reversal potentials from I–V curves to assess how selectivity depends on pH (Figure 4). At pH >5, graphene shows a high selectivity, becoming gradually nonselective at a pH less than 3 (red line, Figure 4).
Figure 4.
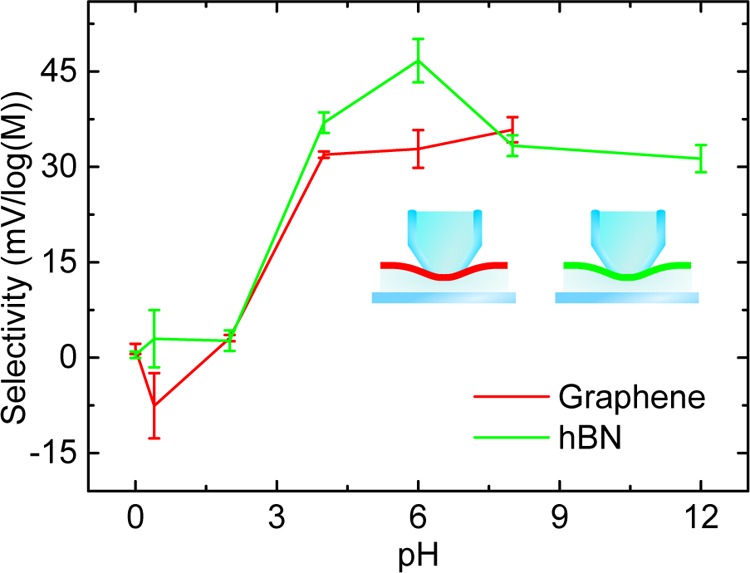
Effect of pH on selectivity for K+ over Cl– for graphene and h-BN. The capillary concentration was 0.1 M, and the reservoir varied from 1 to 100 mM. The pH of the reservoir and the capillary was set using HCl and KOH. The graphene membrane and h-BN both demonstrate increasing selectivity as pH increases to pH 6. For control measurements, see Supporting Information.
In order to clarify the molecular origin of this pH-dependent charge, we compared membrane materials with very different characteristics. Figure 4 depicts the selectivity for graphene and h-BN (positive control measurements for Nafion are shown in the Supporting Information). We observe no significant difference in selectivity between the 2D materials over the entire pH range. Since h-BN and graphene behave almost the same, we propose that selectivity arises as a result of external factors. The different chemical composition of graphene and h-BN makes it unlikely that negative surface charge arises due to edge chemistry alone. Likewise, the different electrical properties, where graphene is conducting and h-BN is insulating, suggest that the glass surface charge is not transferred to the pores.
Previous studies of the selectivity of defects in graphene membranes have largely focused on the chemical functionalization of the pores18 or the precise pore size.16 However, it is well-known that properties of 2D materials like electron mobility are often strongly dependent on the substrate.36 For 2D membranes submerged in aqueous solution, adsorption of OH– ions was suggested recently as the origin of both selectivity of BN4 and carbon nanotubes.37 We also observe slight shifts in the peaks and changes of the G to 2D ratio and fwhm of the peaks in the Raman spectra for graphene floating on water compared to graphene on SiO2, which correspond with the graphene acquiring charge in solution (see Supporting Information).38 The exact origin of charge at the liquid–2D interface is still under debate. Any surface exposed even briefly to air may acquire hydrocarbon molecules, reactions of which can contribute to negative surface charge.39−42 The impact of adsorbed molecules is much more significant on 2D materials as they are composed almost entirely of interfaces. Interestingly, our explanation is also supported by the recent work of Rollings et al.,43 who have studied single graphene nanopores fabricated by voltage breakdown. They found that 2–20 nm engineered pores are cation selective with a similar dependence on pH. OH– absorption is fully consistent with our observation that at low pH the high concentration of H+ will passivate the charges and hence reduce selectivity for both h-BN and graphene.
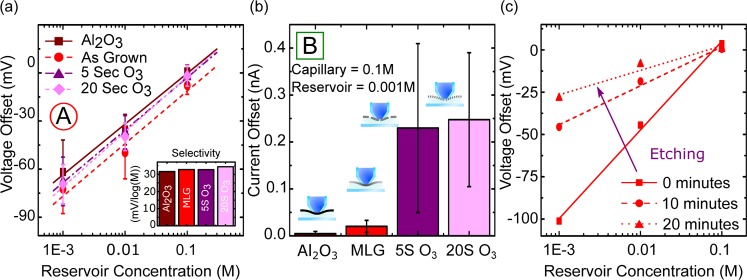
Having established the source of selectivity for 2D membranes to be surface charge, we now focus on the technologically important question: how flux can be increased while maintaining high selectivity. One method of opening new pores in graphene is brief exposure to ozone.8 We investigated graphene that had been exposed to ozone at 200 °C for 5 and 20 s. As a reference, we compare these samples to one decorated with Al2O3. Atomic layer deposition (ALD) of Al2O3 directly on graphene44−47 with tightly controlled nucleation behavior significantly reduces the size of defects due to the poor wetting of the precursors.10,21 We have previously shown that the Al2O3 treatment decreases the current flowing through the defects by at least an order of magnitude, while ozone treatments controllably create new defects, resulting in higher current flows.8,21
Figure 5a shows the reversal potentials associated with each of these samples. All the samples are selective to positive ions with selectivity in the range of 31–34 mV/log(M). However, this measure does not capture the significant differences in the current flowing through each of these membranes. Figure 5b shows the magnitude of the selective current dramatically increasing with the number of defects. This crucial result of enhanced diffusive current while maintaining high reversal potential shows that the ozone treatment on this short time scale has predominately created new pores which are as selective as the intrinsic defects. The Al2O3-decorated graphene has a much lower current due to diffusion, even though the selectivity is maintained. This demonstrates that the defects blocked by the Al2O3 are the selective pathways.
Figure 5.
Effect of blocking and creating defects on selectivity to KCl. The defects in a graphene sample were blocked by depositing 2 nm of Al2O3 and created by exposing the graphene to ozone. These are compared with a sample of as-grown monolayer graphene (MLG). The capillary (180 nm) is at 0.1 M KCl, and the reservoir varied between 1 mM and 0.1 M (all solutions unbuffered at pH 7). (a) All four membranes show a positive voltage offset, indicating they are selective to the positive ion. The gradients are 31.7, 32.8, 32.8, and 34.4 mV/log(M). (b) Current due to diffusion at 0 V when there is 100× concentration difference across the membrane. This demonstrates that the ozone treatment creates new defects which are as selective as the intrinsic defects in graphene. (c) Voltage offsets showing how the selectivity of a graphene sample to K+ over Cl– changes as it is etched in acidic KMnO4. The capillary (180 nm) is 0.1 M KCl, and the reservoir is 1 mM and 0.1 M. Initially, the selectivity is 52.4 mV/log(M); after 10 min of etching, the selectivity is 23.0 mV/log(M), and after 20 min, the selectivity has reduced to 14.4 mV/log(M).
To further increase the flux, the size of defects could be increased, though this may cause selectivity to decrease. We etched our samples with acidic potassium permanganate (2 mM KMnO4·0.5 M H2SO4) to grow the defects (Figure 5c). It has been established by us and others that acidic KMnO4 attacks defects.9 Over a period of up to 20 min, we observed the resistance of the membrane decrease by a factor of 4. At regular intervals, we stopped the etching process and exchanged the reservoir solution to determine the selectivity. We observed a decrease in selectivity from 52 mV/log(M) initially to 14 mV/log(M) after 20 min. By assuming that the defect density remains constant, we can estimate the change in defect size from the change in resistance. From this calculation, we estimate the defects to be 1–6 nm when selectivity is removed after 20 min of etching. Recent work by Rollings et al.(20) has suggested that pores drilled in graphene are selective up to 20 nm diameter; this may highlight the importance of intrinsic defects.
While the ozone treatment creates new defects that are clearly selective, etching using KMnO4 allows for fine-tuning of the resulting pore diameter. Thus, optimization of the membrane permeability and selectivity to specific types of ions should be achievable. Combining ozone and etching treatments is a potential pathway to maximize the selective flux. Importantly, brief ozone treatments are industrially relevant as they can be applied to large areas to create many pores. Parallel fabrication of pores has distinct advantages over methods relying on drilling pores using TEM or voltage-induced etching.20 Due to the charge selective nature of the defects, precise control over the pore size is not required.16 This remarkable finding also strengthens our interpretation that we see transport through intrinsic defects in graphene membranes and that leakage currents are negligible.
The high flux through our selective membranes could be utilized within energy generation. A promising approach is the osmotically driven current created from salinity gradients. We calculate that at pH 7 the osmotically driven current through the ozone-treated graphene equates to a power of 700 Wm–2 compared to 500 Wm–2 for Nafion. We note that 1100 Wm–2 has been demonstrated for a boron nitride nanotube. However, the BN nanotube samples require more complex fabrication.4 Given the scalability of CVD graphene and the ozone process used, porous 2D materials could be used for renewable energy generation or desalination if anion selectivity is demonstrated.
Conclusions
In summary, we have carried out a comprehensive study of the selectivity of CVD-grown two-dimensional membranes to different ions. Our results have shown that charge selectivity is the dominant effect. It follows that precise control of the pore size is not required to create an ion selective membrane. We found that at high pH, positive ions are strongly selected for, but selectivity decreases as pH decreases. Given that this is observed in different 2D materials, clearly extrinsic factors due to the aqueous environment such as adsorbed OH– are the likely cause of the negative surface charge. Our results demonstrate that ozone and etching treatments can increase the number of pores, thus greatly enhancing flux while maintaining high selectivity of the 2D membranes.
Methods
Glass nanocapillaries are pulled using a laser capillary puller (Sutter P2000) to give 180 nm tips. These are filled with the appropriate salt solution.
Graphene is grown by chemical vapor deposition in an Aixtron BM Pro (4 in.) reactor, using 25 μm thick Cu foil (Alfa Aesar, 99.8%) as the catalyst and CH4 (diluted in Ar and H2) as the precursor at 1050 °C.6 Hexagonal boron nitride is grown by chemical vapor deposition on an Fe catalyst using HBNH3 at a temperature of 940 °C and a pressure of 1 × 10–3 mbar.25
After growth, it is transferred to a single salt crystal using a standard PMMA wet transfer process.48 The 2D material is floated on the surface of a water reservoir by placing the salt crystal carrying the material into the reservoir and allowing it to dissolve. As it dissolves, the material is released so that it is floating freely on the surface.8
The nanocapillary is mounted on a micromanipulator, and Ag/AgCl electrodes in the capillary and reservoir connect to a patch clamp amplifier (Axopatch 200B) to apply voltages and measure currents. The capillary is lowered slowly onto the graphene so that it forms a seal which can be assessed using the I–V characteristic. A coated electrode is used to maintain the reservoir electrode at a constant potential, and the amplifier offset is set to zero when the solution in the reservoir matches the capillary. The reservoir electrode is coated in agarose made up in 0.1 M of the solution under test, usually KCl. The reservoir solution is then exchanged and an I–V curve obtained for each from which the reversal potential is extracted.21
The short ozone treatments are carried out in a Cambridge Nanotech Savannah system at 200 °C.45 A constant flow of N2 (20 sccm) provides a background pressure of 6 × 10–1 mbar to which ozone pulses of ∼200 mbar and 0.5 s duration are added with 20 s purges between them.46 The ozone is generated using a Del Ozone LG-7 corona discharge ozone generator. Total ozone exposure times of 5 and 20 s are used, and the resulting increase in defect density can be observed in Raman spectroscopy and as a decrease in the resistance of the membrane.8 CVD graphene is decorated with 2 nm of Al2O3 by atomic layer deposition using a 20 cycle process at 200 °C in a Cambridge Nanotech Savannah ALD system. The cycles consist of alternating pulses of trimethylaluminum and water both carried in N2 (20 sccm) separated by 8 s purges between them.45,47 This would typically yield a 2 nm thick film on Si with a native oxide. However, this relatively high-temperature, water-based process leads to preferential decoration at defects because of the poor wetting of the Al2O3 on graphene.44−46,49
The potassium permanganate etching is conducted by immersing the tip of the graphene-coated capillary in 0.5 M H2SO4 and 2 mM KMnO4 for a timed period.9 This causes the resistance of the membrane to decrease as well as the selectivity change shown above.
Acknowledgments
This work was supported by the EPSRC Cambridge NanoDTC, EP/G037221/1, and EPSRC grant GRAPHTED, EP/K016636/1. R.S.W. acknowledges a Research Fellowship from St. John’s College, Cambridge, and a Marie Skłodowska-Curie Individual Fellowship (Global) under Grant ARTIST (No. 656870) from the European Union’s Horizon 2020 research and innovation programme. V.S. acknowledges funding from the Commonwealth Scholarship Commission in the UK. S.C. acknowledges funding from EPSRC (doctoral training award). U.F.K. was partly supported by an ERC consolidator grant DesignerPores 647144. All data accompanying this publication are directly available within the publication.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.6b06034.
The authors declare no competing financial interest.
Supplementary Material
References
- Prifti H.; Parasuraman A.; Winardi S.; Lim T. M.; Skyllas-Kazacos M. Membranes for Redox Flow Battery Applications. Membranes 2012, 2, 275–306. 10.3390/membranes2020275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu S.; Lozada-Hidalgo M.; Wang F. C.; Mishchenko A.; Schedin F.; Nair R. R.; Hill E. W.; Boukhvalov D. W.; Katsnelson M. I.; Dryfe R. A. W.; Grigorieva I. V.; Wu H. A.; Geim A. K. Proton Transport Through One-Atom-Thick Crystals. Nature 2014, 516, 227–230. 10.1038/nature14015. [DOI] [PubMed] [Google Scholar]
- Cohen-Tanugi D.; Grossman J. C. Mechanical Strength of Nanoporous Graphene as a Desalination Membrane. Nano Lett. 2014, 14, 6171–8. 10.1021/nl502399y. [DOI] [PubMed] [Google Scholar]
- Siria A.; Poncharal P.; Biance A.-L.; Fulcrand R.; Blase X.; Purcell S. T.; Bocquet L. Giant Osmotic Energy Conversion Measured in a Single Transmembrane Boron Nitride Nanotube. Nature 2013, 494, 455–8. 10.1038/nature11876. [DOI] [PubMed] [Google Scholar]
- Geim A. K. Nobel Lecture: Random Walk to Graphene. Rev. Mod. Phys. 2011, 83, 851–862. 10.1103/RevModPhys.83.851. [DOI] [Google Scholar]
- Hofmann S.; Braeuninger-Weimer P.; Weatherup R. S. CVD-Enabled Graphene Manufacture and Technology. J. Phys. Chem. Lett. 2015, 6, 2714–2721. 10.1021/acs.jpclett.5b01052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bunch J. S.; Verbridge S. S.; Alden J. S.; van der Zande A. M.; Parpia J. M.; Craighead H. G.; McEuen P. L. Impermeable Atomic Membranes from Graphene Sheets. Nano Lett. 2008, 8, 2458–62. 10.1021/nl801457b. [DOI] [PubMed] [Google Scholar]
- Walker M. I.; Weatherup R. S.; Bell N. A. W.; Hofmann S.; Keyser U. F. Free-Standing Graphene Membranes on Glass Nanopores for Ionic Current Measurements. Appl. Phys. Lett. 2015, 106, 023119. 10.1063/1.4906236. [DOI] [Google Scholar]
- O’Hern S. C.; Boutilier M. S. H.; Idrobo J.-C. C.; Song Y.; Kong J.; Laoui T.; Atieh M.; Karnik R. Selective Ionic Transport through Tunable Sub-Nanometer Pores in Single-Layer Graphene Membranes. Nano Lett. 2014, 14, 1234–1241. 10.1021/nl404118f. [DOI] [PubMed] [Google Scholar]
- O’Hern S. C.; Jang D.; Bose S.; Idrobo J.-C.; Song Y.; Laoui T.; Kong J.; Karnik R. Nanofiltration across Defect-Sealed Nanoporous Monolayer Graphene. Nano Lett. 2015, 15, 3254–3260. 10.1021/acs.nanolett.5b00456. [DOI] [PubMed] [Google Scholar]
- Koenig S. P.; Wang L.; Pellegrino J.; Bunch J. S. Selective Molecular Sieving Through Porous Graphene. Nat. Nanotechnol. 2012, 7, 728–32. 10.1038/nnano.2012.162. [DOI] [PubMed] [Google Scholar]
- Russo C. J.; Golovchenko J. A. Atom-by-Atom Nucleation and Growth of Graphene Nanopores. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 5953–7. 10.1073/pnas.1119827109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Achtyl J. L.; Unocic R. R.; Xu L.; Cai Y.; Raju M.; Zhang W.; Sacci R. L.; Vlassiouk I. V.; Fulvio P. F.; Ganesh P.; Wesolowski D. J.; Dai S.; van Duin A. C. T.; Neurock M.; Geiger F. M. Aqueous Proton Transfer Across Single-Layer Graphene. Nat. Commun. 2015, 6, 6539. 10.1038/ncomms7539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Surwade S. P.; Smirnov S. N.; Vlassiouk I. V.; Unocic R. R.; Veith G. M.; Dai S.; Mahurin S. M. Water Desalination Using Nanoporous Single-Layer Graphene. Nat. Nanotechnol. 2015, 10, 459–464. 10.1038/nnano.2015.37. [DOI] [PubMed] [Google Scholar]
- Striolo A.; Michaelides A.; Joly L. The Carbon-Water Interface: Modeling Challenges and Opportunities for the Water-Energy Nexus. Annu. Rev. Chem. Biomol. Eng. 2016, 7, 533–56. 10.1146/annurev-chembioeng-080615-034455. [DOI] [PubMed] [Google Scholar]
- Cohen-Tanugi D.; Grossman J. C. Water Desalination across Nanoporous Graphene. Nano Lett. 2012, 12, 3602–3608. 10.1021/nl3012853. [DOI] [PubMed] [Google Scholar]
- Kang Y.; Zhang Z.; Shi H.; Zhang J.; Liang L.; Wang Q.; Agren H.; Tu Y. Na+ and K+ Ion Selectivity by Size-Controlled Biomimetic Graphene Nanopores. Nanoscale 2014, 6, 10666–72. 10.1039/C4NR01383B. [DOI] [PubMed] [Google Scholar]
- Sint K.; Wang B.; Král P. Selective Ion Passage Through Functionalized Graphene Nanopores. J. Am. Chem. Soc. 2008, 130, 16448–16449. 10.1021/ja804409f. [DOI] [PubMed] [Google Scholar]
- Vlassiouk I.; Smirnov S.; Siwy Z. Ionic Selectivity of Single Nanochannels. Nano Lett. 2008, 8, 1978–1985. 10.1021/nl800949k. [DOI] [PubMed] [Google Scholar]
- Rollings R.; Kuan A. T.; Golovchenko J. A. Ion Selectivity of Graphene Nanopores. Nat. Commun. 2016, 7, 11408. 10.1038/ncomms11408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker M. I.; Braeuninger-Weimer P.; Weatherup R. S.; Hofmann S.; Keyser U. F. Measuring the Proton Selectivity of Graphene Membranes. Appl. Phys. Lett. 2015, 107, 213104. 10.1063/1.4936335. [DOI] [Google Scholar]
- Hille B.Ion Channels of Excitable Membranes, 3rd ed.; Sinauer Associates, 2001; pp 441–470. [Google Scholar]
- Mauritz K. A.; Moore R. B. State of Understanding of Nafion. Chem. Rev. 2004, 104, 4535–4585. 10.1021/cr0207123. [DOI] [PubMed] [Google Scholar]
- Corso M.; Auwärter W.; Muntwiler M.; Tamai A.; Greber T.; Osterwalder J. Boron Nitride Nanomesh. Science 2004, 303, 217–220. 10.1126/science.1091979. [DOI] [PubMed] [Google Scholar]
- Caneva S.; Weatherup R. S.; Bayer B. C.; Brennan B.; Spencer S. J.; Mingard K.; Cabrero-Vilatela A.; Baehtz C.; Pollard A. J.; Hofmann S. Nucleation Control for Large, Single Crystalline Domains of Monolayer Hexagonal Boron Nitride via Si-Doped Fe Catalysts. Nano Lett. 2015, 15, 1867–1875. 10.1021/nl5046632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caneva S.; Weatherup R. S.; Bayer B. C.; Blume R.; Cabrero-Vilatela A.; Braeuninger-Weimer P.; Martin M.-B.; Wang R.; Baehtz C.; Schlögl R.; Meyer J. C.; Hofmann S. Controlling Catalyst Bulk Reservoir Effects for Monolayer Hexagonal Boron Nitride CVD. Nano Lett. 2016, 16, 1250. 10.1021/acs.nanolett.5b04586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cassabois G.; Valvin P.; Gil B. Hexagonal Boron Nitride is an Indirect Bandgap Semiconductor. Nat. Photonics 2016, 10, 262–266. 10.1038/nphoton.2015.277. [DOI] [Google Scholar]
- Marcus Y. Ionic Radii in Aqueous Solutions. Chem. Rev. 1988, 88, 1475–1498. 10.1021/cr00090a003. [DOI] [Google Scholar]
- Jain T.; Rasera B. C.; Guerrero R. J. S.; Boutilier M. S. H.; O’Hern S. C.; Idrobo J.-C.; Karnik R. Heterogeneous Sub-Continuum Ionic Transport in Statistically Isolated Graphene Nanopores. Nat. Nanotechnol. 2015, 10, 1053–1057. 10.1038/nnano.2015.222. [DOI] [PubMed] [Google Scholar]
- Geim A. K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. 10.1126/science.1158877. [DOI] [PubMed] [Google Scholar]
- Meyer J. C.; Kisielowski C.; Erni R.; Rossell M. D.; Crommie M. F.; Zettl A. Direct Imaging of Lattice Atoms and Topological Defects in Graphene Membranes. Nano Lett. 2008, 8, 3582–3586. 10.1021/nl801386m. [DOI] [PubMed] [Google Scholar]
- Zan R.; Ramasse Q. M.; Bangert U.; Novoselov K. S. Graphene Reknits its Holes. Nano Lett. 2012, 12, 3936–40. 10.1021/nl300985q. [DOI] [PubMed] [Google Scholar]
- Robertson A. W.; Lee G.-d. D.; He K.; Gong C.; Chen Q.; Yoon E.; Kirkland A. I.; Warner J. H. Atomic Structure of Graphene Subnanometer Pores. ACS Nano 2015, 9, 11599–11607. 10.1021/acsnano.5b05700. [DOI] [PubMed] [Google Scholar]
- Hashimoto A.; Suenaga K.; Gloter A.; Urita K.; Iijima S. Direct Evidence for Atomic Defects in Graphene Layers. Nature 2004, 430, 870–873. 10.1038/nature02817. [DOI] [PubMed] [Google Scholar]
- Drahushuk L. W.; Wang L.; Koenig S. P.; Bunch J. S.; Strano M. S. Analysis of Time-varying, Stochastic Gas Transport through Graphene Membranes. ACS Nano 2016, 10, 786–795. 10.1021/acsnano.5b05870. [DOI] [PubMed] [Google Scholar]
- Chan J.; Venugopal A.; Pirkle A.; McDonnell S.; Hinojos D.; Magnuson C. W.; Ruoff R. S.; Colombo L.; Wallace R. M.; Vogel E. Reducing Extrinsic Performance Limiting Factors in Graphene Grown by Chemical Vapor Deposition. ACS Nano 2012, 6, 3224–3229. 10.1021/nn300107f. [DOI] [PubMed] [Google Scholar]
- Secchi E.; Nigues A.; Jubin L.; Siria A.; Bocquet L. Scaling Behavior for Ionic Transport and its Fluctuations in Individual Carbon Nanotubes. Phys. Rev. Lett. 2016, 116, 154501. 10.1103/PhysRevLett.116.154501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das A.; Pisana S.; Chakraborty B.; Piscanec S.; Saha S. K.; Waghmare U. V.; Novoselov K. S.; Krishnamurthy H. R.; Geim a. K.; Ferrari A. C.; Sood A. K. Monitoring Dopants by Raman Scattering in an Electrochemically Top-Gated Graphene Transistor. Nat. Nanotechnol. 2008, 3, 210–5. 10.1038/nnano.2008.67. [DOI] [PubMed] [Google Scholar]
- Kudin K. N.; Car R. Why Are Water - Hydrophobic Interfaces Charged ?. J. Am. Chem. Soc. 2008, 130, 3915–3919. 10.1021/ja077205t. [DOI] [PubMed] [Google Scholar]
- Roger K.; Cabane B. Uncontaminated Hydrophobic/Water Interfaces are Uncharged: A Reply. Angew. Chem., Int. Ed. 2012, 51, 12943–12945. 10.1002/anie.201207114. [DOI] [Google Scholar]
- Roger K.; Cabane B. Why are Hydrophobic/Water Interfaces Negatively Charged?. Angew. Chem., Int. Ed. 2012, 51, 5625–5628. 10.1002/anie.201108228. [DOI] [PubMed] [Google Scholar]
- Aria A. I.; Kidambi P. R.; Weatherup R. S.; Xiao L.; Williams J. A.; Hofmann S. Time Evolution of the Wettability of Supported Graphene under Ambient Air Exposure. J. Phys. Chem. C 2016, 120, 2215–2224. 10.1021/acs.jpcc.5b10492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rollings R.; Graef E.; Walsh N.; Nandivada S.; Benamara M.; Li J. The effects of geometry and stability of solid-state nanopores on detecting single DNA molecules. Nanotechnology 2015, 26, 044001. 10.1088/0957-4484/26/4/044001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X.; Tabakman S.; Dai H. Atomic Layer Deposition of Metal Oxides on Pristine and Functionalized Graphene. J. Am. Chem. Soc. 2008, 130, 8152–8153. 10.1021/ja8023059. [DOI] [PubMed] [Google Scholar]
- Dlubak B.; Kidambi P. R.; Weatherup R. S.; Hofmann S.; Robertson J. Substrate-Assisted Nucleation of Ultra-Thin Dielectric Layers on Graphene by Atomic Layer Deposition. Appl. Phys. Lett. 2012, 100, 173113. 10.1063/1.4707376. [DOI] [Google Scholar]
- Martin M. B.; Dlubak B.; Weatherup R. S.; Yang H.; Deranlot C.; Bouzehouane K.; Petroff F.; Anane A.; Hofmann S.; Robertson J.; Fert A.; Seneor P. Sub-nanometer Atomic Layer Deposition for Spintronics in Magnetic Tunnel Junctions Based on Graphene Spin-Filtering Membranes. ACS Nano 2014, 8, 7890–7895. 10.1021/nn5017549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weatherup R. S.; Baehtz C.; Dlubak B.; Bayer B. C.; Kidambi P. R.; Blume R.; Schloegl R.; Hofmann S. Introducing Carbon Diffusion Barriers for Uniform, High-Quality Graphene Growth from Solid Sources. Nano Lett. 2013, 13, 4624–4631. 10.1021/nl401601x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Arco L. G.; Zhang Y.; Kumar A.; Zhou C. Synthesis, Transfer, and Devices of Single- and Few-Layer Graphene by Chemical Vapor Deposition. IEEE Trans. Nanotechnol. 2009, 8, 135–138. 10.1109/TNANO.2009.2013620. [DOI] [Google Scholar]
- Robinson J. A.; Labella M.; Trumbull K. A.; Weng X.; Cavelero R.; Daniels T.; Hughes Z.; Hollander M.; Fanton M.; Snyder D. Epitaxial Graphene Materials Integration: Effects of Dielectric Overlayers on Structural and Electronic Properties. ACS Nano 2010, 4, 2667–2672. 10.1021/nn1003138. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.