Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Feb 3;11(2):2094–2102. doi: 10.1021/acsnano.6b08287

Condensation and Demixing in Solutions of DNA Nanostars and Their Mixtures

Emanuele Locatelli †,*, Philip H Handle ‡, Christos N Likos †, Francesco Sciortino ‡,§, Lorenzo Rovigatti †,⊥
PMCID: PMC5333195  PMID: 28157331

Abstract

graphic file with name nn-2016-08287b_0009.jpg

We present a numerical/theoretical approach to efficiently evaluate the phase diagram of self-assembling DNA nanostars. Combining input information based on a realistic coarse-grained DNA potential with the Wertheim association theory, we derive a parameter-free thermodynamic description of these systems. We apply this method to investigate the phase behavior of single components and mixtures of DNA nanostars with different numbers of sticky arms, elucidating the role of the system functionality and of salt concentration. Specifically, we evaluate the propensity to demix, the gas–liquid phase boundaries and the location of the critical points. The predicted critical parameters compare very well with existing experimental results for the available compositions. The approach developed here is very general, easily extensible to other all-DNA systems, and provides guidance for future experiments.

Keywords: DNA nanostars, Wertheim theory, binary mixtures, coexistence, DNA hydrogels

The pivotal role played by DNA in biology cannot be understated.1 Its outstanding pairing specificity, embodied by the famous Watson–Crick mechanism, lies at the core of its biological functionality. Exploiting such a specificity in synthetic applications, an idea which dates back to the seminal work of Seeman in the 1980s, provides researchers from many different fields, ranging from nanotechnology to material science, with a powerful tool.2,3 Since then, DNA has been used in nanotechnogy to build, just to name a few examples, nanomachines,4 logic gates,5 and nanoscale objects of predetermined shape thanks to DNA origami6,7 or DNA Lego-like bricks.8,9 On the materials side, recent advances have made it possible to synthesize DNA-coated colloids that self-assemble into both ordered and disordered structures10−13 as well as to produce materials made exclusively of DNA.14−17 These all-DNA materials are synthesized through a multistep self-assembly process: the basic constituents are short strands with sizes ranging from a few to a few tens of nucleotides and with sequences specifically designed to self-assemble into well-defined constructs at intermediate temperature. These DNA constructs can, in turn, bind to each other to form higher order structures at lower T. The strategy outlined here has been exploited to synthesize two-dimensional ordered lattices14 as well as DNA hydrogels with unique characteristics.15,17,18

Owing to the high degree of control provided by DNA, these building blocks can be used not only to synthesize biocompatible materials with tunable properties but also to investigate fundamental questions. For instance, trivalent and tetravalent DNA constructs (nanostars) have been recently used to assess the dependence of the gas–liquid phase separation on the maximum number of bonds that each particle can form (also called valence). In fact, the experimental work of Biffi et al.(17) confirmed that, as predicted by theory and simulation,19 the gas–liquid phase coexistence region can be shrunk by decreasing the maximum number of bonds that each particle can form. The importance of this result is 2-fold. First, the experimental verification of the effect of the valence on the gas–liquid instability provides an innovative route for the generation of low-density physical gels, also known as empty liquids.17 Second, it strengthens the idea that carefully designed DNA constructs can be used as experimental realizations of patchy particles, which have recently gained much interest for their ability to self-assemble materials with exotic thermodynamic and dynamic properties, such as low-density gels, re-entrant gels, open crystals, ultrastable liquids, and much more.20−24 Remarkably, many of the features that make these materials so unique and interesting can be theoretically predicted by means of the Wertheim thermodynamic perturbation theory (TPT).25,26

Here, we introduce a method to predict the phase behavior of a system composed by interacting DNA nanostars (NST) with valence f = 2–4, identical to the ones employed in recent experimental studies17,18 (see Figure 1a–c). Each DNA nanostar is formed by f DNA strands made of 49 nucleotides, which hybridize to form the body of the construct. The sequence of each strand terminates with six self-complementary bases that allow for internanostar bonding (see the Supporting Information). Therefore, each DNA nanostar carries a functionality (or valence) f. When the strands composing the NST are mixed in solution in the proper stochiometric ratio, they self-assemble into well-defined NST constructs, interacting among themselves via the sticky ends, as schematically shown in Figure 1d.

Figure 1.

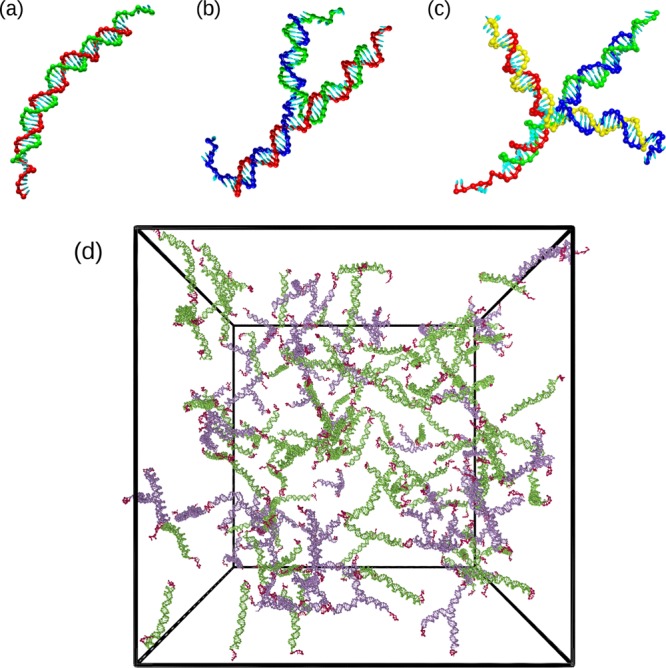
Figure 1

Open in a new tab

(a–c) Representative snapshots of DNA nanostars with different functionalities. (a) A DNA dimer (f = 2), (b) a DNA trimer (f = 3), and (c) a DNA tetramer (f = 4). The f strands composing each nanostar are colored differently. (d) Simulation snapshot of a binary mixture composed of 50 trimers and 100 dimers at a nanostar number density ρ = 2.4 × 10–4 nm–3 and T = 48 °C. Trimers are colored violet, dimers are green, and sticky ends are red.

To describe the temperature and density dependence of the system we exploit the Wertheim theory, a theory originally designed to model associating liquids but which was proved to qualitatively (and, in some cases, quantitatively) reproduce the numerical results obtained in systems of patchy particles.21,27 The Wertheim theory evaluates the free energy of the system as a sum of two contributions: a reference part, which is often the free energy of a purely repulsive system, and a bonding part, which takes into account the formation of interparticle bonds. In the case of patchy colloids, the former is provided by the Carnahan–Starling expression for the free-energy of hard spheres,28 while the parameters that determine the latter are embedded in the definition of the interparticle interaction, which is set a priori. Extending the Wertheim approach to all-DNA systems requires one to provide a way of evaluating these two contributions.

We propose (i) to evaluate the reference free energy building on an existing accurate coarse-grained model for DNA, oxDNA2,29 which allows us to evaluate numerically the effective potential between pairs of constructs and the associated virial coefficient, in the absence of sticky interaction between the NST. This requires short, small-scale simulations. The reference free energy is then evaluated as a virial expansion truncated to the second order. We also propose (ii) to evaluate the probability of association between the sticky ends via the well-known SantaLucia nearest neighbor model.30,31 We independently test (i) and (ii) by running large-scale bulk simulations, which confirm the validity of the approach. The theoretical expressions and the numerical techniques are detailed in the Methods.

Finally, we test the resulting theory by evaluating the critical points and coexistence regions of pure tetramer and trimer systems, carrying out comparisons with the experimental and numerical data available in the literature. We find good agreement with experimental results for the critical temperature and for the density of the coexisting phases away from the critical point, while comparisons with the experimental critical densities are less favorable, as it is often the case with patchy models.19 We also show that the salt concentration plays a major role in determining the phase behavior of these DNA constructs, which helps rationalizing recent experimental results on their dynamical properties.32 We demonstrate the generality of our theoretical approach by computing the critical points, coexistence regions, the degree of demixing as well as the cloud/shadow curves of binary mixtures of DNA nanostars with different valences, for several values of the salt concentration.

Results and Discussion

Effective Interactions and Second Virial Coefficients

The evaluation of the effective interaction potentials βV(r) between DNA NST in the absence of binding sites and, consequently, of the second virial coefficients B2 (as detailed in the Methods) is key to our investigation methodology, which is based on a separation of the free energy into a reference part, accounting for the repulsion, plus a binding contribution computed using the SantaLucia model (see the Methods). We start the discussion of the results by reporting the reference interaction potentials and the second virial coefficients, computed for tetramers. Similar results for trimers are reported in the Supporting Information.

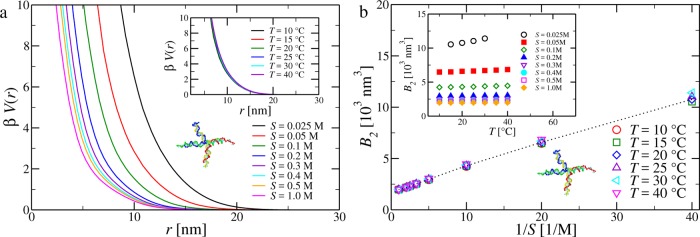
Figure 2 shows examples of the effective interaction potential and of the second virial coefficients for DNA tetramers. Both βV(r) and B2 have a negligible T dependence, which reflects the weak T-dependence of the Debye screening length as well as the small absolute-T range relevant for DNA. By contrast, the salt concentration has a substantial effect on the effective interaction. Indeed, the screening length depends on the inverse of the square root of S, which varies by more than a factor of 10 in the explored range. The resulting V(r) is well-described for distances comparable to the construct size by an exponential decay characterizing the softness and interpenetrability of the NST. The decay length of βV(r) increases on decreasing S, consistent with the increasing of the screening length. The behavior of B2 is consistent with a bare excluded volume contribution of 1.7 × 103 nm3 and displays a linear growth controlled by S–1. Even though we have not carried out a direct comparison, these results are in qualitative agreement with the experimentally measured salt dependence of the second virial coefficient of small DNA fragments.33,34

Figure 2.

Figure 2

Open in a new tab

(a) Effective interaction potential between two DNA tetramers, excluding the sticky ends, as a function of the distance r between the tetramers’ centers of mass for fixed temperature T = 20 °C and different salt concentrations (main panel) and for fixed salt concentration S = 0.05 M and different temperatures (inset). (b) Second virial coefficient B2 for DNA tetramers (f = 4) as a function of the inverse of the salt concentration for different temperatures (main panel) and as a function of the temperature for different salt concentrations (inset). The second virial coefficient is evaluated according to eq 11.

Comparison with Large-Scale Simulations: Test of βV(r)

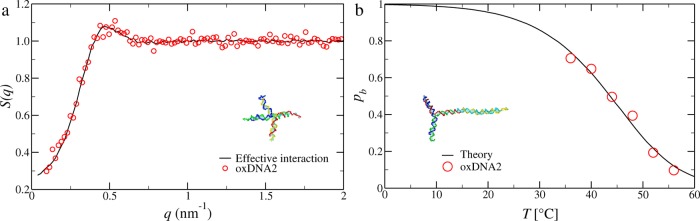
To validate the numerical procedure designed to evaluate the repulsive part of the effective potential and B2, we resort to a comparison between a bulk simulation of DNA–NST interacting with oxDNA (156800 nucleotides) and a simulation of particles interacting via βV(r). Indeed, the accurate investigation of the structure and thermodynamics of disordered all-DNA materials is a recent topic, and a large corpus of experimental results that can be used as terms for comparison is not yet available. In particular, no scattering data for inter-NST correlations are presently available to compare with the theoretical predictions. Remarkably, oxDNA2 has been shown to quantitatively reproduce the form factor of tetravalent nanostars, as measured by small-angle neutron scattering experiments.35

Figure 3a shows the structure factor of a system of 800 DNA tetramers at T = 50 °C, S = 0.1 M, and NST number density ρ = 1.8 × 10–4 nm–3 interacting with either oxDNA2 or βV(r). The structure factors of the two systems are indistinguishable within our numerical accuracy, validating the use of the effective potential, at least up to the large density investigated (which is higher than the range of densities we will consider in the following).

Figure 3.

Figure 3

Open in a new tab

(a) Structure factors for a system made of 800 DNA tetramers simulated with oxDNA2 (circles) and with the effective interaction reported in Figure 2 (lines), simulated at T = 50 °C, S = 0.1 M, and nanostar number density ρ = 1.8 × 10–4 nm–3. (b) Probability of forming a bond, pb, as a function of temperature for a binary mixture composed by 50 DNA trimers and 100 DNA dimers at nanostar number density ρ = 2.4 × 10–4 nm–3 and S = 1.0 M as a function of T. The line is the theoretical estimate, eq 6; circles are simulation data.

Comparison with Large-Scale Simulations: Test of the Bonding T-Dependence

The second assumption on which we build to develop a thermodynamic description of the association process assumes that the bonding free energy depends on S, T, and the sequence of the sticky ends but not the remaining parts of the nanostars. Testing such an assumption requires a full-scale simulation to also take into account internanostar bonding. We thus run simulations of a binary mixture made of 50 DNA trimers and 100 DNA dimers (17150 nucleotides) at NST number density ρ = 2.4 × 10–4 nm–3, S = 1.0 M and for several T, down to T = 36 °C. Below this temperature, 2 weeks of GPU computing time are not sufficient to observe the convergence of observables such as the potential energy or the total number of bonds. Such a lack of equilibration highlights the demanding nature of these large-scale simulations, and as a consequence, the usefulness of the proposed theoretical approach. From the simulated configurations we evaluate the probability to form a bond, pb, and compare it to the theoretical estimate based on the well-known SantaLucia model (see the Methods (eq 6) and SI). Figure 3b shows such a comparison, confirming the validity of the theoretical expression.

Pure Systems

The theoretical and numerical expressions reported in the Methods, complemented with the oxDNA-based B2, provide a close expression for the free energy of any mixture or pure solution of DNA NST of arbitrary valence. We begin by evaluating the phase diagram for pure solutions of trivalent and tetravalent NST, for which experimental data for S = 0.035 M and S = 0.025 M are available.

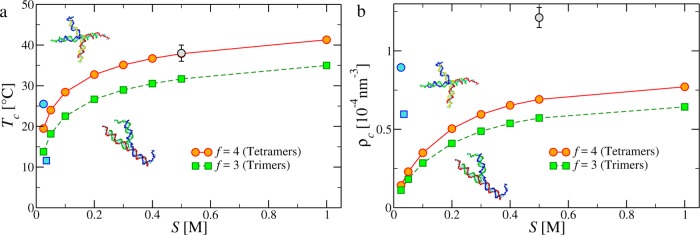
Figure 4a shows the gas–liquid critical temperatures as a function of the salt concentration for DNA tetramers and trimers. The same figure also reports the available experimental data from ref (17). The theoretical estimates, based on calculations that do not require a significant amount of numerical resources, are in very good agreement with the experimental data, being less than 2% off.

Figure 4.

Figure 4

Open in a new tab

Gas–liquid (a) critical temperatures and (b) critical densities as functions of the salt concentration for DNA tetramers (circles) and trimers (squares). Red and green symbols and lines refer to the theoretical estimates (see the Methods). Blue circles and squares are experimental values for tetramers and trimers, respectively, from ref (17); the gray circle is a numerical estimate from ref (36).

Figure 4b shows the gas–liquid critical densities as a function of the salt concentration for DNA tetramers and trimers. The critical density increases monotonically with salt concentration, similar to the critical temperature. Such behavior suggests that the coexistence region of the system, in the (ρ – T) plane, broadens with salt concentration, following the progressive softening of the particles (see Figure 2b and Figure S3) as suggested in ref (36).

Figure 5 shows the theoretical and experimental17 coexistence curves for pure systems of tetramers and trimers in the ρ – T plane. We observe that the extent of the coexistence region is comparable with the experimental data. For trimers, the shape of the region is particularly well reproduced; for tetramers, the theory underestimates the location of the binodal at high densities. Nevertheless, a good estimate for the highest coexistence density, as well as for the coexistence curve at small ρ, is found.

Figure 5.

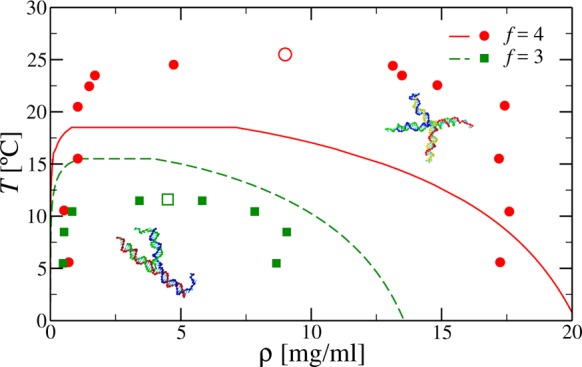
Figure 5

Open in a new tab

Coexistence region for tetramers at S = 0.025 M (red line and symbols) and trimers at S = 0.035 M (green line and symbols). Lines refer to theoretical data, symbols refer to experimental data, taken from ref (17). Empty symbols are the experimental critical points.

As a general remark, we note that the salt concentration has a strong influence on the location of the critical points. Its effect on the thermodynamics of the system is a result of two contributions. First, S controls the flexibility and overall shape of the NST (see the Supporting Information),35,37 as well as the repulsion between the DNA nanostars and, hence, the value of the second virial coefficient. Second, S enters in the bonding free energy, as prescribed by the SantaLucia model (see eq 7 in the Methods). We find that the critical T depends on S through both B2 and the bonding free-energy, whereas the S-dependence of the critical density is exclusively encoded in B2 (see the Supporting Information).

In the past, the numerical determination of critical points in DNA NST systems has been attempted only through expensive numerical simulations,36 with a substantial computational effort. We show here, through direct comparison of our results with data available in the literature, that the present far less demanding methodology is able to yield equally good estimates but for all possible values of the ionic strength.

Binary Mixtures

As predicted by theory and simulations19,38 and later confirmed by experiments,17 the gas–liquid phase coexisting region shrinks as the overall valence of the system tends to 2. Approaching this limit with continuity requires a noninteger average valence which can be achieved by employing mixtures of fixed-valence objects. We thus study mixtures of constructs with valence 4–2 and 3–2. We also investigate 4–3 mixtures, where both limiting cases (pure trimers and pure tetramers) exhibit a gas–liquid phase separation. For all these systems, we compute the loci of the critical points. We also compute some representative coexistence curves as well as shadow and cloud curves for the 4–2 mixture. In all cases considered here, the nature of the phase separation is found to be compatible with a gas–liquid phase separation close to the critical point and becomes more demixing-like as T decreases.

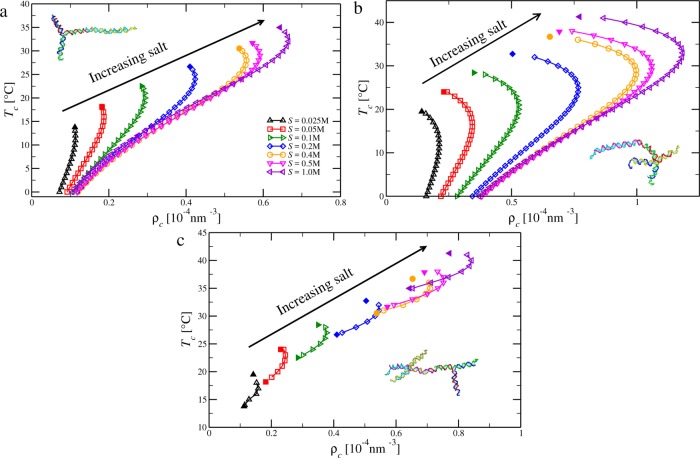
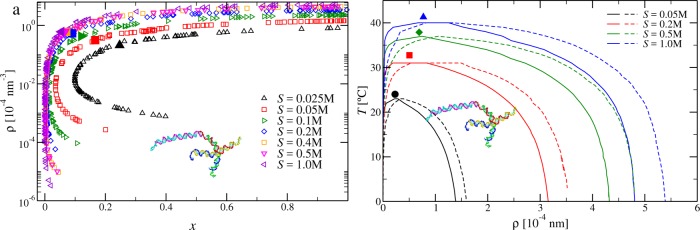
Figure 6a shows the critical parameters for mixtures of trimers and dimers at different salt concentrations. We observe that the trend of the curve is similar for all the values of salt considered. In particular, the critical density increases with temperature until a maximum is reached and then converges smoothly toward the critical point of the pure system. The maximum is less pronounced for smaller salt concentrations. Interestingly, the curves at different S seem to collapse below a certain T, even though such a collapse is not reached for the smallest values of S considered here.

Figure 6.

Figure 6

Open in a new tab

Theoretical critical densities at different temperatures for mixtures of (a) trimers and dimers, (b) tetramers and dimers, and (c) trimers and tetramers at different salt concentrations. Open symbols refer to the binary mixtures; full symbols refer to the critical points of the pure systems. In (c), the trimer critical point is always at lower density with respect to the tetramer critical point.

The critical points of mixtures of tetramers and dimers at different salt concentrations, reported in Figure 6b, exhibit the same trends seen for the trimer–dimer mixture. However, the nonmonotonic behavior of the critical density is much more pronounced here. In addition, compared to the 3–2 case, the collapse of the curves starts at higher salt concentrations.

Figure 6c shows the critical densities at different temperatures for mixtures of tetramers and trimers at different S. This case is qualitatively different from the previous ones in that both critical points of the pure system exist. Indeed, it can be seen that the line of critical densities at intermediate compositions connects the critical points of the associated pure systems. Since the critical points of the pure systems are separated by small T and ρ differences, the lines of critical points of the mixtures are quite short in this representation. We note that, in contrast with the previous cases, we do not observe a collapse of the curves at low temperatures. We also note that similarly to pure systems, the salt concentration plays a big role in determining the critical parameters of the mixtures, monotonically moving the critical points to higher T and ρ.

Next, we focus on the full coexistence region of the mixtures. The three mixtures have the same qualitative behavior, and thus, we discuss only the 4–2 mixture. Since a state point in a binary mixture of species A and B is identified by three thermodynamic quantities, the phase diagram of binary mixtures requires a three-dimensional representation. The most common thermodynamic variables used to represent such phase diagrams are T and the density of each species, ρA and ρB, or T, the total density ρ, and the composition x = ρA/ρ. In both these representations, the region of phase coexistence is a volume in the three-dimensional phase diagram. Therefore, for the sake of clarity, it is common procedure to plot two-dimensional slices of the phase diagram by setting one of the three thermodynamic variables to some constant value.

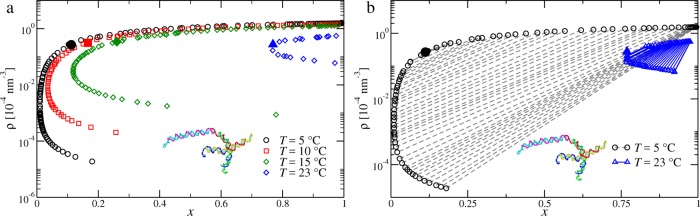
We start by taking cuts of the T, ρ, and x = ρ4/ρ phase diagram at constant temperature. In Figure 7a, we report the coexistence curves, i.e., the binodals, of the 4–2 mixture at salt concentration S = 0.05 M and different temperatures. At high T, that is, close to the critical point of the pure system, the average valence is large, and hence, all of the coexisting points have high x. However, as T decreases below the critical temperature of the pure system, the density of dimers increases in both the gas and the liquid phases, whereas the density of tetramers grows in the liquid phase while remains small in the gas phase. In Figure 7b, we report two examples of tie lines, which connect coexisting points of the two phases, for the 4–2 mixture at salt concentration S = 0.05 M and different temperatures, one rather low (T = 5 °C) and one close to the Tc of the pure system, (T = 23 °C). The tie lines confirm the picture sketched above. As discussed in ref (39), we see that the low-temperature tie lines connect points with increasingly different compositions, signaling a change in the nature of the phase separation, which acquires a more significant demixing character as T decreases while maintaining the liquid–gas character witnessed by a marked density gap.

Figure 7.

Figure 7

Open in a new tab

(a) Theoretical coexistence curves for a mixture of tetramers and dimers at salt concentration S = 0.05 M and different temperatures. (b) Theoretical tie lines for a mixture of tetramers and dimers at salt concentration S = 0.05 M and different temperatures T = 5 °C (black circles) and T = 23 °C (blue triangles). Open symbols refer to the coexistence points, full symbols refer to critical points, and dashed or full lines refer to tie lines.

We also assess the effect of salt concentration on the phase coexisting region. Figure 8a shows the binodal curves at fixed temperature T = 10 °C and different salt concentrations. As discussed in the context of the critical parameters, the main effect of the salt is to enlarge the two-phase region, which retains its shape but moves to more extreme ρ as S increases.

Figure 8.

Figure 8

Open in a new tab

(a) Theoretical coexistence curves for a mixture of tetramers and dimers at fixed temperature T = 10 °C and different salt concentrations. (b) Theoretical cloud (full lines) and shadow (dashed lines) curves for a mixture of tetramers and dimers at x = 0.7 at different salt concentrations. Full symbols refer to critical points.

Another common two-dimensional representation of the phase diagram can be constructed by fixing the overall concentration x and then plotting the resulting binodal, which is called the cloud curve and contains all of the coexisting points having the chosen composition as a function of T and ρ. Each point on the cloud curve coexists with another phase which has, in general, a different composition. The set of points coexisting with the cloud points is called the shadow curve, and it is often plotted together with the cloud curve, even though all its points have different compositions, not only with respect to the cloud points but also with respect to each other.

In Figure 8b, we report the cloud and shadow curves for a mixture of tetramers and dimers at fixed composition x = ρ4/ρ = 0.7 and different salt concentrations. First, we note that the critical points always lie at the intersection of the two curves, as expected.40 The effect of the salt, similar to what happens for the locus of the critical point, is to move the curves to substantially higher temperatures and densities.

Conclusions

The advances in the synthesis of DNA-based materials call for the development of numerical and theoretical methods for the evaluation of their macroscopic properties. Here, we developed a theoretical approach for the quantitative prediction of the low-density phase diagram of one-component and binary systems composed of DNA constructs with fixed valence. We have shown that these complex systems can be modeled as collections of supramolecular particles that, depending on temperature, can bond to each other but also experience an effective mutual repulsion, which is controlled mainly by the salt concentration. These two contributions can be readily evaluated via short two-body simulations employing a realistic DNA model29 and by means of the well-established nearest-neighbor SantaLucia model,30,31 respectively. By comparing these estimates with numerical results obtained through large-scale GPU simulations, we have confirmed that the assumptions underlying these two contributions hold very well, even at high density. The free energy of the system can then be computed in a parameter-free fashion in the framework of Wertheim TPT. In turn, the free energy can be used to evaluate the phase behavior. We have shown that this procedure yields results that are in semiquantitative (for the critical temperature and the off-critical coexisting densities) and qualitative (for the critical density) agreement with experimental results for one-component systems. We have also extended this method to binary mixtures, providing predictions for critical parameters and coexisting curves. Our results shed light on the dependence of the phase behavior on temperature and salt concentration, providing guidance for future experimental work. We stress that the hybrid numerical/theoretical approach developed here is very general: since it takes into account DNA–DNA interactions in a realistic fashion, it can be extended to investigate the behavior of all-DNA systems that incorporates complex DNA nanotechnology motifs such as strand displacements (e.g., DNA re-entrant gels,18 DNA vitrimers.41)

Methods

Theoretical Framework

In order to to estimate the gas–liquid critical parameters and the coexistence regions of DNA nanostar systems, we combine Wertheim TPT with an accurate mass-action law describing DNA binding. The Helmholtz free energy per particle for binary mixtures of DNA nanostars of different valence fA and fB using Wertheim TPT as in ref (39) is

graphic file with name nn-2016-08287b_m001.jpg 1

where v = 1/ρ, β = 1/kBT, kB is the Boltzmann constant, βfref(T, x, v) is the free-energy per particle of the reference state, i.e., the state in which bonding sites are not present, and βfb(T, x, v) is the free energy per particle associated with the bond formation between the sticky ends. βfref(T, x, v) is evaluated by considering a system in which the sticky end sequences are scrambled in such a way that Watson–Crick pairing does not occur and no interstar bond can form; the residual interaction is thus purely repulsive. In the binary mixture case, we express the free energy in terms of the concentration of one of the two species A and B, x = NA/N, N = NA + NB, and the reduced volume per particle v ≡ 1/ρ, ρ being the total number density. The reference free energy is given by the two contributions

graphic file with name nn-2016-08287b_m002.jpg 2

where the ideal gas free-energy density is given by βfid(T, x, v) = ln(v0/v) – 1 + x ln(x) + (1 – x) ln(1 – x), where v0 is a reference volume whose value has no effect on the derivatives of the free energy.

We approximate the excess free energy per particle via a second virial coefficient approximation for binary mixtures42

graphic file with name nn-2016-08287b_m003.jpg 3

where B2AA, B2, and B2AB are the second virial coefficients of the pure systems of species A and B and of the mixed system, respectively. These quantities are computed at different salt concentrations and temperatures, using the formula

graphic file with name nn-2016-08287b_m004.jpg 4

where Vij(r) is the effective intramolecular pair potential, computed through dedicated numerical simulations (see Numerical Methods). Note that Vij(r) is an average over the mutual orientations of the nanostars and thus depends solely on the distance r between the centers of mass of the two objects considered.

Finally, as all bonds are identical, the bonding free energy per particle is given by19

graphic file with name nn-2016-08287b_m005.jpg 5

where ⟨f⟩ = fAx + fB(1 – x), fA and fB are the valences of the first and second species, respectively, and pb is the fraction of formed bonds. The latter, which is function of T, x, and v, can be evaluated via a law of mass action, yielding

graphic file with name nn-2016-08287b_m006.jpg 6

where Δ is linked to the free-energy difference between bonded and nonbonded pairs of sticky ends. Following refs (30) and (31)

graphic file with name nn-2016-08287b_m007.jpg 7

where ΔH = −42790 cal is the enthalpy gain upon bonding, ΔSnosalt = −119.84 cal/K, and ΔSsalt = 0.368·(Ldna – 1)·ln(S) cal/K are the salt-independent and salt-dependent entropy variations again upon bonding, respectively. These quantities refer to the sticky end sequences, for which Ldna = 6. The expression for Δ thus encodes the salt, temperature, and sequence-length dependence of the free-energy difference between bonded and nonbonded states. Furthermore, vb = 1.6606 nm3 is the reference volume of the nonbonded single strands.9 Indeed, in a two-state system the condition for chemical equilibrium is given by

graphic file with name nn-2016-08287b_m008.jpg 8

where ρd is the density of the products (double strands), ρs is the density of the reagents (single strands), ρ̅ = ρ/ρref, where ρref = 6.022 × 1023 dm–3 = 0.6022 nm–3 is the standard state density, and ΔG is the free-energy difference associated with the bonding reaction. Δ, introduced in eq 6, is defined as

graphic file with name nn-2016-08287b_m009.jpg 9

as in eq 7, which implies vb = 1/ρref = 1.6606 nm3.

For pure systems, i.e., systems composed of particles of the same species and same valence, eq 2 simplifies to

graphic file with name nn-2016-08287b_m010.jpg 10

where B2(T) is, again, the second virial coefficient of the particular species considered, while eqs 5 and 6 hold, with x = 1 and fA = 4 (tetramers) or fA = 3 (trimers). For pure systems, the locus of critical points is given by (Tc, ρc) at fixed salt concentration; for binary mixtures, it is given by (xc, ρc) at fixed temperature and salt concentration. Critical points always satisfy the standard thermodynamical stability conditions.43

We also evaluate the coexistence region of both pure systems and binary mixtures. We do so by employing a standard common tangent construction.39 Different points that yield phases with the same pressure and chemical potentials for both species lie on a tie line. We complete the analysis of the phase diagram of the binary mixtures by looking at the cloud and shadow curves. The locus of the cloud points in the x – T plane is obtained by considering the intersection of a line at fixed x with the phase boundary in the ρA – ρB plane at fixed T. Each point on a cloud curve has a corresponding shadow point, which is the state on the coexistence curve connected to the cloud point through a tie line.40,44 We note that, as a consequence of this construction, shadow points on the same shadow curve have, in general, different compositions, whereas cloud points have, by construction, always the same composition.

As a general remark, we note that, in addition to the conditions for phase coexistence one should also require Donnan equilibrium; i.e., the chemical potential of the salt in the two phase should be the same, μsalt1 = μsalt. However, since the absolute values of the concentration of the coexisting phases are small fractions of the overlap density, one can safely ignore it, assuming that the salt has the same concentration in both coexisting phases.

Numerical Methods

We perform simulations of DNA nanostars with oxDNA2, a DNA model coarse-grained at the level of single nucleotides. The interaction forms and parameters in oxDNA2 are chosen to reproduce structural and thermodynamical properties of both single- and double-stranded DNA molecules in B-form. The interactions between nucleotides, modeled as rigid bodies, account for excluded volume, electrostatic repulsion between the negatively charged backbones, backbone connectivity, Watson–Crick hydrogen bonding, stacking, cross-stacking, and coaxial stacking. The interaction parameters have been adjusted in order to be consistent with experimental data on the structure and thermodynamics of DNA.29,45 The electrostatic repulsion is provided by a Yukawa term characterized by a screening length which is an increasing function of T and a decreasing function of S. We note that we also present results for S = 0.025 M, a salt concentration which is slightly below the lowest value for which oxDNA2 has been parametrized.

In order to calculate the second virial coefficient, we evaluate the interstar interaction potential V(r) in the infinite dilution limit. We compute V(r) between two isolated nanostars, for different values of S and T, using a generalized Widom insertion method.46 We first separately simulate the two nanostars for long enough that they lose memory of their previous conformation. We then take the two equilibrated configurations, fix the first one and randomly rotate and insert the other so that their relative center-to-center distance is r, with 0 < r < 30 nm. We perform 500 insertions for every different value of r considered. For each insertion, we calculate the Boltzmann factor of the insertion, e–βΔU, where ΔU is the potential energy difference between the initial state (where the two nanostars are very far apart) and the new configuration, and average it over all trial insertions at fixed r. We repeat the whole procedure for at least 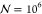Inline graphic iterations, obtaining the radial distribution function, g2(r) = ⟨e–βΔU⟩r, from which the interaction potential between the DNA nanostars in the limit of infinite dilution is readily obtained as

graphic file with name nn-2016-08287b_m012.jpg 11

Given the small scale of the simulations, which involve only two DNA constructs, and the purely repulsive nature of the interactions, convergence is reached very rapidly. Indeed, the evaluation of a single B2(T, S) value takes from few minutes to few hours (depending on the size of the nanostars and on salt concentration) on a single CPU core. The code we use is based on oxDNA,47 and it is available upon request.

We also run large-scale simulations (800 purely repulsive tetramers and a binary mixture of 50 trimers and 100 dimers) to test the assumptions underlying the proposed theoretical approach. We perform these simulations on NVIDIA K80 GPUs,48 and equilibration takes between a few days to a few weeks of computer time.

Acknowledgments

L.R. acknowledges support from the Austrian Science Fund (FWF) through the Lise-Meitner Fellowship No. M 1650-N27 and from the European Commission through the Marie Skłodowska–Curie Fellowship No. 702298-DELTAS. P.H.H. acknowledges support from the Austrian Science Fund (FWF) through the Erwin Schrödinger Fellowship No. J3811-N34. Computer time at the Vienna Scientific Cluster (VSC) is gratefully acknowledged.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.6b08287.

  • Strand sequences, additional information on the effect of the salt concentration on the effective interactions, second virial coefficients, and the DNA nanostar conformations, and a thorough description of the methods used for the determination of the thermodynamics of both pure systems and mixtures (PDF)

The authors declare no competing financial interest.

Supplementary Material

nn6b08287_si_001.pdf (542.4KB, pdf)

References

  1. Egli M.; Saenger W.. Principles of Nucleic Acid Structure; Springer Science & Business Media, 2013. [Google Scholar]
  2. Seeman N. C. Nucleic Acid Junctions and Lattices. J. Theor. Biol. 1982, 99, 237–247. 10.1016/0022-5193(82)90002-9. [DOI] [PubMed] [Google Scholar]
  3. Seeman N. C. DNA Nanotechnology: Novel DNA Constructions. Annu. Rev. Biophys. Biomol. Struct. 1998, 27, 225–248. 10.1146/annurev.biophys.27.1.225. [DOI] [PubMed] [Google Scholar]
  4. Wollman A. J. M.; Sanchez-Cano C.; Carstairs H. M. J.; Cross R. A.; Turberfield A. J. Transport and Self-Organization Across Different Length Scales Powered by Motor Proteins and Programmed by DNA. Nat. Nanotechnol. 2013, 9, 44–47. 10.1038/nnano.2013.230. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Soloveichik D.; Seelig G.; Winfree E. DNA as a Universal Substrate for Chemical Kinetics. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 5393–5398. 10.1073/pnas.0909380107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Rothemund P. W. K. Folding DNA to Create Nanoscale Shapes and Patterns. Nature 2006, 440, 297–302. 10.1038/nature04586. [DOI] [PubMed] [Google Scholar]
  7. Zhao Y.-X.; Shaw A.; Zeng X.; Benson E.; Nyström A. M.; Högberg B. DNA Origami Delivery System for Cancer Therapy with Tunable Release Properties. ACS Nano 2012, 6, 8684–8691. 10.1021/nn3022662. [DOI] [PubMed] [Google Scholar]
  8. Ke Y.; Ong L. L.; Shih W. M.; Yin P. Three-Dimensional Structures Self-Assembled from DNA Bricks. Science 2012, 338, 1177–1183. 10.1126/science.1227268. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Reinhardt A.; Frenkel D. DNA Brick Self-Assembly with an Off-Lattice Potential. Soft Matter 2016, 12, 6253–6260. 10.1039/C6SM01031H. [DOI] [PubMed] [Google Scholar]
  10. Theodorakis P.; Fytas N.; Kahl G.; Dellago C. Self-Assembly of DNA-Functionalized Colloids. Condens. Matter Phys. 2015, 18, 22801. 10.5488/CMP.18.22801. [DOI] [Google Scholar]
  11. di Michele L.; Eiser E. Developments in Understanding and Controlling Self-Assembly of DNA-Functionalized Colloids. Phys. Chem. Chem. Phys. 2013, 15, 3115–3129. 10.1039/c3cp43841d. [DOI] [PubMed] [Google Scholar]
  12. Jones M. R.; Seeman N. C.; Mirkin C. A. Programmable Materials and the Nature of the DNA Bond. Science 2015, 347, 1260901. 10.1126/science.1260901. [DOI] [PubMed] [Google Scholar]
  13. Rogers W. B.; Manoharan V. N. Programming Colloidal Phase Transitions with DNA Strand Displacement. Science 2015, 347, 639–642. 10.1126/science.1259762. [DOI] [PubMed] [Google Scholar]
  14. Winfree E.; Liu F.; Wenzler L. A.; Seeman N. C. Design and Self-Assembly of Two-Dimensional DNA Crystals. Nature 1998, 394, 539–544. 10.1038/28998. [DOI] [PubMed] [Google Scholar]
  15. Park N.; Um S. H.; Funabashi H.; Xu J.; Luo D. A Cell-Free Protein-Producing Gel. Nat. Mater. 2009, 8, 432–437. 10.1038/nmat2419. [DOI] [PubMed] [Google Scholar]
  16. Nakata M.; Zanchetta G.; Chapman B. D.; Jones C. D.; Cross J. O.; Pindak R.; Bellini T.; Clark N. A. End-to-End Stacking and Liquid Crystal Condensation of 6 to 20 Base Pair DNA Duplexes. Science 2007, 318, 1276. 10.1126/science.1143826. [DOI] [PubMed] [Google Scholar]
  17. Biffi S.; Cerbino R.; Bomboi F.; Paraboschi E. M.; Asselta R.; Sciortino F.; Bellini T. Phase Behavior and Critical Activated Dynamics of Limited-Valence DNA Nanostars. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 15633–15637. 10.1073/pnas.1304632110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Bomboi F.; Romano F.; Leo M.; Fernandez-Castanon J.; Cerbino R.; Bellini T.; Bordi F.; Filetici P.; Sciortino F. Re-entrant DNA Gels. Nat. Commun. 2016, 7, 13191. 10.1038/ncomms13191. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Bianchi E.; Largo J.; Tartaglia P.; Zaccarelli E.; Sciortino F. Phase Diagram of Patchy Colloids: Towards Empty Liquids. Phys. Rev. Lett. 2006, 97, 168301. 10.1103/PhysRevLett.97.168301. [DOI] [PubMed] [Google Scholar]
  20. Bianchi E.; Blaak R.; Likos C. N. Patchy Colloids: State of the Art and Perspectives. Phys. Chem. Chem. Phys. 2011, 13, 6397–6410. 10.1039/c0cp02296a. [DOI] [PubMed] [Google Scholar]
  21. Roldán-Vargas S.; Smallenburg F.; Kob W.; Sciortino F. Phase Diagram of a Reentrant Gel of Patchy Particles. J. Chem. Phys. 2013, 139, 244910. 10.1063/1.4849115. [DOI] [PubMed] [Google Scholar]
  22. Romano F.; Sanz E.; Sciortino F. Crystallization of Tetrahedral Patchy Particles in Silico. J. Chem. Phys. 2011, 134, 174502. 10.1063/1.3578182. [DOI] [PubMed] [Google Scholar]
  23. Smallenburg F.; Sciortino F. Liquids More Stable than Crystals in Particles with Limited Valence and Flexible Bonds. Nat. Phys. 2013, 9, 554–558. 10.1038/nphys2693. [DOI] [Google Scholar]
  24. Millan J. A.; Ortiz D.; van Anders G.; Glotzer S. C. Self-Assembly of Archimedean Tilings with Enthalpically and Entropically Patchy Polygons. ACS Nano 2014, 8, 2918–2928. 10.1021/nn500147u. [DOI] [PubMed] [Google Scholar]
  25. Wertheim M. S. Fluids with Highly Directional Attractive Forces. I. Statistical Thermodynamics. J. Stat. Phys. 1984, 35, 19–34. 10.1007/BF01017362. [DOI] [Google Scholar]
  26. Wertheim M. S. Fluids with Highly Directional Attractive Forces. II. Thermodynamic Perturbation Theory and Integral Equations. J. Stat. Phys. 1984, 35, 35–47. 10.1007/BF01017363. [DOI] [Google Scholar]
  27. Marshall B. D.; Ballal D.; Chapman W. G. Wertheim’s Association Theory Applied to One Site Patchy Colloids: Beyond the Single Bonding Condition. J. Chem. Phys. 2012, 137, 104909. 10.1063/1.4751480. [DOI] [PubMed] [Google Scholar]
  28. Carnahan N. F.; Starling K. E. Equation of State for Nonattracting Rigid Spheres. J. Chem. Phys. 1969, 51, 635–636. 10.1063/1.1672048. [DOI] [Google Scholar]
  29. Snodin B. E. K.; Randisi F.; Mosayebi M.; Šulc P.; Schreck J. S.; Romano F.; Ouldridge T. E.; Tsukanov R.; Nir E.; Louis A. A.; Doye J. P. K. Introducing Improved Structural Properties and Salt Dependence into a Coarse-Grained Model of DNA. J. Chem. Phys. 2015, 142, 234901. 10.1063/1.4921957. [DOI] [PubMed] [Google Scholar]
  30. SantaLucia J. A Unified View of Polymer, Dumbbell, and Oligonucleotide DNA Nearest-Neighbor Thermodynamics. Proc. Natl. Acad. Sci. U. S. A. 1998, 95, 1460. 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. SantaLucia J. Jr; Hicks D. The Thermodynamics of DNA Structural Motifs. Annu. Rev. Biophys. Biomol. Struct. 2004, 33, 415–440. 10.1146/annurev.biophys.32.110601.141800. [DOI] [PubMed] [Google Scholar]
  32. Bomboi F.; Biffi S.; Cerbino R.; Bellini T.; Bordi F.; Sciortino F. Equilibrium Gels of Trivalent DNA-Nanostars: Effect of the Ionic Strength on the Dynamics. Eur. Phys. J. E: Soft Matter Biol. Phys. 2015, 38, 1–8. 10.1140/epje/i2015-15064-9. [DOI] [PubMed] [Google Scholar]
  33. Nicolai T.; Mandel M. The Ionic Strength Dependence of the Second Virial Coefficient of Low Molar Mass DNA Fragments in Aqueous Solutions. Macromolecules 1989, 22, 438–444. 10.1021/ma00191a080. [DOI] [Google Scholar]
  34. Stigter D.; Dill K. A. Theory for Second Virial Coefficients of Short DNA. J. Phys. Chem. 1993, 97, 12995–12997. 10.1021/j100151a057. [DOI] [Google Scholar]
  35. Fernandez-Castanon J.; Bomboi F.; Rovigatti L.; Zanatta M.; Paciaroni A.; Comez L.; Porcar L.; Jafta C. J.; Fadda G. C.; Bellini T.; Sciortino F. Small-Angle Neutron Scattering and Molecular Dynamics Structural Study of Gelling DNA Nanostars. J. Chem. Phys. 2016, 145, 084910. 10.1063/1.4961398. [DOI] [PubMed] [Google Scholar]
  36. Rovigatti L.; Bomboi F.; Sciortino F. Accurate Phase Diagram of Tetravalent DNA Nanostars. J. Chem. Phys. 2014, 140, 154903. 10.1063/1.4870467. [DOI] [Google Scholar]
  37. Toan N. M.; Micheletti C. Inferring the Effective Thickness of Polyelectrolytes from Stretching Measurements at Various Ionic Strengths: Applications to DNA and RNA. J. Phys.: Condens. Matter 2006, 18, S269. 10.1088/0953-8984/18/14/S11. [DOI] [Google Scholar]
  38. Fantoni R.; Pastore G. Wertheim Perturbation Theory: Thermodynamics and Structure of Patchy Colloids. Mol. Phys. 2015, 113, 2593–2607. 10.1080/00268976.2015.1061150. [DOI] [Google Scholar]
  39. Rovigatti L.; de las Heras D.; Tavares J.; da Gama M. T.; Sciortino F. Computing the Phase Diagram of Binary Mixtures: a Patchy Particle Case Study. J. Chem. Phys. 2013, 138, 164904. 10.1063/1.4802026. [DOI] [PubMed] [Google Scholar]
  40. Sollich P. Predicting Phase Equilibria in Polydisperse Systems. J. Phys.: Condens. Matter 2002, 14, R79. 10.1088/0953-8984/14/3/201. [DOI] [Google Scholar]
  41. Romano F.; Sciortino F. Switching Bonds in a DNA Gel: An All-DNA Vitrimer. Phys. Rev. Lett. 2015, 114, 078104. 10.1103/PhysRevLett.114.078104. [DOI] [PubMed] [Google Scholar]
  42. Beattie J.; Stockmayer W. The Second Virial Coefficient for Gas Mixtures. J. Chem. Phys. 1942, 10, 473. 10.1063/1.1723750. [DOI] [Google Scholar]
  43. Debenedetti P. G.Metastable Liquids: Concepts and Principles; Princeton University Press, 1996. [Google Scholar]
  44. Koningsveld R. Phase Relationship and Fractionation in Multicomponent Polymer Solutions. Pure Appl. Chem. 1969, 20, 271–308. 10.1351/pac196920030271. [DOI] [Google Scholar]
  45. Doye J. P.; Ouldridge T. E.; Louis A. A.; Romano F.; Šulc P.; Matek C.; Snodin B. E.; Rovigatti L.; Schreck J. S.; Harrison R. M.; Smith W. P. Coarse-Graining DNA for Simulations of DNA Nanotechnology. Phys. Chem. Chem. Phys. 2013, 15, 20395. 10.1039/c3cp53545b. [DOI] [PubMed] [Google Scholar]
  46. Mladek B. M.; Frenkel D. Pair Interactions between Complex Mesoscopic Particles from Widom’s Particle-Insertion Method. Soft Matter 2011, 7, 1450–1455. 10.1039/C0SM00815J. [DOI] [Google Scholar]
  47. http://dna.physics.ox.ac.uk (accessed Feb 1, 2017).
  48. Rovigatti L.; Šulc P.; Reguly I. Z.; Romano F. A Comparison between Parallelization Approaches in Molecular Dynamics Simulations on GPUs. J. Comput. Chem. 2015, 36, 1–8. 10.1002/jcc.23763. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn6b08287_si_001.pdf (542.4KB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES