Integrative Spatial Data Analytics for Public Health Studies of New York State

Abstract

Increased accessibility of health data made available by the government provides unique opportunity for spatial analytics with much higher resolution to discover patterns of diseases, and their correlation with spatial impact indicators. This paper demonstrated our vision of integrative spatial analytics for public health by linking the New York Cancer Mapping Dataset with datasets containing potential spatial impact indicators. We performed spatial based discovery of disease patterns and variations across New York State, and identify potential correlations between diseases and demographic, socio-economic and environmental indicators. Our methods were validated by three correlation studies: the correlation between stomach cancer and Asian race, the correlation between breast cancer and high education population, and the correlation between lung cancer and air toxics. Our work will allow public health researchers, government officials or other practitioners to adequately identify, analyze, and monitor health problems at the community or neighborhood level for New York State.

Introduction

Open data initiatives supported by the governments are providing unprecedented information about our health. New York State Cancer Mapping dataset¹, for example, consists the number of people diagnosed with cancer (cancer counts, 2005-2009) in small geographic areas. New York State data from Statewide Planning and Research Cooperative System (SPARCS)² collects patient level detail on patient characteristics, diagnoses and treatments, services, and charges for each hospital inpatient stay and outpatient visit. Such data also provides street level location information for each patient and healthcare facility site. The improved availability of health data combined with improved geospatial analysis and spatial statistics techniques has significant potential to uncover the spatial patterns of diseases in a population and provide insight as to their causes and controls.

Integrative spatial data analytics for public health has a strong focus on locating patients and the agents of disease, studying the community and region level patterns and variations, and assessing demographic, socio-economic, and environmental factors on diseases and human health. In the past, due to limited accessibility of heath outcome data, public health studies were often limited at macro scale levels such as county level or ZIP code tabulation areas (ZCTAs), and may not allow public health researchers and health officials to adequately identify most at-risk populations, analyze, and monitor health events at the community or neighborhood level^3-5.

One critical challenge for spatial epidemiology and public health research is the isolated datasets with different spatial resolutions, data formats, or data quality. The patient addresses from hospitals, for example, have to be converted into geolocations (latitude, longitude) and then get approximated into a standard geographic identifier (such as census tract or census block group IDs) to protect the privacy of human subjects. Another common issue is the problem of spatial interpolation that combines both point and areal data through the use of area-to-area, area-to-point, and point-to-point covariances⁶. To align spatial data with different geographical granularities, we also need to either aggregate values from small areas into larger ones or vice versa.

Our goal is to integrate fine-grained open health data with a comprehensive set of spatial “exposure” data, which is ranging from levels of various environmental pollutants to the socioeconomic status of persons at risk¹⁴.We focus on the spatial public health research at the community level and consolidate a variety of spatial datasets into a data warehouse system, supported by a scalable computing infrastructure for spatial data integration and spatial analytics. We take advantage of Hadoop-GIS^7-8, a MapReduce based spatial data warehouse system to perform spatial query based data integration. Integrative spatial data analytics is built on top of the integrative spatial data warehouse to support various spatial query types and analytic methods.

In this paper, we verified our methodology for integrative spatial data analytics by linking the New York Cancer Mapping Dataset (Table 1) with three categories of spatial impact indicators (Table 2) generated from representative spatial exposure data sources such as census statistics, geospatial and map data from TIGER (Topologically Integrated Geographic Encoding and Referencing), the American Community Survey (ACS) data, and air toxics data from Environmental Protection Agency (EPA). We first studied spatial distributions and clustering of the cancer risk and spatial impact factors at the level of census block group or census tract. We then correlated the cancer risk ratios with spatially varying demographic, socio-economic, and environmental factors (Tables 3-5), using both non-spatial correlation analysis (ordinary least square regression) and spatial correlation analysis (geographically weighted regression). The results were consistent with three well-established relationships: that between stomach cancer and Asian and Hispanic race, that between breast cancer and high income and high education population, and that between lung cancer and air toxics. At last, we undertook three case studies to identify the detailed spatial trends for each of these three pairs of relationship separately (Figures 1-3).

Table 1.

Statistics of New York Cancer Mapping Dataset at Census Block Group Level, 2005-2009.

Category of Cancer	Sum of Cases	Relative Risk (RR)			Moran’s I Index
		Minimum	Maximum	Mean (St. Dev.)
Total	524,503	0.18	17.14	1.02 (0.29)	0.09*
Prostate	78,162	0	12.08	1.03 (0.56)	0.20*
Female breast	72,296	0	10.89	1.01 (0.53)	0.07*
Lung and bronchus	67,217	0	21.83	1.04 (0.67)	0.19*
Colon and rectum	49,801	0	21.50	1.03 (0.67)	0.03*
Bladder, including in situ	25,134	0	13.68	1.00 (0.90)	0.11*
Non-Hodgkin lymphoma	22,279	0	8.93	1.01 (0.89)	0.02*
Uterus	17,194	0	79.63	1.03 (1.24)	0.01
Kidney and renal pelvis	16,371	0	39.27	1.02 (1.13)	0.03*
Thyroid	15,109	0	12.75	1.01 (1.12)	0.11*
Leukemia	14,091	0	25.05	1.01 (1.13)	0.03*
Pancreas	13,927	0	54.31	1.02 (1.25)	0.03*
Oral cavity and pharynx	10,799	0	16.50	1.03 (1.32)	0.03*
Stomach	9,285	0	36.70	1.05 (1.50)	0.06*
Liver and intrahepatic bile duct	8,342	0	15.63	1.04 (1.57)	0.10*
Ovary	7,582	0	55.14	1.02 (1.60)	0.01
Brain and other nervous system	6,714	0	22.33	1.02 (1.62)	0.01
Esophagus	5,467	0	17.13	1.03 (1.84)	0.02*
Larynx	4,179	0	23.65	1.06 (2.15)	0.02*
Soft tissue	3,385	0	23.83	1.03 (2.26)	0
Testis	2,690	0	33.61	1.09 (2.79)	0.01*
Bone and joint	1,026	0	61.12	1.04 (4.15)	-0.01*
Mesothelioma	979	0	60.42	1.03 (4.32)	0.01
Nasal cavity and nasopharynx	689	0	84.97	1.02 (5.04)	0

^*Significant at 1% confidence interval

Table 2.

Statistics of Demographic, Socio-economic, and Environmental Indicators from Spatial Exposure Data.

Spatial Impact Indicators		Min.	Max.	Mean (St. Dev.)	Moran’s I Index
Demographic Indicators	Asian*	0	0.96	0.07 (0.12)	0.86*
	White*	0	1	0.68 (0.31)	0.91*
	Black*	0	0.98	0.15 (0.24)	0.91*
	American Indian*	0	0.95	0.01 (0.02)	0.34*
	Pacific Islander*	0	0.05	0 (0)	0.13*
	Hispanic*	0	0.94	0.16 (0.19)	0.88*
Socio-economic Indicators	Poverty Population*	0	0.90	0.13 (0.14)	0.54*
	Low Education Population*	0	0.78	0.15 (0.13)	0.60*
	Num. of Persons per Household	0	5.75	2.63 (0.52)	0.70*
Environmental Indicators**	Formaldehyde	6×10-6	62×10-6	25×10-6 (11×10-6)	0.98*
	Carbon tetrachloride	2×10-6	4×10-6	3×10-6 (0)	0.05*
	PAHPOM	0	26×10-6	2×10-6 (2×10-6)	0.71*
	Chromium VI	0	43×10-6	2×10-6 (2×10-6)	0.84*
	Acetaldehyde	1×10-6	8×10-6	4×10-6 (1×10-6)	0.94*
	Benzene	1×10-6	57×10-6	15×10-6 (8×10-6)	0.93*
	T etrachloroethylene	0	19×10-6	4×10-6 (3×10-6)	0.93*
	Naphthalene	0	33×10-6	7×10-6 (4×10-6)	0.92
	1,3-butadiene	0	14×10-6	4×10-6 (2×10-6)	0.92*
	Arsenic	0	9×10-6	2×10-6 (1×10-6)	0.94*

^*Population Proportion among Total Population

^**The air toxics data from EPA are at the level of census tract.

Table 3.

Summary of Correlation Analysis for Demographic and Socio-economic Indicators.

Spatial Impact Indicators		Stomach Cancer RR			Breast Cancer RR
		OLS (Std. Error)	GWR	Bivariate Moran’s I	OLS (Std. Error)	GWR	Bivariate Moran’s I
Demographic Indicators	Asian	1.87* (0.11)	-10.46 - 17.79	0.14*	-0.08* (0.04)	-	-0.06*
	White	-	-	-0.19*	0.11* (0.02)	-	0.17*
	Black	0.82* (0.06)	-1.83 - 3.45	0.12*	-	-	-0.11*
	American Indian	-0.46	-	0.01*	-0.67* (0.24)	-0.04*
	Pacific Islander	1.70	-	0.03*	-10.95* (3.66)	-	-0.04
	Hispanic	0.32* (0.09)	-2.41 - 3.93	0.11*	-0.08* (0.03)	-	-0.15*
Socio-economic Indicators	Poverty Population	0.33* (0.12)	-1.56 - 3.34	0.10*	-0.08	-1.26 - 0.31	-0.12*
	Low Education Population	0.57* (0.15)	-2.15 - 3.67	0.13*	-0.47* (0.05)	-1.15 - 0.12	-0.17*
	Num. of Persons per Household	0.01	-	0.08*	-0.04* (0.01)	-0.40 - 0.21	-0.09*

^*Significant at 1% confidence interval

Table 5.

Comparison of Non-Spatial Regression Model (OLS) and Spatial Regression Models (GWR).

Model	Adjusted R-Squared	AICc
Stomach Cancer RR
OLS	0.0s	49,72s
GWR	0.07	49^32
Breast Cancer RR
OLS	0.05	20,925
GWR	0.0s	20,755
Lung Cancer RR
OLS	0.18	4s82
GWR	0.25	435s

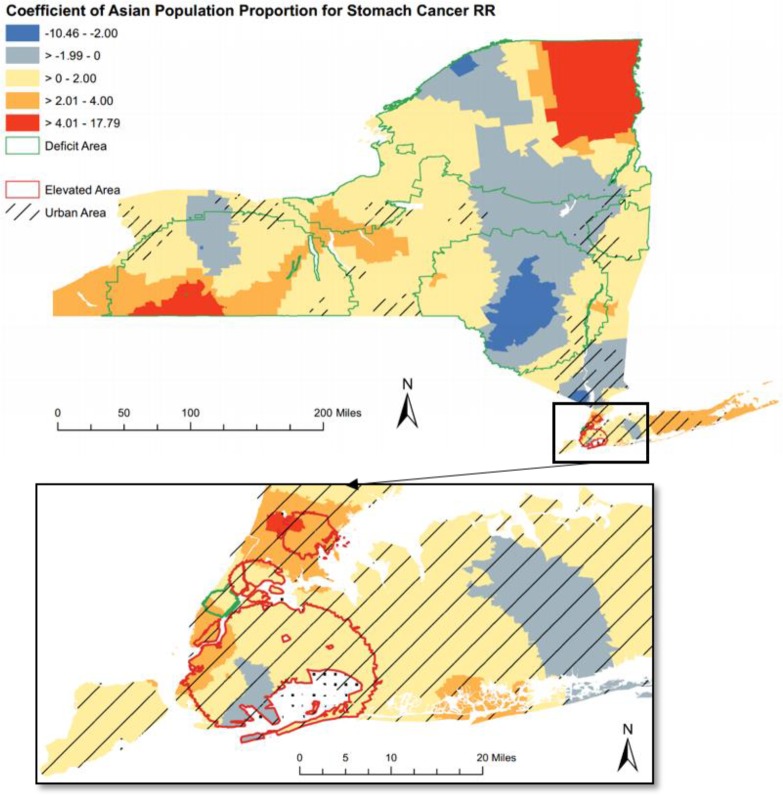
Figure 1.

The choropleth map that visualizes Geographically Weighted Regression (GWR) local coefficient of Asian population for stomach cancer Relative Risk (RR).

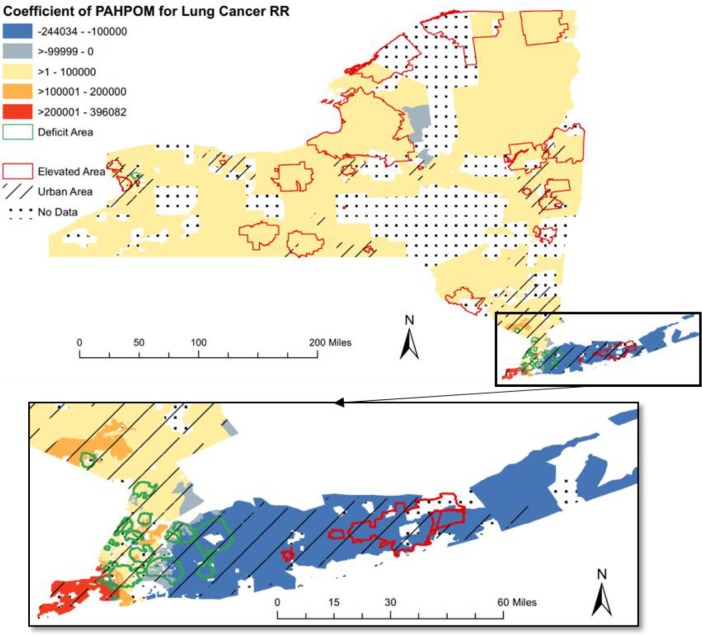
Figure 3.

The choropleth map that visualizes Geographically Weighted Regression (GWR) local coefficient of PAHPOM for lung cancer Relative Risk (RR).

Methods

Data Sources

Spatial Public Health Data: Cancer Incidence Data in New York State.

There has long been a demand for cancer incidence data at a fine geographic resolution for use in etiologic hypothesis generation, methodological evaluation and teaching⁹. We demonstrated our vision of integrative spatial analytics by linking the New York Cancer Mapping Dataset with a comprehensive set of spatial impact indicators from representative spatial exposure data sources such as census and TIGER data, the ACS data, and air toxics data from EPA.

The cancer data set consists of observed counts for 23 anatomic sites of cancer at the neighborhood scale, diagnosed between 2005 and 2009 (Table 1). The data include 524,503 diagnoses of cancer distributed across 13,823 Census block groups with an average population of about 1,400. A census block group is an area containing about 1,000 to 2,000 people as defined by the US Census. Cancer data are reported for a five-year time period because the number of cases in single years can vary dramatically, particularly for outside metropolitan areas¹.

Besides the observed counts of diagnosed cancers, expected counts are also calculated using the indirect standardization method, adjusted for sex and 5-year age groups up to 85+, using the 2010 census counts for New York State⁹. The data set thus contains both observed counts and expected counts per census block group for each of the 23 cancer sites.

Spatial Exposure Data.

We linked three categories of spatial impact indicators to the cancer incidence data using both non-spatial correlation analysis and spatial correlation analysis as shown in Table 2. 1) For demographic indicators, we examined the population proportion for different groups of individuals based on self-identified race and ethnicity, including Asian, Hispanic, White, Black, Pacific Islander, and American Indian. 2) For socio-economic indicators, we examined the number of persons per household, the proportion of poverty population and the population with less than high school education. 3) For environmental indicators, we examined 10 most frequently found air toxics with national average cancer risk greater than one in a million¹⁰.

The demographic indicators here were generated from the 2010 United States Census¹¹ and the socio-economic indicators were from the 2006-2010 American Community Survey¹². The environmental indicators for New York State were generated from Environmental Protection Agency (EPA) National-scale Air Toxins Assessment^{13, 18}. As the EPA air toxics data were at census tract level, we aggregated lung cancer counts per census block group into the counts per census tract.

Analyses

Relative Risk (RR).

We calculated RR through dividing observed counts by expected counts per census block group for different cancer categories (Table 1). The RR estimates provide useful information about how common cancer incidence in a specific location is as compared to the global baseline.

Spatial Clustering.

To test whether there is spatial autocorrelation of the cancer RR, we used Moran’s I (Tables 1 and 2). Moran’s I is a widely used global cluster test, which determines the degree of clustering or dispersion within a data set. The resulting values may range from 1 (perfect correlation), 0 (complete spatial randomness) to -1 (perfect dispersed)¹⁴. For the cancer incidence data, a positive spatial autocorrelation means that the areas with high cancer RR are close to other areas with high cancer RR.

To assess colocation (= spatial correlation) between cancer incidence and each of the spatial impact indicators, we calculated the bivariate Moran’s I for each spatial impact indicator with the cancer RR (Tables 3 and 4). Such bivariate measure of spatial autocorrelation relates the value of a cancer RR at a location to that of a spatial indicator at neighboring locations, as a straightforward generalization of the concept of spatial autocorrelation. This measure of spatial autocorrelation shows the association between cancer incidence at a given location and the local indicator value in neighboring area⁴. The Moran’s I index and the bivariate Moran’s I index were conducted in GeoDa (v 1.6.7)¹⁷.

Table 4.

Summary of Correlation Analysis for Environmental Indicators^**.

Spatial Impact Indicators		Lung Cancer RR
Air Toxics**	Cancer Type	OLS (Std. Error)	GWR	Bivariate Moran’s I
Acetaldehyde	Lung Cancer	-	-	-0.33*
Arsenic	Lung Cancer	0.50x106* (0.14x106)	-0.38x106- 0.s5x106	-0.25*
Benzene	Leukemia	-	-	-0.22*
1,3-butadiene	Leukemia	-	-	-0.29*
Carbon tetrachloride	Adrenal Tumors	0.71x106* (0.14x106)	-	0.00
Chromium VI	Lung Cancer	0.27x106* (0)	-0.88x106 - 0.33x106	-0.12*
Formaldehyde	Nose Cancer	-	-	-0.33*
Naphthalene	Nose Cancer	-0.01x106	-	-0.28*
PAHPOM	Lung Cancer	0.43*106* (0)	-0.24X106 - 0.40X106	0.24*
Tetrachloroethylene	Liver Cancer	-0.80x106* (0.01x106)	-	-0.36*

^*Significant at 1% confidence interval

^**The lung cancer RR and the cancer risk due to 10 air toxics are at the level of census tract.

In addition to observed and expected counts, the New York Cancer Mapping Dataset also includes an indicator variable used to highlight block groups with unusually high or low cancer incidence, as determined using the spatial scan statistic⁹. The spatial scan statistic is a local cluster test, which detects local clusters with statistically significant elevated or deficit risk of diseases. A block group is defined as a high incidence area if 1) it was included in the most likely high incident rate cluster detected by the spatial scan statistic, or 2) it was included in a non-overlapping secondary cluster, and 3) the observed rate was at least 50% higher than the expected rate⁹. A block group was defined as a low incident area in the same manner.

Spatial Regression.

To identify potential correlations between diseases and spatial impact indicators, we assessed both non-spatial and spatial correlation. Ordinary least square regression analyses (OLS) was used to determined nonspatial correlation between cancer RR and each of the spatial impact indicators. We then used Geographically Weighted Regression (GWR) to assess the spatial trends of relevant indicators at a local level.

OLS is a linear regression method that closely fits a function by minimizing the sum of squared errors. To determine potential candidate indicators, we evaluated several possible indicator combinations that form a properly specified OLS regression model. GWR is a local form of linear regression used to model spatially varying relationships. To evaluate the correlation between cancer incidence and spatial impact indicators accounting for data in surrounding areas, we then conducted GWR with a selected indicator combination based on OLS results. Specifically, a fixed kernel type function was used to calculate the GWR regression coefficients. The extent of the kernel is determined using the Akaike Information Criterion (AICc)^{16, 20}. The OLS, GWR and resulting choropleth maps (Figures 1-3) were conducted in ArcGIS (v 10.3).

Results

In this section, we verified our methodology for integrative spatial analytics by linking cancer incidence data (Table 1) with three categories of spatial impact indicators from spatial exposure data (Table 2). The results were consistent with three well-established relationships: the correlation between stomach cancer and Asian race, the correlation between breast cancer and high education population, and the correlation between lung cancer and air toxics. Our results also included detailed spatial trends between cancer RR and spatial impact indicators through three case studies.

Linking Spatial Impact indicators to Health Events

We first modeled all demographic and socio-economic indicators into OLS for both stomach cancer and breast cancer, and then excluded White population for stomach cancer and Black population for breast cancer due to the redundancy issue among different indicators²⁰. For the OLS results of stomach cancer RR, we included all indicators except the White population proportion. For the OLS results of breast cancer RR, we included all indicators except the Black population proportion.

Based on OLS results, we then tried different indicator combinations for GWR model and further excluded several indicators due to the global or local multicollinearity issue¹⁶. As shown in Table 3, we separately chose 5 indicators for GWR model with stomach cancer RR and 3 indicators for GWR model with breast cancer RR. For lung cancer RR (Table 4), 6 out of the 10 air toxics were included in the final OLS model and the 3 air toxics related to lung cancer were included in the final GWR model in the same manner.

The proportion of Asian population was most strongly correlated with stomach cancer RR (Table 3). Among the other significant indicators, the proportions of Black, Hispanic, poverty, and low education population all positively influenced stomach cancer RR. Such finding is consistent with the high stomach cancer rates found among Asian-Americans¹⁵.

Among socio-economic indicators, the proportion of low education population most strongly correlated with breast cancer RR (Table 3). The proportions of different ethnicity groups all negatively influenced breast cancer RR, except the White population proportion. Such findings confirmed the risk factors of higher socio-economic status (SES), race and ethnicity for female breast cancer¹⁹. High SES, which is most often defined by high income and/or high education level, has been linked to an increased risk of breast cancer. This increased risk is not due to the higher SES itself, but rather to differences in risk factors found in women of different education and income levels. For example, compared to women of lower SES, women of higher SES are more likely to 1) have their first child at a later age, 2) have fewer children, 3) use menopausal hormone therapy, 4) use birth control pills, and 5) drink alcohol¹⁹. Since many of these behaviors tend to occur in combination as part of broader lifestyle patterns, the high education can be considered as a direct risk factor for breast cancer.

Most indicators that were significantly correlated with stomach and breast cancer (based on OLS coefficients) also displayed significant colocation relationships (based on bivariate Moran’s I index). However, the bivariate Moran’s I index (spatial correlation) was generally lower than OLS coefficient value (non-spatial correlation), indicating that such correlation was only partly determined by location.

For lung cancer, we examined the 10 most frequently found air toxics with national average cancer risk greater than one in a million (Table 4). The cancer types associated with the air toxics were also listed. We included several air toxics that affected nose cancer, leukemia, and adrenal tumors other than lung cancer for comparison purpose. Among the significant OLS coefficient results, all 3 air toxics related to lung cancer (arsenic, chromium VI, and PAHPOM) were positively correlated with lung cancer. For the air toxics not related to lung cancer, their relationship to lung cancer RR displayed certain randomness. For example, while the carbon tetrachloride (related to adrenal tumors) had the largest positive coefficient value, tetrachloroethylene (related to liver cancer) had a negative coefficient value.

The colocation relationship (Bivariate Moran’s I Index) also displayed inconsistent results as compared to OLS model. For example, while arsenic and chromium VI were positively correlated to lung cancer according to the significantly positive coefficient value, their bivariate Moran’s I indexes were negative which indicated negative spatial correlation.

Among the 3 air toxics related to lung cancer, only PAHPOM had consistent positive correlation relationship with lung cancer. We then chose PAHPOM in the following case study for spatial trend of GWR coefficient.

The model comparison results were shown in Table 5. The GWR was the overall best-fitting regression model in terms of adjusted R-squared as well as the goodness-of-fit AICc statistic. The adjusted R-squared value represented the percentage of local deviance explained. In general, the higher the R-squared, the better the model fits your data. In terms of the AICc statistic, the model with the lowest AICc value is the model with the best fit. Based on this criterion, GWR regression had a slightly better fit than the OLS regression. For lung cancer, the adjusted R-squared increased from 0.18 (OLS as a non-spatial model) to 0.25 (GWR as a spatial model), which suggests a stronger correlation when information from the surrounding areas was taken into account in the spatial regression model.

Most GWR coefficients fluctuated widely across the research area and exceeded the confidence intervals found in the OLS regression (Tables 3 and 4), indicating a more or less varying relation between cancer RR and spatial indicators across research area. In the following section, we then had a closer examination for the spatial trends of local coefficients through case studies.

Case Study 1: Stomach Cancer RR and Demographic Indicators

For stomach cancer RR, the local coefficients of Asian population proportion varied across New York State and were mostly positive (84.4%), indicating a positive association for most part of New York state (Figure 1). The positive association was strongest in the southwest and northeast corner of upper state.

The association also displayed strong regional and intra-urban differences. All the elevated clusters were located at the New York City where the Asian proportion generally had a positive impact. The deficit stomach cancer clusters (with green boundary in Figure 1), on the other hand, mainly appeared at the rural area (areas with line fill symbol in Figure 1) and the coefficient values had a strong local differences within the cluster boundaries.

Case Study 2: Breast Cancer RR and Socio-economic Indicators

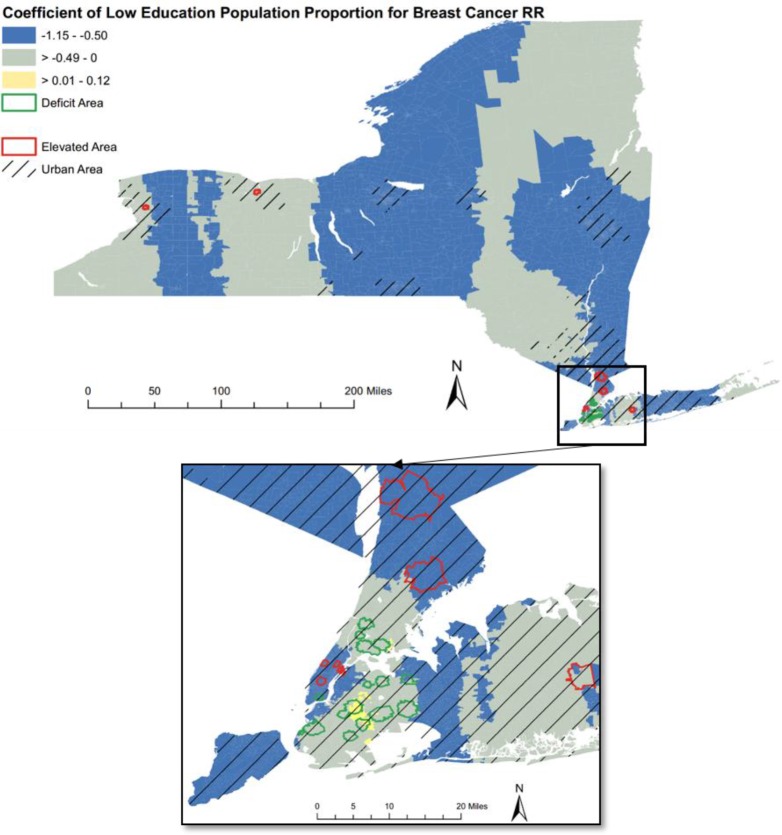
As shown in Figure 2 for breast cancer RR, the local coefficients of low education proportion were overall negative (98.6%), indicating that lower education was associated with a lower breast cancer risk. The small portion of positive coefficient was mainly located at the adjacent area between Brooklyn and Queens Boroughs in New York City.

Figure 2.

The choropleth map that visualizes Geographically Weighted Regression (GWR) local coefficient of low education population for breast cancer Relative Risk (RR).

Most of the highlighted clusters, either elevated clusters or deficit clusters, were located at urban areas in the downstate New York. While all the elevated clusters were located at three urban areas throughout the New York state, all the deficit clusters gathered in the New York City area.

Case Study 3: Lung Cancer RR and Environmental Indicators

As shown in Figure 3 for lung cancer, the coefficient values of PAHPOM were mostly positive throughout the New York State, which is consistent with the well-established relationship between PAHPOM and lung cancer¹⁰. One exception was the area of long island where had an overall negative correlation to PAHPOM.

In general, areas with higher than expected lung cancer incidence (elevated clusters) were located in upstate New York and areas with lower than expected incidence (deficit clusters) were located in downstate New York. The only exception was the area of long island where two elevated clusters were located.

Most of the highlighted clusters, either elevated clusters or deficit clusters, were located at urban areas, with a small portion of elevated clusters appeared at the rural areas. Such inconsistent relationships may require further research for the potential driving factors.

Discussion

This study linked the New York Cancer Mapping Dataset with spatial exposure data sources, thus supporting spatial correlation analyses that draw consistent results with previous work about cancer risks in relation to spatially varying risk factors. In addition, we provided three case studies that mapped the varying values of the local coefficient with improved resolution, which is useful for refined evaluation into spatial trends between cancer risk and spatial indicators.

While our ultimate goal is to provide integrative spatial analytics at fine grained spatial resolution, for this initial work, we focused on the analysis of cancer counts, without patient level demographic details such as gender, age or age ranges, race and ethnicity groups. While the expected case counts capture certain demographic structure of the population, it does not satisfy age-specific or race-specific analysis⁹. The data also lack temporal information such as patient admission or discharge date for discovery of temporal patterns.

In our future work, we will take advantage of data from New York Statewide Planning and Research Cooperative System (SPARCS), which comes with fine grained spatial information. SPARCS data comes with patient level details on patient characteristics, diagnoses and treatments, services, and charges for each hospital inpatient stay and outpatient². Such data also provide street level location information for each patient and healthcare facility site.

After geocoding and de-identifying addresses into census block group identifiers, our framework for integrative spatial data analytics will provide spatial queries based on coordinates or boundaries, thus linking and integrating the health records with spatial exposure data at multiple resolutions. We will first provide multi-dimensional analysis by grouping patients according to their demographic or socio-economic attributes. We will then study potential spatial clusters of disease distributions and correlations between disease risk and spatial impact factors. For example, we are interested in exploring potential hotspots of Hepatitis C or potential environment and weather factors that may have correlations with asthma.

Conclusions

Vast amounts of spatial big data are being increasingly generated and provided in the public health domain. Integrating multiple sources of spatial big data could provide new insights and create new forms of value at much higher spatial resolutions to support community or neighborhood level public health studies. In this paper, we present our initial work on integrative spatial data analytics combining cancer incidence data in New York State, Census data and air toxics data. We focus on three representative case studies: correlation between stomach cancer and ethnicity groups, correlation between breast cancer and high education population, and correlation between lung cancer and air toxics. Our results not only are consistent with traditional studies, but also provide much refined results with improved spatial resolution. Our methods are generic and will be applied to New York State SPARCS data in the future.