Classification-by-Analogy: Using Vector Representations of Implicit Relationships to Identify Plausibly Causal Drug/Side-effect Relationships

Abstract

An important aspect of post-marketing drug surveillance involves identifying potential side-effects utilizing adverse drug event (ADE) reporting systems and/or Electronic Health Records. These data are noisy, necessitating identified drug/ADE associations be manually reviewed – a human-intensive process that scales poorly with large numbers of possibly dangerous associations and rapid growth of biomedical literature. Recent work has employed Literature Based Discovery methods that exploit implicit relationships between biomedical entities within the literature to estimate the plausibility of drug/ADE connections. We extend this work by evaluating machine learning classifiers applied to high-dimensional vector representations of relationships extracted from the literature as a means to identify substantiated drug/ADE connections. Using a curated reference standard, we show applying classifiers to such representations improves performance (+≈37%AUC) over previous approaches. These trained systems reproduce outcomes of the manual literature review process used to create the reference standard, but further research is required to establish their generalizability.

Introduction

In 2007, the Institute of Medicine estimated that 1.5 million preventable adverse drug events (ADEs) occur each year in the United States¹. One report in JAMA indicated that ADEs are the most common nonsurgical adverse events that occur in hospitals,² and another meta-analysis indicated that ADEs were between the fourth and sixth leading cause of patient mortality³. Additionally, 25 drug products were removed from market due to safety issues over the last decade, highlighted by high-profile cases such as Vioxx (rofecoxib)⁴, which was removed from market on account of increased risk of potentially fatal cardiovascular side effects. The seriousness and prevalence of postmarketing ADEs is a motivation for modern pharmacovigilance systems – systems that actively monitor adverse event reports and clinical records for the emergence of yet undetected associations between drugs and side effects. A key challenge to this process, however, is determining whether there is sufficiently compelling evidence to support the belief that an observed drug/side-effect relationship is plausibly causal⁵. In order to make this assessment, information from a variety of data sources, including randomized clinical trials, observational studies, and spontaneous ADE reporting systems, is integrated by subject matter experts⁵. This process is extremely time- and resource-intensive, and doesn’t scale well to the vast and growing amount of such data. Though there has been a considerable amount of methodological research focused on the problem of signal detection – the selective identification of meaningful drug/ADE associations using statistical methods – an urgent need exists for informatics methods to support the process of critical clinical review to establish the plausibility of such associations once identified⁶.

In this paper, we evaluate a novel approach to this problem by applying machine learning methods to vector representations of implicit relationship patterns that connect a given drug/ADE pair in the literature. We call this approach “Classification-by-Analogy”, as classification is thought to occur on the basis of the alignment between the relational structures connecting pairs of entities – a defining characteristic of analogical reasoning⁷. Our hypothesis is that the structure (rather than just the content) of the relations that connect pairs of entities in the literature can serve as a meaningful basis for categorization of the nature of the relationship between them. As an initial case study, we set out to determine whether a drug/ADE pair has a plausibly causal relationship substantiated in the literature, as determined by expert review.

Background

In the field of Literature-based Discovery (LBD), relationships extracted from the literature are used to establish the plausibility of an observed or hypothetical relationship (known as “closed discovery”)^8–10. The main idea is that two concepts (such as a drug and disease) that are not connected directly in the literature, may be connected implicitly by relations involving other concepts (for example a drug might inhibit a gene associated with a disease). Though originally intended to assess potentially therapeutic relationships¹⁰, this approach can also be applied to drug/ADE relationships¹¹’¹². Several systems have been deployed in an effort to automate LBD analyses, many of which operate on a co-occurrence based approach^13-16. In this paradigm, co-occurrence of concepts or terms are taken as indications of relationship between concepts of interest. In general, these methods do not consider the nature of a particular relationship, even if assertions that specify it occur in the text. These linking words are of particular interest in LBD methods, however, as they can add additional information to constrain the search space of intermediate concepts. Natural language processing systems such as SemRep have been developed to extract these relational assertions from the biomedical literature¹⁷. SemRep preserves relational assertions by extracting concept-predicate-concept triplets – such as (ibuprofen-TREATS-pain) – which have been used effectively for LBD in a number of applications^15,18. As noted by LBD’s originator, Don Swanson, however, exhaustive exploration of every implicit relationship occurring between concepts is unlikely to be computationally tractable¹⁰, motivating the development of methods that operate on reduced-dimensional approximations of the relationship matrix between concept pairs^19,20. In one approach, concept-predicate-concept triplets form the basis for a vector representation scheme, Predication-based Semantic Indexing (PSI)^19,21, that encodes concepts and their relational connections (or predicates) in a hyper-dimensional semantic vector space. These PSI encodings can be used to query the relationships between concepts by using an approximate form of reasoning in which the potentially intractable task of exploring large numbers of implicit relationships is converted to the computationally convenient task of comparing the similarity between semantic concept vector representations²¹. Although PSI represents concepts as vector encodings in a high-dimensional vector space similar to those of neural embedding approaches (e.g. word2vec²²), these encodings are derived differently. Neural word embeddings are derived directly from natural language using a neural network optimized to predict the context of a given term (or vice versa). In contrast, PSI representations are derived from semantic predications by explicitly encoding the nature of the relationships between concepts using compositional operators.

PSI accomplishes encoding and query functions by leveraging reversible vector transformations provided by a family of representational approaches: Vector Symbolic Architectures (VSAs)^23-25. The vector transformations are algebraic operations, and can be characterized as follows: a bundling operation (+), which adds (or superposes) vectors to generate a vector product that is similar to its component vectors; and binding (⊗), which results in a vector that is dissimilar from its component vectors and is functionally analogous to multiplication. These vector transformations are reversible by subtraction of component vectors and release (Ø) of the binding operation respectively, and vary in technical implementation between VSAs. In our work, we employ the Binary Spatter Code (BSC) as the VSA, which uses high- (or “hyper-”) dimensional binary vectors with dimensionality on the order of 1,000s as a representational unit²⁶. On account of the statistical properties of high-dimensional space, large numbers of such vectors can be generated stochastically – by randomly assigning a one or zero in each dimension with equal probability – with a high probability of their being far apart in space. This means these vectors are exceedingly unlikely to be confused with one another, despite their being distorted during the superposition process: large numbers of such random vectors can be superposed before their signal is lost. The BSC’s bundling transformation takes a majority rule vote between component vectors (ones are assigned to dimensions with more ones than zeros, and ties are broken at random), and employs Pairwise Exclusive OR (XOR) to bind and release (since XOR is its own inverse). These operations provide the basis for training in PSI. The semantic vector for a concept is generated by superposing the bound product of the random vectors for the predicate and argument of each predication it occurs in. For example, the predication “ibuprofen-TREATS-pain” would be encoded into the semantic vector for the concept “ibuprofen” by superposing the bound product of the random vectors for “TREATS” and “pain”. In symbols, where S(concept) is the semantic vector for a concept, and E(concept/PREDICATE) is the elemental (or random) vector for a concept or a predicate, S(ibuprofen) += E(TREATS) ⊗ E(pain). A consequence of this encoding process is that when applied to two semantic vectors, the release operator reveals the two-predicate path (if any) that connects them:

If S(ibuprofen) += E(TREAT S) ⊗ E(pain)

$$\begin{array}{ll}\text{If}\hfill & S\left(\text{ibuprofen}\right)+=E\left(\text{TREATS}\right)\otimes E\left(\text{pain}\right)\hfill \\ \text{and}\hfill & S\left(\text{arthritis}\right)+=E\left(\text{CAUSES}\right)\otimes E\left(\text{pain}\right)\hfill \\ \text{then}\hfill & S\left(\text{ibuprofen}\right)\varnothing S\left(\text{arthritis}\right)=E\left(\text{TREATS}\right)\otimes E\left(\text{pain}\right)\varnothing \left(E\left(\text{CAUSES}\right)\otimes E\left(\text{pain}\right)\right)\hfill \\ \hfill & =E\left(\text{TREATS}\right)\otimes E\left(\text{pain}\right)\varnothing E\left(\text{pain}\right)\varnothing E\left(\text{CAUSES}\right)\hfill \\ \hfill & =E\left(\text{TREATS}\right)\varnothing E\left(\text{CAUSES}\right)\hfill \end{array}$$

For example, in the PSI semantic space for the current work, the nearest-neighboring bound products of predicate pairs to the vector product S (valdecoxib) Ø S(gastrointestinal_hemorrhage) are shown in Table 1. Importantly, these pathways contain only bridging relationship information (structure), and not the bridging concepts themselves (content).

Table 1.

The closest five predicate paths to S(valdecoxib)ØS(gastrointestinal_hemorrhage). –INV indicates directionality, such that CAUSES-INV can be read as “is caused by”. The rank amongst predicate pathways, and the standard deviation above the mean similarity score across these vectors are shown in the first column.

Rank (std > mean)	Neighboring Predicate Pathway	Explanation
1 (4.979988)	E(COMPARED_WITH) Ø E (PREDISPOSES-INV)	Valdecoxib was compared with (e.g. in a clinical trial) a drug that predisposes toward gastrointestinal hemorrhage (gih).
2 (4.031143)	E(COMPARED_WITH) Ø E(CAUSES-INV)	Valdecoxib was compared with a drug that causes gih.
3 (2.931345)	E(ISA) Ø E(CAUSES-INV)	Valdecoxib is of a class of agents that causes gih.
4 (2.801957)	E(COMPARED_WITH) Ø E(TREATS-INV)	Valdecoxib was compared with an agent that treats gih.
5 (2.780393)	E(COEXISTS_WITH) Ø E(PREDISPOSES-INV)	Valdecoxib coexists with a condition that predisposes toward gih.

Once inferred, these predicate based (or reasoning) pathways can be used to direct a search through the space for other concepts that relate to a third concept in a manner similar to the relationship between the cue concept pair – a process referred to as Discovery-by-Analogy (DbA)²⁷, as the reasoning employed follows the pattern: “what is to myocardial infarction as valdecoxib is to gastrointestinal hemorrhage”. We have previously applied this methodology to estimate the plausibility of drug/ADE relationships⁴, using a procedure that restricts the search to a small number of two- and three-predicate pathways (termed “discovery patterns”) inferred from known therapeutic or drug/ADE relationships.

In this paper, we take previous PSI approaches a step further: rather than inferring and applying discrete reasoning pathways from known examples (the “discovery patterns”), we evaluate the utility of applying machine-learning methods to the vector products of semantic PSI representations directly. As these vector products represent patterns of relationships (predicates), we call this approach Classification-by-Analogy (CbA). Our hypothesis is that this will lead to improved performance in a classification task, as the distribution of reasoning pathways between pairs of concepts, rather than the strength of relatedness across a set of discrete pathways, is considered.

By way of novelty, these models have not yet been utilized as a representational framework for machine learning in the biomedical domain, aside from in the context of DbA, so the literature provides little guidance as to which algorithms might be best applied to them. For the current analyses, we chose to utilize k-Nearest Neighbors (kNN), a support vector machine (SVM), and a logistic regression (LR) model. kNN is a nonparametric classifier that functions in simple deployments by taking a majority vote amongst the closest k-neighbors to an unknown data point. Since VSAs generate a vector space populated by vectors in such a way that similar vectors co-localize to a similar geometric region, we anticipated that kNN would provide reasonable performance. SVMs are parametric models that learn a dividing hyperplane defined by a subset of the data (so-called support vectors) in high dimensional spaces to classify examples occurring on either side. As one previous example exists of an SVM applied to vector symbolic representations with success on a text categorization task²⁸, an SVM with similar parameters was chosen. Finally, LR was chosen due to both its popularity and its simplicity in defining a classifying hyperplane as a function of coefficients on the input data alone (i.e., it does not learn the hyperplane as a function of support vectors). Cost functions differ between SVMs and LR, and they differ slightly in their handling of regularization despite sharing the same hyperparameter, C, a term to encourage sparsity.

Labeled data are required input for these supervised machine learning algorithms. In pharmacovigilance, such labeled data has historically been difficult to acquire, as it requires the very human-intensive process that makes pharmacovigilance itself a costly expenditure. The Observational Medical Outcomes Partnership (OMOP)^5,29,30 research initiative endeavored to meet this data need, and produced a drug/side-effect database to facilitate methodological research for drug safety surveillance. This manually curated reference set consists of 165 positive and 234 negative test cases. Each test case is a drug-ADE pair, and each drug is one of 181 unique drugs in the set, including NSAIDs, beta-blockers, ACE inhibitors, antidepressants, antibiotics, and more. The four side-effects chosen – acute myocardial infraction, acute renal failure, acute liver failure, and gastrointestinal bleeding – are four of the most significant ADEs for a risk identification system³¹. Together, these combinations provide a widely used methodological evaluation set and the current benchmark in PV.

Methods

To facilitate our research, we utilized the semantic predications extracted from the literature by SemRep housed in the Semantic Medline Database (SemMedDB) version 2.2 database and the 2012 MetaMapped Medline Baseline (MMB) for PSI and co-occurrence approaches respectively. The SemMedDB extractions were generated by SemRep version 1.5. The MMB was derived from 20,494,848 citations up to November 2011, and contains 399,701 distinct concepts, while SemMedDBv2.2 was derived from 22,252,812 citations up to March 2013, and contains 63,795,467 predications spanning 58 predicates and 257,350 distinct concepts. These versions are identical to those used in the previously published analyses, and were chosen to facilitate methodological comparison. As in previous work, negative predications, such as drug DOES NOT TREAT side-effect, were excluded, comprising only 1.2% of the total predications.

Of the OMOP data set, we utilized 164 positive and 230 negative test cases. For our analysis, we did not use test cases for the drugs darunavir and sitagliptin, as they did not occur in the vector representation stores used for the analyses. The four side-effects in the OMOP set can be defined by a list of International Classification of Diseases (ICD) 9 codes, and so we expanded the list of terms encompassing each ADE to all of its ICD-9 codes and subcodes. Table 2 represents some of the expanded query terms used for myocardial infarction. Drug names were not expanded, and were queried in all cases as named in the OMOP reference set except for niacin, which was translated to nicotinic acid.

Table 2.

Example expanded terms for myocardial infarction.

OMOP Term	ICD-9 Code	Expansion Term
acute myocardial infarction	410	acute_myocardial_infarction
	411	acute_coronary_syndrome
	414	silent_myocardial_infarction

As our co-occurrence approach, we employed reflective random indexing (RRI) which considers both direct cooccurrence and indirect relatedness (between terms co-occurring with the same other terms). RRI was implemented using the Semantic Vectors package version 3.7 with 32,000 dimensional binary vectors in accordance with the BSC. Briefly, document vectors are built by superposing the elemental vectors for each distinct concept that occurs in each document in the MMB, using a log entropy weighting metric (which reduces the effect of high-frequency terms across and within documents). Semantic concept vectors – i.e. S(concept) – are then built by superposing the document vectors that the given concept occurs in. These semantic vectors are then rank ordered based on (1 – the normalized Hamming distance), a similarity measure, between drugs and (expanded) ADEs in the reference set. To expand each ADE into a query that reflected the sum of its ICD-9 codes, we superposed the available vector representations of expanded list terms reflecting the given condition.

For both producing results as in previous PSI analyses using discrete pathways (i.e. DbA) and for our classification analysis, we utilized vector stores from previous analyses, whereby 32,000 dimensional binary vectors were generated consistent with the BSC using Semantic Vectors version 3.7¹¹. A maximum frequency threshold of 1M terms was used to prune uninformative high-level concepts, and negative predications were removed as mentioned above. In order to further mitigate the effect of highly frequent, uninformative terms, superposition of bound products were weighted by predicate frequency multiplied by the sum of the inverse document frequency of the predicate and bound concept such that (using ibuprofen as an example):

$$\begin{array}{ll}\hfill & S\left(\text{ibuprofen}\right)+=E\left(\text{TREATS}\right)\otimes E\left(\text{pain}\right)\cdot f_{TREATS}\cdot \left(id{f}_{TREATS}+id{f}_{pain}\right)\hfill \\ \text{where}\hfill & f_{TREATS}=\log \left(1+\text{occurrences of predication ibuprofen-TREATS-pain}\right)\hfill \\ \hfill & id{f}_{TREATS}=\log \left(\text{number of total predications / number of predications containing TREATS}\right)\hfill \\ \hfill & id{f}_{pain}=\log \left(\text{number of total predications / number of predications containing pain}\right)\hfill \end{array}$$

Additionally, ADE terms were expanded as in RRI for DbA and CbA. For each drug/ADE pair in the reference set, the semantic vectors for the respective drug and ADE are then released as shown above (Table 1), giving us the abstract pathway vector representation for that pair. This vector is then projected into a subspace composed of two predicate discrete reasoning pathways (Table 3) and rank ordered by magnitude to generate DbA results, and passed as input to the machine learning algorithms in our CbA work. Only double predicate pathways were utilized for DbA to facilitate a fair comparison with CbA (in previous work, triple-predicate pathways were also considered). With our goal to classify these vectors according to ground truth relationship, we labeled the vectors representing each drug/ADE pair relationship with the OMOP ground truth state (Figure 1) for input into machine learning algorithms.

Table 3.

The double predicate discrete reasoning pathways that make up the subspace for DbA. gih = gastrointestinal hemorrhage.

Predicate Subspace Component	Explanation
P(INTERACTS_WITH)⊗P(CAUSES-INV)	Valdecoxib interacts with something that causes gih.
P(ASSOCIATED_WITH)⊗P(COEXISTS_WITH)	Valdecoxib associated with something that coexists with gih.
P(COMPARED_WITH)⊗P(CAUSES-INV)	Valdecoxib compared with something that causes gih.
P(ASSOCIATED_WITH)⊗P(INTERACTS_WITH)	Valdecoxib associated with something that interacts with gih.
P(ISA)⊗P(CAUSES-INV)	Valdecoxib is a type of something that causes gih.

Figure 1.

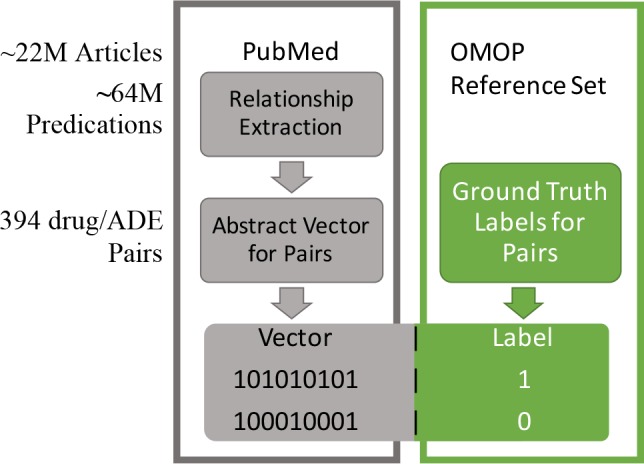
Feature vectors, which represent the abstract pathways that link concepts, are derived from processed literature. The OMOP reference assertions are then used to label these feature vectors as either positive or negative examples.

All machine learning development and deployment was done in the Python programming language version 3.5 using the scikit-leam³² package. The specific Python deployment was from Continuum Analytics Anaconda³³ platform, version 2.5, and a development environment was created using the conda command line utility packaged with Anaconda specifically for the purpose of these analyses and to ease reproducibility. This environment file, along with saved data arrays, code files used, and additional information on software versions utilized, are available upon request.

Within scikit-learn, we utilized the LibLinear library through the scikit-learn.LinearSVC() front end; for k-Nearest Neighbors (kNN) we utilized the scikit-learn.kNN() front end; and for LR we utilized the LibLinear library through the scikit-learn.LogisticRegression() front end. Hyperparameters for the SVM (the regularization C parameter), for LR (C parameter) and for kNN (the k number of neighbors) were chosen using cross-validation grid search functionality built into the scikit learn package (scikit-learn.GridSearchCV). For the SVM and LR, an L1 penalty parameter was chosen to enforce sparsity in the learned model. ROC AUC curves for SVM and LR models were generated by passing the results of the decision function, which calculates the distance from the dividing hyperplane of the classifier for each example in the case of the SVM, as the rank ordering. Additionally, Stratified 5-Fold crossvalidation was used to generate the mean ROC AUC curve by averaging each fold’s performance on a held out test set. Learning curves were generated for the F1 metric by varying the number of training examples and the dimensions of the data. Test data was never utilized in the training phase of any supervised machine learning approach in an attempt to mitigate over-fitting. All plotting was done using the matplotlib package in Python.

Results

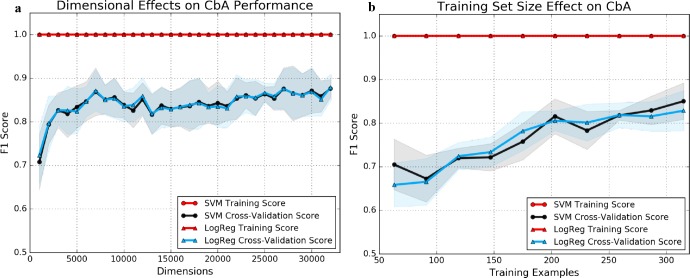
A comparison of kNN performance results with 5, 10, and 15 nearest neighbors are reported below in Table 4. kNN typically performed best with k≈5 in our analysis. For comparison, see F1 scores in Figure 4.

Table 4.

kNN precision, recall, and F1 scores reported with two times the standard deviation across crossvalidation runs in error per number of k neighbors used.

k Neighbors	Precision	Recall	F1 Score
5	0.88 +/- 0.06	0.87 +/- 0.06	0.87 +/- 0.06
10	0.86 +/- 0.05	0.86 +/- 0.05	0.86 +/- 0.05
15	0.83 +/- 0.05	0.81 +/- 0.06	0.82 +/- 0.05

Figure 4.

The effect that truncating dimensions (a) and limiting training samples (b) has on cross-validation performance of CbA parametric methods, as measured by an F1 metric.

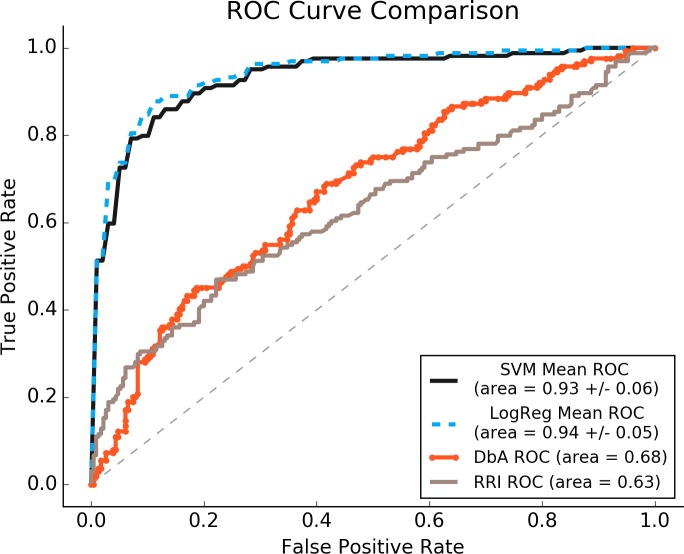
A summary of the ROC results between DbA, RRI, and SVM and LR models both utilizing a C of 1, including AUCs, can be found in Figure 2. All variants of CbA outperformed DbA (+≈37% over 0.68 AUC) and RRI (+≈48% over 0.63 AUC) models, with AUCs around 0.93-0.94. Additional context for these results can be found in the learning curves presented in Figure 4.

Figure 2.

ROC Curves for tested models. AUCs are listed +/- two times the standard deviation (across cross-validation runs).

For C=1, SVM coefficient vectors contained approximately 300/32000 nonzero weights when trained, with similar levels of nonzero weights in LR models. Coherence of nonzero features, including sign and strength of weight, is shown in Figure 3. These nonzero features are distributed across the coefficient vectors for these models. There are approximately 70% shared nonzero positions between them.

Figure 3.

Coherence among LR and SVM models. Negative weights are colored in white, zero values colored in grey, and positive values colored in black. In either case, the 32k weights – one for each dimension of input data – are reshaped into a 200x160 matrix for visualization. Nonzero elements are distributed across the weight vectors. Contrast adjusted for visibility.

LR and SVM models both have one hundred percent accuracy on training sets when trained with full dimensional vectors with C=1. Cross-validation performance is consistently above 0.80 when considering an F1 scoring metric with even a small portion of the training data set and significantly diminished input vector dimensions.

Discussion

To our knowledge, these results represent the first evaluation of classification based on vector representations of abstract relational structures. kNN performance indicates that relational neighborhood as defined by abstract predicate pathways is of value for this task. Although we believe that performance metrics indicate the LR and SVM models are over-fitting, the strong cross-validation performance implies remarkable self-consistency in the representations of the literature for the OMOP reference set. Additionally, LR and SVM models both have striking coefficient vector homology. Since the OMOP set derived its positive examples using automated NLP methods to extract drug reactions from package inserts as the first pass, and then incorporated manual review; and since negative examples were likewise selected as those that did not show up in drug packaging inserts, Tisdale evidence, and had nonexistent or only negative linkings to the ADE in question in the literature during manual review, it is possible that their selection criterion generated a reference set that is internally coherent amongst examples of each class. While more work needs to be done to assess generalizability, presented results indicate that there exists a selfconsistent structure to the OMOP reference set as represented here that provides CbA approaches sufficient information to make accurate classifications on it.

The machine learning algorithms we chose are particularly simple and incorporate no prior information; we anticipate the incorporation of priors will improve performance and likely lend to more generalizable models. Unsurprisingly, it also seems that the models would be well served with additional examples, as evidenced by the learning curves. Such examples would ideally introduce more variance, and trained models would be less prone to over-fitting. Experimentation with additional weighting strategies within the representation itself may also be warranted, as the weighting procedures can influence which predicate pathways are encoded more influentially.

In addition to only being characterized in the context of a single data set, our study has other limitations worth mentioning. First, we didn’t attempt to optimize any statistical weighting metrics or other PSI parameters in the development of this work. Second, we didn’t systematically evaluate how performance changes cross different initializations of the random vectors, opting instead for pseudo-random instantiation per [33]. Additionally, work is presented in comparison to similar approaches that operate on literature information exclusively; other studies have been published on the data set utilizing different methods and data, including observational data^34,35, which is not considered here.

One major benefit of the DbA approach, and one current limitation to CbAs, is clearly defined interpretability. For DbA, confidence scores are generated based on vector-subspace similarity, and the subspace is constructed from elected double predicate pathways. If something has high similarity to the subspace, then the interpretation is that it has high similarity to those predicate pathways which make up the subspace. In our CbA approaches, it is difficult to directly map nonzero coefficients to interpretable pathways or features. Since a fully distributed representation encodes information across vectors, individual features are primarily important in their context of other features. The primary challenge we see facing this work is in mapping learned nonzero parameters from these classifiers back to more interpretable predicate pathways, and to the literature sources that plausibly link these entities themselves. In this same vein, it is likely that more information than just common relations are being utilized by classification algorithms as presented here. The vector space, as a function of its structured encoding scheme, likely incorporates common object information as well when comparing our derived relational representations. For example, in comparing drugs A and B that inhibit the same target C, A⊗C would be similar to B⊗C, and is functionally similar to a direct object comparison in that context (i.e. similarity(A⊗C, B⊗C) = similarity(A,B)). The information used in this case is not exclusively relational, though relational information plays a role (A inhibits y, A causes C; B inhibits Y therefore B may cause C). Further research is needed to identify the extent to which these different sorts of information contribute toward classifier performance.

Conclusion

Each model accurately predicted across a variety of drugs and four ADEs, learning only one set of parameters to distinguish between plausibly causal as defined by the OMOP set and not, substantiating that the representation itself is a meaningful basis for classification tasks. Our original hypothesis that the basis of the relational structure between pairs of biomedical entities could provide the necessary information for categorization of higher level relational status was substantiated by our results on the OMOP reference set.