Interpretable Deep Models for ICU Outcome Prediction

Abstract

Exponential surge in health care data, such as longitudinal data from electronic health records (EHR), sensor data from intensive care unit (ICU), etc., is providing new opportunities to discover meaningful data-driven characteristics and patterns ofdiseases. Recently, deep learning models have been employedfor many computational phenotyping and healthcare prediction tasks to achieve state-of-the-art performance. However, deep models lack interpretability which is crucial for wide adoption in medical research and clinical decision-making. In this paper, we introduce a simple yet powerful knowledge-distillation approach called interpretable mimic learning, which uses gradient boosting trees to learn interpretable models and at the same time achieves strong prediction performance as deep learning models. Experiment results on Pediatric ICU dataset for acute lung injury (ALI) show that our proposed method not only outperforms state-of-the-art approaches for morality and ventilator free days prediction tasks but can also provide interpretable models to clinicians.

Introduction

The national push¹ for electronic health records (EHR) has resulted in an exponential surge in volume, detail, and availability of digital health data. This offers an unprecedented opportunity to infer richer, data-driven descriptions of health and illness. Clinicians are collaborating with computer scientists to improve the state of health care services towards the goal of Personalized Healthcare². Unlike other data sources, medical/hospital data such as EHR is inherently noisy, irregularly sampled (or have missing value), and heterogeneous (data come from different sources such as lab tests, doctor’s notes, monitor readings etc). These data properties make it very challenging for most existing machine learning models to discover meaningful representations or to make robust predictions. This has resulted in development of novel and sophisticated machine learning solutions^3,4,5,6,7,8. Among these methods, deep learning models (e.g., multilayer neural networks) have achieved the state-of-the-art performance on several tasks, such as computational phenotype discovery^9,10 and predictive modeling^8,11.

Even though powerful, deep learning models (usually with millions of model parameters) are difficult to interpret. In today’s hospitals, model interpretability is not only important but also necessary, since clinicians are increasingly relying on data-driven solutions for patient monitoring and decision-making. An interpretable predictive model is shown to result in faster adoptability among clinical staff and better quality of patient care^12,13. Decision trees¹⁴, due to their ease of interpretation, have been successfully employed in the health care domain^15,16,17, and clinicians have embraced them for predictive tasks such as disease diagnosis. However, decision trees can easily overfit and perform poorly on large heterogeneous EHR datasets. Thus, an important question naturally arises: how can we develop novel data-driven solutions which can achieve state-of-the-art performance as deep learning models and at the same time can be easily interpreted by health care professionals and medical practitioners?

Recently, machine learning researchers have conducted preliminary work aiming to interpret the learned features from deep models. An early work¹⁸ investigated visualizing the hierarchical representations learned by deep networks, while a followup work¹⁹ explored feature generalizibility in convolutional neural networks. More recent work²⁰ argued that interpreting individual units of deep models can be misleading. This line of work has shown that interpreting deep learning features is possible but the behavior of deep models may be more complex than previously believed, which motivates us to find alternative strategies to interpreting how deep model work.

In the meanwhile, recent work²¹ showed empirically that shallow neural networks are capable of achieving similar prediction performance as deep neural networks by first training a state-of-the-art deep model, and then training a shallow neural networks using predictions by the deep model as target labels. Similarly, Hinton et. al²² proposed an efficient knowledge distillation approach to transfer (dark) knowledge from model ensembles into a single model following the idea of model compression²³. Another work²⁴ takes a Bayesian approach to distill knowledge from a deep neural network to a shallow neural network. Furthermore, mimic learning has also been successfully applied to multitask learning, reinforcement learning and speech processing applications^25,26,27. These work motivate us to explore the possibility of employing mimic learning to learn an interpretable model and at the same time achieves similar performance as a deep neural network.

In this paper, we introduce a simple yet effective knowledge-distillation approach called interpretable mimic learning, to learn interpretable models with robust prediction performance as deep learning models. Unlike standard mimic learning²¹, which uses shallow neural networks or kernel methods, our interpretable mimic learning framework uses gradient boosting trees (GBT)²⁸ to learn interpretable models from deep learning models. GBT, as an ensemble of decision trees, provides good interpretability along with strong learning capacity. We conduct extensive experiments on several deep learning architectures including feed-forward networks²⁹ and recurrent neural networks³⁰ for mortality and ventilator free days prediction tasks on Pediatric ICU dataset. We demonstrate that deep learning approaches achieve state-of-the-art performance compared to several machine learning methods. Moreover, we show that our interpretable mimic learning framework can maintain strong prediction performance of deep models and provide interpretable features and decision rules.

Background and Deep Models

In this section, we will first introduce notations and describe two state-of-the-art deep learning models, namely feedforward neural networks and gated recurrent unit. We use these two models (and their extensions) as baselines in our experiments as well as components of the proposed interpretable mimic learning.

A. 2.1 Notations

EHR data from ICU contains both static variables such as general descriptors (demographic information collected during admission) and temporal variables, which possibly come from different modalities, such as injury markers, ventilator settings, blood gas values, etc. We use X to represent all the input variables, and a binary label y∈ {0,1} to represent the prediction task outcome such as ICU mortality or Ventilator free days (VFD). We also use x_t to denote the temporal variables observed at time t. Our goal is to learn an effective and interpretable function F() which can be used to predict the value of y given the input X.

2.2 Deep Learning Models

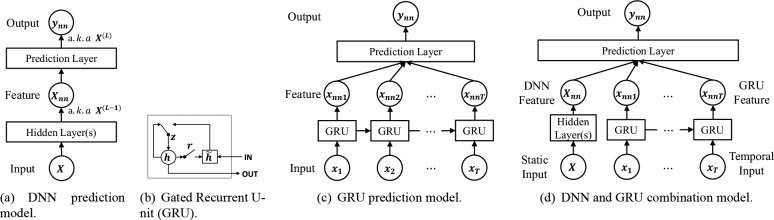
Feedforward Networks A multilayer feedforward network²⁹ (DNN) is a neural network with multiple nonlinear layers and possibly one prediction layer on the top to solve classification task. The first layer takes the concatenation of static and flattened temporal variables as the input X, and the output from each layer is used as the input to the next layer. The transformation of each layer l can be written as

$$X^{\left(l+1\right)}=f^{\left(l\right)}\left(X^{\left(l\right)}\right)=s^{\left(l\right)}\left(W^{\left(l\right)}{X}^{\left(l\right)}+b^{\left(l\right)}\right)$$

where W^(l) and b^(l) are respectively the weight matrix and bias vector of layer l, and s^(l) is a nonlinear activation function, which usually takes one of logistic sigmoid, tanh, or ReLU³¹. For a feed-forward network with L layers shown in Figure 1(a), the output of the top-most layer y_nn = X^(L) is the prediction score, which lies in [0, 1]. People also usually treat the output of second top layer X^(L-1) as the features extracted by DNN, and these features are usually helpful as inputs for other prediction models. We show the structure of DNN model in Figure 1(a). During training, we optimize the cross-entropy prediction loss between the prediction output and the true label.

Figure 1.

Illustration of deep learning models. (a) DNN prediction model. (b) Gated Recurrent U- nit (GRU). (c) GRU prediction model. (d) DNN and GRU combination model.

Gated Recurrent Unit Recurrent neural network (RNN) models, such as Long Short Term Memory (LSTM)³² and Gated Recurrent Unit (GRU)³³, have been shown to be successful at handling complex sequence inputs and capturing long term dependencies. In this paper, we use GRU to model temporal modalities since it has a simpler architecture compared to classical LSTM and has been shown to achieve the state-of-the-art performance among all RNN models for modeling sequential data ³⁰. The structure of GRU is shown in Figure 1(b). Let $x_t\in {ℝ}^p$ denotes the variables at time t, where 1 ≤ t ≤ T. At each time t, GRU has a reset gate r_j^t and an update gate z_j^t for each of the hidden state h_j^t. The update function of GRU is shown as follows:

$$\begin{array}{l}{z}_t=\sigma \left(W_z{x}_t+U_z{h}_{t-1}+b_z\right)r_t=\sigma \left(W_r{x}_t+U_r{h}_{t-1}+b_r\right)\\ {\tilde{h}}_t=tanh\left(W{x}_t+U\left(r_t\odot h_{t-1}\right)+b\right)h_t=\left(1-z_t\right)\odot h_{t-1}+z_t\odot {\tilde{h}}_t\end{array}$$

where matrices W_z, W_r, W, U_z, U_r, U and vectors b_z, b_r, b are model parameters. At time t, we take the hidden states h_t and treat it as the output of GRU x_nnt at that time. As shown in Figure 1(c), we flatten the output of GRU at each time step and add another sigmoid layer on top of them to get the prediction y_nn.

Combinations of deep models One limitation of GRU is that it only aims to model temporal data, while usually both static and temporal features are available in EHR data from ICU. Therefore we propose a combination model of feedforward network (DNN) and GRU. As shown in Figure 1(d), in the combination model, we use one DNN model to take static input features and one GRU model to take temporal input features. We then add one shared layer on top, which takes the features from both GRU and DNN to make prediction, and train all the parts jointly.

Interpretable Mimic Learning

In this section, we introduce the interpretable mimic learning method, which learns interpretable models and achieves similar performance as deep learning models. The proposed approach is motivated by recent development of deep learning in machine learning research and specifically designed for the health care domain.

3.1 Knowledge Distillation

The main idea of knowledge distillation²² is to first train a large, slow, but accurate model and transfer its knowledge to a much smaller, faster, yet still accurate model. It is also known as mimic learning²¹, which uses a complex model (i.e., deep neural network, or an ensemble of network models) as a teacher/base model to train a student/mimic model (such as a shallow neural network or a single network model). The way of distilling knowledge, a.k.a. mimicking the complex models, is to utilize the soft labels learned from the teacher/base model as the target labels while training the student/mimic model. The soft label, in contrast to the hard label from the raw data, is the real value output of the teacher model, whose value usually ranges in [0,1]. It is worth noting that a shallow neural network model is usually not as accurate as a deep neural network model, if trained directly on the same training data. However, with the help of the soft labels from deep models, the shallow model is capable of learning the knowledge extracted by the deep model and can achieve similar or better performance.

The reasons that the mimic learning approach works well can be explained as follows: Some potential noise and error in the training data (input features or labels) may affect the training efficacy of simple models. The teacher model may eliminate some of these errors, thus making learning easier for the student model. Soft labels from the teacher model are usually more informative than the original hard label (i.e. 0/1 in classification tasks), which further improves the student model. Moreover, the mimic approach can also be treated as an implicit way of regularization on the teacher model, which makes the student model robust and prevents it from overfitting. The parameters of the student model can be estimated by minimizing the squared loss between the soft labels from the teacher model and the predictions by the student model. That is, given a set of data {X_i} where i=1,2,...,N as well as the soft label y_s,i from the teacher model, we estimate the student model F(X) by minimizing ${{\displaystyle {\sum }_{i=1}^N\Vert y_{s,i}-F\left(X_i\right)\Vert }}^2$.

While existing work on mimic learning focus on model compression (via shallow neural networks or kernel methods), they cannot lead to more interpretable models, which is important and necessary in health care applications. To address this, we introduce a simple and effective knowledge-distillation approach called interpretable mimic learning, to learn interpretable models that mimic the performance of deep learning models. The main difference of our approach from existing mimic learning approaches is that we use Gradient Boosting Trees (GBT) instead of another neural network as the student model since GBT satisfies our requirements for both learning capacity and interpretability. In the following sections, we describe GBT and our proposed interpretable mimic learning in more details.

3.2 Gradient Boosting Trees

Gradient boosting machines^28,34 are a method which trains an ensemble of weak learners to optimize a differentiable loss function by stages. The basic idea is that the prediction function F(X) can be approximated by a linear combination of several functions (under some assumptions), and these functions can be sought using gradient descent approaches. Gradient Boosting Trees (GBT) takes a simple classification or regression tree as weak learner, and add one weak learner to the entire model per stage. At m-th stage, assume the current model is F_m(X), then the Gradient Boosting method tries to find a weak model h_m(X) to fit the gradient of the loss function with respect to F(X) at F_m(X). The coefficient γ_m of the stage function is computed by the line search strategy to minimize the loss. To keep gradient boosting from overfitting, a regularization method called shrinkage is usually employed, which multiplies a small learning rate v to the stage function in each stage. The final model with M stages can be written as:

$$F_M\left(X\right)={\displaystyle \sum _{i=1}^{M}v{\gamma }_i{h}_i\left(X\right)+const}$$

3.3 Interpretable Mimic Learning Framework

We present two general training pipelines within our interpretable mimic learning framework, which utilize the learned feature representations or the soft labels from deep learning models to help the student model. The main difference between these two pipelines is whether to take the soft labels directly from deep learning models or from a helper classifier trained on the features from deep networks.

In Pipeline 1 (Figures 2), we directly use the predicted soft labels from deep learning models. In the first step, we train a deep learning model, which can be a simple feedforward network or GRU, given the input X and the original target y (which is either 0 or 1 for binary classification). Then, for each input sample X, we obtain the soft prediction score y_nn∈ [0,1] from the prediction layer of the neural network. Usually, the learned soft score y_nn is close but not exactly the same as the original binary label y. In the second step, we train a mimic Gradient boosting model, given the raw input X and the soft label y_nn as the model input and target, respectively. We train the mimic model to minimize the mean squared error of the output y_m to the soft label y_nn.

Figure 2.

Illustration of mimic method training pipeline 1.

In Pipeline 2 (Figures 3), we take the learned features from deep learning models instead of the prediction scores, input them to a helper classifier, and mimic the performance based on the prediction scores from the helper classifier. For each input sample X, we obtain the activations X_nn of the highest hidden layer, which can be X^(L-1) from an L-layer feed forward network, or the flattened output at all time steps from GRU. These obtained activations can be considered as the extracted representations from the neural network, and we can change the its dimension by varying the size of the neural networks. We then feed X_nn into a helper classifier (e.g., logistic regression or support vector machines), to predict the original task y, and take the soft prediction score y_c from the classifier. Finally, we train a mimic Gradient boosting model given X and y_c.

Figure 3.

Illustration of mimic method training pipeline 2.

In both pipelines, we apply the mimic model trained in the last step to predict the labels of testing examples.

Our interpretable mimic learning approach has several advantages. First, our proposed approach can provide models with state-of-art prediction performance. The teacher deep learning model outperforms the traditional methods, and student gradient boosting tree model is good at maintaining the performance of the teacher model by mimicking its predictions. Second, our proposed approach yields more interpretable model than the original deep learning model, which is complex to interpret due to its complex network structures and the large amount of parameters. Our student gradient boosting tree model has better interpretability than original deep model since we can study each feature’s impact on prediction and, we can also obtain simple decision rules from the tree structures. Furthermore, our mimic learning approach uses the soft targets from the teacher deep learning model to avoid overfitting to the original data. Thus, our student model has better generalizations than standard decision tree methods or other models, which tend to overfit to original data.

Experiments

We conduct experiments on a Pediatric ICU dataset to answer the following questions: (a) How does our proposed mimic learning framework perform when compared to the state-of-the-art deep learning methods and other machine learning methods? (b) How do we interpret the models learned through the proposed mimic learning framework? In the remainder of this section, we will describe the dataset, methods, empirical results and interpretations to answer the above questions.

4.1 Dataset and Experimental Design

We conduct experiments on a Pediatric ICU dataset³⁵ collected at the Children’s Hospital Los Angeles. This dataset consists of health records from 398 patients with acute lung injury in the Pediatric Intensive Care Unit at Children’s Hospital Los Angeles. It contains a set of 27 static features such as demographic information and admission diagnoses, and another set of 21 temporal features (recorded daily) such as monitoring features and discretized scores made by experts, for the initial 4 days of mechanical ventilation. We apply simple imputation to fill in missing values, where we take the majority value for binary variables, and empirical mean for other variables. Our choice of imputation may not be the optimal one and finding better imputation methods is another important research direction beyond the scope of this paper. For fair comparison, we used the same imputed data for evaluation of all the methods.

We perform two binary classification (prediction) tasks on this dataset: (1) Mortality (MOR): we aim to predict whether the patient dies within 60 days after admission. 20.10% of all the patients are mortality positive (i.e., patients died). (2) Ventilator Free Days (VFD): we aim to evaluate a surrogate outcome of morbidity and mortality (Ventilator free Days, of which lower value is bad), by identifying patients who survive and are on a ventilator for longer than 14 days within 28 days after admission. Since here lower VFD is bad, it is a bad outcome if the value < 14, otherwise it is a good outcome. 59.05% of all the patients have VFD > 14.

4.2 Methods and Implementation Details

We categorize the methods in our experiments into the following groups:

• Baseline machine learning methods which are popular in healthcare domains: Linear Support Vector Machine (SVM), Logistic Regression (LR), Decision Trees (DT) and Gradient Boosting Trees (GBT).

• Deep network models: We use deep feed-forward neural network (DNN), GRU, and the combinations of them (DNN + GRU).

• Proposed mimic learning models: For each of the deep models shown above, we test both the mimic learning pipelines, and evaluate our mimic model (GBTmimic).

We train all the baseline methods with the same input, i.e., the concatenation of the static and flattened temporal features. The DNN implementations have two hidden layers and one prediction layer. We set the size of each hidden layer twice as large as input size. For GRU, we only use the temporal features as input. The size of other models are set to be in the same scale. We apply several strategies to avoid overfitting and train robust deep learning models: We train for 250 epochs with early stopping criterion based on the loss on validation dataset. We use stochastic gradient descent (SGD) for DNN and Adam³⁶ with gradient clipping for other deep learning models. We also use weight regularizer and dropout for deep learning models. Similarly, for Gradient Boosting methods, we set the maximum number of boosting stages 100, with early stopping based on the AUROC score on validation dataset. We implement all baseline methods using the scikit-learn³⁷ package and all deep networks in Theano³⁸ and Keras³⁹ platforms.

4.3 Overall Classification Performance

Table 1 shows the prediction performance (area under receiver operating characteristic curve (AUROC) and area under precision-recall curve (AUPRC)) of all methods. The results are averaged over 5 random trials of 5-fold cross validation. We observe that for both tasks, all deep learning models perform better than baseline models. The best performance of deep learning models is achieved by the combination model, which use both DNN and GRU to handle static and temporal input variables, respectively. Our interpretable mimic approach achieves similar (or even slightly better performance) as deep models. We found that Pipeline 1 yields slightly better performance than pipeline 2. For example, Pipeline 1 and 2 obtain AUROC score of 0.7898 and 0.7670 for MOR task, and 0.7889 and 0.7799 for VFD task, respectively. Therefore, we use pipeline 1 model in the discussions in Section 4.4.

Table 1.

Interpretable mimic learning classification results for two tasks. (mean ± 95% confidence interval)

Methods		MOR (Mortality)		VFD (Ventilator Free Days)
		AUROC	AUPRC	AUROC	AUPRC
Baselines	SVM	0.6437 ± 0.024	0.3408 ± 0.034	0.7251 ± 0.023	0.7901 ± 0.019
	LR	0.6915 ± 0.027	0.3736 ± 0.038	0.7592 ± 0.021	0.8142 ± 0.019
	DT	0.6024 ± 0.013	0.4369 ± 0.016	0.5794 ± 0.022	0.7570 ± 0.012
	GBT	0.7196 ± 0.023	0.4171 ± 0.040	0.7528 ± 0.017	0.8037 ± 0.018
Deep Models	DNN	0.7266 ± 0.089	0.4117 ± 0.122	0.7752 ± 0.054	0.8341 ± 0.042
	GRU	0.7666 ± 0.063	0.4587 ± 0.104	0.7723 ± 0.053	0.8131 ± 0.058
	DNN + GRU	0.7813 ± 0.028	0.4874 ± 0.051	0.7896 ± 0.019	0.8397 ± 0.018
Best Mimic Model		0.7898 ± 0.030	0.4766 ± 0.050	0.7889 ± 0.018	0.8324 ± 0.016

4.4 Interpretations

Next, we discuss a series of solutions to interpret Gradient Boosting trees in our mimic models, including feature importance measure, partial dependence plots and important decision rules.

4.4.1 Feature Influence

One of the most common interpretation tools for tree-based algorithms is feature importance (influence of variable)²⁸. The influence of one variable j in a single tree T with L splits is based on the numbers of times when the variable is selected to split the data samples. Formally, the influence Inf is defined as

$$In{f}_i\left(T\right)={\displaystyle \sum _{l=1}^{L-1}{I}_l^2{\rm I}\left(S_l=j\right),}$$

where I²_l refers to the empirical squared improvement after split l, and I is the identity function. The importance score of GBT is defined as the average influence across all trees and normalized across all variables. Although importance score is not about how the feature is actually used in the model, it proves to be a useful metric for feature selection.

Table 2 shows the most useful features for MOR and VFD tasks, respectively, from both GBT and the best GBTmimic models. We find that some important features are shared by several models, e.g., MAP (Mean Airway Pressure) at day 1, δPF (Change of PaO2/FIO2 Ratio) at day 1, etc. Besides, almost all the top features are temporal features. Among the static features, PRISM (Pediatric Risk of Mortality) score, which is developed and commonly used by doctors and medical experts, is the most useful static variable. As our mimic method outperforms original GBT significantly, it is worthwhile to investigate which features are considered as more important or less important by our method.

Table 2.

Top features and their corresponding importance scores.

Task	MOR (Mortality)		VFD (Ventilator Free Days)
Model	GBT	GBTmimic	GBT	GBTmimic
Features	PaO2-Day2 (0.0539)	BE-Day0 (0.0433)	MAP-Day1 (0.0423)	MAP-Day1 (0.0384)
	MAP-Day1 (0.0510)	δPF-Day1 (0.0431)	PH-Day3 (0.0354)	PIM2S (0.0322)
	BE-Day1 (0.0349)	PH-Day1 (0.0386)	MAP-Day2 (0.0297)	VE-Day0 (0.0309)
	FiO2-Day3 (0.0341)	PF-Day0 (0.0322)	MAP-Day3 (0.0293)	VI-Day0 (0.0288)
	PF-Day0 (0.0324)	MAP-Day1 (0.0309)	PRISM12 (0.0290)	PaO2-Day0 (0.0275)

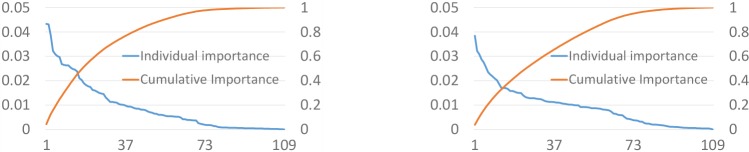
Figures 4 shows the individual (i.e. feature importance of a single feature) and cumulative (i.e. aggregated importance of features sorted by importance score) feature importance of the two tasks. From this figure, we observe that there is no dominant feature (i.e. feature with high importance score among all features) and the most dominant feature has a importance score less than 0.05, which implies that we need more features for obtaining better predictions. We also noticed that for MOR task, we need less number of features compared to the VFD task based on the cumulative feature importance scores (Number of features when cumulative score > 0.8 is 41 for MOR and 52 for VFD).

Figure 4.

Individual (with left y-axis) and cumulative (with right y-axis) feature importance for MOR (top) and VFD (bottom) tasks. x-axis: sorted features.

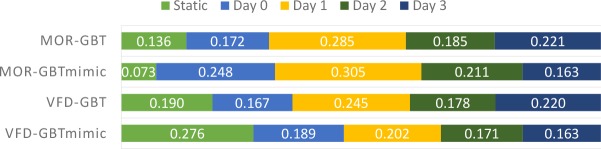
We show the aggregated feature importance scores on different days in Figures 5. The trend of feature importance for GBTmimic methods is Day 1 > Day 0 > Day 2 > Day 3, which means early observations are more useful for both MOR and VFD prediction tasks. On the other hand, for GBT methods, the trend is Day 1 > Day 3 > Day 2 > Day 0 for both the tasks. Overall, Day-1 features are more useful across all the tasks and models.

Figure 5.

Feature importance for static features and temporal features on each day for two tasks.

4.4.2 Partial Dependence Plots

Visualizations provide better interpretability of our mimic models. We visualize GBTmimic by plotting the partial dependence of a specific variable or a subset of variables. The partial dependence can be treated as the approximation of the prediction function given only a set of specific variable(s). It is obtained by calculating the prediction value by marginalizing over the values of all other variables.

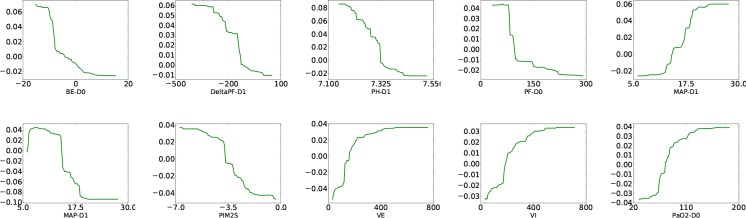
One-way Partial Dependence Table 2 shows the list of important features selected by our model (GBTmimic) and GBT. It is interesting to study how these features influence the model predictions. Furthermore, we can compare different mimic models by investigating the influence of the same variable in different models. Figures 6 shows oneway partial dependence scores from GBTmimic for the two tasks. The results are easy to interpret and match existing findings. For instance, our mimic model predicts a higher chance of mortality when the patient has value of PH-Day0 below 7.325. This conforms to the existing knowledge that human blood (in healthy people) stays in a very narrow pH range around 7.35 - 7.45. Base blood pH can be low because of metabolic acidosis (more negative values for base excess), or from high carbon dioxide levels (ineffective ventilation). Our findings that pH and Base excess are associated with higher mortality corroborate clinical knowledge. More useful rules from our mimic models can be found via the partial dependence plots, which provide deeper insights into the results of the deep models.

Figure 6.

One-way partial dependence plots of the top features from GBTmimic for MOR (top) and VFD (bottom) tasks. x-axis: variable value; y-axis: dependence value.

Two-way Partial Dependence In practical applications, it would be more helpful to understand the interactions between most important features. One possible way is to generate 2-dimensional partial dependence for important feature pairs. Figures 7 demonstrates the 2-way dependence scores of the top three features used in our GBTmimic model. From the left figure in Figures 7, we can see that the combination of severe metabolic acidosis (low base excess) and big reduction in PF ratio may indicate that the patients are developing multiple organ failures, which leads to mortality (area in red). However, big drop in PF ratio alone, without metabolic acidosis, is not associated with mortality (light cyan). From the middle figure, we see that low PH value from metabolic acidosis (i.e., with low base excess) may lead to mortality. However, respiratory acidosis itself may not be bad, since if pH is low but not from metabolic, the outcome is milder (green and yellow). The rightmost figure shows that a low pH with falling PF ratio is a bad sign, which probably comes from a worsening disease on day 1. But a low pH without much change in oxygenation is not important in mortality prediction. These findings are clinically significant and has been corroborated by the doctors.

Figure 7.

Pairwise partial dependence plots of the top features from GBTmimic for MOR (top) and VFD (bottom) tasks. Red: positive dependence; Blue: negative dependence.

4.4.3 Top Decision Rules

Another way to evaluate our mimic methods is to compare and interpret the trees obtained from our models. Figures 8 shows two examples of the most important trees (i.e., the tree with the highest coefficient weight in the final prediction function) built by interpretable mimic learning methods for MOR and VFD tasks. Some observations from these trees are as follows: Markers of lung injury such as lung injury score (LIS), oxygenation index (OI), and ventilator markers such as Mean Airway Pressure (MAP) and PIP are the most discriminative features for the mortality task prediction, which has been reported in previous work³⁵. However, our selected trees provide more fine-grained decision rules. For example, we can study how the feature values on different admission days can impact the mortality prediction outcome. Similar observations can be made for the VFD task. We notice that the most important tree includes features, such as OI, LIS, Delta-PF, in the top features for VFD task, which again agrees well with earlier findings³⁵.

Figure 8.

Sample decision trees from best GBTmimic models for MOR (top) and VFD (bottom) tasks. % and leaf color: class distribution for samples belong to that node; S: # of samples to that node; V: prediction value of that node.

Summary

In this paper, we proposed a simple yet effective interpretable mimic learning method to distill knowledge from deep networks via Gradient Boosting Trees to learn interpretable models and strong prediction rules. Our preliminary experimental results show that our proposed approach can achieve state-of-the-art prediction performance on Pediatric ICU dataset, and can identify features/markers important for mortality and ventilator free days prediction tasks. For future work, we will build interactive interpretable models which can be readily used by clinicians.