Using Monte Carlo/Gaussian Based Small Area Estimates to Predict Where Medicaid Patients Reside

Abstract

Electronic Health Records (EHR) are rapidly becoming accepted as tools for planning and population health^1,2. With the national dialogue around Medicaid expansion¹², the role of EHR data has become even more important. For their potential to be fully realized and contribute to these discussions, techniques for creating accurate small area estimates is vital. As such, we examined the efficacy of developing small area estimates for Medicaid patients in two locations, Albuquerque and Chicago, by using a Monte Carlo/Gaussian technique that has worked in accurately locating registered voters in North Carolina¹¹. The Albuquerque data, which includes patient address, will first be used to assess the accuracy of the methodology. Subsequently, it will be combined with the EHR data from Chicago to develop a regression that predicts Medicaid patients by US Block Group. We seek to create a tool that is effective in translating EHR data’s potential for population health studies.

Introduction

Electronic Health Records (EHR) are a promising data source for examining population health and for community health needs assessments^1,2. For high density populations, zip codes may be used as the units for location analyses, but zip codes are widely considered to be insufficiently granular for modelling environmental/human interactions^3,4,5,6,7. While geo-statistical methods exist for interpolating probable location from known points^8,9,10, the literature is sparse on evaluating how accurate these techniques really are at predicting where the modeled event occurs. Understanding the accuracy of these methods, at spatial & demographic resolutions that are meaningful to health related processes, is vital for epidemiological studies based on EHRs to be successful.

We set out to evaluate the accuracy of one such technique for predicting probable patient location, a Gaussian Geo-statistical & Monte Carlo methodology that has proven effective for estimating probable voter location¹¹. For this analysis, we selected Medicaid status as our condition of interest. We selected Medicaid status for two reasons. First, recent expansion of Medicaid status to new populations presents a controversial effect of the Affordable Care Act ripe for analyses of effects on population health¹². Secondly, it represents a definite, unique indicator of patient socio-economic status that is most likely also associated with both patient health outcomes & exposure to potential health related environmental influences^13,14. Thus, the goal of our study is to ensure that patient location can be accurately imputed from zip code aggregated EHR data using U.S. Block Group Census counts as a tool to weight that imputation, just as it was for voter location.

Methods

Using only registered Medicaid patients in 2 different cities (Chicago & Albuquerque), we developed small area estimates of Medicaid patients for both study areas from aggregated zip code patient counts to block group using a combination Monte Carlo/Gaussian Geo-statistical simulation technique. Chicago Medicaid patients were represented using HealthLNK EHR records. HealthLNK represents a total of 6 years (2006-2011) of de-identified & de-duplicated Electronic Health Records (EHR) obtained from 6 different sites across Chicago and are thus only a sample of the total Medicaid patients in the Chicago area¹⁶. The geo-imputation for Chicago was meant as a comparison and will be used in future steps of the project. Conversely, in Albuquerque, where we have all Medicaid records & patient address data, we compared accuracy to another study done using the same methods but on registered voters in central North Carolina. The accuracy assessment in Albuquerque will be done separately over two years (2012 & 2014), using the most recent address for each Medicaid patient in each year to represent where that patient lives.

We address matched Albuquerque Medicaid patients using ArcGIS 10.3¹⁵ and subsequently aggregated by zip code. Because the methodology weights probable patient location using U.S. Census Block Group counts, Albuquerque zip code to block group geographic coincidence was established in ArcGIS using a spatial join. We imputed probable patient block group location by performing a Monte Carlo simulation that uses limited personal data (age, gender, & ethnicity) & associated US Census Block Group totals to establish the probable average number of zip code aggregated Medicaid patients that live within each associated block group. These probable Medicaid patient block group averages were distributed among associated census blocks proportionally & kriged in ArcGIS.

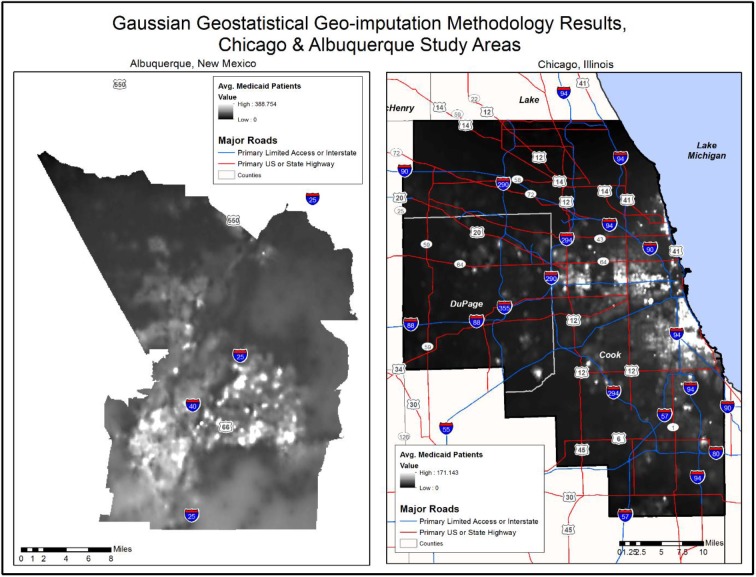
A krig is a raster based statistical surface, similar to a digital elevation model, where the raster cells represent a probability, in this case the number of Medicaid patients living there. The resulting krig was fed into a Gaussian Geo-statistical Simulation to generate an average & standard deviation probability raster to evaluate the accuracy of the predicted average number of Medicaid patients living in each raster cell (Figure 1).

Figure 1.

Probable Average Medicaid Patients, Albuequerque & Chicago Study Areas

We assessed accuracy for each of the three years, separately, using the Root Mean Square Error (RMSE), Error Product, and Error Product/RMSE for each (Table 1). We compared the values for each year to the North Carolina Voter results from our prior study. RMSE is a common measure of accuracy which is calculated as the square root of the average squared error for each prediction made. Since the results here involve geography, the RMSE assesses the average number of patients that the raster has over or under predicted at every point/raster cell within the study area. It follows logically that the smaller the RMSE the better. The Error Product measures how consistent the results are. It has two separate components, which are multiplied together. The first is the percentage of checked locations used in the RMSE that fall within 3 Standard Deviations of the mean. The second is the percentage of checked raster cells with a predicted average number of Medicaid patients that is greater than the 1 standard deviation measured at that same location. The goal is to have 100% of observations comply with each of these criteria, a situation that would yield an Error Product of 1. These two measures are important because they are an indicator of the quality of the simulation as an approximation of the Medicaid patient distribution. Deviations that are far from 1 indicate that the methodology is faulty, and that the RMSE should not be trusted regardless of its magnitude. Finally, the Error Product RMSE is simply the Error Product divided by the RMSE. Since the goal for each measure is a value of 1, where an RMSE of 1 would indicate that the raster has an error of at maximum one Medicaid patient at any given point in the study area, the Error Product RMSE should also be evaluated relative to a value of one.

Table 1.

RMSE, Error Product, & Error Product RMSE, Albuquerque Medicaid Patients & North Carolina Voters

Accuracy Measure	Albuquerque Medicaid		North Carolina – 2014
	2012	2014	Urban Plus - 10%	Urban Plus - 30%
RMSE	5.3	11.61	3.06	11.43
Error Product	0.853	0.859	0.789	0.882
Error Product RMSE	0.161	0.074	0.257	0.078

Results

A total of 108,308 Albuquerque Medicaid patients who had received care within the last year and who were living within 482 block groups were selected for the study. This included, by year, 27,143 Medicaid patients in 2012 & 81,165 Medicaid patients in 2014. In Chicago, 88,198 Medicaid patients were selected who falliwithin 217 zip codes in the Cook, DuPage, & Will County areas. These patients represent all patients in those zip codes whose final insurance status in HealthLNK was Medicaid,

Table 1 shows the results of the accuracy comparison for Albuquerque & the North Carolina Voter dataset project.

Given that the number of Albuquerque Medicaid patients in each year number between around 30 to 80,000, and are represented in a Gaussian raster with a resolution less than 0.01 mi², the most appropriate comparison to the North Carolina Voter project is at both 10% & 30% in the Urban Plus study area, which has 27,125 & 81,367 total voters, respectively. As table 1 shows, the RMSE is virtually identical in both study areas, with greater variability in error at 10% than 30%, which may be caused by sampling error at these lower population levels.

The higher RMSE in Albuquerque in 2012 may also be a result of population distribution. Chicago is very densely populated near the lake, & that population drops as one moves west, toward the suburbs. While Albuquerque has areas that are similar in density to Chicago, these areas are much smaller. Furthermore, the population density drops at a much more rapid rate as one moves out from these areas and into the surrounding desert. These stark contrast between the population distribution in Chicago & Albuquerque can be seen in a block group map of the two study areas. As block groups increase in size, the population density decreases. The krig, which is used as a base for the Gaussian simulation, can account for much of these variations, but it may be that the stark contrast in population distribution around Albuquerque may stretch its limits.

The reason for this stems from the algorithm and mathematical methods that constitute a krig. In effect, it is the same thing as fitting a curve in traditional statistics, it’s just being applied to data that has the added complexity of being spatially explicit. As is common in non-spatial statistics, binning, or grouping, data can create a sort of bias. As such, in a normal statistical project that requires binning, much time and attention is paid to how the underlying data is broken out into its groups. This, of course, includes the problematic question of how many bins to include. With spatial data such as that found in the US Census & ACS data, the binning choices have already been made. Because those bins also have the added complexity of representing an area on the ground with a specific extent and a specific spatial relationship to all of the other bins, the bias introduced by binning is not only found in the underlying counts, but in where the boundaries for that bin have been set. In spatial analysis, the two primary types of error introduced by binning are commonly called spatial clustering and spatial trend. Kriging corrects as much as possible for these two types of bias. By removing this type of bias, we can use the Gaussian to examine the degree to which the underlying data is actually spatially clustered minus that bias. Other forms of small area estimates don’t account for these types of error and bias, making the Gaussian methodology presented here unique.

Thus, after adjusting the observations for these two data aggregation errors, the krig uses a type of machine logic to ‘fit’ a three dimensional surface to those observations. The more normally distributed, or spatially disperse, the underlying data is, the better the equation developed for the krig will fit it. That goodness of fit will lead to a lower RMSE after the Gaussian simulation is run. As the Gaussian RMSE increases, within the confines of a similar or unchanging Error Product, that increase will most likely be due to non-normally distributed, or spatially clustered, underlying data.

Discussion

In this project, we created small area estimates of Medicaid patients using the same methods applied in two distinct geographies. When visualized on a map, our estimates correlate with known areas of low socioeconomic status (SES) in both cities. Compared with a prior validation study applied to voter registration records in North Carolina, our estimates of Medicaid patient distribution generated a slightly larger RMSE at low population counts, but essentially the same. When one considers that, as a rule, population rarely distributes itself ‘normally’ in space, the fact that Medicaid status is dependent on SES & registering to vote is not indicates that it is most likely these socio-economic factors that are responsible for the additional RMSE at low population levels in 2012. Fortunately, the RMSE increase is not that much relative to the total population being simulated & the Error Product for both projects is almost identical. These facts, taken together, strongly indicate that the krig & subsequent Gaussian simulation provide a strong model for Medicaid patient location. Furthermore, the increase in RMSE, most likely due to the clustering effects of low SES, indicates that the block group aggregate average Medicaid patients will serve as a strong dependent variable for future work by our group to apply regression analysis to estimate Medicaid patient population in areas based on socio-economic factors alone

Our group is currently studying the impact of Medicaid expansion on diabetes outcomes across ten states, half of which are non-Medicaid expansion states. Developing accurate methods to estimate Medicaid patients per block group nationally will help us identify a comparison population of patients in non-Medicaid expansion states who would have qualified for Medicaid had their states chosen to participate in the Medicaid expansion program. Accurate imputation methods enable researchers to study the impact of policies or other external shocks on clinical outcomes when data are sparse or missing.