A K-Reversible Approach to Model Clinical Trajectories

Abstract

A clinical trajectory can be defined as the path followed by patients between an initial heath state S_i such as being healthy to another state S_j such as being diagnosed with a specific clinical condition. Being able to identify the common trajectories that a group of patients take can benefit clinicians at identifying the current state of patient and potentially provide early treatment to avoid going towards specific paths. In this paper we present our approach that enables a clinical dataset of patient encounters to be clustered into groups of similarity and run through our algorithm which produces an automaton displaying the most common trajectories taken by patients. Furthermore, we explore a dataset of patients that have experienced mild traumatic brain injuries (mTBI) to show that our approach is effective at clustering and identifying common trajectories for patients that develop headaches, sleep, and post traumatic stress disorder (PTSD) post concussion.

Introduction

A clinical trajectory can be defined as the path followed by patients between an initial heath state s_i such as being healthy to another state S_j such as being diagnosed with a specific clinical condition. Commonly clinicians review a patient’s medical history to better put the medical findings within the context of the patient. While collecting and reviewing medical history is essential to providing personalized treatment, current clinical decision support systems are not effective at aggregating and understanding how a group of patients go from state S_i to another state S_j. Therefore, being able to identify the common trajectories that a group of patients take can benefit clinicians at identifying the current state for a particular patient and potentially providing early treatment to avoid going towards some specific paths. Despite the significant amount of longitudinal information that Electronic Health Records (EHRs) include related to patients’ clinical encounters, determining the most frequent clinical trajectories followed by a given group of patients is still a challenging task. Often within a given cohort of patients, a group of patients take similar paths to a certain disease while others take a vastly different path. Due to the increased interest in understanding how a patient’s condition will develop over time, understanding these varying paths can benefit healthcare by providing physicians and patients crucial information in preparation for the future. Clinical trajectories possess the power of providing physicians and patients with a visual representation that can easily be understood and analyzed. They have the potential to uncover hidden information in data that could not be seen otherwise. With these goals in mind, in this paper we present a framework for creating meaningful clinical trajectories using longitudinal clinical data. First we describe the challenges faced by researchers in using clinical data, next we describe some of the previous work, then we present our approach to cluster patients and to build a condensed model that can be analyzed, followed by discussing how we’ve applied our approach to a large clinical dataset, and finally we conclude the paper and describe some of the future work.

Healthcare data has been predicted to exceed 25,000 petabytes in 2020 compared to 500 petabytes in 2012, an increase by a multiplier of 501. With this rise in the amount of available big data in healthcare, there exists an opportunity to apply machine learning techniques on a large scale to identify key information in patient trends. Understanding what causes patient deaths, what is effective at improving a patient’s life, and how a population of patients end up in a certain diagnosis are just a few examples of the insightful analytics that can be discovered in this data.

However, even though there are many points of information that are desired to be studied, the vast amount of data provided along with the many different types of patients poses extreme challenges to researchers. Not only are efficient algorithms and powerful systems required to extract and perform computations, but understanding the wide variety of patients is key in identifying breakthroughs in healthcare research to assist future patients. It may be easy for a physician to analyze one individual patient to understand their medical history, but at a large scale of data it is not feasible to analyze each patient individually in an attempt to get an overall view of the population. The amount of time it would take to analyze, with more data being added by the minute, would not provide tangible benefits for the short term. Therefore, methods that attempt to combine similar patients and produce a model of the patient population will prove to be effective at providing physicians with a condensed representation of the population in order to assist in preventative care and supporting future patients that will undergo similar conditions.

Background

Research in the area of clustering big data has proposed methods in which an ensemble model of statistics information and word sense information is used to cluster documents ², a framework in which the popular k-means algorithm applied to a weighted linear co-association matrix to cluster biomedical data consisting of text and images ³, and applying data clustering algorithms to the problem of big data ⁴. All of these approaches have shown the benefit that clustering has: the power to be able to identify groupings in data that otherwise could not be found with alternate methods.

In the clinical realm, approaches to understanding the clinical trajectory of a patient, by means of clustering, have focused on a specific disease with the intention of being able to predict whether a new patient will develop a similar diagnosis or not. In the realm of PTSD patients, Bryant et al. studied the long-term trajectory of PTSD patients over 6 years and classified them in chronic, recovery, worsening/recovery, worsening, and resilient groupings. The study found that analyzing patients over time provides a more accurate means to identifying and predicting PTSD rather than relying on hospital admission analysis ⁵;⁶. A similar study analyzed patients 12 months after a burn and also found four different trajectories for patients with PTSD ⁷. In addition, it was found that the risk factors differed between trajectories indicating that each group possessed similar traits which could be used in clinical practice. Another study concentrated on children after an accidental, but traumatic, injury in which they developed Post Traumatic Stress Symptoms (PTSS). In this study the researchers utilized group-based trajectory modeling to identify patterns of PTSS and found three distinct trajectory groups where pre-injury risk factors were predictive of the corresponding group. With this information the researchers concluded that identification of distinct trajectory groups can help understand the course from traumatic injury to PTSS and the necessary treatment for a child ⁸. Gotz et al. utilized patient similarity metrics to visually analyze patient clusters ⁹. In addition, various Bayesian and mathematical models have been utilized to build disease models and cluster patients¹⁰¹¹¹², but lack the ability to provide a simple visualization of disease trajectory. Furthermore, several Harvard researchers have shown their ability to classifying and predicting long-term medication adherence using group-based trajectory models ¹³. All of these studies alike indicate that patients’ trajectories can be grouped together to find a common path and give clinicians an insight into the expected diagnosis path and optimal treatment.

Approach

For our approach we attempted to classify the patients into their respective groups, based on the trajectory that they underwent, followed by representing each group’s trajectory with the most common paths highlighted in a visual manner using automata. Below we will outline the steps taken for each aspect of our approach.

Clustering

With the knowledge that not all patients are the same and that patients take varying, but similar paths, we used the popular clustering algorithm, k-means clustering, to identify the various groups. The k-means algorithm takes a set of feature vectors and a value of k which it then attempts to find k unique groups using a distance metric, in this case the Euclidean distance.

Our first attempt at clustering the patients was to associate each diagnosis with an integer and thus create a feature vector of the diagnoses in order. However, because patients have varying number of diagnoses and k-means requires uniform length, the algorithm ultimately clustered the patients based on the length of their original trajectory. With this we had to find an alternate method that did not discriminate between the patients based on their varying trajectory length. Using our previous work in which we predicted patient outcomes based on their medical history, from Electronic Health Records (EHR) data, ¹⁴;¹⁵ we created a sparse matrix representation of each patient which we will briefly describe next.

To create meaningful input for the k-means algorithm, first the encounters / diagnosis tuples were transformed into a sparse matrix where each row was a diagnosis and each column corresponded to a different time point.

With the sparse matrix defined, we used the Bayesian Information Criterion (BIC) and the elbow criterion method to identify the optimal number of k as this method identifies the point at which additional clusters would result in overfitting.

Model Automata

In an attempt to design a model to estimate the common trajectory followed by most patients from their initial injury to the first diagnosis of PTSD, we model the longitudinal clinical encounters as an automata and employ grammar induction algorithms to minimize the complexity of large automata. This approach allows us to simultaneously consider the path of N patients and minimize the graph into a single automaton that represents the common path. In order to understand our approach, we will first give a brief overview of automata

Automata are self-operating machines that consist of states and transitions, where the input is compared against the transitions in order to move between states in the machine. Two forms of machines exist in finite automata: deterministic (DFA) and non-deterministic (NFA). For a given state and input symbol, deterministic machines only have one possible transition, whereas non-deterministic machines can have multiple transitions.

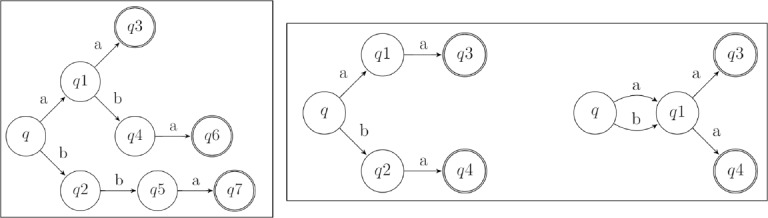
Using the two forms of automata, nondeterministic (NFA) and deterministic (DFA), will allow us to visualize the trajectory of patients over time. Both of these approaches represent the data in a unique way allowing for us to evaluate different aspects of the trajectories. It should be noted that both the NFA’s and DFA’s were run through a simple minimization algorithm that reduced the number of nodes for each individual patient trajectory. For example, a patient that followed the path of: “A ->A->A ->B ->C ->C ->A” would be reduced to: “A ->->B ->C->->A”, as can be seen in Figure 1.

Figure 1:

Example of a DFA (Top) before minimization and (Bottom) after being minimized.

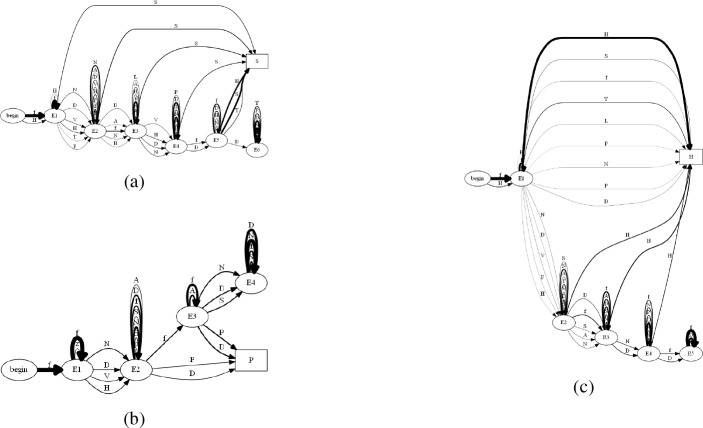
The first approach, using an NFA, treats each diagnosis as an individual node and stacks into a column representing an encounter. An example of a single patient’s NFA can be seen in Figuree 2 where “f” corresponds to a Concussion, “P” corresponds to PTSD, “D” corresponds to Depression, and “E” corresponds to a diagnosis related to Speech. In this example we can see that the patient was diagnosed with P, D, and f in their first encounter, followed by P and D in their second encounter, etc. Representing a patient as an NFA allows us to understand the change in the number of diagnoses over time and represent the concept that a patient can take the path from any disease in a single encounter to any disease in the next.

Figure 2:

An NFA representing six encounters corresponding to the path followed by a particular patient between his/her first concussion to PTSD.

The second approach, using a DFA, represents each encounter as a node with the diagnoses acting as paths leading into the node. This representation is shown for the previously presented patient in Figure 3, where the automaton looks to be smaller due to the lesser amount of nodes. This DFA approach will allow us to utilize a grammar induction algorithm for identifying a common trajectory amongst a group of patients.

Figure 3:

A DFA representing six encounters corresponding to the path followed by a particular patient between his/her first concussion to PTSD.

Furthermore, both of these approaches can be augmented by placing a scale for the amount of days between encounters in order to understand the timeframe of the patient’s encounters better. The previous patient’s NFA and DFA were modified to display the amount of days between encounters in Figure 4.

Figure 4:

Patient’s DFA (Top) and NFA (Bottom) with a timeline of days between encounters in the first row of each automaton. The timeline represents the number of days between mTBI and PTSD, which is 24 days in this patient’s case.

Using the previously demonstrated NFA and DFA’s of a patient’s trajectory, we applied a grammar induction algorithm to the automata with the goal of identifying the most common paths that a group of patients take within their trajectories. The specific algorithm that we chose was the K-Reversible algorithm as it treats all input as being equal, compared to other algorithms such as Gold’s Algorithm that requires positive and negative data.

Merging

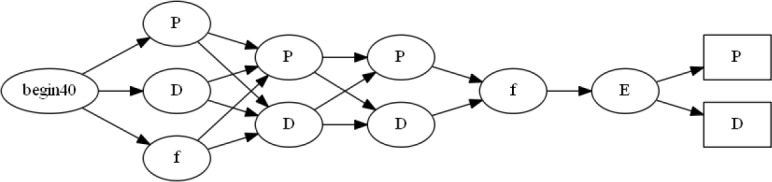
A prefix tree acceptor (PTA) is a tree-like DFA built from a learning sample of strings P = p₁, p₂, …, p_n by converting all of the prefixes pi in the sample P into states Q = q₁, q₂, …, q_m and constructing the smallest DFA that is a tree and consistent with the learning samplelO. For example, given a sample string set P = aa, aba, bba it can be converted into a set of states Q = q₁, q₂,…, q₇ as illustrated in Figure 5a.

Figure 5:

(a) Example of prefix tree acceptor built from strings P = aa, aba, bba. (b) Example of merging states q1 and q2.

One of the basic operations that can be performed on a PTA is a merging operation, which takes two states (q_i, q_j) from an automaton and merges them into a single state ¹⁶. An example of the merging algorithm is shown in Figure 5b. The algorithm takes in two states, q_i and q_j, that are to be merged together and then takes everything that points into q_j and makes it point into q_i. In addition, everything that q_j points to is now made to originate from q_i. This removes all of the transitions into and out of q_j and transfers them to q_i, allowing the algorithm to now remove q_j from the finite state machine.

Algorithms such as Gold’s Algorithm ¹⁷, RPNI ¹⁸, and K-Reversible ¹⁶ start from a PTA and perform operations on it to try and create a DFA that recognizes the target language. By using these algorithms, we can input an automaton of clinical trajectories that will be merged leaving behind the most common paths taken by patients.

Minimizing the Automata

The specific algorithm that we chose was the K-Reversible Grammars Algorithm ¹⁶;¹⁹ as it treats all input as being equal, compared to other algorithms such as Gold’s Algorithm that requires positive and negative data.

The K-Reversible Algorithm is classified as a look-ahead language that takes into account a length k sub-sequence of diagnoses at a time. This means that the algorithm starts at a state and looks backwards for up to k states, combining the diagnoses on the backwards path into a sequence. Subsequently, two states can be compared by contrasting their sequences of k length diagnoses. An example of this is shown in Figure 6, where states p and q are similar for k = 0 as “a” equals “a”, but for k = 1 or k = 2 they are not similar as “ad” does not equal “ab” and “adc” does not equal “abc”. This K-Reversible algorithm was ultimately chosen for its ability to merge similar states based on a length k sequence of diagnoses as similar sequences of diagnoses can potentially lead to the same condition in a patient.

Figure 6:

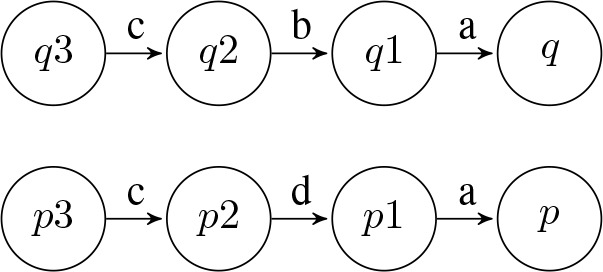
Example of comparing k diagnoses at a time.

Breaking down the K-Reversible Algorithm, there are three cases that need to be considered. The first case looks for a state, p, that has two identical transitions to two different states, q and q’. Once this case has been matched then the states q and q’ are merged together. This is shown in Figure 7a. The second case of the algorithm looks for two final states, q and q’, that have identical paths leading into them of length k, and merges them together. This is shown in Figure 7b. Continuing on with the algorithm, the subsequent states, p and p’, are also merged. The third case of the algorithm looks for a state p that has two identical transitions leading into it from two different states, q and q’, that also have an identical path leading into them of length k. Once again, q and q’ are merged together by this case. This is shown in Figure 7c.

Figure 7:

The three cases (a, b, and c respectively) of the K-Reversible algorithm where q and q are merged.

Algorithm Modifications

We found that the three cases of the K-Reversible algorithm did not achieve an optimal automaton, through visual inspection, such that:

1. similar, but not identical, paths were not merged

2. duplicate paths were not removed

3. a patient’s path was merged with itself

With these flaws present, we modified the algorithm by adding three cases in addition to the original three cases.

First Modification The K-Reversible algorithm strictly considers paths without taking into account that two distinct paths may in fact be the same despite a difference in order of diagnoses. For example, there could be a state q that has paths of [b, a] and [a, b] leading into it, as shown in Figure 8a. In these types of occurrences, we assumed that the ordering of the diagnoses does not matter as both paths lead to the same state of the patient. This property of the algorithm required a modification, accomplished by reordering the less probable path to be equivalent to the more probable path. Upon reordering and running the algorithm further, it will eventually merge these two paths into one.

Figure 8:

The two modifications, a and b respectively, made to the K-Reversible algorithm where q and q are merged.

Second Modification The second modification to the K-Reversible Algorithm was to remove identical paths to the same state, that was generally caused by the first modification. During the minimization of the grammar, the algorithm would cause there to be two states, p and q, where more than one path went from p to q with the same value as the transition. Therefore, by merging these paths, the grammar would be minimized to the furthest extent. An example of this modification is provided in Figure 8b, where the duplicate path of ‘a’ is merged into one single path.

Third Modification The third modification to the algorithm was with the goal of not allowing the algorithm to merge a patient’s trajectory into itself. What this means is that instead of treating a patient’s trajectory as one entire path, the algorithm would attempt to alter the trajectory to be minimal, resulting in only one node and the patient not being represented accurately. We therefore modified the algorithm to track the patient ID’s at each node and did not allow two nodes to be merged if the intersection of the ID’s contained a patient. This ultimately forced the algorithm to ensure that the diagnosis trajectory of each patient was treated as an individual sequence.

Fourth Modification Due to the large size of automata that can result from running the algorithm on an extensive dataset and due to the nature of clinical encounters: in that patients can take many varying, unique paths which cannot be merged together, it can become difficult to understand the common trajectories on a large automaton. This limitation in understanding resulted in us making one final modification which involved pruning the resulting automata to only consider the most probable/most taken paths. During the execution of the K-Reversible algorithm, we kept a count of the number of patients that took each path. Then, once the algorithm finished running we used the patient counts to compute the probability of each path being taken from a node, thus leaving us with a patient count and probability at each path. Using these two metrics, we were able to set varying probability and count cut-offs such that the resulting automaton would only include paths that were above the cut-off. This allowed for the size of the automata to be reduced as can be seen in the next section.

With these modifications made to the algorithm we will explore, in the next section, the automata that result from running our modified algorithm on longitudinal clinical data.

Application Domain

For our results we will explore a dataset available to us centered around the application domain of patients that experience a concussion or a mild traumatic brain injury (mTBI) and the long term affects associated with this injury. Specifically, we will be looking at patients that develop diagnoses related to either headaches, sleep, and/or PTSD post concussion.

TBI Data

A concussion is a poorly understood mild traumatic brain injury (mTBI) that can alter the way the brain functions. During the last decade a significant amount of attention has been given to the acquisition of clinical data from patients suffering mTBI and psychological health (PH) problems after a concussion. The increased awareness has been in part driven by the Department of Defense (DoD), the National Football League (NFL), and many other government and private organizations that have been leading different efforts to raise awareness about the short- and long-term effects of concussions.

A traumatic brain injury (TBI) is defined and indicated by “Any period of loss of or a decreased level of consciousness, Any loss of memory for events immediately before or after the injury, Any alteration in mental state at the time of the injury, Neurological deficits that may or may not be transient, or intracranial lesion following the traumatic event” ²⁰. In the United States alone, an estimated 1.7 million TBIs occur each year, leading to more than 1.3 million emergency room visits, a quarter million hospitalizations, and 52 thousand deaths ²¹. The leading causes of TBIs are falls, physical assault/injury, and motor vehicle accidents. In the U. S. Military, over 307,000 cases of TBI have been diagnosed since 2000, 80% of which were in a non-deployed setting ²².

Patients who have been screened positive with mTBI are at an increased risk of psychological problems that can have a significant impact in the recovery time. Early detection of psychological conditions such as PTSD following a concussion might improve the overall outcome of a patient and could potentially reduce the cost associated with treatment.

Dataset

The original dataset consisted of EHR data for 98,342 mTBI patients. The data was filtered to only include patients with more than thirty days of data and no history of moderate or severe TBI. The resulting subsets of 89,840 patients had 5.3 million TBI-related clinical encounters and 8.7 million clinical diagnoses. In this study, a TBI-related encounter was defined as a visit to the doctor regardless of inpatient/outpatient where the patient is treated with one or more of the conditions that are commonly known to be related to concussions such as behavioral disorder, sleep problems, cognitive deficiencies, and audiology complaints. Note that only TBI-related encounters were taken into consideration. The patients under consideration had an average of 59 encounters.

To build our model the dataset was defined to be P = {P₁, P₂, …, P_n} where P is a set containing each patient P. Each patient P_i had an associated sequence of encounters E_i E {E₁, E₂, …, E_m} representing unique clinical appointments or hospital visits. Each encounter E_i had an associated set of diagnoses represented by D E {D₁, D₂, … , D_k}. To build the sparse matrix representation, as was described in Section, for clustering we set the splitting diagnosis as the first mTBI event and the timeframe of the matrix to be T = ((–60, –30], (–30, 0], [0, 30)), where (-30, 0] represents t_-30 → t_-1 (i.e. 30 days prior to a concussion not including the day of the concussion). The reason for choosing this timeframe was that in our previous work we found that 30 day intervals best capture the critical information of patients and that the first thirty days post concussion are crucial in differentiating between patients.

For our results, we will be analyzing the trajectory that patients took to develop diagnoses of headaches, sleep, and/or PTSD post concussion, with a minimum of at least 15 days between the concussion and diagnoses being required. We will only be using patients that have enough data to cover the time intervals defined previously, which amounts to 6,473 patients. For generating the automata, we will only be using the first 5,000 patients as any number larger than that requires substantial processing power which is beyond the scope of this paper.

Results

With our dataset defined, we set out to apply the approach that we previously defined in order to construct and analyze a model of the clinical trajectories that patients undergo post concussion to headaches, sleep, and PTSD.

First, we built an automaton consisting of 5,000 patients and ran it against our modified K-Reversible algorithm to identify the usefulness of our algorithm. Figure 9 shows an example of an automaton of 20 patients before being input to our algorithm. In this Figure it can be seen that understanding the similarities and differences between patients is near impossible and this difficulty would grow even more as the number of patients would increase. In Figure 10 we see the computed trajectory for all patients that experience a concussion and end up with a diagnosis of either headache, sleep, and/or PTSD. Analyzing this computed automaton, Figure 10, compared to the initial automaton, Figure 9, reveals that it is much easier to understand the path that most patients take. It should be noted that for the automaton in Figure 10, as with the rest of the computed automata that we will show, we set the line thickness of each transition to be equivalent to the probability of getting the specified diagnosis from that state. These varying thicknesses allow for a viewer to understand the flow of patients visually.

Figure 9:

Example of an automaton, before running through the modified K-Reversible algorithm built from 20 patients that had a concussion (f) and a diagnosis of headaches (H), sleep (S), and/or PTSD (P) with more than 15 days between.

Figure 10:

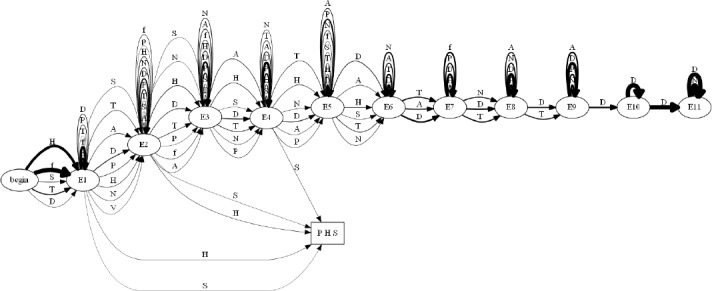
Automaton of all patients developing a diagnosis of headaches (H), sleep (S), and/or PTSD (P) post concussion (f).

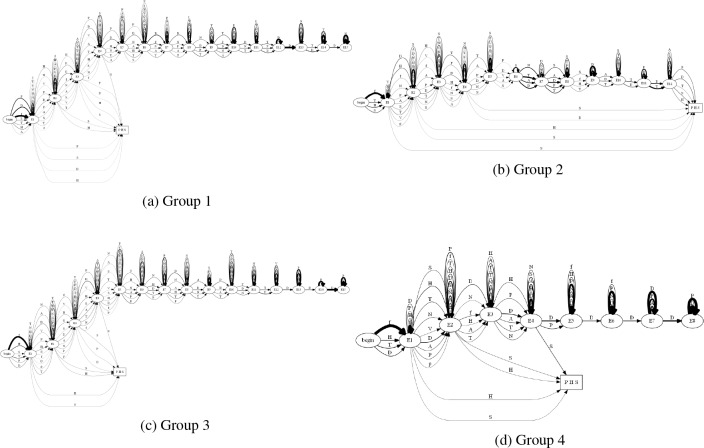
Next, breaking down the trajectories for each individual diagnosis we see headaches in Figure 12a, sleep in Figure 12b, and PTSD in Figure 12c. All of these automata are able to show us clear paths that patients took to each diagnosis, however breaking the patients down into clusters based on their similarity may produce easier to understand trajectories, as well as show trends in the patients.

Figure 12:

The first four groups of patients (a, b, c, d respectively) developing a diagnosis of headaches (H), sleep (S), and/or PTSD (P) post concussion (f).

To understand how the patients can be broken down we input our patients into the k-means clustering algorithm, as defined in the Clustering section of the Approach, to identify the various groups of patients and ran it for 2 j k j 30. Using k versus the BIC and the elbow method we found a value of 5 to be the most optimal for splitting the patients into clusters. With this value of 5 for k the number of patients in each group varied, with the counts being: 2543, 95, 820, 3002, and 138 respectively. With the patients clustered into 5 groups, we now would be able to analyze the automata for each group and identify the various trajectories taken.

Using these defined patient clusters, we analyzed the five groups for patients that experienced a diagnosis of headache, sleep, and/or PTSD post concussion. We see the four of the five groups in Figure 12.

In these figures we are able to see the various paths that patients took to these diagnoses and from this we are able to characterize the groups as such:

• Group 1 Early diagnosis, but long history of encounters afterwards.

• Group 2 Early diagnosis, encounters, followed by late diagnoses.

• Group 3 Early diagnoses, followed by a long history of encounters (similar to Group 1).

• Group 4 Early diagnoses and a short length of encounters with high probabilities.

• Group 5 Early diagnosis, breaks, followed by late diagnoses with a short length of encounters.

With these five groups of encounters we are able to see that we can identify the varying, but most common trajectories that patients take in their diagnoses of headaches, sleep, and/or PTSD post concussion. This information could be passed along to clinicians in the TBI discipline so that they could gain insights that they could not otherwise discover.

Conclusion

In this paper we have defined our approach that enables a clinical dataset of patient encounters to be clustered into groups of similarity, represented as NFA’s and DFA’s that include a timeline indicating the number of days between each encounter, and finally run through our modified K-Reversible algorithm to produce automata that display the most common trajectories taken by patients. In our results we applied our approach to an extensive clinical dataset of 89,840 patients that were diagnosed with headache, sleep, and/or PTSD post concussion and showed that with our clustering and grammar induction algorithms we are able to produce trajectories that clearly show the path that each cluster of patients take. With this information we were able to identify and characterize the five different groups of patients that existed in our dataset and with this information we have shown that our approach is effective at clustering and visually representing the clinical trajectory of patients. We anticipate that the automata that we have generated will assist clinicians in understanding the path that their patients take and then being able to provide early treatment to help patients avoid going down specific paths.

Figure 11:

Automata of all patients post concussion developing a diagnosis of (a) headaches, (b) sleep, and (c) PTSD.