Predicting Prolonged Stay in the ICU Attributable to Bleeding in Patients Offered Plasma Transfusion

Abstract

In blood transfusion studies, plasma transfusion (PPT) and bleeding are known to be associated with risk of prolonged ICU length of stay (ICU-LOS). However, as patients can show significant heterogeneity in response to a treatment, there might exists subgroups with differential effects. The existence and characteristics of these subpopulations in blood transfusion has not been well-studied. Further, the impact of bleeding in patients offered PPT on prolonged ICU-LOS is not known. This study presents a causal and predictive framework to examine these problems. The two-step approach first estimates the effect of bleeding in PPT patients on prolonged ICU-LOS and then estimates risks of bleeding and prolonged ICU-LOS. The framework integrates a classification model for risks prediction and a regression model to predict actual LOS. Results showed that the effect of bleeding in PPT patients significantly increases risk of prolonged ICU-LOS (55%, p=0.00) while no bleeding significantly reduces ICU-LOS (4%, p=0.046).

Introduction

Great progress has been made in improving patient outcomes associated with major surgical operations in recent years. This has been manifested by the reduction in intraoperative and postoperative mortality and the overall reduction in transfusion requirements¹. Despite these advances, bleeding is still the most frequent serious complication during or early after major surgical procedures. For example, bleeding in the immediate postoperative period occurs in approximately 20% of patients undergoing liver transplant and about 12% in patients exposed to cardiopulmonary bypass². Bleeding in the perioperative¹ period has been found in many studies to be significantly associated with increased health care resource utilization as reflected by increased intensive care unit (ICU) length of stay (LOS)^3;4, morbidity and mortality⁵.

After major surgical operations patients are typically managed in the ICU, thus the duration of stay is an important indicator of the quality of care a patient receives as well as resource utilization. Patients with prolonged ICU-LOS generally comprised a very small proportion of all ICU patients, yet studies have repeatedly shown that they consume a significant share of ICU resources^6;7. Early identification of patients who might stay longer in the ICU can help improve resource utilization and efficiency of ICU care.

Many studies have reported risk factors for prolonged ICU-LOS and bleeding and a few have reported accurate models for early identification of patients who might experienced these outcomes^6–8. The majority of these studies have considered the outcomes independently. Little attention has been given to the identification of patients groups with prolonged ICU-LOS or increased risk of bleeding attributable to other important clinical outcomes or interventions. A number of studies have investigated the attributable mortality and ICU-LOS of major bleeding using matched cohort analysis or Cox regression models^3;4;7. In the analysis, variables observed in the intraoperative and early postoperative periods are typically incorporated in the models for improved performance. For example, in Kramer and Zimmerman⁷ predictive models for prolonged ICU-LOS that incorporate patient data observed as late as day 5 of ICU admission produced more accurate results than day 1 data. However, as such studies assume the availability of intraoperative and/or post-operative data they are inapplicable when only preoperative data is available. The authors of this study are unaware of any study that has investigated the causal relationship between prolonged ICU-LOS in patients intervened on with a treatment as plasma transfusion, and methods to early identify patients who might experienced these outcomes using only predictor variables observed at the preoperative period.

A key step to identify patients who might stay long in the ICU attributable to bleeding is to assess preoperatively, patients who might bleed during or early after surgery. Across many centers in the US, substantial emphasis is often placed on preoperative screening tests, such as the international normalized ratio (INR): a major driver of decisions about preoperative plasma transfusion⁹. Fresh frozen plasma (FFP) infusions are commonly used to improve coagulation or clotting and are the main therapy option for patients with elevated INR. A large proportion of plasma components are transfused in the perioperative environment^9;10, however, they are frequently administered prophylactically in the absence of significant active bleeding. This practice persists despite a growing body of literature questioning its efficacy^10;11. Through the use of machine learning methods, a recent study¹² conducted by the authors confirmed previous findings that population wise, preoperative plasma transfusion (PPT) significantly increases the risk of bleeding, ICU-LOS, re-operation due to bleeding, and other important outcomes for patients undergoing non-surgical procedures.

The goal of this study is to present a causal and predictive framework where in a first step, the causal effect (attributable risk) of bleeding in patients offered PPT on prolonged ICU-LOS is estimated. Then in a second step, a predictive model estimates the risk of (1) bleeding and prolonged ICU-LOS attributable to bleeding in patients offered PPT, and (2) all causes of prolonged ICU-LOS. The predictive risk modeling step is designed as a two level structure where in the first level, a classification model estimates the probability of bleeding given that a patient was offered PPT. In the second level, a regression model is constructed specifically for patients identified by the first level model to be at high risk of bleeding to predict the actual ICU-LOS. Given that bleeding patients tend to have longer ICU-LOS as determined by the causal framework, the regression model therefore targets a more homogeneous group of patients at risk of prolonged ICU-LOS compared to the overall heterogeneous ICU population.

Prediction results for patients undergoing non-surgical procedures from the Mayo Clinic perioperative datamart showed that the classification model can effectively identify patients at risk of all courses of prolonged ICU-LOS and bleeding in patients offered PPT with AUC as high as 0.84, sensitivity of 0.79 and G-mean of 0.75. The regression model on the other hand can identify patients at risk of prolonged ICU-LOS attributable to bleeding in patients offered PPT with acceptable accuracy (MAE=0.86, median predictions within 2 day of true median ICU-LOS). Through a simple transformation of the bleeding and PPT variables, the causal inference showed that the effect of bleeding in PPT patients significantly increases the risk of prolonged ICU-LOS (55%, p=0.00) and “no” bleeding in patients offered PPT significantly reduces ICU-LOS (4%, p=0.046).

Study Setting and Datasets

Over the past few years, there has been a significant increased in the application of machine learning methods to solve medical and health care problems. Often the problem reduces to applying standard classification or regression models. However, there are some problems that challenges standard application of machine learning methods. Two of such problems are considered in this study: to find a meaningful association between longer ICU-LOS and bleeding due to PPT before surgery, and to identify patients who are at elevated risk of bleeding due to PPT and those at risk of all causes of extended ICU-LOS. This section presents a causal and predictive framework in attempt to address these problems.

Outcome-Treatment Variable Transformation

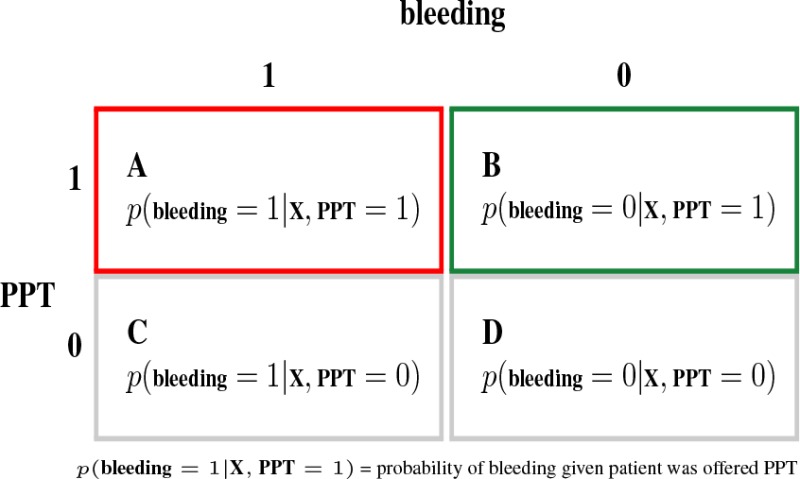
To facilitate the estimation of the effect of bleeding in patients offered PPT on prolonged ICU-LOS and prediction of the risk of bleeding, the training data is grouped into 4 mutually exclusive classes as shown in Table 1. Class A represents patients who bled and were given PPT while class B are patients who did not bleed but were also given PPT. A similar interpretation can be made for the other classes. Using baseline covariates measured before PPT, causal and predictive models can be constructed to to make inference on the four classes. Specifically, the causal inference considers each of the classes in Table 1 as a treatment or exposure variable and then computes its effect on prolonged ICU-LOS. Thus estimates of the treatment effect in class A can be interpreted as the cuasal effect of bleeding as a “complication” of PPT on prolonged ICU-LOS. The predictive inference on the other hand simply constructs binary classification models for each of the four classes. A multiclass classification model can equally be constructed for the 4 classes.

Table 1:

Outcome-Treatment Variable Transformation

Effect of Bleeding as complication of PPT on prolonged ICU-LOS

The standard approach to investigate the causal relationship between a treatment or exposure (e.g PPT or bleeding) and an outcome (e.g ICU-LOS) is to construct statistical regression models in which the outcome is regressed against baseline covariates and the treatment variable. The attributable effect of the treatment is then read off as the corresponding regression coefficient. This study takes a different approach and estimates the treatment effect through application of machine learning methods. The theory of causal inference or technical details of the considered estimation procedure are beyond the scope of this study. The interested reader is referred to^13,14–15 for more details. However, for the purposes of this study, a brief discussion of the data structure required to compute these estimators is presented next.

Data structure and likelihood. The observations for each patient in the data set can be written as O = (X, Y, Z) where Z ∈ {0,1} is the treatment indicator (e.g. class A, B, C or D in Table 1) with Z = 1 if patient was treated and Z = 0 if patient was not treated. X is a vector of baseline covariates that records information specific to each patient prior to treatment. Y is the outcome such as prolonged ICU-LOS (e.g. Y = 1 if ICU-LOS ≥ 7 days and Y = 0 if ICU-LOS < 7 days). The relationship between the observed variables in O can be written in a factorize data likelihood as Pr(X) and

$$\mathrm{Pr}\left(X,Y,Z\right)=\stackrel{g}{\overbrace{\mathrm{Pr}\left(Z|X\right)}}\stackrel{g}{\overbrace{\mathrm{Pr}\left(Y|X,Z\right)\mathrm{Pr}\left(X\right).}}$$ (1)

Pr(Y|X, Z) are referred to as the Q component of the likelihood while Pr(Z|X) is the g component. g(Z|X) represents the propensity or the causal disposition of the treatment to produce some outcome. Q(Z, X) = E[Y|Z,X] is the expected potential outcomes conditional on the observed characteristics. Estimates of g and Q can be obtained by standard regression or machine learning methods.

For a binary outcomes and in the presence of no confounding variables, a straightforward approach to obtain the treatment effect is to compute the expectations ψ₁ = E[Y_Z=1] and ψ₀ = E[Y_Z=0], where E[Y_Z=1] is the mean of Y assuming every patient in the population was exposed at level Z = 1. These two statistics can then be combined in useful ways to assess the effect of different levels of the treatment. Three commonly reported summary statistics include; (1) Additive Treatment Effect: ATE = ψ₁ – ψ₀, (2) Risk Ratio: RR = ψ₁/ψ₀, and (3) Odds Ratio: RO = RR × (1 – ψ₀)/(1 – ψ₁).

The ATE quantifies the additive effect of every patient being exposed to the event versus not being exposed. Thus if the event is class A i.e. bleeding as a complication of PPT, a meaningful interpretation of ATE = 0.05 could read: “being exposed to the event of bleeding as a complication of PPT versus not increases the risk of prolonged ICU-LOS by 5%”¹⁵. The RR quantifies the multiplicative effect of being exposed versus not. A RR of 5 can be interpreted as: “ being exposed to the event of bleeding as a complication of PPT versus not would lead to a 5 times increase in the risk of prolonged ICU-LOS”. Since the OR is a function of RR, a similar interpretation can be given for OR.

Targeted maximum likelihood estimation. In observational studies, estimators of treatment effect need to account for possible confounding, i.e the (apparent) effect of the treatment is actually the effect of another characteristic which is associated with the treatment and with the outcome. Several methods have been proposed for the estimation of ATE, RR and OR that can mitigate the effects of confounding (and model misspecification), e.g. G-computation formula, propensity score matching, inverse probability of treatment weighting (IPTW), and doubly-robust estimation. See^13;14 for more in-depth discussion of these estimators. In this study, the Targeted maximum likelihood estimation (TMLE)^15;16 method is considered because of its double robustness and bias reduction properties. TMLE is a two stage doubly robust semi-parametric estimation methodology designed to minimize the bias of the parameters of interest. The first stage of the method estimates the density of the data generating distribution (specifically Q) while the second stage solves an efficient influence curve estimating equation. The influence curve describes the behavior of the target parameter under slight changes of the initial density estimates. In TMLE, if either g or Q are consistently estimated, then the TMLE estimator is guaranteed to be asymptotically unbiased. However, TMLE will not return consistent estimates of the parameter of interest when both g and Q are misspecified. Thus it is important to avoid overfitting these measures.

As discussed above, estimating the two statistics ψ₁ and ψ₀ allows for calculating any of the causal effects ATE, RR and OR. The TMLE estimate of ψ_z(z ∈ {0,1}) is given by

$${\widehat{\psi }}_z=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\widehat{Q}}^{*}\left(z,x_i\right)}$$ (2)

where ${\widehat{Q}}^{*}\left(z,x_i\right)$ is an update of ${\widehat{Q}}^{*}{\left(z,x_i\right)}^{\mathrm{ }}$². The targeting step for updating $\widehat{Q}\left(z,x_i\right)$ is done by fluctuating ${\widehat{Q}}^{*}\left(z,x_i\right)$ through a parametric sub-model of the form: $logit\left({\widehat{Q}}^{*}\left(z,x\right)\right)=logit\left(\widehat{Q}\left(z,x\right)\right)+\epsilon {\widehat{H}}_z\left(z,x\right)$, where ε is the fluctuation parameter, $\widehat{H}\left(z,x\right)=I\left(Z=z\right)/\widehat{g}\left(z,x\right)$ is the efficient influence curve equations, and I is the indicator function. The MLE of ε is obtained by a logistic regression of Y on ${\widehat{H}}_z\left(z,x\right)$ with offset $\left(\widehat{Q}\left(z,x\right)\right)$. Confidence intervals and p-value for TMLE can be obtained through the variance of the influence curve.

TMLE can use initial estimates of Q and g from any fixed parametric model such as generalized linear models (GLM) (e.g logistic regression). However, parametric models require assumptions regarding the functional form, distribution of variables and variable selection which are often not realistic such that model misspecification is difficult to avoid. It is therefore recommended to used machine learning methods that makes little or no assumptions and are able to estimate complex relationships between the outcome and observed variables.

Two Level Predictive Model

In the proposed two level predictive model, classification models are constructed to predict each of the classes in Table 1. Specifically, a classifier is trained on a modified training set defined by {X, Y}, where X is a matrix containing the patients baseline covariates and Y is a binary variable representing one of the classes in Table 1 such that Y = 1 for all patients in the corresponding class and 0 otherwise. During training, the classifier is trained on the complete training set to predict Y and a regression model is trained to predict ICU-LOS using a subset of the training set for which Y = 1. In the case where class A is the outcome of interest, the second level regression model is trained to specifically target patient at high risk of longer ICU-LOS. This is as a consequence of the known relationship between PPT, bleeding, and prolonged ICU-LOS from the literature^3;4;12, and specifically from causal relationship between these variables derived in this study.

Model validation proceeds as follows; given a new patient, the classification model is first applied to predict the outcome Ŷ for the patient. If Ŷ = 1, then the regression model is applied to predict the corresponding ICU-LOS. Figure 1 illustrates the training and testing steps of the two level predictive model.

Figure 1:

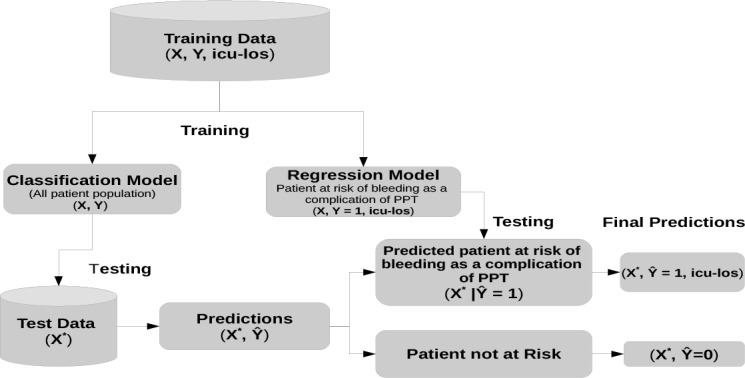
Two Level Predictive Model

Predicting prolonged ICU-LOS attributable to Bleeding as a complication of PPT. Given that class A in Table 1 represents patients who bled and were administered PPT and the fact that bleeding has been found to be significantly associated with prolonged ICU-LOS^3;4;12, a regression model to predict ICU-LOS is constructed only for patients in this sub-population. The rationale behind this strategy is that since this sub-population is relatively homogeneous, the approach allows for optimal targeting of patients at risk of longer ICU-LOS attributable to bleeding as a complication of PPT compared to a model constructed on the general ICU population. Similar regression models can also be constructed for patients identified in each of the other classes in Table 1 to predict the actual ICU-LOS. Class B is of particular interest as these patients did not bleed but were administered PPT. The study of these sub-groups with respect to prolonged ICU-LOS could potentially shed lights on the characteristics of patients who stand to benefit from plasma transfusions.

Predicting all causes of prolonged ICU-LOS. Without taking into account any particular cause, prolonged ICU-LOS was defined as ICU-LOS ≥ 7 days and classification models were constructed to predict this binary outcome. The 7 days threshold was chosen because it represented a reasonable number of days where physicians might be concern about a prolonged stay. This variable was also used in TMLE estimation to estimate the effects of the four exposures in Table 1 on ICU stays of 7 days or more.

Experiments

This section describes the study population and presents empirical evaluation results.

Study Population

The data used in this study are derived from the Mayo Clinic transfusion datamart¹⁷ that captures demographics, disease conditions, laboratory test results, medications, operative and postoperative measurements and outcomes for all patients admitted to acute care environments. To be considered for study participation, patients must meet the following criteria: age ≥ 18 years, noncardiac surgery and an INR ≥ 1.5 in the 30 days preceding surgery. Between 2008 and 2011, a total of 1,233 patients were identified and comprised the study population.

Baseline Variables. Baseline patient demographics include age, height, weight, gender and the ASA status I-V clas- sifcations. Disease conditions included myocardial infarction, congestive heart failure, cerebrovascular disease, dementia, chronic pulmonary disease, diabetes mellitus, etc. Preoperative laboratory values included INR, hemoglobin, platelet counts, creatinine, albumin, and APTT. A total of 51 predictors were considered for inclusion in the analyses. Table 2 presents the characteristics segmented according to the four classes in Table 1. The table show that the four groups are significantly different across demographics (except gender), laboratory, medications, and planned procedure types. The groups are however similar across majority of disease conditions. Further, patients who bled and were offered PPT had significantly longer ICU-LOS compared to those who did not.

Table 2:

Patient characteristics by classes in Table 1

	A N = 73	B N = 66	C N = 349	D N = 745	p-value
Demographics
Age	51 61 72	62 73 81	52 62 74	57 69 80	P < 0.0011
Weight	69 8 5 97	71 83 104	69 82 95	74 87 102	P < 0.0011
Gender: M	62%	64%	59%	60%	P = 0.922
ASA Physical Status
2	1%	12%	5%	19%	P < 0.0012
3	33%	74%	46%	68%	P < 0.0012
4	52%	14%	46%	12%	P < 0.0012
5	12%	0%	3%	0%	P < 0.0012
Disease conditions
Cancer	23%	32%	27%	28%	P = 0.712
Cerebrovascular Disease	22%	23%	14%	23%	P = 0.0062
Congestive Heart Failure	36%	41%	26%	36%	P = 0.0072
Pulmonary Disease	18%	17%	12%	12%	P = 0.332
Chronic Renal Failure	32%	17%	23%	18%	P = 0.0182
Dementia	0%	5%	3%	2%	P = 0.0112
Diabetes	40%	30%	35%	36%	P = 0.712
Leukemia	0%	2%	2%	2%	P = 0.62
Connective Tissue Disease	10%	5%	3%	5%	P = 0.0812
Lymphoma	5%	2%	3%	3%	P = 0.562
MI	19%	15%	12%	15%	P = 0.452
Peptic Ulcer	4%	5%	3%	5%	P = 0.822
Peripheral Vascular Disease	5%	3%	3%	5%	P = 0.422
Mild Liver Disease	18%	9%	37%	8%	P < 0.0012
Moderate/Severe Liver Disease	11%	2%	20%	3%	P < 0.0012
Charlson score	1 4 8	1 3 9	1 4 7	1 3 8	P = 0.0911
Laboratory test results
INR	1.6 1.8 2.0	1.6 1.7 1.9	1.51.8 2.1	1.51.7 2.1	P = 0.341
Platelets Transfusion	11%	3%	3%	1%	P < 0.0012
APTT	95 167 233	128 184 244	66 129 224	160 205 251	P < 0.0011
Creatinine	0.9 1.4 2.0	0.8 1.1 1.6	0.9 1.2 1.7	0.8 1.0 1.3	P < 0.0011
Hemoglobin	8.7 10.1 11.9	10.8 12.9 14.0	8.6 9.8 11.2	10.9 12.3 13.6	P < 0.0011
PLT	29%	14%	41%	8%	P < 0.0012
Medications
Aspirin	68%	53%	62%	52%	P = 0.0022
Clopidogrel	8%	8%	3%	4%	P = 0.0532
Coumadin	55%	71%	43%	69%	P < 0.0012
Heparin	36%	24%	20%	19%	P = 0.0062
Planned Procedure
ENT/Oral	0%	6%	4%	10%	P < 0.0012
General	58%	59%	25%	28%	P < 0.0012
Neurology	3%	3%	1%	2%	P = 0.772
O/G	1%	2%	1%	4%	P = 0.0782
Orthopedic	4%	5%	16%	22%	P < 0.0012
Thoracic	10%	5%	4%	5%	P = 0. 242
Transplatation	19%	2%	37%	2%	P < 0.0012
Urology	1%	3%	2%	9%	P < 0.0012
Vascular	3%	9%	6%	5%	P = 0.292
Emergency	63%	38%	48%	12%	P < 0.0012
ICU LOS	1.25.1 8.4	0.00.0 1.8	0.0 1.1 2.9	0.0 0.0 0.0	P < 0.0011

a b c represent the lower quartile a, the median b, and the upper quartile c for continuous variables. Tests used:

¹Wilcoxon test

²Pearson test

Outcomes and Treatment. Bleeding was taken as the World Health Organization (WHO) grade 3 bleeding events, defined as the need for early perioperative RBC transfusion¹⁸. The term perioperative RBC transfusion was defined as the administration of allogeneic RBC components during the interval beginning with entry into the operating room and ending 24 hours after exit from the operating room. ICU-LOS is the number of days spent in the ICU after surgery. The treatment indicator PPT indicates if a patient was offered plasma transfusion after INR test and before surgery. ICU-LOS

Figure 2 shows the distribution of observed ICU-LOS for the entire population truncated at 250 patients with no ICU admission and 30 days length of stay. It can be seen that the distribution of ICU stays is highly skewed to the right. Learning to identify extreme values at the tail of the distribution can be a very challenging task for a regression model constructed using the entire data. However, this task can be made easier if one focuses only on the extreme values.

Figure 2:

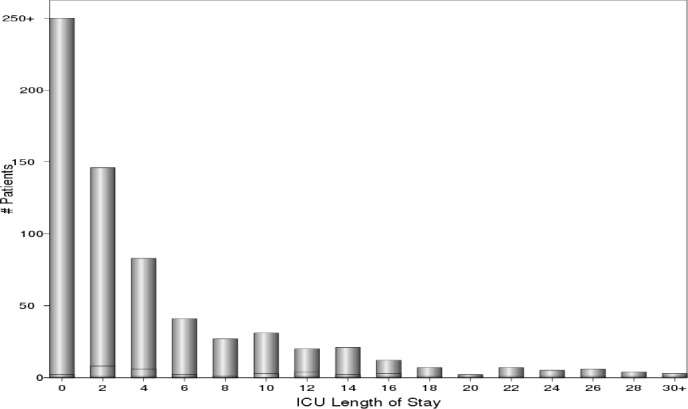
ICU-LOS Distribution

Results

To demonstrate the effectiveness of the two level approach in identifying patients at risk of longer ICU-LOS attributable to bleeding as a complication of PPT, the second level regression model is compared with a regression model trained on the complete training data.

The AUC, sensitivity, and geometric mean $\left(\text{G-mean}=\left(\sqrt{\text{sensitivity}\times \text{specificity}}\right)\right)$ are used to evaluate the classification models, while mean absolute error (MAE) and root mean square error (RMSE) are used to evaluate regression models. The median predicted ICU-LOS and the true median ICU-LOS are also reported for the complete test set and for the top 75% percentile of the true distribution of ICU-LOS.

The random forest (RF) and the gradient boosting machine (GBM) algorithms were considered for classification and regression. The algorithms were trained and evaluated using 100 bootstraps. On each bootstrap iterate, the algorithms are trained on approximately 63% of the data and the left out samples was used for testing. Model selection, i.e. hyperparamter tuning (by grid search) was done using a 5-fold cross-validation procedure. Random forest was trained with 1000 trees.

In calculating estimates of TMLE, RF and GBM along with 6 other algorithms: logistic regression, k-nearest neighbors, support vector machines, neural networks, decision trees, and lasso and elastic net were combined in a Super Learner algorithm¹⁵. Super Learning is a strategy for combining several data-adaptive estimators into one improved estimator. Specifically, the functions g and Q_z in equation (2) are each estimated by these algorithms and combined by the Super Learner to produce better estimates. For comparison, estimates of TMLE are also computed using standard logistic regression (GLM).

Effect of Bleeding as a complication of PPT on prolonged ICU-LOS. Table 3 presents the TMLE estimates of ATE, RR, and OR quantifying the effect of each of the exposures in Table 1, all causes of bleeding, and PPT on prolonged ICU-LOS. Results for TMLE using the Super Learner and a simple main effect GLM are shown for comparison. However, it should be noted that diagnostic tests to ensure that the GLM model fit the data were not performed, thus subsequent discussions will be based on the Super Learner. To save on space, the discussions will also be restricted to the ATE summary statistics; interpretations for RR and OR can be similarly made.

Table 3:

Effect of bleeding as a complication of PPT on prolonged ICU-LOS

		Super Learner		GLM
Exposure	ψ	estimate	p.value	estimate	p.value
	ATE	0.57 (0.55,0.59)	0.00	0.14 (0.08,0.21)	0.00
A	RR	8.43 (6.973,10.20)	0.00	2.97 (2.11,4.18)	0.00
	OR	22.17 (17.95,27.37)	0.00	3.52 (2.32,5.34)	0.00
	ATE	-0.04 (-0.08,00)	0.05	-0.07 (-0.09,-0.05)	0.00
B	RR	0.52 (0.22,1.26)	0.15	0.17 (0.08,0.38)	0.00
	OR	0.50 (0.20,1.26)	0.14	0.16 (0.07,0.35)	0.00
	ATE	0.09 (0.07,0.11)	0.00	-0.09 (-0.17,-0.01)	0.04
C	RR	2.08 (1.71,2.53)	0.00	0.49 (0.28,0.86)	0.01
	OR	2.31 (1.86,2.88)	0.00	0.45 (0.23,0.85)	0.01
	ATE	-0.03 (-0.05,-0.01)	0.00	-0.03 (-0.064,0.00)	0.07
D	RR	0.69 (0.56,0.86)	0.00	0.65 (0.39,1.08)	0.10
	OR	0.67 (0.53,0.85)	0.00	0.6319 (0.37,1.08)	0.10
	ATE	0.17 (0.15,0.20)	0.00	-0.27 (-0.38,-0.15)	0.00
bleeding	RR	3.57 (2.86,4.44)	0.00	0.29 (0.20,0.44)	0.00
	OR	4.38 (3.44,5.58)	0.00	0.21 (0.12,0.36)	0.00
	ATE	0.04 (0.04,0.08)	0.00	0.02 (-0.03,0.06)	0.43
PPT	RR	1.73 (1.40,2.147)	0.00	1.23 (0.76,2.01)	0.39
	OR	1.85 (1.45,2.35)	0.00	1.26 (0.74,2.15)	0.40

Results in Table 3 show that bleeding as a complication of PPT (exposure A in Table 1), all causes of bleeding, andPPT significantly increases the risk of prolonged ICU-LOS by 57%, 17% and 4% respectively (95% confidence intervals are shown in brackets). The event of no bleeding in patients offered PPT (exposure B) was found to reduce the risk of prolonged ICU by 4% (p-value = 0.05) while the event of bleeding when no PPT was administered (exposure C) increases the risk of prolonged ICU-LOS by 9%. These results illustrates that by a simple transformation of the treatment variable, one can identify groups of patients with differential effects of the treatment. Patients identified in group B might show beneficial effects of PPT and thus can be targeted for treatment to mitigate bleeding and reduce ICU-LOS.

Performance of Classification Models. Table 4 presents performance results for predicting the four classes in Table 1. Overall, the models performed very well. Best results for all classes was obtained for RF with AUC as high as 0.84 (class A) and 0.67 (class B). However, no significant difference was observed in the performances. For completeness, Table 4 also show the average per-class performance of a multiclass RF model trained using all four classes in Table 1. The the sensitivity of the multiclass model is however inferior to that of the least performing binary RF model.

Table 4:

Performance of classification models

Model	Class	AUC	sensitivity	G.mean
	A	0.82 (0.76,0.88)	0.67 (0.20,0.94)	0.72 (0.43,0.79)
RF	B	0.67 (0.55,0.79)	0.50 (0.06,0.83)	0.58 (0.25,0.70)
	C	0.83 (0.77,0.88)	0.72 (0.56,0.85)	0.74 (0.69,0.79)
	D	0.84 (0.79,0.86)	0.78 (0.59,0.89)	0.75 (0.70,0.79)
	A	0.80 (0.72,0.88)	0.65 (0.19,0.95)	0.70 (0.41,0.81)
GBM	B	0.65 (0.51,0.73)	0.48 (0.13,0.75)	0.58 (0.35,0.68)
	C	0.83 (0.80,0.87)	0.69 (0.56,0.87)	0.74 (0.69,0.78)
	D	0.83 (0.80,0.86)	0.79 (0.66,0.89)	0.74 (0.70,0.78)
Muticlass RF		0.78 (0.75,0.81)	0.38 (0.35,0.42)	0.57 (0.54,0.60)
		All causes of prolonged ICU-LOS (ICU-LOS ≥ 7 days)
RF		0.80 (0.79,0.80)	0.69 (0.68,0.74)	0.74 (0.74,0.74)
GBM		0.79 (0.73,0.79)	0.70 (0.45,0.72)	0.70 (0.61,0.72)

Performance of Regression Models. Results for the two level predictive model (TwoLevel) as previously described is compared with regression models trained on the complete training set (OneLevel). Table 5 shows that the TwoLevel training approach makes smaller errors for classes A and D while OneLevel training makes smaller errors for classes B and C. These differences were however not significant. A close look at the actual predicted median ICU-LOS in days (see Table 6) for the top 75% percentile of the true distribution of ICU-LOS (i.e. longer ICU-LOS) show that TwoLevel regression models tend to make smaller errors for all classes. Overall, the predicted median ICU length of stay from the TwoLevel model were off from the observed median value by less than 2 days while OneLevel was at least 4 days.

Table 5:

Performance of regression models for predicting log(ICU-LOS)

		TwoLevel Model		OneLevel Model
Model	Class	MAE	RMSE	MAE	RMSE
	A	0.86 (0.59,1.04)	1.04 (0.73,1.19)	1.00 (0.77,1.36)	1.16(0.99,1.51)
RF	B	0.71 (0.53,1.01)	0.88 (0.61,1.30)	0.64 (0.42,0.86)	0.81 (0.53,1.13)
	C	0.68 (0.61,0.76)	0.85 (0.77,0.96)	0.66 (0.57,0.78)	0.85 (0.74,1.02)
	D	0.44 (0.39,0.48)	0.68 (0.59,0.77)	0.48 (0.44,0.54)	0.68 (0.61,0.79)
	A	0.88 (0.66,1.01)	1.05 (0.80,1.19)	0.99 (0.80,1.23)	1.18(0.97,1.42)
GBM	B	0.69 (0.42,0.97)	0.85 (0.56,1.30)	0.64 (0.41,0.87)	0.79 (0.58,1.13)
	C	0.70 (0.61,0.77)	0.87 (0.77,0.97)	0.67 (0.60,0.81)	0.86 (0.75,1.07)
	D	0.42 (0.37,0.47)	0.70 (0.61,0.78)	0.46 (0.41,0.52)	0.69 (0.60,0.77)

Table 6:

Predicted and observed median ICU-LOS (in days)

Model	Class	TwoLevel	OneLevel	Observed
	A	3.99 (2.55,5.36)	1.86 (1.00,2.42)	5.00 (2.18,6.66)
RF	B	0.83 (0.48,1.40)	0.70 (0.41,1.53)	0.00 (0.00,0.98)
	C	1.36 (1.12,1.50)	1.19 (0.95,1.37)	1.15 (0.93,1.73)
	D	0.26 (0.20,0.36)	0.37 (0.28,0.46)	0.00 (0.00,0.00)
	A	4.05 (2.70,5.90)	1.78 (1.08,3.15)	5.14 (2.26,7.01)
GBM	B	0.69 (0.47,1.31)	0.71 (0.37,1.39)	0.00 (0.00,0.81)
	C	1.31 (1.05,1.53)	1.07 (0.75,1.29)	1.11 (0.83,1.60)
	D	0.22 (0.14,0.31)	0.32 (0.25,0.41)	0.00 (0.00,0.00)
		Top 75% predicted and observed median ICU-LOS
	A	12.08 (8.67,37.04)	9.01 (8.44,9.57)	15.19 (8.41,47.63)
RF	B	2.91 (1.85,9.54)	2.65 (1.84,4.53)	4.37 (1.79,50.33)
	C	3.97 (2.95,9.84)	3.59 (2.96,7.08)	5.99 (2.93,37.02)
	D	0.33 (0.02,1.94)	0.48 (0.03,2.72)	0.00 (0.00,12.96)

These results show that using only pretreatment variables, with the TwoLevel model one can predict with high accuracy the risk of a patient bleeding as a complication of PPT and then use this information to determine if the patient is likely going to stay longer in the ICU with sufficient accuracy.

Important Characteristics of Patients at Risk of Prolonged ICU-LOS. Table 7 presents the top 10 important variables for the RF regression model (averaged over 100 bootstrap). The TwoLevel model identified the INR for patients who bled and PLT (platelet count) for patients who did not bleed in the case where these patients were offered PPT as the most predictive variables. Hemoglobin level was the most predictive characteristics for all patients. Though appearing in different order, six top variables are common to all models.

Table 7:

Random Forest Regression Model Top 10 Variable Importance

TwoLevel Model					OneLevel Model
Class A		Class B
Variables	Importance	Variables		Importance	Variables	Importance
INR	85.6 (60.05,100.00)	PLT		95.67 (82.79,100.00)	Hemoglobin	99.34 (95.02,100.00)
PLT	77.5 (46.61,100.00)	Age		91.95 (78.81,100.00)	Emergency	94.29 (82.83,100.00)
Congestive HeartFailure	77.35(36.50,100.00)	Congestive Heart Failure		89.97 (70.63,100.00)	PLT	94.22 (85.37,100.00)
Hemoglobin	72.85(27.30,100.00)	Creatinine		87.79 (72.18,100.00)	ASA:4	90.13 (82.33,97.60)
Age	70.91 (42.76,93.12)	Hemoglobin		87.32 (72.42, 98.06)	Age	87.96 (79.08,96.73)
Creatinine	70.2 (40.70,100.00)	Charlson score		85.1 (71.45, 98.74)	Creatinine	87.87 (77.44,96.74)
Procedure:ENT/Oral	65.13(0.00,100.00)	ASA:3		83.89 (71.70, 96.97)	Weight	85.29 (75.03,94.53)
Emergency	65.02 (30.75,100.00)	Weight		82.2 (70.21, 96.69)	INR	80.62 (70.96,89.70)
Weight	62.97 (30.42, 97.50)	Liver Disease		81.65 (67.06,98.39)	Charlson score	80.34 (70.47,90.24)
ASA:3	61.34(28.24, 92.29)	Emergency		80.92 (63.92, 99.55)	Heparin	77.45 (59.86,89.27)

Conclusion

This study establishes a previously unknown causal relationship between prolonged ICU-LOS, bleeding, and PPT. Through a simple transformation of the bleeding and PPT variables, it was shown that the effect of bleeding in patients offered PPT more than doubled the risk of prolonged ICU-LOS, and that the event of no bleeding in patients also offered PPT significantly reduces the risk of prolonged ICU-LOS. Motivated by these results, this study developed a predictive framework for early identification of patients with (1) increased risk of all causes of prolonged ICU-LOS, and prolonged ICU-LOS attributable to bleeding as a complication of PPT, and (2) increased risk of bleeding as a complication of PPT. Given that the performance of models for ICU-LOS often deteriorate for patients with extended ICU-LOS, a two level predictive modeling approach was proposed to improve performance at the tail of the ICU-LOS distribution. The two level model was shown through a series of experiments using data for patients undergoing non-surgical procedures to be capable of identifying patient at risk or bleeding and longer ICU-LOS with acceptable accuracy. Based on the characteristics and predicted risk scores generated by the framework, patients at risk of extended ICU stays can be targeted and special intervention procedures implemented to reduce ICU-LOS and improve perioperative care.

A possible weakness of this study is the use of the treatment effects ATE, RR and OR. As these are population averages, their use entails that the effect is uniform across sub-populations or individuals and therefore not very useful for characterizing the effect of the treatment for each patient. Thus, an interesting potential future study of this work is to investigate methods of combining the four probabilities in Table 1 to derive individualized treatment effects.