An Empirical Study for Impacts of Measurement Errors on EHR based Association Studies

Abstract

Over the last decade, Electronic Health Records (EHR) systems have been increasingly implemented at US hospitals. Despite their great potential, the complex and uneven nature of clinical documentation and data quality brings additional challenges for analyzing EHR data. A critical challenge is the information bias due to the measurement errors in outcome and covariates. We conducted empirical studies to quantify the impacts of the information bias on association study. Specifically, we designed our simulation studies based on the characteristics of the Electronic Medical Records and Genomics (eMERGE) Network. Through simulation studies, we quantified the loss of power due to misclassifications in case ascertainment and measurement errors in covariate status extraction, with respect to different levels of misclassification rates, disease prevalence, and covariate frequencies. These empirical findings can inform investigators for better understanding of the potential power loss due to misclassification and measurement errors under a variety of conditions in EHR based association studies.

Introduction

Along with the widely use of electronic health record (EHR) systems over the last decade, huge amounts of longitudinal patient information, including coded/structured data (e.g., the International Classification of Disease codes) and clinical narratives (e.g., as admission notes and discharge notes), have been accumulated and are available electronically. These large clinical databases are valuable data sources for clinical, epidemiologic, genomic, and translational research, where identifying patients with specific diseases is often the critical step. However, manual review of patients’ charts is extremely time-consuming and costly as the decision criteria are often complex and require review of different sources of information by domain experts. Many studies have shown that structured data such as the ICD codes are not sufficient enough^1–3 to determine the patient cohorts as much of the detailed patient information was recorded in clinical narratives. Therefore, a large number of phenotyping methods have been developed to combine the clinical narratives with coded data to identify patients with certain diseases.

Due to the sensitiveness of clinical data and intrinsic difference between diseases, current phenotyping studies are often performed in a disease-specific manner⁴, where training and test corpus are developed for each disease. Many studies have focused on the prevalent diseases, such as diabetes^5,6, hypertension^7,8, and rheumatoid arthritis^9,10, or some common healthcare problems associated with significant morbidity and mortality, such as heart failure^11,12, colorectal cancer¹³, and venous thromboembolism^14,15. Some studies also focus on observational characteristics such as smoking status^16,17, obesity^7,18. Various clinical NLP systems have been applied to extract clinical information from text to facilitate phenotype identification, e.g., MedLEE¹⁹, MetaMap²⁰, KnowledgeMap²¹ and cTAKES²². Some of them provide individual module to identify common phenotypes, e.g., the smoking status detection module¹⁶ in cTAKES. Both rule-based and machine learning based systems have been developed to determine phenotypes. Most of the rule-based methods heavily involve domain experts’ knowledge, and the machine learning based phenotype identification methods often achieve better performances by leveraging different sources of information. The performances of phenotyping methods vary greatly among different diseases, and perfect genotype identification is difficult to achieve.

Although EHR-based clinical observational studies have been successfully performed based on automated phenotyping solutions, there is no systematic study to examine the misclassification of outcome and/or measurement error in covariates caused by imperfect phenotyping algorithms. In epidemiologic studies designed for EHR data, researchers have already noticed that the statistical models suffered from the information bias caused by the misclassification and/or measurement errors. Many studies have demonstrated that naive analyses ignoring misclassification lead to biased results in a variety of settings²⁸. As a result, the last 15 years have seen a rise in statistical methods to accommodate misclassification of disease status and measurement error in covariates, specifically when estimating odds ratios (ORs) or relative risks (RRs) in binomial regression; unbiased estimation of these parameters is typically of interest in pharmacoepidemiologic research. Several statistical methods have been developed to correct for a misclassified outcome²⁹ or to correct for a misclassified covariate, for example using matrix methods³⁰, inverse matrix methods³¹ and maximum likelihood methods. However, the loss of power due to the misclassification of outcomes and measurement error in covariates has not been fully understood.

In this study we perform a systematic analysis on the power loss of EHR-based association studies due to misclassified outcomes and measurement errors in covariates through simulation studies. We aim to discuss this problem in two general types of studies. In the settings of genetic association studies using EHR-based phenotypes, we focus on the impact of misclassified binary outcomes (i.e., misclassified phenotypes) only. In the settings of epidemiological association studies using EHR-based disease status and covariates, we investigate the further impact of measurement errors in covariates on the association test. Various settings of misclassification rates, magnitudes of measurement errors and levels of factors that would influence the power are considered. Simulation designs, parameter settings and models to be compared are introduced in the Methods section. Power curves and other simulation results are shown and discussed in the Simulation Results section. Further discussion on the power loss, type I error and effect size estimation are shown in the Discussion section. Our study highlights the issue of power loss in association test with the presence of measurement inaccuracy, which should be considered in all association studies that use data from the EHR systems.

Methods

Simulation setups

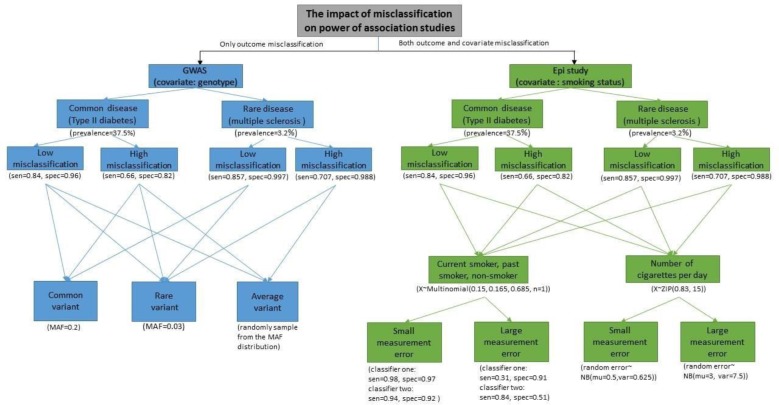
To investigate the impacts of misclassification of binary outcome (disease status) and measurement error in covariates on association studies, we start with the non-differential misclassification where the misclassification rates do not vary across covariate categories. Also, the measurement error of the covariate is assumed to be independent with the outcome. We consider two general types of studies: the genome-wide association studies (GWAS) where the outcome is EHR-based binary disease status and the covariate is the genotype at a single nucleotide polymorphism (SNP) locus, and the epidemiological studies where both the outcome and covariate are EHR-based (e.g., type II diabetes and smoking status). In this empirical study, we conduct simulations to mimic the setups of these two types of studies. We consider different scenarios by choosing different parameters of disease prevalence, covariate frequency, and misclassification rates in both outcome and covariate.

The prevalence of type II diabetes and multiple sclerosis are chosen to represent the common disease and the rare disease respectively. The prevalence for the common disease is 37.5% and for the rare disease is 3.2% according to recent literatures³². To mimic the performance of some commonly used phenotyping algorithms, we choose the misclassification rates of the outcomes to be similar with the eMERGE algorithm of identifying phenotypes from EHR clinical texts. This algorithm has been used in many EHR related studies and its performance has been reported in different literatures^32,33. According to Ritchie et al (2010), in a relatively high-performance situation for phenotyping type II diabetes, the positive predicted value (PPV) of the algorithm is approximately 0.9 and the sensitivity is 0.84. The specificity is then calculated to be 0.96 as in Ritchie et al (2010)³². In a relatively low-performance situation, the sensitivity and specificity of the eMERGE algorithm are reported to be around 0.665 and 0. 819, respectively³³. The misclassification rates of the phenotyping algorithm often depend on the prevalence of the disease. Phenotyping a rare disease tends to be more accurate than a common disease. For rare diseases (e.g., multiple sclerosis), the sensitivity of the eMERGE algorithm is around 0.857 and the specificity is 0.997 in a high-performance situation, and 0.707 and 0.988 in a low-performance situation. We fix the sample size at 5,000, and consider a sequence of effect sizes (in the scale of log odd ratio) in a logistic regression to evaluate the statistical power. These settings are the same for both genetic and epidemiological studies, and number of simulation is 1,000 for each setting.

In genetic association studies, the genetic information (i.e., genotypes) is often quite accurate with low genotyping errors. Therefore, we consider only the outcome misclassification in the GWAS settings. Minor allele frequency (MAF) of SNPs is set to be 0.2 for common variant scenarios and 0.03 for rare variant scenarios. In each scenario, two logistic regressions are fitted using the true outcomes and the misclassified outcomes, respectively. The reject rates are reported for each effect size, and power curves are plotted. The difference in power between using the true outcome and the misclassified outcome quantifies the impact of misclassification in each.

In almost all GWAS, a large number of SNPs are investigated. In order to understand the overall power loss for a typical genetic association study, averaged powers are obtained by sampling MAFs from a real genetic dataset (1000 Genomes Project Consortium, 2012) without replacement in each simulation to mimic the situation in a real GWAS.

In epidemiological studies, however, categorical covariates such as smoking status are often measured with different amount of measurement errors. Hence, we considered both the outcome misclassification and covariate measurement error in the epidemiological settings in order to evaluate the further impact of the measurement error in the covariate on association test. In some EHR systems, smoking status is recorded as a discrete variable with three categories (i.e. the classified smoking status): non-smoker, past-smoker, and current smoker. In this case, we use a single categorical variable which takes values 0, 1 and 2 to mimic the smoking status (non-smoker, past-smoker, and current smoker). The true status of the covariate is then generated from a multinomial distribution where the proportions of the three smoking status categories are based on the results in Liu et al (2012)¹⁷. The misclassified covariate is generated by mimicking the performance of the cTAKES smoking status detection module¹⁷. More precisely, as discussed in the paper, the algorithm first classifies subjects into non-smokers and smokers, and then classifies the smokers into past smokers and current smokers. Both classifiers involve misclassification and the misclassification rates are listed in Liu et al (2012)¹⁷. For scenarios with small amount of measurement errors (e.g., customized cTAKES module for eMERGE data), the sensitivity and specificity are approximately 0.98 and 0.97 for the first classifier and 0.94 and 0.92 for the second classifier. For scenarios with relatively large amount of measurement errors (e.g., direct use of cTAKE module without customization), the sensitivity and specificity are around 0.31 and 0.91 for the first classifier and 0.84 and 0.51 for the second classifier. In some other EHR systems, smoking status is recorded as the self-reported number of cigarettes per day (i.e. the quantified smoking status). To mimic this type of covariate data, we generate the smoking status as a variable taking non-negative integers using a zero-inflated Poisson distribution, considering a lot of patients are non-smokers. According to Kiviniemi et al (2011) ³⁷, the non-smoking proportion in the US is around 83% and the average number of cigarettes per day for one person is 15. The measurement error in smoking status is generated by randomly adding or subtracting a random error which follows a negative binomial distribution. For the situation with relatively small amount of measurement errors, we generated the random error from a negative binomial distribution with mean 0.5 and variance 0.625; and for large amount of errors, the random error are generated from a negative binomial distribution with mean 3 and variance 7.5. Figure 1 shows the scenarios what we consider and the corresponding parameter we choose in this paper.

Figure 1.

Flow chart of all the simulation scenarios and parameter settings. The sensitivities and specificities for diseases status mimick the performance of eMERGE algorithm. The numbers could be found in Ritchie (2010) and Wei (2012). For GWAS setting, no covariate misclassification is considered. MAF is set to be 0.2 for the common variant and 0.03 for the rare variant. By randomly sampling from the MAF distribution of the 1000 Genomes Project Consortium, the averaged power loss is studied. The sensitivities and specificities for the first and second classifiers of smoking status mimic the cTAKES smoking status detection module from Liu (2012). To simulate the number of cigarettes per day, the prevalence of current smoker and mean value of number of cigarettes are the same as Kiviniemi(2011).

In all scenarios, the smoking status is treated as ordinal variable assuming the effect of smoking on presence of disease is additive. Powers are calculated for different effect sizes from 0 to 1 (in the scale of log odds ratio) in the GWAS setting and the epidemiological setting with classified smoking status, and for different effect sizes from 0 to 0. 05.in the epidemiological setting with quantified smoking status.

Methods under comparison

Under genetic settings, we compare the model using true disease status with the model using misclassified outcome. Under epidemiological settings, we compare the model using true disease status and true smoking status with the model using misclassified disease status and misclassified smoking status. The models to be compared are described below:

1. Logistic regression using true disease status and true covariate.

   Let Y denote the true disease status (e.g. type II diabetes) of a patient, and X denote the true covariate status (e.g., genotype at a SNP locus, or true smoking status), we assume a logistic regression model: logit (Pr(Y = 1)) = β₀ + β₁X, where Pr(Y = 1) is the probability of a patient having the disease.

2. Logistic regression using misclassified disease status and true covariate.

   In the genetic association studies using the EHR-based phenotypes, instead of observing the true disease status, we could only obtain the disease status of the patients with misclassification. Let Y* denote the surrogate of the true disease (e.g. type II diabetes status extracted from EHR data), and X denote the genotype at a certain SNP. The logistic regression model using the surrogate as the true type II diabetes status could be expressed as: logit (Pr(Y* = 1)) = γ₀ + γ₁X. Here, the probability of having type II diabetes (Pr(Y = 1)) is replaced by the probability of observing the patient in the disease category (Pr(Y* = 1)). This model is not correct since these two probabilities are not equal and: Pr(Y* = 1|Y = 1) = α₁, Pr(Y* = 1|Y = 0) = 1 — α₂, where α₁ is known as the sensitivity and α₂ is the specificity of the phenotyping algorithm.

3. Logistic regression using misclassified disease status and covariate with measurement error.

   In epidemiological studies using EHR-based phenotypes and covariate (e.g., type II diabetes and smoking status), both the outcome misclassification and covariate measurement error are considered. Let Y^* denote the surrogate of the true disease status and X^* denote the surrogate of true smoking status. The logistic model using surrogates of both disease status and smoking status could be expressed as: logit (Pr(Y* = 1)) = η₀ + η₁X*.

   It also holds that Pr(Y* = 1|Y = 1) = α₁, Pr(Y* = 1|Y = 0) = 1 — α₂. When the smoking status is recorded as non-smoker, past-smoker and current smoker, the misclassification of smoking status involves two classifiers and satisfies:

   $$\begin{array}{ll}\mathrm{Pr}\left({\text{X}}^{*}=1,2|\text{X}=1,2\right)={\text{α}}_{\text{a}},\hfill & \mathrm{Pr}\left({\text{X}}^{*}=1,2|\text{X}=0\right)=1-{\text{α}}_{\text{b}}\hfill \\ \mathrm{Pr}\left({\text{X}}^{*}=1,2|\text{X}=1,2\right)=1-{\text{α}}_{\text{c}},\hfill & \mathrm{Pr}\left({\text{X}}^{*}=2|\text{X}=1\right)=1-{\text{α}}_{\text{d}}\hfill \end{array}$$

   where α_a and α_b are the sensitivity and specificity for the first classifier and α_c and α_d are the sensitivity and specificity for the second classifier of the smoking status detection algorithm. When the covariate X is the selfreported number of cigarettes per day, we assume a measurement error model that X = X ± ∈; ∈~NB(μ, σ²).

In each setting, we are interested in testing for an association between the covariate (smoking status) and disease (type II diabetes) by testing the association parameter being 0, i.e., H₀: β₁ = 0, γ₁ = 0, or η₁ = 0 in the models.

In the simulation studies, we generate the true status of disease and covariate from model 1, and generate the surrogates using the assumed misclassification rates and error distribution. Powers are compared between the misclassified model and the true model in order to quantify the impacts of misclassifications of outcomes and measurement errors of covariates on association test.

Simulation results

1. Genetic settings

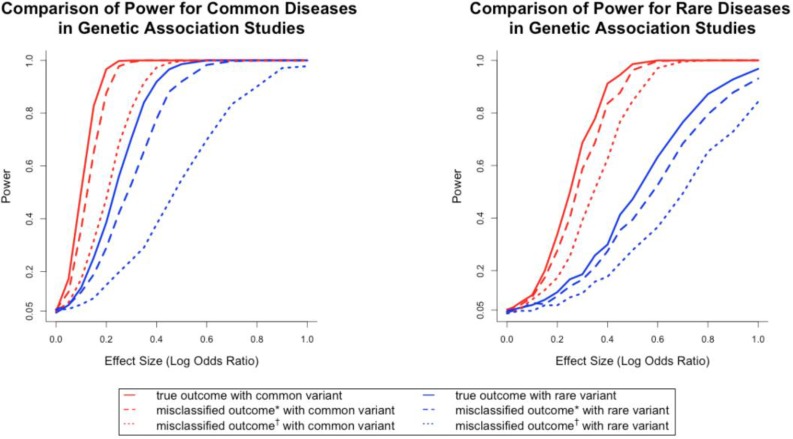
Figure 2 presented the power curves of the genetic association tests in settings with common and rare diseases. When true disease statuses were known, the power for detecting association was higher for common diseases compared to rare diseases, and higher for common variant compared to rare variant when controlling for other parameter values. Such a finding also held when true disease statuses were unknown and surrogates were used. This finding was consistent with the experiences in association studies³⁴. To evaluate the impact of misclassifications, we compared the power of using true outcomes against using the surrogates within the same setting of disease prevalence and allele frequency. The left panel in Figure 2 suggested that for a common variant (i.e., high allele frequency), the loss of power was relatively small as long as the misclassification rates were low (the maximal loss of power is around 15%). On the other hand, if the variant was rare (i.e., low allele frequency), the loss of power due to the misclassification was sizable (up to 20%) when misclassification rates were low. However, when misclassification rates were high, the losses of power were all larger than 50% for both common and rare variant scenarios. The right panel in Figure 2 suggested a similar finding, except the corresponding power was lower due to the fact that the disease was rarer.

Figure 2.

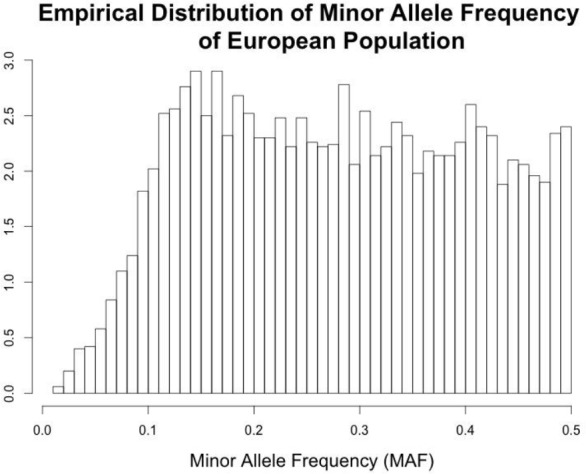
Empirical Distribution of Minor Allele Frequency of Utah residents (CEPH) with northern and western European ancestry.

Another observation from the solid and dashed curves in the left panel of Figure 2 was that when the true log odds ratio was 0.3 (i.e., odds ratio of 1.35), the association test based on the true outcome (or misclassified outcome with small misclassification rates) had a power of 100%. In other words, misclassification had no impact on loss of power, provided the effect size was moderately strong, both disease and covariate were common, and misclassification rates were relatively small. If any of these conditions failed to hold, the loss of power due to misclassification was still substantial. For example, for the same effect size, when considering the common disease and rare variant scenario, the power loss due to misclassification was 17.3% for small misclassification rates and 46.2% for high misclassification rates. These numbers were 10% and 29.6% respectively, for rare disease and common variant, and 2% and 7.2% for rare disease and rare variant. In the setting of no misclassification, the power for the rare disease and common variant scenario and the rare disease and rare variant scenario were 68.7% and 18.6%. Therefore the power loss could not be ignored.

Figure 3 presented the power for association tests at a single SNP in different settings. For a typical GWAS, millions of SNPs are tested where both rare variants and common variants are included. We are often more interested in the averaged loss of power due to misclassifications, where the loss of power in association test at each SNP is averaged over millions of SNPs. To obtain the averaged power, we sampled the allele frequencies without replacement from the data from the reference panels of The 1000 Genomes Project (here we used Utah Residents with Northern and Western European Ancestry, or CEU) (1000 Genomes Project Consortium, 2012). The empirical distribution of the minor allele frequencies was displayed in Figure 2. The SNPs with a MAF greater than 0.1 were distributed approximately evenly, and SNPs with MAF less than 0.05 were considered rare in this population.

Figure 3.

Comparison of power for common and rare disease in genetic association studies. Misclassified outcome* stands for high sensitivity and specificity (Sensitivity=0.84, specificity=0.96 for common diseases; sensitivity=0.857, specificity=0.997 for rare diseases). Misclassified outcome† stands for low sensitivity and specificity (Sensitivity=0.665, specificity=0.819 for common diseases; sensitivity=0.707, specificity=0.988 for rare diseases). MAF=0.2 for common variant and 0.03 for rare variant.

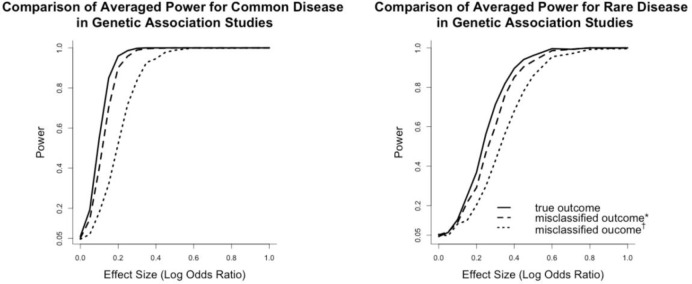
Figure 4 showed the averaged power curves for a genetic association study based on the CEU population. Power curves in the left and right panels showed the impact of misclassified phenotypes on association testing for common and rare diseases. These power curves implied that from an overall perspective how much power was lost due to misclassified outcomes in different settings of misclassification rates. Since the minor allele frequency of most SNPs in the genetic association study was distributed from 0.1 to 0.5, the averaged power curves were similar as the common variant scenarios in Figure 3. It suggested that when misclassification rates were low, the power loss was relatively mild compared to the power loss when misclassification rates were high. For common diseases, when the testing allele had an effect size (log odds ratio) larger than 0.3 and under low misclassification rates, using the surrogates did not cause power loss greater than 1%. When misclassification rates were high, however, the log odds ratio had to be at least 0.5 to reach a power loss less than 5%. When diseases were rare, the log odds ratio had to be greater than 0.4 for the low misclassification scenario, and 0.6 for the high misclassification scenario to ensure a power loss less than 5%.

Figure 4.

Comparison of averaged power for common and rare diseases. The averaged powers were obtained by sampling without replacement from the MAF distribution of CEU population. Misclassified outcome* stands for high sensitivity and specificity (Sensitivity=0.84, specificity=0.96 for common diseases; sensitivity=0.857, specificity=0.997 for rare diseases). Misclassified outcome† stands for low sensitivity and specificity (Sensitivity=0.665, specificity=0.819 for common diseases; sensitivity=0.707, specificity=0.988 for rare diseases).

To evaluate the power loss in extreme situations, we calculated the maximal power loss when the effect size was varying from 0 to 1. When misclassification rates were low, the maximal power loss was 15% for common disease and 11% for rare disease. While when misclassification rates were high, the maximal power losses were 50% and 29% for common and rare diseases correspondingly. Therefore, when the sensitivity and specificity of the phenotyping algorithm were not high enough, the average power loss could be huge for SNPs with relatively moderate effect sizes for both rare and common diseases.

2. Epidemiological settings

In this section, we mimicked the settings of epidemiological studies using EHR-based disease and covariate status (i.e. smoking status). Besides the misclassified binary outcomes, we evaluated the further impact of measurement errors in covariates on the power loss of association test. The misclassification settings for the disease status and smoking status could be found in Figure 1.

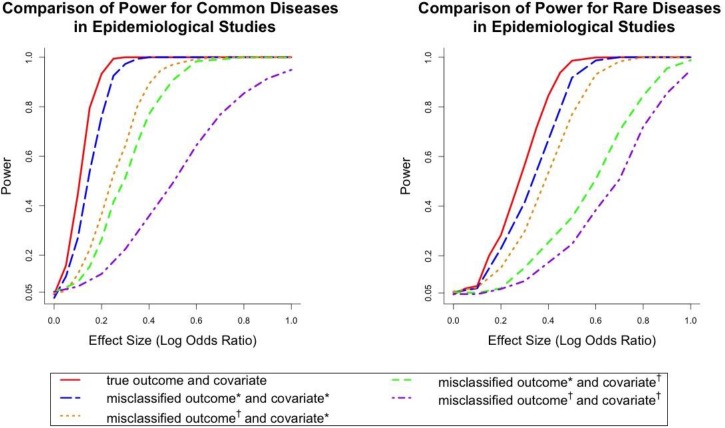
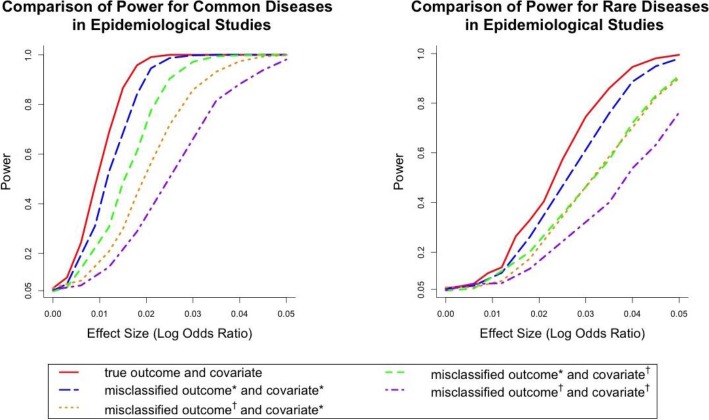
When the smoking status only contained three classes, Figure 5 showed the power curves in different settings of misclassification and measurement errors for common and rare diseases. The previous finding that the power for rare diseases is lower than common diseases when controlling for other settings also held in the epidemiological studies. The comparison between the solid line and the four dashed lines within each panel showed the impact of different levels of misclassification and measurement errors on the power of association testing.

Figure 5.

Comparison of Power for common and rare diseases in epidemiological settings where the covariate contains three categories (nonsmoker, past smoker and current smoker). Misclassified outcome* stands for high sensitivity and specificity (Sensitivity=0.84, specificity=0.96 for common diseases; sensitivity=0.857, specificity=0.997 for rare diseases). Misclassified outcome† stands for low sensitivity and specificity (Sensitivity=0.665, specificity=0.819 for common diseases; sensitivity=0.707, specificity=0.988 for rare diseases). Covariate* stands for small amount of covariate misclassification (sensitivity and specificity were chosen as 0.98 and 0.97 for the first classifier and 0.94 and 0.92 for the second classifier). Covariate† stands for large amount of covariate misclassification (the sensitivity and specificity were set to be 0.31 and 0.91 for the first classifier and 0.84 and 0.51 for the second classifier).

Combined with Figure 3 and Figure 5, it suggested that adding the measurement error increased the power loss compared with models with only the outcome misclassification. For example, when the effect size (log odds ratio) was 0.3 for common disease, the power losses of the four scenarios in the plots (low misclassification small measurement error, high misclassification small measurement error, low misclassification large measurement error and high misclassification large measurement error) were 2.7%, 35.8%, 48.8% and 77.6%. For rare disease, the powers of the four scenarios were 15.1%, 30.6%, 45.8% and 48%, respectively. It also showed that only when both misclassification and measurement error were small, the power loss was relatively small. When either outcome or exposure had a high misclassification rate, the power loss was severe.

When using the number of cigarettes to code the smoking status, the power curves under different scenarios were showed in Figure 6. The major findings under this scenario were the same as the previous scenario in which the smoking status was recorded as three categories. When the outcome misclassification was low and measurement error of the covariate was small, the power loss was within 18.2% for common diseases and 12.4% for rare diseases.

Figure 6:

Comparison of Power for common and rare diseases in epidemiological settings where the covariate is the self-reported number of cigarettes per day. Misclassified outcome* stands for high sensitivity and specificity (Sensitivity=0.84, specificity=0.96 for common diseases; sensitivity=0.857, specificity=0.997 for rare diseases). Misclassified outcome† stands for low sensitivity and specificity (Sensitivity=0.665, specificity=0.819 for common diseases; sensitivity=0.707, specificity=0.988 for rare diseases). Covariate* stands for small amount of covariate measurement error in number of cigarettes which was generated from NB(0.5,0.625). Covariate† stands for large amount of covariate measurement error which was generated from NB (3, 7.5).

However, when either the outcome misclassification or the covariate measurement error was large, the power loss was severe up to 50%.

Through this simulation study, we quantified the impact of misclassification and measurement error in association studies. It was showed that rare diseases, compared to common diseases, had lower power for testing the association controlling for the prevalence of covariate, misclassification rates and measurement error amount. The prevalence of the covariate (minor allele frequency in this study) also influenced the power in the sense that rare variant scenarios had lower power than the common variant scenarios when controlling for other settings. Therefore, in practical researches, study designs should account for these factors to adjust the sample size to achieve a proper testing power. When only outcomes were misclassified, the power loss was small when the misclassification rates were low, and it was sizable when misclassification rates were high. Moreover, when the covariate and the outcome were not measured accurately, the power loss increased compared to the models with only the outcome misclassification. In these scenarios, power loss was relatively large when either the measurement error or the outcome misclassification rates were large.

Discussion

In this empirical study, we conducted simulation studies under different values of misclassification rates and amount of measurement errors to evaluate the loss of power in both genetic and epidemiological association study settings. We concluded that factors including disease prevalence, covariate frequency, misclassification rates of the disease status as well as the amount of measurement errors all influenced the power of association test. The power loss was relatively small as long as the misclassification rates and/or measurement error were low. Otherwise, power loss could be substantial and was increased with higher misclassification rates and/or measurement error rates. From the simulation results, we also observed that the type I error of the association test that ignored misclassification and measurement errors were not inflated under all scenarios. In other words, although the outcome and covariate could be measured with errors, the naive logistic regression ignoring these errors can still control type I error well as long as the misclassification is nondifferential. This is consistent with the findings of Neuhaus (1999) and Li & Duan (1989)^35,36. Therefore, the only issue of using the naive logistic regression is the power loss.

However, while the EHR data are widely used in all kinds of association studies, the problem of power loss due to inaccuracy of EHR-based phenotypes and covariate records are sometimes ignored. Our study investigated this problem in two major types of studies and showed that when observations were measured with certain amount of errors, the power loss could be quite substantial. If no adjustment is made to account for the misclassification and measurement errors, sample size should be recalculated to deal with the loss of power.

In practical studies, when sample size is fixed and misclassification exists, association tests that account for the misclassification are needed. Moreover, the estimations of the effect sizes can also be biased and need to be corrected. Neuhaus (1999) and Li & Duan (1989) pointed out that when the outcome and covariate were misclassified, the estimated effect size (log odds ratio) is biased towards the null if using naive logistic regression^35,36. One limitation of our empirical study is that we only considered two levels of disease prevalence, minor allele frequency, misclassification rates and measurement error amount. The scope of scenarios that we have discussed in this paper is still limited. For example, in real applications, the disease prevalence could be lower than 3.2% as we considered here, and misclassification rates could vary from a wider range. However, the results of this study are useful to inform and guide investigators on the magnitude of loss of power in certain scenarios. And the conclusions about the relationships between powers and each factor could help the investigators obtain a rough estimation of potential loss of power in their studies.

In this study, we considered a relatively simple situation where the misclassification of the outcome is independent of the covariate, as well as the measurement error of the covariates. This assumption might not hold in some practical situations since the error probabilities might differ across different covariate levels. Moreover, the amount of measurement error of the covariate might be correlated with the disease misclassification rates. Empirical evaluation of power loss in these more complicated situations will be reported in the near future.

Furthermore, as we concluded that the power of the association test is influenced by various factors such as the disease prevalence, frequency of the covariate, as well as the misclassification rates, it is of interest to investigate how the power loss is attributable to these factors individually and jointly. Our future work also includes the extension from simple univariate logistic regression to multivariate regression to better understand the impact of misclassification on the power loss of association test in the presence of confounders.

Conclusion

Over the last decade, EHR systems have been increasingly implemented at US hospitals. Substantial amounts of detailed patient information, including lab tests, medications, disease status, and treatment outcome, have been accumulated and are available electronically. These large clinical databases are valuable sources for clinical and translational research. Despite their great potential, the complex and uneven nature of clinical documentation and data quality brings additional challenges for analyzing EHR data. A critical challenge is the information bias due to the measurement errors in outcome and/or covariates. We conducted empirical studies to quantify the impacts of measurement errors on EHR based associated study. More specifically, we designed our simulation studies based on the disease prevalence, covariate frequencies and misclassification rates using data from the Electronic Medical Records and Genomics (eMERGE) Network. Through simulation studies, we quantified the loss of power due to misclassifications in case ascertainment with respect to different levels of misclassification rates (e.g., an algorithm with high precision and recall vs one with low precision and recall), disease prevalence (e.g., common disease vs rare disease), and covariate frequencies (e.g., common allele frequency vs rare allele frequency). We also evaluated the further loss of power if the covariate conditions were subjected to measurement errors, such as smoking status extracted from medical records by a certain algorithm. These empirical findings can help to inform investigators for better understanding the potential power loss due to different types of measurement errors under a variety of conditions in EHR based association studies.