Active delineation of Meyer's loop using oriented priors through MAGNEtic tractography (MAGNET)

Abstract

Streamline tractography algorithms infer connectivity from diffusion MRI (dMRI) by following diffusion directions which are similarly aligned between neighboring voxels. However, not all white matter (WM) fascicles are organized in this manner. For example, Meyer's loop is a highly curved portion of the optic radiation (OR) that exhibits a narrow turn, kissing and crossing pathways, and changes in fascicle dispersion. From a neurosurgical perspective, damage to Meyer's loop carries a potential risk of inducing vision deficits to the patient, especially during temporal lobe resection surgery. To prevent such impairment, achieving an accurate delineation of Meyer's loop with tractography is thus of utmost importance. However, current algorithms tend to under‐estimate the full extent of Meyer's loop, mainly attributed to the aforementioned rule for connectivity which requires a direction to be chosen across a field of orientations. In this article, it was demonstrated that MAGNEtic Tractography (MAGNET) can benefit Meyer's loop delineation by incorporating anatomical knowledge of the expected fiber orientation to overcome local ambiguities. A new ROI‐mechanism was proposed which supplies additional information to streamline reconstruction algorithms by the means of oriented priors. Their results showed that MAGNET can accurately generate Meyer's loop in all of our 15 child subjects (8 males; mean age 10.2 years ± 3.1). It effectively improved streamline coverage when compared with deterministic tractography, and significantly reduced the distance between the anterior‐most portion of Meyer's loop and the temporal pole by 16.7 mm on average, a crucial landmark used for preoperative planning of temporal lobe surgery. Hum Brain Mapp 38:509–527, 2017. © 2016 Wiley Periodicals, Inc.

INTRODUCTION

Diffusion MRI (dMRI) allows for the non‐invasive quantification of the diffusion of water molecules in biological tissues [Basser and Jones, 2002; Le Bihan and Breton, 1985; LeBihan et al., 2001]. Tractography algorithms aim to virtually reconstruct the WM fiber architecture of the human brain based on directional information derived from dMRI acquisitions. These algorithms operate by taking as input a set of tensors, orientation distributions functions (ODFs), or precomputed peaks [Chamberland et al., 2014], and by connecting adjacent voxels based on directions that are similarly aligned [Conturo et al., 1999]. This rule has ever been the definition of the probability of connectivity, whether it is deterministic or probabilistic streamline tractography [Behrens et al., 2003; Conturo et al., 1999; Jeurissen et al., 2011; Parker et al., 2003; Sherbondy et al., 2008a]; or whether tractography is based on diffusion orientation inferred from single tensors [Conturo et al., 1999; Mori et al., 1999; Lazar et al., 2003], constrained spherical deconvolution (CSD) [Descoteaux et al., 2009; Girard et al., 2014; Jeurissen et al., 2011; Tournier et al., 2012; Smith et al., 2012], ball and sticks models [Behrens et al., 2003; Sotiropoulos et al., 2012], DIAMOND models [Scherrer et al., 2015], or model free representations such as diffusion spectrum imaging (DSI) [Wedeen et al., 2005]. However, when multiple peaks are estimated at each voxel, not all WM fascicles are organized so that consecutive peaks along their courses in the brain are maximally aligned.

A perfect example of such caveat is Meyer's loop, a highly curved portion of the OR, commonly known to exhibits a narrow turn, kissing and crossing regions, and changes in fascicle dispersion. The OR is commonly described in three parts, namely the superior, central, and inferior parts, each corresponding to different areas of the visual field [Ebeling and Reulen, 1988]. In particular, Meyer's loop is part of the inferior bundle, which originates from the lateral geniculate nuclei (LGN), propagates anteriorly from the LGN to the temporal lobe, hooks around the inferior horn (IH) of the lateral ventricle (sharp turn) and back projects toward the occipital pole (OP) to form a continuous layer of fibers [Benjamin et al., 2014; Ebeling and Reulen, 1988; Rubino et al., 2005]. This fascicle is well understood from conventional Klingler dissection and histological analysis as it has been studied intensively in the past [Choi et al., 2006; Chowdhury and Khan, 2010; Ebeling and Reulen, 1988; Peltier et al., 2006; Peuskens et al., 2004; Pujari et al., 2008; Rubino et al., 2005; Sincoff et al., 2004; Ture et al., 2000], mainly because of its primary function: transmitting visual information. The OR is also amongst the few primary white matter fiber pathways to attain complete myelination in the early developmental stages [Kinney et al., 1988]. It is generally believed that the OR uniquely projects to the calcarine fissure (in the primary visual cortex, V1), though it has been shown recently that it may reach V2 and V3 as well [Alvarez et al., 2015].

From a neurosurgical perspective, any surgery targeting the visual system has potential risk of inducing vision deficits to the patient [Lilja and Nilsson, 2015; Schmitt et al., 2014; Winston et al., 2011]. For example, anterior temporal lobe resection is a well‐established and effective treatment for temporal lobe epilepsy [Wiebe et al., 2001], a frequent neurological disorder characterized by recurrent and unprovoked seizures. However, while performing such resection, it is crucial for neurosurgeons to minimize the risk of new morbidity to the patient while maximizing the extent of resection. More specifically, any damage to the OR will most likely result in vision deficits, as the resected area in these surgeries often includes parts of Meyer's loop. Neurosurgeons are increasingly using tractography to improve their knowledge of the location and extent of the optic radiation, in order to facilitate the design and execution of an optimal surgical resection [Lilja and Nilsson, 2015; Lilja et al., 2015].

A large number of studies have attempted to reconstruct the OR using diffusion tensor imaging (DTI) [Benjamin et al., 2014; Clatworthy et al., 2010; Dayan et al., 2015; Hofer et al., 2010; Lilja et al., 2014; Sherbondy et al., 2008b; Tax et al., 2014a; Winston et al., 2011; Wu et al., 2012; Yamamoto et al., 2005; Yogarajah et al., 2009] and high order models based on high angular resolution diffusion imaging (HARDI) acquisitions [Bernier et al., 2014; Kammen et al., 2015; Martinez‐Heras et al., 2015; Nowell et al., 2015]. The clinical motivation behind most of these studies was to obtain an accurate model of the OR for the preoperative planning in anterior temporal lobe resection surgery. It is generally believed that HARDI‐based techniques can overcome the limitations of DTI to make tractography more robust by solving the fiber crossing limitations and reconstructing high curvature fiber bundles [Descoteaux, 2015; Farquharson et al., 2013; Neher et al., 2015; Nimsky et al., 2016; Seunarine and Alexander, 2009; Tournier et al., 2011]. However, a better local representation of the diffusion does not imply that tracking algorithms knows how to propagate through these crossing regions. The local angular reconstructions generated from HARDI data can be ambiguous, because several underlying crossing, curving, and branching configurations can lead to the same angular profile. Additionally, it is has been shown that HARDI‐based methods can be inaccurate as they increases the amount of false positive connections [Cote et al., 2013]. For example, Figure 1 show a non‐negligible portion of streamlines exiting the LGN to propagate toward the TP (red), mainly because the local choice of direction complies with the connectivity rule aforementioned. The result is then an under‐estimation of Meyer's loop, as these undesired streamlines do not contribute to the final extracted bundle. To achieve a dense coverage of Meyer's loop, the majority of aforementioned techniques employ brute force probabilistic tractography of all possible streamlines, then rely on multiple regions of interest (ROIs) to eliminate a considerable amount of false positive streamlines. Clustering techniques [Garyfallidis et al., 2012; O'Donnell and Westin, 2007] are also employed to extract the final bundle and increase accuracy [Kammen et al., 2015]. These pipelines can take several hours to compute structural connectivity and may be suboptimal for neurosurgical planning where time is often a key‐factor. Sherbondy et al. [2008b] recently proposed the ConTrack approach [Sherbondy et al., 2008a] for reconstructing the optic radiation, which was evaluated in 8 volunteers (7 males; mean age 26.9 years ± 4.5; range 23–35). Their method aims at finding the most probable connectivity between the LGN and the calcarine sulcus by generating a large amount of candidate streamlines and then by assigning validity indices to every streamline. In this way, they were able to reconstruct the anterior extent of the OR. Their findings matched those of [Ebeling and Reulen, 1988], with an average distance between the anterior‐most tip of Meyer's loop and the temporal pole of 28 ± 3.0 mm. Despite exhaustive attention, the virtual reconstruction of Meyer's loop with tractography typically remains incomplete [Benjamin et al., 2014; Mandelstam, 2012].

Figure 1.

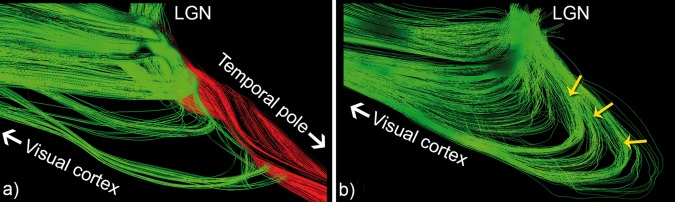
(a) Optic radiation tractography based on deterministic tractography shows incomplete coverage of Meyer's loop (lateral view). A considerable amount of seeds exiting the LGN prefer to propagate toward the temporal pole (red) instead of entering the highly curved Meyer's loop (b, yellow arrows). [Color figure can be viewed at http://wileyonlinelibrary.com]

Notwithstanding, the human TP is prominently composed of multiple interdigitating association fascicles [Schmahmann and Pandya, 2006] that can confound tractography algorithms. For example, Figure 2 shows an anatomical T1‐weighted image with multiple kissing and crossing peaks in Meyer's loop area. In this illustration, the red strokes represent streamlines propagating toward the TP from the LGN, complying with the connectivity rule which dictates that similarly aligned diffusion profiles should be connected [Conturo et al., 1999]. Conversely, the green lines outline the expected anatomical course of Meyer's loop. Figure 3 illustrates a sagittal view of the human brain, where streamlines issued from tractography rapidly become entangled in a bird's nest, such as the uncinate fasciculus (Un), the temporal projections of the cingulum (Cg) and of the fornix (Fx), the medial and inferior longitudinal fasciculi (MLF, ILF), and the inferior fronto‐occipital fasciculus (iFOF) [Catani and Thiebaut De Schotten, 2012; Catani et al., 2003]. This highly complex configuration can impede tractography and lead to an inadequate representation of Meyer's loop, as the many local diffusion directions may confound a tracking algorithm attempting to connect maximally aligned peaks (Fig. 1). To encode our knowledge of the anatomy and disentangle such cluttered configuration (e.g., include or eliminate streamline bundles), common methods employ a mixture of Boolean ROIs which are typically derived from atlas segmentation or manually defined [Catani and Thiebaut De Schotten, 2012; Conturo et al., 1999; Wakana et al., 2004]. For example, the “AND” operator often serves as an inclusion command between different regions of the brain. The “OR” operator is also used as the union of different regions. Additionally, a “NOT” operator can be used to exclude streamlines or simply prune them by stopping their course. In Meyer's loop tractography, Boolean operators typically ensure that streamlines forming the optic radiation will connect the LGN and V1 by the means of an AND operator. Further delineation can also include NOT operators to ensure that streamlines do not propagate toward the frontal and contralateral lobes.

Figure 2.

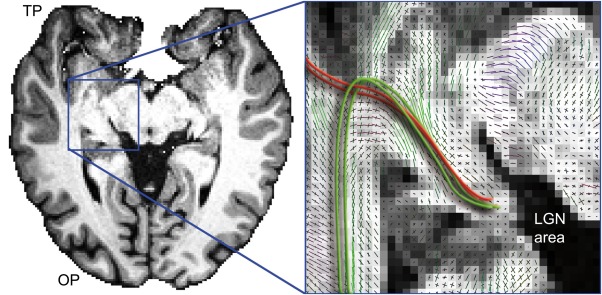
Anatomical T1‐weighted image at the level of Meyer's loop (axial slice). Zoomed view shows multiple kissing and crossing peaks in Meyer's loop area. Red lines represents streamlines propagating toward the TP from the LGN when following similarly aligned peaks in the field of orientations. Green lines illustrate the expected anatomical course of Meyer's loop. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 3.

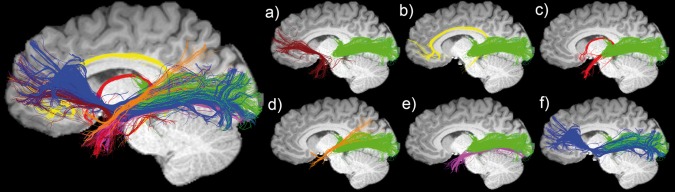
Temporal lobe streamline tractography shows multiple pathways interdigitating with the optic radiation (green) and more specifically, with Meyer's loop. (a) uncinate fasciculus (Un), (b) cingulum (Cg), (c) fornix (Fx), (d) medial longitudinal fasciculus (MLF), (d) inferior longitudinal fasciculus (ILF), (e) inferior fronto‐occipital fasciculus (iFOF). Data source: Boston Children's Hospital. [Color figure can be viewed at http://wileyonlinelibrary.com]

An inherent problem to the reconstruction of Meyer's loop is related to the underlying streamline integration step, which requires a direction to be chosen across a field of orientations. When this field consists of DTs, there is merely one choice of integration [e.g., tensorlines‐based algorithms; Basser et al., 2000; Mori et al., 1999; Weinstein et al., 1999; Wedeen et al., 2005]. These first order integration techniques can also be extended to take into account the full shape of the DT [Lazar et al., 2003; Westin et al., 2002]. HARDI‐based tractography has been proposed for multiple peaks to generalize these DT‐based methods. Second order integration is also possible [Tournier et al., 2010b]. In any cases, deterministic tractography algorithms selects the principal direction associated to the closest diffusion profile to its incoming direction while probabilistic streamline tractography randomly draws directions from to the full orientation distribution. Both methods propose a stepping rule that aims to maximally connect directional manifolds with each other. Taken together, there is a need for a generalized simplification of the integration rule to increase the fidelity of streamline propagation. Moreover, while Meyer's loop reconstruction has been extensively studied in adults, this is still under‐explored in children, despite the fact that temporal lobe epilepsy is prevalent in this age group [Dayan et al., 2015; Gataullina et al., 2015].

In this work, we propose a novel alternative to delineate Meyer's loop using MAGNEtic Tractography (MAGNET). MAGNET is a new ROI‐mechanism that aims to facilitate Meyer's loop delineation by incorporating anatomical knowledge of the expected fiber orientation to streamline reconstruction algorithms. This new ROI‐mechanism not only selects streamlines that reaches it, but also suggests a user‐defined trajectory, if supported by the underlying diffusion profiles. We hypothesize that this new directional‐ROI can help incorporate a priori information about the course of the pathway and lead to an improved delineation of Meyer's loop by using a tailored and interactive approach. The main goals of MAGNET are thus to (1) increase the accuracy of tractography by selecting a specific diffusion direction based on a prior anatomical knowledge, and (2) reduce the total streamline calculation burden by avoiding an exponential search of all possibilities (i.e., computationally infeasible).

METHODS

In this section, we first describe how MAGNET differs from a traditional streamline propagation algorithm [Chamberland et al., 2014]. To measure the effect of our new ROI mechanism in vivo, the virtual reconstruction of Meyer's loop was performed in 15 healthy child controls using both MAGNET and deterministic tractography. MAGNET was also compared with probabilistic tractography on a single‐subject derived from the Human Connectome Project (HCP) [Sotiropoulos et al., 2013; Van Essen et al., 2013].

Propagation Equation

To introduce the concept of MAGNET, we first recall a general streamline propagation equation [Conturo et al., 1999]: V _next = argmin_k α(V _in,V _k) [Eq. (1)], where V _next is the next direction to propagate in the three‐dimensional (3D) space, V _in represents the incoming direction and α is the angle between V _in and V _k, V _k being the kth peak in the voxel. Existing derivative versions of Eq. (1) can also include weighted factors between V _in and V _k to smooth the resulting streamlines [Chamberland et al., 2014; Lazar et al., 2003; Weinstein et al., 1999; Westin et al., 2002].

With MAGNET, we now propose to follow the V _k peak that is most aligned with a preferential tracking direction in a ROI (given by V _magnet), based on anatomical knowledge of the analyst. The incorporation of anatomical priors is achieved by applying an oriented magnetic field (V _magnet) inside the boundaries of a given ROI. Specifically, when the tracking is happening inside the new directional‐ROI, the propagation equation becomes then: V _next = argmin_k α(V _magnet,V _k) if inside the directional‐ROI; Eq. (1) otherwise. Note that if a voxel only contains a single direction, the propagation naturally resumes with Eq. (1).

Datasets

Fifteen healthy controls (8 males; mean age 10.2 years ± 3.1; range 4–14) completed MR imaging at the Boston Children's Hospital, Boston, MA, USA. MR acquisitions were performed on a Siemens 3T Trio MRI. Diffusion scans were acquired using a multidirection (n = 90) and multi‐b‐value scheme ranging from 400 to 3,000 s/mm² according to the Cube and Sphere (CUSP) gradient set of Scherrer and Warfield [2012] (12 at b = 0 s/mm², 6 at b = 400 s/mm², 6 at b = 600 s/mm², 6 at b = 800 s/mm², 30 at b = 1000 s/mm² and 30 gradients on the cube of constant TE, with b‐values in the interval 1,000 < b < 3000 s/mm²). Other acquisition parameters were: 128 × 128 matrix, FOV 220 mm, TR/TE: 5,700/89 ms, 1.7 × 1.7 × 2 mm³. Eddy currents were minimized by using a twice refocused spin echo sequence [Reese et al., 2003]. An anatomical T1‐weighted 1 mm isotropic MPRAGE image was also acquired for each subject (256 × 256 matrix, FOV 200‐256 mm, TR/TE 2530/3.54 ms). The study was approved by the Institutional Review Board and all participants provided informed consent. Finally, a separate HCP dMRI dataset with an isotropic voxel size of 1.25 mm was also analyzed. Only the b = 3,000 s/mm² shell with 90 diffusion directions was used.

Comparison of MAGNET and Deterministic Tractography in 15 Healthy Child Controls

Diffusion data processing

MR image analysis of the group datasets was done using the CRKit (http://crl.med.harvard.edu) and visualization was performed using the Fibernavigator (https://github.com/scilus/fibernavigator, Chamberland et al. [2015]). The intracranial cavity was segmented into WM (including deep nuclei), GM, cortex (CX), and cerebrospinal fluid (CSF) using a previously validated segmentation algorithm [Akhondi‐Asl et al., 2014; Grau et al., 2004; Weisenfeld and Warfield, 2009] based on individual T1‐weighted images. The diffusion images of each participant underwent affine registration and upsampling to anatomical space (1 mm isotropic), correcting for patient motion and potential residual eddy current distortion. Multi‐fiber model estimation was done using DIstribution of Anisotropic MicrOstructural eNvironments in Diffusion compartment imaging (DIAMOND) [Scherrer et al., 2015], resulting in up to three main peaks per voxel. DIAMOND allows the representation of arbitrary fiber configurations together with vasogenic or cytotoxic edema and free water compartments without the need to specify the number and type of compartments a priori. By modeling the signal generated by fascicle crossings as a finite mixture of continuous distributions of tensors (matrix variate gamma distributions), DIAMOND generates a sharp representation of the fascicles at each voxel, while also characterizing the dispersion of each fascicle, and characterizing to the micro‐structural integrity of each fascicle.

Deterministic tractography

Meyer's loop tractography was performed using real‐time multi‐peak tractography [Chamberland et al., 2014, 2015], allowing for interactive 3D visualization of streamlines during the tracking process and facilitating the manual positioning of ROIs. Specifically, streamlines were generated instantaneously while the seed‐ROI was positioned. This allowed for the precise localization of the streamlines starting point in the thalamic area. A 4 × 4 × 9 mm³ seed‐ROI with 15 randomly spaced seeds per axis (total: 3,375) was interactively placed anterolaterally to the left LGN of each subject (localized during streamline propagation), with initial seed direction oriented in the left direction (Fig. 4a, “S”). An inclusion (AND) planar‐ROI centered in the sagittal stratum and an exclusion (NOT) mid‐sagittal plane acted as filtering regions for all subjects (Fig. 4b). To maximize the extent and coverage of Meyer's loop, directional‐ROIs with varying sizes across subjects (see section “Deterministic tractography” under Results section) were placed around the medial, anterior and lateral tip of Meyer's loop (Fig. 4). These directional‐ROIs favored the selection of peaks that form Meyer's loop in a subject‐specific approach. In particular, the medial directional‐ROI (primarily extending along the X‐axis) allows streamlines exiting the LGN to directly enter Meyer's loop instead of propagating toward the TP (Figs. 3a and 4a). The anterior directional‐ROI (also prolonging primarily along the X‐axis) acted as a waypoint to select the peaks exhibiting a sharp turn by prioritizing a lateral diffusion direction (Figs. 1 and 4). This directional‐ROI was interactively moved anteriorly until no loop could be found. This step insured that streamlines did not enter prematurely into the loop, by allowing them to reach the tip of Meyer's loop. Finally, a lateral directional‐ROI (elongated along the Y‐axis) ensured that streamlines did not diverge toward the lateral aspect of the temporal pole, by selecting the peaks which were predominantly aligned toward the visual cortex (Figs. 1 and 4). Once more, we highlight the fact that MAGNET only selects existing peaks from underlying data and does not create artificial diffusion directions toward V _magnet.

Figure 4.

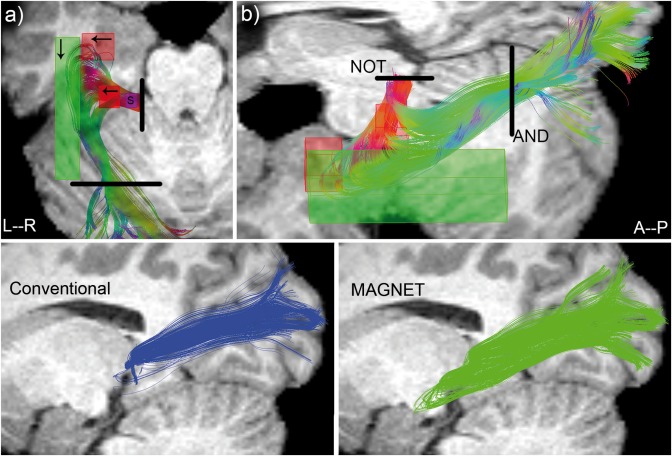
Top: ROIs positioning illustrated for a single subject (S11). Purple box: seed region. Black lines: Boolean ROIs. Arrows indicate the direction of V _magnet. (a) superior view. (b) lateral view (oblique). Bottom: qualitative comparison between deterministic (left, blue) and MAGNET (right, green) reconstruction of Meyer's loop for the same subject. A deeper anterior extent is noticeable with MAGNET (green). [Color figure can be viewed at http://wileyonlinelibrary.com]

WM and GM segmentations were used in our tracking algorithm to provide a better tracking domain (Ω) as opposed to fractional anisotropy (FA)‐based methods where streamline propagation is often prematurely halted in crossing regions [Descoteaux, 2015; Girard et al., 2014; Nimsky et al., 2016; Seunarine and Alexander, 2009; Smith et al., 2012]. Specifically, streamlines were allowed to propagate freely inside the WM, and up to a maximum of five consecutive steps once they reached the GM. The step count was reset if a streamline propagated in GM below this threshold. Deep nuclei were included in the WM masks to ensure propagation of streamlines inside the thalamus (i.e., and the LGN). The final tracking masks were then defined as: $\Omega =\text{WM}+(\text{GM}-\text{CX})$. Tractography parameters were set as follows: step size (s): 1 mm, θ _max: 45°, streamline min/max length: 60/200 mm. Tractography results of both methods were then qualitatively observed for quality assurance.

Comparison between MAGNET and Probabilistic Tractography in a HCP Subject

Diffusion data processing

Recursive calibration of the response function [Tax et al., 2014b] was performed on the HCP data. This response function was used as input to constrained spherical deconvolution (CSD) [Descoteaux et al., 2009; Tournier et al., 2007] to compute the fiber orientation distribution function (fODF) at each voxel of the brain. In this work, we used the efficient implementation publicly available in MRtrix [Tournier et al., 2012] with a maximal spherical harmonics order of 8 and the default parameters. The three main directions of each fODFs were then extracted and given as inputs to MAGNET.

Probabilistic tractography

A WM mask was derived from the T1‐weighted image using FSL‐Fast [Zhang et al., 2001], which was further dilated by 1 voxel. Both MAGNET and probabilistic tractography (IFOD2) [Tournier et al., 2010a] were then initialized using the same positioning for the seed (4 × 6 × 8 mm³) and Boolean ROIs (Fig. 4), as well as with the same tracking parameters aforementioned.

Statistical Analysis

Streamline metrics

To evaluate the anatomical relevance of MAGNET, three bundle‐based metrics were used: (i) the percentage of initial seeds that were rejected, (ii) the mean length and (iii) the volume coverage. These metrics (coupled with quantitative observation) aim a quantifying the spatial extent achieved by MAGNET over the other techniques by generating a significantly lower amount of false positives. A valid streamline was registered if it effectively connected the LGN to the visual cortex once the tractography process was terminated (i.e., met Boolean ROIs requirement illustrated in Fig. 4b). The rejection ratio metric is a compelling measure of algorithmic performance as opposed to the number of streamlines itself and that is directly in line with one aim of the article, which is to reduce the computation burden of current algorithms. The mean length was defined by the integral along a streamline as opposed to the absolute y‐distance. The length (δ) of a streamline is given by: $\delta =s\mathbf{n}$; where s is the step size and n the number of line segments forming the streamline. The mean length μ is then: ${\Sigma }_{\mathrm{i}}({\delta }_{\mathrm{i}})/N$; where N is the number of streamlines forming the OR. Finally, probabilistic streamline occurrence maps were derived from each individual's bundle and group‐normalized to a standard space of reference using non‐linear image registration. The volume coverage (mm³) of the bundles was then computed based on the voxel count of binarized streamline maps. Paired t‐tests were used to compare means across distance metrics for the group analysis. A paired‐sample Wilcoxon signed rank test was used to compare medians between mean lengths as measurements did not follow a normal distribution. A value of P < 0.05 (two‐tailed) was considered statistically significant.

Distance metrics

Conventional metrics reported in the evaluation of Meyer's loop reconstructions often consist of distance measurements depicting the relationship of Meyer's loop with key‐structures of the human brain such as the TP (ML‐TP) [Sherbondy et al., 2008b] and the IH (ML‐IH) of the homotopic ventricle. Most of the existing measurements are done on a two‐dimensional (2D) basis which is the absolute y‐coordinate difference between two anatomical landmarks. However, this measuring technique does not reflect the proximity of Meyer's loop with the TP or IH as MRI images may be tilted due to subject head rotation and inter‐individual anatomy (e.g., angulated loops). For this reason, we performed all of our anatomical measurements using an absolute 3D ruler. Paired t‐tests were used to compare means across distance metrics for the group analysis. A value of P < 0.05 (two‐tailed) was considered statistically significant.

ML‐TP

Measurements were done from the anterior most tip of Meyer's loop to the anterior most tip of the TP (based on the brain‐extracted T1‐weighted image). Distances were relative to head size (e.g., ML‐TP/TP‐OP) [Nowell et al., 2015].

ML‐IH

An isosurface generated from the CSF segmentation maps allowed the precise localization of the IH in 3D. Measurements were done from the anterior most tip of Meyer's loop to the anterior extent of the IH. Distances were relative to head size (e.g., ML‐IH/TP‐OP) [Nowell et al., 2015].

RESULTS

Deterministic Tractography

Figure 5 shows a comparison between MAGNET‐based delineation of Meyer's loop (middle) and histological studies. The left image represent an anatomical model of the OR (green). In the middle, a single subject (S5) MAGNET‐based streamlines shows close agreement with histological studies. Ventricle segmentation (blue) was added to display the relationship between Meyer's loop and the inferior horn. Ventricles are highlighted in blue for qualitative contextual comparison. The right image shows an inferior view of the left hemisphere of an ex vivo human brain [Goga and Ture, 2015]. Klingler dissection of the OR reveals a large sheet of fibers leaving the LGN, forming a particularly deeply projected Meyer's loop.

Figure 5.

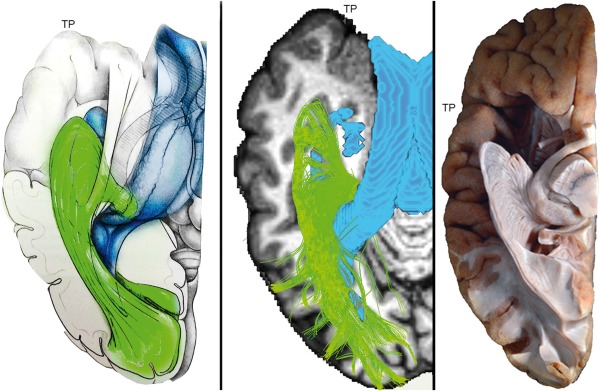
Single subject (S5) MAGNET reconstruction of Meyer's loop shows close agreement with histological studies. Left: Anatomical drawing courtesy of Dr. Patrick Roth. Middle: Streamlines generated using MAGNET. Ventricle segmentation (blue) was added to display the relationship between Meyer's loop and the inferior horn. Colormap: T1‐weighted image. Right: Klingler dissection (ex vivo human brain, inferior view) of the optic radiation reveals a large and angulated anterior extent of Meyer's loop. Adapted from: Goga and Ture [2015], “The anatomy of Meyer's loop revisited: changing the anatomical paradigm of the temporal loop based on evidence from fiber microdissection,” J Neurosurg 2015;122:1253–1262 with permission of Rockwater, Inc. Note that the anatomical drawing omits the direct pathway linking the LGN to the occipital cortex. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 6 qualitatively shows that MAGNET successfully recovered a larger and denser extent of Meyer's loop for all of our 15 child subjects in comparison with Boolean‐based deterministic tractography. For each subject, the final tractography datasets were interactively visualized in context with subject‐specific anatomical T1‐weighted images and ventricle segmentation. Blue bundles were obtained with deterministic streamline tractography using Boolean‐operator as selection objects. Green streamlines indicate the added extension provided by MAGNET, resulting in an improved delineation of Meyer's loop and the OR (i.e., ${\text{OR}}_{\text{magnet}}={\text{OR}}_{\text{green}}\cup {\text{OR}}_{\text{blue}}$).

Figure 6.

MAGNET reconstruction of Meyer's loop (green) shows visual improvements in volume coverage and anterior extent as opposed to deterministic tractography using Boolean operators (blue). Overlapping green streamlines may obscure underlying blue pathways due to an increased bundle density. Visualization was done using the FiberNavigator [Chamberland et al., 2014]. Demo available online at: http://www.youtube.com/watch?v=0m3AoYcl6mA. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 7 illustrates streamline probability maps of the OR averaged over our 15 child subjects for both deterministic and MAGNET methods. Axial slices (Fig. 7a) show representative views where MAGNET (right) effectively increased the streamline density homogeneously through the OR, as opposed to deterministic tractography (left). A larger anterior extent of Meyer's loop using MAGNET was also revealed by those occurrence maps (16.7 mm on average).

Figure 7.

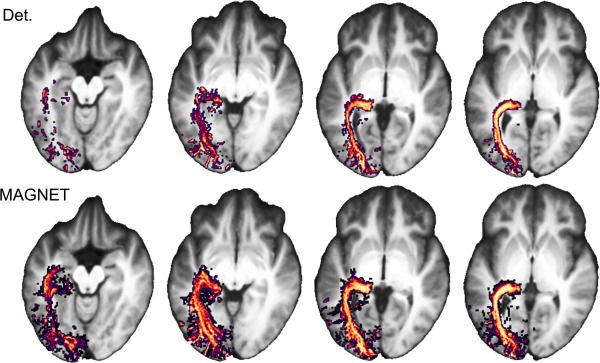
Streamline occurrence maps averaged across 15 child subjects reveals a larger anterior extent (16.7 mm on average) and an increased density coverage of Meyer's loop. Left: Deterministic method; Right: MAGNET. [Color figure can be viewed at http://wileyonlinelibrary.com]

Finally, Figure 8 illustrates an occurrence map of ROIs positioning across subjects. To produce the occurrence maps, all ROIs were binarized, spatially normalized to a standard space of reference using non‐linear image registration and summed at each voxel. Values represent the number of subject having a ROI at this specific brain location. A low value indicates disagreements in the ROI positioning, and is a surrogate of inter‐subject variability. The seed‐ROIs show consistent overlap (Fig. 8a) with a concentrated seed probability for at least 12 subjects. Directional‐ROIs also show coherent overlap across subjects (Fig. 8b) where at least 13 subjects showed consistent directional‐ROI overlap. The mean dimensions and standard deviations were (11 ± 5) × (9 ± 4) × (19 ± 4) mm³ for the medial ROI, (16 ± 5) × (8 ± 2) × (22 ± 5) mm³ for the anterior ROI and (8 ± 1) × (28 ± 9) × (23 ± 7) mm³ for lateral ROI. Size variations of the directional‐ROIs were performed with the aim of maximizing Meyer's loop extent and coverage, while accounting for various loop sizes and shapes of each individual [Goga and Ture, 2015].

Figure 8.

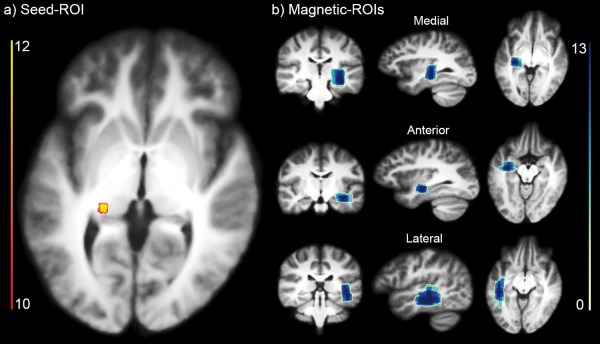
Probability‐map of ROIs positioning shows coherent overlap between different subjects. (a) Seed‐ROI overlap. (b) Directional‐ROIs overlap (medial, anterior, lateral). Scale indicates the amount of subjects sharing an ROI at every voxel. [Color figure can be viewed at http://wileyonlinelibrary.com]

Statistical analysis

Quantitative streamline metrics are summarized in Table 1. A significant decrease in the streamline rejection ratio, and increase in volume coverage and mean length were found for all subjects (Fig. 9). The mean rejection ratio went from 74% ± 11% to 65% ± 11% (P = 1.32E‐05). A 43.7% expansion in volume coverage was also significantly observed (from 4,177 to 6,003 mm³, P = 3.35E‐04). Note that two subjects (S4 and S11) showed a volume increase greater than 100%. Additionally, the mean length of streamlines also increased from 79.22 ± 5.61 cm to 83.04 ± 7.71 cm (P = 3.4E‐03) for a percentage change of 4.8%.

Table 1.

Quantitative evaluation of Meyer's loop tractography using deterministic (Det.) and MAGNET techniques performed on a group of 15 child healthy controls

Subjects	Rejection ratio (%) ***		Volume (mm3) **		Mean length (cm) *
	Det.	MAGNET	Bool	MAGNET	Det.	MAGNET
1	82	70	4,451	6,418	88.38	92.55
2	68	61	4,934	6,037	71.96	76.02
3	83	79	2,926	4,166	86.32	88.57
4	82	70	3,081	9,792	76.22	80.55
5	69	61	4,835	6,168	80.16	90.12
6	68	65	5,036	5,255	75.40	78.75
7	94	72	4,128	5,209	79.20	74.90
8	70	67	3,952	5,997	76.52	78.48
9	70	62	3,715	6,053	77.33	81.54
10	54	50	4,638	5,422	74.60	76.51
11	77	62	2,251	4,919	81.03	86.45
12	87	74	4,100	5,922	91.22	102.21
13	54	37	2,141	4,065	80.71	84.84
14	75	68	7,792	9,226	73.00	77.18
15	83	80	4,672	5,403	76.18	76.91
$\overline{S}$	74	65	4,177	6,003	79.22	83.04
σ	11	11	1,369	1,584	5.61	7.71

Significant differences are observed in rejection ratio, volume, and mean length. $\overline{S}$: mean, σ: standard deviation, *: P < 0.005, **: P < 0.0005, ***: P < 0.00005. Bold font indicates a volume increase >50%.

Figure 9.

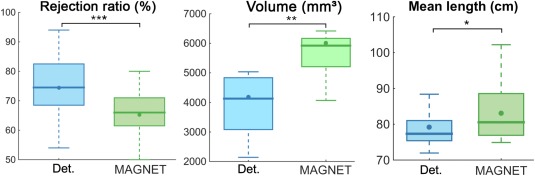
Box plot with 95% confidence interval shows a significant difference between the # of streamlines, volumes and mean lengths of the reconstructed streamlines as measured by deterministic tractography and MAGNET with n = 15, *: P < 0.005, **: P < 0.0005, ***: P < 0.00005 line: median, dot: mean. [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 2 reports decreased 3D distance measurements from Meyer's loop to IH and TP for all subject (Fig. 10). Average measured values for ML‐TP went from 43.7 ± 3.8 mm using Boolean‐based deterministic tractography to 36.0 ± 3.8 mm with MAGNET (P = 4.59E‐07), averaging a 17.4% decrease. A third of the subjects (S1, S3, S5, S9, S11) showed a ML‐TP 3D distance less than 35.0 mm. A 35.6% ML‐IH 3D distance decrease was also measured (from 20.1 ± 4.0 mm to 12.9 ± 4.2 mm, P = 2.36E‐06). Six subjects (S5, S8, S9, S11, S14, S15) also showed absolute ML‐IH 3D distance less than 12.0 mm.

Table 2.

Quantitative evaluation of Meyer's loop tractography using deterministic (Det.) and MAGNET techniques performed on a group of 15 child healthy controls

Subjects	3D ML‐TP (mm)***		3D ML‐IH (mm)***
	Det.	MAGNET	Det.	MAGNET
1	37.7	33.6	23.3	20.8
2	50.7	40.8	27.3	15.8
3	44.1	33.5	22.5	13.0
4	43.0	37.1	19.3	14.7
5	32.9	27.1	13.4	8.3
6	46.9	40.5	19.3	14.1
7	44.0	40.5	24.6	20.9
8	48.7	36.9	20.1	6.3
9	41.7	32.9	15.2	8.1
10	43.0	36.5	19.9	12.7
11	45.7	32.2	20.3	10.3
12	40.2	35.6	18.2	13.8
13	49.1	39.0	23.8	13.7
14	49.1	38.5	20.1	9.5
15	38.2	36.0	13.6	11.8
$\overline{S}$	43.7	36.0	20.1	12.9
σ	5.0	3.8	4.0	4.2

Significant differences are observed in absolute 3D distance measurements. ML, Meyer's loop; TP, temporal pole; IH, inferior horn. ***: P < 0.000005.

Figure 10.

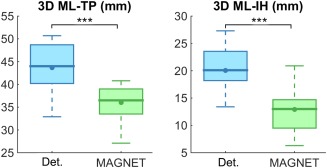
Box plot with 95% confidence interval shows a significant difference between the ML‐TP and ML‐IH 3D absolute distances as measured by deterministic tractography (blue) and MAGNET (green) with n = 15, ***: P < 0.000005, line: median, dot: mean. [Color figure can be viewed at http://wileyonlinelibrary.com]

Probabilistic Tractography

Figure 11 shows a qualitative comparison between MAGNET (green) and MRtrix's probabilistic tractography (red). The top row shows the spatial relationship between the two techniques when using the same amount of seeds (i.e., 3,375). Statistical analysis revealed a volume coverage of 12,086 mm³ (MAGNET) and 10,686 mm³ (MRtrix) and a mean streamline length of 124.98 mm and 120.77 mm, respectively. The streamline rejection ratios of the two methods were 70% (MAGNET) and 91% (MRtrix). In addition, the measured 3D ML‐TP distance for MAGNET was 32.1 and 37.0 mm for the probabilistic method. Finally, the ML‐IH distances were 7.5 and 10.5 mm, respectively. Purple arrow indicates spurious streamlines looping in the target‐ROI for the MRtrix reconstruction.

Figure 11.

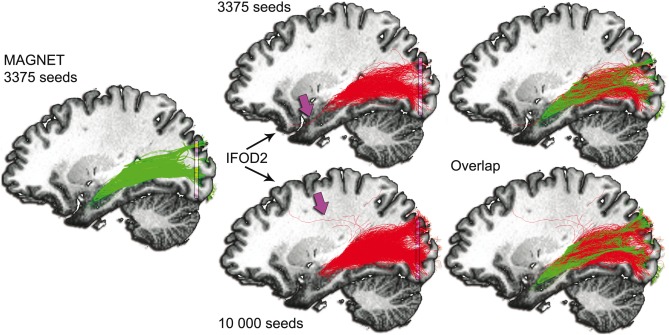
Comparison with probabilistic tractography using MRtrix [Tournier et al., 2012]. Green: MAGNET streamlines. Red: Probabilistic tractography (IFOD2) [Tournier et al., 2010b]. Seeds were initialized from a 4 × 6 × 8 mm³ seed‐ROI located anterolaterally to the LGN. Streamlines were then filtered using a target planar‐ROI located in the occipital lobe (purple, 40 × 2 × 40 mm³). Top row: 3,375 seeds. Bottom row: 10,000 seeds. Purple arrow indicates spurious streamlines looping in the target‐ROI for the MRtrix reconstruction. The last column shows notable agreement between the two techniques. However, the anterior extent of Meyer's loop using probabilistic tractography appears under‐represented, as opposed to MAGNET. [Color figure can be viewed at http://wileyonlinelibrary.com]

Given the high amount of rejected streamlines using MRtrix, an additional comparison between MAGNET and iFOD2 was performed by increasing the amount of initial seeds of the MRtrix pipeline by a factor of approximately 3 (i.e., 10,000 seeds). This increase in number of seeds allowed for a fair comparison between MAGNET and iFOD2 regarding the remaining number of streamlines (i.e., 1,012 vs. 1,005, respectively). Figure 11 (bottom row) demonstrates that Meyer's loop reconstruction remains improved using MAGNET despite increasing the number of seeds for probabilistic tractography. The appearance of spurious streamlines is also denoted by the purple arrow, that is, streamlines looping between the LGN and the target‐ROI. In addition, the streamline rejection ratio of the probabilistic method remained 90%. The volume coverage and mean streamline length for this increased seeding version were 11,035 mm³ and 124.55 mm, respectively. Interestingly, the ML‐TP (38.6 mm) and ML‐IH (12.0 mm) distances also retrogressed.

DISCUSSION

In the present study, we accurately delineated the course of Meyer's loop in 15 healthy child subjects using a novel way of incorporating anatomical priors, generating tractography results that are in line with ex vivo studies. By applying a directional operator to conventional ROIs, streamlines were encouraged to propagate according to our knowledge of Meyer's loop and to back‐project toward the visual cortex once exiting the sharp bend.

Streamline Analysis

In this study, we report absolute 3D ML‐TP measurements in a group of healthy child controls (mean age: 10.2 years) of 36.0 ± 3.8 mm on average (range: 27.1 to 40.8 mm). For comparison purposes, a recent study by Dayan et al. [2015] reported 2D ML‐TP measurements between 36.2 ± 0.7 mm (range: 22.5–45.0 mm) and 38.7 ± 0.7 mm (range: 30.0–47.5 mm) for young males and females, respectively (mean age: 10.8 years). In comparison, ex‐vivo dissections from Ebeling and Reulen [1988] reported an average ML‐TP distance of 27 ± 3.5 mm (range: 22–37 mm). Similarly, Sherbondy et al. [2008b] reported a 2D average ML‐TP distance of 28 ± 3.0 mm (range: 24–34 mm) on a database of 8 young adults (mean age: 26.9 years). For the HCP dataset, we report a 3D ML‐TP distance of 32.1 mm, which fall in the range values reported by the study of Kammen et al. [2015], also performed using the HCP database (19.7–43.4 mm, mean: 30.7 ± 4.0 mm).

Generally speaking, our results are in line with previous work and anatomically‐based predictions considering the average age of our subjects. The resulting streamlines were highly consistent with anatomical descriptions of the Meyer's loop as each bundle included a large and dense anterior extent of the inferior portion of the optic radiation. Yet, we acknowledge that some reconstructions were achieved at the expense of less accurate termination points in the visual cortex. It is important to recall that these extrastriate projections are typically not part of the optic radiations (predominantly located in the superior aspect of the bundles shown in Fig. 6). We believe that two factors may have induced such connectivity patterns. First, the posterior inclusion‐ROI located at the sagittal stratum level could have been place more posteriorly, closer to the occipital cortex. We believe that streamlines reaching this waypoint freely projected to the extrastriate cortex afterward. Next, the initial seed placement may have encompassed not only the LGN, but also the pulvinar region, as it is challenging to accurately identify the exact boundary between these two nuclei. It is generally believed that the pulvinar connects to the extrastriate cortex [Leh et al., 2007; Rushworth et al., 2006] and to regions of higher visual processing (e.g., medial occipital gyrus involved in visuospatial processing [Whittingstall et al., 2014]). However, Meyer's loop is part of the inferior bundle and these projections are predominantly happening superiorly. For these reason, we believe our Meyer's loop reconstruction remain well‐founded.

Across the group, S5 (Fig. 5, middle) showed the smallest ML‐TP 3D distance with 27.1 mm. When measured from the LGN, streamlines forming the loop of S5 extended 35.2 mm anteriorly before initiating their course back to the OP. Importantly, visual inspection confirmed that the delineated Meyer's loop of this subject was formed of a continuous sheet of streamlines, and that our distance measurements were not affected by isolated thread of spurious streamlines. In addition, for some subjects, we found that while ML‐TP measurements where comparable between Boolean‐based deterministic tractography and MAGNET (e.g., ΔML‐TP <6 mm), the density and completeness of Meyer's loop was still underachieved using a deterministic approach (Fig. 6, S1, S4, S5, S7, S12, and S15). A 50% volume increase was also observed in a third of our subjects (Table 1, bold font). This volume increase is essentially the result of a deeper anterior projection of Meyer's loop, alongside with an increase in the coverage of the sheet‐like part of the bundle (Fig. 3, right).

We emphasize that that quantitative metrics are only useful to the extent that they support our knowledge of the anatomical architecture of the brain. Most importantly, major intracranial and ventricular volume changes are occurring during the maturation of the brain, especially during the first 15 years of development [Sgouros et al., 1999; Xenos et al., 2002]. These important changes certainly induce a significant variability in conventional distance measurements (i.e., ML‐TP and ML‐IH). Subsequently, a shorter average ML‐TP or ML‐IH distance does not imply that a technique is valid, or should be prioritize over another, as the distance between ML‐TP and ML‐IH can be differ according to technique employed to measure it. That is, our current data also underscores the problems arising with the validation of Meyer's loop tractography. A possible solution to further validate the method would imply the blunt dissections of a post‐mortem brain combined with the acquisition of high‐resolution dMRI data. Subsequently, our group‐average probability map illustrated in Figure 7 also represents a probabilistic atlas of the OR in children that can be used for validation.

Inter‐Subject Variability of Meyer's Loop

The morphology of the brain substantially differs between individuals [Gu and Kanai, 2014; Mueller et al., 2013]. Importantly, Meyer's loop's exceptional inter‐individual variation [Ebeling and Reulen, 1988] also means it is a difficult task to take an individual's result and compare it with population metrics. Dissection studies recently reported a large inter‐subject variability of the OR, mainly disclosing a significant variation in the anterior extension and angulation of Meyer's loop [Ebeling and Reulen, 1988; Goga and Ture, 2015]. These findings suggest that subject‐to‐subject anatomical variability can account for differences in Meyer's loop's tractography. In this study, our mean streamline length measurements show that the smallest OR was 74.90 cm long while the largest one was 102.21 cm. This 36.5% increase in length is consistent with the observed large inter‐subject structural variability of Meyer's loop. This variability may be one source of tractography failure, especially when propagating conventional tracking parameters and ROIs across different subjects (e.g., template‐based analysis [Thiebaut de Schotten et al., 2011]). A key goal in the future will be to qualitatively and quantitatively validate Meyer's loop tractography against its known anatomy using ex vivo dissection [Lilja and Nilsson, 2015; Goga and Ture, 2015].

Inference of Connectivity

Streamlines are recovered by propagating through a field of DTs, ODFs, fiber ODFs, or any other pre‐computed set of directions. However, how to numerically integrate over them remains an open question. Many families of algorithms aim to propagate through these sets of directions, such as deterministic, probabilistic, geodesic, and global tractography algorithms. Conventional streamline tractography algorithms based on dMRI infer connectivity by following directions which are maximally aligned at every voxel. This rule has ever been the definition of the probability of connectivity, with the difference in current and next orientation being defined as uncertainty in connectivity. However, our experiments demonstrate that in regions where multiple fiber pathways interdigitate (e.g., temporal lobe), this heuristic is insufficient and does not necessarily reflect the underlying human brain architecture. As a result, deterministic tractography methods have been shown to under‐estimate of the anterior extent of Meyer's loop [Lilja et al., 2014, 2015].

To capture the anterior extent of Meyer's loop, studies have largely relied on passive waypoints [Clatworthy et al., 2010; Hofer et al., 2010; Yogarajah et al., 2009; Winston et al., 2011] coupled with the generation of a large number of candidate streamlines. However, even a precise positioning of Boolean operators by experts may return a void selection of streamlines as these passive ROIs have no influence on the underlying tractography algorithm. A multitude of factor will indeed dictate if tractography is allowed to propagate inside these manually positioned Boolean ROIs (e.g., seed sparsity and positioning, threshold of tracking domain, choice of tracking parameters).

Conversely, it is generally assumed that probabilistic tractography can overcome this problem by exploring a broader range of possible connections. However, unless probabilistic tractography algorithms are initialized with large angular threshold, streamline generation still obey to Eq. (1) with the difference in current and next orientation being defined as uncertainty in connectivity. For example, fODF sampling methods can be performed on the fly by restricting directions within a certain angular threshold, associated with the current direction of tracking [Tournier et al., 2012]. As a result, depending on the underlying diffusion data, a large amount of streamlines may still ends up propagating toward an undesired direction because of the restriction applied to the peak selection (e.g., streamlines entering the TP instead of Meyer's loop when seeded from the LGN, Figs. 1 and 3a). This was further confirmed by comparing MAGNET with probabilistic tractography. When looking at the rejection ratio computed for the HCP data comparison, 30% of the initial seeds contributed to the reconstruction of final bundle using MAGNET, as opposed to approximately 10% to for both probabilistic experiments. This implies that differences observed in MAGNET reconstructions are not only the results of a more computationally efficient method that requires fewer seeded streamlines to recover the same anatomical extent, but also a significant advance in Meyer's loop tractography.

Other techniques have explored the possibility to infer brain connectivity using global approaches (i.e., global tractography) [Neher et al., 2012; O'Donnell et al., 2002; Reisert et al., 2011], which implicitly consider the set of all possible pathways, with the most likely pathway being defined as that which maximizes the similarity of orientation of neighboring tensors. Generally, these techniques are computationally demanding as they yield large sets of streamlines to be handled in post‐processing, but can be made more practical by optimization and robust implementation. Yet, streamline tractography can still outperform global tracking in handling crossing regions in vivo [Neher et al., 2015].

In contrast, our experiments suggest that MAGNET enhance the reconstruction of Meyer's loop by injecting anatomical prior to the tractography algorithm and by employing a low amount of strategically placed ROIs. Our choice of directional‐ROIs positioning was based on the following, straightforward hypothesis: anatomically, the radiations form a sharp bend in the temporal pole, respectively looping in a medial, anterior, and then lateral fashion [Ebeling and Reulen, 1988]. We showed that selecting directional‐ROIs representing each of these spatial components benefits Meyer's loop delineation. MAGNET does not generate artificial directions but instead, selects diffusion orientations present in the underlying data. Additionally, integrating priors is most commonly done at multiple levels during tractography (e.g., tracking in WM masks, stopping in the GM, refraining from entering the ventricles, starting at the interface between WM/GM, adding ROIs to select streamlines) [Girard et al., 2014; Kasenburg et al., 2016; Smith et al., 2012]. Connectomes built from pairs of ROIs and atlases also represent an integration of prior knowledge where connectivity is directly imposed between cortical parcels. Thereupon, MAGNET can be perceived as adding very specific orientational priors to tracking existing algorithms (e.g., deterministic or probabilistic).

Characteristics of MAGNET

An important point to stress out here is that part of the procedure presented in this work relies upon the expertise of the user. Visual inspection and quality assurance of tractography data are important procedures that should always be carried out. In addition, it can be debated that the use of larger magnetic‐ROIs may reduce problems related to precise placement of these ROIs, as they would encompass the desired anatomical areas. For instance, careful attention to the position of the anterior magnetic‐ROI should be elicited to the future users. As mentioned in the Results section, it is important to progressively glide the ROI anteriorly, to avoid a premature bend of streamlines toward Meyer's loop. In this regard, we believe that MAGNET is intuitive to the user as it relies on existing ROI‐based techniques and ROI positioning is facilitated with 3D interactive navigation. Yet, further inter‐user agreement evaluation study is needed, similarly done for other software tools [Böttger et al., 2011; Dini et al., 2013].

Another limitation of the current implementation is that the directional operator was only applied to sizeable cubic ROIs. A straightforward extension of MAGNET is to automatically define ROIs based on a binary segmentation mask of a particular anatomical structure. Therefore, an extension to conventional Boolean‐based extraction methods, such as the white matter query language (WMQL) [Wassermann et al., 2016], would allow the user to define a set of rules for the extraction of a fascicle using directional‐ROIs, in the form of:if inside(amygdala):

$$V_{\text{magnet}}=v\left(-1, 0, 0\right);$$

$$V_{\text{next}}={\text{argmin}}_{\mathrm{k}}\hspace{0.17em}\alpha \left(V_{\text{magnet}},V_{\mathrm{k}}\right);.$$

In this example, the resulting operator suggests a left turn (i.e., −X) for any fascicle entering the amygdala, if supported by the data. Note that the application of directional‐ROIs inside anatomical regions can still conveniently be paired with a mixture of conventional Boolean operators between cortical regions. In this study, tractography was performed in real‐time [Chamberland et al., 2014]. The close inspection of streamline propagation allowed the manual positioning of all ROIs in an interactive and subject‐specific manner. An experienced user took on average 10 minutes to extract Meyer's loop for a single subject. The steps performed included positioning and sizing the seed‐ROI, defining exclusion planes, positioning magnetic‐ROIs, performing tractography and finally, extracting fascicle metrics (e.g., 3D distance measurements). As the proposed technique evolves to other bundles, one can imagine an atlas of orientations priors that would be used in future offline tracking algorithms.

A video tutorial demonstrating the interactive use of MAGNET is available online1 and the source‐code of the technique is open to all contributors2. Finally, since MAGNET operates on a set of peaks, we also demonstrated that our approach can be used in association with any local reconstruction model other that outputs multiple directions per voxel (e.g., fODFs and multitensor models).

Neurosurgical Perspective

It has been recently shown that multipeak tractography gives rise to a larger number of false‐positive and false‐negative connections [Cote et al., 2013]. The use of real‐time interactive tools have facilitated the querying and quality assurance in the recent years [Chamberland et al., 2015; Tax et al., 2015] but the translation toward routine application remains a continuous process. As of today, tractography has been shown valuable for surgical planning, and neurosurgeons and radiologists are mostly convinced of the importance of tractography for neurosurgical planning [Duffau, 2005; Leclercq et al., 2010; Nimsky et al., 2016].

The method proposed in this work is likely to change pre‐operative planning approaches. As mentioned before, a complete delineation of the anterior extension of Meyer's loop is of great importance, especially for neurosurgeons who want to prevent visual deficits in patients who undergo temporal lobe surgery resection. Defining accurate boundaries is critical in surgery targeting medial, occipital, and temporal regions, or when the course of the OR is affected by a space‐occupying lesion (e.g., tumor). In future work, we plan to evaluate MAGNET on non‐healthy controls such as tumor and epilepsy patients to see how directional‐ROIs can help facilitating the delineation of Meyer's loop using pre and post‐operative data. With the advent of personalized‐medicine [Wang et al., 2015], we believe that such a tailored approach may improve decision making, especially in a surgical planning context. Nevertheless, the virtual fiber dissection results are subject to the individual skills and anatomy knowledge of the analyst.

On a final note, the bundle of interest of this study (OR) was chosen based on its relevance for neurosurgical planning. We expect that other fiber bundles not studied here can be similarly be delineated using the proposed method, by virtue of addressing the kissing/crossing problem. In particular, potential applications of MAGNET also include the delineation of other controversial fascicles of the human brain such as the vertical occipital fasciculus (VOT) [Takemura et al., 2015; Yeatman et al., 2014], the frontal aslant tract (FAT) [Catani et al., 2013] and the superior fronto‐occipital fasciculus (sFOF) [Forkel et al., 2014; Meola et al., 2015]. Like other streamline tractography methods, our magnetic‐ROI approach can also be used in combination with existing streamline evaluation techniques [Daducci et al., 2015; Pestilli et al., 2014; Smith et al., 2013; Takemura et al., 2016; Tax et al., 2014a].

CONCLUSION

In this work, we introduced a new ROI‐based mechanism to encode our knowledge of the human brain anatomy in tractography studies. We showed that MAGNET can accurately reconstruct Meyer's loop in all of our subjects. It effectively improved streamline coverage, and significantly reduced ML‐TP and ML‐IH distances, crucial information for preoperative planning of temporal lobe surgery. We provide a convenient 3D interactive tool for the virtual dissection of the temporal lobe in individuals. In future work, we plan to apply the magnetic operator inside automatically segmented anatomical structures (e.g., parcels) and to apply MAGNET to the delineation of other WM pathways. This could in turn reveal new anatomical details, currently not achievable with conventional tracking algorithms.

Supporting information

Supporting Information Movie 1.