Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Jan 25;33(7):1629–1638. doi: 10.1021/acs.langmuir.6b04322

Mechanical History Dependence in Carbon Black Suspensions for Flow Batteries: A Rheo-Impedance Study

Aditya Narayanan 1, Frieder Mugele 1, Michael H G Duits 1,✉
PMCID: PMC5333906  PMID: 28122184

Abstract

graphic file with name la-2016-04322n_0014.jpg

We studied the effects of shear and its history on suspensions of carbon black (CB) in lithium ion battery electrolyte via simultaneous rheometry and electrical impedance spectroscopy. Ketjen black (KB) suspensions showed shear thinning and rheopexy and exhibited a yield stress. Shear step experiments revealed a two time scale response. The immediate effect of decreasing the shear rate is an increase in both viscosity and electronic conductivity. In a much slower secondary response, both quantities change in the opposite direction, leading to a reversal of the initial change in the conductivity. Stepwise increases in the shear rate lead to similar responses in the opposite direction. This remarkable behavior is consistent with a picture in which agglomerating KB particles can stick directly on contact, forming open structures, and then slowly interpenetrate and densify. The fact that spherical CB particles show the opposite slow response suggests that the fractal structure of the KB primary units plays an important role. A theoretical scheme was used to analyze the shear and time-dependent viscosity and conductivity. Describing the agglomerates as effective hard spheres with a fractal architecture and using an effective medium approximation for the conductivity, we found the changes in the derived suspension structure to be in agreement with our qualitative mechanistic picture. This behavior of KB in flow has consequences for the properties of the gel network that is formed immediately after the cessation of shear: both the yield stress and the electronic conductivity increase with the previously applied shear rate. Our findings thus have clear implications for the operation and filling strategies of semisolid flow batteries.

1. Introduction

In light of climate change, recent years have seen a rapid adoption of renewable energy production.1 Because of their inherently variable nature, renewables have placed considerable strain on the power grid which must match energy production to demand. A possible solution to this problem is to store energy in batteries.2 Semisolid flow batteries (SSFBs), a recently developed configuration,3−10 are considered to be especially promising for such applications. SSFBs use two fluid electrodes, an anolyte and a catholyte, in place of traditional solid electrodes. The use of fluid electrodes decouples the energy of a SSFB, which depends on the size of storage tanks, from its power, which depends on the size of the reactor. Additionally, SSFBs may allow easy lifecycle management through the modification or replacement of their fluid electrodes.

SSFB electrodes are mixtures of conductive nanoparticles (CNPs) and electrochemically active particles (EAPs) dispersed in an electrolyte solution. In most SSFBs, the EAPs intercalate and deintercalate lithium whereas the CNPs wire the EAPs to the current collectors. The continuous phase, a mixture of linear and cyclic carbonate solvents with a high concentration of dissolved lithium salt, provides an ion-conducting medium and a source of lithium ions. The CNPs used in SSFBs are typically superconductive carbon blacks such as Ketjen black (KB) or Timcal SuperP.3,11 These carbon blacks are submicrometer-sized permanently fused aggregates of hollow spherical subunits.12,13

The self-assembly of the CNPs, which depends on their morphology, colloidal interactions, and shear conditions, is of crucial importance to both the electrical and mechanical performance of SSFBs. For colloidal carbon black (CB) units in SSFB media,3,5,11,14 the van der Waals attractions should be dominant because their electrostatic interactions are strongly screened.11,15 As a result, CB particles tend to form large cohesive structures. At rest (assuming a high enough concentration), they form a space-filling network that can conduct electrons and suspend EAPs against gravity through yield stress.3,11 In flow (e.g., pumping and stirring), this network will be broken down into agglomerates. This leads to shear thinning and much lower electronic conductivity.3,11 Henceforth in this article we differentiate a permanently fused primary aggregate from a reversibly flocculated cluster of these particles, which we will call an agglomerate.

Given the novelty of SSFBs, significant developments are still required to optimize their performance. Mechanical protocols should be a part of this optimization: fluids containing adhesive particles generally produce nonequilibrium structures that can depend on mechanical history.16−19 In this article, we focus on how shear and its history influence the electrical and rheological properties of CB suspensions in an SSFB solvent.

Although the case of CB in an SSFB solvent is rather new,3,11,15 we anticipate that some existing insights into the behavior of CB suspensions will also be applicable to our system. Suspensions of reversibly agglomerating colloids, including those of CB, are known to be strongly shear- and history-sensitive.11,20−25 The storage modulus and yield stress of CB gels in oils have even been found to depend predictably on the preshear used to prepare them.23,24 In flow, the viscosity of agglomerating colloidal suspensions typically decreases in time after an increase in shear stress or rate, a well-studied property known as thixotropy.21,22 The opposite effect, a temporal increase in viscosity after an increase in shear stress or rate, known as rheopexy or antithixotropy, is much less common but has been observed in CB suspensions.23,26−28 On a mechanistic level, rheopexy is thought to be caused by flow-induced flocculation26 or by the ability of fractal structures to rearrange (when shear is lowered) into more densified agglomerates.23,24

The electrical impedance of CB suspensions in shear flow has been studied much less often, but also here a dependence on the shear rate was found.11,14,29 The study of the suspension’s rheology and impedance in conjunction capitalizes on the tight connection of both behaviors to the (dynamic) microstructure of the agglomerates, which can be difficult to measure with optical or scattering techniques, especially for concentrated suspensions.

The present study makes use of a home-built rheo-impedance setup to characterize the influence of the mechanical history on both rheological and electrical properties. This approach addresses both the practical aspect of optimizing SSFB performance via mechanical protocols and the more fundamental aspect of understanding the underlying processes. Both stepwise changes in shear rate and prolonged shear are explored to identify transient responses. The cessation of shear is included as a special case, where the system is left with only Brownian forces to possibly reorganize its structure. Our analysis of the structural changes at the microscale is supported by a theoretical model in which the viscosity of effective hard-sphere agglomerates30 is combined with an effective medium theory for the conductivity.31

2. Materials and Methods

2.1. Suspension Preparation

Ethylene carbonate (EC) and dimethyl carbonate (DMC) were obtained from Sigma-Aldrich (anhydrous, 99%+ purity). Binary mixtures of EC and DMC were 1:1 by mass. LiPF6 was purchased from Alfa Aesar (98% purity). Ketjen black EC 600JD powder (KB) was obtained from AkzoNobel (The Netherlands). Thermax N990 powder was donated by Cancarb. SEM samples were dispersed in acetone, dried on silica wafers, and then imaged. All other sample preparations and experiments were carried out in an MBraun argon-filled glovebox (O2, H2O below 5 ppm).

The two types of CB used in this study differ in morphology (see also Figure 8): for N990, the unit particles are more or less compact spheres, whereas for KB, they are more fractal-like as a result of fusion between spherical subunits. In this article, we designate the KB units as aggregates, whereas clusters formed via reversible flocculation are called agglomerates. All suspensions of KB (of key interest for this work) were prepared at a concentration of 1% by weight (wf = 0.01). Because the KB aggregates are highly porous and their subunits are hollow shells, the occupied volume fraction in suspension is much higher than wf. A crude estimate can be obtained by multiplying wf by the ratio of the density of graphite (2267 kg/m3) to the tap density of KB (100 kg/m3), giving a volume fraction of 23%. Particles were first wetted by the pure (binary) solvent in polypropylene containers. After 8 h, LiPF6 salt was added via a concentrated solution to bring its concentration to 1 M (viscosity 4 mPa·s32). After hand shaking, at least 8 h was allowed to let the particles equilibrate. Samples were then homogenized by rotor stator mixing (Ultraturrax) at 15 000 rpm for 2 min and subsequently loaded into the rheometer.

Figure 8.

Figure 8

Open in a new tab

Morphology of KB (left) and N990 (right). Particles are agglomerated by drying.

In exploratory experiments, we found similar trends as reported in this article. However, the quantitative behavior of KB suspensions in SSFB media appeared to be sensitive to preparation protocols. This could be related to the poor wetting by the solvents, the sensitivity of the media,15 and the strong dependence of macroscopic properties on the volume fraction (S.I. Figure S1 and ref (11)). Thus, for KB we performed all reported measurements (except those in Figure 4) on the same sample.

Figure 4.

Figure 4

Open in a new tab

Intrinsic flow curve of agglomerates formed at different indicated shear rates (lines to guide the eye). The data point indicated by (x) represents the viscosity at 10 000 s–1 after prolonged shearing.

2.2. Rheoimpedance Measurements

Parallel rheological and electrical measurements on CB suspensions were performed on a stress-controlled Haake Rheostress RS600 rheometer with a home-built adaptation for electrical impedance spectroscopy (EIS) measurements (Figure 1). A 60-mm-diameter parallel plate geometry was designed with both stainless steel plates also acting as electrodes. The rheometer rotates and measures torques on the upper geometry. To allow a frictionless low-noise electrical connection to the rotating plate, a mercury-based solvent trap was designed. A glass disk was used to electrically isolate the lower plate from the rheometer body. Because of its high thermal conductivity, glass also allows accurate temperature control (at 25 °C for all experiments). Argon was used to drive the rheometer air bearing.

Figure 1.

Figure 1

Open in a new tab

Schematic of rheo-impedance setup. (Gray) Measuring geometry with stationary lower and rotating upper plates. (Light gray) Mercury solvent trap. (Red) Sample. (Blue) Isolating dielectric. (Brown) Polypropylene body. (White) Cover.

EIS was performed using a four-terminal configuration. The top plate was excited by a sinusoidal voltage, and the bottom was connected to the virtual ground of a transimpedance preamplifier (HF2TA, Zurich Instruments). A buffer preamplifier (HF2CA, Zurich Instruments) was used to measure the potential difference between the plates. An impedance spectroscope (HF2IS, Zurich Instruments) was used to extract the complex impedance from the current and voltage signals. AC frequency sweeps were performed from 10 to 100 MHz (total time 550 s) with a maximum applied voltage amplitude of ∼100 mV, which was within the linear response range of the samples. The frequency-dependent impedance of the empty measurement setup was calibrated out using the open short technique. Custom LabVIEW programs were used to synchronize rheological and electrical measurements.

Rheo-impedance experiments were performed with a plate–plate gap of 250 μm. Suspensions of CB have been reported to exhibit nonideal rheometric behaviors such as wall slip, shear banding,23 and vorticity alignment of flocs,33 especially during start up and in low-shear-rate regimes. We avoided these effects in shear flow experiments by employing relatively high shear rates, where the samples behave as low-viscosity liquids. To obtain a reproducible starting state (Figure 2), the suspensions were presheared at 10 000 s–1 for 200 s, after which the shear rate was slowly ramped down to 316 s–1 and then held for 200 s. Step changes in shear rate were followed by a dwell time (τ) that was different per type of experiment.

Figure 2.

Figure 2

Open in a new tab

Schematic of the general experimental protocol for preshearing and subsequent measurements of the electrical impedance and yield stress.

Measurements of the impedance during shear were made at a frequency of 0.5 Hz to allow real-time monitoring of the electronic resistance (Section 2.3). Measurements after the cessation of shear were made after a 200 s rest period. Impedance spectra were measured before the yield stress. In the measurement of the latter, the shear stress was ramped up at 62 s per stress decade while measuring the strain. The log(strain) versus log(stress) curve was fitted with two straight lines, and the stress at the intersection was taken to be the yield stress.34

2.3. Impedance Analysis

Because flow battery electrodes contain conductive carbon in an electrolyte solution, they are capable of both ionic and electronic conduction. To monitor the KB network electrically, it is necessary to separate these contributions. This is done using AC impedance spectroscopy. The KB suspensions have two ionic charge carriers (Li+, PF6–) and an electron-conducting carbon network. During measurements, the sample is in contact with electrodes that are ionically blocking but electronically reversible. Ignoring geometric capacitance, the response of this system can be simplified35 to that of an ionic resistor and an ionic double layer capacitor, both in parallel to the electronic resistance of the carbon black network. Thus, the high-frequency real impedance gives us a parallel combination of both resistances whereas the low-frequency real impedance gives the electronic resistance. The data in Figure 3 illustrate that the behavior of our KB suspension at rest can be analyzed with this approach. The very high frequencies (Figure 3 insets) are affected by uncompensated parasitics.36

Figure 3.

Figure 3

Open in a new tab

Nyquist with equivalent circuit (left) and Bode (right) plots of the impedance response of the KB suspension. The insets show a zoom around high-frequency data (>10 kHz). Filled symbols: KB at rest. Open symbols: KB under 1000 s–1 shear (only two frequencies measured). The 50 Hz points have been removed.

Under strong shear, it is unlikely to have a continuous percolated network. (For low shear rates, dynamic percolation may be possible.37) However, a measurement at two frequencies on the same KB suspension, but now under high shear (open symbols of Figure 3), shows that the low-frequency real impedance is finite whereas the imaginary impedance is close to zero. This implies that the sheared suspension has a finite electronic resistance.35 Our measurements on other carbon black samples show that the overall impedance response under shear is similar in shape to that at rest (Figure S2 in S.I.), justifying our use of a single low frequency to probe the electronic resistance. Additionally, this is in qualitative agreement with earlier findings on carbon black filled polymers, which are known to conduct electrons via two mechanisms. (At high volume fractions, when the network is continuous, conduction is graphitic.38 The resistance is still determined by constriction and ohmic contributions.39) When the network is broken, the electrons can tunnel across small gaps (<10 nm) modulated by thermal voltage fluctuations.11,12,38,39 For larger gaps, however, the intrinsic electronic conductivity of the medium dominates.39

3. Results and Discussion

3.1. Intrinsic Flow Curves

We first consider the mechanical properties of our material in flow. To characterize KB, we measured a series of so-called “intrinsic” flow curves23 where each of the curves corresponds to a unique preshear rate (PSR) that was maintained for 1000 s in order to reach a steady state. Data points within each curve were then obtained by stepping from the PSR to the shear rate of interest and recording the viscosity quickly. (As shown later, the viscosity almost immediately reached an extremum; it was this extremum that was recorded.) All intrinsic flow curves (Figure 4) are strongly shear-thinning, as expected for agglomerating suspensions.27,30,40−43

Their dependence on the PSR reveals interesting information that is specific to our KB system. First, the three curves with the highest PSR coincide, indicating that a PSR of 1000 s–1 or more brings the material to a similar microstructural state. This suggests that the agglomerates are largely broken down under these conditions: generally for agglomerating systems a stronger shear flow causes more breakup. After prolonged (2000 s) shearing at the highest accessible shear rate of 10 000 s–1 (from an arbitrary starting state), the sample showed a similar viscosity to the corresponding points of the intrinsic flow curves for PSR ≥ 1000 s–1: this again suggests that the agglomerates are largely broken down (i.e., into primary aggregates) by prolonged shear above 1000 s–1. Second, it becomes clear that in order to reach a steady state even the highest preshears need to be maintained for a significant duration, i.e., much longer than the data acquisition time (of O(1 s)) of the intrinsic flow curve. This is shown by the curves with PSR ≤ 316 s–1, for which the viscosities are different from the curves at higher PSRs, even for measurement shear rates ≥1000 s–1. Third, the fact that the intrinsic flow curves with smaller PSRs have lower viscosities is remarkable. In earlier suggested mechanistic pictures,30 where shear leads to both breakdown and the densification of agglomerates into smaller units, a lower PSRs should have resulted in higher viscosities, which is the opposite of what we observe. This points to a mechanism that can enhance the viscosity via agglomerate breakup in KB suspensions. The remarkable fact that the lowest possible viscosity (21 mPa·s) for our system was measured after the smallest preshear rate (100 s–1) also points in this direction.

3.2. Transient Behavior

To examine this intriguing behavior, we performed experiments in which the material’s response to shear rate steps was followed over time.21 Both the viscosity and the electronic resistance (Section 2.3) were measured in parallel. All steps in the shear rate were taken from the same reference condition, for which we chose 316 s–1, based on Figure 4. Some typical results of these measurements are found in Figure 5, where both steps up (to 562 and 1000 s–1) and down (to 177 and 100 s–1) are illustrated.

Figure 5.

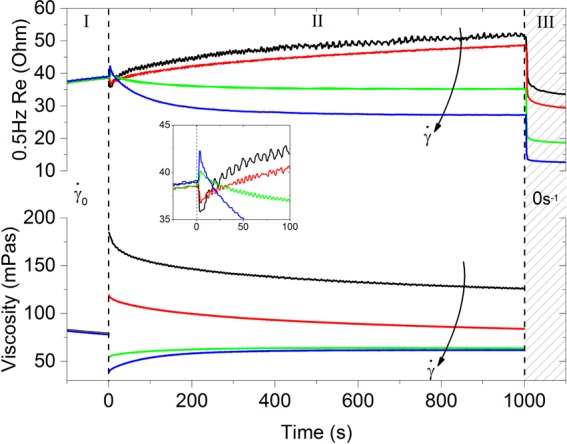
Figure 5

Open in a new tab

Evolution of viscosity and low-frequency real impedance of the KB suspension after a shear rate step from 316 to 100 (black), 177 (red), 562 (green), and 1000 s–1 (blue). The inset is a close-up view of the response of the electronic resistance around the step.

Both the viscosity and the electronic resistance show a two-staged response. The initial response, a large increase in viscosity and a small decrease in electronic resistance for a step down in rate (transition from region I to region II) is fast, with a time scale of O(1 s). It is not resolvable, considering the short time that the rheometer needs to step the shear rate and the low frequency of the impedance measurement. For the steps to higher shear rates, the opposite trends were observed. The secondary response (region II) is significantly slower O (100–1000 s). The slow changes in the viscosity and resistance appear to have similar time scales, suggesting that they both probe changes in the microstructure of the KB.

Remarkably, for both signals, the secondary response opposes the direction of the initial response. For the viscosity, this amounts to a relatively small correction (rheopexy, shear thinning), but for the electronic resistance, the secondary effect is strong and causes a reversal of the overall effect. The shape of the decays of the viscosity and electronic resistance is well described by stretched exponentials; such behavior has been found for the viscosity of thixotropic systems.21 The opposing change in the second stage is found irrespective of whether the shear rate is increased or decreased. Yet the direction in which the shear rate is changed still determines the sign of all changes. This is consistent with a picture in which all structural transitions can be reversed via the shear rate.

3.3. Mechanistic Picture

We interpret our findings in Figures 4 and 5 with a picture in which KB reversibly agglomerates via two distinct mechanisms (each with its own time scale and influence on the microstructure). Both the viscosity and electronic resistance depend on the concentration and morphology of the agglomerates, but in different ways.

Flow curves of weakly agglomerating suspensions have been successfully described by modeling the agglomerates along with their immobilized solvent as effective hard spheres.40,44 Shear thinning is then explained via a lowering of the effective hard sphere volume fraction. As the shear rate is increased, higher shear stress causes the agglomerates to break down into smaller structures. Because of the fractal build up, the latter then occupy less total volume (Figure 6). Although (strictly speaking) perfectly fractal scaling is rarely observed, it is has often been found that the structure of agglomerates can be fairly well described with this concept.30,40,43,44

Figure 6.

Figure 6

Open in a new tab

Cartoon of fractal agglomeration and imperfect percolation (left) in shear flow.

To understand the (changes in) electronic conductivity of the suspension under flow, we need to take into account the formation of (transient) pathways with missing links (Figure 6, left). As such gaps dominate the resistance (Section 2.3), the macroscopic electronic resistance of the sheared suspension should be determined by the concentration of agglomerates and their typical distance of closest approach.

We now proceed to a qualitative interpretation of Figure 5, focusing first on the instant process. The jumps in viscosity and electronic resistance may be explained by agglomeration due to lower shear forces when the rate is stepped down. The immediate sticking between colliding fractal entities leads to more open agglomerates that enclose (and hence immobilize) more solvent, causing the hydrodynamic volume fraction and thus the suspension viscosity to increase. (Note: if the shear step were small, then a binary collision would lead to an unstable agglomerate, which would be quickly eroded.) The same agglomerate restructuring also changes the ensemble of interrupted conductive pathways. The formation of fewer but larger agglomerates after a step down in shear rate diminishes both the average gap between agglomerates and the number of gaps an electron needs to traverse along a conductive path. Both of these effects should lower the electronic resistance. However, they are counteracted by a decrease in the number of electronic pathways. This could explain why the overall decrease in resistance is small.

As shear is continued after the step down in rate, the population of agglomerates is rejuvenated continually: bonds between KB units are incessantly broken and formed by shear. This provides a means for the agglomerates to overcome kinetic barriers and discover more stable states. As the unit particles (and their agglomerates) are (roughly) fractal in nature, the randomness of collisions will occasionally cause two particles to interpenetrate (Figure 7). Because of the enhanced contact area and generally lower aspect ratio, these agglomerates will be more stable (compared to those formed by peripheral contacts). However, if the shear stress gets high enough, they can be torn apart again, making the process reversible. Clearly, a consolidated interpenetration should lead to an overall densification of agglomerates, leading to a lower hydrodynamic volume fraction and hence a reduced viscosity. It also follows from mass conservation that the average gap between agglomerates will increase in this scenario. Additionally, the number of conduction pathways will decrease. Both effects should lead to the observed increase in the electronic resistance (after a stepdown in shear rate).

Figure 7.

Figure 7

Open in a new tab

Cartoon of interpenetrating agglomeration.

The dependence of the interpenetrating agglomeration on shear rate can be understood as follows: the stability of interpenetrating KB units will depend on how deeply they are lodged within the agglomerate because only the peripheral zone will be exposed to local shear flow. This explains why a complete reversal of the process can only be achieved at high shear rates: here, the shear stresses are high and the agglomerates are small, thus exposing all KB units to shear. (This is also why we defined our samples by preshearing them at 10000 s–1.)

In our proposed mechanism of interpenetrating agglomeration, the shape of the KB units plays an important role. To test this hypothesis, we performed an experiment comparable to that in Figure 5 but now with spherical unit particles (N990). This system was also strongly shear-thinning, indicating reversible agglomeration. A weight fraction of 30% was chosen to achieve a high shear viscosity similar to that of KB. Assuming that the hydrodynamic volume fractions of both suspensions are comparable when they are broken down to the unit particles, the only relevant difference should be the shape of the unit particle (Figure 8).

The electrical resistance of the N990 suspensions turned out to be too high to be accessible at experimental frequencies (<10 mHz). As shown in Figure 9, similar to KB the N990 suspension also exhibits an immediate jump in viscosity when the shear rate is stepped down, consistent with instant open agglomeration. However, when shear is continued, the viscosity slightly increases (thixotropy, shear thinning), in contrast to KB where it decreases. This supports our explanation that the fractal morphology of KB is responsible for the occurrence of interpenetrating agglomeration.

Figure 9.

Figure 9

Open in a new tab

Evolution of the viscosity of an N990 suspension after a shear rate step from 316 s–1. The colors correspond to shear rate steps described in Figure 5. Viscosity axis breaks and their scales are not uniform. One tick corresponds to 1 mPa·s.

3.4. Modeling

To further examine the mechanistic explanations proposed so far (as sketched in Figures 6 and 7), we combined previously developed concepts for describing the viscosity of agglomerating systems30 and the conductivity of filled polymers39 into a simplistic theoretical scheme. A complete description of this scheme is given in the Appendix. The scheme uses the measured viscosity and electronic resistance as inputs, and the collision radius and fractal dimension of the agglomerates (along with other derived geometrical properties) are output. The Krieger–Dougherty equation45 is used to calculate the hydrodynamic volume fraction from the relative viscosity, while part of the Potanin model30,46 is used to set a relation between the agglomerate radius and the fractal dimension. An effective medium approach for the electronic resistance is used to construct an additional relation between the agglomerate radius and the fractal dimension. In this approach, agglomerates are assumed to occupy centers in a lattice. The resistivity of the suspension then depends on the resistance between adjacent occupied lattice sites and depends asymptotically on the fraction of occupied sites. Because the agglomerates have a fractal architecture, the resistance of a conductive contact depends not only on proximity but also on the local (sub)unit particle density in the outer shells of the agglomerate.

The above relations are solved numerically for each measured viscosity and electronic resistance combination to yield a solution (fractal dimension, collision radius). Several other structure parameters can then be derived. Application of the scheme to the measurements of Figure 5 leads to the data shown in Figure 10. We observe that the trends used in our qualitative interpretation are reproduced by the model. For steps down in shear rate, the fast restructuring response leads to larger and less dense agglomerates while reducing both their concentration and spacing. During the slow interpenetrating agglomeration process, densification leads to a strong increase in the interagglomerate distance (and hence electronic resistance). For steps up in shear rate, the opposite trends occur, in line with expectations.

Figure 10.

Figure 10

Open in a new tab

Analysis of the experiments of Figure 5 with our theoretical model. Shear rate steps are made from 316 to 100 (black), 177 (red), 562 (green), and 1000 s–1 (blue).

3.5. Cessation of Shear

We revisit the experiment shown in Figure 5, now focusing on the last stage (region III) in which the flow is terminated after 1000 s of maintained shear at a constant rate. The (still monitored) electronic resistance shows an immediate sharp drop, indicating the formation of a space-filling network. After 200 s, the resistance reaches a steady state, justifying measurements of the full impedance spectra (Figure S3 in the S.I.) and the yield stress. Remarkably, both the low-frequency real impedance and the yield stress show a systematic dependence on the previously applied shear rate, with higher preshear leading to a higher yield stress and a lower electronic resistance (Figure 11). This effect is of strong significance to SSFBs where a high yield stress and low electronic resistance are both required for efficient operation.

Figure 11.

Figure 11

Open in a new tab

Rest impedance and yield stress of KB suspensions after preshearing for 1000 s at indicated rates. (Lines are drawn to guide the eye.) Figure 5 was used as the preshear protocol.

To explain these trends, we propose that the agglomerate structures as defined by the shear history are the building blocks of the solid network that forms after shear cessation. In other words, the agglomerates remain intact up to the point where they connect with other agglomerates to form a space-filling network. This freezing-in effect is plausible, as agglomerates can still undergo Brownian motion47 while thermal forces are too weak to break bonds between the KB units.

The qualitative dependences of the electronic resistance and yield stress on the preshear rate can be rationalized using the same shear (history) induced changes in the agglomerate structure as discussed earlier. High preshears result in small agglomerates, which assemble into a highly branched network when shear is stopped. Conversely, preshearing at low rates leads to networks with fewer and thicker branches because the agglomerates were larger in size and fewer in number. The contact areas between the agglomerates that form the low preshear gel should be similar (peripheral contacts) and thus no more effective at transferring charge and mechanical force than those of the high preshear gel. However, in the latter material, the number density of branches will be higher, leading to a higher yield stress and a lower electronic resistance.

To further examine the role of the secondary response (region II in Figure 5) in light of the results of Figure 11, we explored the effect of shear cessation at different times (Figure 12 left). As before, a 200 s rest time was given between the cessation of shear and the measurement of the impedance spectrum (complete spectrum in S.I. Figure S4). The yield stress was subsequently measured. As shown in Figure 12 right, both the final electronic resistance and yield stress were found to evolve in an S shape from their starting value. (In the case of the step to 100 s–1, steady state is not completely reached even after 1000 s.) Remarkably, their values for just 1 s of shear after the step are fairly similar to those without the step. This indicates that the structures of the gelled networks must also be very similar, despite the instant agglomeration (viscosity and resistance jumps) that occurred during the 1 s step. This suggests that the instant agglomeration process and gel formation on shear cessation have similar mechanisms. Additionally, it shows that the process responsible for the secondary response (interpenetration) is almost exclusively responsible for the change in rest network properties.

Figure 12.

Figure 12

Open in a new tab

(Left) Evolution of viscosity and low-frequency real impedance after a shear rate step from 316 to 1000 (up) or 100 s–1 (down) with shear cessation at different (indicated) times. (Right) Rest network resistance and yield stress measured after shear cessation at the indicated time. (Lines are drawn to guide the eye.)

4. Conclusions

The influence of shear and its history on the rheology and electrical impedance of Ketjen black suspensions in SSFB solvent was studied with two objectives: to understand the microscopic origin of the shear-history-dependent behaviors and to identify the implications for the performance of SSFBs. Both aspects revolve around the microstructure of the agglomerated suspension and how it adapts to mechanical conditions. Given the difficulty of measuring relevant structural properties directly via microscopy or scattering, our simultaneous study of the rheology and electrical impedance provided a good alternative method.

The fast and slow transient responses to a change in shear rate clearly indicate that KB agglomerates exhibit two buildup (breakup) mechanisms after decreasing (increasing) the shear rate. The fast response was attributed to open agglomeration, and the slower response was ascribed to an interpenetration of the fractal-like KB units. The combination of these processes leads to a shear- and time-dependent agglomerate structure that gets frozen in on cessation of flow, with a higher preshear leading to a stronger gel with a lower electronic resistance, both critical to SSFB performance.

An implication of our findings is that for SSFBs operated in the absence of flow, a high preshear (through fast pumping or stirring) would be the best for minimizing the electronic resistance and maximizing the yield stress. For SSFBs operated in continuous flow, a high flow rate would minimize the electronic resistance. We expect that our findings will be of relevance not just to SSFBs but also to other systems that use fractal carbon blacks such as flow supercapacitors. Additionally, we foresee electrochemical cycling to play an important role in the rheo-impedance of fluid electrodes (and vice versa) and are currently investigating the same.

Acknowledgments

The authors thank Duc Nguyên, Yan Zhang, Dirk van den Ende, and Martien Cohen Stuart for discussions. The authors also thank Daniel Wijnperlé for SEM imaging. The research leading to these results has received funding from the European Union Seventh Framework Program (FP7/2007-2013) under grant agreement no. 608621.

Appendix

In this section, we describe a scheme for calculating the structure in an agglomerated suspension, using measured data for the viscosity and conductivity as input.

To describe the viscosity, we model the fractal agglomerates as effective hard spheres with a hydrodynamic radius Rh that depends on the shear rate and history. The Krieger–Dougherty equation45 is used to calculate the hydrodynamic volume fraction ϕhyd from the viscosity η

graphic file with name la-2016-04322n_m001.jpg 1

where η0 is the solvent viscosity and ϕmhyd is the maximum hydrodynamic volume fraction. From scaling laws for fractal agglomerates made of spherical subunits (of radius a), the number N of subunits enclosed by a shell of radius R is given by30

graphic file with name la-2016-04322n_m002.jpg 2

Note that we do not distinguish between subunits originating from different primary aggregates. Setting N0 equal to unity for simplicity and invoking mass conservation, Rh can be related to df.30

graphic file with name la-2016-04322n_m003.jpg 3a
graphic file with name la-2016-04322n_m004.jpg 3b

ϕparticles is the volume fraction of the particles, in our case, the volume fraction of the solvent-filled KB subunits. Rc is the radius of the smallest sphere that completely encloses the agglomerate, the collision radius. κ is the ratio of the hydrodynamic to collision radius and is β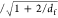Inline graphic.30 This equation contains two unknowns (Rc, df), and thus we use the impedance data to impose an additional constraint.

The electronic resistance of the CB suspension is governed by the macroscopic paths that electrons can take (percolation) and the conductivity of the paths themselves, i.e., the suspension behaves as a network of resistors. The effective medium approximation can be used to obtain an analytical expression for the conductivity of the entire system.31 It consists of replacing the random conductances by a single value Gm such that the overall electrical properties are unchanged. Sheared concentrated CB suspensions present a rather special case, as the concentration is high enough that conductive chains can form; however, the shear keeps these chains from being continuous; despite percolation, the electrons still need to cross insulating gaps between agglomerates. We assume that CB agglomerates behave as conductive spheres whose centers are randomly distributed in a lattice. As the electronic conductivity of carbon is much higher than that of the solvent, we assume a binomial probability distribution of conductivities between lattice sites. If both neighboring sites are occupied, then the conductance Gl will be finite; otherwise, it will be zero. From the effective medium approximation, it then follows that

graphic file with name la-2016-04322n_m006.jpg 4

where z is the coordination number of the lattice, ϕ is the lattice occupation fraction, and ϕm is its maximum value (taken equal to that of their hydrodynamic counterparts for simplicity). For a lattice edge length of l, the suspension resistivity ρ then becomes

graphic file with name la-2016-04322n_m007.jpg 5

In our case, l is equal to the total of the agglomerate diameter 2Rc and the (typical) gap between agglomerates d. The latter is given by48

graphic file with name la-2016-04322n_m008.jpg 6

The conductivity σl of the gapped connection depends on the geometry and the prevailing conduction mechanism. Agglomerates separated by very small gaps (a few nanometers) conduct through fluctuation-induced quantum tunneling.12 For larger gaps, the (low) intrinsic electronic conductivity of the solvent dominates. As interagglomerate distances of tens of nanometers are expected (shown later), Gl is given by

graphic file with name la-2016-04322n_m009.jpg 7

where σs is the intrinsic electronic conductivity of the solvent and act is the charge-transfer area. To determine act, we assume that conduction is effective up to a depth h into the agglomerate as shown in Figure 13.

Figure 13.

Figure 13

Open in a new tab

Geometry of the lattice cells.

From the geometry of the system, it is evident that

graphic file with name la-2016-04322n_m010.jpg 8

where F accounts for the fact that the perimeter of the agglomerate is not completely occupied. To evaluate F, we consider a shell of thickness dRc around a fractal of radius Rc. The number of primary particles enclosed in this shell dN is given by

graphic file with name la-2016-04322n_m011.jpg 9

To get the area fraction F, we simply divide the projected area of these particles by the surface area of a sphere of radius Rc.

graphic file with name la-2016-04322n_m012.jpg 10

Collecting the above relations, we get an equation for the impedance of the suspension:

graphic file with name la-2016-04322n_m013.jpg 11

Equations 3 and 11 can be numerically solved to obtain df and Rc. To make a numercial analysis of the data in Figure 5, some numerical constants need to be specified; these can be found in Table 1. To obtain the magnitude of ϕparticles in eq 3, we use the assumption that for a sufficiently prolonged shearing at 1000 s–1 the agglomerates are completely broken down.

Table 1. Parameter Estimates Used in the Model.

parameter value  
η0 4 mPa·s ref 32
a 5 nm ref 12
ϕmhyd 0.71 high-shear limit for hard spheres
β 0.72 ref 49
z 12  
df primary aggregate 1.8 ref 13
Rh primary aggregate 90 nm DLS (S.I. Figure S5)
Open in a new tab

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.6b04322.

  • Detailed Nyquist plots of impedance spectra, weight fraction dependence of KB suspension properties, and DLS measurement of KB (PDF)

The authors declare no competing financial interest.

Supplementary Material

la6b04322_si_001.pdf (557.6KB, pdf)

References

  1. Chen H. N.; Lu Y. C. A High-Energy-Density Multiple Redox Semi-Solid-Liquid Flow Battery. Adv. Energy Mater. 2016, 6 (8), 1502183. 10.1002/aenm.201502183. [DOI] [Google Scholar]
  2. Smith K. C.; Chiang Y. M.; Carter W. C. Maximizing Energetic Efficiency in Flow Batteries Utilizing Non-Newtonian Fluids. J. Electrochem. Soc. 2014, 161 (4), A486–A496. 10.1149/2.011404jes. [DOI] [Google Scholar]
  3. Duduta M.; Ho B.; Wood V. C.; Limthongkul P.; Brunini V. E.; Carter W. C.; Chiang Y. M. Semi-Solid Lithium Rechargeable Flow Battery. Adv. Energy Mater. 2011, 1 (4), 511–516. 10.1002/aenm.201100152. [DOI] [Google Scholar]
  4. Ventosa E.; Buchholz D.; Klink S.; Flox C.; Chagas L. G.; Vaalma C.; Schuhmann W.; Passerini S.; Morante J. R. Non-aqueous semi-solid flow battery based on Na-ion chemistry. P2-type NaxNi0.22Co0.11Mn0.66O2-NaTi2(PO4)(3). Chem. Commun. 2015, 51 (34), 7298–7301. 10.1039/C4CC09597A. [DOI] [PubMed] [Google Scholar]
  5. Madec L.; Youssry M.; Cerbelaud M.; Soudan P.; Guyomard D.; Lestriez B. Surfactant for enhanced rheological, electrical, and electrochemical performance of suspensions for semisolid redox flow batteries and supercapacitors. ChemPlusChem 2015, 80 (2), 396–401. 10.1002/cplu.201402042. [DOI] [Google Scholar]
  6. Fan F. Y.; Woodford W. H.; Li Z.; Baram N.; Smith K. C.; Helal A.; McKinley G. H.; Carter W. C.; Chiang Y. M. Polysulfide Flow Batteries Enabled by Percolating Nanoscale Conductor Networks. Nano Lett. 2014, 14 (4), 2210–2218. 10.1021/nl500740t. [DOI] [PubMed] [Google Scholar]
  7. Li Z.; Smith K. C.; Dong Y. J.; Baram N.; Fan F. Y.; Xie J.; Limthongkul P.; Carter W. C.; Chiang Y. M. Aqueous semi-solid flow cell: demonstration and analysis. Phys. Chem. Chem. Phys. 2013, 15 (38), 15833–15839. 10.1039/c3cp53428f. [DOI] [PubMed] [Google Scholar]
  8. Hamelet S.; Larcher D.; Dupont L.; Tarascon J. M. Silicon-Based Non Aqueous Anolyte for Li Redox-Flow Batteries. J. Electrochem. Soc. 2013, 160 (3), A516–A520. 10.1149/2.002304jes. [DOI] [Google Scholar]
  9. Hamelet S.; Tzedakis T.; Leriche J. B.; Sailler S.; Larcher D.; Taberna P. L.; Simon P.; Tarascona J. M. Non-Aqueous Li-Based Redox Flow Batteries. J. Electrochem. Soc. 2012, 159 (8), A1360–A1367. 10.1149/2.071208jes. [DOI] [Google Scholar]
  10. Richards J. J.; Scherbarth A. D.; Wagner N. J.; Butler P. D. Mixed Ionic/Electronic Conducting Surface Layers Adsorbed on Colloidal Silica for Flow Battery Applications. ACS Appl. Mater. Interfaces 2016, 8 (36), 24089–24096. 10.1021/acsami.6b07372. [DOI] [PubMed] [Google Scholar]
  11. Youssry M.; Madec L.; Soudan P.; Cerbelaud M.; Guyomard D.; Lestriez B. Non-aqueous carbon black suspensions for lithium-based redox flow batteries: rheology and simultaneous rheo-electrical behavior. Phys. Chem. Chem. Phys. 2013, 15 (34), 14476–14486. 10.1039/c3cp51371h. [DOI] [PubMed] [Google Scholar]
  12. Sichel E. K.; Gittleman J. I.; Sheng P. Transport properties of the composite material carbon-poly(vinyl chloride). Phys. Rev. B: Condens. Matter Mater. Phys. 1978, 18 (10), 5712–5716. 10.1103/PhysRevB.18.5712. [DOI] [Google Scholar]
  13. Donnet J.-B.Carbon Black: Science and Technology; CRC Press, 1993. [Google Scholar]
  14. Youssry M.; Madec L.; Soudan P.; Cerbelaud M.; Guyomard D.; Lestriez B. Formulation of flowable anolyte for redox flow batteries: Rheo-electrical study. J. Power Sources 2015, 274, 424–431. 10.1016/j.jpowsour.2014.10.076. [DOI] [Google Scholar]
  15. Zhang Y.; Narayanan A.; Mugele F.; Stuart M. A. C.; Duits M. H. G. Charge inversion and colloidal stability of carbon black in battery electrolyte solutions. Colloids Surf., A 2016, 489, 461–468. 10.1016/j.colsurfa.2015.08.041. [DOI] [Google Scholar]
  16. Vanvliet T.; Vandijk H. J. M.; Zoon P.; Walstra P. Relation between Syneresis and Rheological Properties of Particle Gels. Colloid Polym. Sci. 1991, 269 (6), 620–627. 10.1007/BF00659917. [DOI] [Google Scholar]
  17. Rueb C. J.; Zukoski C. F. Viscoelastic properties of colloidal gels. J. Rheol. 1997, 41 (2), 197–218. 10.1122/1.550812. [DOI] [Google Scholar]
  18. Mewis J.; Wagner N. J. Thixotropy. Adv. Colloid Interface Sci. 2009, 147-148, 214–227. 10.1016/j.cis.2008.09.005. [DOI] [PubMed] [Google Scholar]
  19. Mewis J.; Wagner N. J.. Colloidal Suspension Rheology; Cambridge University Press, 2012. [Google Scholar]
  20. Tadros T. F.Rheology of Dispersions: Principles and Applications; John Wiley & Sons, 2011. [Google Scholar]
  21. Barnes H. A. Thixotropy—a review. J. Non-Newtonian Fluid Mech. 1997, 70 (1), 1–33. 10.1016/S0377-0257(97)00004-9. [DOI] [Google Scholar]
  22. Mewis J. Thixotropy-a general review. J. Non-Newtonian Fluid Mech. 1979, 6 (1), 1–20. 10.1016/0377-0257(79)87001-9. [DOI] [Google Scholar]
  23. Ovarlez G.; Tocquer L.; Bertrand F.; Coussot P. Rheopexy and tunable yield stress of carbon black suspensions. Soft Matter 2013, 9 (23), 5540–5549. 10.1039/c3sm27650c. [DOI] [Google Scholar]
  24. Osuji C. O.; Kim C.; Weitz D. A.. Shear thickening and scaling of the elastic modulus in a fractal colloidal system with attractive interactions. Phys. Rev. E 2008, 77 ( (6), ). 10.1103/PhysRevE.77.060402 [DOI] [PubMed] [Google Scholar]
  25. Purnomo E. H.; van den Ende D.; Mellema J.; Mugele F. Rheological properties of aging thermosensitive suspensions. Phys. Rev. E 2007, 76 (2), 021404. 10.1103/PhysRevE.76.021404. [DOI] [PubMed] [Google Scholar]
  26. Kawaguchi M.; Okuno M.; Kato T. Rheological properties of carbon black suspensions in a silicone oil. Langmuir 2001, 17 (20), 6041–6044. 10.1021/la010560r. [DOI] [Google Scholar]
  27. Potanin A. Thixotropy and rheopexy of aggregated dispersions with wetting polymer. J. Rheol. (Melville, NY, U. S.) 2004, 48 (6), 1279–1293. 10.1122/1.1807844. [DOI] [Google Scholar]
  28. Medalia A.; Hagopian E. Rheology of dispersant-free aqueous slurries of carbon black. Rheol. Acta 1963, 3 (2), 100–111. 10.1007/BF01979460. [DOI] [Google Scholar]
  29. Helal A.; Divoux T.; McKinley G. H. Simultaneous rheo-electric measurements of strongly conductive complex fluids. Phys. Rev. Appl. 2016, 6, 064004. 10.1103/PhysRevApplied.6.064004. [DOI] [Google Scholar]
  30. Wolthers W.; Duits M. H. G.; Van Den Ende D.; Mellema J. Shear history dependence of the viscosity of aggregated colloidal dispersions. J. Rheol. (Melville, NY, U. S.) 1996, 40 (5), 799–811. 10.1122/1.550783. [DOI] [Google Scholar]
  31. Kirkpatrick S. Classical transport in disordered media: scaling and effective-medium theories. Phys. Rev. Lett. 1971, 27 (25), 1722. 10.1103/PhysRevLett.27.1722. [DOI] [Google Scholar]
  32. Dougassa Y. R.; Jacquemin J.; El Ouatani L.; Tessier C.; Anouti M. Viscosity and carbon dioxide solubility for LiPF6, LiTFSI, and LiFAP in alkyl carbonates: lithium salt nature and concentration effect. J. Phys. Chem. B 2014, 118 (14), 3973–3980. 10.1021/jp500063c. [DOI] [PubMed] [Google Scholar]
  33. Osuji C. O.; Weitz D. A. Highly anisotropic vorticity aligned structures in a shear thickening attractive colloidal system. Soft Matter 2008, 4 (7), 1388–1392. 10.1039/b716324j. [DOI] [PubMed] [Google Scholar]
  34. Schramm G.A Practical Approach to Rheology and Rheometry; Haake Karlsruhe, 1994. [Google Scholar]
  35. Jamnik J.; Maier J. Treatment of the impedance of mixed conductors equivalent circuit model and explicit approximate solutions. J. Electrochem. Soc. 1999, 146 (11), 4183–4188. 10.1149/1.1392611. [DOI] [Google Scholar]
  36. Barsoukov E.; Macdonald J. R.. Impedance Spectroscopy: Theory, Experiment, and Applications; John Wiley & Sons, 2005. [Google Scholar]
  37. Dullaert K.; Mewis J. Stress jumps on weakly flocculated dispersions: Steady state and transient results. J. Colloid Interface Sci. 2005, 287 (2), 542–551. 10.1016/j.jcis.2005.02.018. [DOI] [PubMed] [Google Scholar]
  38. Sheng P.; Sichel E.; Gittleman J. Fluctuation-induced tunneling conduction in carbon-polyvinylchloride composites. Phys. Rev. Lett. 1978, 40 (18), 1197. 10.1103/PhysRevLett.40.1197. [DOI] [Google Scholar]
  39. Sherman R.; Middleman L.; Jacobs S. Electron transport processes in conductor-filled polymers. Polym. Eng. Sci. 1983, 23 (1), 36–46. 10.1002/pen.760230109. [DOI] [Google Scholar]
  40. Potanin A. A.; Derooij R.; Vandenende D.; Mellema J. Microrheological Modeling of Weakly Aggregated Dispersions.. J. Chem. Phys. 1995, 102 (14), 5845–5853. 10.1063/1.469317. [DOI] [Google Scholar]
  41. Derooij R.; Potanin A. A.; Vandenende D.; Mellema J. Rheological Behavior of Weakly Aggregating Colloids - Viscosity of the Structure Formed in a Steady Shear-Flow. Colloid J. 1994, 56 (4), 476–486. [Google Scholar]
  42. Derooij R.; Potanin A. A.; Vandenende D.; Mellema J. Steady Shear Viscosity of Weakly Aggregating Polystyrene Latex Dispersions. J. Chem. Phys. 1993, 99 (11), 9213–9223. 10.1063/1.465537. [DOI] [Google Scholar]
  43. Tolpekin V. A.; Duits M. H. G.; van den Ende D.; Mellema J. Aggregation and breakup of colloidal particle aggregates in shear flow, studied with video microscopy. Langmuir 2004, 20 (7), 2614–2627. 10.1021/la035758l. [DOI] [PubMed] [Google Scholar]
  44. Genovese D. B. Shear rheology of hard-sphere, dispersed, and aggregated suspensions, and filler-matrix composites. Adv. Colloid Interface Sci. 2012, 171-172, 1–16. 10.1016/j.cis.2011.12.005. [DOI] [PubMed] [Google Scholar]
  45. de Kruif C. G.; Van Iersel E.; Vrij A.; Russel W. Hard sphere colloidal dispersions: Viscosity as a function of shear rate and volume fraction. J. Chem. Phys. 1985, 83 (9), 4717–4725. 10.1063/1.448997. [DOI] [Google Scholar]
  46. Potanin A.; De Rooij R.; Van den Ende D.; Mellema J. Microrheological modeling of weakly aggregated dispersions. J. Chem. Phys. 1995, 102 (14), 5845–5853. 10.1063/1.469317. [DOI] [Google Scholar]
  47. Cerbelaud M.; Lestriez B.; Ferrando R.; Videcoq A.; Richard-Plouet M.; Caldes M. T.; Guyomard D. Numerical and Experimental Study of Suspensions Containing Carbon Blacks Used as Conductive Additives in Composite Electrodes for Lithium Batteries. Langmuir 2014, 30 (10), 2660–2669. 10.1021/la404693s. [DOI] [PubMed] [Google Scholar]
  48. Hao T.; Riman R. E. Calculation of interparticle spacing in colloidal systems. J. Colloid Interface Sci. 2006, 297 (1), 374–377. 10.1016/j.jcis.2004.10.014. [DOI] [PubMed] [Google Scholar]
  49. Wolthers W.; Van den Ende D.; Duits M.; Mellema J. The viscosity and sedimentation of aggregating colloidal dispersions in a Couette flow. J. Rheol. (Melville, NY, U. S.) 1996, 40 (1), 55–67. 10.1122/1.550784. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

la6b04322_si_001.pdf (557.6KB, pdf)

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES