Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2017 Mar 3;7:43482. doi: 10.1038/srep43482

Towards an accurate description of perovskite ferroelectrics: exchange and correlation effects

Simuck F Yuk 1, Krishna Chaitanya Pitike 2, Serge M Nakhmanson 2, Markus Eisenbach 3, Ying Wai Li 3, Valentino R Cooper 1,a
PMCID: PMC5335310  PMID: 28256544

Abstract

Using the van der Waals density functional with C09 exchange (vdW-DF-C09), which has been applied to describing a wide range of dispersion-bound systems, we explore the physical properties of prototypical ABO3 bulk ferroelectric oxides. Surprisingly, vdW-DF-C09 provides a superior description of experimental values for lattice constants, polarization and bulk moduli, exhibiting similar accuracy to the modified Perdew-Burke-Erzenhoff functional which was designed specifically for bulk solids (PBEsol). The relative performance of vdW-DF-C09 is strongly linked to the form of the exchange enhancement factor which, like PBEsol, tends to behave like the gradient expansion approximation for small reduced gradients. These results suggest the general-purpose nature of the class of vdW-DF functionals, with particular consequences for predicting material functionality across dense and sparse matter regimes.

ABO3 perovskite oxides, such as PbTiO3 and Pb(Zr, Ti)O3, are an important family of multifunctional compounds due to their high dielectric and piezoelectric responses1,2,3. These materials are attractive for numerous technological applications such as electronics, catalysis, superconductors, and electromechanical energy conversion4,5. Recently, major efforts have been invested in designing new lead-free piezoelectric oxides in order to minimize environmental damage6,7,8,9,10. First-principles methods based on density functional theory (DFT) have been routinely used to explore the ferroelectric phase transition of transition metal oxides at the atomistic level. A key challenge is the fact that complex behavior such as order-disorder transitions and domain wall motion typically require a large number of atoms in order to adequately simulate this behavior. Thus, some of the most common tactics for efficiently studying ferroelectric phase transitions include: (1) Monte Carlo simulations employing DFT parameterized effective Hamiltonians11,12,13,14,15,16,17 or (2) molecular dynamic simulations with atomistic potentials, such as the shell-model18,19,20 or bond-valence21,22,23 approach. While the above methods correctly reproduce the overall sequence of phase transitions for various perovskite oxides, the values of transition temperatures were generally underestimated relative to the experiments11,12,24. Such discrepancies in transition temperatures is likely caused by a combination of issues including an insufficient description of thermal expansion effects, failure to capture the important cooperative effects of ferroelectric distortions, and/or the error associated with the choice of DFT exchange-correlation functional25,26,27,28,29.

It is known that the practical error of DFT is closely related to its treatment of exchange and correlation effects. The binding energy between atoms tends to be overestimated by the local density approximation (LDA), resulting in an underestimation of optimized lattice parameters, particularly in perovskite oxides30,31. In contrast, the generalized gradient approximation (GGA) overcorrects the LDA errors, resulting in an overestimation of lattice parameters. Due to the strong volume dependence of structural instabilities in ferroelectric materials31,32,33,34,35,36,37, even modest errors in the values of their lattice parameters may sometimes lead to sizeable inaccuracies in predicting their functional properties with DFT. To overcome this issue, numerous approaches have been proposed to improve the exchange and correlation part of the density functional. Wu and Cohen modified the GGA functional (WC-GGA) by tuning the exchange enhancement factor of Perdew-Burke-Erzenhoff (PBE), which resulted in a better description of ferroelectric PbTiO3 and BaTiO3 phases compared to GGA and meta-GGA38. A similar approach was also adopted by Perdew and co-workers for their modified PBE for solids (PBEsol) functional, which gives predicted lattice parameters in good agreement with experimental values for various materials39. Hybrid exchange-correlation functionals, such as HSE and B1-WC, have also been developed to provide accurate descriptions of structural and electronic structures of ferroelectric oxides40,41. More recently, the class of van der Waals density functionals (vdW-DF), which account for long-range dispersion interactions, has shown remarkable success in representing not only dispersion-bound, but also densely-packed systems, including ferroelectric bulk oxides and metals42,43,44,45,46,47,48,49,50,51,52,53,54.

In this paper, we study how the choice of exchange-correlation functionals affects the prediction of the structural and ferroelectric properties of prototypical PbTiO3 (PTO), BaTiO3 (BTO), and KNbO3 (KNO) perovskites. As expected, LDA underestimates both the lattice parameters and spontaneous polarizations, while PBE overestimates them. In contrast, we observed the opposite trend when evaluating the bulk modulus due to the inverse relationship between total energy and optimized volume. Overall, vdW-DF with C09 exchange (vdW-DF-C09), followed by PBEsol, provides the best agreement with the experimental values, demonstrating its utility as a general-purpose functional for studying ferroelectric perovskite oxides. Additional analyses of the double-well potential surfaces and phase transition temperatures clearly confirm that the choice of the exchange and correlation functional may significantly impact the values of predicted ferroelectric properties of perovskite oxides. Recent studies on the application of a similar functional, vdW-DF-cx, to various systems, ranging from the ferroelectric response in PTO to the adsorption of small molecules, further supports the robustness of such vdW-DF-type functionals52,53,55. The overall trends in the performance of different functionals can be strongly correlated with the behavior of the exchange enhancement factor in the small reduced gradient region.

Computational Details

All DFT calculations were performed using the plane-wave-based Quantum Espresso software package56. The energy cutoff for the plane-wave basis set was 50 Ry (200 Ry for the charge density cutoff), along with ultrasoft pseudopotentials57 (scalar-relativistic for A- and B-site cations and non-relativistic for O) to represent the electron-ion interaction. This cutoff criterion has also been employed in high-throughput DFT calculations using the ultrasoft pseudopotential library proposed by Garrity, Bennett, Rabe, and Vanderbilt58. Ba (5s, 5p, 5d, 6s, 6p), K (3s, 3p, 4s, 4p), Nb (4s, 4p, 4d, 5s, 5p), Pb (5d, 6s, 6p), Ti (3s, 3p, 3d, 4s), and O (2s, 2p) were considered as valence orbitals. A Monkhorst-Pack k-point mesh of 4 × 4 × 4 was determined to be sufficient for sampling the Brillouin zone. The quasi-Newton BFGS algorithm was used to optimize the bulk geometry with a force convergence criterion of 3.0 × 10−4 Ry/Bohr. To compare the effects of various exchange-and-correlation parameterizations on the structural and ferroelectric properties of perovskite oxides, we considered four types of functionals: LDA59, PBE60, PBEsol39, and vdW-DF43,44 with C09 exchange (vdW-DF-C09)47.

A 2 × 2 × 2 unit cell, consisting of 40 atoms, was first constructed to represent the centrosymmetric bulk structure of cubic PTO, BTO, and KNO perovskites. Subsequent displacements of B-site cations along [001], [011], and [111] directions were then induced to create tetragonal, orthorhombic, and rhombohedral phases, respectively. The detailed structural information of each crystal phase for PTO, BTO, and KNO can be found in Table S1 of Supplementary Information. In all cases, the cell parameters were relaxed together with the ionic coordinates, using a stress convergence criterion of 0.5 kbar. The Berry phase approach61 was applied to calculate spontaneous polarizations, P, from the optimized bulk geometries. The bulk modulus, B, of each crystal phase was evaluated using the Birch-Murnaghan62 equation of state:

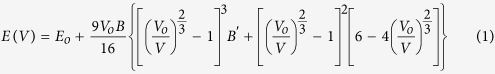graphic file with name srep43482-m1.jpg

where Eo and Vo are the total energy and optimized volume of each phase, respectively. Thus, B and its first derivative, B′, can be computed by fitting the above equation with DFT energies and volumes near the energy minimum.

Results and Discussion

Influence of exchange-correlation functionals on structural properties

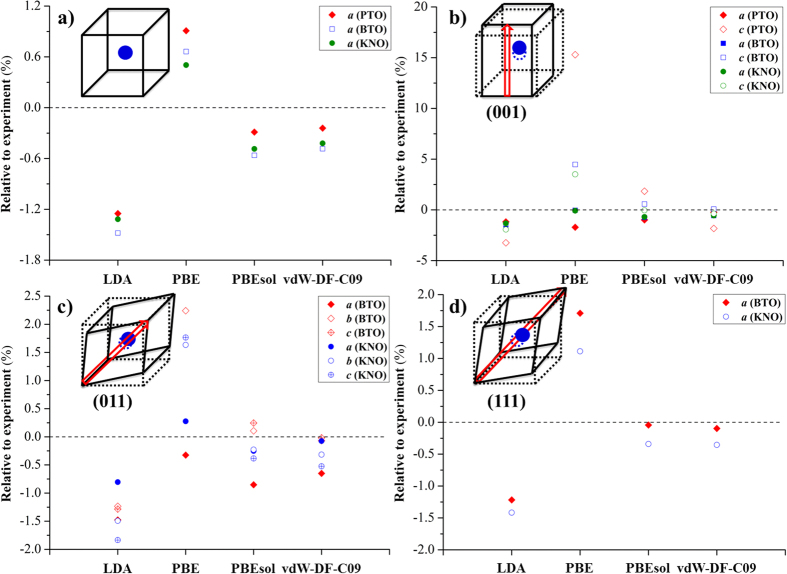
Figure 1 shows the percent error of DFT lattice parameters for PTO, BTO and KNO in different crystal phases relative to the experimental values (the magnitudes of the lattice parameters are presented in Table 1). As expected, LDA always underestimates the lattice parameters, while PBE overestimates them. In particular, there is a significant overestimation of the c lattice parameter (as large as ~15% deviation) in the tetragonal phase when using the latter. In contrast, PBEsol and vdW-DF-C09 predicted lattice parameters close to the experimental values (less than ~3% deviation).

Figure 1.

Figure 1

Open in a new tab

Percent error(%) of DFT lattice parameters evaluation for PTO, BTO, and KNO in the (a) cubic, (b) tetragonal, (c) orthorhombic, and (d) rhombohedral phases compared to the experimental values.

Table 1. Structural and ferroelectric properties of PTO, BTO, and KNO in the different crystal phases using LDA, PBE, PBEsol, and vdW-DF-C09.

Phase   LDA PBE PBEsol vdW-DF-C09 Expt.
PbTiO3
Cubic a (Å) 3.881 3.966 3.919 3.921 3.93073
B (GPa) 205.27 173.21 190.08 190.76 195.0074
Tetragonal a (Å) 3.858 3.837 3.865 3.895 (3.8955)52 3.90475
c (Å) 4.017 4.787 4.228 4.076 (4.0788)52 4.15275
B (GPa) 145.69 85.60 114.85 131.74 110.4476
P (C/m2) 0.78 1.28 0.98 0.78 (0.75)52 0.7577
Tc (K) 813 2162 1276 814 74778
BaTiO3
Cubic a (Å) 3.941 4.026 3.977 3.981 4.00079
B (GPa) 195.96 162.65 179.25 178.65 195.0080
Tetragonal a (Å) 3.933 3.991 3.962 3.969 3.99281
c (Å) 3.980 4.216 4.059 4.039 4.03681
B (GPa) 169.47 123.59 148.44 153.08 139.2080
P (C/m2) 0.26 0.48 0.35 0.30 0.2782
Tc (K) 373 1226 658 496 39383
Orthorhombic a (Å) 3.931 3.977 3.956 3.964 3.99084
b (Å) 5.599 5.796 5.675 5.665 5.66984
c (Å) 5.609 5.848 5.696 5.681 5.68284
B (GPa) 155.68 105.75 133.21 138.24 —
P (C/m2) 0.31 0.61 0.31 0.30 0.3082
Tc (K) 293 1139 299 287 27883
Rhombohedral a (Å) 3.951 4.068 3.998 3.996 4.00085
B (GPa) 151.17 95.95 121.73 129.36 —
P (C/m2) 0.31 0.50 0.39 0.35 0.3382
Tc (K) 165 419 260 208 18383
KNbO3
Cubic a (Å) 3.952 4.025 3.986 3.988 4.00586
B (GPa) 204.27 176.77 189.62 185.49 —
Tetragonal a (Å) 3.944 3.994 3.969 3.975 3.99786
c (Å) 3.984 4.205 4.061 4.048 4.06386
B (GPa) 184.85 127.17 157.36 163.93 165.0087
P (C/m2) 0.27 0.51 0.38 0.34 0.3788
Tc (K) 378 1322 739 613 70889
Orthorhombic a (Å) 3.941 3.984 3.963 3.970 3.97386
b (Å) 5.610 5.788 5.682 5.677 5.69586
c (Å) 5.616 5.822 5.699 5.691 5.72186
B (GPa) 174.15 108.42 139.82 148.63 146.0090
P (C/m2) 0.32 0.61 0.47 0.45 0.4191
Tc (K) 301 1109 654 594 49889
Rhombohedral a (Å) 3.959 4.061 4.002 4.002 4.01686
B (GPa) 168.67 101.61 136.40 141.67 —
P (C/m2) 0.31 0.52 0.42 0.39 0.4286
Tc (K) 142 397 261 226 26389
Open in a new tab

B and P are the bulk modulus and spontaneous polarization obtained for the optimized crystal structures, respectively. Tc represents the phase transition temperature of crystal phases predicted using Equation (4). Experimental values are provided for comparison.

Reference values in parentheses were obtained using the vdW-DF-cx functional52.

As mentioned above, some of the most responsive piezoelectrics are perovskite oxides. Piezoelectricity is closely related to the following properties: the compressibility of the materials and the magnitude and orientation of polarization63,64,65. In this regard, correctly estimating the spontaneous polarization and elastic properties is the key to understanding phase transition temperatures and electromechanical coupling. Thus, it is an important task to study the exchange and correlation effects on the prediction of these properties for the accurate measurement of piezoelectric responses in perovskites. The bulk modulus and spontaneous polarizations of PTO, BTO, and KNO in different crystal phases were computed and compared to experiment (Table 1). Figure 2 depicts the ratio of the DFT spontaneous polarization (PDFT) relative to the experimental value (PExpt) as a function of the ratio of the DFT bulk modulus (BDFT) relative to experiment (BExpt). Again, using LDA and PBE leads to the under- and overestimation of spontaneous polarizations, respectively. The opposite trend was observed for the bulk modulus, generally with larger errors compared to the lattice parameters. The trend in bulk moduli is a direct consequence of the inverse dependence of total energy on optimized volume as shown in Equation (1). In other words, overestimations in volume are translated to underestimations in bulk moduli66. Overall, we found that vdW-DF-C09 produces the best agreement with experiments when predicting the structural properties of perovskite oxides, while PBEsol yields a slightly lower accuracy in property evaluations compared to the former. In fact, similar performance was also seen with vdW-DF-cx when predicting the material properties for cubic and tetragonal phase of PTO52. Thus, vdW-DF-C09 and PBEsol functionals should be suitable for further studies on the phase transitions of ferroelectric oxides.

Figure 2. Comparison of bulk modulus (BDFT) and spontaneous polarizations (PDFT) of PTO, BTO, and KNO in the different crystal phases relative to the experimental values.

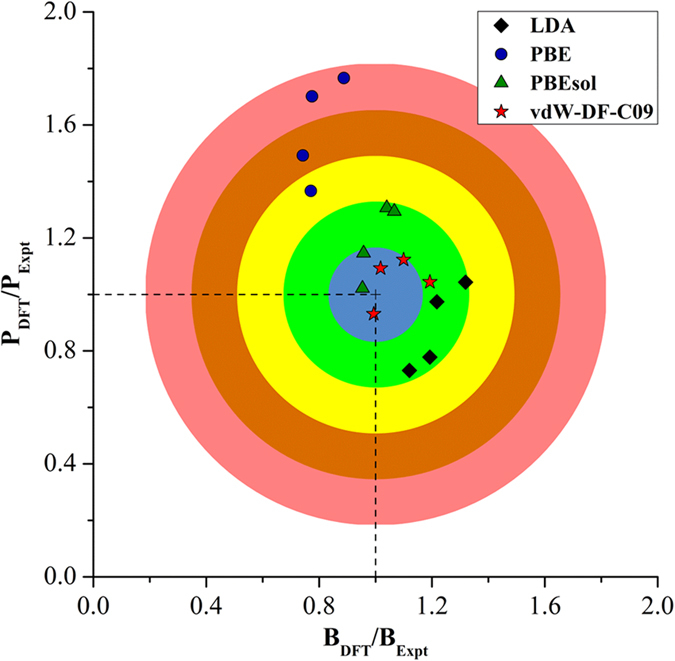
Figure 2

Open in a new tab

Each color region represents the DFT/Experiment ratio of ±0.165.

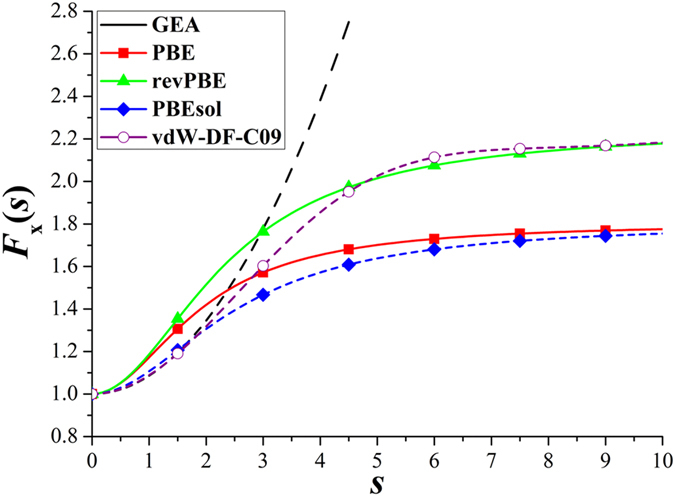
A closer look at the exchange enhancement factor (Fx(s)), which is a function of the reduced density gradient (s = ∇ρ/ρ), shows a clear difference in the overall trends with respect to the form of the exchange functionals, as displayed in Fig. 3. For a standard GGA, the exchange energy, Ex(s), can be written as:

Figure 3. Exchange enhancement factor (Fx(s)) for GEA, PBE, revPBE, PBEsol, and vdW-DF-C09 functionals.

Figure 3

Open in a new tab
graphic file with name srep43482-m2.jpg

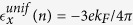where Inline graphic is the exchange energy per particle in a uniform gas with KF = 3π2n. For s < 2, Fx(s) of vdW-DF-C09 matches PBEsol, which tends to the form of the gradient expansion approximation (GEA)67; where F_x(s) = 1 + \mu s2 with \mu=0.0864. On the other hand, Fx(s) of PBE significantly deviates from the GEA in the small s region. For large s, vdW-DF-C09 recovers the behavior of the revised PBE (revPBE)68 exchange, while PBEsol asymptotes to the PBE limit. Since reducing Fx(s) for small s values leads to a decrease in short-range repulsion39,47, the treatment of Fx(s), and thus, short-range repulsion by PBE leads to the overestimation of structural properties, while the opposite holds true for LDA (whose Fx(s) = 1). Fx(s) of PBEsol and vdW-DF-C09 sits between LDA and PBE and behaves similarly in the small s region, providing a more suitable prediction in structural properties compared to both LDA and PBE.

Influence of exchange-correlation functionals on ferroelectric properties

It is generally thought that the magnitude of the ferroelectric double well potential depth scales with the magnitude of the polarization. Changes in the predictions of ferroelectric well depths, consequently, may have large effects on predictions of ferroelectric phase transitions as well as responses to the application of an external electric field. The double well potential for the cubic-to-tetragonal transition can be expressed as a function of DFT-derived spontaneous polarizations based on the Landau theory (without considering strain couplings)69:

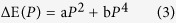graphic file with name srep43482-m4.jpg

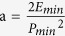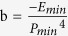where ΔE is the total energy relative to the saddle point and P is the spontaneous polarization from DFT calculations. At the ferroelectric minimum, Equation (3) can be rearranged to find the value of constants: Inline graphic and Inline graphic. Greater potential well depths are expected for PTO, due to the presence of Pb lone pairs which results in a stronger hybridization between Pb 6s and O 2p orbitals resulting in larger polarizations in PTO as compared to BTO and KNO33. More importantly, we observed that the potential well depth increases by the following order of functionals regardless of the material: LDA ≤ vdW-DF-C09 < PBEsol < PBE, as presented in Fig. 4. This is consistent with the notion that the well depth scales with the magnitude of the polarization40,70. Thus, the energy barrier is changed, already hinting at a variation in phase transition behavior when using different exchange-correlation functionals.

Figure 4. A double well potential for PTO, BTO, and KNO for cubic-to-tetragonal transition obtained with using LDA, PBE, PBEsol, and vdW-DF-C09.

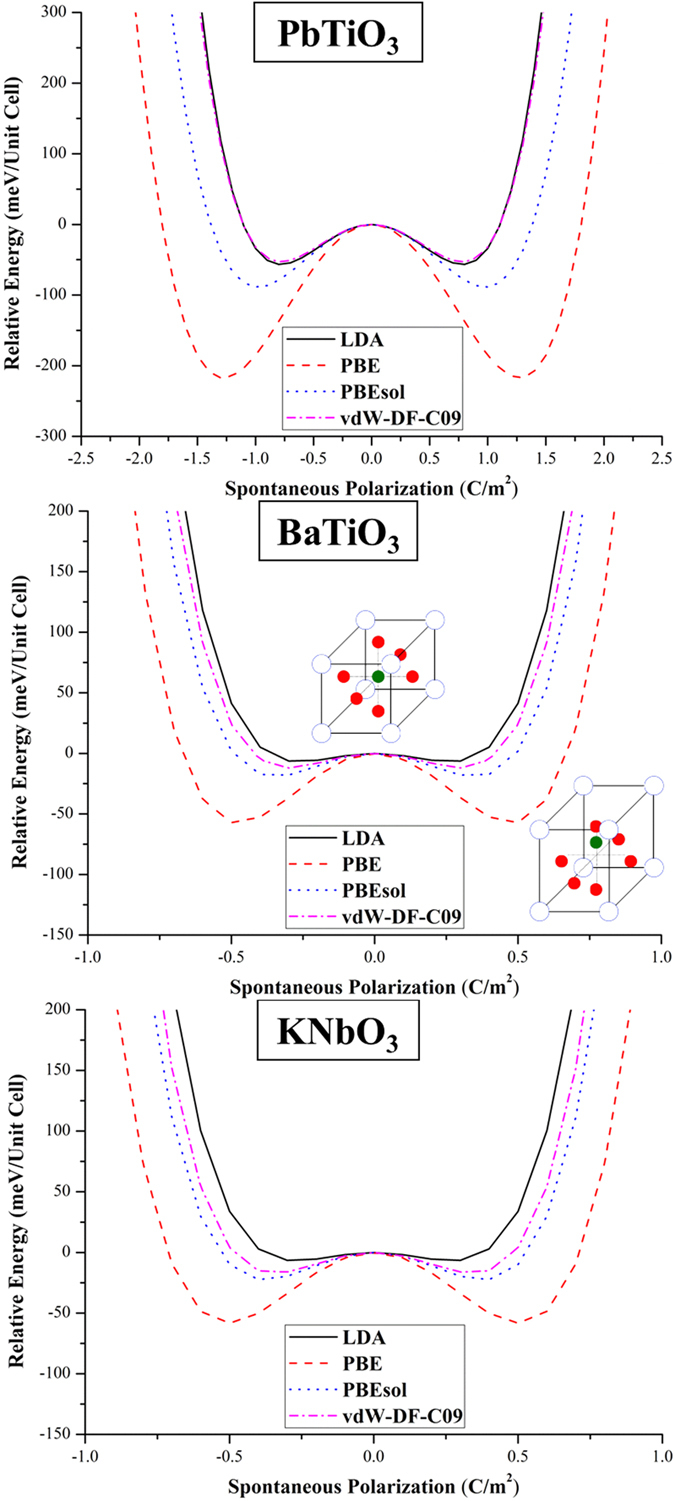
Figure 4

Open in a new tab

The fully optimized cubic structure was initially used for each perovskite. The lattice constants for the DFT optimized cubic structures are listed in the Supplementary information.

Ultimately, we would like to understand the effects of exchange correlation functionals on dynamic phenomena such as phase transitions, domain wall motion and piezoelectric response; thus requiring the need to perform Monte Carlo or molecular dynamics simulations. However, as a first approximation it is possible to estimate phase transition temperatures (Tc) from the cubic phase to the tetragonal phase in these materials using Landau theory. In this regards, Grinberg and Rappe demonstrated that there exists a strong dependence of Tc on the local structures of Pb- and Bi-based solid solutions71,72. Such dependence was expressed as a linear relationship between Tc and spontaneous polarization (P) in Landau theory as follows69:

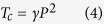graphic file with name srep43482-m7.jpg

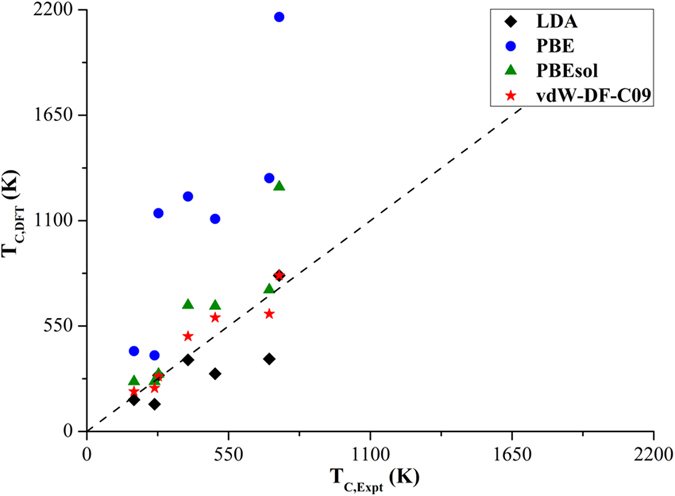
The constant γ of each crystal phase can be found by using the experimental spontaneous polarizations and temperatures. Thus, using such an approach, we can approximate Tc solely based on P from DFT calculations, as already summarized in Table 1. Of course, this approach cannot be used in a predictive sense as it requires experimental parameters to obtain the constant γ. Nevertheless, it emphasizes how small deviations in predictions of polarizations may be magnified in the prediction of other material behaviors. The estimated values of Tc from Equation (4) were determined over a large temperature range for different crystal phases of oxide perovskites, as shown in Fig. 5. Naturally, the phases with predicted P that are close to the experimental P yield the best agreement in Tc with experiment due to the nature of Equation (4). Again, the large variation in predicted temperatures is another indication that the exchange-correlation functional needs to be carefully chosen in order to accurately describe the ferroelectric phase transition of perovskite oxides.

Figure 5. Comparison of phase transition temperatures (TC,DFT) of PTO, BTO, and KNO in the different crystal phases relative to the experimental values.

Figure 5

Open in a new tab

Conclusions

In conclusion, we studied how the choice of exchange-correlation functional influences both the structural and ferroelectric properties of prototypical PbTiO3, BaTiO3, and KNbO3 perovskites. As expected, under- and overestimations of lattice parameters and spontaneous polarizations were observed for LDA and PBE, respectively. In contrast, the opposite trend was seen in estimating the bulk modulus arising from the dependence of total energy on volume. Such variations in spontaneous polarizations and bulk moduli are a good (first) indication of exchange and correlation effects in predicting the responses in these materials. We found that a functional designed to describe sparse matter, vdW-DF-C09, gives the best agreement with experimental values for the structural properties. Similar performance was previously observed for a limited test of the vdW-DF-cx functional for the cubic and tetragonal phases of PTO. Both potential-well depths and transition temperatures were also greatly affected by choice of functionals. Detailed analyses of the exchange enhancement factor reveal that the variations in properties are strongly tied to the behavior of enhancement factor observed in the small s region. The PBEsol and C09 exchange functionals reproduce the form of GEA, thereby being more appropriate functionals when studying dense solids. It is worth noting that other exchange functionals that are often paired with the vdW-DF nonlocal correlation functional, including cx and optB86b, have similar forms in the small s region and may behave similarly for dense matter53,54. Overall, the selection of exchange-correlation functionals can induce non-negligible variations in predicting macroscopic properties of ferroelectric perovskite oxides, stressing the importance of exchange-correlation effects on such systems. In any event, these results provide benchmarks for the class of vdW-DF functionals that help to emphasize the role that the exchange functional plays in defining structural (and perhaps dynamic) properties of materials. Nevertheless, such considerations should be taken into account in the design or parameterization of new empirical/phenomenological models for studying dynamic and temperature- and pressure-dependent properties of bulk complex oxides.

Additional Information

How to cite this article: Yuk, S. F. et al. Towards an accurate description of perovskite ferroelectrics: exchange and correlation effects. Sci. Rep. 7, 43482; doi: 10.1038/srep43482 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Information
srep43482-s1.pdf (363.6KB, pdf)

Acknowledgments

S.F.Y., M.E., and V.R.C. are supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division and the Office of Science Early Career Research Program. K.C.P. and S.M.N. are supported by the National Science Foundation (DMR 1309114). K.C.P. also acknowledges the internship through the Advanced Short Term Research Opportunity (ASTRO) program at Oak Ridge National Laboratory (ORNL), supported by the U.S. DOE, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division and the Office of Science Early Career Research Program. Y.W.L. is sponsored by the U.S. DOE, Office of Advanced Scientific Computing Research. We gratefully acknowledge the computational resources provided by the National Energy Research Scientific Computing Center (NERSC), which is supported by the Office of Science of the U.S. DOE under Contract No. DE-AC02-05CH11231 and the Oak Ridge Leadership Computing Facility (OLCF), which is supported by the Office of Science of the U.S. DOE under Contract No. DE-AC05-00OR22725.

Footnotes

The authors declare no competing financial interests.

Author Contributions V.R.C. conceived the original idea and S.F.Y. performed all the DFT calculations. S.F.Y., K.C.P., S.M.N., M.E., Y.W.L., and V.R.C. discussed and interpreted the results. S.F.Y. and V.R.C. led the writing and analysis efforts. S.F.Y. prepared the figures and table for the manuscript. All the authors reviewed and edited the manuscript.

References

  1. Jaffe B., Roth R. & Marzullo S. Piezoelectric Properties of Lead Zirconate-Lead Titanate Solid-Solution Ceramics. J. Appl. Phys. 25, 809–810 (1954). [Google Scholar]
  2. Jaffe B., Roth R. & Marzullo S. Properties of piezoelectric ceramics in the solid-solution series lead titanate-lead zirconate-lead oxide: tin oxide and lead titanate-lead hafnate. J. Res. Nat. Bur. Stand. 55, 239–254 (1955). [Google Scholar]
  3. Ouchi H., Nagano K. & Hayakawa S. Piezoelectric properties of Pb(Mg1/3Nb2/3)O3—PbTiO3—PbZrO3 solid solution ceramics. J. Am. Ceram. Soc. 48, 630–635 (1965). [Google Scholar]
  4. Ramesh R. Thin Film Ferroelectric Materials and Devices (Springer, 2013). [Google Scholar]
  5. Scott J. F. Ferroelectric Memories (Springer, 2013). [Google Scholar]
  6. Takenaka T., Maruyama K. & Sakata K. (Bi1/2Na1/2)TiO3-BaTiO3 system for lead-free piezoelectric ceramics. Jpn. J. Appl. Phys 30, 2236 (1991). [Google Scholar]
  7. Guo Y., Kakimoto K. & Ohsato H. (Na0.5K0.5)NbO3–LiTaO3 lead-free piezoelectric ceramics. Mater. Lett. 59, 241–244 (2005). [Google Scholar]
  8. Takenaka T. & Nagata H. Current status and prospects of lead-free piezoelectric ceramics. J. Eur. Ceram. Soc. 25, 2693–2700 (2005). [Google Scholar]
  9. Shrout T. R. & Zhang S. J. Lead-free piezoelectric ceramics: Alternatives for PZT? J. Electroceram. 19, 113–126 (2007). [Google Scholar]
  10. Yejing D., Xiaowen Z. & Kepi C. Morphotropic phase boundary and electrical properties of K1-xNaxNbO3 lead-free ceramics. Appl. Phys. Lett. 94, 042905 (2009). [Google Scholar]
  11. Zhong W., Vanderbilt D. & Rabe K. M. Phase Transitions in BaTiO3 from First Principles. Phys. Rev. Lett. 73, 1861 (1994). [DOI] [PubMed] [Google Scholar]
  12. Zhong W., Vanderbilt D. & Rabe K. M. First-principles theory of ferroelectric phase transitions for perovskites: the case of BaTiO3. Phys. Rev. B 52, 6301 (1995). [DOI] [PubMed] [Google Scholar]
  13. Waghmare U. V. & Rabe K. M. Ab initio statistical mechanics of the ferroelectric phase transition in PbTiO3. Phys. Rev. B 55, 6161 (1997). [Google Scholar]
  14. Vanderbilt D. First-principles based modelling of ferroelectrics. Curr. Opin. Solid State Mater. Sci. 2, 701–705 (1997). [Google Scholar]
  15. Cohen R. E. Theory of ferroelectrics: a vision for the next decade and beyond. J. Phys. Chem. Solids 61, 139–146 (2000). [Google Scholar]
  16. Walizer L., Lisenkov S. & Bellaiche L. Finite-temperature properties of (Ba, Sr)TiO3 systems from atomistic simulations. Phys. Rev. B 73, 144105 (2006). [Google Scholar]
  17. Bin-Omran S., Kornev I. A. & Bellaiche L. Wang-Landau Monte Carlo formalism applied to ferroelectrics. Phys. Rev. B 93, 014104 (2016). [Google Scholar]
  18. Sepliarsky M., Stachiotti M. G. & Migoni R. L. Ferroelectric soft mode and relaxation behavior in a molecular-dynamics simulation of KNbO3 and KTaO3. Phys. Rev. B 56, 566 (1997). [Google Scholar]
  19. Sepliarsky M., Asthagiri A., Phillpot S. R., Stachiotti M. G. & Migoni R. L. Atomic-level simulation of ferroelectricity in oxide materials. Curr. Opin. Solid State Mater. Sci. 9, 107–113 (2005). [Google Scholar]
  20. Sepliarsky M., Phillpot S. R., Stachiotti M. G. & Migoni R. L. Ferroelectric phase transitions and dynamical behavior in KNbO3/KTaO3 superlattices by molecular-dynamics simulation. J. Appl. Phys. 91, 3165–3171 (2002). [Google Scholar]
  21. Grinberg I., Cooper V. R. & Rappe A. M. Relationship between local structure and phase transitions of a disordered solid solution. Nature 419, 909–911 (2002). [DOI] [PubMed] [Google Scholar]
  22. Cooper V. R., Grinberg I. & Rappe A. M. In AIP Conference Proceedings. (eds Davies P. K. & Singh D. J.) 220–230 (American Institute of Physics, 2003). [Google Scholar]
  23. Shin Y.-H., Cooper V. R., Grinberg I. & Rappe A. M. Development of a bond-valence molecular-dynamics model for complex oxides. Phys. Rev. B 71, 054104 (2005). [Google Scholar]
  24. Tinte S., Stachiotti M. G., Sepliarsky M., Migoni R. L. & Rodriguez C. O. Atomistic modelling of BaTiO3 based on first-principles calculations. J. Phys. Condens. Matter 11, 9679 (1999). [Google Scholar]
  25. Bersuker I. B. Recent development of the vibronic theory of ferroelectricity. Ferroelectrics 164, 75–100 (1995). [Google Scholar]
  26. Tinte S., Íñiguez J., Rabe K. M. & Vanderbilt D. Quantitative analysis of the first-principles effective Hamiltonian approach to ferroelectric perovskites. Phys. Rev. B 67, 064106 (2003). [Google Scholar]
  27. Bersuker I. B. The Jahn-Teller Effect (Cambridge University Press, 2006). [Google Scholar]
  28. Lejaeghere K., Van Speybroeck V., Van Oost G. & Cottenier S. Error estimates for solid-state density-functional theory predictions: an overview by means of the ground-state elemental crystals. Crit. Rev. Solid State Mater. Sci. 39, 1–24 (2014). [Google Scholar]
  29. Lejaeghere K. et al. Reproducibility in density functional theory calculations of solids. Science 351, aad3000 (2016). [DOI] [PubMed] [Google Scholar]
  30. Tinte S., Stachiotti M. G., Rodriguez C. O., Novikov D. L. & Christensen N. E. Applications of the generalized gradient approximation to ferroelectric perovskites. Phys. Rev. B 58, 11959 (1998). [Google Scholar]
  31. King-Smith R. D. & Vanderbilt D. First-principles investigation of ferroelectricity in perovskite compounds. Phys. Rev. B 49, 5828 (1994). [DOI] [PubMed] [Google Scholar]
  32. Cohen R. E. & Krakauer H. Lattice dynamics and origin of ferroelectricity in BaTiO3: Linearized-augmented-plane-wave total-energy calculations. Phys. Rev. B 42, 6416 (1990). [DOI] [PubMed] [Google Scholar]
  33. Cohen R. E. & Krakauer H. Electronic structure studies of the differences in ferroelectric behavior of BaTiO3 and PbTiO3. Ferroelectrics 136, 65–83 (1992). [Google Scholar]
  34. Cohen R. E. Origin of ferroelectricity in perovskite oxides. Nature 358, 136–138 (1992). [Google Scholar]
  35. Singh D. J. & Boyer L. L. First principles analysis of vibrational modes in KNbO3. Ferroelectrics 136, 95–103 (1992). [Google Scholar]
  36. Singh D. J. Local density and generalized gradient approximation studies of KNbO3 and BaTiO3. Ferroelectrics 164, 143–152 (1995). [Google Scholar]
  37. Rabe K. M., Triscone J.-M. & Ahn C. H. Modern Ferroelectrics. (Springer, 2007). [Google Scholar]
  38. Wu Z. & Cohen R. E. More accurate generalized gradient approximation for solids. Phys. Rev. B 73, 235116 (2006). [Google Scholar]
  39. Perdew J. P. et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100, 136406 (2008). [DOI] [PubMed] [Google Scholar]
  40. Bilc D. I. et al. Hybrid exchange-correlation functional for accurate prediction of the electronic and structural properties of ferroelectric oxides. Phys. Rev. B 77, 165107 (2008). [Google Scholar]
  41. Wahl R., Vogtenhuber D. & Kresse G. SrTiO3 and BaTiO3 revisited using the projector augmented wave method: Performance of hybrid and semilocal functionals. Phys. Rev. B 78, 104116 (2008). [Google Scholar]
  42. Rydberg H. et al. Van der Waals density functional for layered structures. Phys. Rev. Lett. 91, 126402 (2003). [DOI] [PubMed] [Google Scholar]
  43. Dion M., Rydberg H., Schröder E., Langreth D. C. & Lundqvist B. I. Van der Waals density functional for general geometries. Phys. Rev. Lett. 92, 246401 (2004). [DOI] [PubMed] [Google Scholar]
  44. Thonhauser T. et al. Van der Waals density functional: Self-consistent potential and the nature of the van der Waals bond. Phys. Rev. B 76, 125112 (2007). [Google Scholar]
  45. Klimeš J., Bowler D. R. & Michaelides A. Chemical accuracy for the van der Waals density functional. J. Phys. Condens. Matter 22, 022201 (2009). [DOI] [PubMed] [Google Scholar]
  46. Román-Pérez G. & Soler J. M. Efficient implementation of a van der Waals density functional: application to double-wall carbon nanotubes. Phys. Rev. Lett. 103, 096102 (2009). [DOI] [PubMed] [Google Scholar]
  47. Cooper V. R. Van der Waals density functional: An appropriate exchange functional. Phys. Rev. B 81, 161104 (2010). [Google Scholar]
  48. Lee K., Murray É. D., Kong L., Lundqvist B. I. & Langreth D. C. Higher-accuracy van der Waals density functional. Phys. Rev. B 82, 081101 (2010). [Google Scholar]
  49. Vydrov O. A. & Van Voorhis T. Nonlocal van der Waals density functional: The simpler the better. J. Chem. Phys. 133, 244103 (2010). [DOI] [PubMed] [Google Scholar]
  50. Klimeš J., Bowler D. R. & Michaelides A. Van der Waals density functionals applied to solids. Phys. Rev. B 83, 195131 (2011). [Google Scholar]
  51. Lee K., Kolb B., Thonhauser T., Vanderbilt D. & Langreth D. C. Structure and energetics of a ferroelectric organic crystal of phenazine and chloranilic acid. Phys. Rev. B 86, 104102 (2012). [Google Scholar]
  52. Berland K. et al. van der Waals density functionals built upon the electron-gas tradition: Facing the challenge of competing interactions. J. Chem. Phys. 140, 18A539 (2014). [DOI] [PubMed] [Google Scholar]
  53. Berland K. et al. van der Waals forces in density functional theory: a review of the vdW-DF method. Rep. Prog. Phys. 78, 066501 (2015). [DOI] [PubMed] [Google Scholar]
  54. Berland K. & Hyldgaard P. Exchange functional that tests the robustness of the plasmon description of the van der Waals density functional. Phys. Rev. B 89, 035412 (2014). [Google Scholar]
  55. Gharaee L., Erhart P. & Hyldgaard P. Finite-temperature properties of non-magnetic transition metals: Comparison of the performance of constraint-based semi and nonlocal functionals. arXiv:1612.00425 (2016).
  56. Giannozzi P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009). [DOI] [PubMed] [Google Scholar]
  57. Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892 (1990). [DOI] [PubMed] [Google Scholar]
  58. Garrity K. F., Bennett J. W., Rabe K. M. & Vanderbilt D. Pseudopotentials for high-throughput DFT calculations. Comput. Mater. Sci. 81, 446–452 (2014). [Google Scholar]
  59. Ceperley D. M. & Alder B. J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 45, 566 (1980). [Google Scholar]
  60. Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996). [DOI] [PubMed] [Google Scholar]
  61. King-Smith R. D. & Vanderbilt D. Theory of polarization of crystalline solids. Phys. Rev. B 47, 1651 (1993). [DOI] [PubMed] [Google Scholar]
  62. Birch F. Finite elastic strain of cubic crystals. Phys. Rev. 71, 809 (1947). [Google Scholar]
  63. Lines M. E. & Glass A. M. Principles and Applications of Ferroelectrics and Related Materials. (Oxford University Press, 1977). [Google Scholar]
  64. Rabe K. M., Dawber M., Lichtensteiger C., Ahn C. H. & Triscone J.-M. Modern Physics of Ferroelectrics: Essential Background. (Springer, 2007). [Google Scholar]
  65. Ogawa T. In Ferroelectric Materials - Synthesis and Characterization (eds Barranco A. P.) 33–58 (InTech, 2015). [Google Scholar]
  66. Grabowski B., Hickel T. & Neugebauer J. Ab initio study of the thermodynamic properties of nonmagnetic elementary fcc metals: Exchange-correlation-related error bars and chemical trends. Phys. Rev. B 76, 024309 (2007). [Google Scholar]
  67. Sham L. J. Computational Methods in Band Theory. (Plenum, 1971). [Google Scholar]
  68. Zhang Y. & Yang W. Comment on “Generalized gradient approximation made simple”. Phys. Rev. Lett. 80, 890 (1998). [DOI] [PubMed] [Google Scholar]
  69. Landau L. D. On the theory of phase transitions. I. Zh. Eksp. Teor. Fiz. 11, 19 (1937). [Google Scholar]
  70. Dall’Olio S., Dovesi R. & Resta R. Spontaneous polarization as a Berry phase of the Hartree-Fock wave function: The case of KNbO3. Phys. Rev. B 56, 10105 (1997). [Google Scholar]
  71. Grinberg I. & Rappe A. M. Local structure and macroscopic properties in PbMg1∕ 3Nb2∕ 3O3 − PbTiO3 and PbZn1∕ 3Nb2∕ 3O3 − PbTiO3 solid solutions. Phys. Rev. B 70, 220101 (2004). [Google Scholar]
  72. Grinberg I. & Rappe A. M. Nonmonotonic TC Trends in Bi-Based Ferroelectric Perovskite Solid Solutions. Phys. Rev. Lett. 98, 037603 (2007). [DOI] [PubMed] [Google Scholar]
  73. Mabud S. A. & Glazer A. M. Lattice parameters and birefringence in PbTiO3 single crystals. J. Appl. Crystallogr. 12, 49–53 (1979). [Google Scholar]
  74. Sani A., Hanfland M. & Levy D. The equation of state of PbTiO3 up to 37 GPa: a synchrotron x-ray powder diffraction study. J. Phys. Condens. Matter 14, 10601 (2002). [Google Scholar]
  75. Shirane G., Pepinsky R. & Frazer B. X-ray and neutron diffraction study of ferroelectric PbTiO3. Acta Crystallographica 9, 131–140 (1956). [Google Scholar]
  76. Costa S. C., Pizani P. S., Rino J. P. & Borges D. S. Structural phase transition and dynamical properties of PbTiO3 simulated by molecular dynamics. J. Phys. Condens. Matter 17, 5771 (2005). [DOI] [PubMed] [Google Scholar]
  77. Haun M. J., Furman E., Jang S. J., McKinstry H. A. & Cross L. E. Thermodynamic theory of PbTiO3. J. Appl. Phys. 62, 3331–3338 (1987). [Google Scholar]
  78. Jabarov S. G. et al. High-pressure effect on the ferroelectric-paraelectric transition in PbTiO3. Phys. Solid State 53, 2300–2304 (2011). [Google Scholar]
  79. Hellwege K. H. & Hellwege A. M. Ferroelectrics and Related Substances. (Springer, 1969). [Google Scholar]
  80. Fischer G. J., Wang Z. & Karato S.-I. Elasticity of CaTiO3, SrTiO3 and BaTiO3 perovskites up to 3.0 GPa: the effect of crystallographic structure. Phys. Chem. Miner. 20, 97–103 (1993). [Google Scholar]
  81. Kwei G. H., Lawson A. C., Billinge S. J. L. & Cheong S. W. Structures of the ferroelectric phases of barium titanate. J. Phys. Chem. 97, 2368–2377 (1993). [Google Scholar]
  82. Wieder H. H. Electrical behavior of barium titanatge single crystals at low temperatures. Phys. Rev. 99, 1161 (1955). [Google Scholar]
  83. Chiang Y.-M., Kingery W. D. & Birnie D. P. Physical Ceramics: Principles for Ceramic Science and Engineering. (John Wiley & Sons, 1997). [Google Scholar]
  84. Shirane G., Danner H. & Pepinsky R. Neutron Diffraction Study of Orthorhombic BaTiO3. Phys. Rev. 105, 856 (1957). [Google Scholar]
  85. Hewat A. W. Structure of rhombohedral ferroelectric barium titanate. Ferroelectrics 6, 215–218 (1973). [Google Scholar]
  86. Hewat A. W. Cubic-tetragonal-orthorhombic-rhombohedral ferroelectric transitions in perovskite potassium niobate: neutron powder profile refinement of the structures. J. Phys. C: Solid State Phys. 6, 2559 (1973). [Google Scholar]
  87. Chervin J. C., Itié J. P., Gourdain D. & Pruzan P. Energy dispersive X-ray diffraction study of KNbO3 up to 19 GPa at room temperature. Solid State Commun. 110, 247–251 (1999). [Google Scholar]
  88. Kleemann W., Schäfer F. J. & Fontana M. D. Crystal optical studies of spontaneous and precursor polarization in KNbO3. Phys. Rev. B 30, 1148 (1984). [DOI] [PubMed] [Google Scholar]
  89. Shirane G., Newnham R. & Pepinsky R. Dielectric Properties and Phase Transitions of NaNbO3 and (Na, K)NbO3. Phys. Rev. 96, 581 (1954). [Google Scholar]
  90. Gourdain D. et al. Compression of KNbO3 up to 30 GPa: Transition sequence orthorhombic → tetragonal → cubic. Phys. Rev. B 65, 054104 (2002). [Google Scholar]
  91. Michel-Calendini F. M., Peltier M. & Micheron F. Electron paramagnetic resonance of Fe3+ in orthorhombic KNbO3. Solid State Commun. 33, 145–150 (1980). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep43482-s1.pdf (363.6KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES