Abstract.
Recently, a class of no-gold-standard (NGS) techniques have been proposed to evaluate quantitative imaging methods using patient data. These techniques provide figures of merit (FoMs) quantifying the precision of the estimated quantitative value without requiring repeated measurements and without requiring a gold standard. However, applying these techniques to patient data presents several practical difficulties including assessing the underlying assumptions, accounting for patient-sampling-related uncertainty, and assessing the reliability of the estimated FoMs. To address these issues, we propose statistical tests that provide confidence in the underlying assumptions and in the reliability of the estimated FoMs. Furthermore, the NGS technique is integrated within a bootstrap-based methodology to account for patient-sampling-related uncertainty. The developed NGS framework was applied to evaluate four methods for segmenting lesions from F-Fluoro-2-deoxyglucose positron emission tomography images of patients with head-and-neck cancer on the task of precisely measuring the metabolic tumor volume. The NGS technique consistently predicted the same segmentation method as the most precise method. The proposed framework provided confidence in these results, even when gold-standard data were not available. The bootstrap-based methodology indicated improved performance of the NGS technique with larger numbers of patient studies, as was expected, and yielded consistent results as long as data from more than 80 lesions were available for the analysis.
Keywords: no-gold-standard evaluation, positron emission tomography segmentation, quantitative imaging biomarkers, metabolic tumor volume
1. Introduction
Quantitative imaging, i.e., the measurement and use of numerical or statistical features from medical images to facilitate clinical decision making,1 is finding applications in many diagnostic and therapeutic procedures. A particularly important application is quantitative imaging biomarkers (QIBs). Various QIBs are being explored for clinical usage, including tumor standardized uptake value (SUV), metabolic tumor volume (MTV), and total lesion glycolysis (TLG) measured from -Fluoro-2-deoxyglucose positron emission tomography (18F-FDG PET),2–10 apparent diffusion coefficient measured with diffusion magnetic resonance imaging,11,12–13 and dopamine transporter using single-photon emission computed tomography.14
A major challenge in QIB development is that the quantitative metrics should be measured precisely.15–17 Precision is related to variability and defined as the closeness of agreement between measured quantity values obtained by replicate measurements on the same experimental units under specified conditions.18,19 To illustrate the importance of precision, consider a longitudinal study where a change in the MTV value at different time points in a treatment is being proposed to assess whether a patient is responding to therapy, and thus decide if the treatment should be continued. If the measured MTV values at different time points are highly imprecise, then it will be complicated to determine if the measured change in MTV value is due to an actual change in the MTV or simply due to a random error in the measurement.
There could be different sources of imprecision in the imaging chain in a clinical study, ranging from variabilities arising due to tumor biology, patient state, scanner calibration, and the imaging method, where the imaging method includes any combination of image-reconstruction, image-analysis or metric-estimation procedures.20 In a clinical setting, it is usually impossible to separate these sources of variability. In this context, it is highly desirable, as also recommended by the Quantitative Imaging Biomarkers Alliance (QIBA) Terminology Working Group, that the different sources of imprecision be separated.18 In this manuscript, the focus is on isolating and quantifying the imprecision arising due to the imaging method, and more specifically, to develop a framework to evaluate imaging methods based on how precisely they measure the true quantitative metric.
Typically, imaging methods are evaluated using animal, physical-phantom, and realistic simulation studies where information about the ground truth quantitative metric is available. While these studies are important, they suffer from limitations, mainly in their inability to model the complex anatomy and physiology of human systems.20,21 Thus, there is an important need for a procedure to evaluate precision of imaging methods with patient studies. One such procedure could be acquiring repeated measurements of the same quantitative metric in the patient, for example, via test–retest studies.18 In these studies, two or more scans of a patient are acquired assuming there is no biological change in the quantitative metric in the time between these measurements.18,20 However, such studies are expensive, time consuming, and may lead to increased patient dose and patient inconvenience.16,20 Furthermore, the computed precision value could include the variability arising due to the biological, patient, and scanner-calibration-related factors.18,20 Finally, these studies are typically limited to a single repeated measure due to possible risks to patients from reimaging. Thus, the computed precision often includes substantial uncertainty. Therefore, a procedure to estimate the precision of the imaging method without requiring repeated measurements is highly desirable.
While test–retest studies are difficult to perform, obtaining measurements of quantitative values from a population of patients is much easier. If the true quantitative values for these patients were known, or a reliable gold standard was available as a substitute for the true value, and if a relationship between the true and measured quantitative values could be assumed, then a measurement of the precision of the quantitative value over the patient population could be easily obtained using regression techniques. This is explained in detail in Sec. 2.1. However, the true values are typically unknown and gold standards are not easily available with patient data. A procedure to compute the precision of the imaging methods with patient data in the absence of a gold standard would help resolve this issue.
To compute the precision of quantitative imaging methods in the absence of a gold standard, a regression-without-truth (RWT) technique has been proposed.22,23 This technique assumes that the measured quantitative values obtained using each imaging method are linearly related to the true quantitative values, and that the true quantitative values have been sampled from a distribution with known upper and lower limits. This approach has been used to compare software packages24 and segmentation methods25 on the task of measuring the cardiac ejection fraction. However, for some quantitative metrics, such as the MTV, the upper and lower limits on the distribution of true values are not known a priori. To overcome this issue, the RWT procedure has been extended to a more general no-gold-standard (NGS) technique. This technique does not require knowledge of the exact lower and upper bounds of the distribution of true values.21 The technique estimates figures of merit (FoMs) that can quantify the performance of the imaging method based on how precisely they measure the true quantitative value over a population of patients. Validations with numerical experiments21 and realistic simulation studies conducted in the context of evaluating reconstruction methods for quantitative nuclear-medicine imaging21,26 and segmentation methods for diffusion MRI27,28 have provided strong evidence in support of the technique. However, the NGS technique has not yet been applied to patient data.
Application of the NGS technique to patient data poses several practical difficulties. First, the NGS technique assumes that the true and measured quantitative values using each of the methods are related linearly. It has been observed that the technique does not evaluate the methods accurately when this assumption is violated.21 However, it is impossible to validate this assumption in the absence of a gold standard. Another challenge is the difficulty in verifying the reliability of the FoMs estimated by the NGS technique in the absence of a gold standard. Finally, the NGS technique is applied to a random subset of the patient population. This yields an uncertainty in the estimated FoM. This uncertainty must be accounted for so that the results are generalizable to larger patient populations. In this manuscript, our primary objective was to develop an NGS framework that consisted of strategies to overcome these practical challenges in applying the NGS technique.
The NGS framework was applied to evaluate FDG-PET tumor-segmentation methods on the task of estimating the MTV. The tumor segmentation task in PET is complicated due to random factors, such as noise and variability in the shape, texture, and location of tumors.29 A segmentation procedure that is substantially affected by these random factors could yield an imprecise MTV value. Thus, evaluating PET segmentation methods on the task of precisely measuring the MTV value is essential. This evaluation is facilitated by the knowledge of the true MTV value or a suitable gold standard for comparison, but these are often very difficult to obtain for patients. Typically, the only reference standards are obtained from manual segmentations, but these suffer from substantial inter- and intrareader variability.30 Thus, an NGS methodology for the task of evaluating PET segmentation methods is highly significant. Consequently, we chose this task to demonstrate the application of the NGS framework.
2. Development of the No-Gold-Standard Framework
2.1. No-Gold-Standard Evaluation Technique: Theory
A detailed mathematical description and validation of the NGS evaluation technique has been presented previously.21 We provide a brief summary of the NGS evaluation technique here, with a focus on the intuition behind the technique.
Consider the case where a quantitative value is estimated for a particular patient. Suppose that there are different imaging methods available to measure this value. For example, in the context of FDG-PET imaging, the quantitative value could be the MTV. To measure the MTV, the tumor must be delineated, for which different segmentation methods are available. Suppose that we intend to evaluate different imaging methods based on their performance in measuring the true quantitative value. Denote the number of measurements from all the patient images by . For the ’th measurement, denote the true value and the value measured using the ’th segmentation method by and , respectively. Further, let denote the mean value of . For this case, the precision for the ’th method, denoted by , is defined as Ref. 20:
| (1) |
The NGS evaluation method assumes that the true and measured values using each of the methods are related. The relationship consists of a deterministic and a random component. The deterministic component is assumed to be linear, characterized by a slope and bias term. The random component is characterized by a normally distributed noise term. It is assumed that the slope, bias, and noise terms are unique for the different methods and independent of the true value. Denote the slope, bias, and the standard deviation of the noise term for the ’th segmentation method by , , and , respectively. The linear relationship between the true and measured values for the ’th imaging method is given as follows:
| (2) |
where denotes a zero-mean normally distributed noise term with standard deviation . Under this assumption, the mean value of is given as follows:
| (3) |
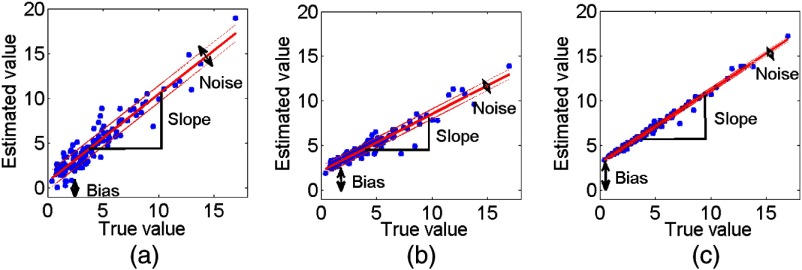
Substituting the expressions from Eqs. (2) and (3) into Eq. (1) shows that the precision is equal to the standard deviation term . Intuitively also, as illustrated in Fig. 1, the method with the highest value of the noise standard deviation would be the most imprecise.20 Thus, under the assumption of this linear relationship, if we could estimate these linear relationship terms, we could design FoMs to evaluate the different methods.
Fig. 1.
Scatter plots of the true versus measured MTV values using three different segmentation methods. The corresponding linear relationships for the three methods are superimposed on each scatter plot. The solid line is the line defined by the slope and bias terms, while the dashed lines denote one standard deviation above and below. The plots illustrate that under the linearity assumption, the segmentation methods that are most imprecise (method 1) over the range of true values have the highest noise standard deviation.
Denote the parameters in Eq. (1) by the vector . Furthermore, assume that the true values have been sampled from a four-parameter beta distribution (FPBD). The FPBD is characterized by two shape parameters ( and ) and upper and lower limits, denoted by and , respectively. The reason for choosing this form for the distribution of true values has been previously described in detail.21 Denote the parameters of the FPBD by the vector . Under these assumptions, using properties of conditional probability, a mathematical expression for the distribution of the values can be obtained that depends only on the linear relationship and FPBD parameters, and does not depend on the true values .21 Using a maximum-likelihood (ML) approach, the linear relationship and FPBD parameters that maximize the probabilities of the measured values using all the imaging methods can be estimated. Denoting the ML estimates of and by and , respectively, the equation to be solved is given as follows:
| (4) |
Note that solving the above equation does not require any knowledge of the true values,. Therefore, the above-formalism allows estimating the linear-relationship parameters without any knowledge of the true values.
The NGS technique has been developed and implemented in software running under MATLAB® using a previously described procedure.21 To determine the ML estimates , a constrained-optimization technique based on the interior-point algorithm was used. This optimization routine searches between reasonable values of the and parameters. This search space typically depends on the evaluation task. The procedure for defining the search space to evaluate the FDG-PET segmentation methods is described in Sec. 3.1.
We have shown through numerical simulations that the noise standard deviation and the slope terms are estimated accurately using the above-described NGS technique.21 As mentioned earlier, the noise term quantifies the precision. Since the slope is estimated accurately, the measured values could be recalibrated using the slope term. In that case, using Eq. (2), the noise standard deviation term would be scaled by the reciprocal of the slope term. It is easy to show that the precision would then be given by the ratio of the noise standard deviation to the slope for each method, also referred to as the noise-to-slope ratio (NSR). The NSR metric has been widely used for evaluating imaging methods using NGS techniques on the basis of precision.21,22,24–27 However, to evaluate the imaging methods, instead of directly comparing the NSRs for the different methods, we suggest an alternative strategy that accounts for the uncertainty in the NSR metric. Before describing that strategy, we provide an intuitive explanation for how the NGS technique estimates the linear-relationship parameters for the different methods.
2.2. Intuitive Explanation of the No-Gold-Standard Technique
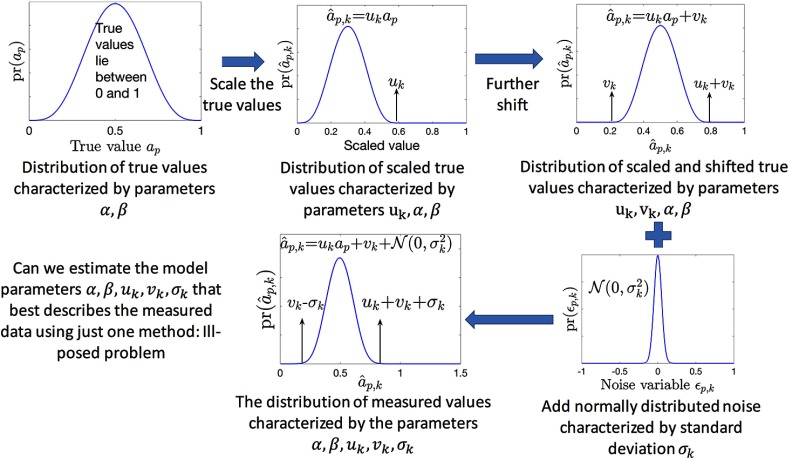
For the sake of simplicity, consider the case where the true values are drawn from a beta distribution, which is a specific case of an FPBD but with the upper and lower limits, i.e., and , equal to 1 and 0, respectively. This beta distribution is only characterized by the two terms and , which describe the shape of this distribution.
Consider that the output from the ’th imaging method follows the relationship defined in Eq. (2). In that case, as illustrated pictorially in Fig. 2, the distribution of measured values for the ’th imaging method can be described by the parameters . Thus, theoretically, a statistical technique could be designed to estimate from all the measurements made with the ’th imaging method. For example, we could design an ML technique that estimates those values of that maximize the probability of all the observed measurements. However, numerical studies indicate that the estimation of these parameters is an ill-posed problem when measurements from just one imaging method are used. This is because, in that case, the parameters are not always identifiable, i.e., two different combinations of these parameters can yield the same distribution of measured values.
Fig. 2.
Schematic illustrating the parameterized form for the distribution of measured values.
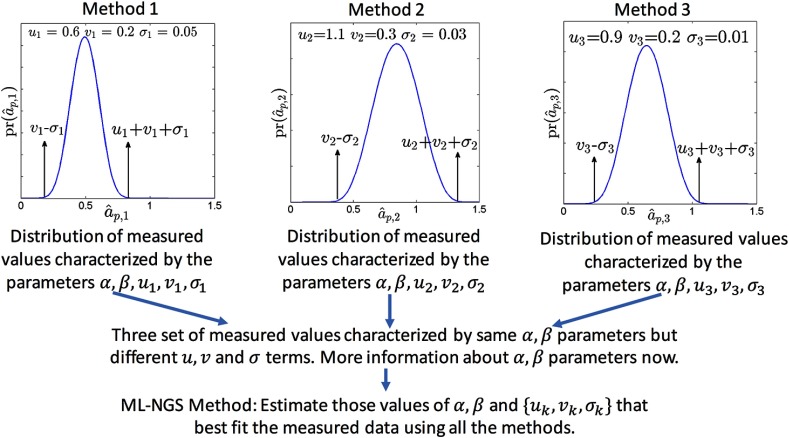
The parameters become more identifiable, or uniquely defined, when we consider measurements from all the imaging methods. This is because the different sets of independent measurements are all characterized by the same parameters but each has a different set of , as illustrated in Fig. 3. Thus, an ML-based technique, similar to the RWT technique, or a method-of-moments technique, similar to that proposed in Dunn and Roberts,31 could be used to estimate these parameters. It has been observed through numerical experiments with the RWT technique that, when data from three or more imaging methods are available, the slope, bias, and standard deviation terms of the different methods are estimated accurately.22
Fig. 3.
Schematic illustrating the intuition behind how the NGS technique estimates the model parameters.
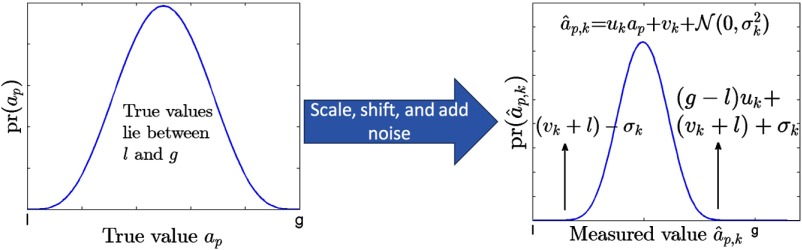
Now, consider the case where both the upper and lower limits of the FPBD are unknown. In this case, the distribution of the measured values with the ’th imaging method is depicted as in Fig. 4. Note that, in this case, the bias term always appears in the expressions for the distribution of the measured values in the form . Thus, it can be argued that the statistical identifiability of the bias term is poor. In fact, it has been observed in several numerical experiments that when the upper and lower limits of the GBD are not known, the bias term is not estimated reliably using the ML-based NGS technique described in Sec. 2.1.21 The slope and noise terms, however, are still estimated reliably.21 Therefore, even when the upper and lower limits of the FPBD are unknown, the NGS method estimates the NSR reliably.
Fig. 4.
The distribution of measured values when the true values are sampled from a GBD with upper and lower limits of g and l. Note that in a heuristic description of the distribution of measured values, the bias term always appears with the lower limit as one unit, .
2.3. Checking the Linearity Assumption with Patient Data
The NGS technique assumes that the measured and true quantitative values are linearly related for each of the imaging methods. In the absence of a gold standard, this assumption cannot be directly validated. However, if the true values are linearly related to the measured value for each of the methods, then the measurements using two different methods must also be linearly related. Stated alternatively, linearity between the measurements using the different methods is a necessary condition for the measurements to be related linearly to the true values, as formally proved in the Appendix.
Using this fact, the linearity between the values from the different imaging methods was assessed before applying the NGS technique. A scatter plot of the measured values using different pairs of segmentation methods was constructed to verify the linearity. Furthermore, the strength of the linearity was quantified using the Pearson’s correlation coefficient between the measured values for different pairs of imaging methods. A value close to unity provided evidence of a linear relationship between the measured values from different pairs of methods.
2.4. Using the No-Gold-Standard Technique Outputs to Evaluate the Segmentation Methods
The ultimate objective with the NGS technique is to determine the most precise of all the compared segmentation methods. As described above, the NGS technique yields the NSR value for each method from one set of patient data. However, this patient dataset is a randomly drawn subset from the entire population of patients. Due to this random sampling, there is an uncertainty in the FoM estimated using the NGS technique. Quantifying this uncertainty and accounting for it while predicting the most precise imaging method is important.
To accomplish this task, we developed a bootstrap-based approach similar to that suggested by Obuchowski et al.20 The basic idea of bootstrapping is that information about some statistic of interest about a population can be obtained from sample data by resampling the sample data with replacement many times and computing the statistic of interest from these. We chose the statistic of interest to be the difference of the NSR values between a candidate for the best imaging method and the other imaging methods. The motivation behind choosing this difference as the statistic of interest was the following. Consider two methods, method A and method B, with their NSR values denoted by and , respectively. A common test to declare that method A is superior to, i.e., in this case, more precise than, method B is to show that the one-sided confidence interval (CI) for is included in .20 In other words, if denotes the upper limit of the CI, then we need to check if . Thus, by determining the CI for using the bootstrap-based procedure, we can assess whether method A is more precise than method B. As is standard practice, we determined the 95% CI by setting .
The following procedure was used to determine the best imaging method using the NGS technique. Denote the vector of measurements for the ’th patient using all imaging methods, i.e., by the vector . The vector of measurements from the patients was sampled times with replacement to form a bootstrap dataset. This bootstrap dataset was input to the NGS technique and the NSR values for all the imaging methods were estimated. The bootstrap process was repeated for multiple trials. The method with the lowest NSR for a majority of the bootstrap trials was chosen as a candidate for the most precise method. Denote the NSR for the candidate for the most precise method by , and the NSR for the ’th method by .
Next, the difference of the NSR values between the candidate method and other methods, i.e., , denoted by , was computed. From the multiple bootstrap trials, the 2.5 and 97.5 percentiles of were computed, providing the upper and lower limits of the 95% CI. We checked whether the upper limit of this CI was less than 0 for each of the considered pair of methods. If so, this demonstrated that the superiority of the candidate method was statistically significant.
2.5. Consistency Checks
In the absence of a gold standard, it is not possible to verify whether the NGS technique has yielded the correct rankings. However, tests can be implemented to indicate whether the parameters estimated using the NGS technique are consistent with the measured data. For this purpose, we extend a consistency check initially proposed in Kupinski et al.24
This consistency check uses the fact that the NGS technique yields parameters that relate the gold standard to measurements from a method with the relationship given in Eq. (2). Using these estimated parameters, we can predict the relationship between the measurements using two different methods. Mathematically, consider the ’th and the ’th segmentation methods. The relationship between the measurements from these methods, as predicted using the NGS technique, is obtained by solving for the gold standard for each of the measurements and , as follows:
| (5) |
If the NGS technique estimated the bias and the slope terms accurately, then the above-predicted relationship between the measurements obtained using the ’th and ’th segmentation methods should match the actual relationship of the measurements using these methods. In other words, the line defined by Eq. (5) should overlap with the scatter plot of the actual measurements obtained using the ’th and ’th methods. We quantify this overlap using the coefficient of determination. If the value is close to unity, this indicates that the relationship between the measured values matches the relationship defined by Eq. (5); smaller values of the coefficient are an indication that the output from the NGS technique is inaccurate.
It must be pointed that the success of this consistency check does not guarantee that the NGS technique has yielded accurate NSR values. However, a failure of this check indicates that the output using the NGS technique must be used with caution.
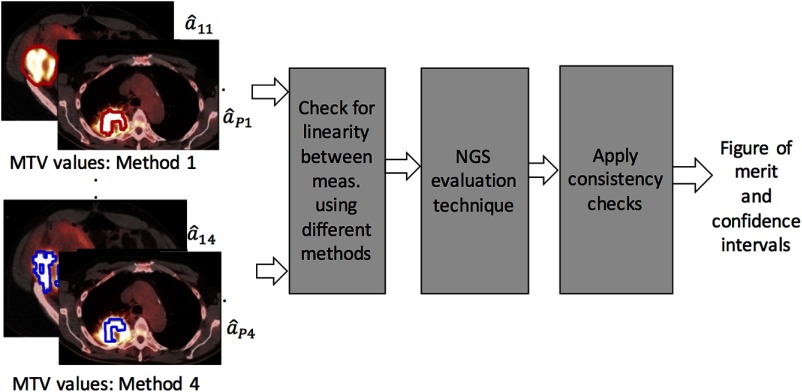
A schematic of the proposed NGS framework is as shown in Fig. 5.
Fig. 5.
A schematic of the proposed NGS framework in the context of evaluating four image-segmentation methods.
3. Application of the No-Gold-Standard Framework to Patient Data
3.1. Patient-Data Acquisition
We retrospectively conducted a PET segmentation study including data from a total of 128 patients (mean age years old, range 29 to 83 years old) with histologically proven newly diagnosed oropharyngeal head and neck squamous cell carcinoma. The patients underwent a baseline PET/CT staging between 2007 and 2014. This was an Institutional review board approved, HIPAA-compliant, retrospective study, with a waiver for obtaining informed consent. None of the patients had surgical intervention, radiation therapy or systemic chemotherapy before being scanned with PET/CT. Patients with uncontrolled diabetes, active inflammation, or with a second primary malignancy, were excluded.
All patients were instructed to fast for at least 4 h before scanning, and the weight, height, and blood glucose level was recorded for each patient before FDG administration. The mean blood glucose level was (range, 61 to ), and the average injected dose was 16.7 mCi (617.9 MBq) [range, 9.4 to 24.7 mCi (347.8 to 913.9 MBq)]. Patients were initially scanned from the base of the skull to mid-thigh region, and then with a second dedicated PET/CT acquisition of the head and neck region acquired in a single field-of-view (FoV). The mean time interval between the injection of and the scan was (range, 51 to 81 min).
Patients were scanned using a 64-MDCT lutetium oxyorthosilicate crystal scanner (Discovery DVT, GE Healthcare), in 3-D acquisition mode with 4.15 min per bed position. The images were reconstructed using the ordered subset-expectation maximization (OS-EM) algorithm, a matrix, two iterations of 21 subsets, a 3-mm postreconstruction Gaussian filter and standard Z filter, a 4.7-mm pixel size, and a 3.27-mm slice thickness. All PET data were reconstructed with and without CT-based attenuation compensation using a noncontrast CT acquisition for attenuation correction and for anatomical co-registration. The CT parameters were 50-cm axial dynamic FoV, weight-based amperage (20 to 200 automated mA), 120 to 40 kVp, 3.75-mm reconstructed slice thickness, pitch of 0.984, 0.5-s gantry rotation speed and matrix.2
3.2. Image Analysis and Segmentation Methods Compared
An experienced board-certified nuclear medicine physician reviewed the FDG-PET/CT images using a MIM workstation (MIM Vista Software, version 5.2). Since inter-reader reliability for automatic PET volumetric segmentation has been previously established,30 only one reader was used for the image analysis. Axial, coronal, and sagittal PET, CT and fused PET/CT images were used for the visual qualitative identification of the oropharyngeal primary malignancy and the cervical lymph node involvement sites. A total of 80 primary tumors and 62 cervical lymph nodes were assessed using an automated semiquantitative PET segmentation. MTV values expressed as tumor volumes in cubic cm (cc) units within the FDG uptake for each lesion were extracted using four different segmentation methods: a gradient-based method32 and fixed intensity thresholds of 50%, 40%, and 30% of .33
The gradient-based method, based on an edge-detection tool, required placing the cursor at the center of the lesion and dragging it out until the three orthogonal guiding lines reached the boundaries of the FDG-avid lesion, while avoiding adjacent structures. The method generated an automated tumor volume-of-interest (VoI) within the tumor lesion outlined in axial, transverse, and sagittal views. For the fixed-percentage threshold segmentation techniques, a spherical VoI predefined by the MIM software tool was placed over the lesion. The VoI was adjusted to include the entire FDG-avid tumor, excluding adjacent structures. Subsequently, all voxels with gray level values more than 50%, 40%, and 30% of the were classified as lesion voxels, for the 50% , 40% , and 30% segmentation methods, respectively, thus defining the tumor boundary with each of these methods.
Subsequently, the physician verified the drawn boundaries in all three orthogonal planes for the four segmentation methods. The MTV values were extracted from the segmented tumor volumes for each of the segmentation methods and exported in a tabulated Excel (version 12.3.6, Microsoft) spreadsheet.
3.3. Application of the No-Gold-Standard Technique
We first verified, using the tests described in Sec. 2.3, if there was a linear relationship between the MTV values measured using different pairs of segmentation methods. If so, the measured MTV values were input to the NGS technique.
In the NGS optimization routine, the search space for the different parameters was set such that the routine searched between reasonable values of these parameters. The search space should be large enough to model all possible relationships between the true and estimated values. However, having the search space too large would increase the possibility of the optimization routine being trapped in local minima. Based on these considerations, the search ranges for the and parameters were chosen to lie in [1, 20]. This allowed modeling a wide variety of shapes of the FPBD distribution, as described previously.21 Similarly, the search range for the slope parameter was chosen to lie in [0.6, 1.4] to model methods that substantially scaled the MTV value. To determine the search ranges for the other parameters, we studied the range of measured MTV values yielded by the different methods. It was observed that the minimum measured MTV values obtained using the four segmentation methods were between 2.4 cc and 3 cc. Similarly, the maximum measured MTV values were between 90 and 170 cc. Using this information, the search ranges for the upper and lower value of the GBD were set to [2.4, 3.0] cc and [90, 170] cc, respectively, and the search ranges for the bias and standard deviation of the noise terms were set to [] cc and [1,10] cc, respectively.
The NGS technique was executed for a total of 500 bootstrap realizations of the MTV data from all the methods, as described in Sec. 2.4, yielding 500 NSR values. The CI of the difference in the NSR values between the candidate for the most precise method and other methods, i.e., was obtained. Analysis of these CIs was performed to determine the most precise segmentation method. We also implemented the consistency check described in Sec. 2.5 on the output of the NGS technique.
3.4. Sensitivity to Patient Dataset
The objective of this experiment was to study the sensitivity of the output of the NGS technique to the choice of the set of MTV measurements considered in the dataset. As mentioned above, the available patient dataset provided MTV measurements from 214 lesions for each method. We created a group of MTV measurements from 150 tumors by sampling without replacement from this dataset. The value of 150 was chosen since that allowed for each combination to have different sets of MTV measurements. Next, using the bootstrap-based procedure, the CI for the difference in the NSR values between the various segmentation methods and the most precise segmentation method, i.e., , was computed. The experiment was repeated for 50 trials. The variation in the estimated CIs over the trials was assessed.
3.5. Effect of Reducing the Number of Patient Studies
In the NGS technique, a number of parameters are estimated. For example, when comparing three segmentation methods, 13 parameters are estimated. To estimate these parameters, measured quantitative values from a large number of patient studies are required. This requirement could limit the utility of the NGS approach to applications where large numbers of patient datasets are available. It was thus of interest to study the reliability of the NGS technique in determining the most precise segmentation method as the number of patient images was reduced.
To study the effect of reducing the number of patient studies on the performance of the NGS technique, we varied the number of lesion measurements input to the NGS technique from 40 to 214. The CI of the difference in the NSR values for the various segmentation methods relative to the most precise method, as determined using data from all 214 MTV measurements, was obtained. The upper limit of the estimated CI and the width of the 95% CI were analyzed.
4. Results
4.1. Testing for Linearity
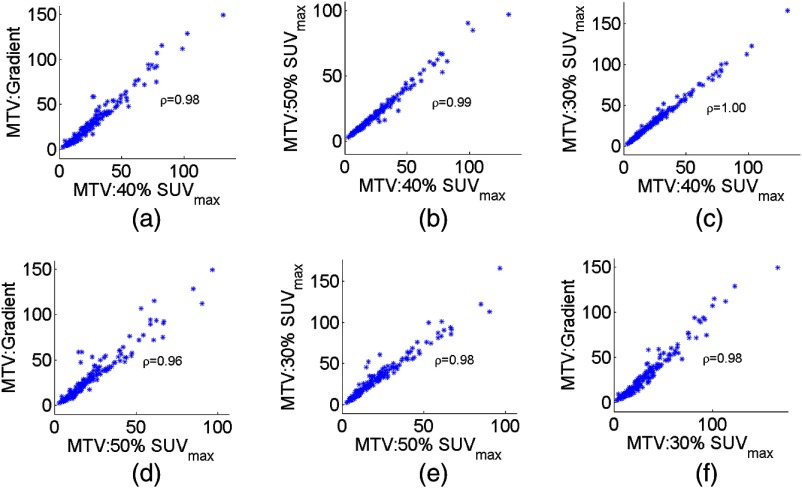
Scatter plots of the measured MTV values between different pairs of segmentation methods are shown in Fig. 6. Pearson’s correlation coefficient between the measurements using the different pairs of methods is reported on the scatter plots. A visual inspection of the plots indicates that these measurements were linearly related. Furthermore, the values of the correlation coefficient were close to unity, providing stronger evidence of this linear relationship. We thus proceeded to apply the NGS technique.
Fig. 6.
Scatter plots depicting the relationships between the true and measured MTV values for different pairs of segmentation methods. The Pearson’s correlation coefficient is given on each plot.
4.2. Determining the Most Precise Segmentation Method
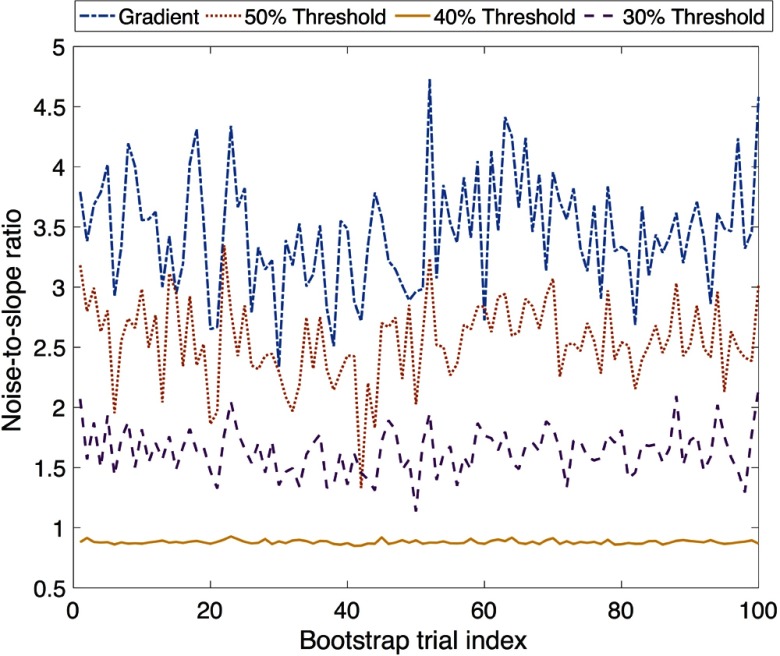
The estimated NSR value for the four segmentation methods for the first 100 bootstrap trials is plotted in Fig. 7. It was observed that the 40% method consistently had the lowest NSR. Thus, the 40% method was chosen as the candidate for the most precise method, and the CI of the difference between the NSR using this method and the other three segmentation methods was obtained. The upper limit of the 95% CIs for this difference estimate was always greater than 0, as shown in Table 1. This result shows that the superiority of the 40% method was statistically significant.
Fig. 7.
The NSR for the different segmentation methods for the first 100 bootstrap trials.
Table 1.
The upper and lower limits of the CI of the difference in the NSR estimates between the 40% and the other segmentation methods.
| 40% versus gradient | 40% versus 50% | 40% versus 30% | |
|---|---|---|---|
| Lower limit of 95% CI | |||
| Upper limit of 95% CI |
4.3. Consistency Check
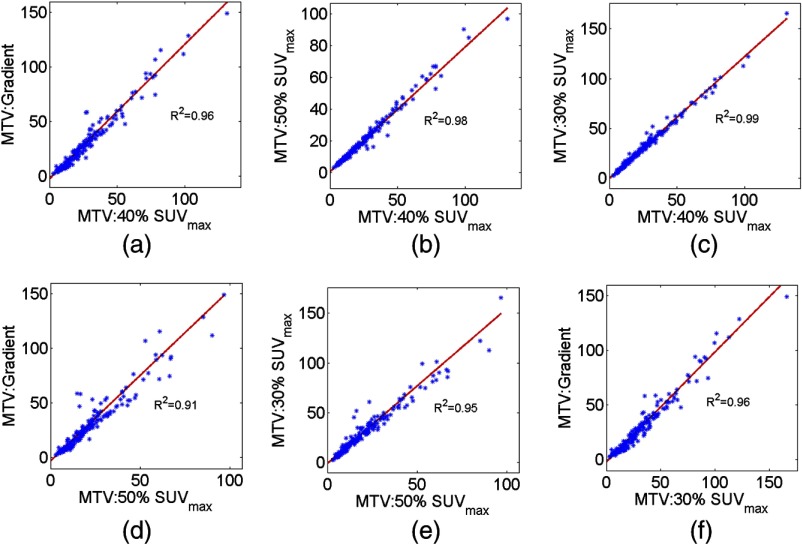
The results for the consistency check are shown in Fig. 8 for a representative bootstrap realization. It was observed that the relationship predicted by the NGS technique between the MTV values obtained using the different segmentation methods coincided with the scatter plot, with the coefficient of determination values close to unity. The same trend was observed in the results with all the bootstrap realizations, as evident from the summary statistics of the values presented in Table 2.
Fig. 8.
The linear relationship between the measurements of the MTV values from the different methods, as predicted by the NGS technique for a representative bootstrap realization, overlaid on the scatter plot between the MTV values measured using the different methods.
Table 2.
The mean and standard deviation of the coefficient of determination values over all the bootstrap realizations.
| Method pairs | value |
|---|---|
| 40% versus gradient | |
| 40% versus 50% | |
| 40% versus 30% | |
| 50% versus gradient | |
| 50% versus 30% | |
| 30% versus gradient |
4.4. Sensitivity to Patient Dataset
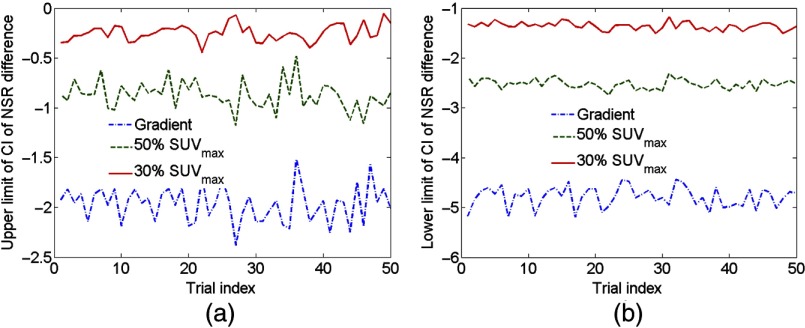
The upper and lower limits of the CI of the difference in the NSR estimates between the 40% method and other segmentation methods for different combinations of 150 patient datasets are shown in Figs. 9(a) and 9(b), respectively. It was observed that both limits were robust to the choice of the patient dataset. Furthermore, the upper limit was less than 0 for all combinations of patient datasets, indicating that the 40% method was the most precise. These experimental results provided evidence that the output of the NGS technique was robust to the choice of the patient dataset.
Fig. 9.
The (a) upper limit and (b) lower limit of the CI of 95% CI for the estimate of the NSR difference between the 40% method and other three segmentation methods for different trials, where in each trial different combinations of lesion datasets input to the NGS technique.
4.5. Effect of Reducing the Number of Measured Metabolic Tumor Volume Measurements
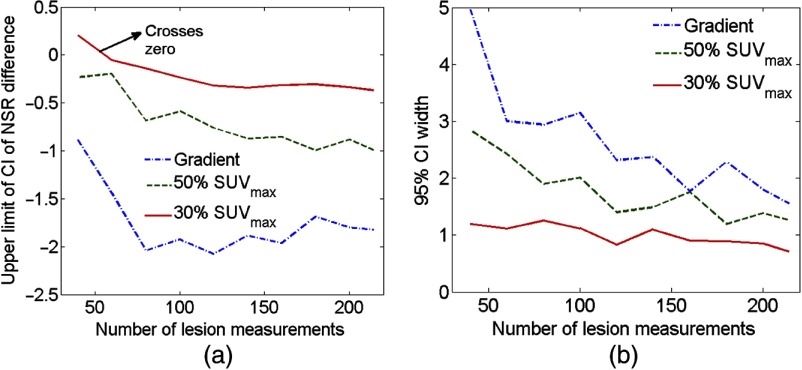
The upper limit of the CI for the difference estimate in the NSR of the 40% method and the other segmentation methods, as a function of the number of MTV measurements input to the NGS technique, is shown in Fig. 10(a). The upper limit of the CI was smaller than 0 cc when MTV measurements from up to 80 lesions were available, so that the NGS technique predicted that the same segmentation method of 40% was the most precise. However, as the number of MTV measurements was further reduced, the upper limit of the CI approached the value 0, and eventually became greater than 0 for the case of 60 patient studies. Thus, assuming that the output of the NGS framework with the 214-lesion dataset was accurate, we infer that using less than 60 measurements was insufficient to determine the most precise segmentation method with the NGS framework.
Fig. 10.
(a) The upper limit of the CI and (b) the width of the 95% CI for the estimate of the NSR difference between the 40% method and other three segmentation methods.
The effect of reducing the number of patient studies is further illustrated in Fig. 10(b), where the width of the 95% CI (i.e., the difference between the upper and lower limits) for the difference in NSR between the 40% method and other segmentation methods is plotted. Again, a reduction in the number of MTV measurements led to an increase in the width of the CI’s, indicating that the availability of a larger number of patient studies is desirable.
5. Discussions and Conclusions
There has been a growing interest in using quantitative PET volumetric metrics such as MTV and TLG to assess disease burden and tumor aggressiveness. Several investigations are being conducted on the role of change in MTV and TLG as an early predictor of therapy response.34–37 Thus, these metrics could provide useful measures of response in response-adaptive therapy regimens. However, for these metrics to be incorporated as a routine predictive biomarker, a PET segmentation methodology that yields precise values of these metrics is needed. Since several PET segmentation methods are available,38 each with their own trade-offs, evaluation of these methods on the task of precisely measuring the metric is highly desirable. The proposed NGS framework is useful in this evaluation by providing an estimate of the precision of the MTV values under the assumption that the true and measured metric values are linearly related.
Conventionally, segmentation methods are evaluated by quantifying some measure of overlap between a reference segmentation and the output yielded by the segmentation method under evaluation using metrics, such as Dice’s coefficient39 and the Jaccard index.40 However, typically, the only reference standards available for comparison are segmentations produced by expert observers, which tend to suffer from observer bias and intra- and interexpert variability.30,41 Obtaining expert segmentation is also tedious, time-consuming, and expensive. Moreover, the precision of manual segmentations depends on the sharpness of the boundaries, the window-level settings for image display, the computer monitor and its settings and the operator’s vision characteristics.42 Consequently, there is an important need to develop tools to evaluate segmentation methods in the absence of ground-truth (or reference) segmentation. For this purpose, algorithms such as simultaneous truth and performance level estimation (STAPLE)43 have been widely used when segmentation outputs from multiple methods or manual experts are available. Additionally, other methods have been proposed to evaluate segmentation methods in the absence of ground truth.44,45 In these approaches, the evaluation metric is the amount of region overlap between the output of the segmentation technique under evaluation and an unknown gold standard segmentation.
More recently, the idea that segmentation algorithms must be evaluated based on the specific task that will be performed using the images has gained interest.24–27,33,46 This is especially true in the context of evaluating FDG-PET segmentation methods, where the task of interest is the estimation of volumetric metrics such as MTV and TLG.33,47,48 However, an issue with these task-based evaluations is the lack of knowledge about the true value of the metric. In this manuscript, the use of the NGS framework to address this issue in evaluating FDG-PET segmentation methods has been demonstrated. While the NGS evaluation technique provides a way to evaluate methods on the specific task of measuring the MTV, in our opinion, it is complementary to the region-overlap-based approaches and should be used in conjunction.
A limitation of the NGS evaluation technique is that it cannot be applied if the relationship between the true and measured values for any of the imaging methods is not linear. In the context of delineating tumors in FDG-PET images of patients with head-and-neck cancer, several segmentation methods are available.47 For some of these methods, it is possible that the true and measured values are not linearly related. Applying the NGS technique to evaluate these methods can yield inaccurate results. Thus, before applying the NGS technique, it is important to assess whether the linearity assumption is satisfied. We have proposed a test that helps to check for nonlinearity between the true and measured values using patient data. In addition to this test, if measurements using the different methods are available from experiments where the ground truth is known, such as realistic simulations or physical-phantom studies, then this could be used to further check the assumption of linearity. Also, in some cases, the linearity assumption could be enforced by the linearity of the image-formation process. For example, in PET, the imaging operator is linear so that the projection data is linearly related to the activity distribution. Thus, any linear functional of the projection data will also be related to the corresponding linear functional of the activity distribution.
In this study, we have compared four segmentation procedures, namely the PET-edge technique and 30%, 40%, and 50% intensity thresholding methods. These methods were chosen due to their wide use in segmenting FDG-PET images of patients with head-and-neck cancer.30,33,49–53 The wide usage of these methods is due to their ease of deployment and their availability in clinical workstations, such as MIM. Our study concluded that the 40% SUV thresholding method was the most precise of the considered segmentation methods. At the same time, several other techniques have been developed to segment FDG-PET images,47 Thus more precise segmentation methods that were not considered here might exist. The primary objective of this paper was to develop the NGS evaluation framework. The use of the framework to evaluate four candidate FDG-PET image-segmentation methods was primarily meant to demonstrate its application to patient data, and not to find the best segmentation method of all methods available. However, the developed framework could be used to comprehensively evaluate various methods for FDG-PET tumor segmentation, and thus determine the most precise method for FDG-PET tumor segmentation. Note that the segmentation outputs could also be affected by the scanner, acquisition, and reconstruction parameters. Thus, for a particular acquisition protocol, a unique segmentation method might be most precise. The NGS framework could also be used to determine this method.
In a previous study, Sridhar et al. have observed that, of the gradient and the 30%, 40%, and 50% threshold methods, the 40% SUVmax thresholding method was not the most accurate on the task of estimating the MTV.33 However, the NGS technique evaluates the imaging methods on the basis of precision, and not accuracy of the estimated metric. Thus, there is no discrepancy in these results and the results presented in this manuscript. In fact, the presented results suggest that while a given segmentation method might yield very accurate values of a metric, these might not be the most precise. In applications, such as radiotherapy, segmentation accuracy might be more desirable, while in applications such as monitoring therapy response, precision of the quantitative value measured from the segmentation results is more important. Thus, care must be exercised in selecting the evaluation criteria, and must consider the clinical task.
The limitation of the NGS framework in not being able to evaluate methods on the basis of accuracy of the estimated metric arises because the NGS technique does not accurately estimate the bias (intercept) term of the linear relationship [Eq. (2)] when the upper and lower limits of the FPBD are not known.21 However, for some applications, the accuracy of the measured QIB values is important. Improvements to the NGS technique for evaluating segmentation methods on the basis of accuracy of the QIB value are definitely desirable. In this context, if the upper and lower limits of the distribution of true values are known, it has been demonstrated using numerical experiments that the NGS technique can yield accurate estimate of the bias terms.22
In summary, an NGS framework was developed to overcome the practical difficulties in applying an NGS technique to patient data. The framework includes the NGS technique itself, a set of statistical tests that provide confidence in the assumptions made by the technique, a bootstrap-based procedure to compute CIs on the FoMs estimated using the NGS technique, and consistency checks to assess the reliability of these FoMs. The application of the framework to patient data was demonstrated by using the framework to objectively evaluate four tumor-segmentation methods for FDG-PET imaging, namely 30%, 40%, and 50% intensity threshold methods and a gradient technique, using data from 128 patients with biopsy-proven head-and-neck squamous cell carcinoma. The results from the application of the framework provided evidence that the 40% thresholding method yielded the most precise MTV values for segmenting tumors in FDG-PET images of head-and-neck cancer acquired following the described imaging protocol. Additionally, the results were relatively stable over subsets of the patient data. Experiments involving application of the NGS framework to smaller subsets of patient data showed that the 40% threshold method was the most precise as long as MTV measurements from more than 80 lesions were available.
Acknowledgments
This work was supported by National Institutes of Health under Grant Nos. R01-EB016231, R01-CA109234, U01-CA140204, and T32EB006351. The authors thank Harrison Barrett, Matthew Kupinski, and Eric Clarkson for helpful discussions.
Biographies
Abhinav K. Jha is an instructor in the Division of Medical Imaging Physics of the Russell H. Morgan Department of Radiology and Radiological Sciences at Johns Hopkins University School of Medicine. He received his PhD from the College of Optical Sciences, University of Arizona. His research interests are in the design, optimization, and evaluation of medical imaging systems and algorithms using objective image-science-based measures of image quality. A major area of focus is quantitative imaging with applications in oncology and neurology.
Esther Mena is a trained nuclear-medicine physician with expertise in molecular imaging and research interests in quantitative PET imaging. She completed her residency in the Nuclear Medicine Program at Johns Hopkins and was chief resident during her last year of residency. Following that, she was a PET/CT fellow in the Division of Nuclear Medicine, Department of Radiology and Radiological Sciences at Johns Hopkins School of Medicine.
Brian Caffo, PhD, is a professor at the Johns Hopkins Department of Biostatistics at the Bloomberg School of Public Health. He graduated from the Department of Statistics at the University of Florida. His research interests are in the areas of statistical computing, categorical data analysis, medical imaging, functional MRI, diffusion tensor imaging, pharmacology, and statistical algorithms. He is a recipient of the Presidential Early Career Award for Scientists and Engineers award.
Saeed Ashrafania is a PhD student in the Department of Electrical and Computer Engineering, Johns Hopkins University. His research interests are in optimized partial volume correction and texture analysis in oncologic positron emission tomography.
Arman Rahmim, PhD, is an associate professor of radiology and electrical & computer engineering at the Johns Hopkins University. His Laboratory of Quantitative Tomography pursues interdisciplinary research toward enhanced quantitative image generation and analysis for tomographic medical imaging devices (PET, SPECT, optical, acoustic) including emphasis on multimodality imaging. He also serves as chief physicist in the Section of High Resolution Brain PET Imaging at the Division of Nuclear Medicine & Molecular Imaging.
Eric Frey is a professor in the Division of Medical Imaging Physics of the Russell H. Morgan Department Radiology and Radiological Science at Johns Hopkins University, with joint appointments in the Departments of Environmental Health Sciences and Electrical and Computer Engineering. His research is in the area of nuclear medicine, with applications to myocardial, neural and cancer imaging, targeted radiopharmaceutical therapy, and task-based assessment of image quality.
Rathan M. Subramaniam, MD, PhD, MPH, FRANZCR, FACNM, is the Robert W. Parkey MD distinguished professor in radiology, chief of the Nuclear Medicine Division, and medical director of the Cyclotron and Molecular Imaging Program at UT Southwestern. He focuses his research on linking imaging biomarkers to patient quality of life and survival outcomes; quantitative imaging using positron emission tomography/computed tomography (PET/CT); single-photon emission computed tomography (SPECT/CT); and MRI for human translational oncologic imaging.
Appendix A.
Theorem 1:
Consider two random variables and related to a common variable . For both and to be linearly related to , a necessary condition is that and must be linearly related to each other.
Proof:
Without loss of generality, consider the case where and have a quadratic relationship given as follows:
(6) where are all constants. Also, assume that and are linearly related so that
(7) where again and are constants. Substituting Eq. (7) in Eq. (6), we obtain
(8)
Thus, the variables and are not linearly related. Thus, the theorem is proved by contraposition.
Appendix B.
The NGS technique has been previously validated using numerical experiments and in the context of evaluating reconstruction methods for quantitative SPECT.21 To further validate the performance of the NGS technique specifically for the segmentation task considered in this manuscript, we conducted another numerical validation study.
The parameters for this validation study were chosen to replicate a scenario similar to the patient study. First, the values of the four-parameter beta distribution estimated from the patient data using the NGS technique were used to define a distribution of true MTV values. 212 MTV values were sampled from this distribution. Next, the slope, bias, and noise standard deviation for each of the four segmentation methods, again as estimated from the patient data using the NGS technique, were used to numerically obtain noisy measurements of MTV values corresponding to the four segmentation methods using Eq. (1). These measured values were input to the NGS technique. The NGS technique, without any knowledge of the true MTV values, estimated the values of the slope, bias, and noise standard deviation terms. These estimates were used to compute the NSR. The true NSR value was determined using knowledge of the true slope and noise standard deviation values. The results, as presented in Table 3, show the similarity between the NSR estimated using the NGS technique, without any knowledge of the true MTV values, and the true NSR, thus numerically validating the NGS technique in the context of this application.
Table 3.
NSR estimated using the NGS technique compared with the true NSR values.
| Method | True slope | Measured slope | True std. dev. | Measured std. dev. | True NSR | Measured NSR |
|---|---|---|---|---|---|---|
| PET-edge | 1.40 | 4.80 | 3.45 | |||
| 50% threshold | 0.92 | 2.34 | 2.56 | |||
| 40% threshold | 1.14 | 1.00 | 0.88 | |||
| 30% threshold | 1.38 | 2.29 | 1.65 |
Disclosures
The authors have no conflicts of interest to declare.
References
- 1.Abramson R. G., et al. , “Methods and challenges in quantitative imaging biomarker development,” Acad. Radiol. 22(1), 25–32 (2015). 10.1016/j.acra.2014.09.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chirindel A., et al. , “Prognostic value of FDG PET/CT-derived parameters in pancreatic adenocarcinoma at initial PET/CT staging,” Am. J. Roentgenol. 204(5), 1093–1099 (2015). 10.2214/AJR.14.13156 [DOI] [PubMed] [Google Scholar]
- 3.Kim J., et al. , “Prognostic value of metabolic tumor volume estimated by (18) F-FDG positron emission tomography/computed tomography in patients with diffuse large B-Cell lymphoma of Stage II or III disease,” Nucl. Med. Mol. Imaging 48(3), 187–195 (2014). 10.1007/s13139-014-0280-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kim T. M., et al. , “Total lesion glycolysis in positron emission tomography is a better predictor of outcome than the international prognostic index for patients with diffuse large B cell lymphoma,” Cancer 119(6), 1195–1202 (2013). 10.1002/cncr.27855 [DOI] [PubMed] [Google Scholar]
- 5.Son S. H., et al. , “Prognostic implications of metabolic tumor volume on 18F-FDG PET/CT in diffuse large B-cell lymphoma patients with extranodal involvement,” J. Nucl. Med. 56(Suppl. 3), 1353 (2015). [Google Scholar]
- 6.Song M. K., et al. , “Prognostic value of metabolic tumor volume on PET / CT in primary gastrointestinal diffuse large B cell lymphoma,” Cancer Sci. 103(3), 477–482 (2012). 10.1111/j.1349-7006.2011.02164.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Carlier T., Bailly C., “State-of-the-art and recent advances in quantification for therapeutic follow-up in oncology using PET,” Front. Med. 2, 18 (2015). 10.3389/fmed.2015.00018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tomasi G., Turkheimer F., Aboagye E., “Importance of quantification for the analysis of PET data in oncology: review of current methods and trends for the future,” Mol. Imaging Biol. 14(2), 131–146 (2012). 10.1007/s11307-011-0514-2 [DOI] [PubMed] [Google Scholar]
- 9.Mena E., et al. , “18F-FDG PET/CT metabolic tumor volume and intratumoral heterogeneity in pancreatic adenocarcinomas: impact of dual-time point and segmentation methods,” Clin. Nucl. Med. 42(1), e16–e21 (2017). 10.1097/RLU.0000000000001446 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mena E., et al. , “Value of intra-tumoral metabolic heterogeneity and quantitative 18F-FDG PET/CT parameters to predict prognosis in patients with HPV-positive primary oropharyngeal squamous cell carcinoma,” Clin. Nucl. Med. (2017). [DOI] [PMC free article] [PubMed]
- 11.Xu Q. G., Xian J. F., “Role of quantitative magnetic resonance imaging parameters in the evaluation of treatment response in malignant tumors,” Chin. Med. J. 128(8), 1128–1133 (2015). 10.4103/0366-6999.155127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Stephen R. M., et al. , “Diffusion MRI with semi-automated segmentation can serve as a restricted predictive biomarker of the therapeutic response of liver metastasis,” Magn. Reson. Imaging 33(10), 1267–1273 (2015). 10.1016/j.mri.2015.08.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jha A. K., Rodríguez J. J., Stopeck A. T., “A maximum-likelihood method to estimate a single ADC value of lesions using diffusion MRI,” Magn. Reson. Med. 76(6), 1919–1931 (2016). 10.1002/mrm.26072 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Djang D. S., et al. , “SNM practice guideline for dopamine transporter imaging with 123I-ioflupane SPECT 1.0,” J. Nucl. Med. 53(1), 154–163 (2012). 10.2967/jnumed.111.100784 [DOI] [PubMed] [Google Scholar]
- 15.Harrison R. L., et al. , “A virtual clinical trial of FDG-PET imaging of breast cancer: effect of variability on response assessment,” Transl. Oncol. 7(1), 138–146 (2014). 10.1593/tlo.13847 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kinahan P. E., et al. , “PET/CT assessment of response to therapy: tumor change measurement, truth data, and error,” Transl. Oncol. 2(4), 223–230 (2009). 10.1593/tlo.09223 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Meyer C. R., et al. , “Quantitative imaging to assess tumor response to therapy: common themes of measurement, truth data, and error sources,” Transl. Oncol. 2(4), 198–210 (2009). 10.1593/tlo.09208 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kessler L. G., et al. , “The emerging science of quantitative imaging biomarkers terminology and definitions for scientific studies and regulatory submissions,” Stat. Methods Med. Res. 24(1), 9–26 (2015). 10.1177/0962280214537333 [DOI] [PubMed] [Google Scholar]
- 19.BIPM I, IFCC I, IUPAC I, ISO O, The International Vocabulary of Metrology—Basic and General Concepts and Associated Terms (VIM), 3rd ed., JCGM 200: 2012, Joint Committee for Guides in Metrology; (2008). [Google Scholar]
- 20.Obuchowski N. A., et al. , “Quantitative imaging biomarkers: a review of statistical methods for computer algorithm comparisons,” Stat. Methods Med. Res. 24(1), 68–106 (2015). 10.1177/0962280214537390 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jha A. K., Caffo B., Frey E. C., “A no-gold-standard technique for objective assessment of quantitative nuclear-medicine imaging methods,” Phys. Med. Biol. 61(7), 2780–2800 (2016). 10.1088/0031-9155/61/7/2780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hoppin J. W., et al. , “Objective comparison of quantitative imaging modalities without the use of a gold standard,” IEEE Trans. Med. Imaging 21(5), 441–449 (2002). 10.1109/TMI.2002.1009380 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kupinski M. A., et al. , “Estimation in medical imaging without a gold standard,” Acad. Radiol. 9(3), 290–297 (2002). 10.1016/S1076-6332(03)80372-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kupinski M. A., et al. , “Comparing cardiac ejection fraction estimation algorithms without a gold standard,” Acad. Radiol. 13(3), 329–337 (2006). 10.1016/j.acra.2005.12.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lebenberg J., et al. , “Nonsupervised ranking of different segmentation approaches: application to the estimation of the left ventricular ejection fraction from cardiac cine MRI sequences,” IEEE Trans. Med. Imaging 31(8), 1651–1660 (2012). 10.1109/TMI.2012.2201737 [DOI] [PubMed] [Google Scholar]
- 26.Jha A. K., et al. , “Objective evaluation of reconstruction methods for quantitative SPECT imaging in the absence of ground truth,” Proc. SPIE 9416, 94161K (2015). 10.1117/12.2081286 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jha A. K., et al. , “Task-based evaluation of segmentation algorithms for diffusion-weighted MRI without using a gold standard,” Phys. Med. Biol. 57(13), 4425–4446 (2012). 10.1088/0031-9155/57/13/4425 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jha A. K., et al. , “Evaluating segmentation algorithms for diffusion-weighted MR images: a task-based approach,” Proc. SPIE 7627, 76270L (2010). 10.1117/12.845515 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Murphy J. D., et al. , “Truong D and others. Correlation between metabolic tumor volume and pathologic tumor volume in squamous cell carcinoma of the oral cavity,” Radiother. Oncol. 101(3), 356–361 (2011). 10.1016/j.radonc.2011.05.040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Paidpally V., et al. , “Interreader agreement and variability of FDG PET volumetric parameters in human solid tumors,” Am. J. Roentgenol. 202(2), 406–412 (2014). 10.2214/AJR.13.10841 [DOI] [PubMed] [Google Scholar]
- 31.Dunn G., Roberts C., “Modelling method comparison data,” Stat. Methods Med. Res. 8(2), 161–179 (1999). 10.1191/096228099668524590 [DOI] [PubMed] [Google Scholar]
- 32.Geets X., et al. , “A gradient-based method for segmenting FDG-PET images: methodology and validation,” Eur. J. Nucl. Med. Mol. Imaging 34(9), 1427–1438 (2007). 10.1007/s00259-006-0363-4 [DOI] [PubMed] [Google Scholar]
- 33.Sridhar P., et al. , “FDG PET metabolic tumor volume segmentation and pathologic volume of primary human solid tumors,” Am. J. Roentgenol. 202(5), 1114–1119 (2014). 10.2214/AJR.13.11456 [DOI] [PubMed] [Google Scholar]
- 34.Kim Y. I., et al. , “Clinical outcome prediction of percutaneous cementoplasty for metastatic bone tumor using (18)F-FDG PET-CT,” Ann. Nucl. Med. 27(10), 916–923 (2013). 10.1007/s12149-013-0771-z [DOI] [PubMed] [Google Scholar]
- 35.Yossi S., et al. , “Early assessment of metabolic response by 18F-FDG PET during concomitant radiochemotherapy of non-small cell lung carcinoma is associated with survival: a retrospective single-center study,” Clin. Nucl. Med. 40(4), e215–e221 (2015). 10.1097/RLU.0000000000000615 [DOI] [PubMed] [Google Scholar]
- 36.Grootjans W., et al. , “Performance of automatic image segmentation algorithms for calculating total lesion glycolysis for early response monitoring in non-small cell lung cancer patients during concomitant chemoradiotherapy,” Radiother Oncol. 119(3), 473–479 (2016). 10.1016/j.radonc.2016.04.039 [DOI] [PubMed] [Google Scholar]
- 37.Kim S. J., Koo P. J., Chang S., “Predictive value of repeated F-18 FDG PET/CT parameters changes during preoperative chemoradiotherapy to predict pathologic response and overall survival in locally advanced esophageal adenocarcinoma patients,” Cancer Chemother Pharmacol. 77(4), 423–431 (2016). 10.1007/s00280-016-2988-8 [DOI] [PubMed] [Google Scholar]
- 38.Foster B., “A review on segmentation of positron emission tomography images,” Comput. Biol. Med. 50, 76–96 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dice L. R., “Measures of the amount of ecologic association between species,” Ecology 26(3), 297–302 (1945). 10.2307/1932409 [DOI] [Google Scholar]
- 40.Jaccard P., “The distribution of the flora in the alpine zone,” New Phytol. 11(2), 37–50 (1912). 10.1111/nph.1912.11.issue-2 [DOI] [Google Scholar]
- 41.Dewalle-Vignion AS, et al. , “Evaluation of PET volume segmentation methods: comparisons with expert manual delineations,” Nucl. Med. Commun. 33(1), 34–42 (2012). 10.1097/MNM.0b013e32834d736f [DOI] [PubMed] [Google Scholar]
- 42.Udupa J. K., et al. , “A framework for evaluating image segmentation algorithms,” Comput. Med. Imaging Graphics 30(2), 75–87 (2006). 10.1016/j.compmedimag.2005.12.001 [DOI] [PubMed] [Google Scholar]
- 43.Warfield S. K., Zou K. H., Wells W. M., “Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation,” IEEE Trans. Med. Imaging 23(7), 903–921 (2004). 10.1109/TMI.2004.828354 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kohlberger T., et al. , “Evaluating segmentation error without ground truth,” in Medical Image Computing and Computer-Assisted Intervention – MICCAI 2012, Vol. 15, No. Pt 1, pp. 528–536 (2012). [DOI] [PubMed] [Google Scholar]
- 45.Shepherd T., Prince S. J., Alexander D. C., “Interactive lesion segmentation with shape priors from offline and online learning,” IEEE Trans. Med. Imaging 31(9), 1698–1712 (2012). 10.1109/TMI.2012.2196285 [DOI] [PubMed] [Google Scholar]
- 46.Jha A. K., et al. , “A clustering algorithm for liver lesion segmentation of diffusion-weighted MR images,” in IEEE Southwest Symp. on Image Analysis & Interpretation (SSIAI ‘12), pp. 93–96 (2010). 10.1109/SSIAI.2010.5483911 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zaidi H., et al. , “Comparative methods for PET image segmentation in pharyngolaryngeal squamous cell carcinoma,” Eur. J. Nucl. Med. Mol. Imaging 39(5), 881–891 (2012). 10.1007/s00259-011-2053-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Greco C., et al. , “Evaluation of different methods of 18F-FDG-PET target volume delineation in the radiotherapy of head and neck cancer,” Am. J. Clin. Oncol. 31(5), 439–445 (2008). 10.1097/COC.0b013e318168ef82 [DOI] [PubMed] [Google Scholar]
- 49.Dibble E. H., et al. , “18F-FDG metabolic tumor volume and total glycolytic activity of oral cavity and oropharyngeal squamous cell cancer: adding value to clinical staging,” J. Nucl. Med. 53(5), 709–715 (2012). 10.2967/jnumed.111.099531 [DOI] [PubMed] [Google Scholar]
- 50.Mena E., et al. , “Value of pre-treatment 18F-FDG PET intratumoral heterogeneity and quantitative parameters: predicting patient outcome in primary oropharyngeal squamous cell carcinoma,” in SNMMI Annual Meeting, San Diego (2016). [Google Scholar]
- 51.Shah B., et al. , “Intra-reader reliability of FDG PET volumetric tumor parameters: effects of primary tumor size and segmentation methods,” Ann. Nucl. Med. 26(9), 707–714 (2012). 10.1007/s12149-012-0630-3 [DOI] [PubMed] [Google Scholar]
- 52.Tahari A. K., et al. , “FDG PET/CT imaging of oropharyngeal squamous cell carcinoma: characteristics of human papillomavirus-positive and -negative tumors,” Clin. Nucl. Med. 39(3), 225–231 (2014). 10.1097/RLU.0000000000000255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Yu J., et al. , “Head and neck squamous cell cancer (stages III and IV) induction chemotherapy assessment: value of FDG volumetric imaging parameters,” J. Med. Imaging Radiat. Oncol. 58(1), 18–24 (2014). 10.1111/1754-9485.12081 [DOI] [PubMed] [Google Scholar]