Multi-Shot Sensitivity-Encoded Diffusion Data Recovery Using Structured Low-Rank Matrix Completion (MUSSELS)

Abstract

Purpose

To introduce a novel method for the recovery of multi-shot diffusion weighted (MS-DW) images from echo-planar imaging (EPI) acquisitions.

Methods

Current EPI-based MS-DW reconstruction methods rely on the explicit estimation of the motion-induced phase maps to recover artifact-free images. In the new formulation, the k-space data of the artifact-free DWI is recovered using a structured low-rank matrix completion scheme, which does not require explicit estimation of the phase maps. The structured matrix is obtained as the lifting of the multi-shot data. The smooth phase-modulations between shots manifest as null-space vectors of this matrix, which implies that the structured matrix is low-rank. The missing entries of the structured matrix are filled in using a nuclear-norm minimization algorithm subject to the data-consistency. The formulation enables the natural introduction of smoothness regularization, thus enabling implicit motion-compensated recovery of the MS-DW data.

Results

Our experiments on in-vivo data show effective removal of artifacts arising from inter-shot motion using the proposed method. The method is shown to achieve better reconstruction than the conventional phase-based methods.

Conclusion

We demonstrate the utility of the proposed method to effectively recover artifact-free images from Cartesian fully/under-sampled and partial Fourier acquired data without the use of explicit phase estimates.

INTRODUCTION

Magnetic resonance diffusion-weighted imaging (DWI) is a unique noninvasive tool used to study the micro-architecture of tissues by modeling the diffusion of water molecules in the tissue (1,2). It is widely used in the clinical diagnosis of acute stroke, tumors and brain abscesses (3–7) and has also become the primary neuroscience research tool for studying white matter connections (8). Single-shot EPI (ss-EPI) acquisition coupled with parallel imaging is currently the preferred method for DWI acquisition, primarily due to its immunity to bulk motion and its short acquisition time (9–11). However, the long readouts of the EPI sequences lead to signal loss and blurring while intrinsically low bandwidth along the phase-encoding direction results in distortions in that direction (12). This is a fundamental limitation, which makes ss-EPI less preferable for many applications. For example, high resolution diffusion imaging requires long EPI readout durations and results in considerable geometric distortion and blurring in the resulting images. Another example where the long echo-train length of EPI is undesirable is diffusion imaging at ultra-high field strength (UHFS) where the T₂ relaxation times are shortened (13). In such situations, the echo-train length, even for a moderate imaging resolution, is long enough to cause loss of SNR. This limits the ability of ss-EPI-based DWI to leverage the advantages of UHFS MR imaging (14–16). Acquisitions with shorter readouts would therefore significantly enhance DWI especially when applied at UHFS.

Multi-shot diffusion weighted imaging (MS-DWI) holds great potential for enabling high spatial resolution diffusion imaging (7). The technique can also achieve shorter echo times (TE) to enhance studies at higher field strengths as well as to examine structures that are proximal to inhomogeneous fields or imaging near metal implants. However, MS-DWI has certain limitations. The main problem is the sensitivity of MS-DWI reconstructions to motion resulting from the use of large diffusion gradients. Subject motion and other kinds of physiologic motion arising from cardiac pulsations, respiratory motion etc. during the diffusion encoding gradients result in the image being corrupted by spatially varying motion-induced phase (17–19). While this phase term does not pose a challenge in single shot imaging, the difference in the phase distortions between shots of a multi-shot acquisition are manifested as ghosting artifacts in the reconstructed image. Moreover, the imaging time of MS-DWI increases by a scale factor proportional to the number of shots.

Special reconstruction schemes have to be employed to eliminate the shot-to-shot ghosting artifacts resulting from bulk and physiological motion for the MS-DWI. Such schemes generally involve a multi-step process, where the shot-to-shot phase variations are first estimated and then applied during image reconstruction. Methods to estimate the phase fall into two categories: (i) methods that rely on navigator scans [16, (20–22)] and (ii) methods that estimates phase from the data itself [19, (23–29)]. Since phase navigation methods require additional scan time and do not accurately capture the bulk motion during the diffusion scans, estimating phase from the data itself is the more attractive option. The data-based techniques work extremely well for non-Cartesian self-navigated trajectories (e.g. SNAILS, PROPELLER) where a low-resolution phase map can be obtained from the fully sampled k-space data of each shot (23–25). The same strategy has been employed for Cartesian MS-DW acquisition, even in the absence of fully sampled center k-space data [19, 26–29]. The estimate of the phase map in this case is obtained by employing highly regularized reconstructions of the individual shot data.

The aim of this work is to introduce a novel reconstruction for MS-DWI data that does not rely on the explicit estimation of motion-induced phase estimates to correct the artifacts resulting from inter-shot motion. This is in contrast to existing methods that depend explicitly on an estimate of motion-induced phase maps to remove these artifacts. Even though phase estimation in itself is not an expensive step, we show here that the reconstruction offered by the proposed phase-independent method is much more robust than those obtained using the phase-based methods. This in-turn lead to better reconstructions of under-sampled and noisy data using the proposed method. This work exploits the recent advances in multichannel MR image recovery, which utilizes the annihilation relations between the sensitivity weighted images or their Fourier samples (30–37). We adopt the above scheme for the recovery of MS-DWI data by constructing a structured matrix by the lifting of the k-space samples of shots, which is low-rank due to the annihilation relations. This property enables us to fill in the missing entries using a structured low-rank matrix completion approach. We also exploit the recent advances in reformulating smoothness regularization as structured low-rank problem, where a similar lifting strategy is adopted [34–36, 38, 39]. We introduce a novel lifting scheme that combines the above structures, which enables the recovery of the motion compensated images from noisy and under-sampled MS-DW data.

THEORY

k-Space Data Matrix Structure of a MS-DW Acquisition

In an N_s-shot EPI-based sensitivity-encoded diffusion acquisition for sampling an N₁ × N₂ imaging matrix, the readout is shortened by collecting only N₂/N_s phase encoding lines during every acquisition. The acquisition is repeated N_s times, each time sequentially collecting the next set of N₂/N_s phase-encoding lines (see Fig. 1a for a cartoon of a 4-shot acquisition). In Figure 1b, we represent the 4-shot acquisition using four k-space data matrices concatenated along the shot dimension. The acquired k-space samples are marked using solid circles and the unacquired k-space samples are marked using hollow circles. Note that if phase differences due to inter-shot motion are absent, then we can fill a single k-space data matrix with the sampled points occupying the appropriate positions in the data matrix. In fact, this method is often used in the recovery of the nondiffusion weighted images collected as part of the MS-DWI acquisition. During a diffusion-weighted acquisition, the diffusion sensitizing gradients add extra phase to the moving spins and the acquired k-space data for each shot will have a different phase due to the shot-to-shot inherent sub-pixel motion of the imaging sample. Hence, the acquired k-space data from the separate shots cannot be combined directly; instead they are stacked into separate matrices. Our aim is to recover the unaliased k-space data samples in each of the four k-space data matrices based on the samples that we collected.

FIG. 1.

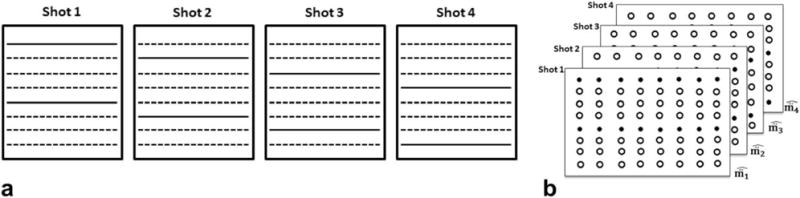
(a) A 4-shot acquisition illustrated. (b) The k-space data matrix of the 4-shot DWI acquisition. The solid circles and the hollow circles represent the acquired and unacquired k-space samples during each shot respectively.

Annihilating Filter Formulation for MS-DW Data

Liu et al showed that by using an encoding function that combines the coil sensitivity with the phase information of the individual shots, the unaliased image could be recovered (40) using an iterative sensitivity encoded reconstruction algorithm [41]. This idea combined with the recent null-space based MR image reconstruction methods (42–45) suggests the possibility of using composite sensitivities as a null-space constraint for the recovery of the MS-DWI data. Since null-space methods can be tied to the notion of annihilating filters in the frequency domain (39), it is likely that shift-invariant k-space filters corresponding to the composite sensitivities or the motion-induced phase maps exist. Utilizing such filters, the above reconstruction problem can be posed as a structured low-rank matrix completion problem (46).

Structured Low-Rank Property of MS-DW Data

In this section, we revisit the relationship between the diffusion weighted data from the different shots by rewriting them in the frequency domain. Assuming that the motion-induced phase maps are smooth functions, these can be represented in k-space as shift-invariant filters of finite support (32). The annihilation relations that we obtain based on the k-space filters lead to a low-rank recovery for the MS-DWI data that do not require motion-induced phase estimates as derived below.

Let the complex DWI of a given diffusion direction be denoted as ρ(x), where x represents spatial co-ordinates. Then, due to inter-shot motion, the measured DWI from the l^th shot (m_l(x)) will have a phase term (40) that will be different from the measured DWI from the i^th shot (m_i(x)), leading us to write

$$m_l\left(\mathbf{x}\right)=\mathrm{\rho }\left(\mathbf{x}\right){\mathrm{\varphi }}_1\left(\mathbf{x}\right);\forall \mathbf{x}.$$ [1]

and

$$m_i\left(\mathbf{x}\right)=\mathrm{\rho }\left(\mathbf{x}\right){\mathrm{\varphi }}_i\left(\mathbf{x}\right);\forall \mathbf{x}.$$ [2]

Here, we assume that the phase ϕ(x) is also a complex quantity such that |ϕ(x)|=1; ∀x. In the case of multi-channel images, the notation m_l(x) corresponds to the channel-combined DWI for the l^th shot. Multiplying Eq. (1) by ϕ_i(x) and Eq. (2) by ϕ_l(x), we can write

$$m_l\left(\mathbf{x}\right){\mathrm{\varphi }}_i\left(\mathbf{x}\right)-m_i\left(\mathbf{x}\right){\mathrm{\varphi }}_l\left(\mathbf{x}\right)=0;\forall \mathbf{x},$$ [3]

which leads to annihilation relations in the image domain, similar to those introduced in (30). Taking the Fourier transform on both sides of (3), we obtain

$$\widehat{m_l}\left[\mathbf{k}\right]\ast \widehat{{\mathrm{\varphi }}_i}\left[\mathbf{k}\right]-\widehat{m_i}\left[\mathbf{k}\right]\ast \widehat{{\mathrm{\varphi }}_l}\left[\mathbf{k}\right]=0;\forall \mathbf{k},$$ [4]

which leads to annihilation relation in the frequency domain as discussed in (32,34–37). Here, $\widehat{m_l}\left[\mathbf{k}\right]$ and ${\widehat{\mathrm{\varphi }}}_l\left[\mathbf{k}\right]$ denote the Fourier coefficients of m_l(x) and ϕ_l(x), respectively for l = 1, ..N_s. Since $\widehat{{\mathrm{\varphi }}_l}\left(\mathbf{k}\right);l=1,\mathrm{..}{N}_s$ are support limited in k-space and assuming the support of $\widehat{{\mathrm{\varphi }}_l}\left(\mathbf{k}\right)$ to be r × r, the convolution with this filter can be implemented as multiplication using block-Hankel matrices:

$$\mathbf{H}\left(\widehat{m_l}\right)·{\widehat{\mathit{\varphi }}}_i-\mathbf{H}\left(\widehat{m_i}\right)·{\widehat{\mathit{\varphi }}}_l=\mathbf{0}.$$ [5]

Here, $\mathbf{H}(\widehat{m_l}))$ is a block-Hankel matrix of size (N₁−r+1) (N₂−r+1)×r² generated from the N₁ × N₂ Fourier samples of $\widehat{m_l}\left[\mathbf{k}\right]$. The rows of $\mathbf{H}\left(\widehat{m_l}\right)$ are vectorized versions of the r ×r rectangular k-space neighborhoods of $\widehat{m_l}\left[\mathbf{k}\right]$. ${\widehat{\mathit{\varphi }}}_l$ is a vector of size r² × 1, which is the vectorized version of the r × r filter ϕ_l. Thus, $\mathbf{H}\left(\widehat{m_l}\right)·{\widehat{\mathit{\varphi }}}_i$ provides a vector that corresponds to the convolution $\widehat{m_l}\left[\mathbf{k}\right]\ast {\widehat{\mathit{\varphi }}}_i\left[\mathbf{k}\right]$ within the rectangular region (N₁−r+1)×(N₂−r+1)×r². Note that this region corresponds to the valid convolutions between the r × r filter ${\widehat{\mathrm{\varphi }}}_i$ and the N₁ × N₂ samples of $\widehat{m_l}\left[\mathbf{k}\right]$. Since, the relation in Eq. (5) holds true for all the shots, we can combine the annihilation relations in the matrix form as:

$$\underset{{\mathbf{H}}_1\left(\widehat{\mathbf{m}}\right)}{\underbrace{\left[\begin{array}{cccc}\mathbf{H}\left(\widehat{m_1}\right)& \mathbf{H}\left(\widehat{m_2}\right)& \dots & \mathbf{H}\left(\widehat{m_{N_s}}\right)\end{array}\right]}}\underset{\widehat{\mathbf{\Phi }}}{\underbrace{\left[\begin{array}{cccccc}\widehat{{\mathit{\varphi }}_2}& 0& & 0& \widehat{{\mathit{\varphi }}_3}& \\ -\widehat{{\mathit{\varphi }}_1}& \widehat{{\mathit{\varphi }}_3}& & 0& 0& \\ 0& -\widehat{{\mathit{\varphi }}_2}& \cdots & ⋮& -\widehat{{\mathit{\varphi }}_1}& \cdots \\ 0& 0& & 0& 0& \\ ⋮& ⋮& & \widehat{{\mathit{\varphi }}_{N_s}}& ⋮& \\ 0& 0& & -\widehat{{\mathit{\varphi }}_{N_s-1}}& 0& \end{array}\right]}}=\left[\begin{array}{cccccc}0& 0& \dots & 0& 0& \dots \end{array}\right].$$ [6]

The above relation can be compactly expressed as ${\mathbf{H}}_1\left(\widehat{\mathbf{m}}\right)\widehat{\mathbf{\Phi }}=0$. Here, H₁ is block-Hankel structured matrix with data from shots stacked along the columns of the block-Hankel matrix. Figure 2 shows the structure of ${\mathbf{H}}_1\left(\widehat{m}\right)$. The same mapping techniques introduced in (31,33) for the multi-channel MRI recovery can be used for the construction of H₁. Our adaptation of this scheme for the multi-shot image recovery results in a final block-Hankel structure where the data of each shot are channel combined as opposed to stacking the individual channel images in (31,33).

FIG. 2.

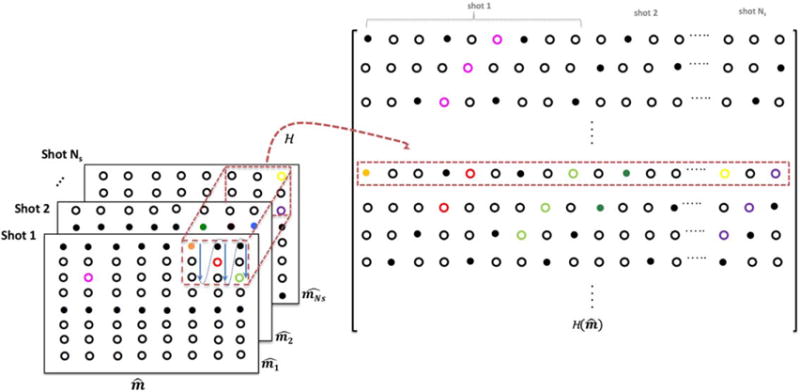
Illustration of the matrix lifting: $\widehat{\mathbf{m}}$ is the k-space data matrix of a given DWI comprising of data from the different shots of the DWI. A sliding window of size r × r as marked by the red dotted box generates the rows of the block-Hankel matrix $\mathbf{H}(\widehat{\mathbf{m}})$ by vectorizing the elements in the red block.

As evident from Eq. (6), for an N_s-shot acquisition, there will be $\left(\begin{array}{c}{N}_s\\ 2\end{array}\right)$ columns in $\widehat{\mathbf{\Phi }}$, which implies that the block-Hankel matrix ${\mathbf{H}}_1\left(\widehat{m}\right)$ has a null-space of dimension ≥N_s, thus establishing the low-rankedness of ${\mathbf{H}}_1\left(\widehat{m}\right)$ (31–34,44,45). It is the above property that enables the recovery of the artifact-free DWI from the measurements without having to explicitly compute the phase ϕ(x). Thus, even if we don’t have an estimate of $\widehat{\mathbf{\Phi }}$ we can enforce a low-rank penalty on the matrix ${\mathbf{H}}_1\left(\widehat{m}\right)$ to guide image recovery. However, because of the high structured under-sampling present in the individual shot data, the above constraint alone will not provide effective recovery of the data. In the next section, we strengthen the reconstruction problem by using additional information available from the data itself.

MUSSELS: MUlti-Shot Sensitivity Encoded Diffusion Data Recovery using Structured Low Rank Matrix Completion

In a typical MS-DWI acquisition, the diffusion weighted data are collected as a multi-channel sensitivity-encoded acquisition. The sensitivity-encoding provides additional constraints to recover the artifact-free DWIs from a multi-shot acquisition. Two sensitivity-encoded formulations are possible for the recovery of the MS-DWI data: (i) using a regular SENSE formulation and (ii) using annihilating filter relations derived from sensitivity encoding. We use the SENSE-based formulation in this work because of the ease of such implementations. For the sake of completion, the second formulation is provided in the appendix. We assume the coil sensitivities to be estimated from the nondiffusion-weighted image are collected as part of the acquisition, which is typically the case. The knowledge of the coil sensitivity information allows us to formulate the recovery of the multi-shot k-space data as follows:

$$\widehat{\stackrel{\sim }{\mathbf{m}}}=\underset{\widehat{\mathbf{m}}}{\arg min}\underset{\text{data consistency}}{\underbrace{\Vert \mathcal{A}\left(\widehat{\mathbf{m}}\right)-\widehat{\mathbf{y}}{\Vert }_{{\mathrm{\ell }}_2}^2}}+\mathbf{\lambda }\underset{\text{regularization}}{\underbrace{\Vert {\mathbf{H}}_1\left(\widehat{\mathbf{m}}\right){\Vert }_{\ast }}}.$$ [7]

Here, $\widehat{\mathbf{y}}$ is the measured multi-channel multi-shot k-space data of dimension N₁ × N₂/N_s × N_c × N_s. The first term imposes data consistency to the measured k-space data using a regular SENSE formulation. The operator $\mathcal{A}$ represents the concatenation of the following operations: ℳ○ℱ○ $\mathcal{S}$○ ℱ⁻¹ where ℱ and ℱ⁻¹ represent the Fourier transform and the inverse Fourier transform operations respectively, $\mathcal{S}$ represents multiplication by coil sensitivities, and ℳ represents multiplication by the k-space sampling mask corresponding to each shot. The second term in Eq. [7] is the nuclear norm of the block-Hankel matrix of the shots, which is the convex relaxation for the rank penalty. λ is a regularization parameter. We will refer to Eq. [7] as the MUSSELS recovery scheme, which can recover the multi-shot k-space data corresponding to the motion-compensated DWI. The magnitude DWI can then be recovered by taking the inverse Fourier transform and doing a sum-of-squares (SOS) of the multi-shot k-space data.

$$\begin{array}{c}{\displaystyle \sum _{l=1}^{N_s}|m_l(\mathbf{x}){|}^2=|\mathrm{\rho }(\mathbf{x}){|}^2}{\displaystyle \sum _{l=1}^{N_s}|{\mathrm{\varphi }}_l(\mathbf{x}){|}^2}\\ |\mathrm{\rho }(\mathbf{x})|=\sqrt{\frac{1}{N_s}{\displaystyle \sum _{l=1}^{N_s}|m_l(\mathbf{x}){|}^2}}\end{array}$$ [8]

Smoothness Regularized Reconstruction

The MUSSELS formulation works well when the data is fully sampled and not noisy. However, the recovery may be ill-conditioned when used with under-sampling or when the measurements are noisy, which is particularly true for the case for DWIs. To improve the conditioning of the reconstruction, additional smoothness penalties such as total-variation (TV) can be imposed in the reconstruction. We instead rely on an annihilation formulation for smoothness regularization, introduced in (34,35,38,39). These methods assume that the partial derivatives of the image vanishes on the zero-crossings of a filter μ band limited to p × p; p < r, which translates to the space domain relation

$$\nabla m\left(\mathbf{x}\right)·\mathrm{\mu }\left(\mathbf{x}\right)=\mathbf{0}$$ [9]

in the distributional sense. Here ∇m(x)=[∂₁m(x)∂₂m(x)] is the gradient operator and ∂₁ and ∂₂ are the partial derivative operators in x- and y- dimensions. The space domain operation (9) translates to the Fourier domain annihilation relations

$$\widehat{{\partial }_{1}m}[\mathbf{k}]\ast \widehat{\mathbf{\mu }}[\mathbf{k}]=0$$ [10]

$$\widehat{{\partial }_{2}m}[\mathbf{k}]\ast \widehat{\mathrm{\mu }}[\mathbf{k}]=0;$$ [11]

Using the derivative property of Fourier transforms, we have $\widehat{{\partial }_{1}m}[\mathbf{k}]=j2\mathbf{\pi }{k}_x\widehat{m}[\mathbf{k}]$ and $\widehat{{\partial }_{2}m}[\mathbf{k}]=j2\mathbf{\pi }{k}_y\widehat{m}[\mathbf{k}]$, where k_x and k_y are the spatial frequencies. The above convolutions can also be replaced by multiplications using block-Hankel matrices as described in the previous section, and the resulting annihilation relations can be compactly represented in the matrix form as

$$\underset{\mathbf{G}\left(\widehat{m}\right)}{\underbrace{\left[\begin{array}{l}\mathbf{H}\left(\widehat{{\partial }_{1}m}\right)\hfill \\ \mathbf{H}\left(\widehat{{\partial }_{2}m}\right)\hfill \end{array}\right]}}\widehat{\mathit{\mu }}=\mathbf{0}.$$ [12]

Here, $\mathbf{H}(\widehat{{\partial }_{1}m})$ and $\mathbf{H}(\widehat{{\partial }_{2}m})$ are defined the same way as in the previous section and has the same dimensions. Note that the support of $\widehat{\mathrm{\mu }}$ is p × p, where p < r; one can consider (r − p)² shifts of $\widehat{\mathrm{\mu }}$ that are support limited in the r × r window, all of which will satisfy (12). This implies that $\mathbf{G}\left(\widehat{m}\right)$ is low-rank. This property was exploited to recover the signal from under-sampled measurements in (34,35,38,39,47). We propose to combine the matrix liftings specified by (6) and (12) to obtain a new structured matrix:

$$F(\widehat{\mathbf{m}})=\left[\begin{array}{llll}\mathbf{H}(\widehat{{\partial }_1{m}_1})\hfill & \mathbf{H}(\widehat{{\partial }_1{m}_2})\hfill & \dots \hfill & \mathbf{H}(\widehat{{\partial }_1{m}_{N_s}})\hfill \\ \mathbf{H}(\widehat{{\partial }_2{m}_1})\hfill & \mathbf{H}(\widehat{{\partial }_2{m}_2})\hfill & \dots \hfill & \mathbf{H}(\widehat{{\partial }_2{m}_{N_s}})\hfill \end{array}\right].$$ [13]

Figure 3 illustrates the creation of the new lifted matrix F, which is highly low-rank. We propose to recover the motion-compensated multi-shot data using the consolidated nuclear-norm minimization problem that incorporates smoothness regularization (SR):

$$\widehat{\stackrel{\sim }{\mathbf{m}}}=\arg {min}_{\widehat{\mathbf{m}}}\Vert \mathbf{A}(\widehat{m})-\widehat{y}{\Vert }_{{\mathrm{\ell }}_2}^2+\lambda \Vert \mathbf{F}(\widehat{m}){\Vert }_{\ast }.$$ [14]

FIG. 3.

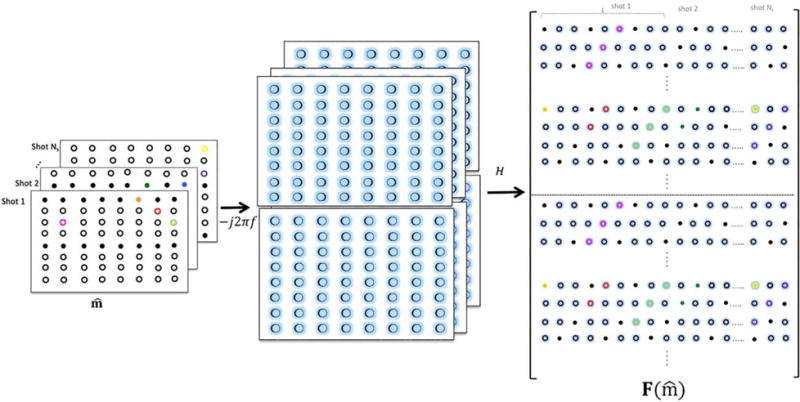
Illustration of joint matrix lifting for multi-shot data: The Fourier coefficients of the partial derivatives along the x-dimension and y-dimensions are obtained by multiplication using −j2πk_x and −j2πk_x, respectively. The block-Hankel matrices of the each partial derivative are generated and stacked as shown.

The above minimization problem, which we will refer to as SR-MUSSELS, can also be solved in the same framework as that of the unconstrained formulation in Eq. (7).

Augmented Lagrangian Optimization Algorithm

We propose to solve the reconstruction problems in Eqs. [7], [14] using an AL scheme (48,49) employing variable splitting. The unconstrained minimization problems in Eqs. [7], [14] are converted to constrained forms using an auxiliary variable D to get the new cost C₁:

$$C_1=\Vert \mathbf{A}\widehat{m}-\widehat{y}{\Vert }_{{\mathrm{\ell }}_2}^2+\mathbf{\lambda }\Vert \mathbf{D}{\Vert }_{\ast }\text{such that }\mathbf{F}(\widehat{\mathbf{m}})=\mathbf{D}$$ [15]

which can be solved by alternatively solving the quadratic subproblem

$$C_2(\widehat{\mathbf{m}})=\Vert \mathbf{A}\widehat{\mathbf{m}}-\widehat{\mathbf{y}}{\Vert }_{{\mathrm{\ell }}_2}^2+\frac{\mathrm{\lambda }\mathrm{\beta }}{2}\Vert \mathbf{D}-\mathbf{F}(\widehat{\mathbf{m}}){\Vert }_{{\mathrm{\ell }}_2}^2+\frac{\mathbf{\lambda }}{2}{\widehat{\mathrm{\gamma }}}^T(\mathbf{D}-\mathbf{F}(\widehat{\mathbf{m}})),$$ [16]

and a singular value shrinkage subproblem (see Table 1 for more details).

Table 1.

Augmented Lagrangian Algorithm for Solving SR-MUSSELS

1: Initialize β > 0; γ

2: Initialize the algorithm by channel combining the measured k-space data to form ${\widehat{\mathbf{m}}}^{(0)}={\mathbf{A}}^H\mathbf{A}(\widehat{\mathbf{y}})$.

3: set n = 0

4: Repeat

5: ${\mathbf{D}}^{(n)}=F({\widehat{\mathbf{m}}}^{(n)})$ where F is the block-Hankel matrix given in Eq. (13).

Compute the singular value decomposition: UΣVT = SVD(D(n))

Perform singular value shrinkage using the rule Σk = diag{(σi−k)+} where σ are the singular values along the diagonal of Σ.

6: Update Dn+1 = ℋ*(UΣkVT)) where ℋ* is the inverse mapping of the block-Hankel elements into the multi-shot data matrix.

7: Update ${\widehat{\mathbf{m}}}^{(n+1)}$ by solving $C_2(\widehat{\mathbf{m}})$ given in Eq. (16) using CG

8: Update Lagrange multipliers: ${\mathrm{\gamma }}^{(n+1)}={\mathrm{\gamma }}^{(n)}-\mathrm{\beta }(\mathbf{D}-\mathbf{F}(\widehat{\mathbf{m}}))$

9: set n = n + 1

10: Until stopping criterion is reached

METHODS

Datasets for Validation

We used in-vivo data collected on a GE 7T 950 MR scanner (maximum gradient amplitude of 50 mT/m and slew rate of 200 T/m/s) using a MS-DW acquisition to test the proposed reconstruction. Several sets of data were collected on four healthy adult volunteers in accordance with the Institutional Review Board of the University of Iowa. A 32-channel receive coil with either a 2-channel transmit coil in quadrature mode or 8-channel parallel transmit coil were used for imaging. The 128x128 data were collected with a Stejskal-Tanner diffusion sequence with the following parameters: b-value = 800–1000 s/ mm²; FOV = 220 220 mm²; slice thickness = 1.7 mm. Single-shot, 2-shot, 4-shot and 8-shot acquisitions with TE = 57–142 ms, one non-diffusion weighted and 6 or 15 DW acquisitions were collected. The 256 × 256 data were collected with a dual-spin-echo diffusion sequence with b-value = 700 s/mm²; FOV = 210 × 210 mm;² slice thickness = 2 mm;TE = 86 ms, 25 directions and three averages. A partial Fourier acquisition (pf) was employed with 20 oversampling ky-lines. To simulate under-sampled multi-shot acquisition, the 4-shot data was retrospectively under-sampled by a factor of 2.

Figure 4 demonstrates the effect of TE on image quality of the DWIs collected at 7T. Because of the short T₂ relaxation times at UHFS, shorter TEs becomes extremely desirable. 4-shot or higher number of shots provide good SNR and a significant reduction in TE. As a result, susceptibility related artifacts are also minimized. The MUSE-based methods (26–29) has been previously shown to be effective in recovering motion-compensated DWIs from a 4-shot acquisition. We compare the performance of the proposed reconstruction to the POCSMUSE method (27) in achieving the same.

FIG. 4.

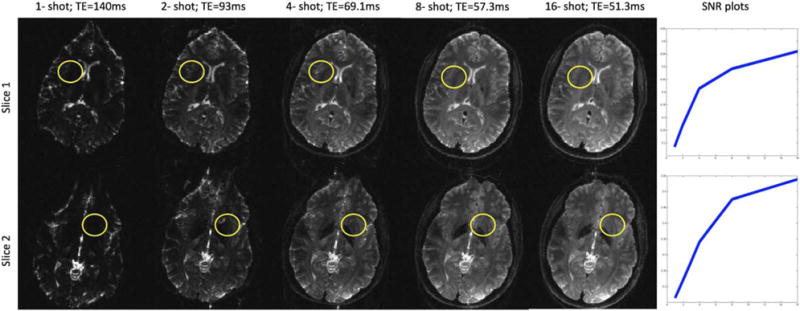
Effect of long echo times at 7T demonstrated on non-diffusion weighted images collected using different number of shots for a 128 × 128 acquisition matrix. The loss of SNR due to the long TE are clearly evident from these images. The SNR computed from the ROIs as a function of the number of shots are shown in the last column. No parallel imaging acceleration was employed in these acquisitions. However, with single-shot imaging, it is common to employ parallel imaging acceleration of at least 2, in which case, the TE becomes comparable to the 2-shot case in column two.

Coil sensitivity information was required for all the reconstruction methods used in this work. The sensitivity maps were estimated from the non-diffusion weighted images by combining the k-space data from all the shots into a single data matrix, performing an inverse Fourier transform along the channel dimension and computing the ratio of each individual coil image to the SOS-combined image (26). Note that any Nyquist ghost artifacts resulting from odd-even shifts of the EPI acquisition needed to be corrected prior to this step. Residual ghosting present in the sensitivity maps resulted in residual artifacts in the final reconstruction. The data used in this manuscript were corrected for odd-even EPI shifts before computing the coil sensitivities using standard reference-scan based methods, which were not fully effective for multi-shot acquisitions. Thus, some residual ghosting was still visible in the images. In addition to the coil sensitivity maps, the MUSE-based algorithms required the motion-induced phase maps corresponding to each shot to reconstruct the DWI, which were obtained using a TV-regularized reconstruction of each k-space shots as described in (26).

Experiments

In the first experiment, we show the capability of MUSSELS in recovering the motion-compensated DWIs from a 4-shot acquisition. The measured 4-shot k-space data were channel combined and stacked into the data matrix as shown in Figure 2 and the Hankel matrix was computed using a filter size of 8 × 8. In the second experiment, we demonstrate the performance of the proposed method in comparison with phase-based methods for a set of q-space down-sampled reconstructions. In the third experiment, we demonstrate the utility of the SR-MUSSELS. We show that SR-MUSSELS can be used for ill-conditioned data reconstruction problems such as in the cases of under-sampled or noisy MS-DW data reconstruction. A filter size of 12 × 12 was used in this case and the low-rank property was imposed on the taller Hankel matrix shown in Figure 3. Finally, we also show the utility of the proposed reconstruction for recovering partial Fourier data which are especially suited for high spatial resolution scans.

We used the AL scheme for the recovery of the data, the pseudo-code for which is provided in Table 1. The proposed implementation is fast, and the speed is determined by the filter size. For example, a 128 × 128 matrix size 4-shot 32-channel data with an 8 × 8 filter took 25 s to reconstruct the artifact-free image on an Intel i7-4770, 3.4 GHz CPU with 8 GB RAM using Matlab. The maximum filter size that we used in our experiments was 12 × 12; however, an 8 × 8 filter gave comparable results in all the cases.

In all experiments, the parameter for the POCSMUSE reconstruction were chosen to give the best visual result for the DWIs and the resulting fractional anisotropy images with directionally encoded color (DEC) maps. The reconstruction might be improved by tuning the parameters for each individual DWI depending upon the amount of phase distortions. However, this is a hard problem and can produce arbitrary results; hence, this approach was not employed. The parameters for the MUSSELS-based reconstructions were also tuned in the same manner.

RESULTS

Motion Compensation Without Phase Estimates

The proposed MUSSELS reconstruction of a 4-shot DW acquisition is shown in Supporting Information Figure S1, with the results from a conventional SENSE reconstruction also included for comparison. The motion-induced artifacts arising from phase mismatch between shots are evident in SENSE reconstruction while the MUSSELS reconstruction successfully removed these artifacts.

Comparison to Methods That Use Phase Estimates

Next we compare the performance of MUSSELS with the standard method that uses motion-induced phase estimates to reconstruct artifact-free DWIs. Figure 5 shows 15 DWIs reconstructed using POCSMUSE, MUSSELS and SR-MUSSELS from a 4-shot 15-direction diffusion data. A careful comparison of the images reconstructed from these methods show some visual differences in the resulting images, some of which are marked using arrows in the figure. To further study the differences, Figure 6 shows the DEC maps corresponding to the three reconstructions. The top row shows the DEC maps computed using all 15 directions from the respective reconstructions. They appear to be comparable visually in terms of the directional information conveyed by the color-coding. To further demonstrate the differences in the reconstructions, the 15-direction data was under-sampled in q-space in two different ways. Two subsets each consisting of seven diffusion directions were chosen from the dataset; the two subsets are marked using yellow and red dots in Figure 5. The first subset included all of the DWIs that were marked using arrows that showed visual differences between the reconstructions. The second subset consisted of mostly DWIs that did not show much difference visually. DEC maps were computed from the two subsets and are plotted in Figure 6b,d. For the purpose of error quantification, the angular error was computed for the under-sampled cases with the 15 direction data of the respective reconstructions used as the ground truth. The angular error computes the error in the primary diffusion direction (PDD) as:

$$\text{error}=\text{acos}\left(v_{\text{ref}}^{\to }·v_{\text{us}}^{\to }\right)\ast 180/\mathrm{\pi },$$ [17]

where $v_{\text{ref}}^{\to }$ and $v_{\text{us}}^{\to }$ are the PDD of the reference and under-sampled data. The maps are included in Figure 6c,e, with the average angular error also reported in the images.

FIG. 5.

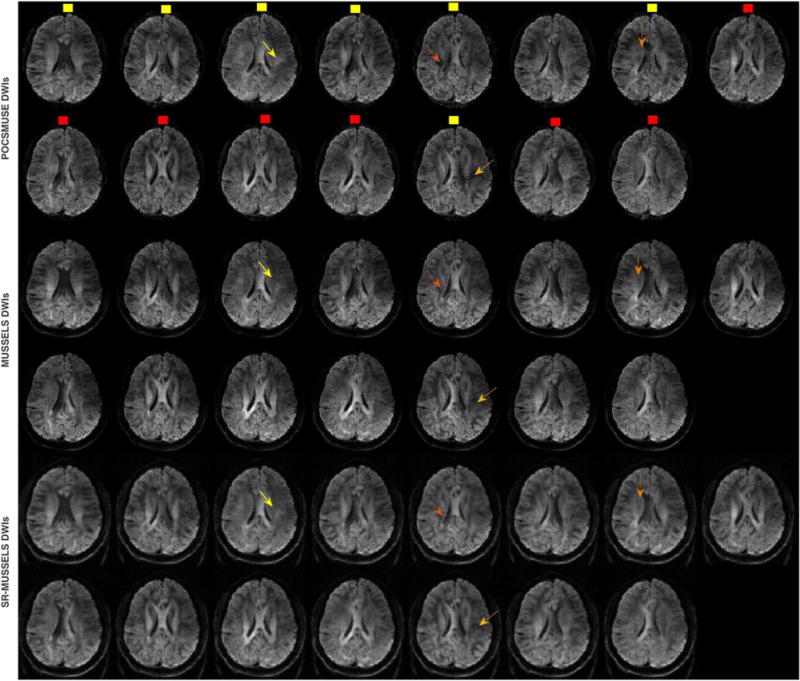
DWIs reconstructed using POCSMUSE, MUSSELS and SR-MUSSELS from a 15-direction (b = 1000 s/mm²) 4-shot acquisition. The arrows indicate the regions where MUSE reconstruction show difference from MUSSELS reconstruction. Two subsets of q-space sub-sampled DWIs are shown using yellow and red dots.

FIG. 6.

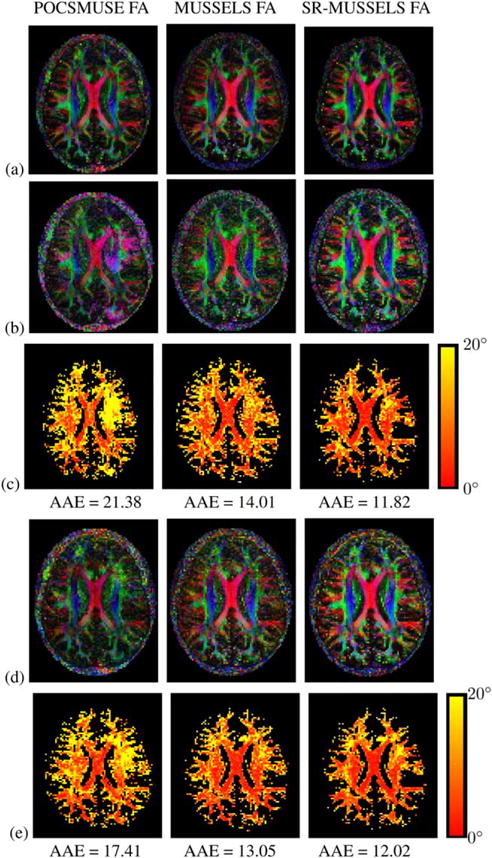
The three columns correspond to the reconstructions of the dataset in figure 6 using POCSMUSE, MUSSELS, and SR-MUSSELS respectively. (a) shows the DEC maps computed using all the 15 DWIs. (b) & (d) correspond to the DEC maps computed using the 7 DWIs marked using the yellow dots and red dots respectively in figure 6. (c) & (e) shows the map of the angular error in (b) and (d) with respect to (a). The average angular error (AAE) corresponding to each of the reconstructions are reported below the figure.

When the number of diffusion directions are high, the estimate of the diffusion directions using tensor fitting and Eigen decomposition gives robust results. Hence, the DEC maps computed from the 15-direction data reconstructed using POCSMUSE appear similar to those reconstructed using MUSSELS. However, the above q-space downsampling experiments show that there are substantial errors in the DWIs obtained using MUSE. For the POCSMUSE reconstruction, the DEC maps computed from the two sets of under-sampled data clearly differ from the DEC map computed using all the 15 DWIs. For the case of MUSSELS reconstruction, the DEC maps are consistent in all the cases, yet they are noisy. For the case of SR-MUSSELS, the DEC maps could be reconstructed with less noise compared to the MUSSELS.

Regularized Reconstruction for Under-Sampled MS-DWI

The previous experiments demonstrate the utility of MUSSELS to recover the fully sampled MS-DWI data. Here we show that the regularized version of MUSSELS can be used to recover under-sampled MS-DWI data as well. For this purpose the 4-shot MS-DWI data was first under-sampled uniformly by skipping every other k-space lines from each of the shots. Figure 7 shows the reconstruction of the 4-shot under-sampled MS-DWI data using POCSMUSE and SR-MUSSELS. The residual aliasing artifacts are evident in all DWIs reconstructed by POCSMUSE. The regularized MUSSELS has performed reasonably well with significantly fewer artifacts seen visually in the reconstructed images. The DEC maps generated from all the 15 DWIs are shown with the angular error map also computed based on the fully-sampled 15-direction data. A plot of the normalized-root-mean-squared-error (NRMSE) for all the 15 DWIs reconstructed from the under-sampled data is also computed (Fig. 7f). Interestingly, if the under-sampling pattern is changed slightly, the performance of both the methods improve significantly. Figure 8 shows the results of reconstruction where a nonuniform under-sampling pattern was employed. Specifically, the three center k-space lines of each of the shots were kept intact. The improvement in the reconstruction results can be appreciated from the DWIs as well as in the DEC maps. This behavior is not surprising and adds evidence to the fact that reconstructions from a slightly nonuniform under-sampling patterns provides more reliable results than a strictly uniform under-sampling pattern while using sparsity/low-rank -based reconstructions (33). For the POCSMUSE reconstruction, aliasing artifacts are still visible in the images. Even in this case, the voxel-wise tensor fitting recovered the diffusion directions reasonably well as evident from the DEC maps. The MUSSELS and SR-MUSSELS reconstruction gives artifact-free images. The noisy MUSSELS reconstructions have been improved by using the smoothness regularization. Note that we used a retrospectively under-sampled example to illustrate the performance of the reconstruction algorithms. However, this simulated version of non-uniform EPI may have unrealistic features and might be easier to reconstruct than real prospective data.

FIG. 7.

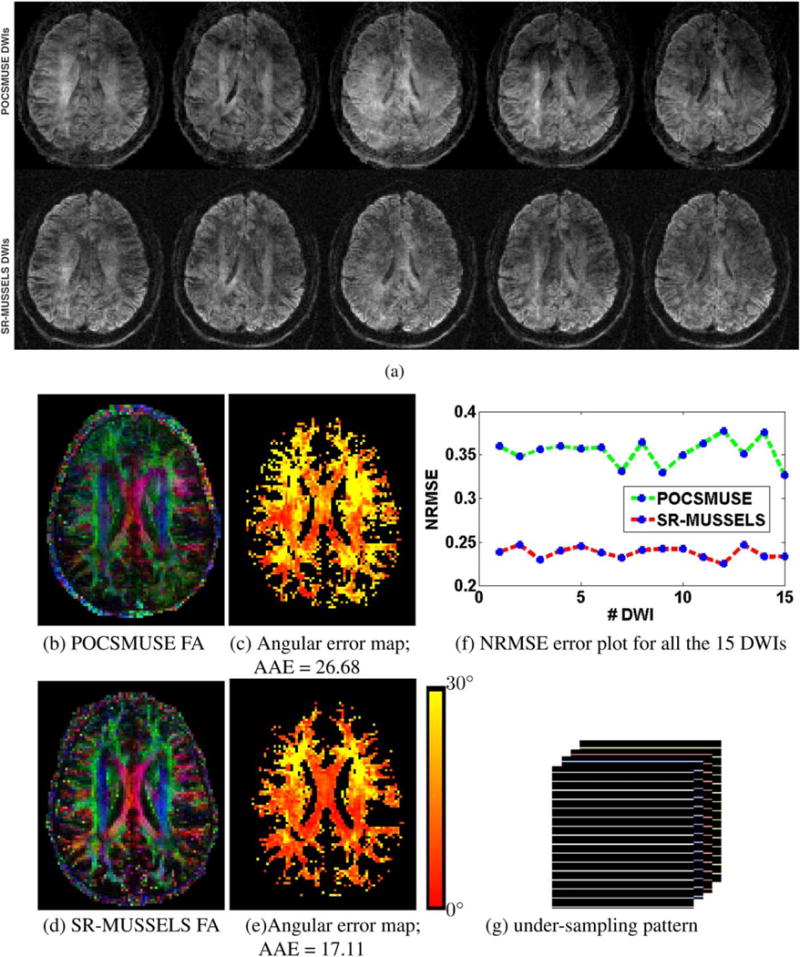
Uniformly under-sampled 4 shot MS-DW data. (a) the top row shows the POCSMUSE and second row shows SR-MUSSELS reconstruction of the first 5 out of 15 DWIs reconstructed from uniformly under-sampled data. The corresponding DEC maps and their angular error maps are shown in (b)–(e). The NRMSE error for each of the DWI are plotted in (f) and the under-sampling pattern used is shown in (g).

FIG. 8.

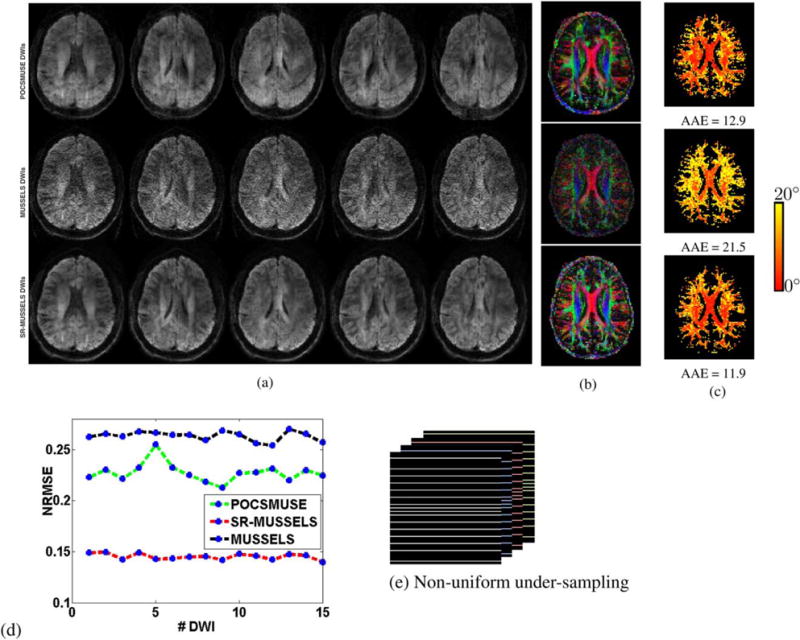
(a) the rows show the POCSMUSE, MUSSELS and SR-MUSSELS reconstruction of the first 5 out of 15 DWIs reconstructed from non-uniformly under-sampled data. The corresponding DEC maps (b) and the angular error maps (c) are shown on the right. Residual aliasing are clearly visible in the POCSMUSE reconstructions although this is not evident in its DEC maps. The NRMSE error for each of the DWI are plotted in (d) and the under-sampling pattern used is shown in (e).

Noisy 4-Shot Data

Another example where the proposed reconstruction performs better compared to the standard phase-based reconstruction is included in Supporting Information Figures S2 and S3. Here, a noisy six-direction 4-shot data is reconstructed using the three methods. POCSMUSE reconstruction shows artifacts in one of the DWIs which are recovered accurately using MUSSELS and SR-MUSSELS. As expected the images are noisy for the unregularized case. However, the SR-MUSSELS can recover the MS-DWI data reasonably well.

Partial Fourier Data

The performance of the proposed reconstructions were also tested on a higher resolution diffusion data, the results of which are provided in Figure 9. For this experiment, the data was collected with partial Fourier acquisition to reduce TE. We observe that the MUSSELS-based reconstruction can recover the pf data without any modifications of the proposed algorithm [50]. An alternate approach is to use the structure as proposed in (33).

FIG. 9.

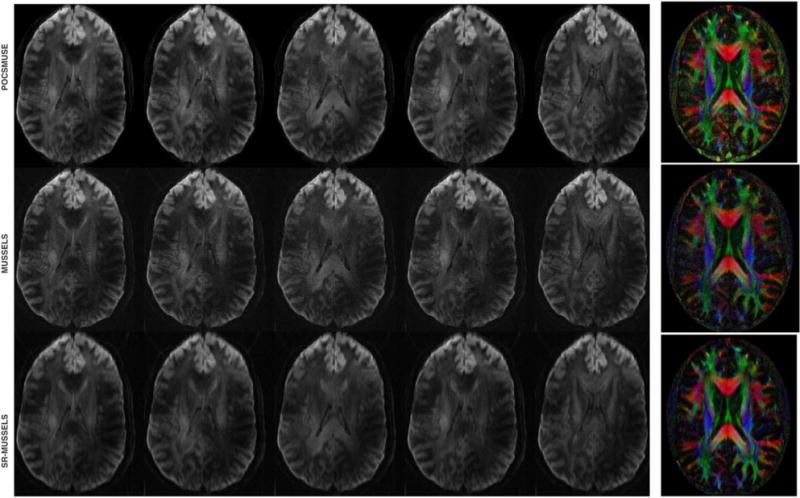
DWIs reconstructed for a high resolution data (voxel size: 0.82 × 0.82 × 2.0 mm²; b = 700 s/mm², 25 directions, 3 averages, using partial Fourier with 20 over-sampling ky-lines) using various reconstructions and the corresponding DEC maps.

DISCUSSION

Recently, several authors have shown that annihilating filter-based methods provide a flexible and generalized framework for reconstruction of MR images exploiting sparsity (32,34) and image smoothness (38,51). These works are also related to finite rate of innovation (FRI) theory (52,53) and the recovery of polynomials from Fourier data (54). Learning shift-invariant annihilating filters from a calibration scan to recover missing k-space data in a local neighborhood is also now well-established in parallel-MRI reconstruction literature (42,43,45). Recently this idea was also extended to calibration-less parallel imaging reconstruction using structured low-rank matrix completion (31,33,35,55). The fundamental performance guarantees and the sampling requirement of the structured low-rank approach for various FRI models have also been theoretically addressed (36,56).

Inspired by the above body of literature, in this work, we modeled the smooth slowly varying phase of the MS-DWI data using a shift invariant k-space filter. By deriving an annihilation formulation based on these filters, we derived a reconstruction framework based on structured low-rank recovery that could learn the filter implicitly to recover the missing k-space data. This led to a new formulation that can recover motion-compensated DWIs from a multi-shot acquisition. Since the k-space data for each shot is recovered using matrix completion, the final DWI can be reconstructed without having to know the motion-induced phase that varies between shots. Thus, the formulation that we introduced here, which we call MUSSELS, is a” phase-calibration-free” method since the motion-induced phase is not required to recover the final DWI. We exploit the known coil sensitivity information to enable the recovery of the uniformly under-sampled k-space samples of the MS-DW acquisition.

The annihilating filter-based approach in this paper is also theoretically similar to the recent ALOHA-based approach introduced in (37) and the SENSE-LORAKS method introduced in (55,57). Specifically, the referenceless Nyquist ghost correction method (37) uses a similar annihilation filter to compensate for the phase between the odd and the even lines of an EPI acquisition. Since this method was primarily intended for data with modest under-sampling (odd/even), it used independent coil-by-coil reconstruction along with a wavelet-based pyramidal decomposition constraint. Note that, in comparison, our proposed method works with data with higher under-sampling and greater phase mismatch by making use of the coil sensitivities and the use of the k-space weighting in both the kx- and ky- direction (as opposed to the kx-only in the ALOHA based approach). Additionally, the ALOHA based methods use the structured low-rankness as a preprocessing step rather than as a penalty as used in the current work. Similarly, recent works from Kim et al have shown that the use of smooth image phase constraint using LORAKS, along with coil sensitivity information, is helpful to recover missing k-space data from uniformly under sampled one-sided Fourier acquisitions (55,57).

We demonstrate the results of the proposed method on in-vivo data collected on 7 Tesla MRI. Diffusion studies on 7T MRI are challenging compared to those on 3T (14,58). The SNR gain offered by the higher field strength are counterbalanced by the reduced T₂ relaxation times at the echo times considered in this study. In addition, B₁ field inhomogeneity and higher susceptibility effects cause local signal dropouts. Hence, the reduced TE offered by the multi-shot acquisitions can make significant impact on 7T diffusion studies and are thus more relevant for 7T diffusion data. Provided short-TE acquisitions are enabled, 7T diffusion studies can offer significant advantages over 3T studies as discussed in (14,16,58) with improved spatial resolution afforded by 7T to study smaller regions being the main advantage. As shown from our results above, the proposed method can enable direct motion-compensated reconstruction for multi-shot acquisitions which in turn can be used more readily for routine imaging. This method is easily adapted to non-Cartesain acquisitions as well.

In conclusion, we proposed a fast and robust reconstruction scheme for fully sampled and under-sampled multi-shot diffusion data recovery that does not rely on motion-induced phase estimates or navigator data.

Supplementary Material

Supplemental

Figure S1: DWIs reconstructed from a 6-direction (b=1000s=mm²) 4-shot acquisition using conventional SENSE method (top row) and the proposed MUSSELS method (bottom row). Both methods use the coil sensitivity information only and do not use motion-induced phase estimates in the reconstruction. Conventional SENSE cannot achieve motion compensation while MUSSELS can recover artifact-free DWIs.

Figure S2: Reconstruction of the 6 DWIs from a noisy 4-shot 6-direction acquisition.

Figure S3: The FA maps computed from the noisy 4-shot 6-direction acquisition. The FA maps clearly show that the SR-MUSSELS offers robust reconstruction of noisy data while POCSMUSE reconstructions show visible artifacts.

APPENDIX

We can derive a different set of annihilating filters based on the coil sensitivities similar to that we derived above using the phase. Writing the DWI for shot l as the multiplication of the object ρ(x) with the coil sensitivities s(x), we have m_il(x) = ρ(x)s_i(x); i = 1: N_c. Thus for coils i, j shot l, we have:

$$m_{il}\left(\mathbf{x}\right)=\mathrm{\rho }\left(\mathbf{x}\right)s_i\left(\mathbf{x}\right)$$ [18]

$$m_{ji}\left(\mathbf{x}\right)=\mathrm{\rho }\left(\mathbf{x}\right)s_j\left(\mathbf{x}\right).$$ [19]

Multiplying Eq. [18] by s_j(x)and Eq. [19] by s_i(x) and subtracting we get the following:

$$m_{il}\left(\mathbf{x}\right)s_j\left(\mathbf{x}\right)-m_{jl}\left(\mathbf{x}\right)s_i\left(\mathbf{x}\right)=0\forall i,j.$$ [20]

Equivalently, in Fourier domain (30,35,36,47),

$$\widehat{m_{il}}[\mathbf{k}]\ast {\widehat{s}}_j[\mathbf{k}]-\widehat{m_{jl}}[\mathbf{k}]\ast {\widehat{s}}_i[\mathbf{k}]=0\forall i,j.$$ [21]

Replacing the convolution operations in Eq. (21) as multiplication using Toeplitz/Hankel matrices, we get

$$\mathbf{H}(\widehat{m_{il}})·{\widehat{s}}_j[\mathbf{k}]-\mathbf{H}(\widehat{m_{jl}})·{\widehat{s}}_i[\mathbf{k}]=0.$$ [22]

Since this is true for all shots l = 1 : N_s, we can derive a set of conditions which can be written in matrix form as:

$$\underset{\widehat{\mathbf{s}}(\mathbf{k})}{\underbrace{\left[\begin{array}{lllll}{\widehat{s}}_2\hfill & -{\widehat{s}}_1\hfill & 0\hfill & \dots \hfill & 0\hfill \\ 0\hfill & {\widehat{s}}_3\hfill & -{\widehat{s}}_2\hfill & \dots \hfill & 0\hfill \\ ⋮\hfill & \hfill & \hfill & \hfill & \hfill \\ {\widehat{s}}_3\hfill & 0\hfill & -{\widehat{s}}_1\hfill & \dots \hfill & 0\hfill \\ ⋮\hfill & \hfill & \hfill & \hfill & \hfill \\ 0\hfill & 0\hfill & \dots \hfill & {\widehat{s}}_{N_c}\hfill & -{\widehat{s}}_{N_c-1}\hfill \end{array}\right]}}\underset{{\mathbf{H}}_2(\widehat{\mathbf{m}})}{\underbrace{\left[\begin{array}{ccc}\mathbf{H}({\widehat{m}}_{11})& \mathbf{H}({\widehat{m}}_{12})\dots & \mathbf{H}({\widehat{m}}_{1N_s})\\ \mathbf{H}({\widehat{m}}_{21})& \mathbf{H}({\widehat{m}}_{22})\dots & \mathbf{H}({\widehat{m}}_{2N_s})\\ ⋮& & \\ \mathbf{H}({\widehat{m}}_{N_{c}1})& \mathbf{H}({\widehat{m}}_{N_{c}2})\dots & \mathbf{H}({\widehat{m}}_{N_c{N}_s})\end{array}\right]}}=0\Rightarrow \widehat{\mathbf{S}}{\mathbf{H}}_2(\widehat{\mathbf{m}})=0.$$ [23]

Since we have access to the non-diffusion weighted image for all imaged slices, which are not affected by the shot-to-shot phase variations, we can compute the coil sensitivity images s(x) using a sum-of-squares (SOS) method or the k-space filters $\widehat{s}\left[\mathbf{k}\right]$ with the center k-space lines of the non-diffusion weighted data acting as the ACS lines using methods such as ESPIRiT (45). The matrix $\widehat{\mathbf{S}}\left(\mathbf{k}\right)$ as defined in (23) can have ${ }^{N_c}{C}_2$ rows which implies that the left null-space of the block-Hankel matrix ${\mathbf{H}}_2\left(\widehat{\mathbf{m}}\right)$ has high dimensionality. With the above filter formulation, we can pose the recovery of the multi-shot k-space data $\stackrel{\sim }{\mathbf{m}}$ as the constrained reconstruction problem:

$$\begin{array}{c}\widehat{\stackrel{\sim }{\mathbf{m}}}=minrank({\mathbf{H}}_1(\widehat{\mathbf{m}}))\text{subject to}\\ \widehat{\mathbf{S}}{\mathbf{H}}_2(\widehat{\mathbf{m}})=0,\text{and}\\ \mathbb{A}\widehat{\mathbf{m}}=\widehat{\mathbf{y}}\end{array}$$ [24]

The last term imposes the data consistency to the measured multi-channel multi-shot k-space data, $\widehat{\mathbf{y}}$, of dimension N₁ × N₂ × N_c × N_s. The operator A applies the mask corresponding to the different multi-shot sampling locations. The equivalent unconstrained reconstruction problem can be written as

$$\widehat{\stackrel{\sim }{\mathbf{m}}}=\underset{\widehat{\mathbf{m}}}{\text{argmin}}\Vert \mathbb{A}\widehat{\mathbf{m}}-\widehat{\mathbf{y}}{\Vert }_{{\mathrm{\ell }}_2}^2+{\mathbf{\lambda }}_1\Vert {\mathbf{H}}_1\left(\widehat{\mathbf{m}}\right){\Vert }_{\ast }+{\mathbf{\lambda }}_2\Vert \widehat{\mathbf{S}}{\mathbf{H}}_2\left(\widehat{\mathbf{m}}\right){\Vert }_{{\mathrm{\ell }}_2}^2,$$ [25]

where λ₁ and λ₂ are two regularization parameters. In practice, numerically solving the above reconstruction problem is highly computation-intensive mainly because of the size of the Hankel matrix ${\mathbf{H}}_2\left(\widehat{m}\right)$, especially with high number of coils. Hence the SENSE-based method is adopted in this work.