Evaluating renal function and age as predictors of amikacin clearance in neonates: model‐based analysis and optimal dosing strategies

Abstract

Aims

We aimed to compare the performance of renal function and age as predictors of inter‐individual variability (IIV) in clearance of amikacin in neonates through parallel development of population pharmacokinetic (PK) models and their associated impact on optimal dosing regimens.

Methods

Amikacin concentrations were retrospectively collected for 149 neonates receiving amikacin (post‐natal age (PNA) between 4–89 days). Two population PK models were developed in parallel, considering at least as predictors current body weight (WT), in combination with either creatinine clearance (CL_cr) or age descriptors. Using stochastic simulations for both renal function or age‐based dosing, we identified optimal dosing strategies that were based on attainment of optimal peak‐ (PCC) and trough target concentration coverage (TCC) windows associated with efficacy and toxicity.

Results

The CL_cr and age‐based population PK models both included current body weight (WT) on CL, central distribution volume and intercompartmental clearance, in combination with either CL_cr or PNA as predictors for IIV of clearance (CL). The WT‐CL_cr model explained 6.9% more IIV in CL compared with the WT‐PNA model. Both models successfully described an external dataset (n = 53) of amikacin PK. The simulation analysis of optimal dose regimens suggested similar performance of either CL_cr or PNA based dosing.

Conclusion

CL_cr predicted more IIV in CL, but did not translate into clinically relevant improvements of target concentrations. Our optimized dose regimens can be considered for further evaluation to optimize initial treatment with amikacin.

What is Already Known about this Subject

• The population pharmacokinetics of amikacin have been established in various neonatal populations.

• Current dosing guidelines for amikacin in neonates are based on weight and/or age descriptors.

• Renal function markers have not yet been reported as potential predictors, even though amikacin is a renally excreted antibiotic.

What this Study Adds

• Creatinine clearance (CL_cr) predicted 6.9% more of the inter‐individual variability of amikacin clearance than post‐natal age (PNA) in neonates.

• A systematic evaluation of optimal dose regimens based on CL_cr and PNA was performed and novel optimal dose regimens were proposed, which could be considered further to optimize initial treatment with amikacin based on body weight and PNA or CL_cr.

• First dose administration of amikacin based on CL_cr and PNA results in comparable attainment of target trough and peak concentrations, when using optimized dose regimens.

Introduction

Aminoglycosides are primarily indicated for the treatment of infections caused by aerobic gram‐negative bacilli 1 including Pseudomonas spp, Escherichia coli, Klebsiella spp, Serratia spp and Staphylococcus infections. Specifically for neonates, amikacin plays an important role in the treatment of neonatal sepsis, necrotizing enterocolitis, meningitis and empirical antibiotic therapy 2.

Therapeutic drug monitoring (TDM) is crucial for treatment optimization of amikacin in neonates. Typically, peak concentrations between 24–35 mg l^–1 and trough concentrations between 1–5 mg l^–1 3 are considered therapeutic target concentrations associated with generally effective yet safe treatment. However, treatment optimization through TDM can only be implemented after initial treatment has been started. In order to reach optimal therapeutic concentrations as early as possible, a priori treatment optimization is therefore also of relevance, especially in this particularly fragile patient population 4.

A priori treatment optimization, e.g. treatment optimization prior to performing TDM‐based dose adjustments, is generally performed by identifying patient‐associated predictors of inter‐individual variation (IIV) in pharmacokinetic (PK) parameters and subsequent development of optimized dose regimens using population PK modelling and simulation 3, 5, 6. Several studies have described amikacin population PK in neonates 3, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 (Table 1) and several dosing guidelines have been published 3, 6, 9, 16 as summarized in Table 2. These guidelines suggest dose adaptations based on combinations of either gestational age (GA), post‐menstrual age (PMA), post‐natal age (PNA) or current body weight (WT). The Neofax guideline 16 is one of the most commonly used guidelines in this matter.

Table 1.

Overview of amikacin population pharmacokinetic (PK) model parameter estimates in neonates reported in the literature.

	Botha et al. 1998 8	Allegaert et al. 2006 7	Allegaert et al. 2008 13	Sherwin et al. 2009 3	De Cock et al. 2012 6
Patients (n)	53	205	715	80	874
Body weight (kg), range	n.r.	0.45‐1.98	0.39‐4.78	0.45‐4.43	0.39‐4.78
Gestational age (w), range	Mean 35.1 (SD 3.6)	24‐30	n.r.	24‐41	24‐43
Postnatal age (d)	3.1 (3.1)	0‐2	0‐28	3‐64	1‐30
Postconceptional age (d)	n.r.	168‐210	n.r.	n.r.	n.r.
Postmenstrual age (d)	n.r.	n.r.	168‐301	172‐308	n.r.
Structural model	1 compartment	1 compartment	1 compartment	1 compartment	2 compartment
PK estimates
ΘCL (L/h)	0.031	0.486†	1.49§	0.23	0.0493¶
ΘV1 (L)	0.316	40.2‡	31.7‡	0.957	0.833**
ΘQ (L/h)	‐	‐	‐	‐	0.415
ΘV2 (L)	‐	‐	‐	‐	0.833
Final covariate model	CL = ΘCL WTΘCL‐WT ΘCL‐G	CL = [ΘCL (WT/70)0.75] EXP [ΘCL‐SLPCL SLPCL (PCA‐24) ΘCL‐FSNAID FNSAID]	CL = ΘCL (WT/70)0.75 (1 + ΘCL‐SLPCL SLPCL (PMA‐40)) (ΘCL‐RF RF) (ΘCL‐Fventilation Fventilation) (ΘCL‐VENT VENT) (ΘCL‐Finotrope Finotrope) (ΘCL‐INO INO) (ΘCL‐Fiugr Fiugr) (ΘCL‐SGA SGA)	CL = ΘCL (WT/2)ΘCL‐WT (PMA/40)ΘCL‐PMA	CL = ΘCL (bWT/median)ΘCL‐bWT+ (1 + ΘCL‐PNA (PNA/median) + (ΘCL‐IBU IBU)
	V = ΘV1 WTΘV‐WT	V = ΘV1 (WT/70)1	V = ΘV (WT/70)1 (1 + ΘV‐SLPV SLPV PNA) (ΘV‐Finotrope Finotrope) (ΘV‐INO INO) (ΘV‐Fventilation Fventilation) (ΘV‐VENT VENT)	V = ΘV1 (WT/2)ΘV‐WT	V1 = ΘV1 (WT/median)ΘV‐WT
					V2 = V1
					Q = ΘQ
Covariate pharmacokinetic estimates	ΘCL‐WT = 1.45; ΘCL‐G = 1.28*; ΘV‐WT = 1.44	ΘCL‐WT = 0.75(fix); ΘCL‐SLPCL = 0.11; ΘCL‐FNSAID = 0.788; ΘV‐WT = 1(fix)	ΘCL‐WT = 0.75(fix); ΘCL‐SLPCL = 0.032; ΘCL‐Fventilation = 0.977; ΘCL‐Finotrope = 0.945; ΘCL‐Fiugr = 0.872; ΘV‐WT = 1(fix); ΘV‐SLPV = 0.005; ΘV‐Finotrope = 1.09; ΘV‐Fventilation = 1.08	ΘCL‐WT = 0.691; ΘCL‐PMA = 3.23; ΘV‐WT = 0.89	ΘCL‐bWT = 1.34; ΘCL‐PNA = 0.213; ΘCL‐IBU = 0.838; ΘV‐WT = 0.919

^* θ‐CLG = 1 for boys;

^† expressed as l h⁻¹ per 70 kg at 24 weeks of postconceptional age, without NSAID;

^‡ expressed as l per 70 kg;

^§ expressed as l h⁻¹ per 70 kg at 40 weeks of postmenstrual age, and RF = 1;

^¶ for a typical individual with bWT of 1750 g and PNA of 2 days;

^** for a typical individual with a WT of 1760 g.

n.r.: non reported; bWT: birthweight; G: Gender; SLPCL: factor relating PCA to developmental changes in CL; FNSAID: scaling factor for those premature neonates given a NSAID; RF: Renal function parameter standardized to creatinine clearance of L/h/70Kg in a 40‐year‐old person with serum creatinine of 85.947 µmol l⁻¹, calculated as CPR(creatinine production rate) = 516 EXP(Kage ((PMA‐30)weeks/52‐40)) µmol h⁻¹ (Kage = 0.00344) and CLcr = CPR/Serum Creatinine L/hCL; Finotrope, Fventilation and Fiugr are scaling factors applied for the use of inotropes (INO), positive pressure artificial ventilation (VENT) or intrauterine growth retardation (SGA); INO, VENT and SGA have a value of 1 if present and 0 if absent

Table 2.

Amikacin dosing recommendations in preterm and term neonates

Gestational age (weeks)	Post‐menstrual age (weeks)	Post‐natal age (days)	Weight (g)	Dose (mg kg –1 )	Dose interval (h)
Neofax 16
‐	≤ 29*	0–7	‐	18	48
‐		8–28	‐	15	36
‐		≥ 29	‐	15	24
* or significant asphyxia, PDA or treatment with indomethacin
‐	30–34	0–7	‐	18	36
‐		≥8	‐	15	24
‐	≥35	ALL	‐	15	24
Langhendries et al. 9
<28	‐	‐	‐	20	42
28–30	‐	‐	‐	20	36
31–33	‐	‐	‐	18.5	30
34–37	‐	‐	‐	17	30
>37	‐	‐	‐	15.5	24
6h prolongation of the dosing interval when ibuprofen is co‐administered
Sherwin et al. 3
‐	≤28	‐	‐	15	36
‐	29–36	‐	‐	14	24
‐	≥37	‐	‐	15	24
Does not apply to neonates of <3 days post‐natal age
De Cock RF et al. 6
‐	‐	<14	0–800	16	48
‐	‐	‐	800–1200	16	42
‐	‐	‐	1200–2000	15	36
‐	‐	‐	2000–2800	13	30
‐	‐	‐	≥2800	12	24
‐	‐	≥14	0–800	20	42
‐	‐	‐	800‐1200	20	36
‐	‐	‐	1200–2000	19	30
‐	‐	‐	2000–2800	18	24
‐	‐	‐	≥2800	17	20

Amikacin is mainly eliminated through glomerular filtration (GFR), which is undergoing maturation after birth until around 2 years of age 7. For the paediatric population, the Schwartz formula is commonly used to estimate GFR 17, even though this equation has limitations when used for (preterm) neonates due to potential interference with maternal serum creatinine (S_cr) concentrations at birth 18, 19. Secondly, besides GFR, current body weight is also a physiologically relevant predictor to be considered in the paediatric population, specifically for renally eliminated drugs such as amikacin 20, 21. However, none of the current dosing guidelines include the use of renal function metrics to optimize a priori dose regimens, even though such descriptors are directly related to variability in amikacin PK. Rather, these guidelines use age, which is a more indirect metric to represent the GFR maturation and if not separately considered, also body size changes.

In this work we aimed to evaluate and compare renal function and age metrics as predictors for inter‐individual variability (IIV) of amikacin clearance in neonates, in addition to current body weight. Secondly, we aimed to compare the clinical dosing implications of using either renal function or age metrics in optimal dosing strategies. To these aims, we systematically developed two population PK models in parallel using a novel dataset of amikacin PK in preterm‐ and term neonates, combining current body weight with either renal function or age descriptors and in addition evaluated a number of other potential predictors. The final two models that contained either age or renal function metrics were then both evaluated using an external dataset not used for model development. Thereafter, a global stochastic simulation analysis was performed using both final models to identify the optimal dose regimens for amikacin in patient subgroups based on either renal function or age descriptors, based on established therapeutic target concentrations for efficacy and toxicity.

Methods

Data collection

TDM data and medical reports were retrospectively collected from all the newborns hospitalized at the Unit of Neonatology and Pediatrics of Hospital Materno‐Infantil of Vall Hebron (Barcelona, Spain) between July 2000 and July 2006. Neonates treated with amikacin having less than 90 days of PNA and with at least two amikacin serum concentrations available were eligible for inclusion. The request to collect of anonymized retrospective data from the hospital database for the purpose of this analysis was reviewed by the local ethics review committee of the Hospital Universitari Vall d'Hebron Clinical Research and was found ethically acceptable.

Amikacin dosing regimens, serum drug concentrations, actual timing of dose administration and blood sampling were collected. Furthermore, the following patient characteristics were collected: gender, gestational age (GA), PNA, post‐menstrual age (PMA), birth weight (BWT), current body weight (WT) and serum creatinine (S_cr) at the same day of amikacin TDM sampling. Creatinine clearance (CL_cr) was computed according to the Schwartz formula 17. The patients included in the study were randomly distributed into a model building dataset (three‐quarters of the patients) and a dataset to external evaluation (one quarter of the patients), used to verify the predictive performance of the final model.

Amikacin treatments and blood sampling

Neonates were started on amikacin according to the judgment of the attending neonatologist for suspected or culture proven infection. According to the established protocol of the neonatal intensive care and paediatric units, based on the recommendations of the reference book Neofax 16, amikacin dosing was done by intravenous infusion over 30–60 min. The individual infusion durations were used for model development. Generally, blood for serum drug concentration measurements was collected just before amikacin administration (trough concentrations) and approximately 1 h after initiation of amikacin infusion (peak concentrations). Each patient could be sampled either on one occasion or on several occasions throughout the treatment, defining each occasion as the PK profile of each dose.

Bio‐analysis

All amikacin concentrations were measured using a fluorescence polarization immunoassay (TDx, Abbott Laboratories). This assay was linear up to 50 mg l^–1, the intra‐ and inter‐assay precision values were lower than 5% and the lower limit of quantification (LLOQ) was 0.1 mg l^–1, as described in more detail elsewhere 22.

Serum creatinine concentrations were determined by the method of Jaffé on a Modular Analytics SWA (Roche/ Hitachi) 23 and CL_cr was estimated according to the Schwartz et al. formula 17, where K has a value of 0.33 for premature and neonates with low weight for gestational age and 0.45 for term infants whose weight is appropriate for gestational age.

Model development

All models were fit using the non‐linear mixed effect modelling package nonmem (version 7.2) 24. The first order conditional estimation method with interaction was used throughout the analysis.

Model selection was guided by the decrease in the –2 log likelihood (–2LL) using a statistical significance criterion of P < 0.01 (likelihood ratio test), adequate precision of parameter estimates, biological plausibility and clinical relevance of parameter estimates. Visual inspection of goodness of fit plots including population and individual predicted vs. observed, and conditional weighted residuals vs. time and population predictions, was also performed.

First, a structural base model was developed where we compared both one and two compartmental linear disposition models with zero order input and first order elimination kinetics. Estimates for IIV associated with PK parameters were modelled according to a log‐normal distribution. Additive, proportional and combined (additive plus proportional) models were considered for the quantification of residual unexplained variability (RUV) variances of drug concentrations. Finally, inter‐occasion variability was also evaluated.

With respect to data below the lower limit of quantification (LLOQ) of 8.8% of observations, we considered the approaches of ignoring the LLOQ samples or the likelihood‐based M3 approach, which both limit the magnitude of bias introduction 25. However, in our analysis the M3 method resulted in model instability. Hence, we chose to discard these observations as it was unlikely these would reduce any relevant bias in the parameters 25.

Parameter–covariate relationships were evaluated according to linear and power relationships and scaled by their median values as follows:

$${\mathrm{P}}_{\mathrm{i}}={\mathrm{\theta }}_{\mathrm{i}}*{\left({\mathrm{COV}}_{\mathrm{i}}/{\mathrm{COV}}_{\text{median}}\right)}^{\mathrm{\theta }\mathrm{COV}}$$

where P_i is the parameter of the individual, θ_i the typical value of the PK parameter, COV_i the individual covariate, COV_median the median covariate value in the population and θ_COV estimated covariate effect parameter.

The following covariates were evaluated for inclusion: gender, GA, PNA, PMA, BWT, WT, S_cr and CL_cr. Information about co‐administration of ibuprofen and peripheral asphyxia, which have been reported previously as potentially important covariates 7, was not available in our dataset and could therefore not be evaluated as covariates.

As the aim of our analysis was to compare age and renal function predictions between two separate models, these were not combined in a single model. In addition to statistical significance (P < 0.01), a decrease of at least 5% in IIV was considered as a clinically relevant threshold for covariate inclusion in the model. First, WT was evaluated as covariate on each PK parameter, as this is an important and direct metric to account for size based differences in PK 21 and in addition partly covers age related changes. In a second step either the effect of renal function or age descriptors was evaluated.

Model evaluation

Aforementioned goodness of fit diagnostics plots were used to evaluate the selected final models that included either at least renal function or an age descriptor as covariate. A visual predictive check (VPC) was generated to evaluate the typical predicted trend and the variability of predicted concentration‐time curves. A non‐parametric bootstrap method with replacement was used to further confirm precision of model parameters, using Perl‐speaks‐nonmem (PsN) version 3.5.2. In addition, normalized prediction distribution errors (NPDEs) 26 were computed to evaluate further model simulated and observed values (n = 1000). Also NPDEs stratified to different categories of PNA and CL_cr were calculated. Overparametrization was evaluated by calculation of the condition numbers. An external evaluation of the two final models was performed by predicting amikacin concentrations for a dataset not included in model development using the final parameter estimates. This external dataset consisted of a random subset of the data (26% of total dataset) not used for model fitting. The predictions were subsequently visualized by generating a VPC for these predictions.

Simulation analysis

The two renal function‐ and age‐based models developed, referred to as WT‐CL_cr and WT‐PNA (see results section), were used to simulate stochastically concentration–time profiles for a complete range of dose amounts and dose intervals and for a complete range of covariate combinations. As such, for both models, all possible ranges for weight–age and weight–renal function were evaluated, allowing to identify the optimal dose regimen. For each scenario (i.e. all covariate ranges), all possible combinations of dose amount–interval scenario from the same set of 250 individual PK parameter values were simulated without residual variability. For each WT, CL_cr and PNA window, the same individual values were used. Residual variability was not included as we were interested in the concentrations without measurement error, but rather the ‘true’ concentrations. The following WT ranges were considered: 500–1000, 1000–1500, (..), 4500–5000 g. For the CL_cr‐WT scenario, CL_cr ranges according to the National Kidney Foundation 27 were defined: 1–15, 15–30, 30–60, 60–90 and 90–120 ml min^–1. For PNA, we considered day intervals of 1–7, 7–14, 14–21, 21–28 and 28–80 days. The range of dose amounts used was from 10 to 120 mg in steps of 5 mg. The range of dose intervals used was from 6 to 84 h, prior to evaluation of trough concentration. The simulation modelled a single dose intravenous infusion of amikacin given over 30 min for all the cases. Subsequently, for each simulation scenario we computed the percentage of patients within the target peak concentration window of 25–35 mg l^–1 3 at 1 h after the start of each infusion. We also computed the percentage of patients within the target trough concentration window of 1–5 mg l^–1 prior to each following (hypothetical) administered dose. We computed the percentage of peak target concentration coverage (PCC) and trough target concentration coverage (TCC), e.g. the percentage of patients within the target peak and trough concentration windows, for each dose amount–interval combination and stratified for each combination of WT and CL_cr or PNA. In a second step, we computed the optimal dose regimen for each subset of values for WT and CL_cr, or WT and PNA, by maximizing the combined percentage of both PCC and TCC. Results of these global dose optimizations were depicted for WT vs. CL_cr or PNA, depicting PCC and TCC, and also the resulting dose interval values, in order to obtain insights in optimal dosing strategies.

Results

Patient and dataset characteristics

A total of 202 neonates were included in the analysis, of whom 149 neonates (73.76%) were included for the model building dataset and the remaining 53 patients (26.24%) for external model qualification. The population group consisted on 86 males (57.7%) and 63 females (42.3%). At the first dose given, 83% of the population had an age lower than 30 days of life. Specifically, 14.3% of the population had age < 7 days of life, 59.2% between 7 and 21 days, 9.5% between 22 and 30 days and 17% more than 30 days. The last, 60% was between 30 and 40 days of life and only 8% were older than 61 days. Further demographic, laboratory values and information regarding administered doses and blood sampling is provided in Table 3. Trough concentrations were taken just before the following dose. However, the actual sampling times of the ‘peak’ concentrations ranged from 1 to 3.25 h after the end of the infusion. Table 3 summarizes the details of the study design for the model building and external validation datasets.

Table 3.

Demographic and biochemical characteristics of patients included into the model building dataset and into the external evaluation dataset

Characteristics	Units	Median (range)
		Model building dataset	External evaluation dataset
Patients
Number of males/female	(n)	86/63	34/19
Gestational age	(weeks)	31.8 (24.3–41)	32.5 (24.3–42)
Post‐natal age	(days)	28 (1–86)	26 (5–89)
Post‐menstrual age	(days)	248 (175–360)	257 (178–374)
Birth weight	(kg)	1.64 (0.45–3.89)	1.76 (0.37–3.82)
Current weight	(kg)	1.92 (0.50–4.65)	2.09 (0.44–5.54)
Serum creatinine	(mg dl–1)	0.58 (0.19–2.50)	0.54 (0.20–1.90)
Creatinine clearance	(ml min–1)	32.28 (5.87–121.5)	36.78 (8.7–110.25)
Amikacin treatment
Total number of administered doses	(n)	2443	255
Number of doses/patient	(n)	3–61	3–54
Dose amount	(mg kg–1)	11.62 (2.8–58.4)	22 (2.8–120)
Dose interval	(h)	8,12,18,24,36,48	8,10,12,18, 24,36,48,72
Amikacin concentrations
Total number of observations	(n)	446	121
Total number of trough concentrations	(n)	203	54
Total number of peak concentrations	(n)	243	67
Number of concentrations/patient	(n)	2–11	1–6

Model development

A two compartment model with first order elimination kinetics best described the PK of amikacin. All fixed effect PK parameters were estimated with adequate precision. IIV was estimated for CL, central distribution volume (V ₁) and inter‐compartmental clearance (Q). The final population PK parameter estimates of the base model are summarized in Table 4. A combined additive and proportional residual error model best described the residual error distribution. Inter‐occasion variability modelling tested on CL and V did not improve the fit.

Table 4.

Population PK parameters of the base, the intermediate and the two full covariate models, shrinkage values and bootstrap results

Description	Parameter		Base model		Full model WT, PNA		Bootstrap *		Full model WT, CL cr		Bootstrap *
			Estimate % (RSE)		Estimate % (RSE)		Median	95% PI	Estimate % (RSE)		Median	95% PI
Structural model parameters
Clearance	θCL	(l h–1)	0.135 (7.2)		0.093 (5.4)		0.093	0.082 – 0.104	0.093 (7.0)		0.093	0.081 – 0.104
~ Body weight	θCL~WT	‐	‐		1.100 (8.4)		1.108	0.916 – 1.330	0.799 (16.0)		0.809	0.622 – 1.042
~ Post‐natal age	θCL~PNA	‐	‐		0.299 (25.3)		0.300	0.140 – 0.438	‐		‐	‐
~ Creatinine clearance	θCL~CLcr	‐	‐		‐		‐	‐	0.659 (9.8)		0.651	0.527 – 0.789
Central distribution volume	θV1	(l)	0.599 (5.4)		0.637 (4.2)		0.628	0.552 – 0.686	0.641 (4.9)		0.636	0.574 – 0.690
~ Body weight	θV1~WT	‐	‐		1.030 (5.4)		1.014	0.857 – 1.140	1.040 (6.2)		1.038	0.905 – 1.160
Inter‐compart. clearance	θQ	(l h–1)	0.113 (15.2)		0.051 (25.3)		0.055	0.027 – 0.123	0.042 (42.5)		0.043	0.022 – 0.086
~ Body weight	θQ~WT	‐	‐		0.995 (21.0)		1.125	0.460 – 2.397	0.909 (55.2)		0.908	0.458 – 2.324
Peripheral distribution volume	θV2	(l)	1.050 (12.5)		0.480 (28.3)		0.500	0.286 – 0.893	0.478 (24.5)		0.491	0.282 – 1.023
Inter‐individual variability				Shrinkage (%)		Shrinkage (%)				Shrinkage (%)
	ωCL	CV%	70.569 (14.4)	15.5	41.833 (16.2)	15.7	16.9	11.4 – 23.4	34.928 (16.5)	17.9	11.5	7.7 – 16.2
	ΔωCL †	CV%	‐		‐28.74				‐35.64
	ωV1	CV%	60.992 (18.2)	28.2	19.570 (32.9)	50.2	3.8	1.3 – 7.1	21.331 (26.2)	42.4	4.4	2.3 – 6.9
	ΔωV1 †	CV%	‐		‐41.42				‐39.66
	ωQ	CV%	102.956 (29.7)	57.8	71.344 (31.8)	73.0	41.8	8.6 – 105.1	50.596 (63.7)		24.4	1.3 – 65.5
	ΔωQ †	CV%	‐		‐31.61				‐52.36
Residual variability				Shrinkage (%)		Shrinkage (%)				Shrinkage (%)
Additive	σadd	mg l–1	0.384 (7.7)	16.5	0.318 (8.5)	16.5	0.312	0.369 – 0.256	0.283 (6.9)	17.3	0.279	0.241 – 0.314
Proportional	σprop	‐	1.010 (36.8)		0.500 (17.9)		0.485	0.374 – 1.038	0.507 (15.9)		0.480	0.360 – 0.916
Δ –2LL ‡, †			‐		‐379.51				‐485.23

RSE Relative standard error; PI non‐parametric prediction interval of 2.5^th and 97.5^th percentiles; PN post‐natal age; WT body weight; CL_cr creatinine clearance; ΔIIV relative change in inter‐individual variability compared with the base model;

^* 1000 bootstrap samples

^† Change in IIV from base model.

^‡ Change in –2LL from base model

Inclusion of WT showed the strongest decreases in –2LL, ultimately leading to inclusion of WT on CL, V ₁ and Q (Table 4). Next, models including either renal function or renal maturation covariates (age‐covariates) on CL were evaluated. Among the renal maturation covariates, PNA showed the best fit. Inclusion of either CL_cr or PNA together with WT resulted in significant drops of –2LL and IIV, with the inclusion of CL_cr resulting in the largest decrease of the –2LL and IIV. Table 4 summarizes the final estimates for the base model and the two full covariate models including WT‐CL_cr or WT‐PNA. All parameters were well estimated, with RSE <25.3, except Q and the effect of WT on Q, for the WT‐CL_cr model (RSE 42.5 and 55.2, respectively). The influence of weight on clearance was different in both models, because of the intrinsic, but different, correlations between both WT and PNA and CL_cr. The bootstrap analysis confirmed the precision of parameter estimates obtained from the asymptotic standard errors. Goodness‐of‐fit diagnostic plots (Figure 1) did not show any relevant trends.

Figure 1.

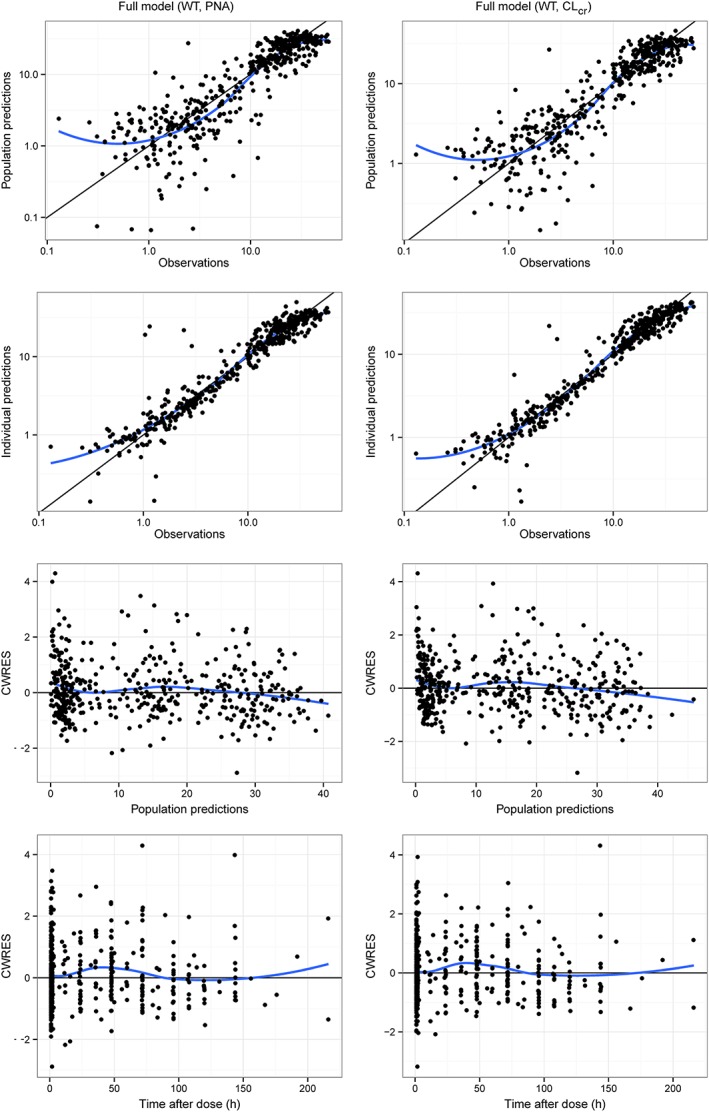
Goodness‐of‐fit comparison of the two full covariate models: WT‐PNA (left) and WT‐CLcr (right). Population predictions (top panel) and individual predictions (middle panel) vs. observations; conditional weighted residuals (CWRES) vs. population predictions and time after dose (bottom panel). The blue lines represent loess smoothers

Model evaluation and qualification

The visual predictive check (VPC) indicated that the median and the 5th and 95th percentiles of the observed data fell within the 95% prediction intervals of the corresponding model predicted percentiles, either including PNA or CL_cr on CL (Figure 2). For both models, the density of predictive model discrepancies (NPDE) went along theoretical normal distribution, without extreme values, indicating that the final model variance estimates was low. Discrepancy errors of predicted concentrations had homogeneous distribution around a mean of 0, without clear trends (Supplemental Material). The results of the stratified NPDEs for both models are represented in Figure 3. As in the case of general NPDEs, the results indicate very good model performance. Nonetheless, NPDE of the full covariate model including WT‐CL_cr shows slightly better performance than the WT–PNA covariate model, especially for lower CL_cr values (< 15 ml min^–1). The condition numbers for the final WT–CL_cr and WT–PNA models were 21.04 and 1.93, respectively, indicating no overparameterization was present (i.e. condition number <1000).

Figure 2.

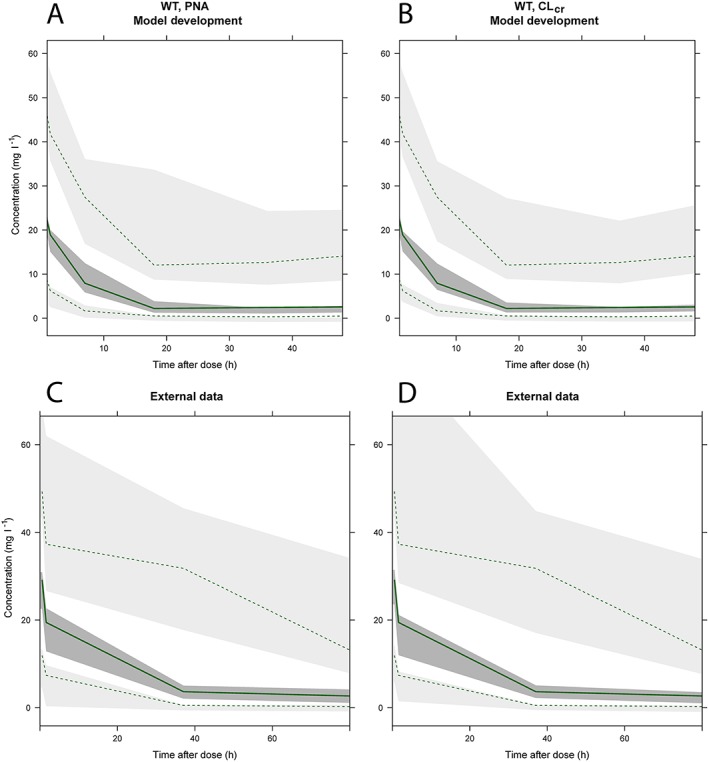
Visual predictive checks (VPC) of full covariate models based on WT‐PNA (A and C) and WT‐CLcr (B and D), for model development (top) and external evaluation (bottom). The dashed lines and light grey areas represent the 2.5th and 97.5th percentiles for observed and simulated concentration‐time profiles. The solid line and dark grey area represent the median observed and simulated concentration‐time profiles

Figure 3.

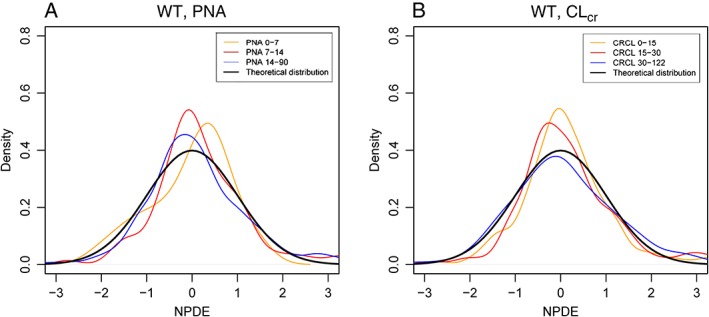
Normalized prediction distribution errors (NPDEs) for the WT‐PNA and WT‐CLCR based models stratified by different strata of postnatal age (PNA)

The remaining dataset not used for model development consisting of 53 patients was used for the external qualification of the model. This was done by building VPCs of the expected concentration–time profiles using either the WT–CL_cr or WT–PNA covariate models (Figure 2), which showed adequate predictive performance.

Simulations of dosing regimens

A simulation study for different dose amounts and intervals was conducted using the WT‐CL_cr or WT‐PNA models. Only a single dose was simulated so, in this case, intervals represent the time after dose prior to which a second dose would be administered. Figure 4 depicts the PCC and TCC values across different covariate combinations for both models for the most optimal dose regimens for each covariate combinations selected. Some differences in PCC and TCC can be seen. However, these were expected to be mostly related to the difference in the CL‐WT effect estimated in the WT‐CL_cr and WT‐PNA models. Moreover, the figures for PCC and TCC cannot be compared one to one because PNA and CL_cr across WT groups were not directly correlated. The PCC and TCC based on WT‐CL_cr or WT‐PNA models both resulted in relatively low coverages, with PCC ranging between 36% to 69% and TCC ranging between 50% to 80%. Overall it appeared there was not a large difference in PCC and TCC, i.e. the increased IIV for CL was not clearly identifiable from these simulations.

Figure 4.

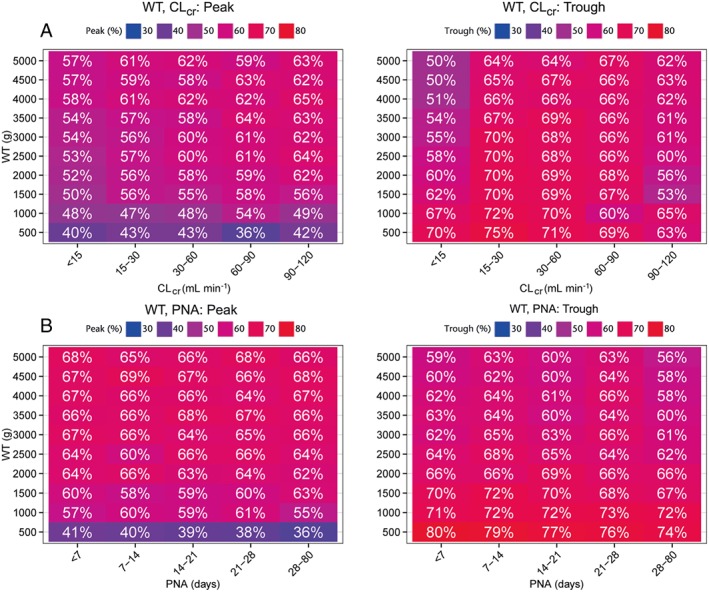
Peak and trough coverages (%) for body weight and post‐natal age (PNA) combination derived from dose optimization simulations using full covariate models based on WT–CLcr (A) and WT–PNA (B)

The optimized dose regimens values (e.g. dose amount and dose interval) are depicted in Figure 5, which shows all the possible sub‐groups of patients with respect to WT and CL_cr or PNA. Some covariate combinations are very unlikely or even impossible to occur, but we have included these values for completeness. In both the optimal dosing regimens, dose intervals identified increased with lower WT, PNA and CL_cr values, i.e. younger neonates. There were significant differences in dose interval values between WT–CL_cr and WT–PNA‐based dosing regimens, but these did not translate into clearly superior differences in terms of PCC and TCC.

Figure 5.

Optimal dosing regimens optimized for best peak and trough target coverage based on WT‐CLcr (left) or WT‐PNA (right) models

Discussion

This study included a substantial number of premature neonates and low birth weight infants, and had a large overall sample size (n = 149) (Table 1). Unlike previous population PK analyses, we have focused specifically on (comparing) the potential relevance of direct renal function markers to account for IIV in neonatal amikacin clearance. Moreover, this analysis also provided a comprehensive simulation‐based analysis of optimal dosing regimens using either renal function or age‐based optimization algorithms, which is of value to optimize initial dosing of amikacin, regardless of the outcomes of our comparison of age vs. renal function.

Assessment of renal function in newborn neonates is challenging because of the bias induced by maternal creatinine concentrations, mainly during the first 3 days of life 18. Potentially, this could be a reason why other population PK models of amikacin in neonates did not evaluate or include GFR markers in their models. However, even though GFR measured in newborn neonates may be associated with some bias, age descriptors may have disadvantages as well, as there will always remain patients who have deviating combinations of their age and renal function, i.e. that deviate from the typical correlation established in age‐based maturation models such as by De Cock et al. 6. Within specific age groups there may still exist wide variation in both organ (renal) function and size related effects, hence potentially resulting in less precise dose adjustments, compared with dose adjustments based on a more physiologically relevant and direct measure for variability in clearance, i.e. markers for GFR. Therefore, we propose that even though CL_cr values in patients may be associated with some bias, this metric may still represent a more clinically relevant descriptor for prediction of individual CL in neonates, especially in extreme combinations of WT and CL_cr/PNA (e.g. older patient with renal failure, extremely low weight or small for gestational neonates).

In the current analysis, the PK of amikacin was best described by a two compartment model with zero order input and first order elimination kinetics. Among all the PK studies on neonates, there is only one other model that used a two compartment model 6. This is related to larger variation in sampling times available around the peak, allowing improved characterization of early distributional kinetics and subsequent identification of a two compartment model. This is of relevance, as it has led to a more accurate prediction of target peak coverage than a one compartment model would have allowed. Finally, the external evaluation of our model using a test dataset confirmed its predictive performance.

Current body weight proved to be the most influential covariate on CL, V ₁ and Q. The final inclusion of either CL_cr or PNA on CL produced considerable reductions of –2LL and IIV values for both models. However, the inclusion of CL_cr produced a more marked decrease on IIV of CL (36%), than inclusion of PNA did (28%).

Previous studies (Table 1) also incorporated WT on CL and V ₁. However, all these studies used age descriptors including PCA 7, PMA 3, 13 or PNA 6, instead of CL_cr, to explain IIV on CL. Age descriptors, such as PNA, are convenient predictors in practice because they do not require any laboratory measurements to be available. However, it intrinsicially contains a composite description of both changes in size and renal function. Hence, PNA does not allow the optimization of dose for atypical patients. Yet, especially for such patients, adequate dose adjustments may be of relevance. In contrast, the use of a model that incorporates CL_cr allows more explicit separation of the two distinct physiological processes underlying IIV in amikacin PK, changes in size and changes in renal function maturation. As such it may be more suited to deal with atypical combinations of WT and renal function than PNA. This is in agreement with De Cock et al. 6, who have recently proposed amikacin clearance maturation as a direct marker of renal maturation in neonates and this concept was, for instance, successfully used to predict changes in GFR for vancomycin in neonates 28. However, for routine patient care this approach may not be directly relevant.

Our optimized dose regimens (Figure 5) suggested prolonged dose intervals for younger (lower WT, PNA) neonates, with dose intervals gradually decreasing towards lower intervals for older neonates. Generally, proposed dose intervals are in accordance with other studies, but there were also a number of clear differences. For the WT‐CL_cr based optimized dosing a larger dose interval (48–54 h) for older (higher WT) patients with renal dysfunction (CL_cr < 15 ml min^–1) was identified, whilst for WT‐PNA based dose regimens the maximum dose interval was 36 h. This illustrates the potential relevance of considering CL_cr‐based dose regimens, even when there is no apparent overall advantage between WT–PNA or WT–CL_cr. In addition, for older neonates (i.e. higher WT, CL_cr) optimal dose intervals based on WT‐CL_cr were shorter than those proposed by others that were based on age (20–24 h) (Table 2). Optimized dose regimens based on WT‐CL_cr resulted in dose intervals between 6–18 h. In contrast, the WT‐PNA based dosing regimens resulted in intervals between 18‐24 h, which were more in line with previously suggested dose regimens. It should be noted that, in contrast to other model‐based optimized dose regimens for amikacin, we have taken into account the IIV of PK parameters. Moreover, the global optimization strategy of optimized dose regimens on the basis of often used target peak and trough concentration windows allowed consideration of the complete range of all possible dose regimens across different covariate combinations and it has not been used in such a way before.

Our analysis used the Jaffé method for the measurement of serum creatinine concentrations. Although this method is known to result potentially in overestimation of serum creatinine, it is still frequently used in clinical practice 29. However, Schmidt et al. 30 have shown that the magnitude of potential bias is lower than biological variation.

The neonates in our analysis had a PNA of ≥4 days, because most patients received amikacin as a part of treatment for late onset infections. Hence, our model and/or simulations may not be directly applicable for neonates PNA ≤3 days and, especially, not using CL_cr as covariate, because of interference of maternal creatinine.

With respect to further extensions of this model‐based analysis, it could be of relevance to also consider bacterial PK–PD and adaptive resistance, such as published for gentamicin 31 explicitly and/or target site concentrations. In addition, the consideration of target site concentration can represent another relevant extension 32, 33.

In conclusion, we developed and externally evaluated population PK models for amikacin based on WT and CL_cr or PNA in a large population of neonates. Our population included a significant number of premature patients, which is representative of the day to day clinical population. Our models suggest that CL_cr is an improved predictor of amikacin CL compared with PNA. On the basis of these models we developed optimized dose regimens using a global stochastic optimization strategy which indicated that the advantage of CL_cr‐based dosing for the first dose does not translate into clinically relevant advantages over the use of PNA, when using our optimized dose regimens. The principle of ‘hit early, hit hard’ is critical for effective antibiotic therapy, hence getting dose regimens right as soon as possible in case of potentially life threatening infections of considerable importance. The optimized dose regimens based on CL_cr or PNA can be further clinically evaluated and compared with current dosing strategies to improve the number of patients who are within target concentrations at the first dose. Nonetheless, even with our optimized dose regimens, a substantial number of patients still remain outside the therapeutic windows, re‐confirming the need for further dose individualization using TDM strategies.

Competing Interests

There are no competing interests to declare.

Supporting information

Figure S1 NPDE for the final model including PNA on CL

Figure S2 NPDE for the final model including WT on CL

Supporting info item

Illamola, S. M. , Colom, H. , and van Hasselt, J. G. C. (2016) Evaluating renal function and age as predictors of amikacin clearance in neonates: model‐based analysis and optimal dosing strategies. Br J Clin Pharmacol, 82: 793–805. doi: 10.1111/bcp.13016.